Teğetler Dörtgeni
Tüm kenarları bir çembere teğet olan dörtgene teğetler dörtgeni denir.

Her üçgenin bir iç teğet çemberi vardır, ancak her dörtgen bir teğetler dörtgeni değildir. Her kare, eşkenar dörtgen ve deltoid aynı zamanda birer teğetler dörtgenidir, kare olmayan dikdörtgen teğetler dörtgeni değildir.
Pitot Teoremi: Teğetler dörtgeninde karşılıklı kenarların uzunlukları toplamı birbirine eşittir. Bunun karşıtı da doğrudur, yani karşılıklı kenar uzunlukları toplamı birbirine eşit olan bir dörtgen teğetler dörtgenidir.
\( u \) teğetler dörtgeninin çevre uzunluğunun yarısı olmak üzere,
\( a + c = b + d = u \)
İSPATI GÖSTER

Teğetler dörtgeninin köşelerinden çembere çizilen teğetlerin uzunluklarına \( x_1 - x_8 \) diyelim.
Çembere bir noktadan çizilen teğet uzunlukları eşittir.
\( x_1 = x_2 \)
\( x_4 = x_3 \)
\( x_5 = x_6 \)
\( x_8 = x_7 \)
Eşitlikleri taraf tarafa toplayalım.
\( x_4 + x_5 + x_1 + x_8 = x_2 + x_3 + x_6 + x_7 \)
Bu eşitliği kirişler dörtgeninin kenar uzunlukları cinsinden yazalım.
\( \underbrace{x_4 + x_5}_{a} + \underbrace{x_1 + x_8}_{c} = \underbrace{x_2 + x_3}_{b} + \underbrace{x_6 + x_7}_{d} \)
\( a + c = b + d \)
Teğetler dörtgeninin köşelerinin açıortayları tek bir noktada ve çemberin merkezinde kesişir. Bunun karşıtı da doğrudur, yani açıortayları tek bir noktada kesişen bir dörtgen teğetler dörtgenidir.
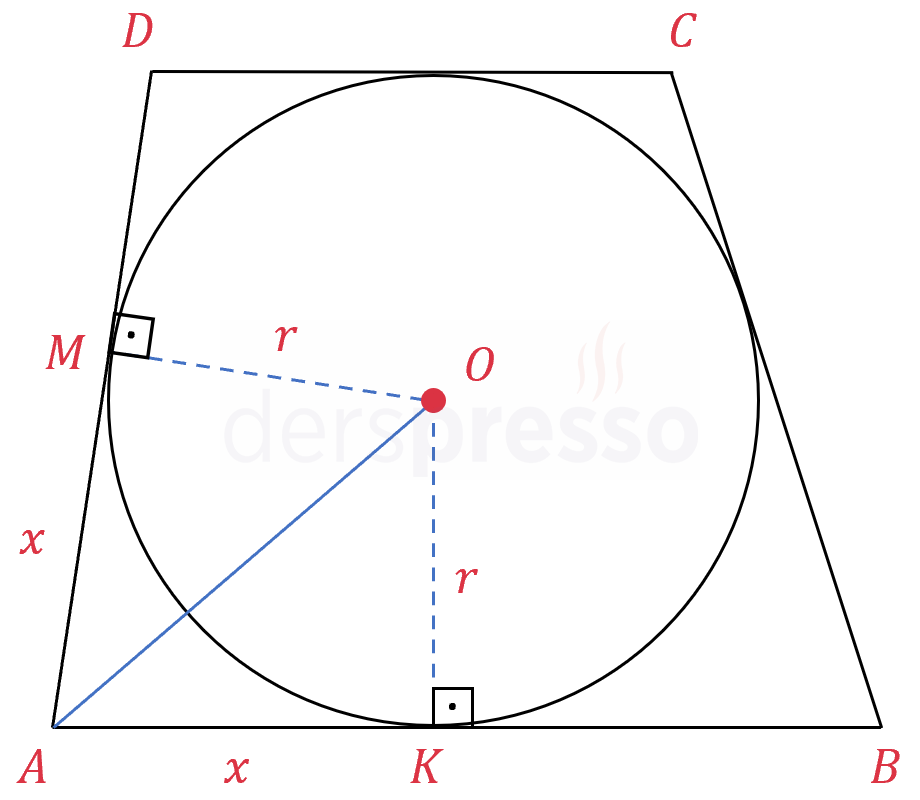
\( A \) köşesi ile çemberin merkezini \( [AO] \) doğru parçası ile birleştirelim.
Çemberin dışındaki \( A \) noktasından çembere çizilen teğetlerin uzunlukları birbirine eşittir.
\( \abs{AK} = \abs{AM} = x \)
Çemberin merkezinden bir teğete çizilen doğru parçası teğeti dik keser ve uzunluğu çemberin yarıçapına eşittir.
\( \abs{OK} = \abs{OM} = r \)
İkişer kenarı (\( x \) ve \( r \)) ve bu iki kenar arasındaki açıları (\( \widehat{AKO} \) ve \( \widehat{AMO} \)) eşit olan iki üçgen, karşı kenar uzunlukları da eşit olacağı için eş üçgenlerdir.
\( \overset{\triangle}{AKO} \cong \overset{\triangle}{AMO} \)
Bu iki üçgen eş üçgenler oldukları için aşağıdaki iki açıları da eşittir.
\( m(\widehat{KAO}) = m(\widehat{MAO}) \)
Dolayısıyla \( [AO] \) doğru parçası \( A \) köşesinin açıortayıdır.
Aynı ispatı diğer köşeler için de tekrarlarsak teğetler dörtgeninin tüm açıortaylarının tek bir noktada ve çemberin merkezinde kesiştiklerini göstermiş oluruz.
Teğetler dörtgeninin alanı, dörtgenin çevre uzunluğunun yarısı olan \( u \) ve çemberin yarıçapı cinsinden aşağıdaki formülle hesaplanabilir.
\( A(ABCD) = ur \)
İSPATI GÖSTER
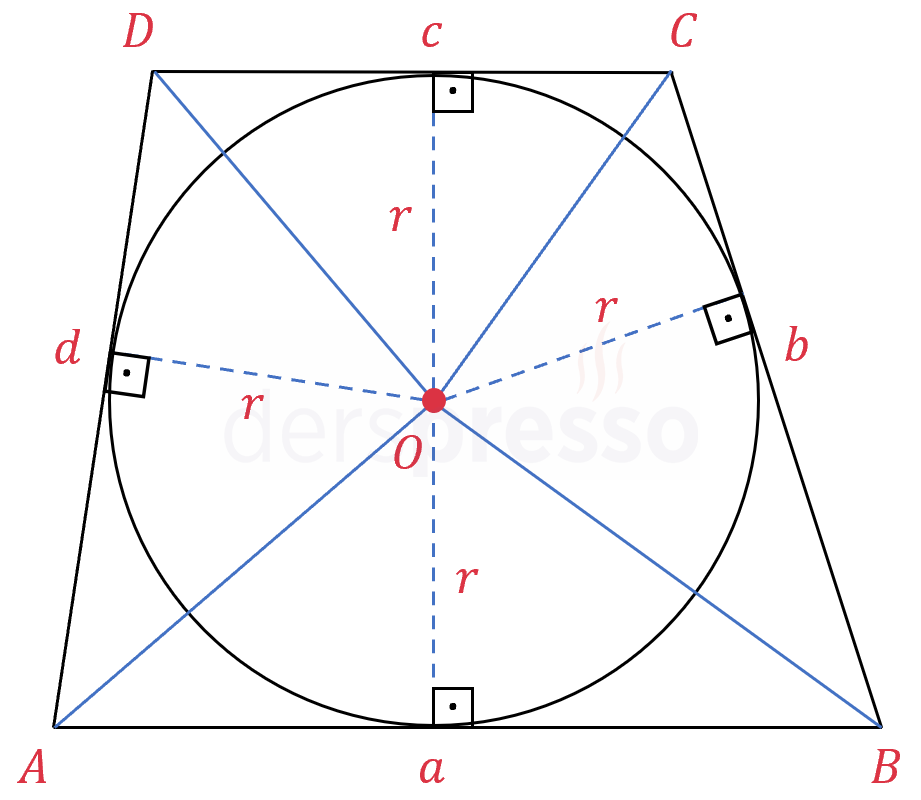
Teğetler dörtgeninin köşelerinden çemberin merkezine doğrular çizelim (mavi çizgiler).
Teğetler dörtgeninin alanını her birinin yüksekliği çemberin yarıçapı olan dört üçgenin alanları toplamı şeklinde yazalım.
\( A(ABCD) = A(ABO) + A(BCO) + A(CDO) + A(DAO) \)
\( A(ABO) = \dfrac{ar}{2} \)
\( A(BCO) = \dfrac{br}{2} \)
\( A(CDO) = \dfrac{cr}{2} \)
\( A(DAO) = \dfrac{dr}{2} \)
\( A(ABCD) = \dfrac{a + b + c + d}{2} \cdot r \)
Teğetler dörtgeninin karşılıklı kenar uzunlukları \( u \)'ya eşittir.
\( = \dfrac{u + u}{2} \cdot r \)
\( = ur \)
Bir diğer formüle göre, teğetler dörtgeninin alanı dörtgenin kenar uzunluklarının çarpımının kareköküne eşittir.
\( A(ABCD) = \sqrt{abcd} \)
Kenar uzunlukları 6, 9, 12 ve 8 br olan teğetler dörtgeninin alanı:
\( A = \sqrt{6 \cdot 9 \cdot 12 \cdot 8} = 72 \)