Kirişler Dörtgeni
Tüm köşeleri bir çemberin üzerinde olan, bir diğer ifadeyle tüm kenarları bir çemberin kirişleri olan dörtgene kirişler dörtgeni denir.
Bir çember üzerinden seçilecek dört farklı noktanın birleştirilmesi ile bir kirişler dörtgeni elde edilebilir.
Önceki bölümde gördüğümüz gibi her üçgenin bir çevrel çemberi vardır, ancak her dörtgen bir kirişler dörtgeni değildir. Her kare, dikdörtgen ve ikizkenar yamuk aynı zamanda birer kirişler dörtgenidir.
Birer kenarı \( [AD] \) doğru parçası olan iki üçgenin tepe açıları eşitse bu noktaların oluşturduğu dörtgen bir kirişler dörtgenidir. Bunun sebebi \( [AD] \) doğru parçasının \( \overparen{AD} \) çember yayını oluşturması ve ölçüleri eşit tepe açılarının bir çember üzerinde aynı yayı gören iki çevre açıya karşılık gelmesidir.
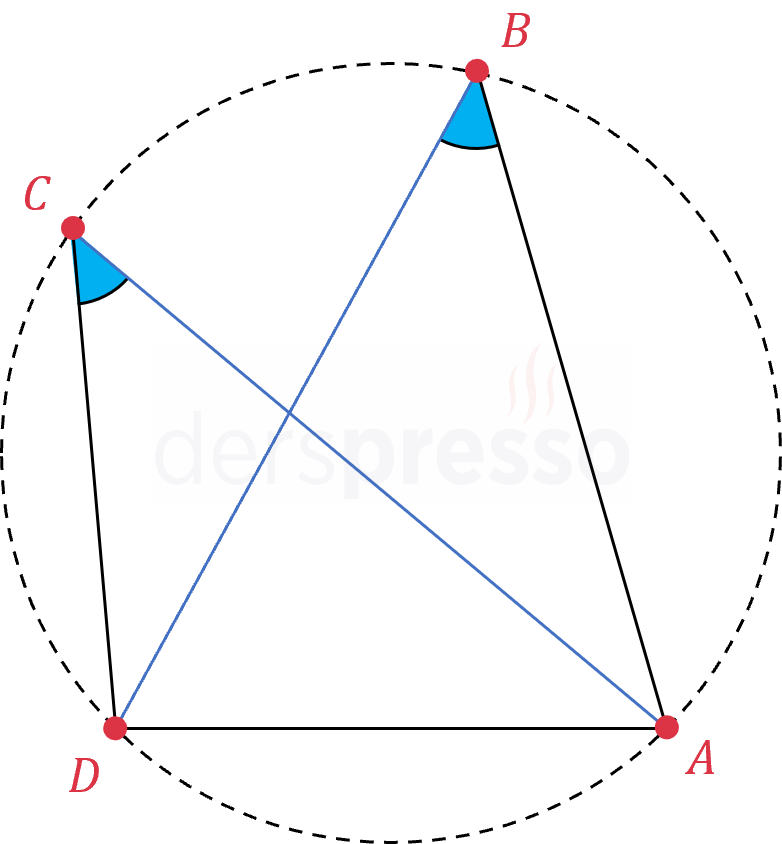
Kirişler dörtgeninde karşılıklı açıların ölçüleri toplamı \( 180° \)'dir ve gördükleri yayların uzunlukları toplamı \( 360° \)'dir. Bunun karşıtı da doğrudur, yani karşılıklı açılarının ölçüleri toplamı \( 180° \) olan bir dörtgen kirişler dörtgenidir.

\( m(\hat{A}) + m(\hat{C}) = m(\hat{B}) + m(\hat{D}) = 180° \)
\( x + y + z + t = 360° \)
İSPATI GÖSTER
Kirişler dörtgeninin köşeleri arasında kalan yayların uzunlukları toplamı 360°'dir.
\( x + y + z + t = 360° \)
Çevre açılarının ölçüleri gördükleri yay uzunluklarının yarısına eşittir.
\( m(\hat{A}) = \dfrac{y + z}{2} \)
\( m(\hat{B}) = \dfrac{z + t}{2} \)
\( m(\hat{C}) = \dfrac{x + t}{2} \)
\( m(\hat{D}) = \dfrac{x + y}{2} \)
Kirişler dörtgeninde karşılıklı açıların toplamını alalım.
\( m(\hat{A}) + m(\hat{C}) = \dfrac{y + z}{2} + \dfrac{x + t}{2} \)
\( = \dfrac{x + y + z + t}{2} = \dfrac{360°}{2} = 180° \)
\( m(\hat{B}) + m(\hat{D}) = \dfrac{z + t}{2} + \dfrac{x + y}{2} \)
\( = \dfrac{x + y + z + t}{2} = \dfrac{360°}{2} = 180° \)
Buna göre kirişler dörtgeninde karşılıklı açıların toplamı 180°'dir.
Bu kurallardan aşağıdaki sonuçlar çıkarılabilir.
- Bir kirişler dörtgeni paralelkenar ise dikdörtgen olmak zorundadır.
- Bir kirişler dörtgeni yamuk ise ikizkenar yamuk olmak zorundadır.
- Kirişler dörtgeni kare olmayan bir eşkenar dörtgen olamaz.
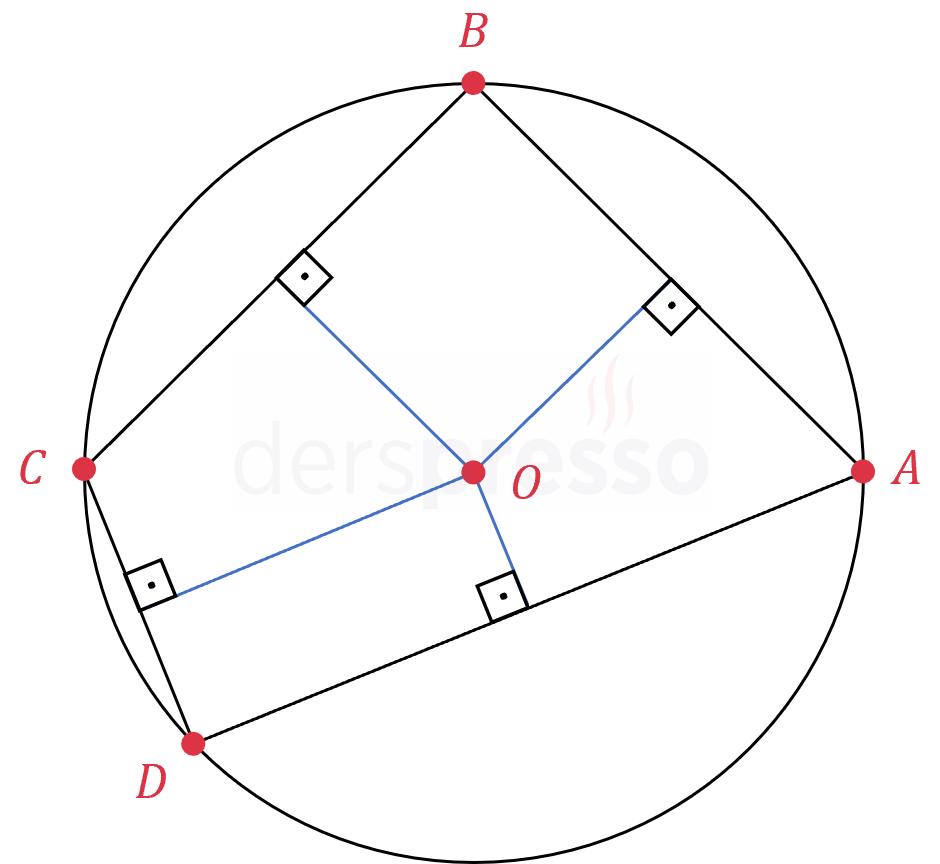
Kirişler dörtgeninin kenarlarının orta dikmeleri tek bir noktada ve çemberin merkezinde kesişir. Bunun karşıtı da doğrudur, yani kenarlarının orta dikmeleri tek bir noktada kesişen bir dörtgen kirişler dörtgenidir.
Batlamyus (Ptolemy) Teoremi: Bu teoreme göre kirişler dörtgeninde karşılıklı kenar uzunluklarının çarpımlarının toplamı, köşegen uzunluklarının çarpımına eşittir. Bunun karşıtı da doğrudur, yani bu eşitliği sağlayan bir dörtgen kirişler dörtgenidir.
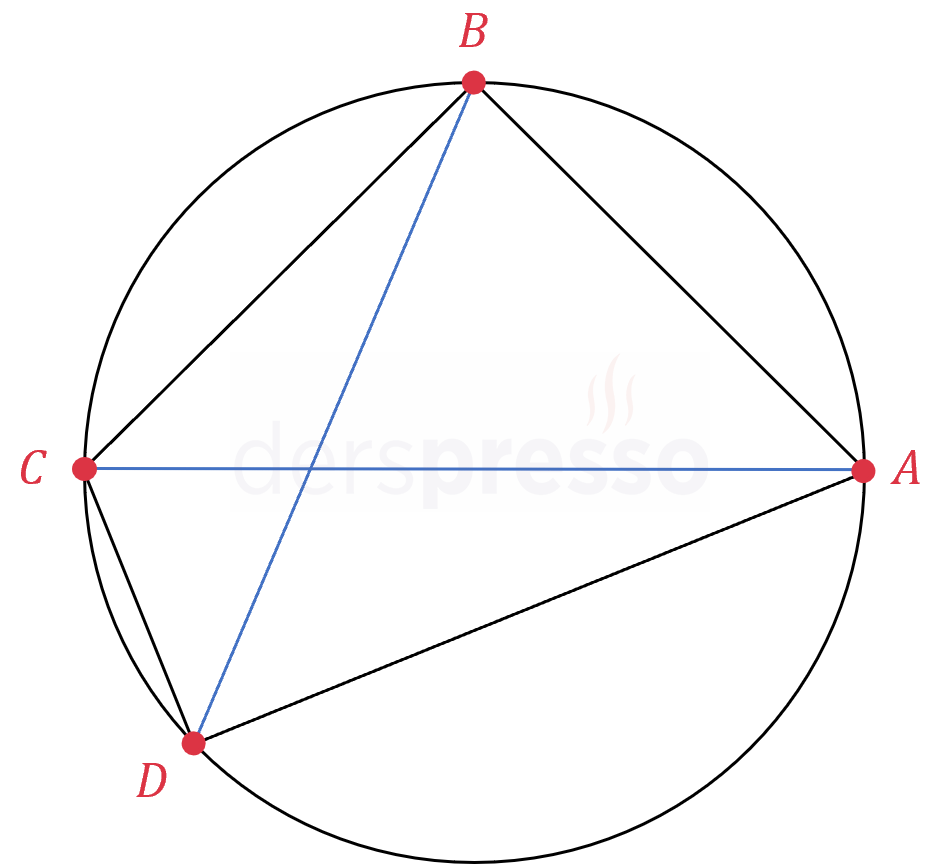
\( \abs{AB} \cdot \abs{DC} + \abs{CB} \cdot \abs{DA} \) \( = \abs{AC} \cdot \abs{DB} \)
İSPATI GÖSTER
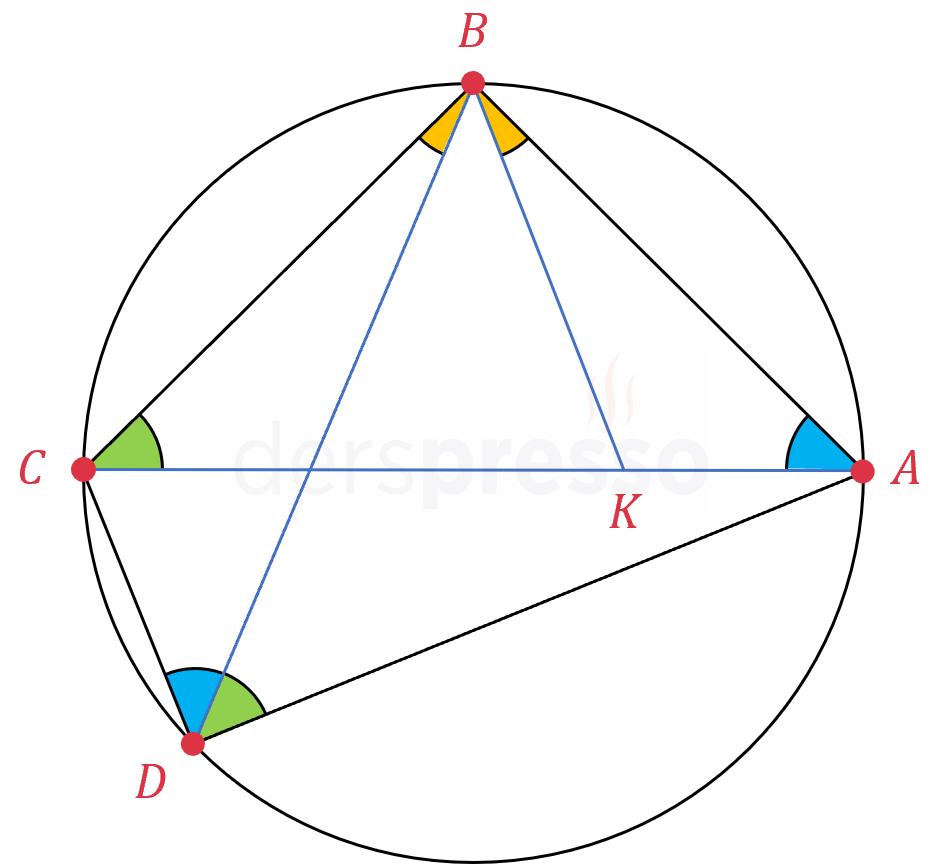
\( ABCD \) kirişler dörtgeninde \( \overparen{AB} \) yayını gören yeşil ile işaretli iki çevre açısı birbirine eşittir.
\( m(\widehat{ACB}) = m(\widehat{ADB}) \)
Ayrıca \( \overparen{BC} \) yayını gören mavi ile işaretli iki çevre açısı birbirine eşittir.
\( m(\widehat{BAC}) = m(\widehat{BDC}) \)
\( B \) köşesinden \( [AC] \) köşegenine aşağıdaki iki açı birbirine eşit olacak şekilde \( [BK] \) doğru parçası çizelim.
\( m(\widehat{ABK}) = m(\widehat{CBD}) \)
Aşağıdaki iki üçgenin ikişer açısı eşit olduğu için üçüncü açıları da eşittir, dolayısıyla bu iki üçgen benzerdir.
\( \overset{\triangle}{ABK} \sim \overset{\triangle}{DBC} \)
Buna göre bu iki üçgenin kenar uzunlukları arasında aşağıdaki benzerliği yazabiliriz.
\( \dfrac{\abs{AB}}{\abs{AK}} = \dfrac{\abs{DB}}{\abs{DC}} \)
\( \abs{AB} \cdot \abs{DC} = \abs{AK} \cdot \abs{DB} \)
Turuncu ile işaretli iki açı eşit olduğu için aşağıdaki iki açı da birbirine eşittir.
\( m(\widehat{ABD}) = m(\widehat{CBK}) \)
Aşağıdaki iki üçgenin ikişer açısı eşit olduğu için üçüncü açıları da eşittir, dolayısıyla bu iki üçgen benzerdir.
\( \overset{\triangle}{CBK} \sim \overset{\triangle}{DBA} \)
Buna göre bu iki üçgenin kenar uzunlukları arasında aşağıdaki benzerliği yazabiliriz.
\( \dfrac{\abs{CB}}{\abs{CK}} = \dfrac{\abs{DB}}{\abs{DA}} \)
\( \abs{CB} \cdot \abs{DA} = \abs{CK} \cdot \abs{DB} \)
Bu iki benzerlikten elde ettiğimiz iki eşitliği taraf tarafa toplayalım.
\( \abs{AB} \cdot \abs{DC} + \abs{CB} \cdot \abs{DA} \) \( = \abs{AK} \cdot \abs{DB} + \abs{CK} \cdot \abs{DB} \)
\( \abs{AB} \cdot \abs{DC} + \abs{CB} \cdot \abs{DA} = (\abs{AK} + \abs{CK}) \cdot \abs{DB} \)
Eşitlikte \( \abs{AK} + \abs{CK} \) yerine \( \abs{AC} \) yazdığımızda Batlamyus teoremi formülünü elde ederiz.
\( \abs{AB} \cdot \abs{DC} + \abs{CB} \cdot \abs{DA} = \abs{AC} \cdot \abs{DB} \)
Brahmagupta Formülü: Kirişler dörtgeninin alanı kenar uzunlukları kullanılarak aşağıdaki formülle hesaplanabilir.
\( u \) kirişler dörtgeninin çevre uzunluğunun yarısı olmak üzere,
\( u = \dfrac{a + b + c + d}{2} \)
\( A(ABCD) = \sqrt{(u - a)(u - b)(u - c)(u - d)} \)
Kirişler dörtgeni, uzunlukları belirli dört kenar ile çizilebilecek dörtgenler içinde alanı en büyük olan dörtgendir.