Artan ve Azalan Fonksiyonlar
Artan Fonksiyon
Bir fonksiyonun belirli bir aralıkta \( x \) değeri arttıkça \( y \) değeri de sürekli artıyorsa ya da sabit kalıyorsa (yani azalmıyorsa) fonksiyon bu aralıkta artan ya da azalmayan bir fonksiyondur. Bir fonksiyonun bir aralıkta artan olabilmesi için fonksiyon değeri bu aralıkta artabilir ya da sabit kalabilir, ama azalamaz.
\( f: A \to \mathbb{R} \) olmak üzere, her \( x_1, x_2 \in (a, b) \) için,
\( x_1 \lt x_2 \) iken \( f(x_1) \le f(x_2) \) ise \( f \) fonksiyonu \( (a, b) \) aralığında artan (azalmayan) bir fonksiyondur.
Bir fonksiyonun belirli bir aralıkta \( x \) değeri arttıkça \( y \) değeri de sürekli artıyorsa fonksiyon bu aralıkta kesin artan bir fonksiyondur. Bir fonksiyonun bir aralıkta kesin artan olabilmesi için fonksiyon değeri bu aralıkta azalamaz ya da sabit kalamaz, sadece artabilir.
\( f: A \to \mathbb{R} \) olmak üzere, her \( x_1, x_2 \in (a, b) \) için,
\( x_1 \lt x_2 \) iken \( f(x_1) \lt f(x_2) \) ise \( f \) fonksiyonu \( (a, b) \) aralığında kesin artan bir fonksiyondur.
Azalan Fonksiyon
Bir fonksiyonun belirli bir aralıkta \( x \) değeri arttıkça \( y \) değeri sürekli azalıyorsa ya da sabit kalıyorsa (yani artmıyorsa) fonksiyon bu aralıkta azalan ya da artmayan bir fonksiyondur. Bir fonksiyonun bir aralıkta azalan olabilmesi için fonksiyon değeri bu aralıkta azalabilir ya da sabit kalabilir, ama artamaz.
\( f: A \to \mathbb{R} \) olmak üzere, her \( x_1, x_2 \in (a, b) \) için,
\( x_1 \lt x_2 \) iken \( f(x_1) \ge f(x_2) \) ise \( f \) fonksiyonu \( (a, b) \) aralığında azalan (artmayan) bir fonksiyondur.
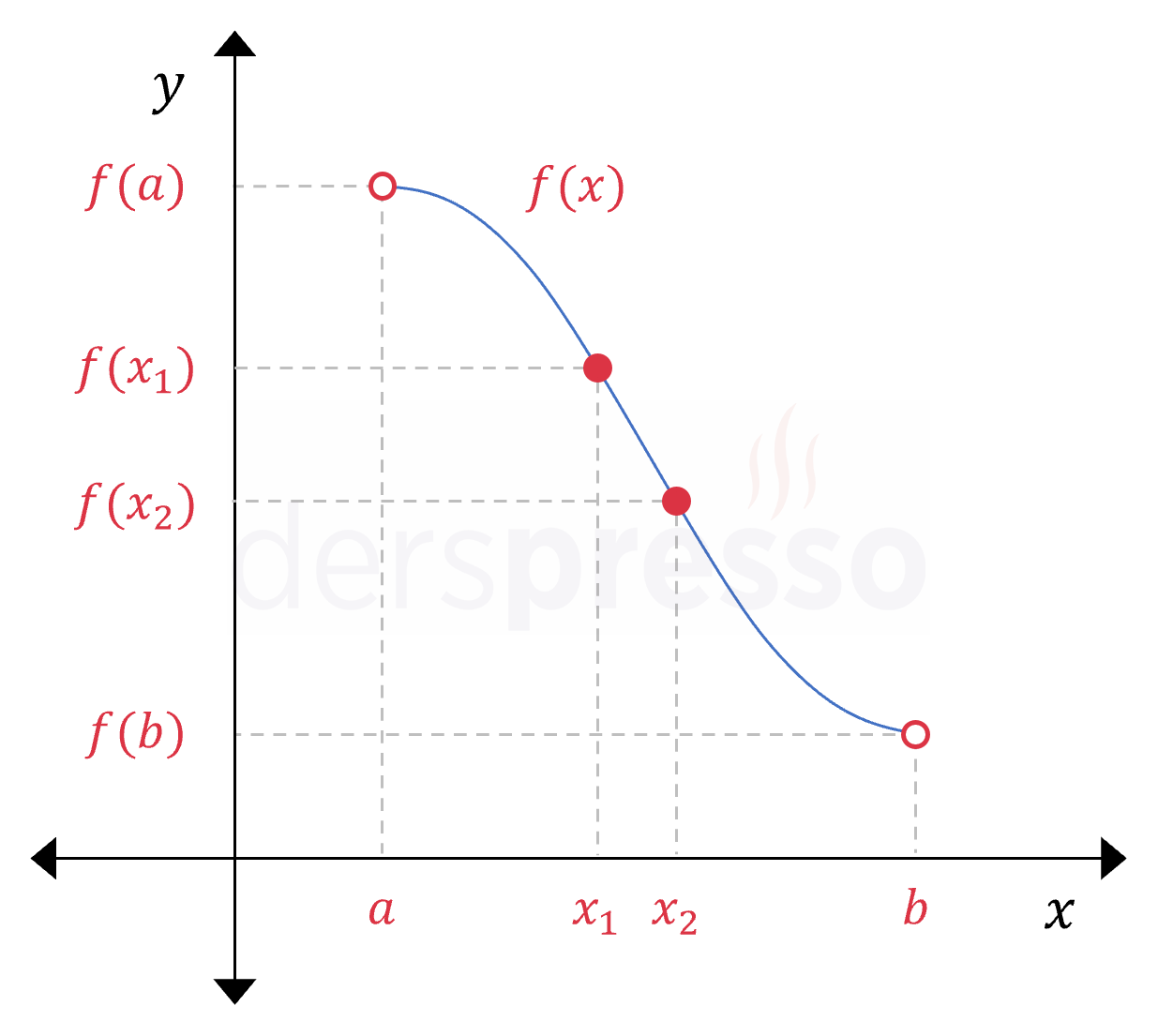
Bir fonksiyonun belirli bir aralıkta \( x \) değeri arttıkça \( y \) değeri sürekli azalıyorsa fonksiyon bu aralıkta kesin azalan bir fonksiyondur. Bir fonksiyonun bir aralıkta kesin azalan olabilmesi için fonksiyon değeri bu aralıkta artamaz ya da sabit kalamaz, sadece azalabilir.
\( f: A \to \mathbb{R} \) olmak üzere, her \( x_1, x_2 \in (a, b) \) için,
\( x_1 \lt x_2 \) iken \( f(x_1) \gt f(x_2) \) ise \( f \) fonksiyonu \( (a, b) \) aralığında kesin azalan bir fonksiyondur.
Yukarıdaki koşullar sağlandığı sürece bir fonksiyonun bir noktada sürekli ya da türevli olmaması artan ya da azalan olmasına engel değildir. Örneğin aşağıdaki fonksiyon \( x = c \) noktasında süreksiz, \( x = d \) noktasında türevsiz olsa da \( (a, b) \) aralığında artandır.
Aşağıda grafiği verilen \( f(x) = x^3 \) fonksiyonu her ne kadar \( x = 0 \) noktasında sabit gözükse de (bu noktadaki teğetinin eğimi sıfır olsa da) tüm tanım aralığında kesin artan bir fonksiyondur. Bunun sebebi (aşağıda ispatını verdiğimiz üzere) fonksiyonun hiçbir iki noktasında aynı değere sahip olmamasıdır.
Fonksiyon grafiği üzerinde apsis değerleri \( a \) ve \( b \) olan ve \( a \gt b \) koşulunu sağlayan iki nokta seçelim.
Her durumda \( a^3 - b^3 \gt 0 \) olduğunu gösterebilirsek bu fonksiyonun tüm tanım aralığında kesin artan olduğunu göstermiş oluruz.
Küp farkı özdeşliğini yazalım.
\( a^3 - b^3 = (a - b)(a^2 + ab + b^2) \)
\( a \gt b \) olduğu için her durumda \( a - b \gt 0 \) olur.
İkinci çarpanı aşağıdaki şekilde yazabiliriz.
\( a^2 + ab + b^2 = \dfrac{1}{2}((a + b)^2 + a^2 + b^2) \)
Eşitliğin sağ tarafı üç kare ifadesinin toplamından oluştuğu için her zaman pozitif olur.
Buna göre \( a^3 - b^3 \) ifadesi iki pozitif sayının çarpımı şeklinde yazılabilir, dolayısıyla her zaman pozitiftir.
\( a^3 - b^3 = \underbrace{(a - b)}_{(+)}\underbrace{(a^2 + ab + b^2)}_{(+)} \)
\( a^3 - b^3 \gt 0 \)
Monoton Fonksiyon
Yukarıda verdiğimiz terimler bir fonksiyonun tüm tanım kümesinde olduğu gibi belirli bir aralıktaki davranışını tanımlamak için de kullanılabilir. Buna göre bir fonksiyon belirli bir aralıkta artan, diğer bir aralıkta azalan, üçüncü bir aralıkta sabit olabilir.
Bir fonksiyon tüm tanım kümesinde artan (ya da azalan) ise bu fonksiyona monoton artan (azalan) ya da daima artan (azalan) fonksiyon denir. Benzer şekilde, bir fonksiyon tüm tanım aralığında kesin artan (azalan) ise bu fonksiyona kesin monoton artan (azalan) fonksiyon denir.
Kesin monoton fonksiyonlar herhangi iki \( x \) değerinin görüntüsü aynı olamayacağı için aynı zamanda birebir fonksiyonlardır.
Temel Fonksiyonlarda Artan/Azalan Aralıklar
Temel bazı fonksiyonların artan/azalan oldukları aralıklar aşağıda verilmiştir.
| Grafik | Fonksiyon |
|---|---|
|
Doğrusal Fonksiyon \( m \gt 0 \) olmak üzere, \( f(x) = mx + c \) Tüm reel sayılarda artan |
|
Doğrusal Fonksiyon \( m \lt 0 \) olmak üzere, \( f(x) = mx + c \) Tüm reel sayılarda azalan |
|
Parabol \( a \gt 0 \) olmak üzere, \( f(x) = ax^2 + bx + c \) \( (-\infty, r) \) için azalan \( (r, \infty) \) için artan |
|
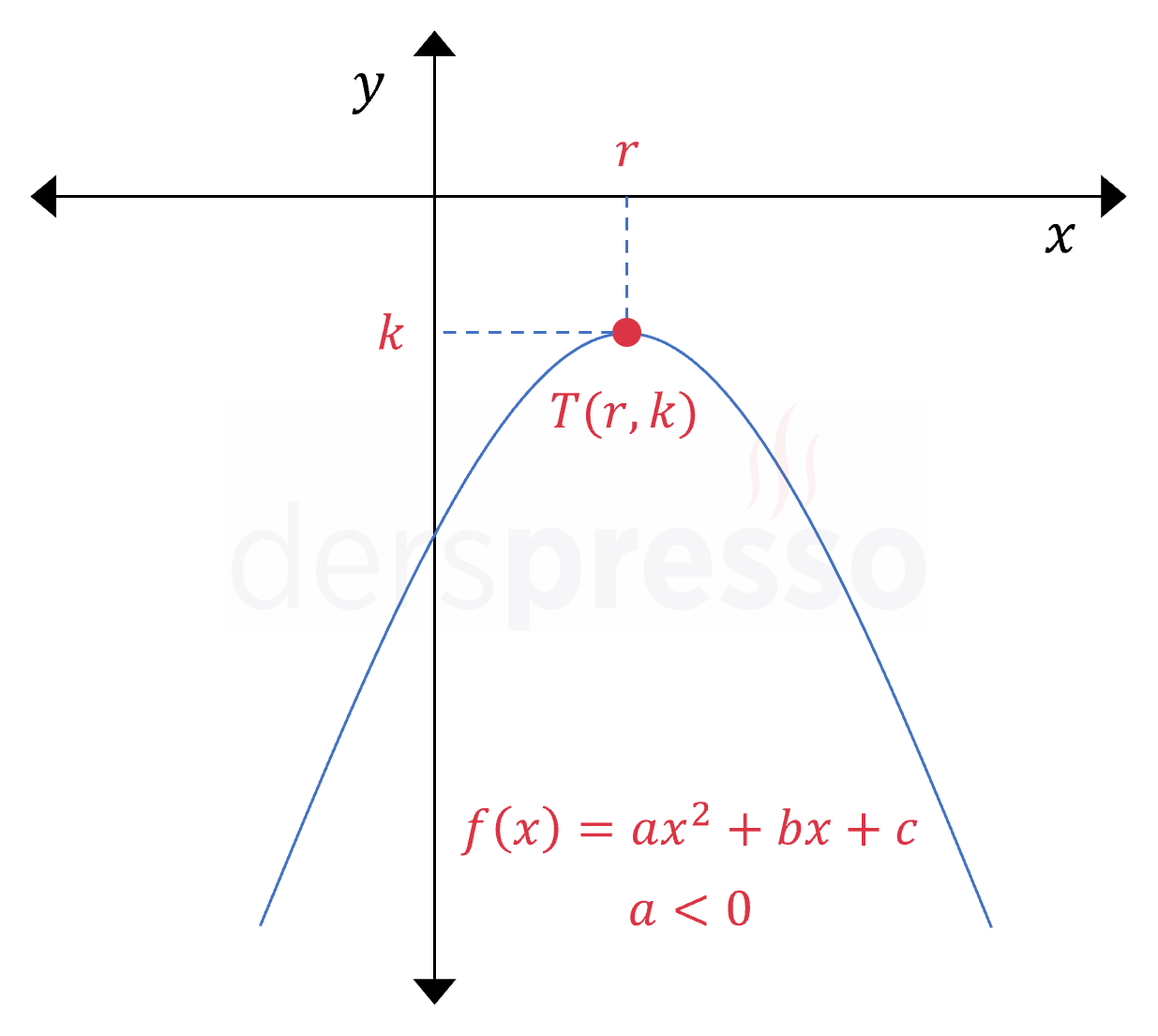
Parabol \( a \lt 0 \) olmak üzere, \( f(x) = ax^2 + bx + c \) \( (-\infty, r) \) için artan \( (r, \infty) \) için azalan |
|
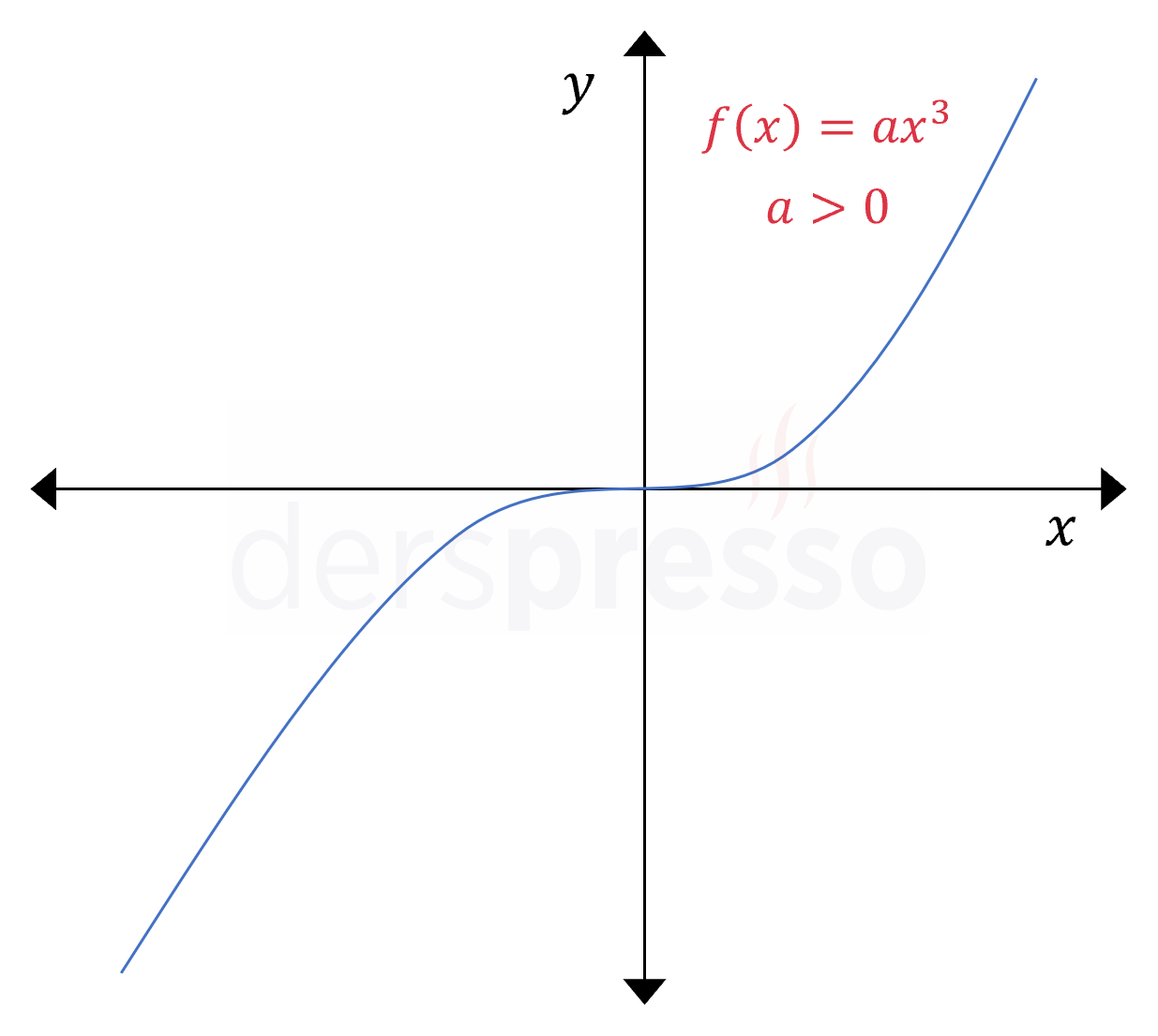
3. Dereceden Polinom Fonksiyonu \( a \gt 0 \) olmak üzere, \( f(x) = ax^3 \) Tüm reel sayılarda artan |
|
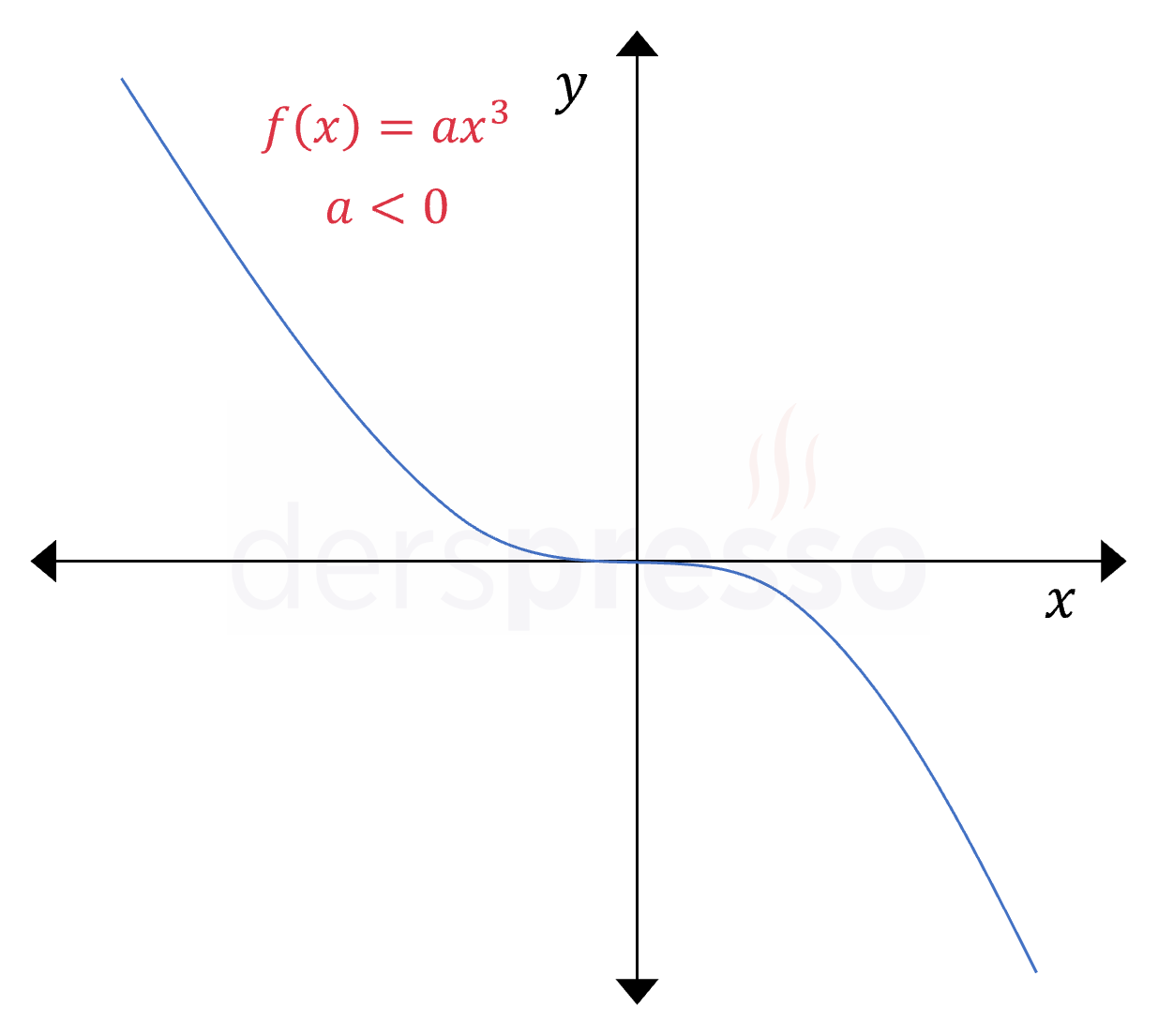
3. Dereceden Polinom Fonksiyonu \( a \lt 0 \) olmak üzere, \( f(x) = ax^3 \) Tüm reel sayılarda azalan |
|
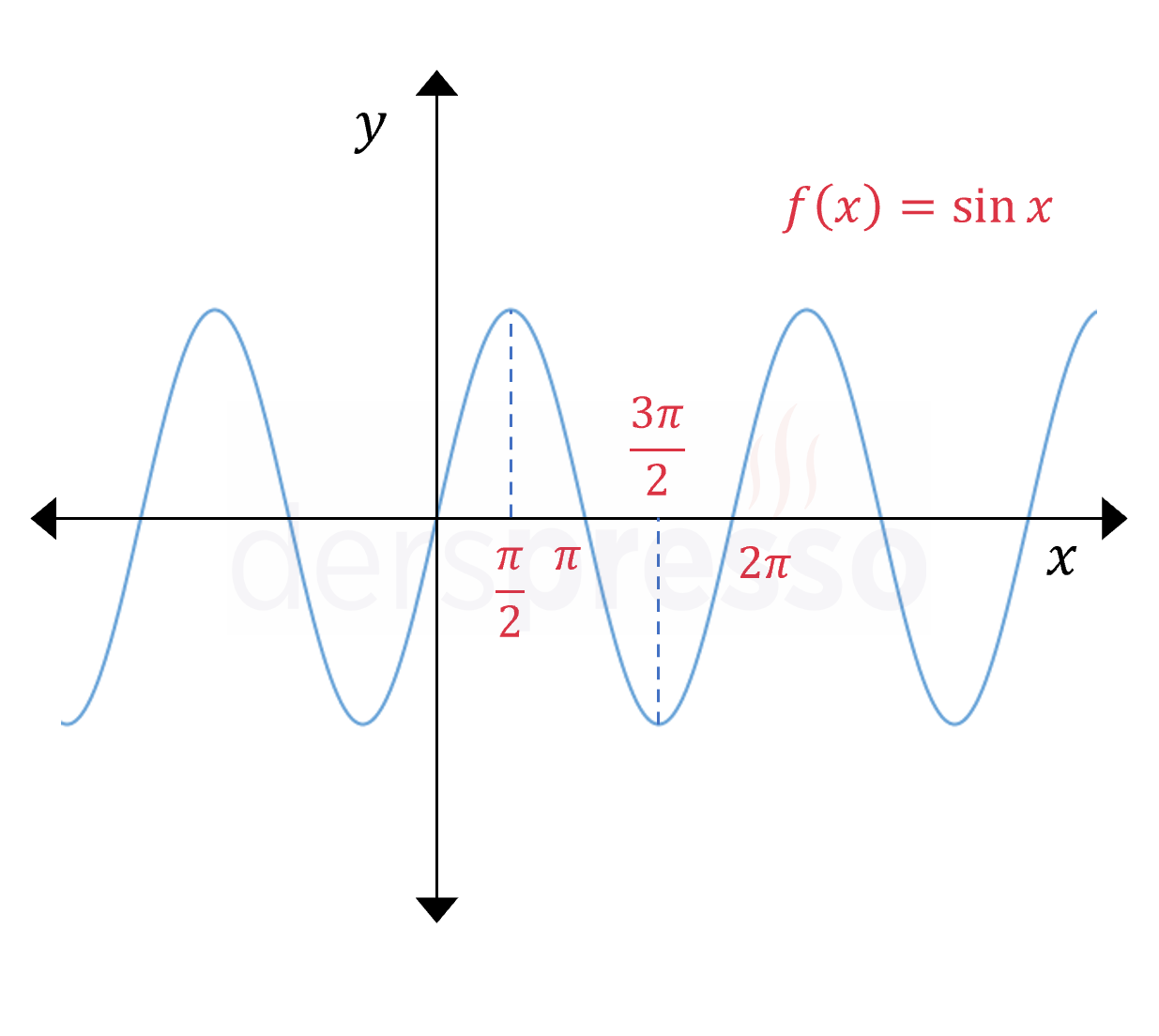
Sinüs Fonksiyonu \( f(x) = \sin{x} \) \( (0, 2\pi) \) aralığında: \( (0, \frac{\pi}{2}) \) için artan \( (\frac{\pi}{2}, \frac{3\pi}{2}) \) için azalan \( (\frac{3\pi}{2}, 2\pi) \)için artan |
|
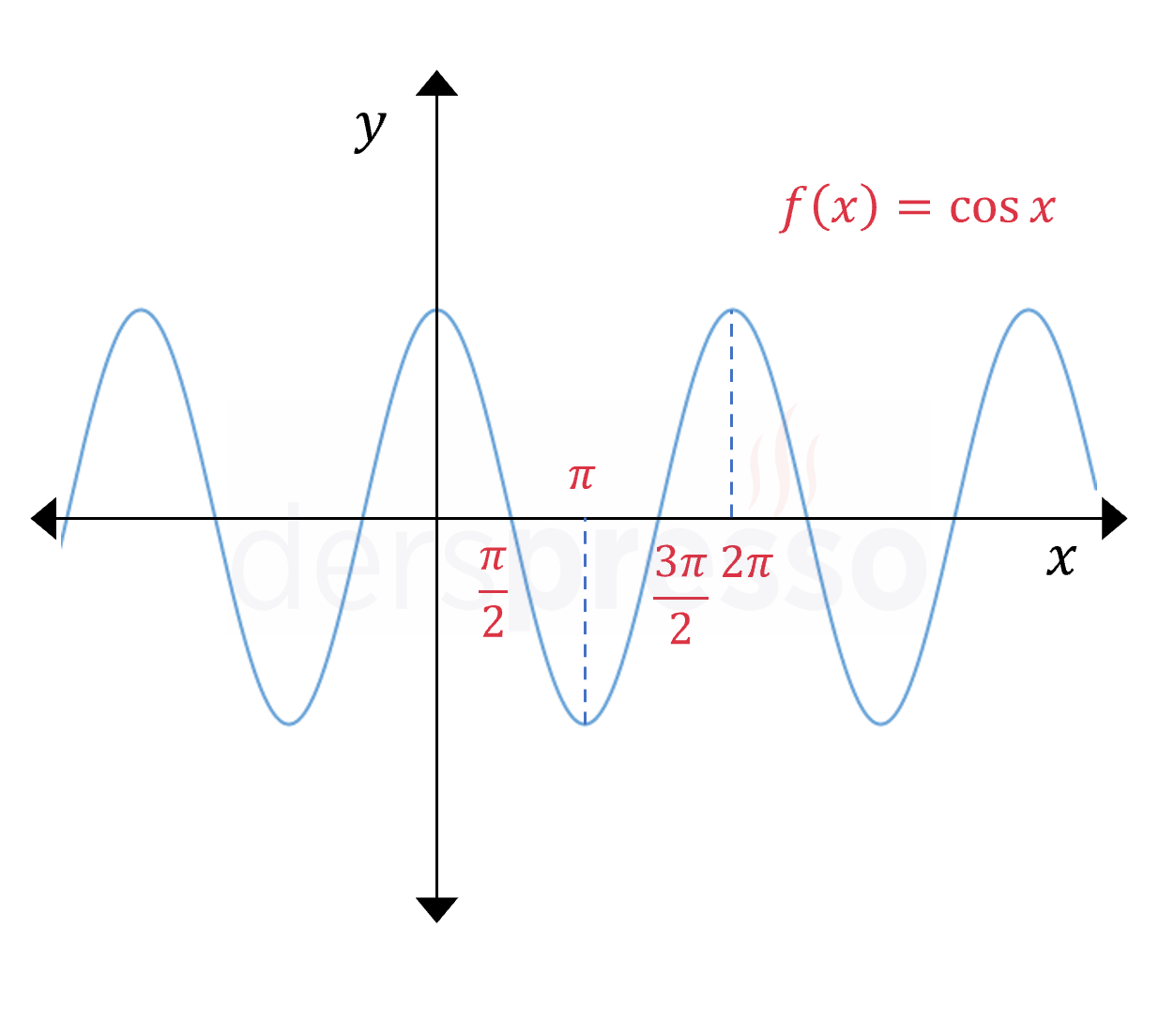
Kosinüs Fonksiyonu \( f(x) = \cos{x} \) \( (0, 2\pi) \) aralığında: \( (0, \pi) \) için azalan \( (\pi, 2\pi) \) için artan |
|
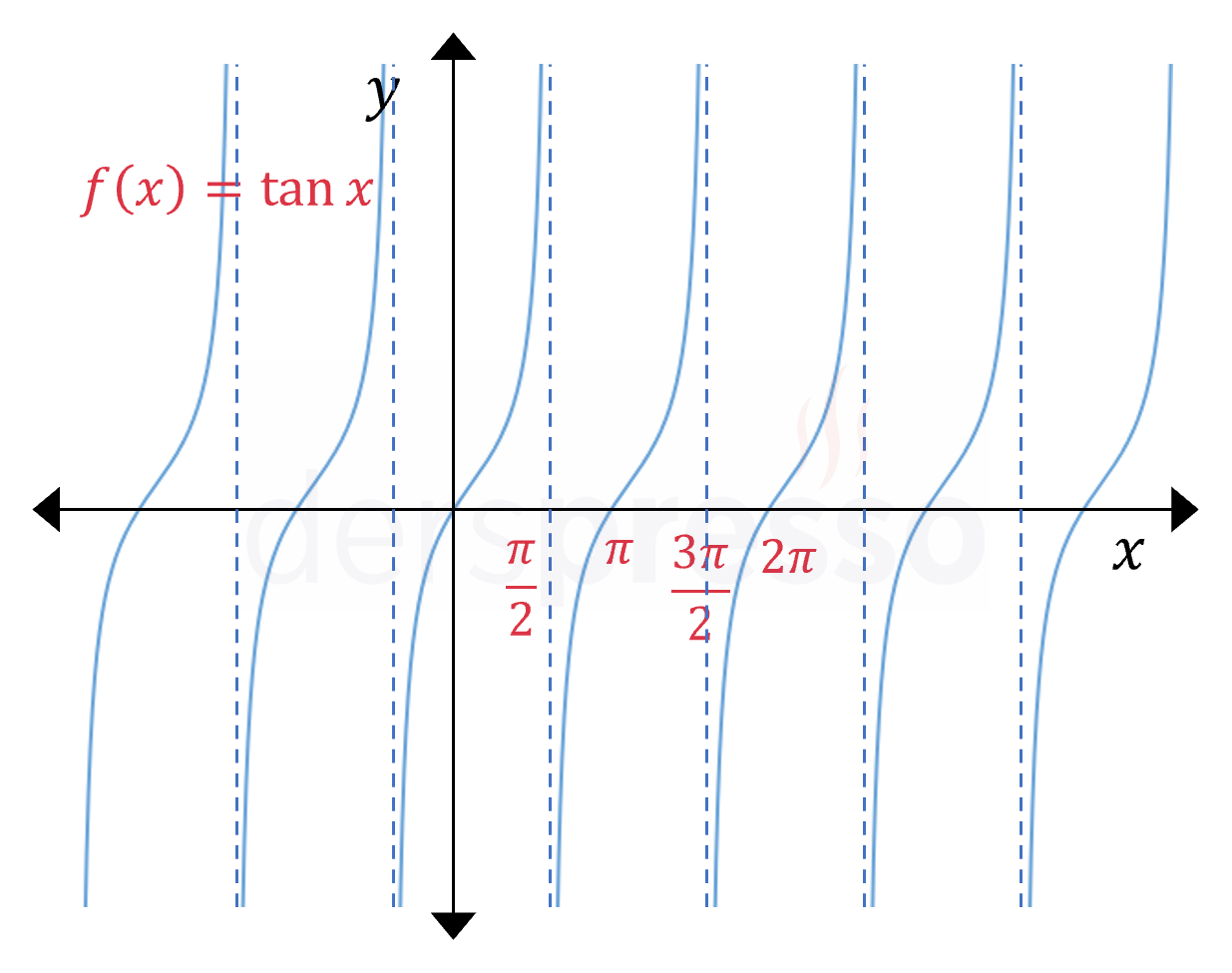
Tanjant Fonksiyonu \( f(x) = \tan{x} \) \( (0, 2\pi) \) aralığında: \( (0, \frac{\pi}{2}) \) için artan \( (\frac{\pi}{2}, \frac{3\pi}{2}) \) için artan \( (\frac{3\pi}{2}, 2\pi) \)için artan |
|
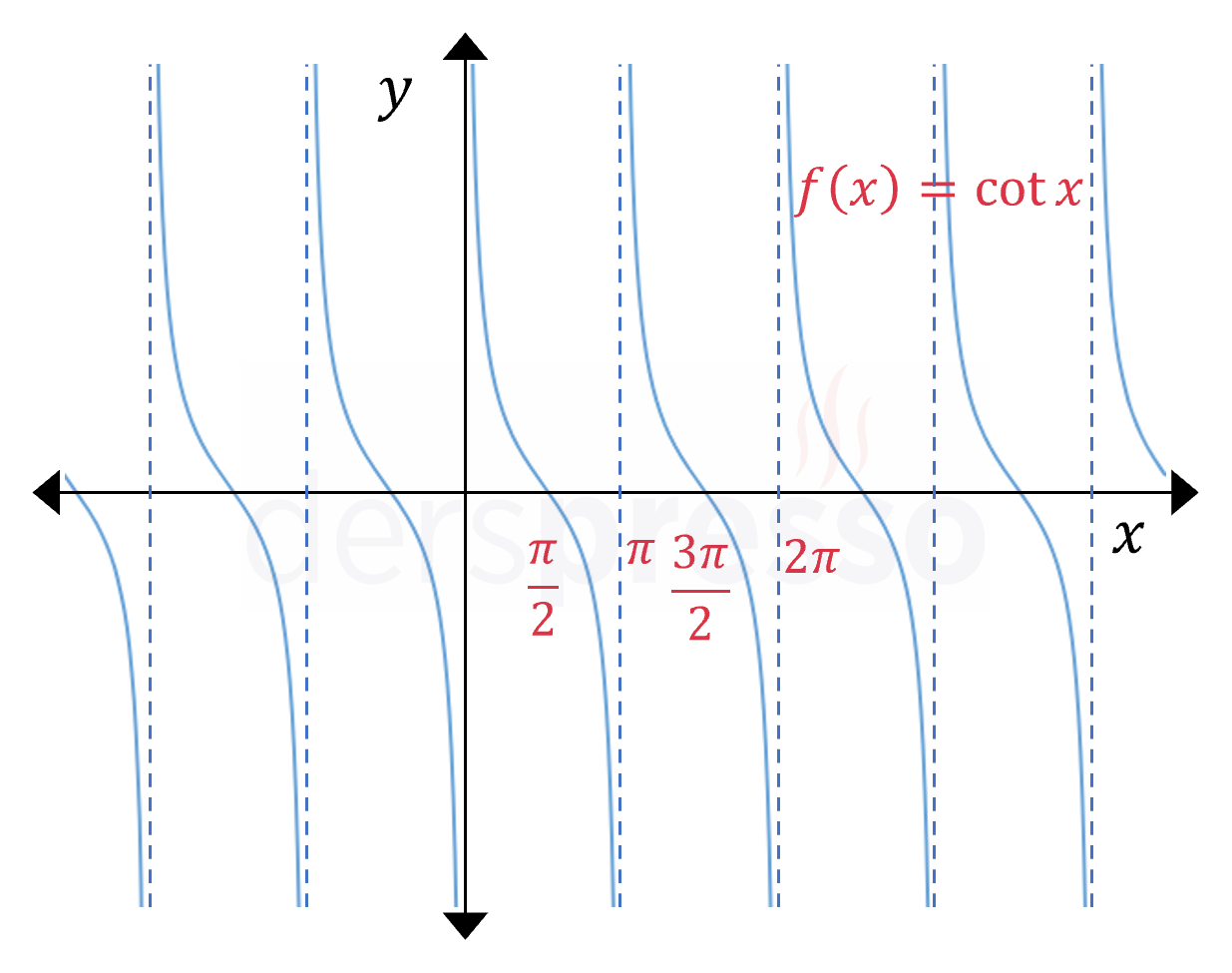
Kotanjant Fonksiyonu \( f(x) = \cot{x} \) \( (0, 2\pi) \) aralığında: \( (0, \pi) \) için azalan \( (\pi, 2\pi) \) için azalan |
|
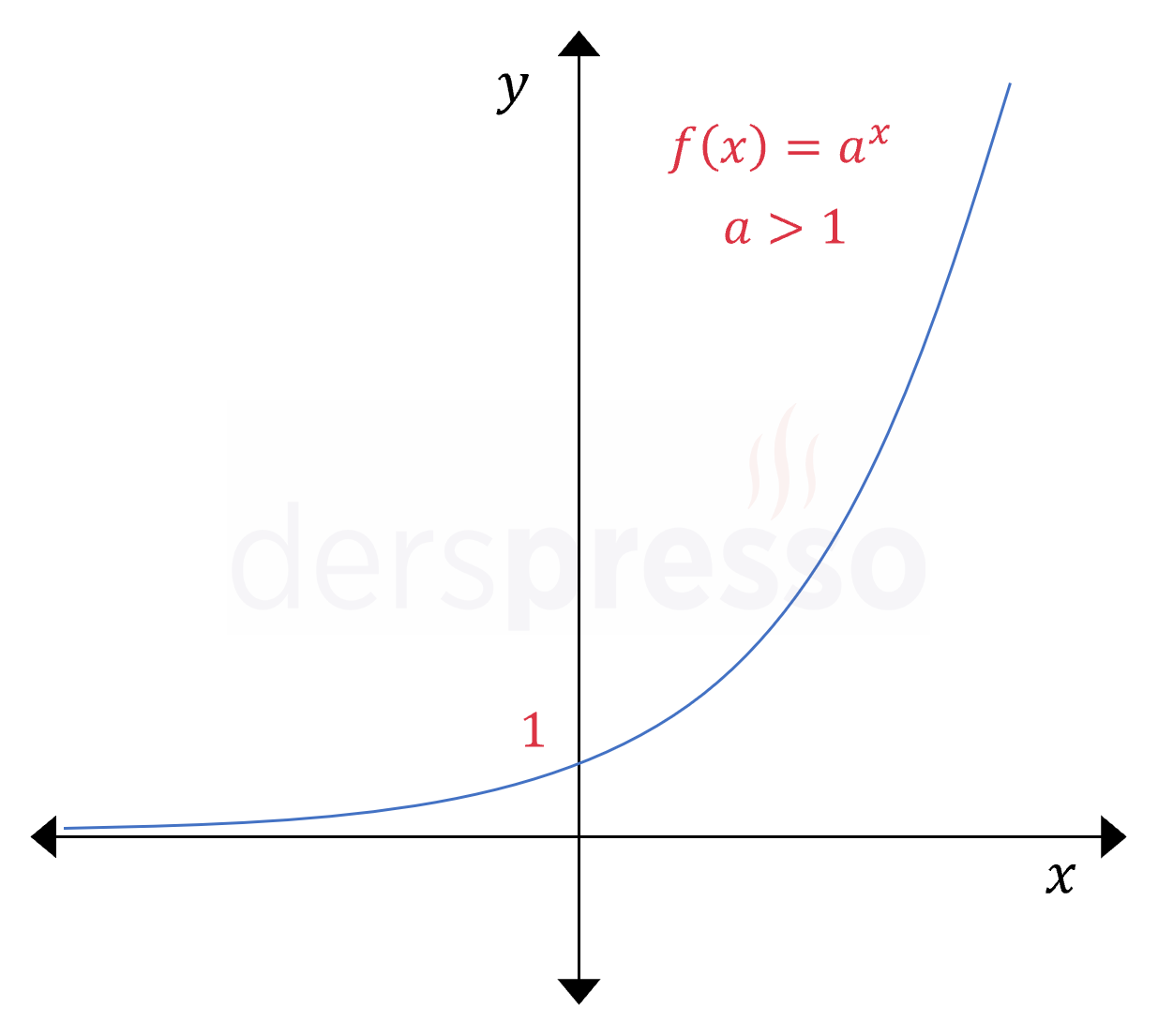
Üstel Fonksiyon \( a \gt 1 \) olmak üzere, \( f(x) = a^x \) Tüm reel sayılarda artan |
|
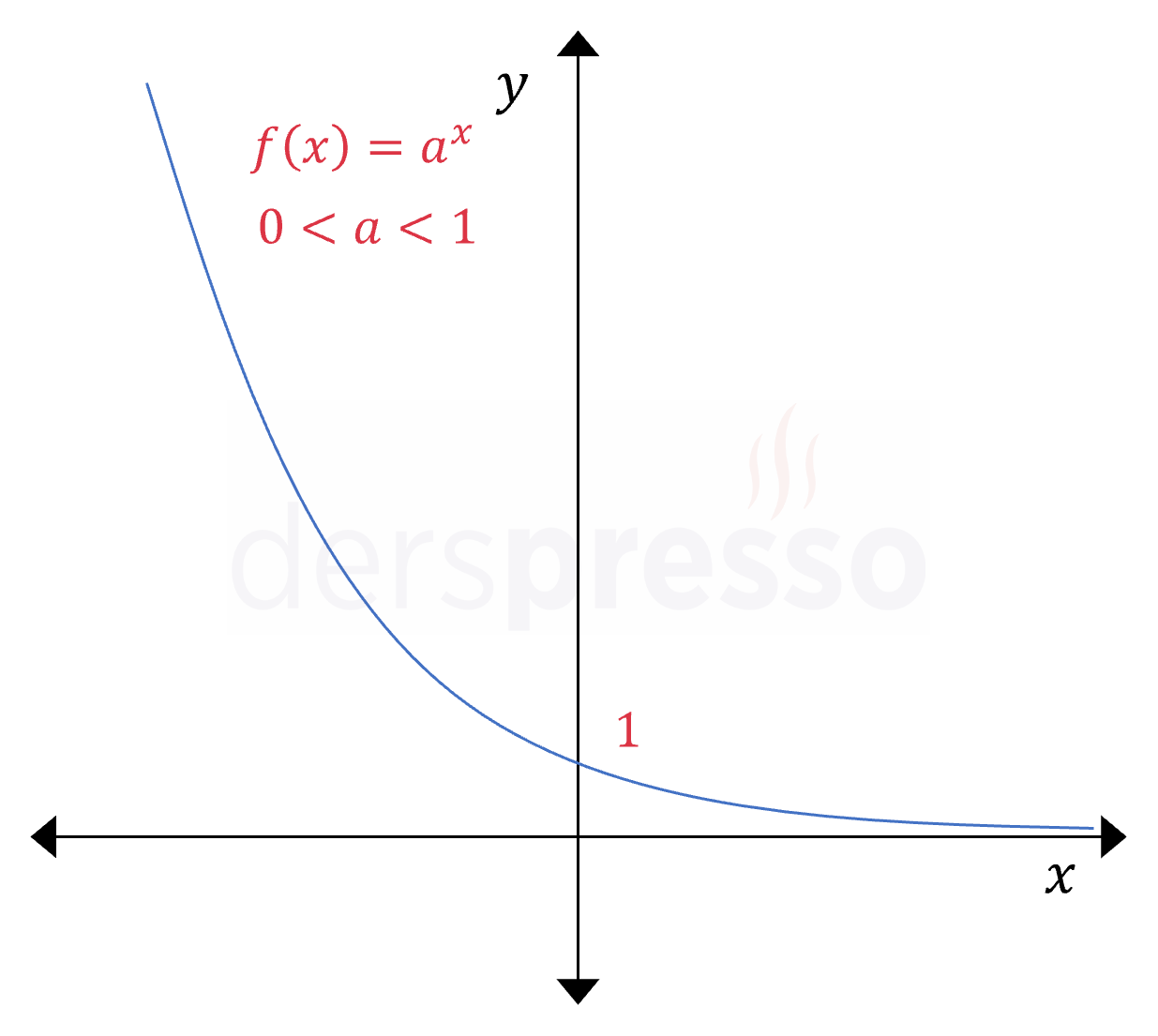
Üstel Fonksiyon \( 0 \lt a \lt 1 \) olmak üzere, \( f(x) = a^x \) Tüm reel sayılarda azalan |
|
Logaritma Fonksiyonu \( a \gt 1 \) olmak üzere, \( f(x) = \log_a{x} \) Pozitif reel sayılarda artan |
|
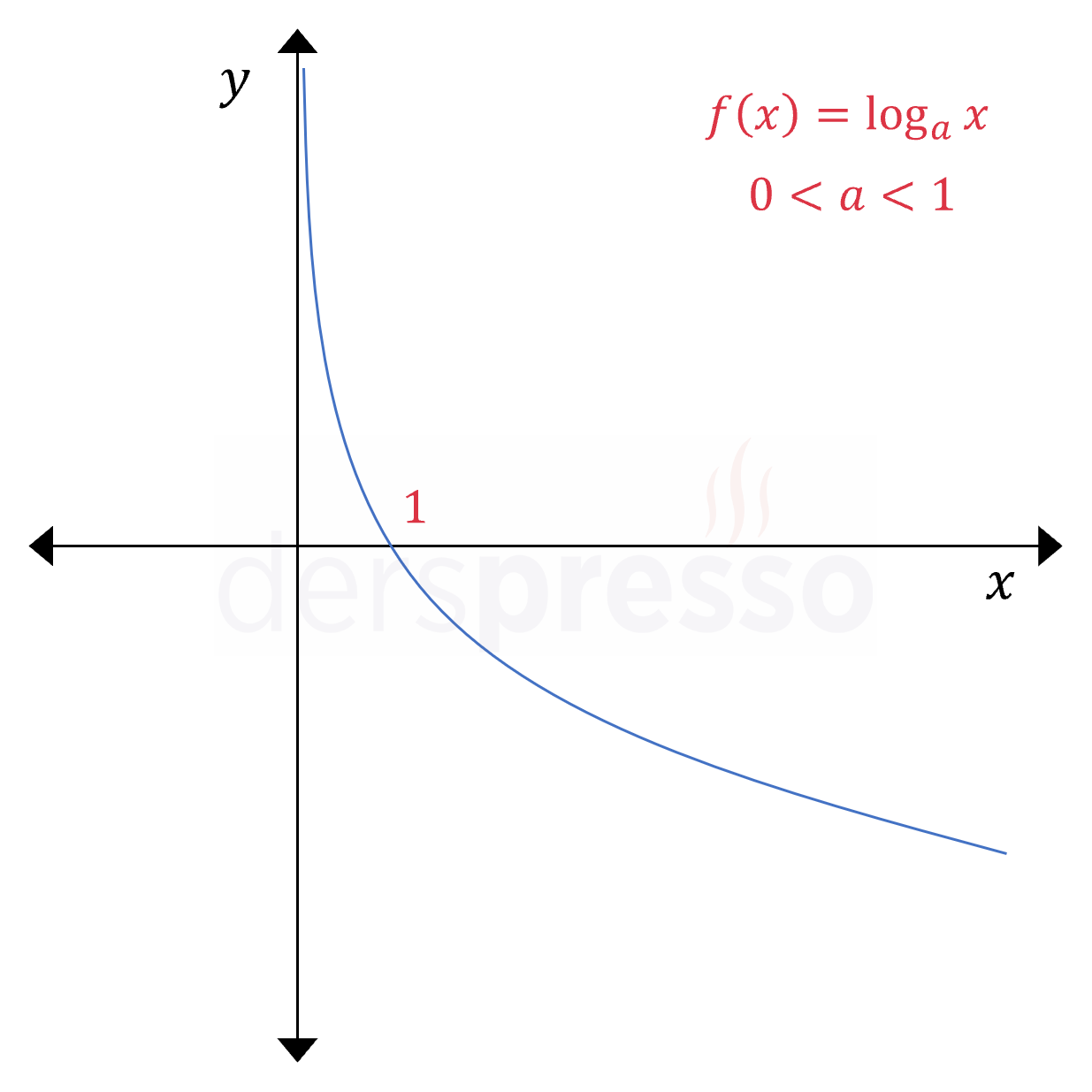
Logaritma Fonksiyonu \( 0 \lt a \lt 1 \) olmak üzere, \( f(x) = \log_a{x} \) Pozitif reel sayılarda azalan |
Artan ve Azalan Fonksiyonlar Arası İşlemler
Artan ve azalan fonksiyonlar arasındaki işlemler sonucunda oluşan fonksiyonların artan ya da azalan olma durumları aşağıdaki gibidir.
\( f \) ve \( g \) fonksiyonları \( (a, b) \) aralığında artan fonksiyonlar olmak üzere,
- \( f + g \) fonksiyonu da aynı aralıkta artan fonksiyondur.
- \( -f \) fonksiyonu aynı aralıkta azalan fonksiyondur.
- \( \frac{1}{f} \) fonksiyonu aynı aralıkta azalan fonksiyondur.
- Belirtilen aralıkta \( f(x) \gt 0 \) ve \( g(x) \gt 0 \) olmak koşuluyla, \( f \cdot g \) fonksiyonu aynı aralıkta artan fonksiyondur.
\( f \) ve \( g \) fonksiyonlarının azalan olması durumunda yukarıdaki işlem sonuçları artan yerine azalan, azalan yerine artan olacaktır.
\( f(x) = (k - 1)x^2 + 2x + k + 4 \) fonksiyonunun tüm reel sayılarda daima artan olması için \( k \) kaç olmalıdır?
Çözümü Gösterİkinci dereceden polinomların (parabol) tepe noktasının iki tarafında artan/azalan olma durumları birbirinden farklıdır, dolayısıyla bir parabol tüm reel sayılarda daima artan ya da daima azalan olmaz.
Buna göre \( x^2 \)'lik katsayısı sıfır olmalıdır.
\( k - 1 = 0 \Longrightarrow k = 1 \)
\( f(x) = 2x + k + 4 = 2x + 5 \)
Elde ettiğimiz doğrusal fonksiyonun eğimi pozitif olduğu için grafiği daima artandır.
\( f(x) = (k - 4)x + 5 \) fonksiyonunun daima azalan olması için \( k \)'nın alabileceği en büyük tam sayı değer kaçtır?
Çözümü GösterBir doğrusal fonksiyonun daima azalan olması için \( x \)'in katsayısı, yani doğrunun eğimi negatif olmalıdır.
\( k - 4 \lt 0 \)
\( k \lt 4 \)
\( k \)'nın alabileceği en büyük tam sayı değer 3 olarak bulunur.
Aşağıdaki fonksiyonlardan hangilerinde \( x \)'in her 1 birim artışında \( f(x) \) değeri %20 azalır?
I. \( f(x) = -(0,8)x \)
II. \( f(x) = -(0,2)^x \)
III. \( f(x) = (0,8)^x \)
IV. \( f(x) = x^{0,8} \)
Çözümü GösterBir fonksiyonun değeri \( x \)'in her 1 birim artışında %20 azalıyorsa \( \frac{f(a + 1)}{f(a)} \) oranı her \( a \) için \( 1- \frac{20}{100} = 0,8 \) olmalıdır.
Tüm seçenekler için bu oranı bulalım.
I. öncül:
\( f(x) = -(0,8)x \)
\( \dfrac{f(a + 1)}{f(a)} = \dfrac{-(0,8)(a + 1)}{-(0,8)a} \)
\( = \dfrac{a + 1}{a} \)
\( a \)'nın her 1 birim artışında \( f(a) \) farklı oranlarda değişir.
II. öncül:
\( f(x) = -(0,2)^x \)
\( \dfrac{f(a + 1)}{f(a)} = \dfrac{-(0,2)^{a+1}}{-(0,2)^a} \)
\( = \dfrac{(0,2)^a \cdot 0,2}{(0,2)^a} \)
\( = 0,2 \)
III. öncül:
\( f(x) = (0,8)^x \)
\( \dfrac{f(a + 1)}{f(a)} = \dfrac{(0,8)^{a+1}}{(0,8)^a} \)
\( = \dfrac{(0,8)^a \cdot 0,8}{(0,8)^a} \)
\( = 0,8 \)
IV. öncül:
\( f(x) = x^{0,8} \)
\( \dfrac{f(a + 1)}{f(a)} = \dfrac{(a + 1)^{0,8}}{a^{0,8}} \)
\( = (\dfrac{a + 1}{a})^{0,8} \)
\( a \)'nın her 1 birim artışında \( f(a) \) farklı oranlarda değişir.
Buna göre sadece III. öncüldeki fonksiyonun değeri \( x \)'in her 1 birim artışında %20 azalır.
\( f \) kesin azalan bir fonksiyondur.
\( f(a + 2) = 4, f(a - 3) = 8, f(2a - 8) = 6 \)
olduğuna göre, \( a \)'nın alabileceği kaç farklı tam sayı değer vardır?
Çözümü GösterBir fonksiyonun belirli bir aralıkta \( x \) değeri arttıkça \( y \) değeri sürekli azalıyorsa fonksiyon bu aralıkta kesin azalan bir fonksiyondur. Bir fonksiyonun bir aralıkta kesin azalan olabilmesi için fonksiyon değeri bu aralıkta artamaz ya da sabit kalamaz, sadece azalabilir.
\( f \) kesin azalan bir fonksiyon ve \( 8 \gt 6 \gt 4 \) olduğuna göre, verilen noktaların apsisleri arasındaki ilişki aşağıdaki gibi olmalıdır.
\( a - 3 \lt 2a - 8 \lt a + 2 \)
Tüm taraflardan \( a \) çıkaralım.
\( -3 \lt a - 8 \lt 2 \)
Tüm taraflara 8 ekleyelim.
\( 5 \lt a \lt 10 \)
\( a \)'nın bu aralıkta alabileceği 4 tam sayı değeri vardır.
\( f \) artan ve \( g \) azalan fonksiyonlar olmak üzere,
\( f(2) = b + f(-1) \)
\( g(0) = g(3) - a \)
olduğuna göre, aşağıdaki ifadelerden hangileri doğrudur?
I. \( f(a) \lt f(b) \)
II. \( g(a) \gt g(b) \)
III. \( f(g(a)) \gt f(g(b)) \)
Çözümü Göster\( f \) fonksiyonu artan olduğu için \( f(-1) \lt f(2) \) olur, dolayısıyla \( b \) pozitiftir.
\( g \) fonksiyonu azalan olduğu için \( g(0) \gt g(3) \) olur, dolayısıyla \( a \) negatiftir.
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( a \lt b \) ve \( f \) fonksiyonu artan olduğu için bu öncül doğrudur.
II. öncül:
\( a \lt b \) ve \( g \) fonksiyonu azalan olduğu için bu öncül doğrudur.
III. öncül:
\( g(a) \gt g(b) \) ve \( f \) fonksiyonu artan olduğu için bu öncül doğrudur.
Buna göre üç öncül de doğrudur.
Aşağıdaki fonksiyonların artan oldukları en geniş aralıklara sırasıyla \( A \), \( B \) ve \( C \) dersek bu üç aralık arasındaki kapsama ilişkisi nedir?
I. \( f(x) = x^2 - 4x \)
II. \( g(x) = x^3 \)
III. \( h(x) = \sqrt{x} \)
Çözümü GösterI. öncül:
\( f \) parabolünün tepe noktasının apsisi \( x = 2 \)'dir.
Parabolün başkatsayısı pozitif olduğu için artan olduğu en geniş aralık \( [2, \infty) \) olur.
II. öncül:
\( x^3 \) fonksiyonu tüm reel sayılarda artandır.
III. öncül:
Karekök fonksiyonu tanımlı olduğu en geniş aralık olan \( [0, \infty) \) aralığında artandır.
Buna göre üç fonksiyonun artan oldukları en geniş aralıklar arasındaki kapsama ilişkisi aşağıdaki gibidir.
\( A \subset C \subset B \)
\( n, m, t \in \mathbb{R} \) olmak üzere,
Pozitif reel sayılarda tanımlı \( f, g, h \) fonksiyonlarıyla ilgili aşağıdaki önermeler veriliyor.
\( p: f(x) = n^x \) fonksiyonu azalandır.
\( q: g(x) = \log_t{x} \) fonksiyonu azalandır.
\( r: h(x) = mx + n \) fonksiyonu artandır.
\( (p \lor r)' \Rightarrow q' \equiv 0 \) olduğuna göre, \( n, m, t \) sayılarını küçükten büyüğe doğru sıralayın.
Çözümü Göster\( (p \lor r)' \Rightarrow q' \) bileşik önermesi yalnız birinci önerme doğru, ikinci önerme yanlış olduğunda yanlış olur.
\( (p \lor r)' \equiv 1, \quad q' \equiv 0 \)
\( p \lor r \equiv 0 \)
\( p \equiv 0, \quad r \equiv 0 \)
\( q \equiv 1 \)
Buna göre \( p \) ve \( r \) önermeleri yanlış, \( q \) önermesi doğrudur.
\( p \) önermesi yanlış olduğuna göre \( f \) fonksiyonu artandır, dolayısıyla \( n \gt 1 \) olmalıdır.
\( q \) önermesi doğru olduğuna göre \( g \) fonksiyonu azalandır, dolayısıyla \( 0 \lt t \lt 1 \) olmalıdır.
\( r \) önermesi yanlış olduğuna göre \( h \) fonksiyonu azalandır, dolayısıyla \( m \lt 0 \) olmalıdır.
Buna göre sayıların sıralaması aşağıdaki gibi olur.
\( m \lt t \lt n \)
\( f(x) = 3^x - 5 \) fonksiyonu veriliyor.
Buna göre aşağıdaki fonksiyonlardan hangileri tüm tanım aralığında artandır?
I. \( -f(x) \)
II. \( f(-x) \)
III. \( -f(-x) \)
Çözümü GösterTabanın 1'den büyük olduğu üstel fonksiyonlar tüm reel sayılarda artandır. Fonksiyonun çıktısından 5 çıkarıldığında tüm noktalar 5 birim aşağı öteleneceği için fonksiyon yine artan olur.
I. öncül: \( -f(x) \)
\( -f(x) \) fonksiyonu \( f(x) \) fonksiyonunun \( x \) eksenine göre simetriğidir, dolayısıyla artan fonksiyon azalan fonksiyona dönüşür.
II. öncül: \( f(-x) \)
\( f(-x) \) fonksiyonu \( f(x) \) fonksiyonunun \( y \) eksenine göre simetriğidir, dolayısıyla artan fonksiyon azalan fonksiyona dönüşür.
III. öncül: \( -f(-x) \)
\( -f(-x) \) fonksiyonu \( f(x) \) fonksiyonunun hem \( x \) hem de \( y \) eksenine göre simetriğidir, dolayısıyla artan fonksiyon yine artan olur.
Buna göre sadece III. önermedeki fonksiyon artandır.