Fonksiyon Grafiklerine Giriş
Bir \( f \) fonksiyonunun grafiği, fonksiyonun tanım aralığında \( y = f(x) \) eşitliğini sağlayan \( (x, y) \) koordinatlarının analitik düzlemde oluşturduğu noktalar kümesidir.

Bir fonksiyonun grafiğinde \( x \) ekseni fonksiyonun tanım kümesine, \( y \) ekseni fonksiyonun değer kümesine karşılık gelir.
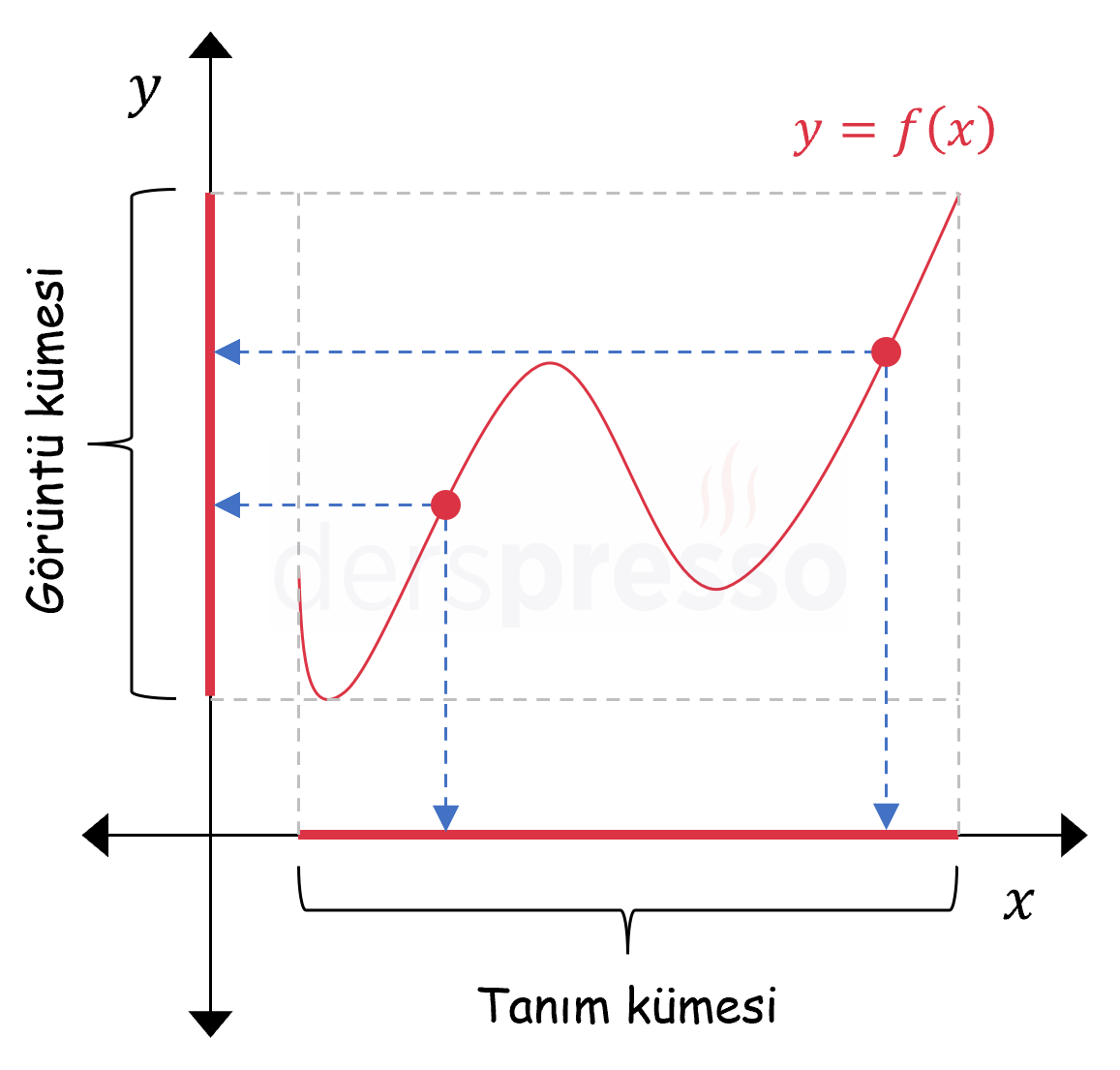
Bir fonksiyonun grafiği, fonksiyonun girdi (\( x \)) ve çıktı (\( y \)) değerleri arasındaki ilişkiyi kolaylıkla anlamamızı sağlar. Fonksiyonun bütününde ya da belirli aralıklarda bu ilişki aşağıdaki şekillerde olabilir:
- \( x \) ve \( y \) değişkenlerinin tanımlı/tanımsız oldukları aralıklar ve değerler
- \( x \) değişkeni artarken \( y \) değişkenindeki değişimin yönü ve hızı
- Grafiğin eksenleri kestikleri noktalar
- \( y \) değişkeninin pozitiflik/negatiflik durumu
- Farklı aralıklarında değişkenler arasında farklı ilişkiler olup olmadığı (parçalı fonksiyon)
- Fonksiyonun simetri özellikleri ve tek/çift olma durumu
- Fonksiyonun örten, içine, birebir fonksiyon olma durumları
- Fonksiyonun sürekli, süreksiz fonksiyon olma durumları
- Fonksiyonun belirli noktalardaki limiti
- Fonksiyonun belirli noktalardaki eğimi
- Fonksiyonun periyodik olma durumu
\( f(x) = cx \) ve \( g(x) = \frac{d}{x} \) fonksiyonlarının grafiklerinin kesişim noktalarından biri \( ( -3, -2 ) \) olduğuna göre, ikinci nokta nedir?
Çözümü GösterFonksiyonlar \( ( -3, -2 ) \) noktasında kesiştiklerine göre, bu noktanın koordinatları iki denklemi de sağlar.
\( y = cx \)
\( -2 = -3c \Longrightarrow c = \dfrac{2}{3} \)
\( y = \dfrac{d}{x}\)
\( -2 = \dfrac{d}{-3} \Longrightarrow d = 6 \)
\( c \) ve \( d \) değerlerini denklemlerde yerlerine yazalım.
\( y = \dfrac{2x}{3} \)
\( y = \dfrac{6}{x} \)
İki denklemi ortak çözerek kesişim noktalarını bulalım.
\( f(x) = g(x) \)
\( \dfrac{2x}{3} = \dfrac{6}{x} \)
\( 2x^2 = 18 \)
\( x \in \{ -3, 3 \} \)
\( x = -3 \) soruda verilen kesişim noktasının apsis değeridir, buna göre ikinci kesişim noktasının apsisi \( x = 3 \) olur.
İkinci kesişim noktasının ordinatını bulmak için denklemlerden birinde \( x = 3 \) koyalım.
\( y = \dfrac{2x}{3} \)
\( = \dfrac{6}{3} = 2 \)
Buna göre ikinci kesişim noktası \( (3, 2) \) noktasıdır.