Dönüşümlerde İşlem Sırası
İki ya da daha fazla dönüşüm bir fonksiyona birlikte uygulandığında oluşan yeni fonksiyonun grafiği bu dönüşümlerin grafiğe ayrı ayrı etkilerinin birleşimini yansıtır. Bu dönüşümler bir fonksiyona herhangi bir sırada uygulanabilecek olsa da bazı noktalara dikkat edilmelidir. Örneğin aşağıdaki fonksiyona iki dikey dönüşüm farklı sıralarda uygulandığında iki farklı fonksiyon elde edilir.
\( f(x) = x^2 \) olmak üzere,
Önce genişleme, sonra öteleme
\( f(x) \longmapsto 2f(x) \longmapsto 2f(x) + 3 \)
\( x^2 \longmapsto 2x^2 \longmapsto 2x^2 + 3 \)
Önce öteleme, sonra genişleme
\( f(x) \longmapsto f(x) + 3 \longmapsto 2(f(x) + 3) \)
\( x^2 \longmapsto x^2 + 3 \longmapsto 2(x^2 + 3) \)
Bu bölümde önce bu noktalara dikkat etmemize gerek kalmadan dönüşümler için bir uygulama sırası önereceğiz, daha sonra bu dönüşümleri herhangi bir sırada uygulayabilmek için dikkat edilmesi gereken noktaları paylaşacağız.
Dönüşümler İçin Önerilen İşlem Sırası
Bir fonksiyona uygulanabilecek dikey ve yatay dönüşümler aşağıdaki şekilde özetlenmiştir.
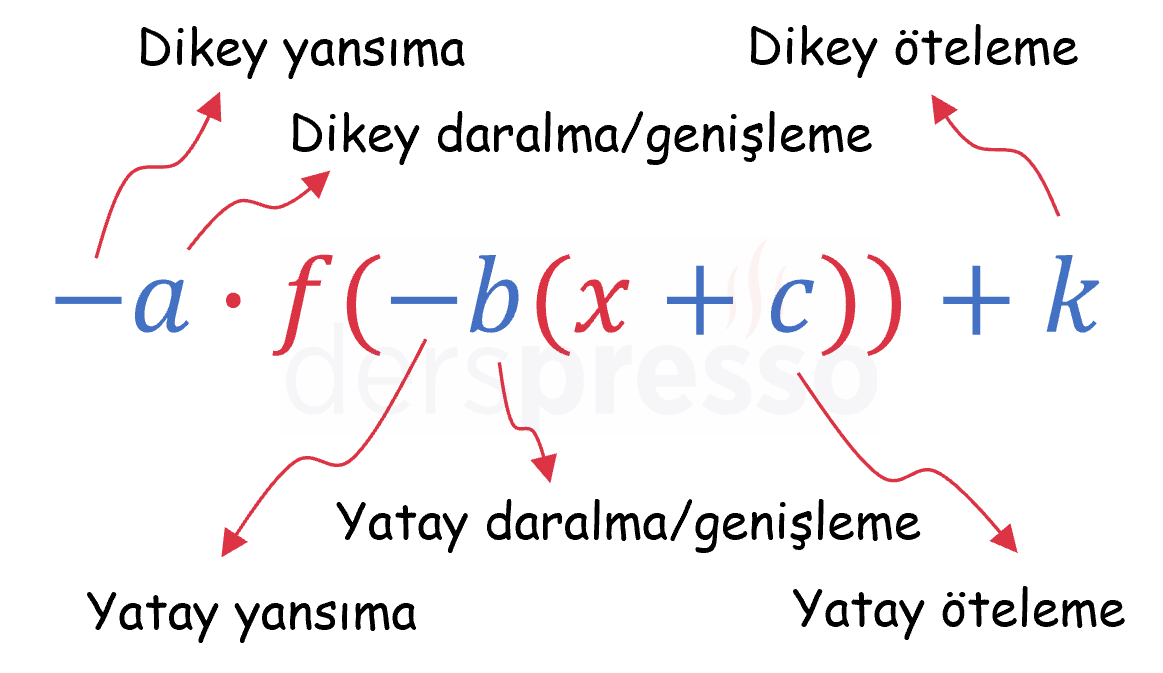
Bir fonksiyona iki ya da daha fazla dönüşümü burada önereceğimiz sırada uygulamak için fonksiyon öncelikle aşağıdaki iki formdan birine getirilmelidir.
Form 1
\( -a \cdot f(-b(x + c)) + k \)
Bu formda önemli nokta \( -b(x + c) \) ifadesinin \( x \)'in katsayısı 1 kalacak şekilde katsayı parantezine alınmış olmasıdır. Bu formdaki bir fonksiyona dönüşümleri aşağıdaki yöntem doğrultusunda uygulayabiliriz.
- Dikey ve yatay dönüşümler birbirinden bağımsızdır, dolayısıyla hangisinin önce uygulandığının bir önemi yoktur.
- Yatay dönüşümlerde önce \( b \) katsayısı ile ilgili dönüşümler (daralma/genişleme ve yansıma), sonra \( c \) ile ilgili dönüşüm (öteleme) uygulanır. Daralma/genişleme ve yansıma dönüşümleri arasındaki uygulama sırası önemli değildir.
- Dikey dönüşümlerde önce \( a \) katsayısı ile ilgili dönüşümler (daralma/genişleme ve yansıma), sonra \( k \) ile ilgili dönüşüm (öteleme) uygulanır. Daralma/genişleme ve yansıma dönüşümleri arasındaki uygulama sırası önemli değildir.
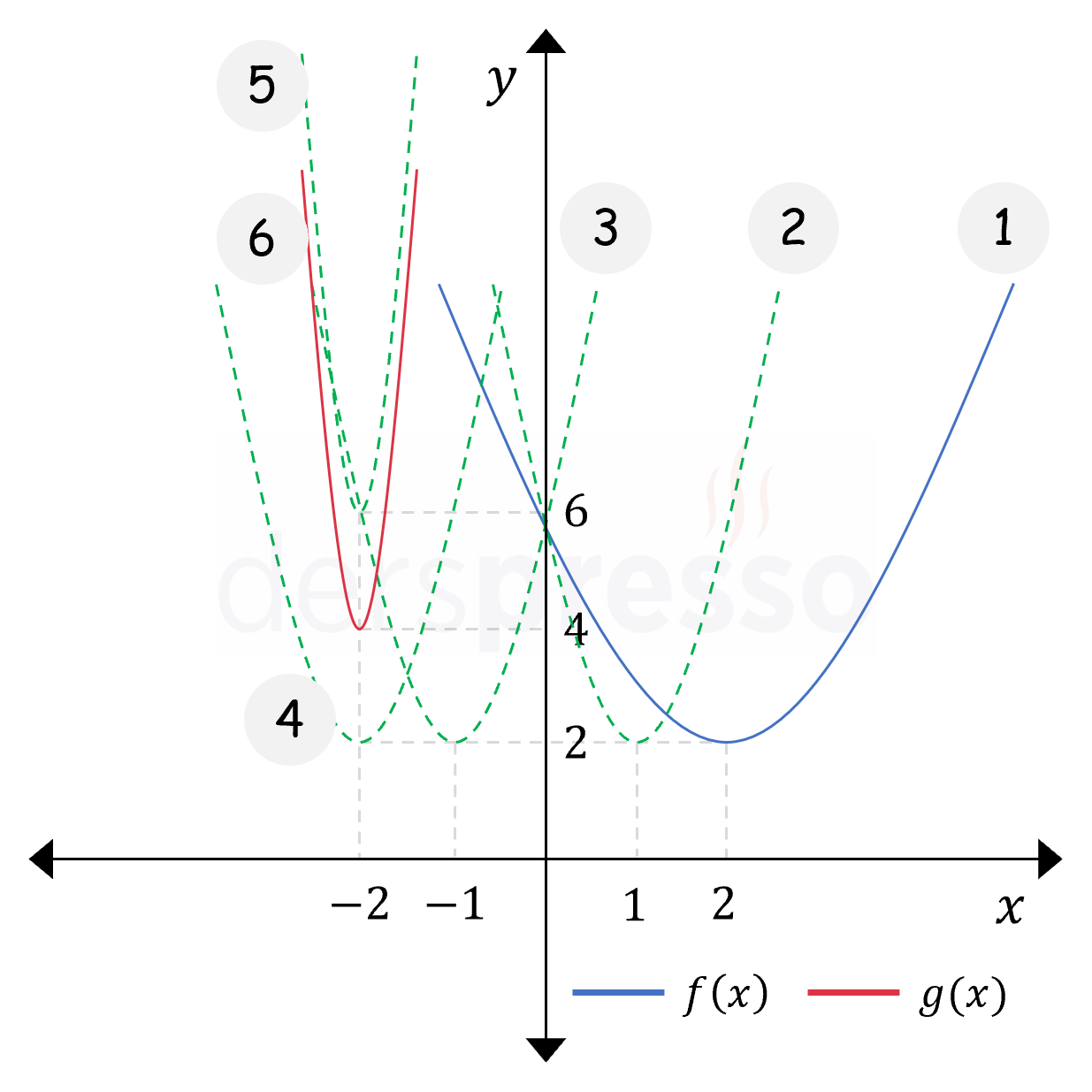
\( g(x) = 3f(-2(x + 1)) - 2 \) olmak üzere,
Tanımı 1. formda verilmiş \( g \) fonksiyonunun grafiğini \( f \) fonksiyonunun grafiğine aşağıdaki dönüşümleri uygulayarak elde edebiliriz.
Yatay dönüşümler:
\( x \) ekseni boyunca \( \frac{1}{2} \) kat daralma
\( y \) eksenine göre yansıma
\( x \) ekseni boyunca \( 1 \) br sola öteleme
Dikey dönüşümler:
\( y \) ekseni boyunca \( 3 \) kat genişleme
\( y \) ekseni boyunca \( 2 \) br aşağı öteleme
Form 2
\( -a \cdot f(-bx + c) + k \)
Bu formda önemli nokta \( -bx + c \) ifadesinde herhangi bir paranteze alma işlemi yapılmamış olmasıdır. Bu formdaki bir fonksiyona dönüşümleri uygularken yukarıda paylaştığımız 2. madde yerine aşağıdaki madde geçerli olacaktır.
- Yatay dönüşümlerde önce \( c \) ile ilgili dönüşüm (öteleme), sonra \( b \) ile ilgili dönüşümler (daralma/genişleme ve yansıma) uygulanır.
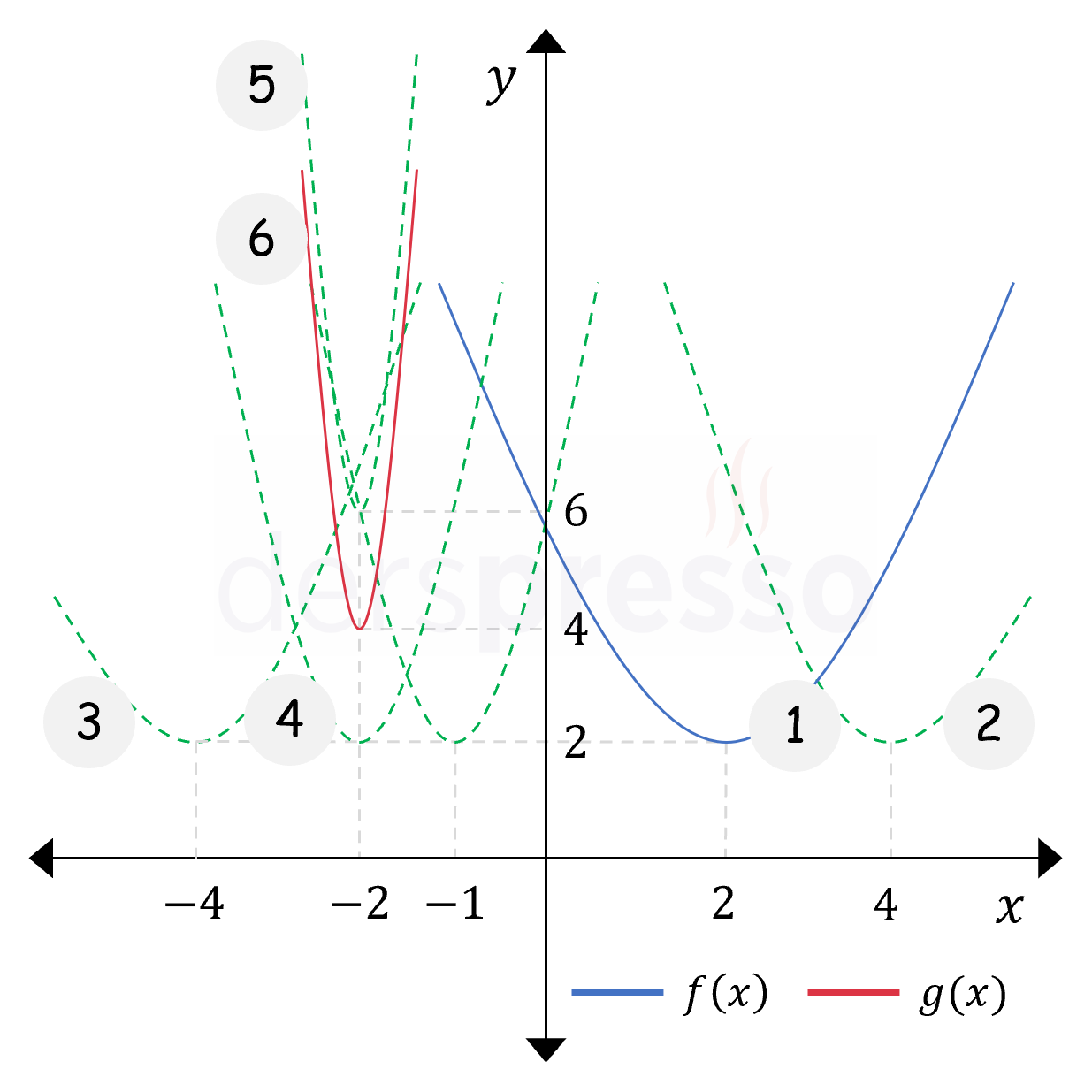
\( g(x) = 3f(-2x - 2) - 2 \) olmak üzere,
Tanımı 2. formda verilmiş \( g \) fonksiyonunun grafiğini \( f \) fonksiyonunun grafiğine aşağıdaki dönüşümleri uygulayarak elde edebiliriz.
Yatay dönüşümler:
\( x \) ekseni boyunca \( 2 \) br sağa öteleme
\( y \) eksenine göre yansıma
\( x \) ekseni boyunca \( \frac{1}{2} \) kat daralma
Dikey dönüşümler:
\( y \) ekseni boyunca \( 3 \) kat genişleme
\( y \) ekseni boyunca \( 2 \) br aşağı öteleme
Dikkat edilirse aynı fonksiyonun iki farklı formda yazılışına dönüşümleri uygularken birinci formda \( x \) ekseni boyunca \( 1 \) br sola öteleme, ikinci formda \( x \) ekseni boyunca \( 2 \) br sağa öteleme yaptık ve sonuçta aynı fonksiyonu ve grafiği elde etmiş olduk.
Genel Uygulama Prensipleri
Dönüşümler bir fonksiyona yukarıda paylaştığımız önerilen sıra dışında herhangi bir sırada da uygulanabilir. Bunun için dikkat edilmesi gereken nokta, dönüşüm uygulanmış fonksiyonu elde etmek için aşağıdaki yerine koyma işlemlerinden her birini adım adım uygulamak ve her adımın fonksiyon grafiğine etkisini ilgili adımla uyumlu şekilde takip etmektir.
| Yerine Koyma | Dönüşüm |
|---|---|
|
\( b \gt 1 \) olmak üzere,
\( x \longmapsto bx \)
|
\( \frac{1}{b} \) kat yatay daralma |
|
\( 0 \lt b \lt 1 \) olmak üzere,
\( x \longmapsto bx \)
|
\( \frac{1}{b} \) kat yatay genişleme |
| \( x \longmapsto -x \) | \( y \) eksenine göre yansıma |
|
\( c \gt 0 \) olmak üzere,
\( x \longmapsto x + c \)
|
\( c \) br sola öteleme |
|
\( c \gt 0 \) olmak üzere,
\( x \longmapsto x - c \)
|
\( c \) br sağa öteleme |
|
\( a \gt 1 \) olmak üzere,
\( f(x) \longmapsto a \cdot f(x) \)
|
\( a \) kat dikey genişleme |
|
\( 0 \lt a \lt 1 \) olmak üzere,
\( f(x) \longmapsto a \cdot f(x) \)
|
\( a \) kat dikey daralma |
| \( f(x) \longmapsto -f(x) \) | \( x \) eksenine göre yansıma |
|
\( k \gt 0 \) olmak üzere,
\( f(x) \longmapsto f(x) + k \)
|
\( k \) br yukarı öteleme |
|
\( k \gt 0 \) olmak üzere,
\( f(x) \longmapsto f(x) - k \)
|
\( k \) br aşağı öteleme |
Verilen bir fonksiyonun dönüşümlerini yorumlarken aşağıda ilk satırdaki \( + 2 \) ifadesini \( x \) ekseni boyunca 2 birim sola öteleme olarak yorumlamamalıyız, bu ifadeyi 2 parantezine aldığımızda aslında bu dönüşümün 1 birim sola ötelemeye karşılık geldiğini görebiliriz. Dolayısıyla bu dönüşümleri adım adım uygularken yöntemimiz cebirsel olarak istenen ifadeyi elde etmek ve uyguladığımız her yerine koyma işleminin karşılık geldiği grafiksel dönüşümü yukarıdaki tablodan not etmek olmalıdır.
\( g(x) = f(2x + 2) \)
\( g(x) = f(2(x + 1)) \)
Örnek 1
Aşağıdaki örnekte iki yatay dönüşümün uygulandığı bir fonksiyona bu dönüşümler farklı sıralarda uygulanmış ve aynı sonucun elde edildiği gösterilmiştir.
| Grafik | Dönüşüm |
|---|---|
|
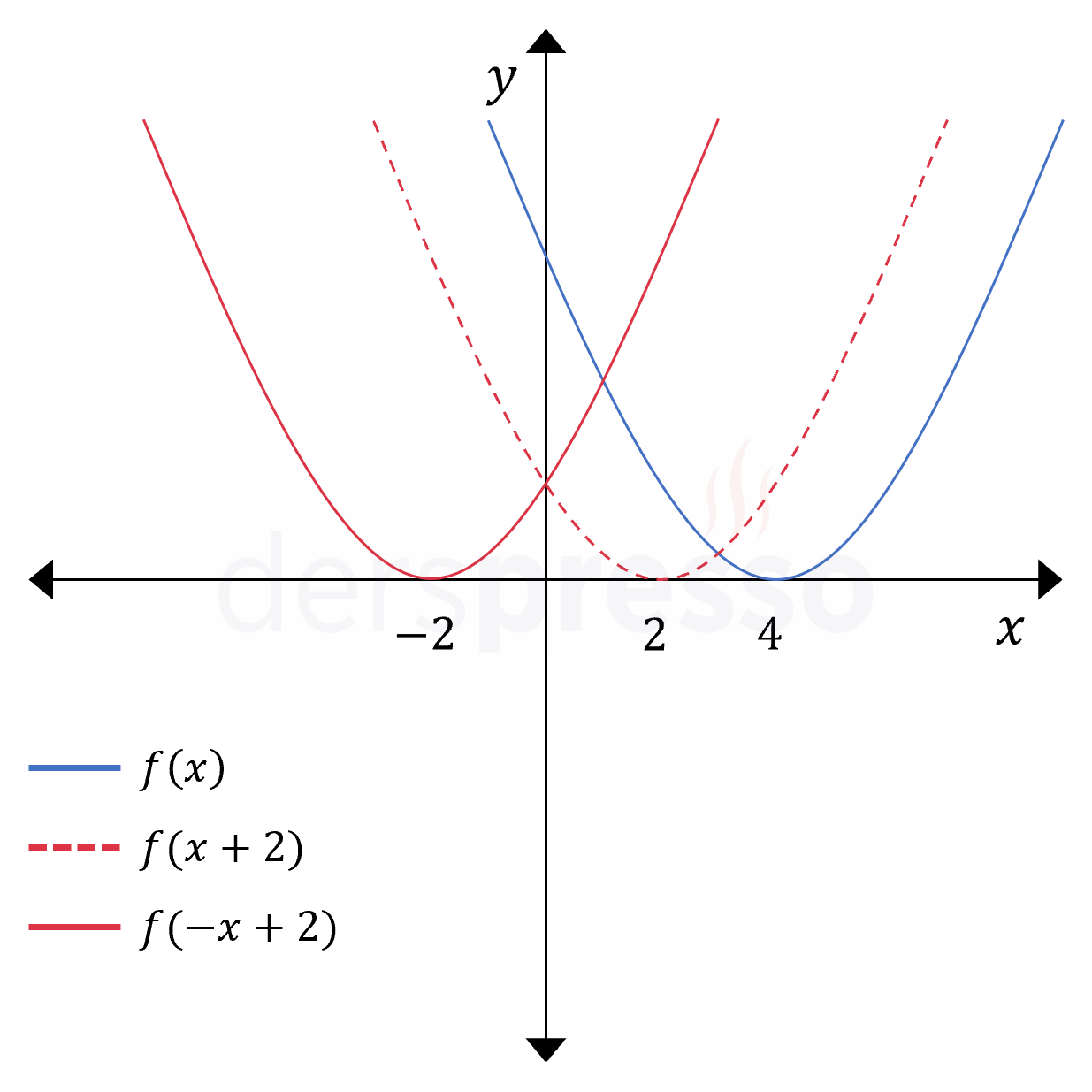
\( f(x) \longmapsto f(-x + 2) \) Solda verilen \( f(x) \) fonksiyonundan \( f(-x + 2) \) fonksiyonunu elde etmek için fonksiyona öteleme ve yansıma dönüşümleri uygulamamız gerekir. Dönüşümleri doğru şekilde uyguladığımız sürece hangi sırada uyguladığımızın bir önemi yoktur. |
|
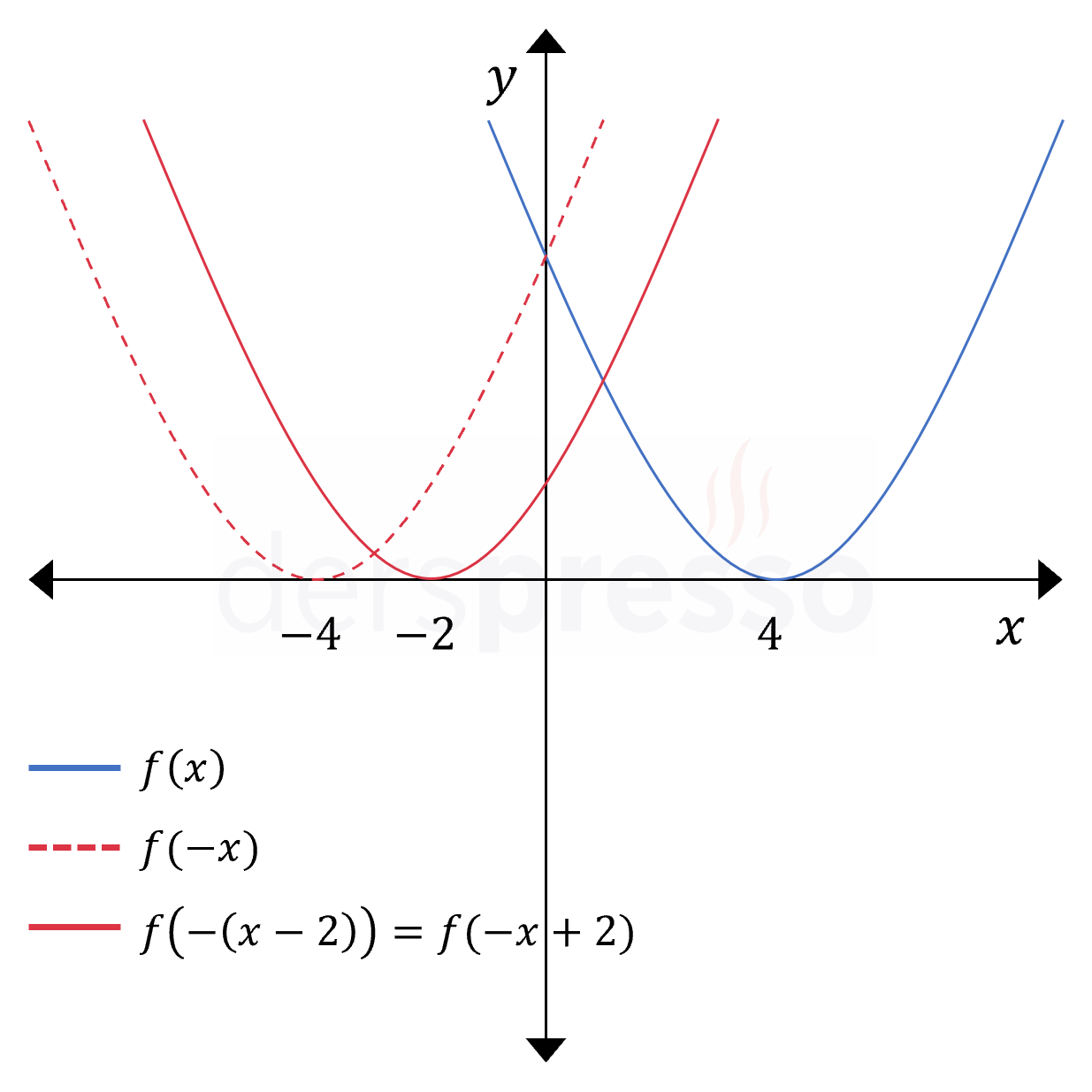
Önce yansıma, sonra öteleme (1) Önce fonksiyonun girdisine \( x \longmapsto -x \) dönüşümü uygulayarak fonksiyonun \( y \) eksenine göre yansımasını alalım. \( f(x) \longmapsto f(-x) \) (2) Sonra fonksiyonun girdisine \( x \longmapsto x - 2 \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca 2 br sağa öteleyelim. Dikkat edilirse, \( x \)'in önündeki negatif işareti dolayısıyla \( f(-x) \longmapsto f(-x + 2) \) dönüşümü için uygulamamız gereken dönüşüm \( x \longmapsto x + 2 \) değil \( x \longmapsto x - 2 \) olmaktadır. \( f(-x) \longmapsto f(-(x - 2)) = f(-x + 2) \) |
|
Önce öteleme, sonra yansıma (1) Önce fonksiyonun girdisine \( x \longmapsto x + 2 \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca 2 br sola öteleyelim. \( f(x) \longmapsto f(x + 2) \) (2) Sonra fonksiyonun girdisine \( x \longmapsto -x \) dönüşümü uygulayarak fonksiyonun \( y \) eksenine göre yansımasını alalım. \( f(x + 2) \longmapsto f(-x + 2) \) |
Örnek 2
Aşağıdaki örnekte üç yatay dönüşümün uygulandığı bir fonksiyona bu dönüşümler farklı sıralarda uygulanmış ve aynı sonucun elde edildiği gösterilmiştir.
| Grafik | Dönüşüm |
|---|---|
|
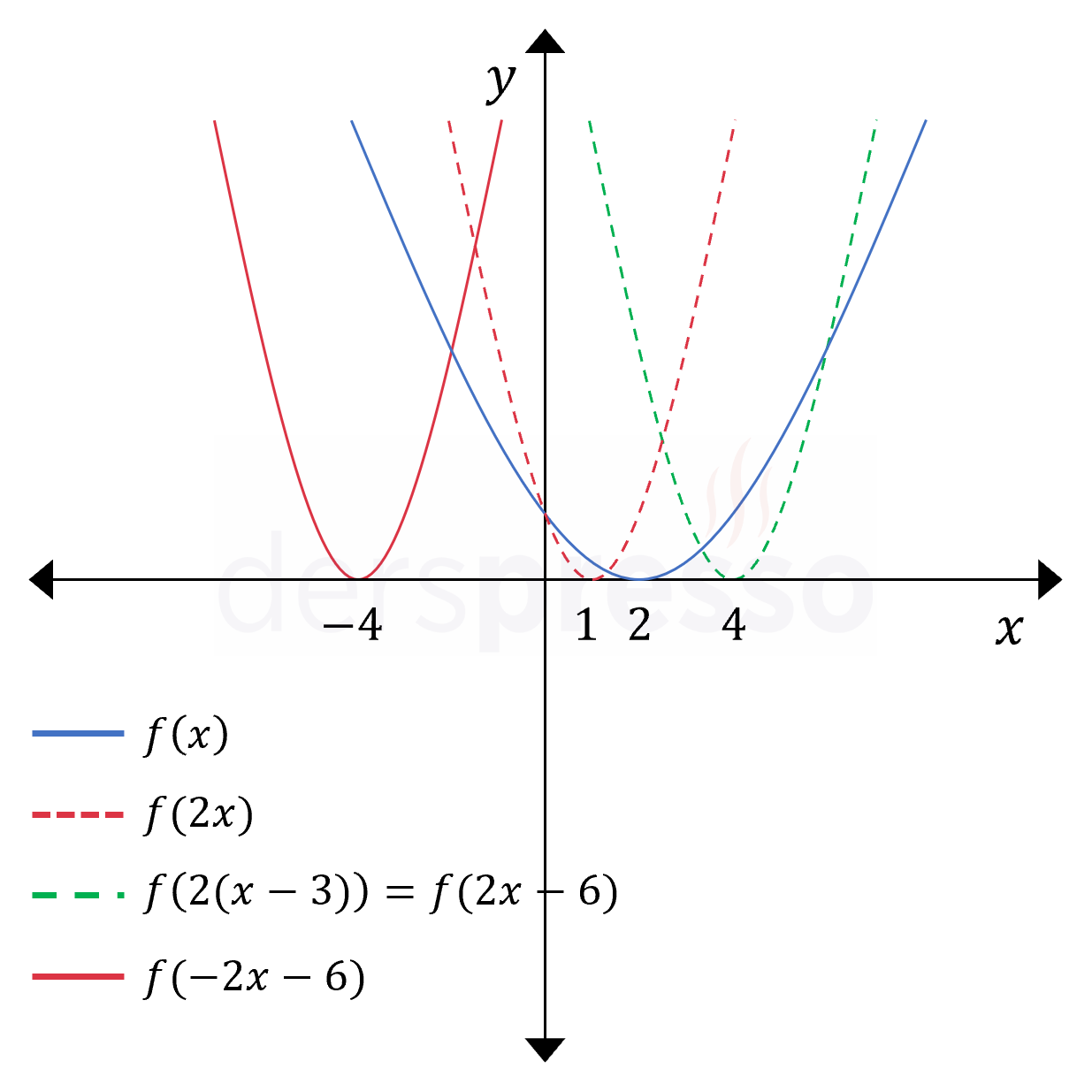
\( f(x) \longmapsto f(-2x - 6) \) Solda verilen \( f(x) \) fonksiyonundan \( f(-2x - 6) \) fonksiyonunu elde etmek için fonksiyona öteleme, daralma ve yansıma dönüşümleri uygulamamız gerekir. Dönüşümleri doğru şekilde uyguladığımız sürece hangi sırada uyguladığımızın bir önemi yoktur. |
|
Önce daralma, sonra öteleme, sonra yansıma (1) Önce fonksiyonun girdisine \( x \longmapsto 2x \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca daraltalım. \( f(x) \longmapsto f(2x) \) (2) Sonra fonksiyonun girdisine \( x \longmapsto x - 3 \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca 3 br sağa öteleyelim. \( f(2x) \longmapsto f(2(x - 3)) = f(2x - 6) \) (3) Sonra fonksiyonun girdisine \( x \longmapsto -x \) dönüşümü uygulayarak fonksiyonun \( y \) eksenine göre yansımasını alalım. \( f(2x - 6) \longmapsto f(-2x - 6) \) |
|
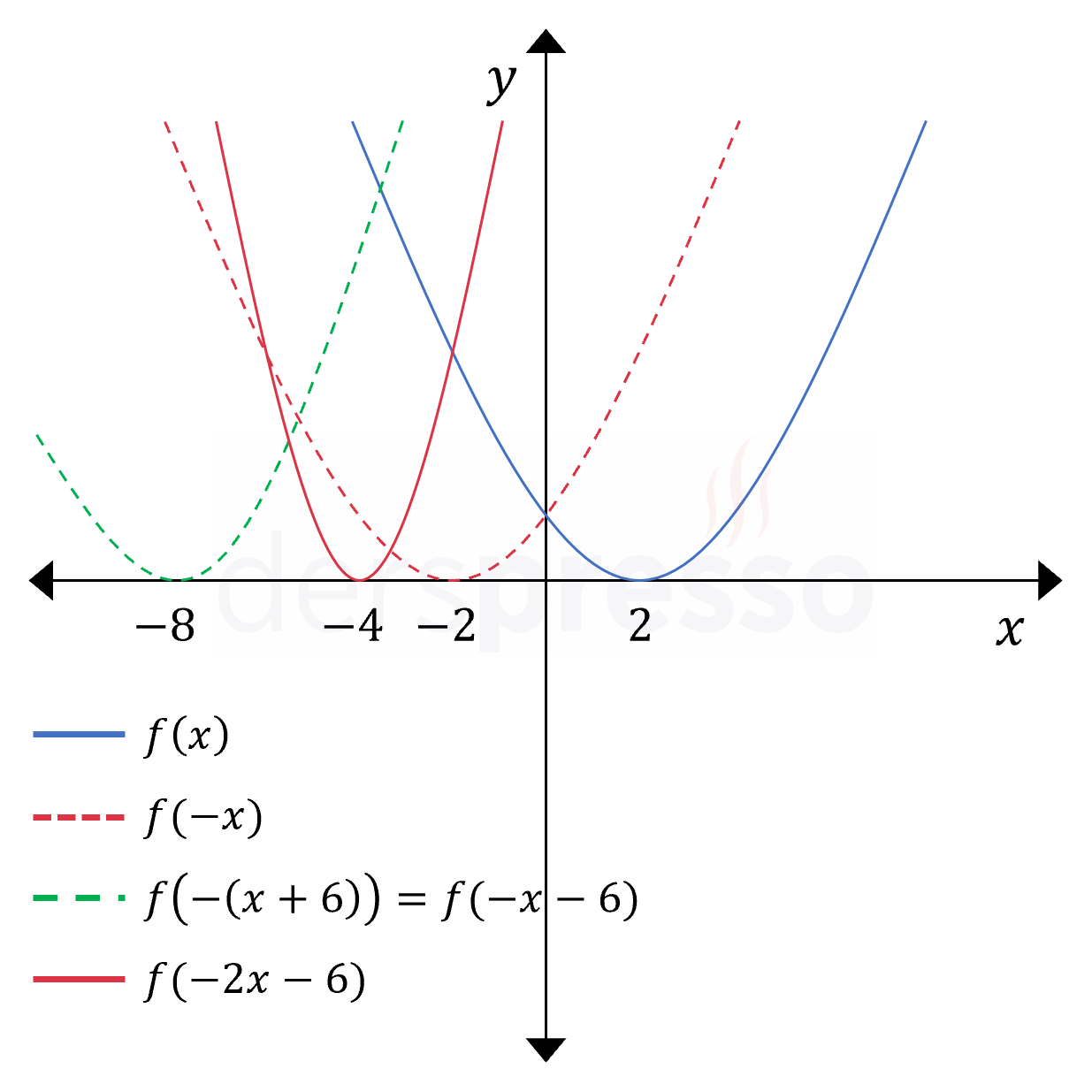
Önce yansıma, sonra öteleme, sonra daralma (1) Önce fonksiyonun girdisine \( x \longmapsto -x \) dönüşümü uygulayarak fonksiyonun \( y \) eksenine göre yansımasını alalım. \( f(x) \longmapsto f(-x) \) (2) Sonra fonksiyonun girdisine \( x \longmapsto x + 6 \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca 6 br sola öteleyelim. \( f(-x) \longmapsto f(-(x + 6)) = f(-x - 6) \) (3) Sonra fonksiyonun girdisine \( x \longmapsto 2x \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca daraltalım. \( f(-x - 6) \longmapsto f(-2x - 6) \) |
|
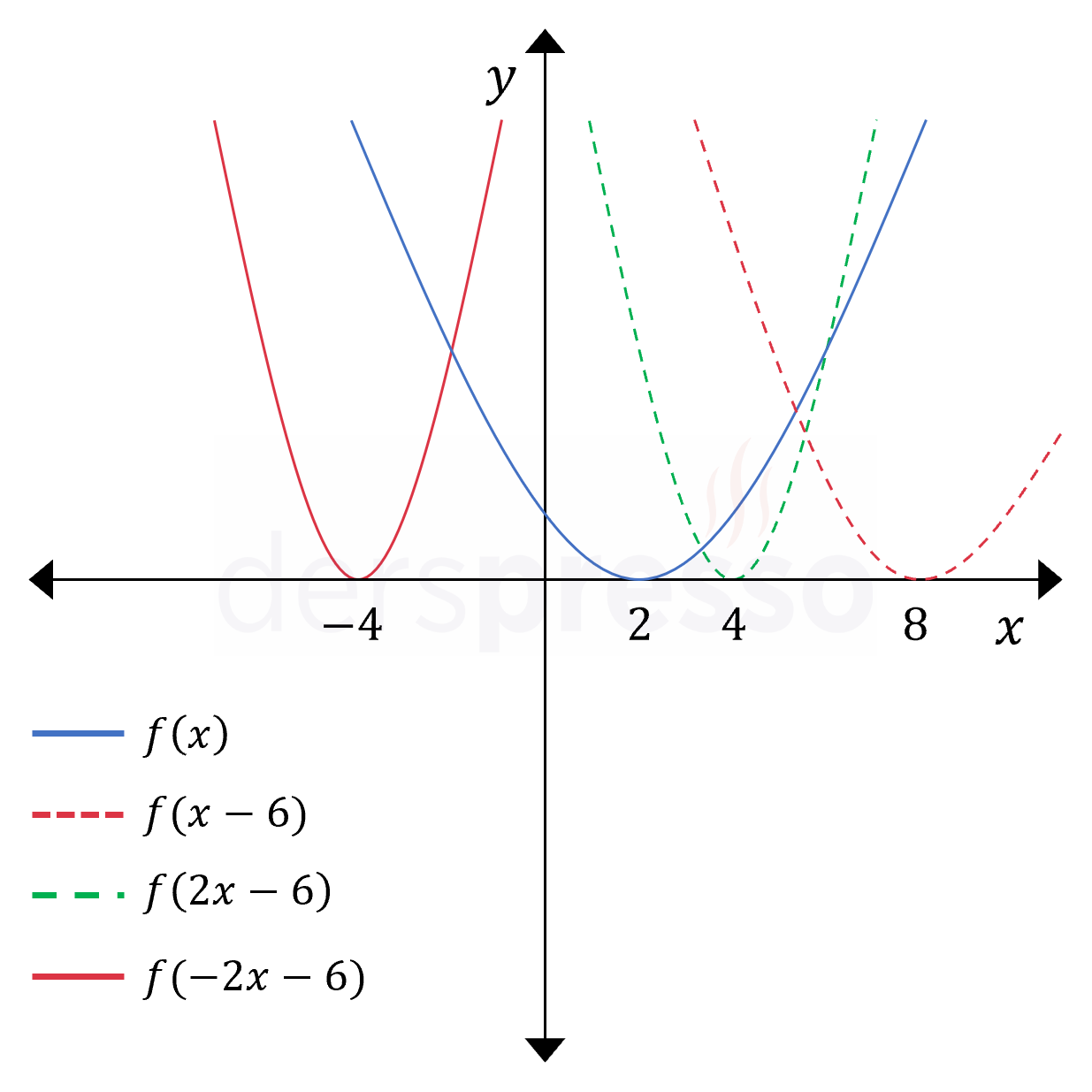
Önce öteleme, sonra daralma, sonra yansıma (1) Önce fonksiyonun girdisine \( x \longmapsto x - 6 \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca 6 br sağa öteleyelim. \( f(x) \longmapsto f(x - 6) \) (2) Sonra fonksiyonun girdisine \( x \longmapsto 2x \) dönüşümü uygulayarak fonksiyonu \( x \) ekseni boyunca daraltalım. \( f(x - 6) \longmapsto f(2x - 6) \) (3) Sonra fonksiyonun girdisine \( x \longmapsto -x \) dönüşümü uygulayarak fonksiyonun \( y \) eksenine göre yansımasını alalım. \( f(2x - 6) \longmapsto f(-2x - 6) \) |
\( A(3,4) \) noktası \( f(x) \) eğrisi üzerinde bir noktadır.
Fonksiyona \( -f(-x) + 4 \) dönüşümü uygulandığında bu noktanın koordinatları ne olur?
Çözümü GösterDönüşümleri sırayla uygulayalım.
(1) \( f(x) \longmapsto f(-x) \)
Yatay yansıma dönüşümü sonucunda noktanın apsisi işaret değiştirir.
\( A(3, 4) \longmapsto A(-3, 4) \)
(2) \( f(-x) \longmapsto -f(-x) \)
Dikey yansıma dönüşümü sonucunda noktanın ordinatı işaret değiştirir.
\( A(-3, 4) \longmapsto A(-3, -4) \)
(3) \( -f(-x) \longmapsto -f(-x) + 4 \)
Dikey öteleme dönüşümü sonucunda noktanın ordinatı 4 birim yukarı ötelenir.
\( A(-3, -4) \longmapsto A(-3, 0) \)
\( f(x) = x^2 \) parabolüne belirli dönüşümler uygulanarak \( g(x) = -3x^2 + 24x - 42 \) parabolü elde ediliyor. Yapılan öteleme işlemlerini ve uygulama sırasını bulunuz.
Çözümü Göster\( g \) parabolünün başkatsayısı -3, tepe noktasının apsisi \( -\frac{24}{2(-3)} = 4 \)'tür.
\( g \) parabolünün tepe noktasının ordinatını bulalım.
\( g(4) = -3(4)^2 + 24(4) - 42 = 6 \)
Buna göre tepe noktası bilinen parabol formülü ile \( g \) parabolünün denklemini aşağıdaki şekilde yazabiliriz.
\( g(x) = -3(x - 4)^2 + 6 \)
\( f \) fonksiyonundan \( g \) fonksiyonunu elde etmek için uygulanması gereken dönüşümleri listeleyelim.
(1) \( f(x) \longmapsto f(x - 4) \)
Yatay öteleme dönüşümü sonucunda grafik 4 birim sağa ötelenir.
(2) \( f(x - 4) \longmapsto 3f(x - 4) \)
Dikey genişleme dönüşümü sonucunda grafik üzerindeki tüm noktalar \( x \) ekseninden 3 kat uzaklaşır.
(3) \( 3f(x - 4) \longmapsto -3f(x - 4) \)
Dikey yansıma dönüşümü sonucunda grafik üzerindeki tüm noktaların \( x \) eksenine göre simetriği alınır.
(4) \( -3f(x - 4) \longmapsto -3f(x - 4) + 6 = g(x) \)
Dikey öteleme dönüşümü sonucunda grafik 6 birim yukarı ötelenir.
3. dereceden bir polinom fonksiyonu olan \( f(x) \) fonksiyonunun büküm noktası \( (1, -3) \) noktasıdır.
Buna göre \( -f(-x + 2) - 3 \) fonksiyonunun büküm noktasının koordinatları nedir?
Çözümü Göster\( -f(-x + 2) - 3 \) fonksiyonunu elde etmek için uygulanması gereken dönüşümleri listeleyelim. Uygulanan her dönüşüm fonksiyon üzerindeki her noktaya aynı şekilde uygulanır.
(1) \( f(x) \longmapsto f(x + 2) \)
Yatay öteleme dönüşümü sonucunda nokta 2 birim sola ötelenir.
\( (1, -3) \longmapsto (-1, -3) \)
(2) \( f(x + 2) \longmapsto f(-x + 2) \)
Yatay yansıma dönüşümü sonucunda tüm noktaların \( y \) eksenine göre simetriği alınır.
\( (-1, -3) \longmapsto (1, -3) \)
(3) \( f(-x + 2) \longmapsto -f(-x + 2) \)
Dikey yansıma dönüşümü sonucunda tüm noktaların \( x \) eksenine göre simetriği alınır.
\( (1, -3) \longmapsto (1, 3) \)
(3) \( -f(-x + 2) \longmapsto -f(-x + 2) - 3 \)
Dikey öteleme dönüşümü sonucunda nokta 3 birim aşağı ötelenir.
\( (1, 3) \longmapsto (1, 0) \)
Buna göre büküm noktasının koordinatları \( (1, 0) \) olur.