Özel Fonksiyonlar
Bazı daha az bilinen fonksiyonlar kimi zaman ismen kimi zaman grafikleriyle karşımıza çıkabilmektedir.
İşaret Fonksiyonu
İşaret fonksiyonu \( x \) sayısı pozitif ise \( +1 \), negatif ise \( -1 \), sıfır ise 0 değeri veren bir parçalı fonksiyondur ve kısaca \( \sgn(x) \) olarak gösterilir. İşaret fonksiyonu bir değişkenin pozitif/negatif olarak işaretini verdiği için bu adı almıştır.
\( \sgn(x) = \begin{cases} 1 & x \gt 0 \\ 0 & x = 0 \\ -1 & x \lt 0 \end{cases} \)
\( \sgn(3) = 1 \)
\( \sgn(0) = 0 \)
\( \sgn(-8) = -1 \)

İşaret fonksiyonu \( x = 0 \) noktasında limitsizdir, süreksizdir ve türevlenebilir değildir.
İşaret fonksiyonuna benzer bir diğer fonksiyon aşağıdaki gibidir. Bu fonksiyonun yukarıdaki fonksiyondan farkı \( x = 0 \) noktasında tanımsız olmasıdır.
\( f: \mathbb{R} - \{ 0 \} \to \mathbb{R} \)
\( f(x) = \dfrac{\abs{x}}{x} = \dfrac{x}{\abs{x}} \)
\( x \lt y \lt 0 \) olmak üzere,
\( \sgn(x + y) + \sgn(x - y) + \sgn(-x) \) ifadesinin sonucu kaçtır?
Çözümü Gösterİşaret fonksiyonu girdi değeri pozitif ise \( 1 \), negatif ise \( -1 \), sıfır ise \( 0 \) değeri verir.
İşlem kolaylığı açısından \( x \) ve \( y \) değişkenlerine \( x \lt y \lt 0 \) koşulunu sağlayacak şekilde aşağıdaki değerleri verebiliriz.
\( x = -2, \quad y = -1 \)
\( \sgn(x + y) = \sgn(-2 + (-1)) \)
\( = \sgn(-3) = -1 \)
\( \sgn(x - y) = \sgn(-2 - (-1)) \)
\( = \sgn(-1) = -1 \)
\( \sgn(-x) = \sgn(-(-2)) \)
\( = \sgn(2) = 1 \)
Bu değerleri verilen ifadede yerine koyalım.
\( \sgn(x + y) + \sgn(x - y) + \sgn(-x) = (-1) + (- 1) + 1 = - 1 \) bulunur.
\( \sgn(x^2 + 3x + 2) = -1 \) denkleminin çözüm kümesini bulunuz.
Çözümü Gösterİşaret fonksiyonu girdi değeri pozitif ise \( 1 \), negatif ise \( -1 \), sıfır ise \( 0 \) değeri verir.
Verilen işaret fonksiyonu \( -1 \)'e eşit olduğuna göre, fonksiyonun içindeki ifade sıfırdan küçüktür.
\( x^2 + 3x + 2 \lt 0 \)
\( (x + 1)(x + 2) \lt 0 \)
Eşitsizliğin sol tarafı \( (-2 , -1) \) aralığında negatif olur.
Çözüm kümesi: \( x \in (-2 , -1) \)
\( f: \mathbb{R} \to \{-1, 0, 1\} \)
\( f(x) = \sgn(x^2 + 4x + 7) \) fonksiyonunun görüntü kümesi nedir?
Çözümü Gösterİşaret fonksiyonu girdi değeri pozitif ise \( 1 \), negatif ise \( -1 \), sıfır ise \( 0 \) değeri verir.
Soruda verilen ifadeyi inceleyelim.
\( x^2 + 4x + 7 = (x + 2)^2 + 3 \)
Bir ifadenin karesi ile pozitif bir reel sayının toplamı daima pozitif olacağı için verilen işaret fonksiyonu her zaman 1 değeri alır.
Görüntü kümesi: \( f(x) \in \{ 1 \} \)
\( a, b, c, d \in \mathbb{R} - \{0\} \) olmak üzere,
\( a + b + c + d = 0 \) eşitliği veriliyor.
\( \sgn(x) \) işaret fonksiyonu olmak üzere, \( \sgn(a) + \sgn(b) + \sgn(c) + \sgn(d) + \sgn(abcd) \) ifadesinin alabileceği farklı değerler toplamı kaçtır?
Çözümü Gösterİşaret fonksiyonu girdi değeri pozitif ise \( 1 \), negatif ise \( -1 \), sıfır ise \( 0 \) değeri verir.
\( a + b + c + d = 0 \) eşitliği 3 durumda sağlanır.
Durum 1: 3 sayı pozitif, 1 sayı negatif
Hangi sayıları pozitif hangilerini negatif seçtiğimiz sonucu değiştirmeyecektir.
3 pozitif 1 negatif sayının çarpımı negatiftir.
\( \sgn(a) + \sgn(b) + \sgn(c) + \sgn(d) + \sgn(abcd) \)
\( = -1 + 1 + 1 + 1 + (-1) = 1 \)
Durum 2: 2 sayı pozitif, 2 sayı negatif
2 pozitif 2 negatif sayının çarpımı pozitiftir.
\( \sgn(a) + \sgn(b) + \sgn(c) + \sgn(d) + \sgn(abcd) \)
\( = -1 + (-1) + 1 + 1 + 1 = 1 \)
Durum 3: 1 sayı pozitif, 3 sayı negatif
1 pozitif 3 negatif sayının çarpımı negatiftir.
\( \sgn(a) + \sgn(b) + \sgn(c) + \sgn(d) + \sgn(abcd) \)
\( = -1 + (-1) + (-1) + 1 + (-1) = -3 \)
İfadenin alabileceği farklı değerlerin toplamı \( 1 + (-3) = -2 \) olarak bulunur.
Taban Fonksiyonu
Taban fonksiyonu girdi olarak aldığı \( x \) değerinden küçük ya da \( x \)'e eşit en büyük tam sayıyı verir. Taban işlemi \( \floor{x} \) şeklinde gösterilir. Bu fonksiyonun bir diğer adı tam değer fonksiyonudur.
\( f: \mathbb{R} \to \mathbb{Z} \)
\( f(x) = \floor{x} \)
\( f(3,2) = f(3) = 3 \)
\( f(-1,5) = f(-2) = -2 \)
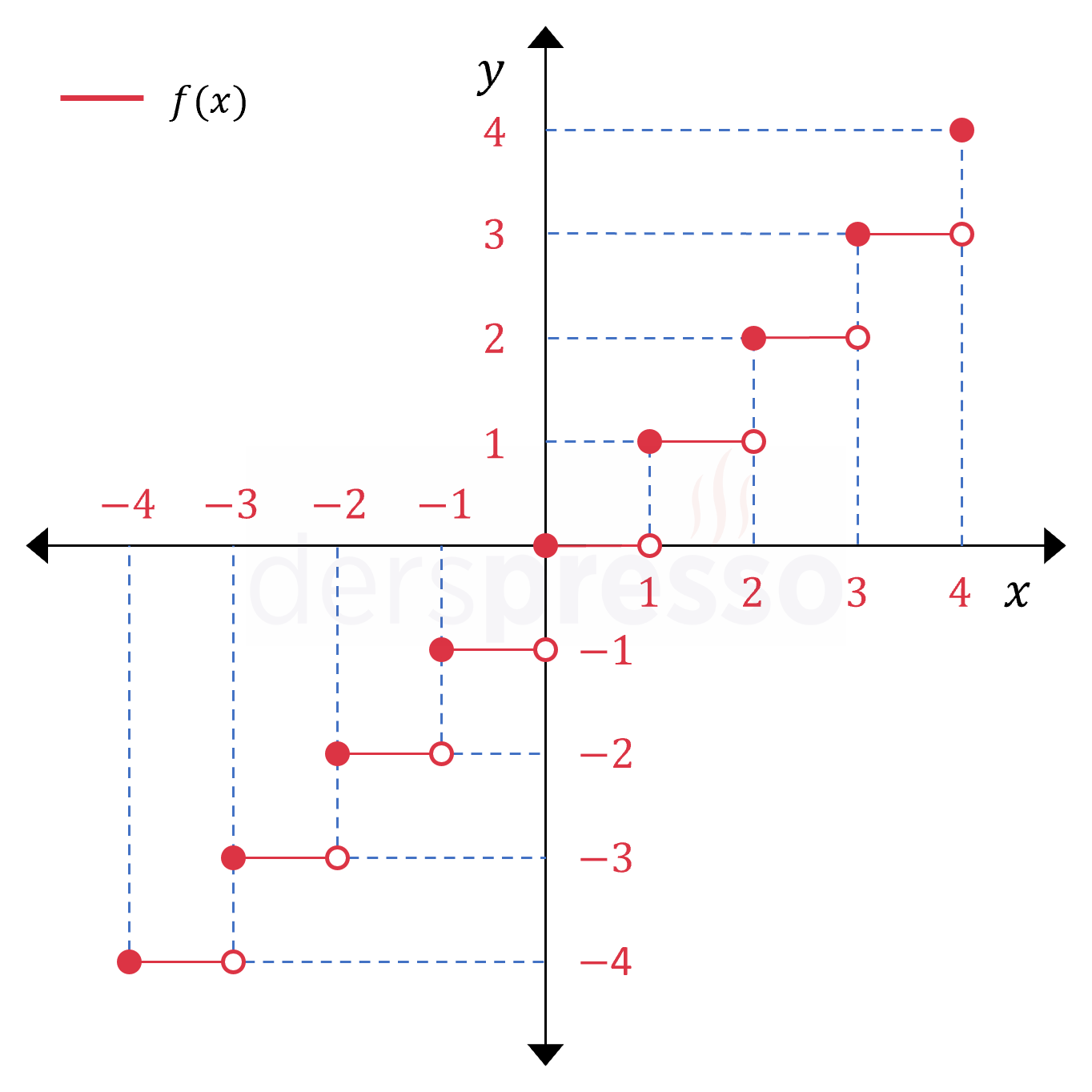
Taban fonksiyonu tam sayı \( x \) değerleri için limitsizdir, süreksizdir ve türevlenebilir değildir.
Tavan Fonksiyonu
Tavan fonksiyonu girdi olarak aldığı \( x \) değerinden büyük ya da \( x \)'e eşit en küçük tam sayıyı verir. Tavan işlemi \( \ceiling{x} \) şeklinde gösterilir.
\( f: \mathbb{R} \to \mathbb{Z} \)
\( f(x) = \ceiling{x} \)
\( f(3,2) = f(4) = 4 \)
\( f(-1,5) = f(-1) = -1 \)
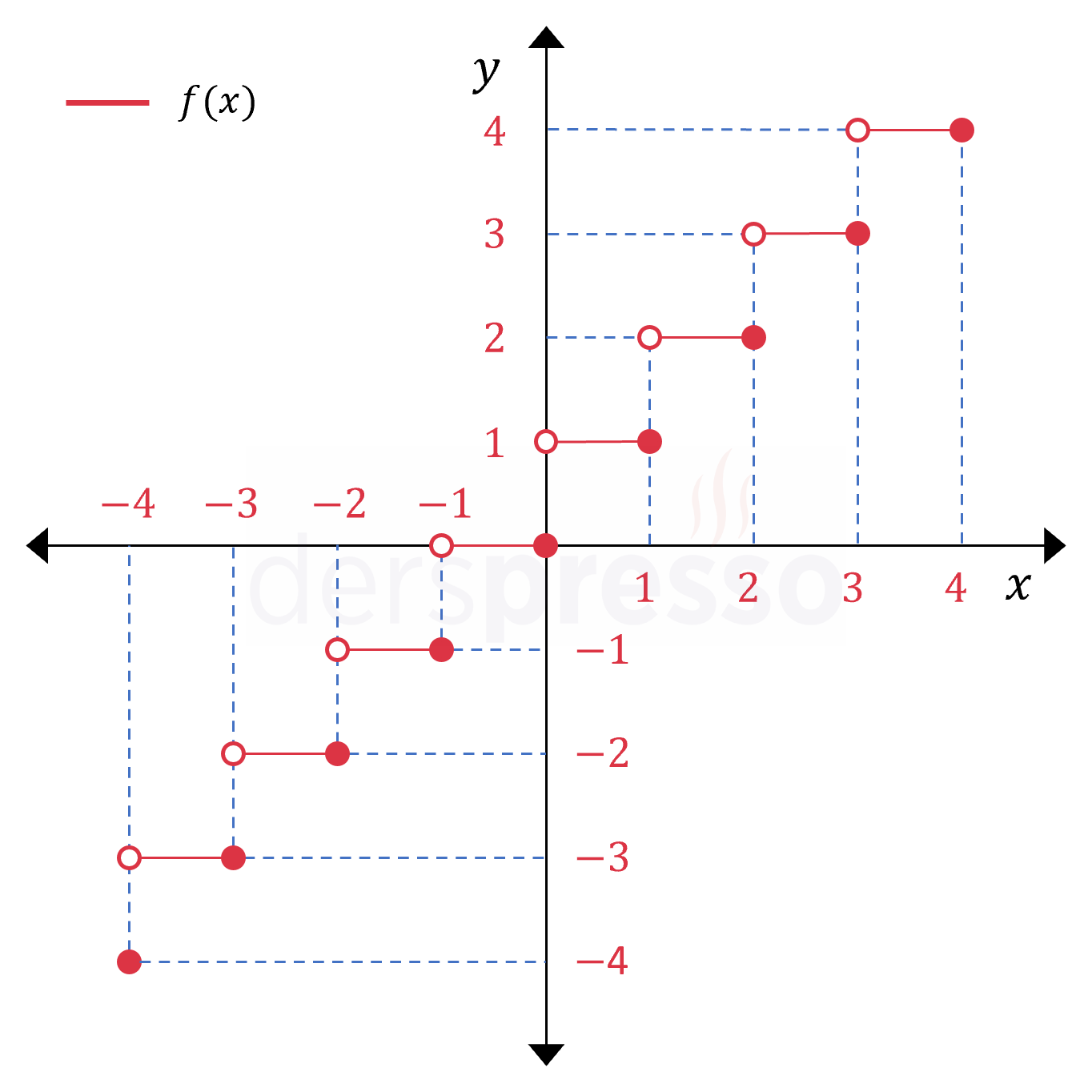
Tavan fonksiyonu tam sayı \( x \) değerleri için limitsizdir, süreksizdir ve türevlenebilir değildir.
\( \ceiling{x} \) tavan fonksiyonu olmak üzere,
\( \displaystyle\sum_{n = 1}^{N} {\ceiling{\dfrac{2}{3} + \dfrac{n}{45}}} = 111 \) ise \( N \) kaçtır?
Çözümü GösterVerilen ifadeyi düzenleyelim.
\( \displaystyle\sum_{n = 1}^{N} {\ceiling{\dfrac{2}{3} + \dfrac{n}{45}}} = \displaystyle\sum_{n = 1}^{N}{\ceiling{\dfrac{30 + n}{45}}} \)
\( n = 1 \) için:
\( \ceiling{\dfrac{30 + 1}{45}} = 1 \)
\( n = 2 \) için:
\( \ceiling{\dfrac{30 + 2}{45}} = 1 \)
\( n = 15 \) için:
\( \ceiling{\dfrac{30 + 15}{45}} = 1 \)
Buna göre \( n = 1 \) ve \( n = 15 \) arasında fonksiyon 1 değerini alır.
\( n \)'nin 1 - 15 arası değerleri için toplam \( 1 \cdot 15 = 15 \) olur.
\( n = 16 \) için:
\( \ceiling{\dfrac{30 + 16}{45}} = 2 \)
\( n = 60 \) için:
\( \ceiling{\dfrac{30 + 60}{45}} = 2 \)
Buna göre \( n = 16 \) ve \( n = 60 \) arasında fonksiyon 2 değerini alır.
\( n \)'nin 16 - 60 arası değerleri için toplam \( 2 \cdot 45 = 90 \) olur.
\( n \)'nin 1 - 60 arası değerleri için toplam \( 15 + 90 = 105 \) olur.
Bulunan değer istenen toplam değerinden \( 111 - 105 = 6 \) eksiktir.
\( n = 61 \) için:
\( \ceiling{\dfrac{30 + 61}{45}} = 3 \)
\( n = 62 \) için:
\( \ceiling{\dfrac{30 + 62}{45}} = 3 \)
Buna göre \( N = 62 \) olarak bulunur.
Ondalık Kısım Fonksiyonu
Ondalık kısım fonksiyonu girdi olarak aldığı \( x \) değeri ile bu değerin taban fonksiyon değeri arasındaki farkı verir. Ondalık kısım fonksiyonu \( \{x\} \) şeklinde gösterilir.
\( f: \mathbb{R} \to [0, 1) \)
\( f(x) = \{x\} = x - \floor{x} \)
\( \{3,2\} = 3,2 - 3 = 0,2 \)
\( \{2\} = 2 - 2 = 0 \)
\( \{-1,75\} = -1,75 - (-2) = 0,25 \)
\( \{\pi\} = \pi - 3 = 0,1415... \)
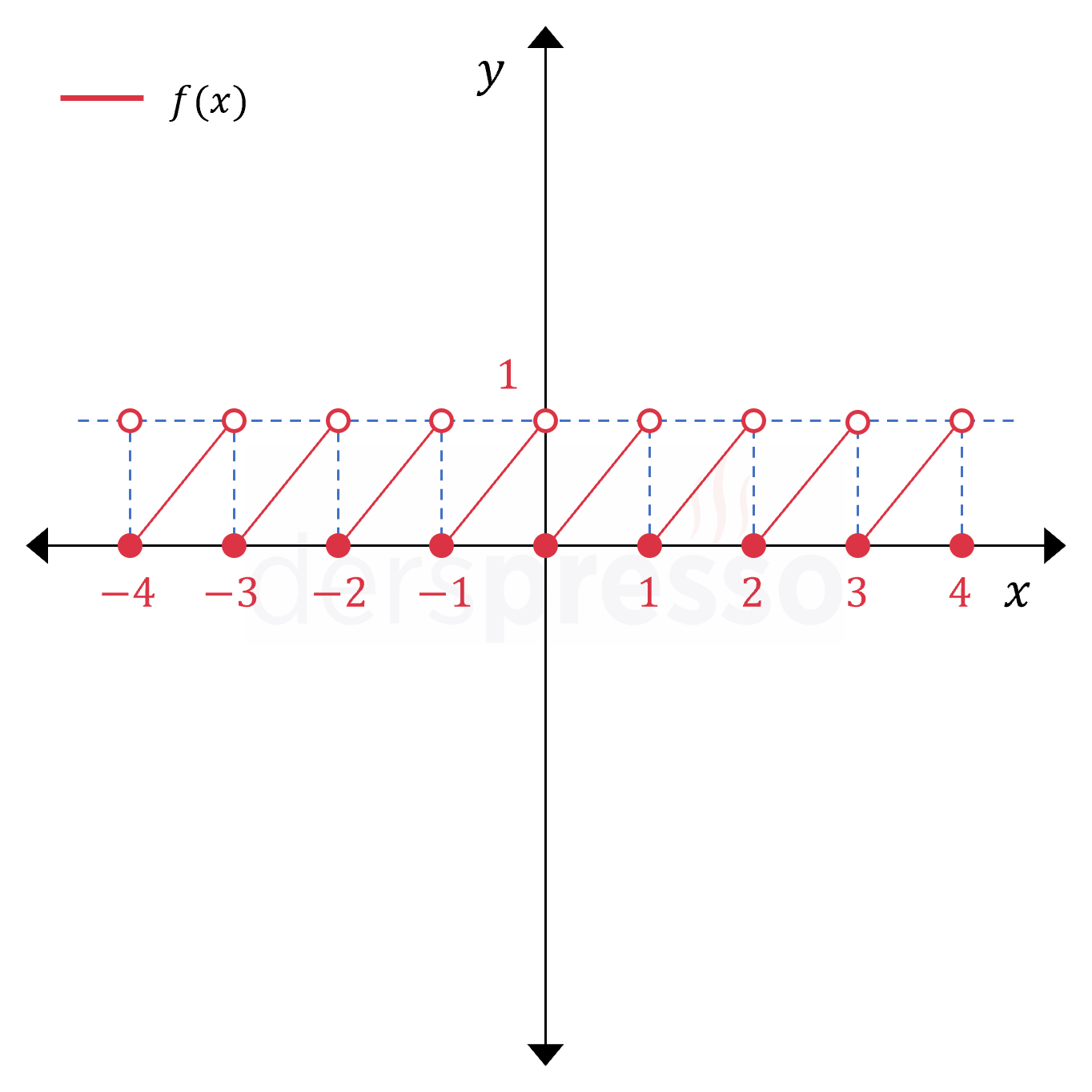
Ondalık kısım fonksiyonu tam sayı \( x \) değerleri için limitsizdir, süreksizdir ve türevlenebilir değildir.