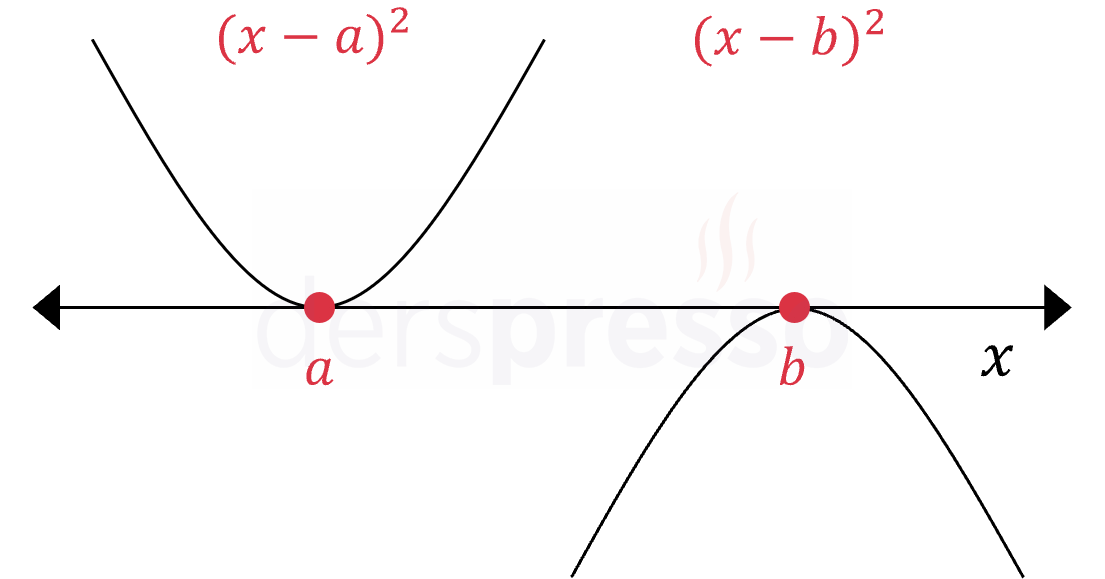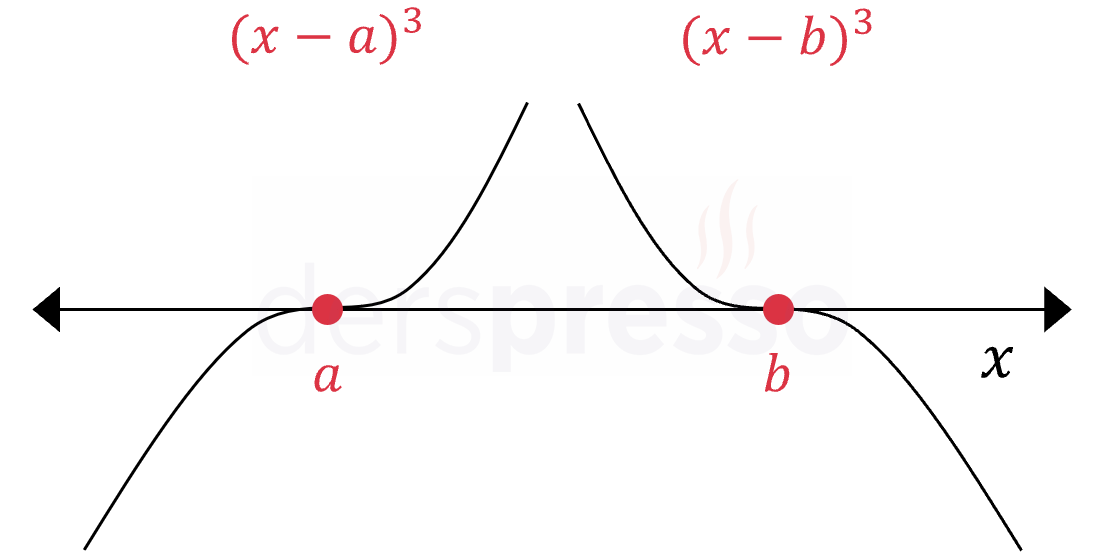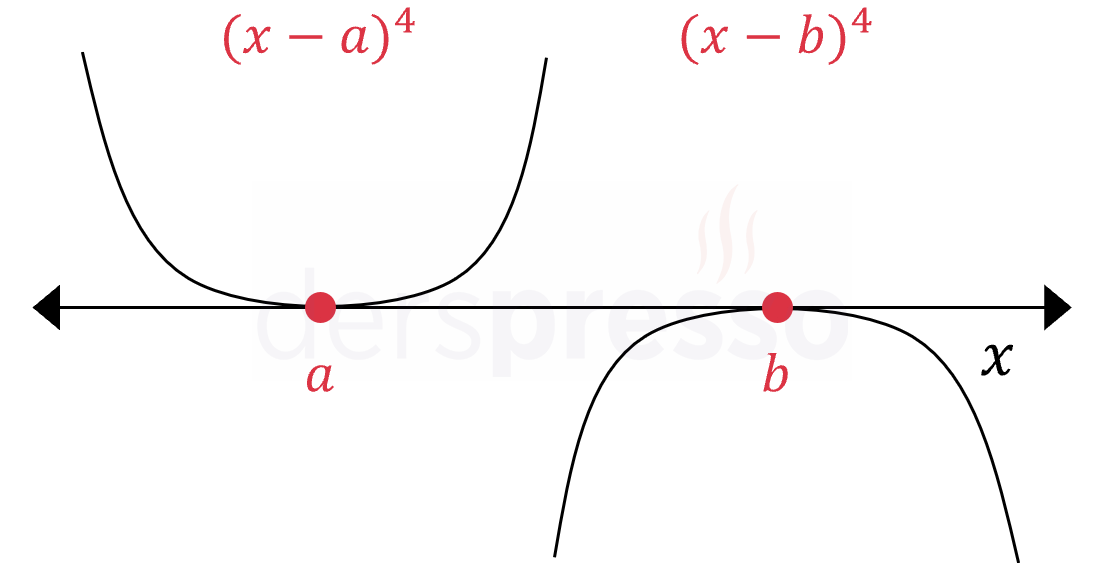Polinomlarda Katlı Kökler
Bir polinom fonksiyonu birinci dereceden kaç çarpana ayrılabiliyorsa denklemin o sayıda reel kökü vardır ve grafiği \( x \) eksenini o kadar noktada keser.
Buna göre, aşağıdaki gibi çarpanlarına ayrılabilen bir fonksiyonun üç reel kökü vardır ve \( x \) eksenini bu üç noktada keser.
\( f(x) = x^3 - 4x^2 -7x + 10 \)
\( f(x) = (x + 2)(x - 1)(x - 5) \)
Grafik \( x \) eksenini \( A(-2, 0) \), \( B(1, 0) \) ve \( C(5, 0) \) noktalarında keser.
Çarpanlarına ayrılmış bir polinom denkleminde bazı kökler birden fazla kez yer alabilir. Eğer bir kök çarpan listesinde \( n \) kez yer alıyorsa, bu \( n \) sayısı bu çarpanın kuvveti olarak yazılır ve bu kök değerine \( n \) katlı kök denir. \( n \)'nin çift sayı olduğu köklere çift katlı kök, tek sayı olduğu köklere tek katlı kök denir.
\( (x + 2)^3 (x - 1)^2 (x - 5) = 0 \) olmak üzere,
\( x = -2 \) denklemin 3 katlı bir köküdür.
\( x = 1 \) denklemin 2 katlı bir köküdür.
\( x = 5 \) denklemin tek katlı bir köküdür.
Bir kökün \( n \) katlı olması o kökün çözüm kümesinde \( n \) kez bulunması anlamına gelir.
Katlı Köklerin x Eksenini Kestiği Noktada Davranışı
Bir kökün kaç katlı olduğu grafiğin \( x \) eksenini kestiği o noktadaki davranışını belirler.
Tek katlı köklerde (n = 1, 3, 5, ...) grafik \( x \) eksenini keser ve eksenin öteki tarafına geçer.
Çift katlı köklerde (n = 2, 4, 6, ...) grafik \( x \) eksenini teğet keser ve eksenin öteki tarafına geçmeden geri döner.
Kökün katının derecesi arttıkça grafik \( x \) eksenini kestiği noktada artan düzeyde düzleşir/basıklaşır.
Aşağıda farklı derecede katlı kökler için fonksiyon grafiğinin \( x \) eksenini kestiği noktadaki davranışı gösterilmiştir.