Kuvvet Fonksiyonlarının Grafikleri
Kuvvet fonksiyonlarının grafiklerini fonksiyonun derecesinin tek ya da çift olmasına göre iki grup altında inceleyebiliriz. Önceki bölümde gördüğümüz gibi bu iki farklı grup için fonksiyonun tanım kümeleri aynı, görüntü kümeleri birbirinden farklıdır.
Çift Dereceli Kuvvet Fonksiyonları
Bu fonksiyonların derecesi çift sayıdır.
\( n \in \mathbb{Z^+}, \quad k \in \mathbb{R}, \quad k \ne 0 \) olmak üzere,
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = k \cdot x^{2n} \)
Aşağıda \( k \gt 0 \) olduğu durum için çift dereceli üç kuvvet fonksiyonunun grafiği verilmiştir. \( k \lt 0 \) olduğu durumda grafiklerin \( x \) eksenine göre yansıması oluşur.
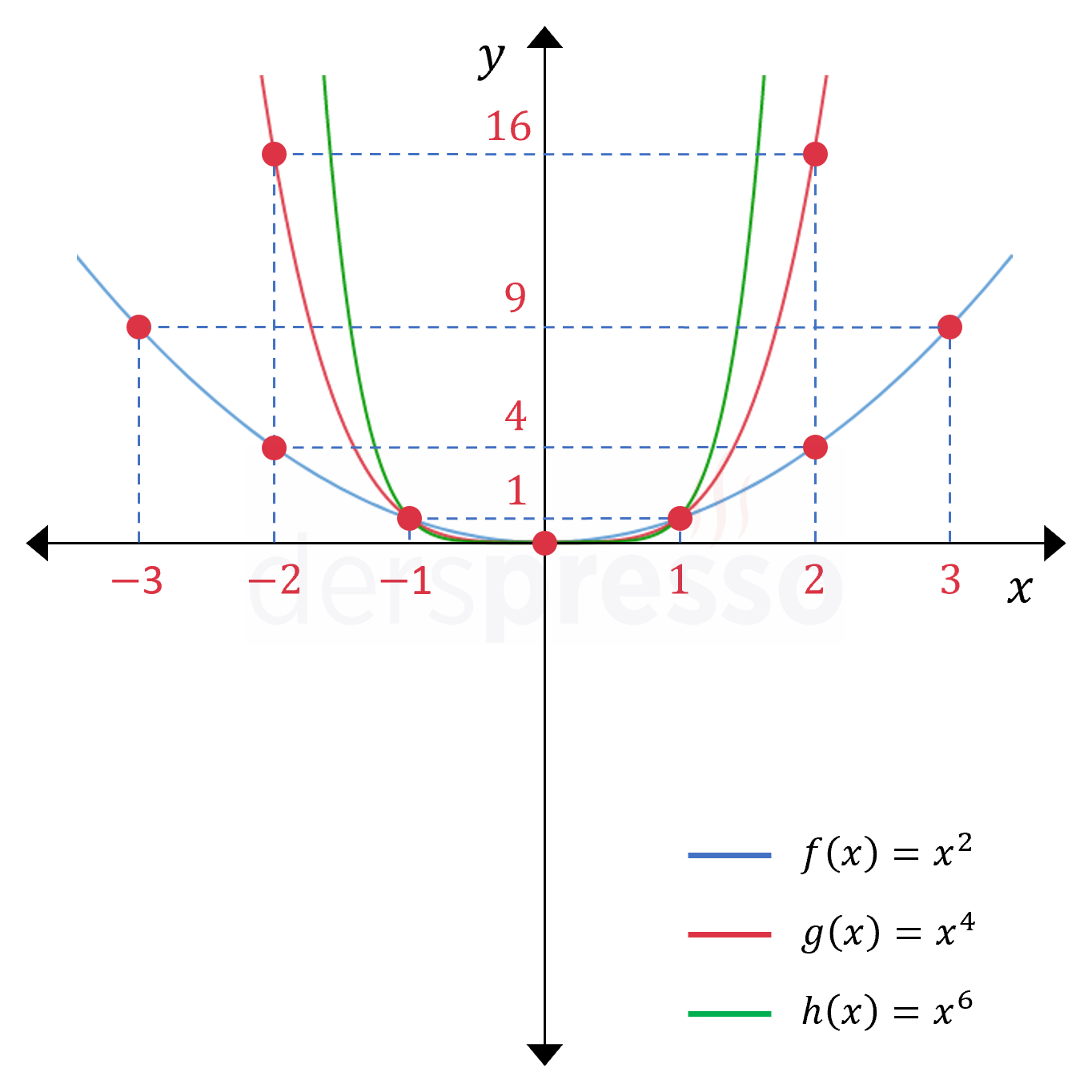
Çift dereceli kuvvet fonksiyonlarının grafikleri ile ilgili şu yorumları yapabiliriz.
- Çift dereceli kuvvet fonksiyonları, parabole benzer grafiği olan fonksiyonlardır.
- Fonksiyonların tanım kümesi tüm reel sayılar, görüntü kümesi \( [0, \infty) \)'dir.
- \( x = 0 \)'ın her dereceden üssü \( 0 \) olduğu için, grafik her zaman orijinden geçer.
- \( x = 1 \)'in her dereceden üssü \( 1 \) olduğu için, grafik her zaman \( (1, 1) \) noktasından geçer.
- \( x = -1 \)'in her çift sayı dereceden üssü \( 1 \) olduğu için, grafik her zaman \( (-1, 1) \) noktasından geçer.
- Fonksiyon \( (-\infty, 0) \) aralığında azalan, \( (0, \infty) \) aralığında artandır.
- \( 0 \lt \abs{x} \lt 1 \) arasında üs büyüdükçe fonksiyon değeri küçülür, dolayısıyla fonksiyon grafiği \( x \) eksenine yaklaşır.
- \( 1 \lt \abs{x} \) olduğunda üs büyüdükçe fonksiyon değeri de büyür, dolayısıyla fonksiyon grafiği \( x \) ekseninden uzaklaşır.
- Çift dereceli kuvvet fonksiyonları çift fonksiyonlardır ve \( y \) eksenine göre simetriktirler.
Tek Dereceli Kuvvet Fonksiyonları
Bu fonksiyonların derecesi tek sayıdır.
\( n \in \mathbb{Z^+}, \quad k \in \mathbb{R}, \quad k \ne 0 \) olmak üzere,
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = k \cdot x^{2n + 1} \)
Aşağıda \( k \gt 0 \) olduğu durum için tek dereceli üç kuvvet fonksiyonunun grafiği verilmiştir. \( k \lt 0 \) olduğu durumda grafiklerin \( x \) eksenine göre yansıması oluşur.
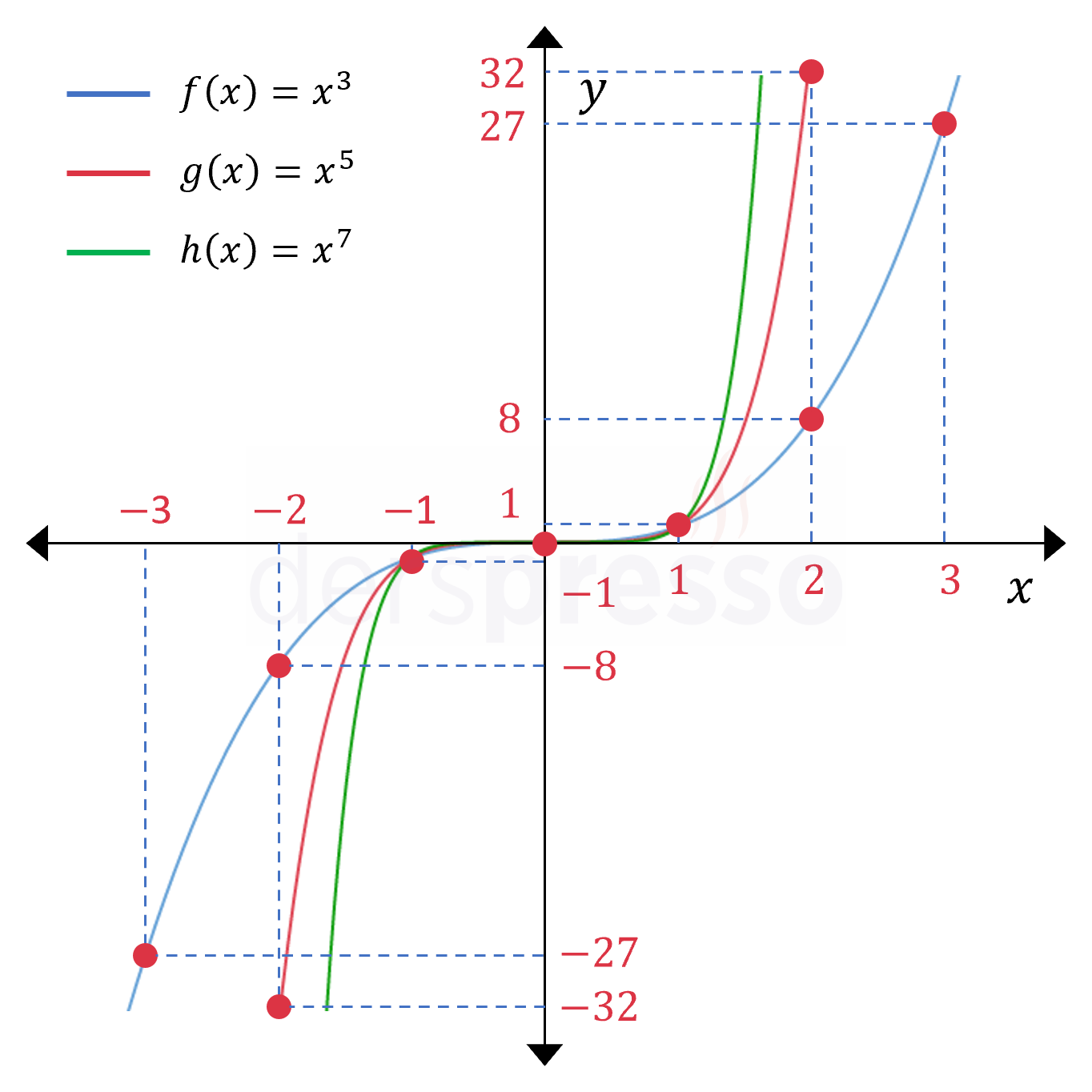
Tek dereceli kuvvet fonksiyonlarının grafikleri ile ilgili şu yorumları yapabiliriz.
- Fonksiyonun tanım ve görüntü kümeleri tüm reel sayılardır.
- \( x = 0 \)'ın her dereceden üssü \( 0 \) olduğu için, grafik her zaman orijinden geçer.
- \( x = 1 \)'in her dereceden üssü \( 1 \) olduğu için, grafik her zaman \( (1, 1) \) noktasından geçer.
- \( x = -1 \)'in her tek sayı dereceden üssü \( -1 \) olduğu için, grafik her zaman \( (-1, -1) \) noktasından geçer.
- Fonksiyon tüm tanım aralığında artandır.
- \( 0 \lt \abs{x} \lt 1 \) arasında üs büyüdükçe fonksiyon değeri küçülür, dolayısıyla fonksiyon grafiği \( x \) eksenine yaklaşır.
- \( 1 \lt \abs{x} \) olduğunda üs büyüdükçe fonksiyon değeri de büyür, dolayısıyla fonksiyon grafiği \( x \) ekseninden uzaklaşır.
- Tek dereceli kuvvet fonksiyonları tek fonksiyonlardır ve orijine göre simetriktirler.