Köklü Fonksiyonlar
Bir değişkenin köklü ifade içinde yer aldığı fonksiyonlara köklü fonksiyon denir.
Kök içindeki \( x \) ifadesi fonksiyonun değişkeni, \( n \) köklü ifadenin derecesidir.
\( n \in \mathbb{Z^+} \) olmak üzere,
Çift dereceli köklü fonksiyonlar:
\( f: [0, \infty) \to [0, \infty) \)
\( f(x) = \sqrt[2n]{x} \)
Tek dereceli köklü fonksiyonlar:
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = \sqrt[2n + 1]{x} \)
Değer Tablosu ve Grafiği
\( f(x) = \sqrt[2]{x} \) ve \( g(x) = \sqrt[3]{x} \) fonksiyonlarının bazı değerleri için değer tablosu aşağıdaki gibidir.
| \( x \) | \( f(x) = \sqrt[2]{x} \) | \( g(x) = \sqrt[3]{x} \) |
|---|---|---|
| \( -27 \) | \( f(-27) \): Tanımsız | \( g(-27) = \sqrt[3]{-27} = -3 \) |
| \( -16 \) | \( f(-16) \): Tanımsız | \( g(-16) = \sqrt[3]{-16} = -2,51984... \) |
| \( -8 \) | \( f(-8) \): Tanımsız | \( g(-8) = \sqrt[3]{-8} = -2 \) |
| \( -4 \) | \( f(-4) \): Tanımsız | \( g(-4) = \sqrt[3]{-4} = -1,58740... \) |
| \( 0 \) | \( f(0) = \sqrt[2]{0} = 0 \) | \( g(0) = \sqrt[3]{0} = 0 \) |
| \( 4 \) | \( f(4) = \sqrt[2]{4} = 2 \) | \( g(4) = \sqrt[3]{4} = 1,58740... \) |
| \( 8 \) | \( f(8) = \sqrt[2]{8} = 2,82842... \) | \( g(8) = \sqrt[3]{8} = 2 \) |
| \( 16 \) | \( f(16) = \sqrt[2]{16} = 4 \) | \( g(16) = \sqrt[3]{16} = 2,51984... \) |
| \( 27 \) | \( f(27) = \sqrt[2]{27} = 5,19615... \) | \( g(27) = \sqrt[3]{27} = 3 \) |
Her iki fonksiyon için bulunan bu noktalar analitik düzlemde işaretlendiğinde aşağıdaki grafikler elde edilir.
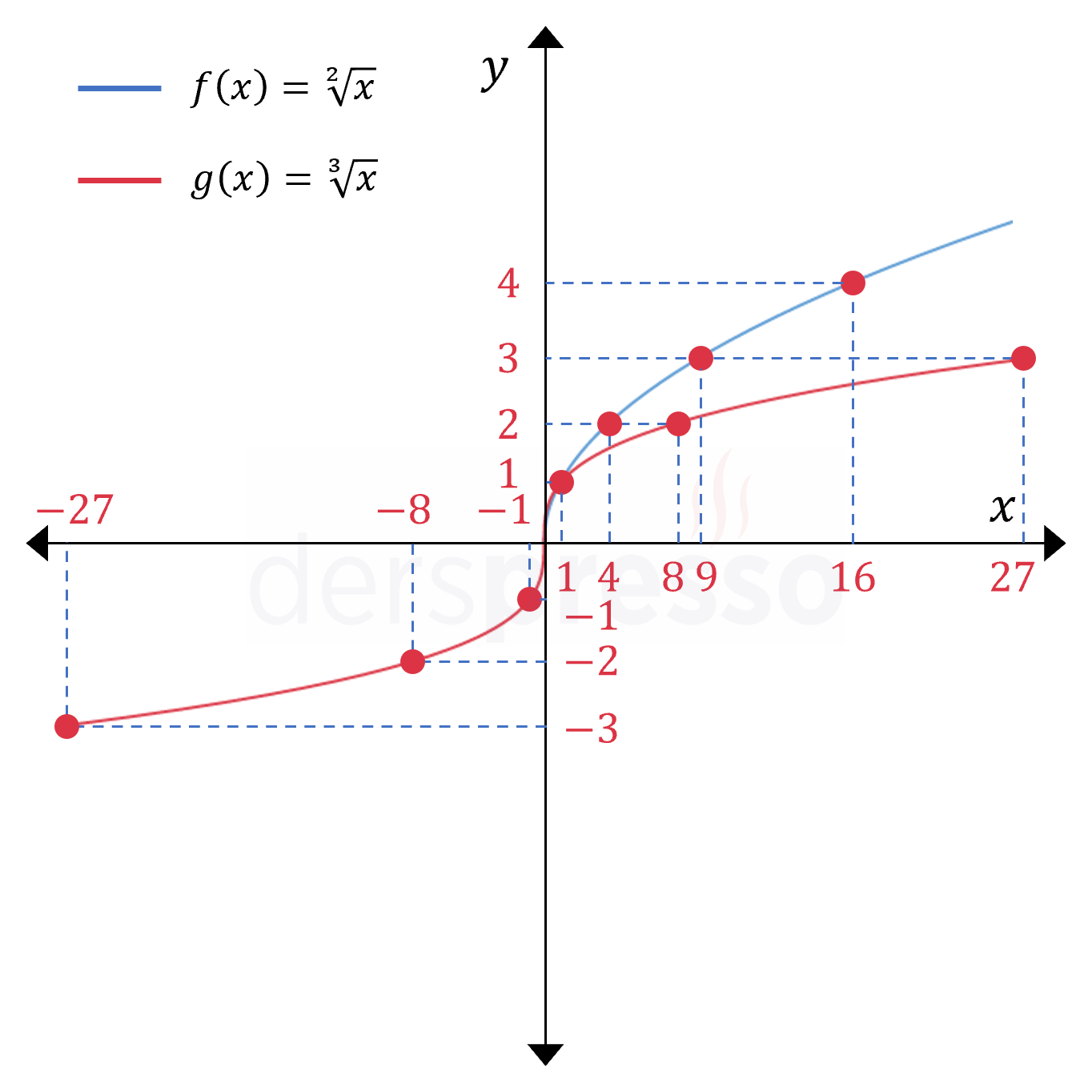
Çift dereceli bir köklü ifade \( x \)'in sadece sıfır ya da pozitif değerleri için tanımlı olduğu için grafiği de sadece bu aralıkta tanımlıdır.
Tek dereceli bir köklü ifade \( x \)'in tüm reel sayı değerleri için tanımlı olduğu için grafiği de tüm reel sayılarda tanımlıdır.
Köklü Fonksiyon Dönüşümleri
Fonksiyonların dönüşümü konusunda gördüğümüz tüm dönüşümler köklü fonksiyonlara uygulanarak fonksiyonun denkleminde, grafiğinin konumunda ve şeklinde değişiklikler meydana getirilebilir.
Bu dönüşümlere aşağıdaki gibi birkaç örnek verilebilir.
\( f(x) = 2\sqrt[3]{x} + 3 \)
\( g(x) = -\sqrt{3x - 5} - 1 \)
\( h(x) = 3\sqrt{-x + 1} + 2 \)
\( 0 \lt a \lt 1 \) olmak üzere,
\( \dfrac{1}{a^3}, \sqrt{a}, a, \dfrac{1}{\sqrt{a}}, a^2, \dfrac{1}{a} \)
ifadelerini küçükten büyüğe doğru sıralayın.
Çözümü GösterVerilen ifadeleri birer fonksiyon olarak düşünürsek bu fonksiyonları ikişerli ortak çözdüğümüzde tümünün \( (1, 1) \) noktasında ve bazılarının \( (0, 0) \) noktasında kesiştiklerini ve \( (0, 1) \) aralığında başka kesişim noktaları olmadığını görebiliriz.
Buna göre bu ifadeler arasındaki küçüklük - büyüklük ilişkisi \( (0, 1) \) aralığı boyunca aynı kalır, dolayısıyla bu aralıkta herhangi bir değer vererek ifadeleri karşılaştırabiliriz.
Tüm ifadelerde \( a = \frac{1}{4} \) verelim.
\( \dfrac{1}{(\frac{1}{4})^3} = \dfrac{1}{\frac{1}{64}} = 64 \)
\( \sqrt{\dfrac{1}{4}} = \dfrac{1}{2} \)
\( \dfrac{1}{4} = \dfrac{1}{4} \)
\( \dfrac{1}{\sqrt{\frac{1}{4}}} = \dfrac{1}{\frac{1}{2}} = 2 \)
\( (\dfrac{1}{4})^2 = \dfrac{1}{16} \)
\( \dfrac{1}{\frac{1}{4}} = 4 \)
Buna göre verilen ifadelerin küçükten büyüğe doğru sıralaması aşağıdaki gibi olur.
\( \dfrac{1}{16} \lt \dfrac{1}{4} \lt \dfrac{1}{2} \lt 2 \lt 4 \lt 64 \)
\( a^2 \lt a \lt \sqrt{a} \lt \dfrac{1}{\sqrt{a}} \lt \dfrac{1}{a} \lt \dfrac{1}{a^3} \)