Ek-1: İrrasyonel Sayılar
Bu bölümde irrasyonel sayılarla ilgili bazı ek bilgiler ve ispatlar vereceğiz.
Köklü Sayıların Sayı Doğrusunda Gösterimi
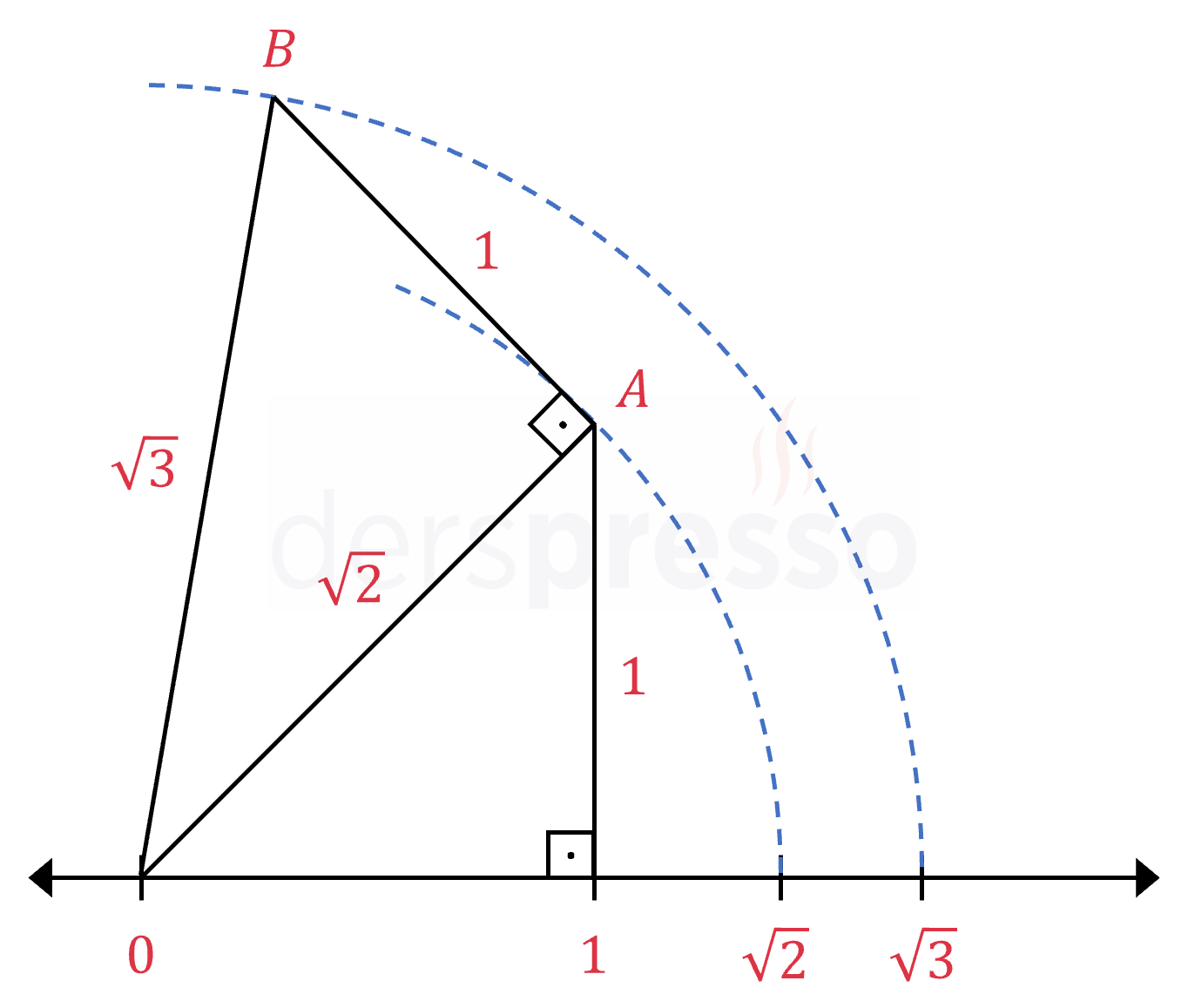
\( \sqrt{2} \) sayısının sayı doğrusu üzerinde karşılık geldiği noktayı işaretleyebilmek için aşağıdaki yöntemi kullanabiliriz.
- Önce bir sayı doğrusu çizilir ve 0 ve 1 noktaları işaretlenir.
- 0-1 noktaları arasındaki uzaklığa 1 birim dersek, uzunluğu 1 birim olacak şekilde 1 noktasından sayı doğrusuna dik bir doğru parçası çizilir. Bu doğru parçasının bitiş noktasına \( A \) diyelim.
- 0 ve \( A \) noktaları birleştirilir. Pisagor teoreminden bu doğru parçasının uzunluğunun \( \sqrt{2} \) olduğunu görebiliriz.
- Bir pergelin bir ucu 0 noktasına diğer ucu \( A \) noktasına yerleştirilir ve 0 noktasındaki uç sabit kalacak şekilde bir yay çizilir. Bu yayın sayı doğrusunu kestiği nokta \( \sqrt{2} \) sayısının sayı doğrusu üzerinde karşılık geldiği noktadır.
\( \sqrt{3} \) sayısının sayı doğrusu üzerinde karşılık geldiği noktayı işaretleyebilmek için aşağıdaki yöntemi kullanabiliriz.
- Yukarıda elde ettiğimiz \( A \) noktasından yine 1 birim uzunluğunda dik bir doğru parçası çizilir. Bu doğru parçasının bitiş noktasına \( B \) diyelim.
- 0 ve \( B \) noktaları birleştirilir. Pisagor teoreminden bu doğru parçasının uzunluğunun \( \sqrt{3} \) olduğunu görebiliriz.
- Bir pergelin bir ucu 0 noktasına diğer ucu \( B \) noktasına yerleştirilir ve 0 noktasındaki uç sabit kalacak şekilde bir yay çizilir. Bu yayın sayı doğrusunu kestiği nokta \( \sqrt{3} \) sayısının sayı doğrusu üzerinde karşılık geldiği noktadır.
Sonraki tam sayıların karekök değerleri için bu adımlar tekrarlanabilir.
İrrasyonel Sayılarla İlgili İspatlar
\( \sqrt{2} \) sayısının irrasyonel olduğunun ispatı aşağıda verilmiştir.
\( \sqrt{2} \)'nin irrasyonel bir sayı olduğunu ispatlamak için çelişkiyle ispat yöntemini kullanalım.
İlk önce \( \sqrt{2} \)'nin rasyonel bir sayı olduğunu varsayalım. \( \sqrt{2} \) rasyonel ise tanım gereği aralarında asal \( a \) ve \( b \) tam sayılarının oranı şeklinde yazılabilir.
\( \sqrt{2} = \dfrac{a}{b} \)
İki tarafın karesini alalım ve \( a^2 \)'yi yalnız bırakalım.
\( 2 = \dfrac{a^2}{b^2} \)
\( a^2 = 2b^2 \)
Eşitliğin sağ tarafında 2 çarpanı olduğu için ifadenin her iki tarafı, dolayısıyla \( a^2 \) çift sayı olmak zorundadır (herhangi bir tam sayının çift bir sayı ile çarpımının sonucu çift olur). \( a^2 \) çift ise \( a \) da çift olmak zorundadır (bir çift sayının karesi çift, bir tek sayının karesi tektir).
\( a \) bir çift sayı olduğu için bir diğer \( k \) tam sayısı cinsinden aşağıdaki şekilde yazılabilir (\( k \in \mathbb{Z} \)).
\( a = 2k \)
\( a^2 = 4k^2 \)
\( a^2 \)'nin eşitini yukarıdaki eşitlikte yerine koyup \( b^2 \)'yi yalnız bırakalım.
\( 4k^2 = 2b^2 \)
\( b^2 = 2k^2 \)
Yukarıda \( a \) için gösterdiğimiz şekilde, eşitliğin sağ tarafında 2 çarpanı olduğu için ifadenin her iki tarafı, dolayısıyla \( b^2 \) çift sayı olmak zorundadır. \( b^2 \) çift ise \( b \) de çift olmak zorundadır.
İspata \( a \) ve \( b \)'nin aralarında asal tam sayılar ve \( \sqrt{2} \)'nin rasyonel bir sayı olduğu varsayımı ile başlamıştık, ama bu varsayımın \( a \) ve \( b \)'nin birer çift sayı olmasını gerektirdiğini bulmuş olduk. 2 sayısı iki çift sayının ortak bir çarpanı olduğu için iki çift sayı aralarında asal olamaz, dolayısıyla ispatın başında yaptığımız aralarında asal varsayımı doğru olamaz.
Sonuç olarak oranları \( \sqrt{2} \)'ye eşit olacak ve aynı zamanda aralarında asal iki tam sayı bulamayacağımızı, dolayısıyla \( \sqrt{2} \)'nin rasyonel olamayacağını ve irrasyonel olmak zorunda olduğunu göstermiş olduk.
Rasyonel ve İrrasyonel Sayılar Arasında İşlemler
İki rasyonel sayının toplamı/farkı bir rasyonel sayıdır.
\( m \) ve \( n \) olmak üzere iki rasyonel sayı tanımlayalım. Bu rasyonel sayıları aşağıdaki şekilde yazabiliriz.
\( a, b, c, d \in \mathbb{Z}, \quad b, d \ne 0 \)
\( m = \dfrac{a}{b} \)
\( n = \dfrac{c}{d} \)
\( m \) ve \( n \)'nin toplamını alalım.
\( m + n = \dfrac{a}{b} + \dfrac{c}{d} \)
\( m + n = \dfrac{ad + bc}{bd} \)
Elde ettiğimiz kesirli ifadenin payı ve paydası birer tam sayıdır ve paydası sıfırdan farklıdır, dolayısıyla \( m + n \) toplamı bir rasyonel sayıdır.
İki rasyonel sayının çarpımı bir rasyonel sayıdır.
\( m \) ve \( n \) olmak üzere iki rasyonel sayı tanımlayalım. Bu rasyonel sayıları aşağıdaki şekilde yazabiliriz.
\( a, b, c, d \in \mathbb{Z}, \quad b, d \ne 0 \)
\( m = \dfrac{a}{b} \)
\( n = \dfrac{c}{d} \)
\( m \) ve \( n \)'nin çarpımını alalım.
\( m \cdot n = \dfrac{a}{b} \cdot \dfrac{c}{d} \)
\( m \cdot n = \dfrac{ac}{bd} \)
Elde ettiğimiz kesirli ifadenin payı ve paydası birer tam sayıdır ve paydası sıfırdan farklıdır, dolayısıyla \( m \cdot n \) çarpımı bir rasyonel sayıdır.
Bir irrasyonel ve bir rasyonel sayının toplamı/farkı bir irrasyonel sayıdır.
Bir irrasyonel ve bir rasyonel sayının toplamının/farkının bir irrasyonel sayı olduğunu ispatlamak için çelişkiyle ispat yöntemini kullanalım.
\( m \) irrasyonel ve \( n \) rasyonel olmak üzere iki sayı tanımlayalım. Bu iki sayının toplamının bir rasyonel sayı olduğunu varsayalım. Bu durumda \( n \) rasyonel sayısını ve iki sayının toplamını aşağıdaki şekilde yazabiliriz.
\( a, b, c, d \in \mathbb{Z}, \quad b, d \ne 0 \)
\( n = \dfrac{a}{b} \)
\( m + n = m + \dfrac{a}{b} = \dfrac{c}{d} \)
\( m \)'yi yalnız bırakırsak aşağıdaki ifadeyi elde ederiz.
\( m = \dfrac{c}{d} - \dfrac{a}{b} \)
\( m = \dfrac{bc - ad}{bd} \)
Elde ettiğimiz kesirli ifadenin payı ve paydası birer tam sayıdır ve paydası sıfırdan farklıdır, dolayısıyla bir rasyonel sayıdır. İspatın başında \( m \)'nin bir irrasyonel sayı olduğunu varsaydığımız için bir çelişki elde etmiş olduk, buna göre bir sayının bir rasyonel sayı ile toplamının sonucu rasyonel ise, bu sayı rasyonel sayı olmak zorundadır.
Sonuç olarak bir irrasyonel sayı ile rasyonel sayının toplamının rasyonel olamayacağını ve irrasyonel olmak zorunda olduğunu göstermiş olduk.
Bir irrasyonel ve sıfırdan farklı bir rasyonel sayının çarpımı bir irrasyonel sayıdır.
Bir irrasyonel ve sıfırdan farklı bir rasyonel sayının çarpımının bir irrasyonel sayı olduğunu ispatlamak için çelişkiyle ispat yöntemini kullanalım.
\( m \) bir irrasyonel ve \( n \) sıfırdan farklı bir rasyonel sayı olmak üzere iki sayı tanımlayalım. Bu iki sayının çarpımının bir rasyonel sayı olduğunu varsayalım. Bu durumda \( n \) rasyonel sayısını ve iki sayının çarpımını aşağıdaki şekilde yazabiliriz.
\( a, b, c, d \in \mathbb{Z}, \quad a, b, d \ne 0 \)
\( n = \dfrac{a}{b} \)
\( m \cdot n = m \cdot \dfrac{a}{b} = \dfrac{c}{d} \)
\( m \)'yi yalnız bırakırsak aşağıdaki ifadeyi elde ederiz.
\( m = \dfrac{c}{d} \cdot \dfrac{b}{a} \)
\( m = \dfrac{bc}{ad} \)
Elde ettiğimiz kesirli ifadenin payı ve paydası birer tam sayıdır ve paydası sıfırdan farklıdır, dolayısıyla bir rasyonel sayıdır. İspatın başında \( m \)'nin bir irrasyonel sayı olduğunu varsaydığımız için bir çelişki elde etmiş olduk, buna göre bir sayının bir rasyonel sayı ile çarpımının sonucu rasyonel ise, bu sayı rasyonel sayı olmak zorundadır.
Sonuç olarak bir irrasyonel sayı ile sıfırdan farklı bir rasyonel sayının çarpımının rasyonel olamayacağını ve irrasyonel olmak zorunda olduğunu göstermiş olduk.
İki irrasyonel sayının toplamı/farkı rasyonel ya da irrasyonel olabilir.
Rasyonel sonuca örnek:
\( \quad \sqrt{2} + (-\sqrt{2}) = 0 \)
İrrasyonel sonuca örnek:
\( \quad \sqrt{2} + 2\sqrt{2} = 3\sqrt{2} \)
İki irrasyonel sayının çarpımı rasyonel ya da irrasyonel olabilir.
Rasyonel sonuca örnek:
\( \quad \sqrt{2} \cdot \sqrt{2} = 2 \)
İrrasyonel sonuca örnek:
\( \quad \sqrt{2} \cdot \sqrt{3} = \sqrt{6} \)
Aşağıdaki sayılardan hangileri irrasyoneldir?
I. \( (\sqrt{2} - 1)(\sqrt{2} + 1) \)
II. \( \sqrt{27} \cdot \sqrt{3} \)
III. \( \sqrt{12,1} \)
IV. \( \sqrt{1000} \)
V. \( \dfrac{\sqrt{18}}{\sqrt{2}} \)
Çözümü GösterI. öncül:
\( (\sqrt{2} - 1)(\sqrt{2} + 1) = (\sqrt{2})^2 - 1^2 = 1 \)
II. öncül:
\( \sqrt{27} \cdot \sqrt{3} = \sqrt{81} = 9 \)
III. öncül:
\( \sqrt{12,1} = \sqrt{\dfrac{121}{10}} = \dfrac{11\sqrt{10}}{10} \)
IV. öncül:
\( \sqrt{1000} = 10\sqrt{10} \)
V. öncül:
\( \dfrac{\sqrt{18}}{\sqrt{2}} = \sqrt{9} = 3 \)
Buna göre III. ve IV. ifadeler irrasyoneldir.