Birim Çember
Analitik düzlemde merkezi orijin ve yarıçapı 1 birim olan çembere birim çember denir. Merkezi
Birim çemberin denklemi merkezi orijin ve yarıçapı 1 birim olan çember denklemidir.
Birim çemberin trigonometride önemli bir yerinin olmasının bazı sebepleri şunlardır.
- Açıların başlangıç kenarını sabitleyerek (aşağıdaki şekilde
- Birim çember üzerindeki noktaların koordinatları üzerinden trigonometrik fonksiyonların değerlerini belirleyebiliriz.
- Birim çemberi kullanarak dar olmayan açıların trigonometrik değerlerini dar açılar cinsinden ifade edebiliriz.
- Kullandığımız pek çok trigonometrik özdeşliği birim çember üzerinde geometrik olarak türetebiliriz.
Sinüs ve Kosinüs Değerleri
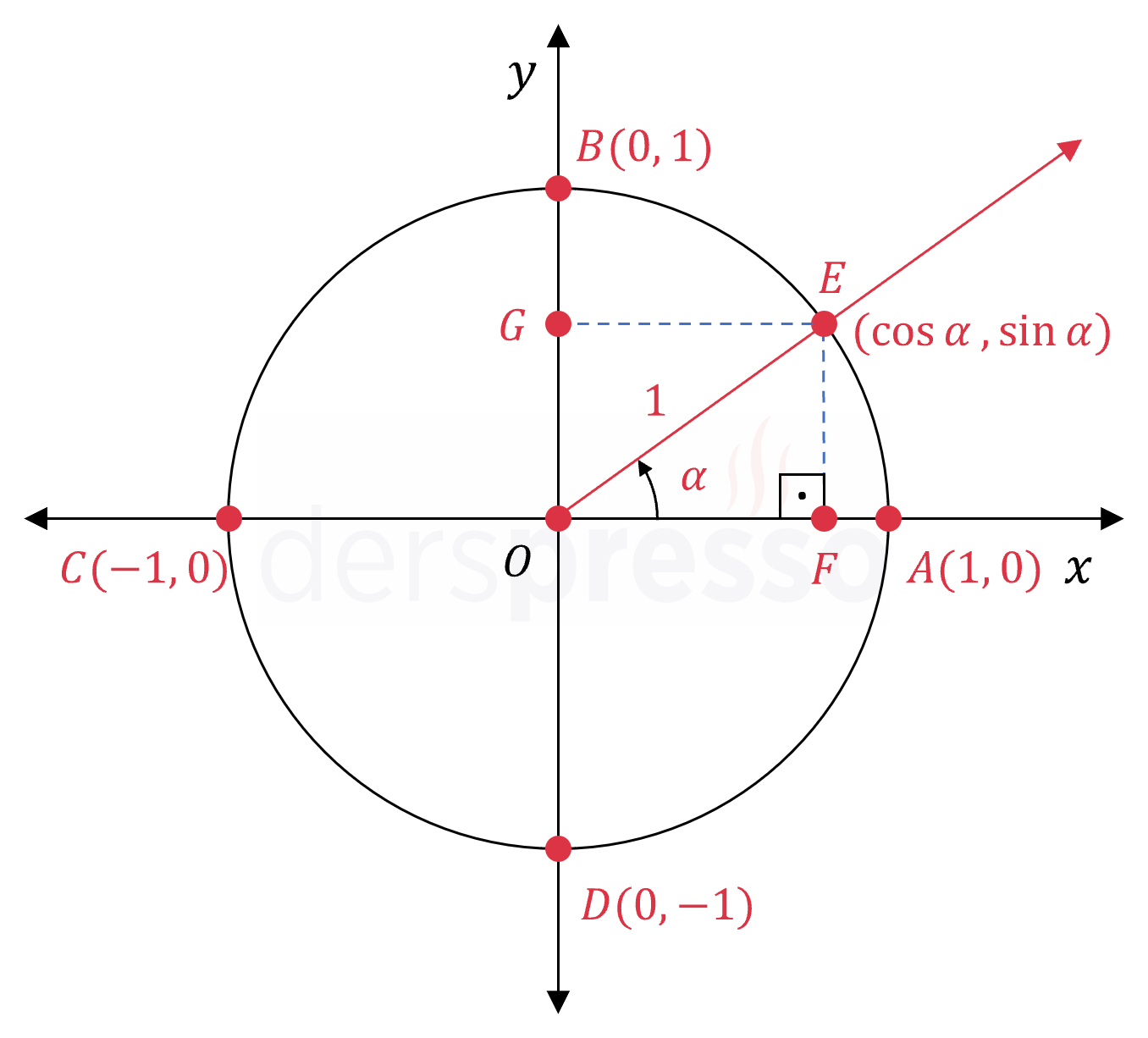
Belirli bir
Buna göre
Buna göre
Dolayısıyla
Birim çemberin eksenleri kestiği noktaların koordinatlarını, bu noktaların karşılık geldikleri açıların sinüs ve kosinüs değerleri cinsinden yazarak bu formülü doğrulayabiliriz.
Ayrıca birim çember üzerindeki herhangi bir noktanın koordinatlarını yukarıda paylaştığımız birim çember denkleminde yerine koyduğumuzda denklemin her zaman sağlandığını görebiliriz.
Birim çemberin denklemi:
Yarıçap uzunluğu tüm birim çember üzerinde 1 birim olduğu ve
Sinüs ve Kosinüs Eksenleri
Bir açının birim çember üzerinde karşılık geldiği noktanın ordinat değeri, yani
Aşağıdaki şekilde 4 bölgedeki birer açı için sinüs değerleri sinüs ekseni üzerinde gösterilmiştir.
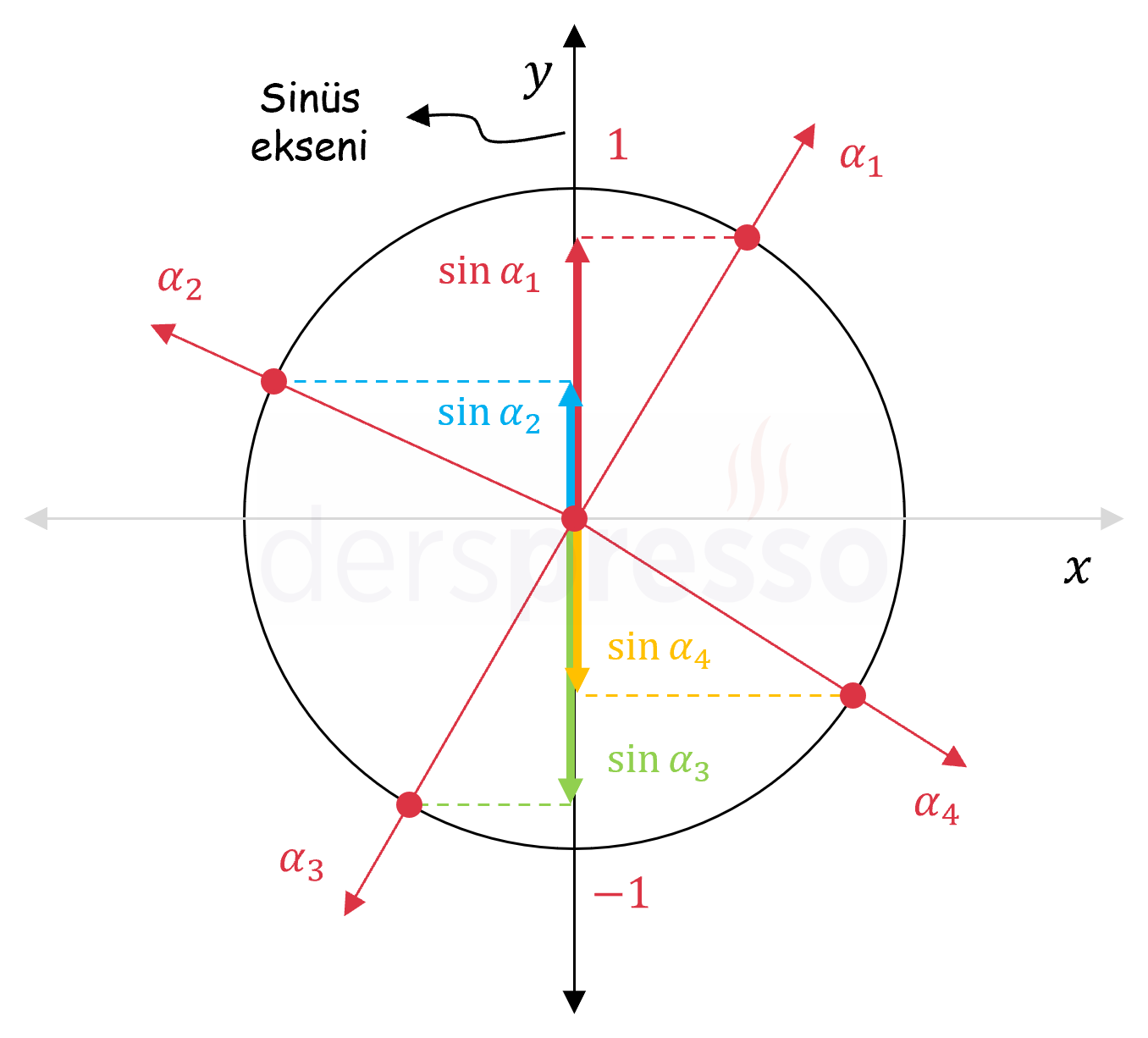
Bir açının birim çember üzerinde karşılık geldiği noktanın apsis değeri, yani
Aşağıdaki şekilde 4 bölgedeki birer açı için kosinüs değerleri kosinüs ekseni üzerinde gösterilmiştir.
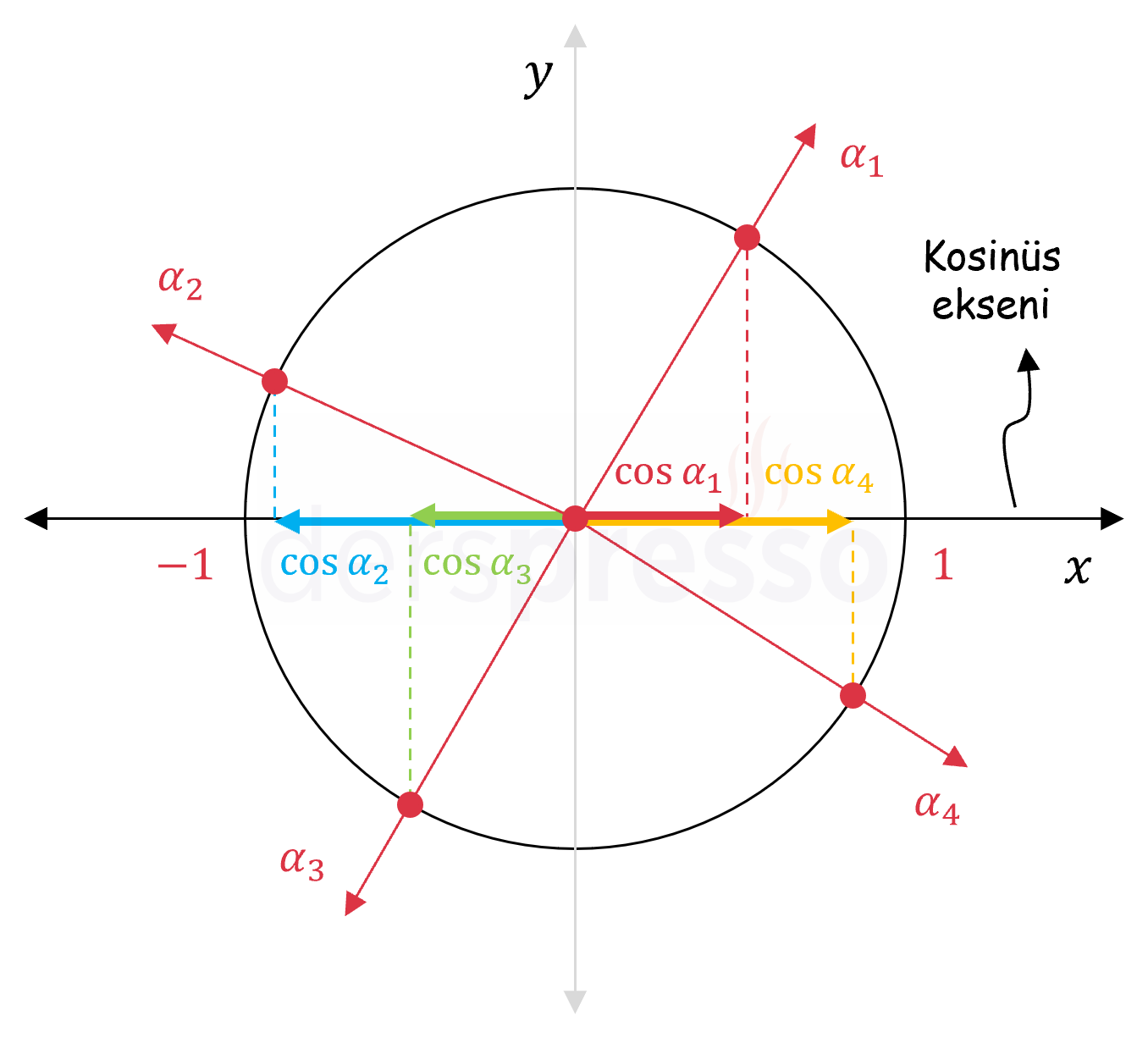
Tanjant Değeri
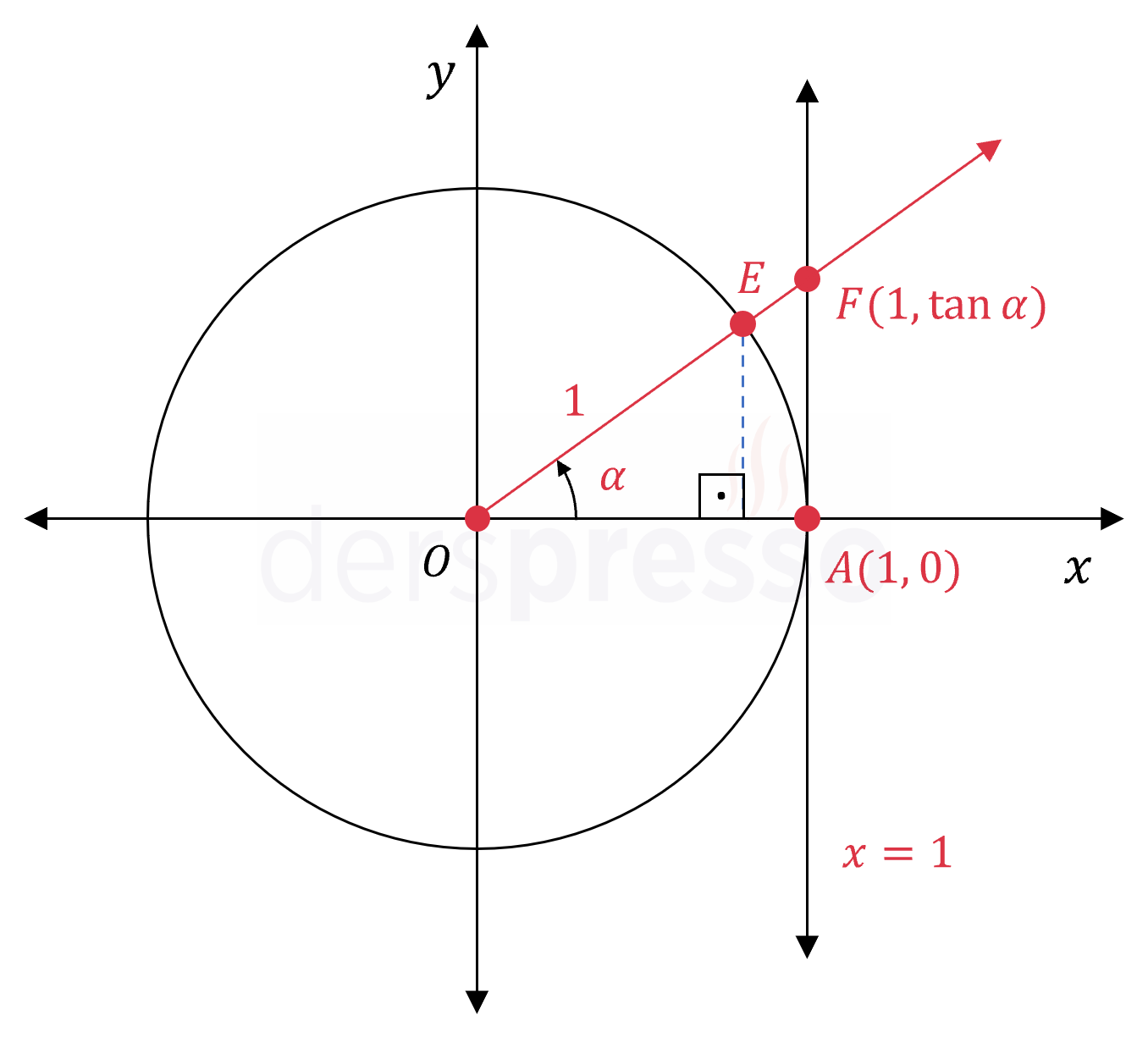
Belirli bir
Buna göre
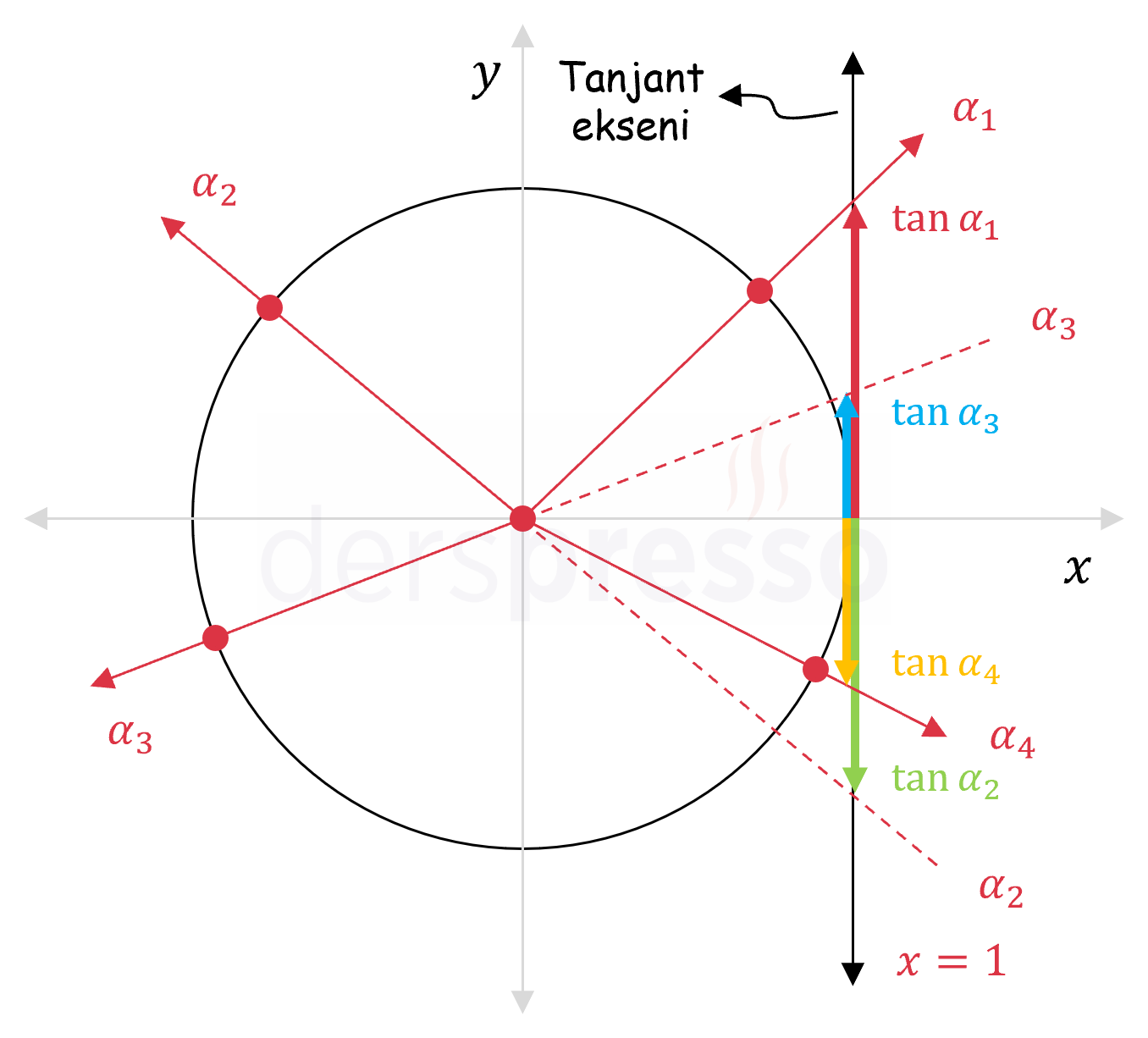
Tanjant Ekseni
Bir açının bitim kolunun
Aşağıdaki şekilde 4 bölgedeki birer açı için tanjant değerleri tanjant ekseni üzerinde gösterilmiştir.
Kotanjant Değeri

Belirli bir
Buna göre
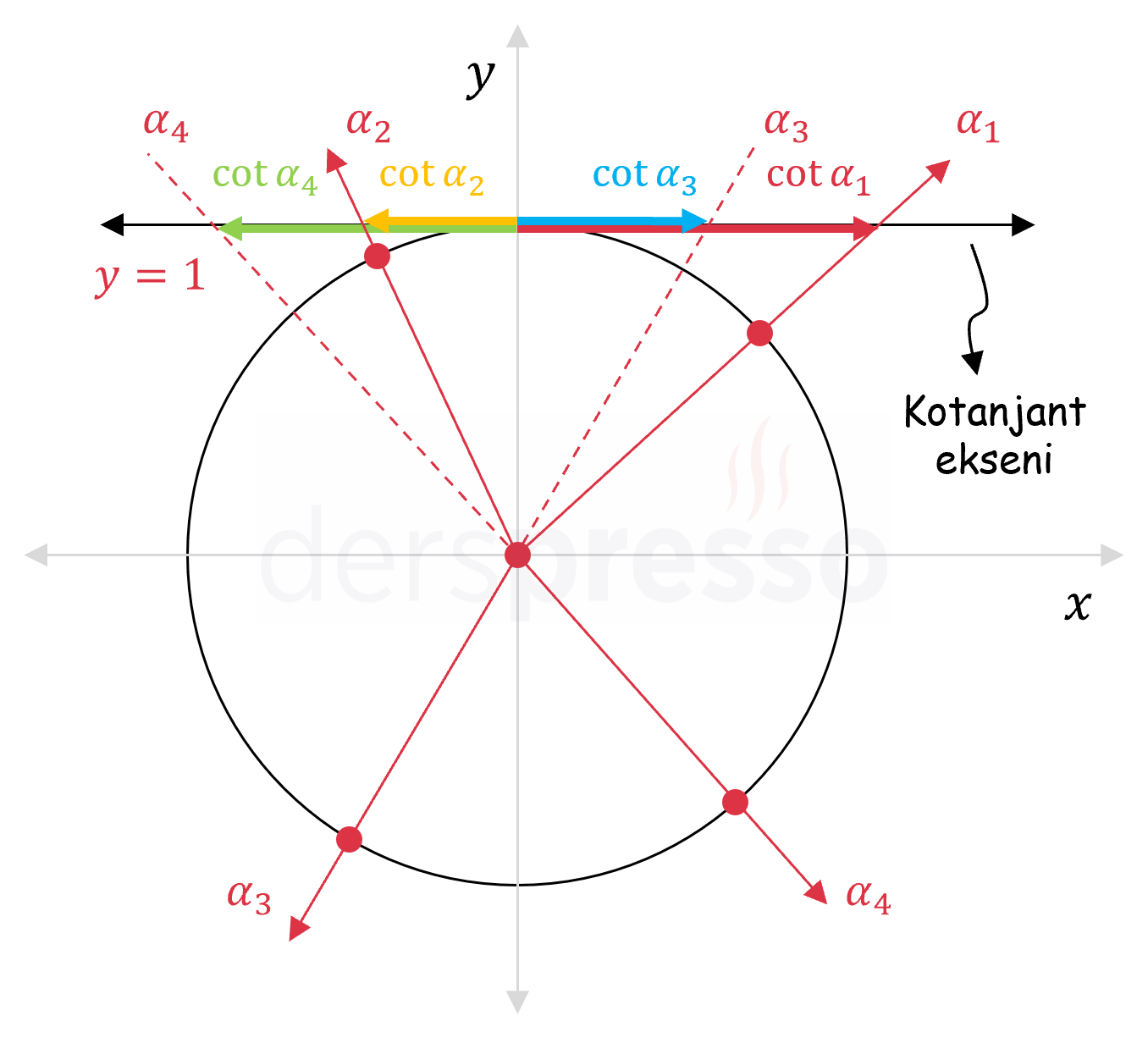
Kotanjant Ekseni
Bir açının bitim kolunun
Aşağıdaki şekilde 4 bölgedeki birer açı için kotanjant değerleri kotanjant ekseni üzerinde gösterilmiştir.
Sekant ve Kosekant Değerleri

Belirli bir
Buna göre
Aynı teğet doğrunun
Buna göre
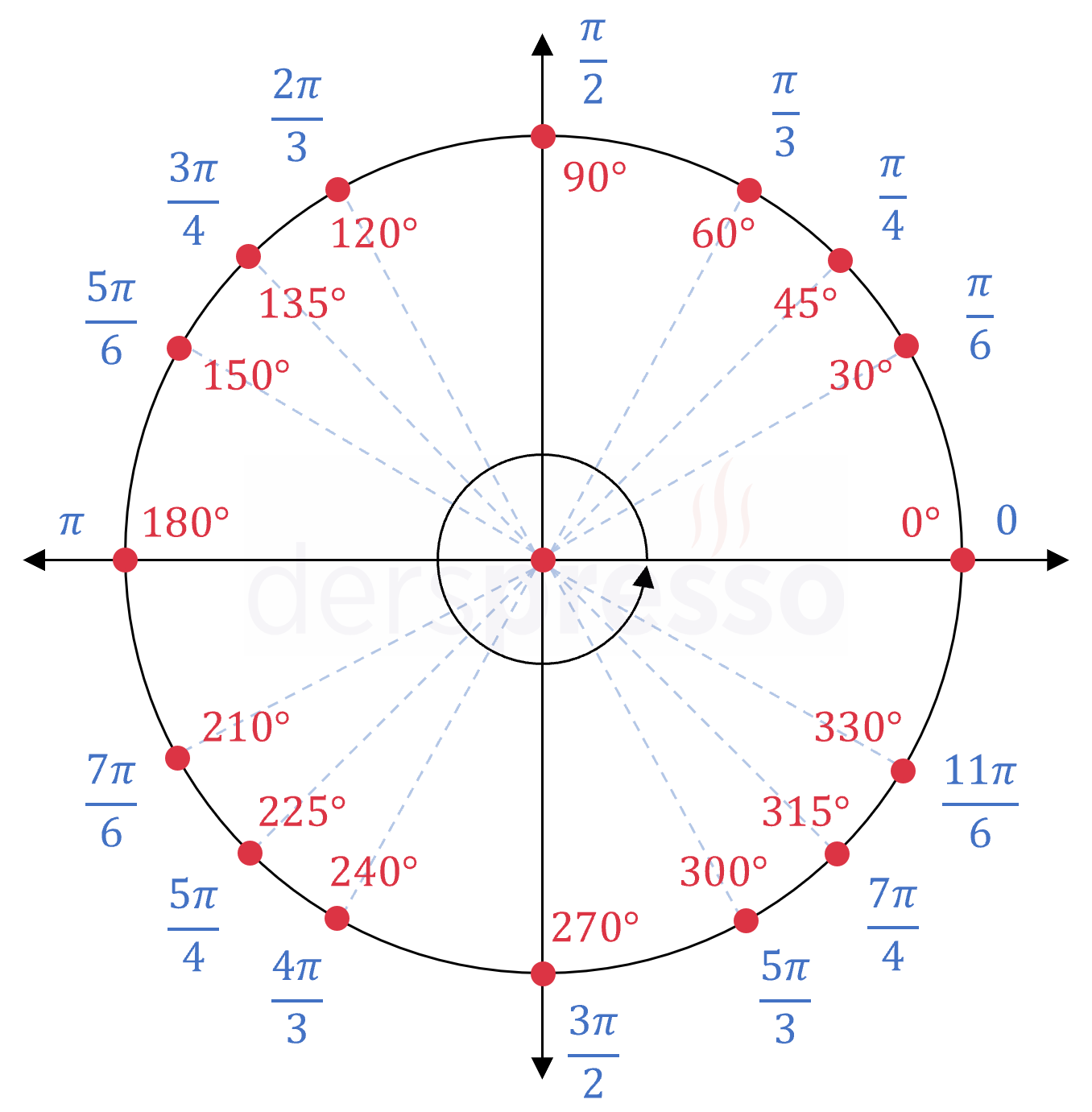
Birim Çember ve Sık Kullanılan Açılar
En sık kullanılan açıların derece ve radyan karşılıkları aşağıdaki şekilde birim çember üzerinde gösterilmiştir. Bu açıların derece ve radyan karşılıklarının ve her birinin trigonometrik fonksiyon değerlerinin bilinmesi ya da hızlı bir şekilde hesaplanabilmesi oldukça önemlidir.
denklemi bir birim çember belirttiğine göre,
Birim çemberin denklemi aşağıdaki gibidir.
Verilen denklem bu denkleme eşit olacak şekilde katsayıları eşitleyelim.
Çember denkleminde
Bu değerleri soruda verilen ifadede yerine yazalım.
Birim çember üzerindeki
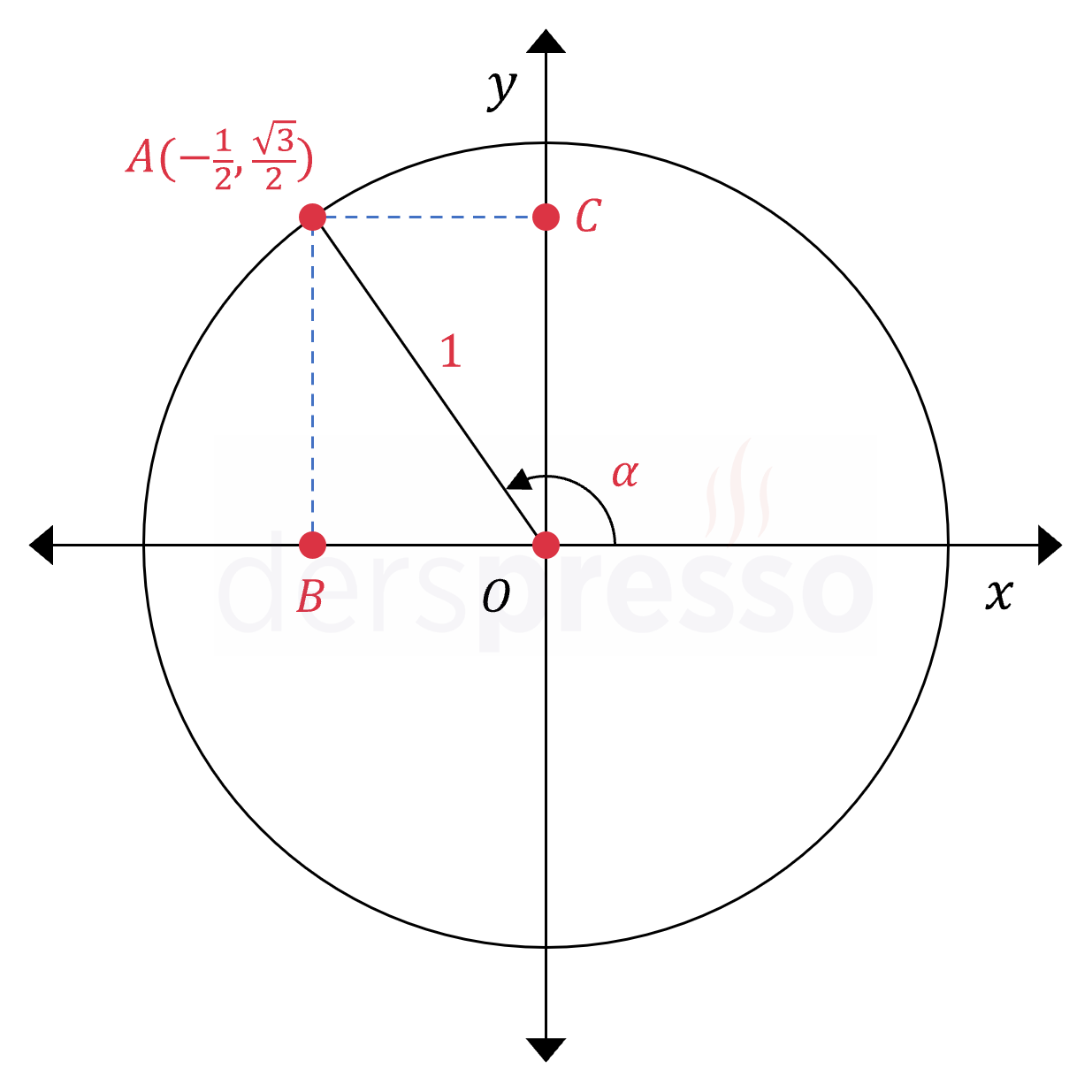
Apsis negatif, ordinat pozitif olduğu için nokta II. bölgededir.
Birim çember üzerindeki bir noktanın apsis ve ordinat değerleri sırasıyla o noktanın karşılık geldiği açının kosinüs ve sinüs değerlerine eşittir.
Noktanın
Kosinüs değeri
Birim çember üzerinde apsisi ordinatının 3 katına eşit olan noktalar nelerdir?
Çözümü Gösterİstenilen noktaların koordinatlarına
Birim çember üzerindeki bir noktanın apsis ve ordinat değerleri sırasıyla o noktanın karşılık geldiği açının kosinüs ve sinüs değerlerine eşittir.
Noktanın
Birim çember üzerindeki tüm noktalar sinüs - kosinüs kare toplamı özdeşliğini sağlar.
O halde istenen koşulu sağlayan noktalar aşağıdaki gibi bulunur.
Dik koordinat düzleminde birim çember üzerinde
Bu nokta saat yönünde 3500° hareket ettirilirse hangi bölgeye ulaşılır?
Çözümü Göster
Saat yönünde hareket negatif yönlü açıya karşılık gelir.
250° III. bölgede bir açıdır.
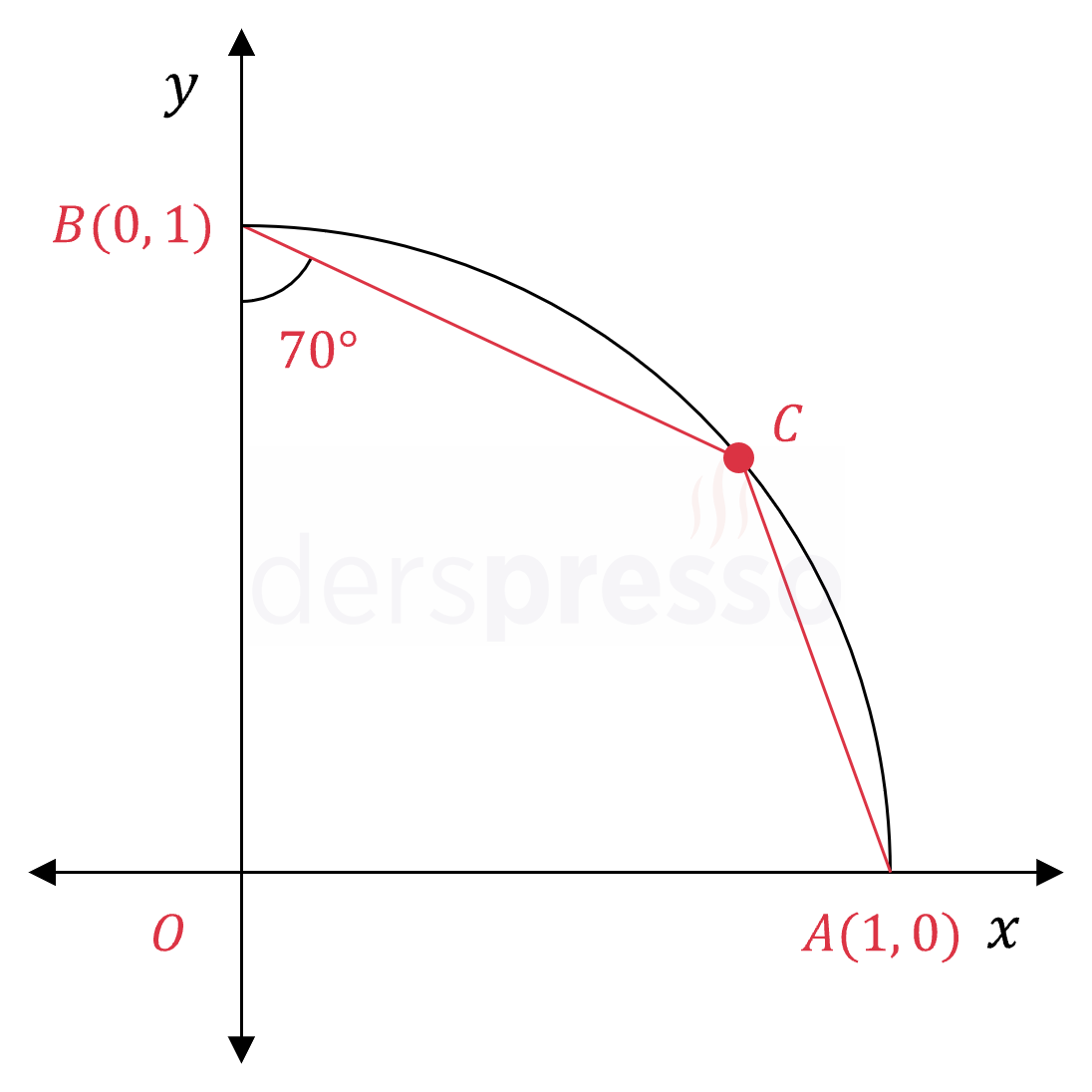
Yukarıda
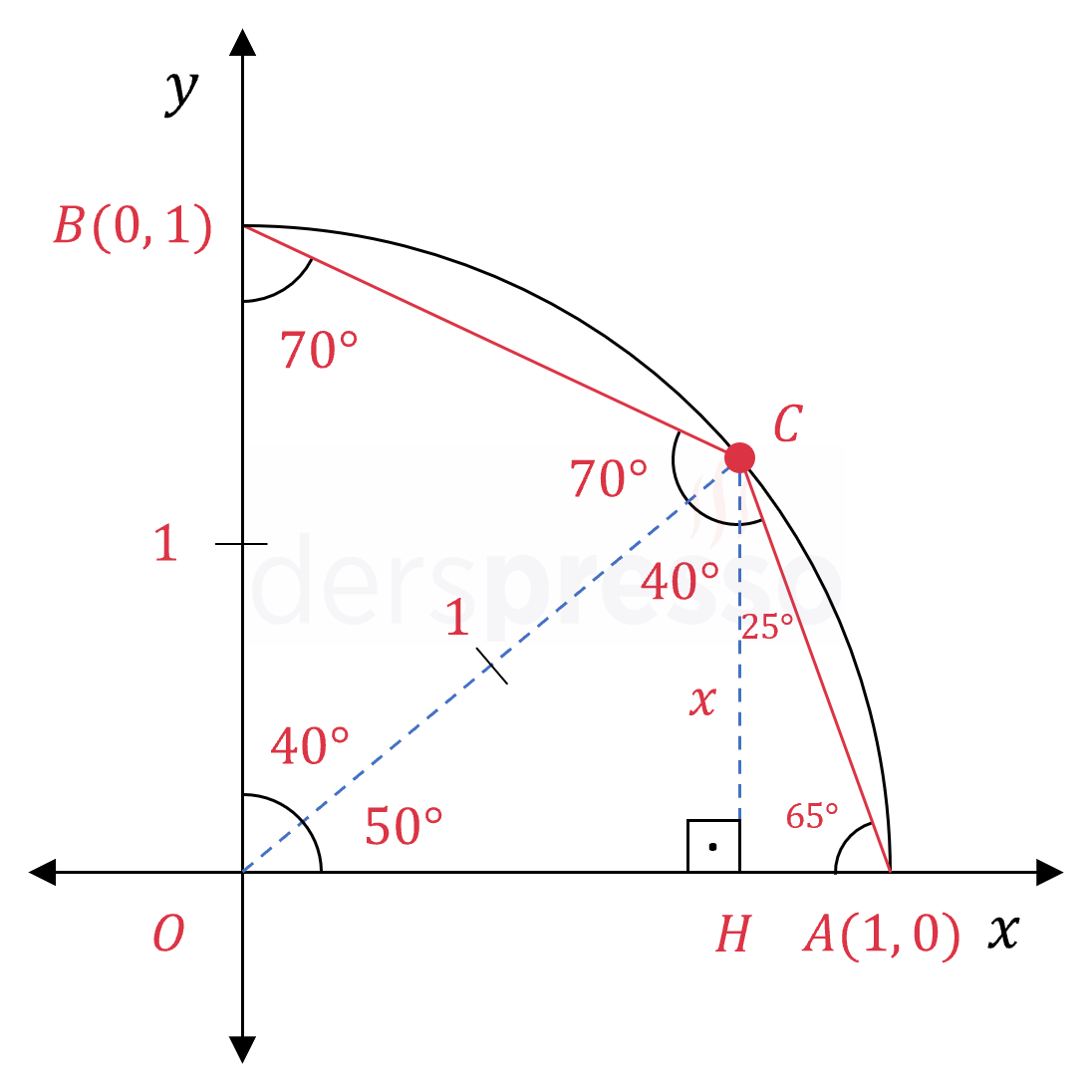
Orijin ile
Sinüs iki kat açı formülünü kullanalım.
ifadelerini değerlerine göre büyükten küçüğe doğru sıralayın.
Çözümü GösterVerilen ifadeleri kosinüs ve kotanjant fonksiyonları ve I. ve II. bölgede açılar cinsinden yazalım.
Tümler açıların tanjant ve kotanjant değerleri eşittir.
Kotanjant fonksiyonunun periyodu 180°'dir.
Bu trigonometrik ifadelerin değerlerini birim çember üzerinde işaretleyelim.
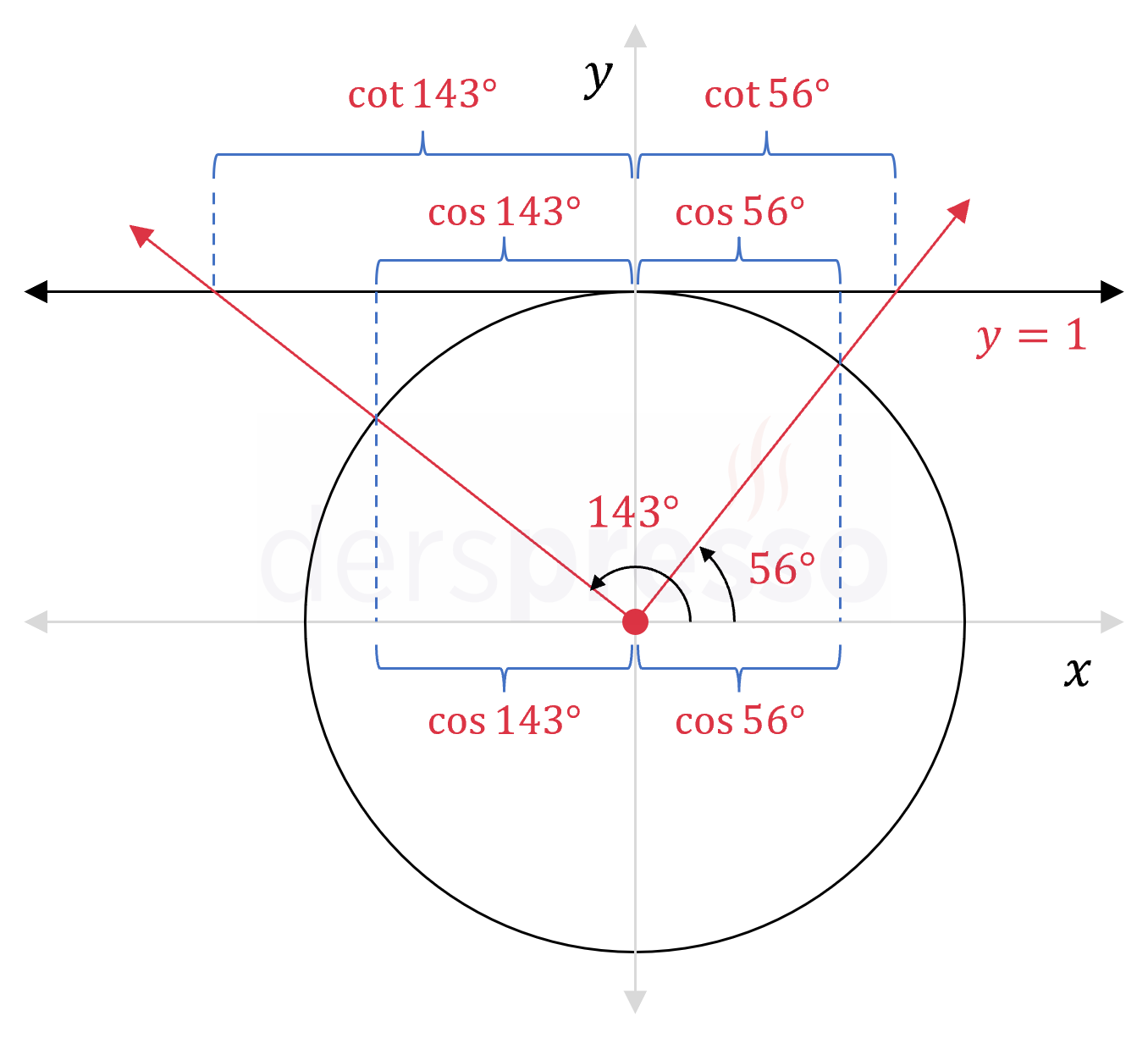
Şekilde kotanjant ifadeleri
Kotanjant ekseni üzerindeki büyüklükleri karşılaştırarak verilen ifadelerin büyükten küçüğe sıralaması aşağıdaki gibi olur.