Toplam, Fark ve İki Kat Açı Formülleri
Toplam ve Fark Formülleri
Bu formüller iki açının toplamının/farkının trigonometrik değerinin her bir açının trigonometrik değerleri cinsinden açılımını verir.
Kosinüs Toplam ve Fark Formülleri
\( \cos(x + y) = \cos{x}\cos{y} - \sin{x}\sin{y} \)
\( \cos(x - y) = \cos{x}\cos{y} + \sin{x}\sin{y} \)
\( \cos{15°} = \cos(45° - 30°) \)
\( = \cos{45°}\cos{30°} + \sin{45°}\sin{30°} \)
\( = \dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{2}}{2} \cdot \dfrac{1}{2} \)
\( = \dfrac{\sqrt{2} \cdot (\sqrt{3} + 1)}{4} \)
İSPATI GÖSTER
Yukarıdaki birim üçgen üzerinde aşağıdaki noktaları işaretleyelim ve her birinin koordinatlarını yazalım.
\( A \): \( x \) ekseninin birim çemberi kestiği nokta
\( A(1, 0) \)
\( B \): \( x \) ekseni ile \( x \) derece açı yapan \( [OB] \) doğru parçasının birim çemberi kestiği nokta
\( B(\cos{x}, \sin{x}) \)
\( C \): \( x \) ekseni ile \( y \) derece açı yapan \( [OC] \) doğru parçasının birim çemberi kestiği nokta
\( C(\cos{y}, \sin{y}) \)
\( D \): \( x \) ekseni ile \( (x - y) \) derece açı yapan \( [OD] \) doğru parçasının birim çemberi kestiği nokta
\( D(\cos(x - y), \sin(x - y)) \)
Aşağıdaki iki açı birbirine eşittir.
\( m(\widehat{BOC}) = m(\widehat{DOA}) = x - y \)
Dolayısıyla, kosinüs teoreminden bu açıların gördükleri kirişlerin uzunlukları da eşittir (iki kenar ve aralarındaki açı eşit).
\( \abs{BC} = \abs{DA} \)
Birinci kirişin uzunluğunu, analitik düzlemde iki nokta arasındaki uzaklık formülünü kullanarak yazalım.
\( \abs{BC} = \sqrt{(\cos{x} - \cos{y})^2 + (\sin{x} - \sin{y})^2} \)
\( = \sqrt{\cos^2{x} - 2\cos{x}\cos{y} + \cos^2{y} + \sin^2{x} - 2\sin{x}\sin{y} + \sin^2{y}} \)
\( = \sqrt{2 - 2\cos{x}\cos{y} - 2\sin{x}\sin{y}} \)
İkinci kirişin uzunluğunu, aynı uzaklık formülünü kullanarak yazalım.
\( \abs{DA} = \sqrt{(\cos(x - y) - 1)^2 + (\sin(x - y) - 0)^2} \)
\( = \sqrt{\cos^2(x - y) - 2\cos(x - y) + 1 + \sin^2(x - y)} \)
\( = \sqrt{2 - 2\cos(x - y)} \)
İki kiriş uzunluğunu birbirine eşitleyip iki tarafın karesini alalım.
\( \abs{BC}^2 = \abs{DA}^2 \)
\( 2 - 2\cos{x}\cos{y} - 2\sin{x}\sin{y} = 2 - 2\cos(x - y) \)
Eşitliği düzenlersek kosinüs fark formülünü elde ederiz.
\( \cos(x - y) = \cos{x}\cos{y} + \sin{x}\sin{y} \)
Yukarıdaki fark formülü bir özdeşlik olduğu için, \( y \) açısı yerine \( -y \) de yazabiliriz.
\( \cos(x - (-y)) = \cos{x}\cos(-y) + \sin{x}\sin(-y) \)
\( \cos(-y) = \cos{y} \)
\( \sin(-y) = -\sin{y} \)
Bu değerleri yerine koyarsak, kosinüs toplam formülünü elde ederiz.
\( \cos(x + y) = \cos{x}\cos{y} - \sin{x}\sin{y} \)
Sinüs Toplam ve Fark Formülleri
\( \sin(x + y) = \sin{x}\cos{y} + \cos{x}\sin{y} \)
\( \sin(x - y) = \sin{x}\cos{y} - \cos{x}\sin{y} \)
\( \sin{75°} = \sin(45° + 30°) \)
\( = \sin{45°}\cos{30°} + \cos{45°}\sin{30°} \)
\( = \dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{2}}{2} \cdot \dfrac{1}{2} \)
\( = \dfrac{\sqrt{2} \cdot (\sqrt{3} + 1)}{4} \)
İSPATI GÖSTER
Sinüs toplam ve fark formüllerinin ispatını, yukarıda ispatıyla birlikte verdiğimiz kosinüs fark formülünü kullanarak yapabiliriz.
Temel özdeşliklerden tümler açıların sinüs ve kosinüs değerlerinin eşit olduğunu biliyoruz.
\( \sin(x + y) = \cos(\frac{\pi}{2} - (x + y)) \)
Eşitliğin sağ tarafında parantez içini düzenleyelim.
\( \sin(x + y) = \cos((\frac{\pi}{2} - x) - y)) \)
Eşitliğin sağ tarafını kosinüs fark formülünü kullanarak açalım.
\( \sin(x + y) = \cos(\frac{\pi}{2} - x)\cos{y} + \sin(\frac{\pi}{2} - x)\sin{y} \)
Tümler açı özdeşliklerini kullanırsak, sinüs toplam formülünü elde ederiz.
\( \sin(x + y) = \sin{x}\cos{y} + \cos{x}\sin{y} \)
Yukarıdaki toplam formülü bir özdeşlik olduğu için, \( y \) açısı yerine \( -y \) de yazabiliriz.
\( \sin(x + (-y)) = \sin{x}\cos(-y) + \cos{x}\sin(-y) \)
\( \cos(-y) = \cos{y} \)
\( \sin(-y) = -\sin{y} \)
Bu değerleri yerine koyarsak, sinüs fark formülünü elde ederiz.
\( \sin(x - y) = \sin{x}\cos{y} - \cos{x}\sin{y} \)
Tanjant Toplam ve Fark Formülleri
\( \tan(x + y) = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
\( \tan(x - y) = \dfrac{\tan{x} - \tan{y}}{1 + \tan{x}\tan{y}} \)
\( \tan{15°} = \tan(60° - 45°) \)
\( = \dfrac{\tan{60°} - \tan{45°}}{1 + \tan{60°}\tan{45°}} \)
\( = \dfrac{\sqrt{3} - 1}{1 + \sqrt{3} \cdot 1} \)
\( = \dfrac{(\sqrt{3} - 1)^2}{(\sqrt{3} - 1)(\sqrt{3} + 1)} \)
\( = \dfrac{(\sqrt{3} - 1)^2}{2} \)
İSPATI GÖSTER
Tanjant toplam ve fark formüllerinin ispatını, yukarıda ispatıyla birlikte verdiğimiz sinüs ve kosinüs toplam ve fark formüllerini kullanarak yapabiliriz.
\( \tan(x + y) = \dfrac{\sin(x + y)}{\cos(x + y)} \)
\( = \dfrac{\sin{x}\cos{y} + \cos{x}\sin{y}}{\cos{x}\cos{y} - \sin{x}\sin{y}} \)
Payı ve paydayı \( \cos{x}\cos{y} \)'ye bölelim.
\( = \dfrac{\dfrac{\sin{x}\cos{y} + \cos{x}\sin{y}}{\cos{x}\cos{y}}}{\dfrac{\cos{x}\cos{y} - \sin{x}\sin{y}}{\cos{x}\cos{y}}} \)
\( = \dfrac{\dfrac{\sin{x}\cos{y}}{\cos{x}\cos{y}} + \dfrac{\cos{x}\sin{y}}{\cos{x}\cos{y}}}{\dfrac{\cos{x}\cos{y}}{\cos{x}\cos{y}} - \dfrac{\sin{x}\sin{y}}{\cos{x}\cos{y}}} \)
İfadeleri sadeleştirelim.
\( = \dfrac{\dfrac{\sin{x}}{\cos{x}} + \dfrac{\sin{y}}{\cos{y}}}{\dfrac{1}{1} - \dfrac{\sin{x}\sin{y}}{\cos{x}\cos{y}}} \)
Sinüs ve kosinüs oranlarını tanjanta çevirirsek tanjant toplam formülünü elde ederiz.
\( \tan(x + y) = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
Yukarıdaki toplam formülü bir özdeşlik olduğu için, \( y \) açısı yerine \( -y \) de yazabiliriz.
\( \tan(x + (-y)) = \dfrac{\tan{x} + \tan(-y)}{1 - \tan{x} \cdot \tan(-y)} \)
\( \tan(-y) = -\tan{y} \)
Bu değeri yerine koyarsak, tanjant fark formülünü elde ederiz.
\( \tan(x - y) = \dfrac{\tan{x} - \tan{y}}{1 + \tan{x}\tan{y}} \)
İki Kat Açı Formülleri
Yukarıdaki toplam ve fark formüllerinde iki açı birbirine eşit alınırsa aşağıdaki formüller elde edilir.
Sinüs İki Kat Açı Formülü
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( x = 30° \)
\( \sin{60°} = 2\sin{30°}\cos{30°} \)
\( = 2 \cdot \dfrac{1}{2} \cdot \dfrac{\sqrt{3}}{2} = \dfrac{\sqrt{3}}{2} \)
İSPATI GÖSTER
Sinüs toplam formülünü kullanalım.
\( \sin(x + y) = \sin{x}\cos{y} + \cos{x}\sin{y} \)
Formülde \( y = x \) yazalım.
\( \sin(x + x) = \sin{x}\cos{x} + \cos{x}\sin{x} \)
\( \sin(2x) = 2\sin{x}\cos{x} \)
Kosinüs İki Kat Açı Formülleri
\( \cos(2x) = \cos^2{x} - \sin^2{x} \)
\( \cos(2x) = 2\cos^2{x} - 1 \)
\( \cos(2x) = 1 - 2\sin^2{x} \)
\( x = 30° \)
\( \cos{60°} = \cos^2{30°} - \sin^2{30°} \)
\( = \left( \dfrac{\sqrt{3}}{2} \right)^2 - \left( \dfrac{1}{2} \right)^2 \)
\( = \dfrac{3}{4} - \dfrac{1}{4} = \dfrac{1}{2} \)
İSPATI GÖSTER
Kosinüs toplam formülünü kullanalım.
\( \cos(x + y) = \cos{x}\cos{y} - \sin{x}\sin{y} \)
Formülde \( y = x \) yazalım.
\( \cos(x + x) = \cos{x}\cos{x} - \sin{x}\sin{x} \)
\( \cos(2x) = \cos^2{x} - \sin^2{x} \)
Sinüs - kosinüs kare toplamı özdeşliğini kullanarak bu özdeşliği bir diğer şekilde yazalım.
\( \sin^2{x} + \cos^2{x} = 1 \)
\( \sin^2{x} = 1 - \cos^2{x} \)
Son satırdaki ifadeyi yukarıdaki özdeşlikte yerine koyalım.
\( \cos(2x) = \cos^2{x} - (1 - \cos^2{x}) \)
\( \cos(2x) = 2\cos^2{x} - 1 \)
\( \cos^2{x} = 1 - \sin^2{x} \)
Son satırdaki ifadeyi yukarıdaki özdeşlikte yerine koyalım.
\( \cos(2x) = (1 - \sin^2{x}) - \sin^2{x} \)
\( \cos(2x) = 1 - 2\sin^2{x} \)
Tanjant İki Kat Açı Formülleri
\( \tan(2x) = \dfrac{2\tan{x}}{1 - \tan^2{x}} \)
\( \tan(2x) = \dfrac{2}{\cot{x} - \tan{x}} \)
\( x = 30° \)
\( \tan{60°} = \dfrac{2\tan{30°}}{1 - \tan^2{30°}} \)
\( = \dfrac{2\frac{\sqrt{3}}{3}}{1 - (\frac{\sqrt{3}}{3})^2} = \sqrt{3} \)
İSPATI GÖSTER
Tanjant toplam formülünü kullanalım.
\( \tan(x + y) = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
Formülde \( y = x \) yazalım.
\( \tan(x + x) = \dfrac{\tan{x} + \tan{x}}{1 - \tan{x}\tan{x}} \)
\( \tan(2x) = \dfrac{2\tan{x}}{1 - \tan^2{x}} \)
Payı ve paydayı \( \tan{x} \)'e bölelim.
\( \tan(2x) = \dfrac{2}{\dfrac{1}{\tan{x}} - \dfrac{\tan^2{x}}{\tan{x}}} \)
\( \tan(2x) = \dfrac{2}{\cot{x} - \tan{x}} \)
\( 0 \lt x \lt \dfrac{\pi}{2} \) olmak üzere,
\( \sin{x} = \dfrac{7}{25} \) olduğuna göre, \( \sin(2x) \) kaçtır?
Çözümü GösterSinüs değeri \( \frac{7}{25} \) olan \( x \) açısının karşı kenarına \( 7k \), hipotenüse \( 25k \) dersek bu açının komşu kenarı Pisagor teoremine göre \( 24k \) olur.
\( (7k)^2 + (24k)^2 = (25k)^2 \)
\( \cos{x} = \dfrac{24k}{25k} = \dfrac{24}{25} \)
Sinüs iki kat açı formülünü kullanalım.
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( = 2 \cdot \dfrac{7}{25} \cdot \dfrac{24}{25} = \dfrac{336}{625} \) bulunur.
\( x, y \in [0, \frac{\pi}{2}] \) olmak üzere,
\( \tan{x} = \dfrac{3}{4}, \quad \cot{y} = \dfrac{8}{15} \)
olduğuna göre, \( \sin(x - y) \) kaçtır?
Çözümü Göster\( x \) açısının tanjant değeri \( \frac{3}{4} \) olduğuna göre, diğer trigonometrik oranları 3-4-5 özel üçgenini kullanarak bulabiliriz.
\( \sin{x} = \dfrac{3}{5}, \quad \cos{x} = \dfrac{4}{5} \)
\( y \) açısının kotanjant değeri \( \frac{8}{15} \) olduğuna göre, diğer trigonometrik fonksiyon değerlerini 8-15-17 özel üçgenini kullanarak bulabiliriz.
\( \sin{y} = \dfrac{15}{17}, \quad \cos{y} = \dfrac{8}{17} \)
Sinüs fark formülünü kullanalım.
\( \sin(x - y) = \sin{x}\cos{y} - \cos{x}\sin{y} \)
\( = \dfrac{3}{5} \cdot \dfrac{8}{17} - \dfrac{4}{5} \cdot \dfrac{15}{17} \)
\( = -\dfrac{36}{85} \) bulunur.
\( \cos(2x + \frac{\pi}{3}) + \cos(2x - \frac{\pi}{3}) \) ifadesinin en sade halini bulunuz.
Çözümü GösterKosinüs toplam ve fark formüllerini kullanalım.
\( \cos(2x)\cos{\dfrac{\pi}{3}} - \sin(2x)\sin{\dfrac{\pi}{3}} + \cos(2x)\cos{\dfrac{\pi}{3}} + \sin(2x)\sin{\dfrac{\pi}{3}} \)
\( = 2\cos(2x)\cos{\dfrac{\pi}{3}} \)
\( = 2\cos(2x) \cdot \dfrac{1}{2} \)
\( = \cos(2x) \) bulunur.
\( \cos(2x) + \tan{x}\sin(2x) \) ifadesinin en sade halini bulunuz.
Çözümü GösterSinüs ve kosinüs iki kat açı formüllerini kullanalım.
\( (1 - 2\sin^2{x}) + \dfrac{\sin{x}}{\cos{x}} \cdot 2\sin{x}\cos{x} \)
\( = 1 - 2\sin^2{x} + 2\sin^2{x} \)
\( = 1 \) bulunur.
\( \tan{105°} \) ifadesinin değerini bulunuz.
Çözümü GösterTanjant toplam formülünü kullanalım.
\( \tan(x + y) = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
Formülde \( x = 60° \) ve \( y = 45° \) verelim.
\( \tan(60° + 45°) = \dfrac{\tan{60°} + \tan{45°}}{1 - \tan{60°}\tan{45°}} \)
Trigonometrik ifadelerin değerlerini yazalım.
\( \tan{105°} = \dfrac{\sqrt{3} + 1}{1 - \sqrt{3} \cdot 1} \)
\( = \dfrac{\sqrt{3} + 1}{1 - \sqrt{3}} \)
Paydayı rasyonel hale getirmek için payı ve paydayı paydanın eşleniği ile çarpalım.
\( = \dfrac{(\sqrt{3} + 1)^2}{1^2 - (\sqrt{3})^2} \)
\( = \dfrac{3 - 2\sqrt{3} + 1}{-2} \)
\( = -2 - \sqrt{3} \) bulunur.
\( \csc{15°} \) ifadesinin değerini bulunuz.
Çözümü GösterSinüs fark formülünü kullanalım.
\( \sin(x - y) = \sin{x}\cos{y} - \cos{x}\sin{y} \)
Formülde \( x = 45° \) ve \( y = 30° \) verelim.
\( \sin(45° - 30°) = \sin{45°}\cos{30°} - \cos{45°}\sin{30°} \)
Trigonometrik ifadelerin değerlerini yazalım.
\( \sin{15°} = \dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{3}}{2} - \dfrac{\sqrt{2}}{2} \cdot \dfrac{1}{2} \)
\( = \dfrac{\sqrt{6} - \sqrt{2}}{4}\)
Kosekantı sinüs cinsinden yazalım.
\( \csc{15°} = \dfrac{1}{\sin{15°}} \)
\( = \dfrac{1}{\frac{\sqrt{6} - \sqrt{2}}{4}} = \dfrac{4}{\sqrt{6} - \sqrt{2}} \)
Paydayı rasyonel hale getirmek için payı ve paydayı paydanın eşleniği ile çarpalım.
\( = \dfrac{4(\sqrt{6} + \sqrt{2})}{(\sqrt{6})^2 - (\sqrt{2})^2} \)
\( = \sqrt{6} + \sqrt{2} \) bulunur.
\( \cos{\dfrac{3\pi}{8}} \) ifadesinin değerini bulunuz.
Çözümü Göster\( \frac{3\pi}{8} \) açısının kosinüs değerini \( \frac{3\pi}{4} \) açısının kosinüs değerini ve kosinüs iki kat açı formülünü kullanarak bulalım.
\( \cos(2x) = 2\cos^2{x} - 1 \)
\( x = \frac{3\pi}{8} \) yazalım.
\( \cos\left( 2 \cdot \dfrac{3\pi}{8} \right) = 2\cos^2{\dfrac{3\pi}{8}} - 1 \)
\( \cos{\dfrac{3\pi}{4}} = 2\cos^2{\dfrac{3\pi}{8}} - 1 \)
Kosinüs II. bölgede negatiftir.
\( -\dfrac{\sqrt{2}}{2} = 2\cos^2{\dfrac{3\pi}{8}} - 1 \)
\( 2\cos^2{\dfrac{3\pi}{8}} = 1 - \dfrac{\sqrt{2}}{2} \)
\( \cos^2{\dfrac{3\pi}{8}} = \dfrac{2 - \sqrt{2}}{4} \)
Kosinüs I. bölgede pozitiftir.
\( \cos{\dfrac{3\pi}{8}} = \dfrac{\sqrt{2 - \sqrt{2}}}{2} \)
\( \sin{\dfrac{\pi}{8}} \) ifadesinin değerini bulunuz.
Çözümü GösterKosinüs iki kat açı formülünü kullanalım.
\( \cos(2x) = 1 - 2\sin^2{x} \)
\( x = \frac{\pi}{8} \) yazalım.
\( \cos{\dfrac{\pi}{4}} = 1 - 2\sin^2{\dfrac{\pi}{8}} \)
\( \sin^2{\dfrac{\pi}{8}} = \dfrac{1 - \cos{\frac{\pi}{4}}}{2} \)
\( = \dfrac{1 - \frac{\sqrt{2}}{2}}{2} \)
\( = \dfrac{2 - \sqrt{2}}{4} \)
Sinüs I. bölgede pozitiftir.
\( \sin{\dfrac{\pi}{8}} = \dfrac{\sqrt{2 - \sqrt{2}}}{2} \) bulunur.
\( x \) açısı II. bölgede, \( y \) açısı III. bölgede olmak üzere,
\( \sin{x} = \dfrac{5}{13}, \quad \sin{y} = -\dfrac{7}{25} \)
olduğuna göre, \( \sin(x + y) \) kaçtır?
Çözümü Göster\( x \) açısının sinüs değeri \( \frac{5}{13} \) olduğuna göre, diğer trigonometrik oranları 5-12-13 özel üçgenini kullanarak bulabiliriz.
\( x \) açısının bulunduğu II. bölgede sinüs pozitif, kosinüs negatiftir.
\( \sin{x} = \dfrac{5}{13}, \quad \cos{x} = -\dfrac{12}{13} \)
\( y \) açısının sinüs değeri \( -\frac{7}{25} \) olduğuna göre, diğer trigonometrik oranları 7-24-25 özel üçgenini kullanarak bulabiliriz.
\( y \) açısının bulunduğu III. bölgede sinüs ve kosinüs negatiftir.
\( \sin{y} = -\dfrac{7}{25}, \quad \cos{y} = -\dfrac{24}{25} \)
Sinüs toplam formülünü kullanalım.
\( \sin(x + y) = \sin{x}\cos{y} + \cos{x}\sin{y} \)
\( = \dfrac{5}{13} \cdot (-\dfrac{24}{25}) + (-\dfrac{12}{13}) \cdot (-\dfrac{7}{25}) \)
\( = -\dfrac{120}{325} + \dfrac{84}{325} \)
\( = -\dfrac{36}{325} \) bulunur
\( \sin{x} + \cos{x} = \dfrac{2}{3} \) olduğuna göre, \( \sin(2x) \) kaçtır?
Çözümü Gösterİki tarafın karesini alalım.
\( (\sin{x} + \cos{x})^2 = \left( \dfrac{2}{3} \right)^2 \)
\( \sin^2{x} + 2\sin{x}\cos{x} + \cos^2{x} = \dfrac{4}{9} \)
Pisagor özdeşliğini kullanalım.
\( 1 + 2\sin{x}\cos{x} = \dfrac{4}{9} \)
Sinüs iki kat açı formülünü kullanalım.
\( \sin(2x) = -\dfrac{5}{9} \) bulunur.
\( \cos\left( x + \dfrac{\pi}{3} \right) = 3\cos\left( x - \dfrac{\pi}{3} \right) \)
olduğuna göre \( \tan{x} \) kaçtır?
Çözümü GösterKosinüs toplam ve fark formüllerini kullanalım.
\( \cos{x}\cos{\dfrac{\pi}{3}} - \sin{x}\sin{\dfrac{\pi}{3}} = 3\cos{x}\cos{\dfrac{\pi}{3}} + 3\sin{x}\sin{\dfrac{\pi}{3}} \)
Trigonometrik ifadelerin değerlerini yazalım.
\( \cos{x} \cdot \dfrac{1}{2} - \sin{x} \cdot \dfrac{\sqrt{3}}{2} = 3\cos{x} \cdot \dfrac{1}{2} + 3\sin{x} \cdot \dfrac{\sqrt{3}}{2} \)
\( \cos{x} - \sqrt{3}\sin{x} = 3\cos{x} + 3\sqrt{3}\sin{x} \)
\( 4\sqrt{3}\sin{x} = -2\cos{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = -\dfrac{2}{4\sqrt{3}} \)
\( \tan{x} = -\dfrac{1}{2\sqrt{3}} = -\dfrac{\sqrt{3}}{6} \) bulunur.
\( 2\cot(2x) + \tan{x} \) ifadesinin en sade halini bulunuz.
Çözümü GösterTanjant ve kotanjant ifadelerini sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{2\cos(2x)}{\sin(2x)} + \dfrac{\sin{x}}{\cos{x}} \)
Kosinüs ve sinüs iki kat açı formüllerini kullanalım.
\( = \dfrac{2(\cos^2{x} - \sin^2{x})}{2\sin{x}\cos{x}} + \dfrac{\sin{x}}{\cos{x}} \)
\( = \dfrac{\cos^2{x}}{\sin{x}\cos{x}} - \dfrac{\sin^2{x}}{\sin{x}\cos{x}} + \dfrac{\sin{x}}{\cos{x}} \)
\( = \dfrac{\cos{x}}{\sin{x}} - \dfrac{\sin{x}}{\cos{x}} + \dfrac{\sin{x}}{\cos{x}} \)
\( = \dfrac{\cos{x}}{\sin{x}} = \cot{x} \) bulunur.
\( a + b = \dfrac{\pi}{6} \) olduğuna göre,
\( (\cos{a} + \cos{b})^2 + (\sin{a} - \sin{b})^2 \) ifadesinin eşiti kaçtır?
Çözümü GösterParantezli ifadelerin açılımını yazalım.
\( (\cos{a} + \cos{b})^2 + (\sin{a} - \sin{b})^2 \)
\( = \cos^2{a} + 2\cos{a}\cos{b} + \cos^2{b} + \sin^2{a} - 2\sin{a}\sin{b} + \sin^2{b} \)
Pisagor özdeşliğini kullanalım.
\( = 1 + 1 + 2(\cos{a}\cos{b} - \sin{a}\sin{b}) \)
Parantez içindeki ifade kosinüs toplam formülüdür.
\( = 2 + 2\cos(a + b) \)
\( = 2 + 2\cos{\dfrac{\pi}{6}} \)
\( = 2 + 2 \cdot \dfrac{\sqrt{3}}{2} \)
\( = \sqrt{3} + 2 \) bulunur.
\( \tan{\dfrac{\pi}{8}} \) ifadesinin değerini bulunuz.
Çözümü GösterTanjant iki kat açı formülünü kullanalım.
\( \tan(2x) = \dfrac{2\tan{x}}{1 - \tan^2{x}} \)
\( x = \frac{\pi}{8} \) yazalım.
\( \tan{\dfrac{\pi}{4}} = \dfrac{2\tan{\frac{\pi}{8}}}{1 - \tan^2{\frac{\pi}{8}}} \)
\( 1 = \dfrac{2\tan{\frac{\pi}{8}}}{1 - \tan^2{\frac{\pi}{8}}} \)
\( \tan{\frac{\pi}{8}} = t \) şeklinde değişken değiştirelim.
\( 1 = \dfrac{2t}{1 - t^2} \)
\( t^2 + 2t - 1 = 0 \)
\( (t + 1)^2 - 2 = 0 \)
Tanjant I. bölgede pozitiftir.
\( t + 1 = \sqrt{2} \)
\( t = \sqrt{2} - 1 \)
\( \tan{\dfrac{\pi}{8}} = \sqrt{2} - 1 \) bulunur.
\( \cos{25°} = x \) olduğuna göre,
\( \cos{130°} - \sin{40°} \) ifadesinin \( x \) cinsinden değeri nedir?
Çözümü Göster\( 130° \) II. bölgededir ve kosinüs bu bölgede negatiftir.
\( \cos{130°} = \cos(180° - 50°) = -\cos{50°} \)
Tümler açıların sinüs ve kosinüs değerleri birbirine eşittir.
\( \sin{40°} = \cos{50°} \)
\( \cos{130°} - \sin{40°} = -\cos{50°} - \cos{50°} = -2\cos{50°} \)
\( = -2\cos(2 \cdot 25°) \)
Kosinüs iki kat açı formülünü kullanalım.
\( = -2(2\cos^2{25°} - 1) \)
\( = -2(2x^2 - 1) \)
\( = 2 - 4x^2 \) bulunur.
\( \cos{200°} = x \) olduğuna göre,
\( \sin{80°} \) ifadesinin \( x \) cinsinden değeri nedir?
Çözümü GösterTümler açıların sinüs ve kosinüs değerleri birbirine eşittir.
\( \sin{80°} = \cos{10°} \)
\( \cos{200°} = -\cos{20°} = x \)
\( \cos{20°} = -x \)
\( \cos{20°} \) değerini kullanarak \( \cos{10°} \) değerini bulmak için kosinüs iki kat açı formülünü kullanalım.
\( \cos{20°} = 2\cos^2{10°} - 1 \)
\( x = 2\cos^2{10°} - 1 \)
\( \cos^2{10°} = \dfrac{-x + 1}{2} \)
\( 10° \) I. bölgede olduğu için kosinüs değeri pozitiftir.
\( \cos{10°} = \sin{80°} = \sqrt{\dfrac{1 - x}{2}} \) bulunur.
\( \tan{x} - \cot{x} = \dfrac{3}{5} \) olduğuna göre, \( \tan(2x) \) kaçtır?
Çözümü GösterTanjant ve kotanjant ifadelerini sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{\sin{x}}{\cos{x}} - \dfrac{\cos{x}}{\sin{x}} = \dfrac{3}{5} \)
\( \dfrac{\sin^2{x} - \cos^2{x}}{\sin{x}\cos{x}} = \dfrac{3}{5} \)
Paydaki ifade için kosinüs, paydadaki ifade için sinüs iki kat açı formüllerini kullanalım.
\( \dfrac{-\cos(2x)}{\frac{1}{2}\sin(2x)} = \dfrac{3}{5} \)
\( \dfrac{\cos(2x)}{\sin(2x)} = -\dfrac{3}{10} \)
Eşitliğin iki tarafının çarpmaya göre tersini alalım.
\( \dfrac{\sin(2x)}{\cos(2x)} = -\dfrac{10}{3} \)
\( \tan(2x) = -\dfrac{10}{3} \) bulunur.
\( ABC \) üçgeninin iç açılarının ölçüleri \( a, b, c \) olarak veriliyor.
\( \cos{a} = \frac{4}{5} \) ve \( \tan{b} = \frac{12}{5} \) olduğuna göre, \( \sin{c} \) kaçtır?
Çözümü Göster\( a \) açısının kosinüs değeri \( \frac{4}{5} \) olduğuna göre, diğer trigonometrik oranları 3-4-5 özel üçgenini kullanarak bulabiliriz.
\( \sin{a} = \dfrac{3}{5}, \quad \cos{a} = \dfrac{4}{5} \)
\( b \) açısının tanjant değeri \( \frac{12}{5} \) olduğuna göre, diğer trigonometrik oranları 12-5-13 özel üçgenini kullanarak bulabiliriz.
\( \sin{b} = \dfrac{12}{13}, \quad \cos{b} = \dfrac{5}{13} \)
Üçgenin iç açıları toplamı 180°'dir.
\( a + b + c = 180° \)
\( c = 180° - (a + b) \)
Ölçüleri eşit açıların trigonometrik değerleri de eşittir.
\( \sin{c} = \sin(180° - (a + b)) \)
Sinüs II. bölgede pozitiftir.
\( = \sin(a + b) \)
Sinüs toplam formülünü kullanalım.
\( = \sin{a}\cos{b} + \cos{a}\sin{b} \)
\( = \dfrac{3}{5} \cdot \dfrac{5}{13} + \dfrac{4}{5} \cdot \dfrac{12}{13} = \dfrac{63}{65} \) bulunur.
\( \dfrac{1 - \tan^2{\frac{x}{2}}}{1 + \tan^2{\frac{x}{2}}} \) ifadesinin en sade halini bulunuz.
Çözümü GösterTanjant ifadesini sinüs ve kosinüs cinsinden yazalım.
\( \dfrac{1 - \tan^2{\frac{x}{2}}}{1 + \tan^2{\frac{x}{2}}} = \dfrac{1 - \frac{\sin^2{\frac{x}{2}}}{\cos^2{\frac{x}{2}}}}{1 + \frac{\sin^2{\frac{x}{2}}}{\cos^2{\frac{x}{2}}}} \)
\( = \dfrac{\frac{\cos^2{\frac{x}{2}} - \sin^2{\frac{x}{2}}}{\cos^2{\frac{x}{2}}}}{\frac{\cos^2{\frac{x}{2}} + \sin^2{\frac{x}{2}}}{\cos^2{\frac{x}{2}}}} \)
\( = \dfrac{\cos^2{\frac{x}{2}} - \sin^2{\frac{x}{2}}}{\cos^2{\frac{x}{2}} + \sin^2{\frac{x}{2}}} \)
Payda kosinüs iki kat açı formülünü, paydada Pisagor özdeşliğini kullanalım.
\( = \dfrac{\cos{x}}{1} = \cos{x} \) bulunur.
\( \dfrac{\sin(2x)}{\sin{x}} - \dfrac{\cos(2x)}{\cos{x}} \) ifadesinin en sade halini bulunuz.
Çözümü GösterTerimlerin paydalarını eşitleyelim.
\( \dfrac{\sin(2x)\cos{x}}{\sin{x}\cos{x}} - \dfrac{\cos(2x)\sin{x}}{\cos{x}\sin{x}} \)
\( = \dfrac{\sin(2x)\cos{x} - \cos(2x)\sin{x}}{\cos{x}\sin{x}} \)
Paydaki ifade sinüs fark formülünün açılımıdır.
\( = \dfrac{\sin(2x - x)}{\sin{x}\cos{x}} \)
\( = \dfrac{\sin{x}}{\sin{x}\cos{x}} \)
\( = \dfrac{1}{\cos{x}} = \sec{x} \) bulunur.
\( \dfrac{\sin(3x)}{\sin{x}} - \dfrac{\cos(3x)}{\cos{x}} \) ifadesinin en sade halini bulunuz.
Çözümü GösterTerimlerin paydalarını eşitleyelim.
\( \dfrac{\sin(3x)\cos{x}}{\sin{x}\cos{x}} - \dfrac{\cos(3x)\sin{x}}{\cos{x}\sin{x}} \)
\( = \dfrac{\sin(3x)\cos{x} - \cos(3x)\sin{x}}{\cos{x}\sin{x}} \)
Paydaki ifade sinüs fark formülünün açılımıdır.
\( = \dfrac{\sin(3x - x)}{\cos{x}\sin{x}} \)
\( = \dfrac{\sin(2x)}{\cos{x}\sin{x}} \)
Sinüs iki kat açı formülünü kullanalım.
\( = \dfrac{2\sin{x}\cos{x}}{\cos{x}\sin{x}} = 2 \) bulunur.
\( \dfrac{1 + \cos{24°}}{1 - \cos{24°}} \) ifadesinin en sade halini bulunuz.
Çözümü GösterKosinüs iki kat açı formülünün iki formu aşağıdaki gibidir.
\( \cos(2x) = 2\cos^2{x} - 1 \)
\( \cos(2x) = 1 - 2\sin^2{x} \)
Bu iki formülden birinciyi payda, ikinciyi paydada kullanalım.
\( \dfrac{1 + \cos{24°}}{1 - \cos{24°}} = \dfrac{1 + 2\cos^2{12°} - 1}{1 - (1 - 2\sin^2{12°})} \)
\( = \dfrac{2\cos^2{12°}}{2\sin^2{12°}} \)
\( = \cot^2{12°} \) bulunur.
\( \cos{20°}\cos{40°}\cos{80°} \) ifadesinin en sade halini bulunuz.
Çözümü Göster\( \cos{20°}\cos{40°}\cos{80°} \)
Payı ve paydayı \( 2\sin{20°} \) ile çarpalım.
\( = \dfrac{2\sin{20°}\cos{20°}\cos{40°}\cos{80°}}{2\sin{20°}} \)
Paya sinüs iki kat açı formülünü uygulayalım.
\( 2\sin{20°}\cos{20°} = \sin{40°} \)
\( = \dfrac{\sin{40°}\cos{40°}\cos{80°}}{2\sin{20°}} \)
Paya tekrar sinüs iki kat açı formülünü uygulayalım.
\( 2\sin{40°}\cos{40°} = \sin{80°} \)
\( = \dfrac{\sin{80°}\cos{80°}}{4\sin{20°}} \)
Paya tekrar sinüs iki kat açı formülünü uygulayalım.
\( 2\sin{80°}\cos{80°} = \sin{160°} \)
\( = \dfrac{\sin{160°}}{8\sin{20°}} \)
Sinüs II. bölgede pozitiftir.
\( \sin{160°} = \sin(180° - 20°) = \sin{20°} \)
\( = \dfrac{\sin{20°}}{8\sin{20°}} = \dfrac{1}{8} \) bulunur.
\( \cos{15°} + \sqrt{3} \sin{15°} \) ifadesinin değerini bulunuz.
Çözümü Göster\( \sqrt{3} = \tan{60°} \) yazalım.
\( \cos{15°} + \tan{60°}\sin{15°} \)
\( = \cos{15°} + \dfrac{\sin{60°}}{\cos{60°}} \cdot \sin{15°} \)
Terimleri aynı paydada birleştirelim.
\( = \dfrac{\cos{15°}\cos{60°} + \sin{15°}\sin{60°}}{\cos{60°}} \)
Paydaki ifade kosinüs fark formülünün açılımıdır.
\( = \dfrac{\cos(60° - 15°)}{\cos{60°}} \)
\( = \dfrac{\cos{45°}}{\cos{60°}} \)
\( = \dfrac{\frac{\sqrt{2}}{2}}{\frac{1}{2}} = \sqrt{2} \) bulunur.
\( \cos{x} = \dfrac{2}{3} \) olduğuna göre,
\( \cos{x}\cos(2x)\cos(4x) \) ifadesinin değeri kaçtır?
Çözümü GösterKosinüs iki kat açı formülünü kullanalım.
\( \cos{x}\cos(2x)(2\cos^2(2x) - 1) \)
\( = 2\cos{x}\cos^3(2x) - \cos{x}\cos(2x) \)
Tekrar kosinüs iki kat açı formülünü kullanalım.
\( = 2\cos{x}(2\cos^2{x} - 1)^3 - \cos{x}(2\cos^2{x} - 1) \)
\( \cos{x} = \dfrac{2}{3} \) yazalım.
\( = 2 \cdot \dfrac{2}{3} \cdot [2(\dfrac{2}{3})^2 - 1]^3 - \dfrac{2}{3} \cdot [2(\dfrac{2}{3})^2 - 1] \)
\( = \dfrac{4}{3} \cdot (-\dfrac{1}{729}) - \dfrac{2}{3} \cdot (-\dfrac{1}{9}) \)
\( = -\dfrac{4}{2187} + \dfrac{2}{27} \)
\( = \dfrac{158}{2187} \) bulunur.
\( \tan{\alpha} + \tan{\beta} = 3 \)
\( \cot{\alpha} + \cot{\beta} = 5 \)
olduğuna göre, \( \tan(\alpha + \beta) \) ifadesinin değeri kaçtır?
Çözümü GösterTanjant toplam formülünü yazalım.
\( \tan(\alpha + \beta) = \dfrac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha}\tan{\beta}} \)
\( \tan{\alpha}\tan{\beta} \) çarpımını bulmak için \( \cot{\alpha} + \cot{\beta} = 5 \) eşitliğini kullanalım.
\( \cot{\alpha} + \cot{\beta} = 5 \)
\( \dfrac{1}{\tan{\alpha}} + \dfrac{1}{\tan{\beta}} = 5 \)
\( \dfrac{\tan{\alpha} + \tan{\beta}}{\tan{\alpha}\tan{\beta}} = 5 \)
\( \dfrac{3}{\tan{\alpha}\tan{\beta}} = 5 \)
\( \tan{\alpha}\tan{\beta} = \dfrac{3}{5} \)
Bu değeri istenen ifadede yerine koyalım.
\( \tan(\alpha + \beta) = \dfrac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha}\tan{\beta}} \)
\( = \dfrac{3}{1 - \frac{3}{5}} = \dfrac{15}{2} \) bulunur.
\( \dfrac{1 + \tan{15°}}{1 - \tan{15°}} \) ifadesinin değeri kaçtır?
Çözümü GösterVerilen ifadeyi tanjant toplam formülüne benzetelim.
\( 1 = \tan{45°} \) yazalım.
\( \dfrac{1 + \tan{15°}}{1 - \tan{15°}} = \dfrac{\tan{45°} + \tan{15°}}{1 - \tan{45°}\tan{15°}} \)
\( x = 45° \) ve \( y = 15° \) olarak kabul edersek bu ifade \( \tan(45° + 15°) \) toplam formülünün açılımıdır.
\( = \tan(45° + 15°) \)
\( = \tan{60°} = \sqrt{3} \) bulunur.
\( \sin(2x) = \dfrac{2}{5} \) olduğuna göre,
\( \cos^6{x} + \sin^6{x} \) ifadesinin sonucu kaçtır?
Çözümü GösterKüpler toplamı formülünü kullanalım.
\( a^3 + b^3 = (a + b)(a^2 - ab + b^2) \)
\( \cos^6{x} + \sin^6{x} = (\cos^2{x})^3 + (\sin^2{x})^3 \)
\( = (\cos^2{x} + \sin^2{x})[(\cos^2{x})^2 - \cos^2{x}\sin^2{x} + (\sin^2{x})^2] \)
Pisagor özdeşliğini kullanalım.
\( = (\cos^2{x})^2 - \cos^2{x}\sin^2{x} + (\sin^2{x})^2 \)
\( a^2 - ab + b^2 = (a + b)^2 - 3ab \) özdeşliğini kullanalım.
\( = (\cos^2{x} + \sin^2{x})^2 - 3\cos^2{x}\sin^2{x} \)
Pisagor özdeşliğini kullanalım.
\( = 1^2 - 3\cos^2{x}\sin^2{x} \)
\( = 1 - \dfrac{3}{4}(4\cos^2{x}\sin^2{x}) \)
Sinüs iki kat açı formülünü kullanalım.
\( = 1 - \dfrac{3}{4}\sin^2(2x) \)
\( \sin(2x) = \dfrac{2}{5} \) olarak veriliyor.
\( = 1 - \dfrac{3}{4} \cdot (\dfrac{2}{5})^2 \)
\( = 1 - \dfrac{3}{25} = \dfrac{22}{25} \) bulunur.
\( \sin^4{x} + \cos^4{x} \) ifadesinin alabileceği en küçük değer kaçtır?
Çözümü GösterVerilen ifadeyi düzenleyelim.
\( \sin^4{x} + \cos^4{x} = (\sin^2{x} + \cos^2{x})^2 - 2\sin^2{x}\cos^2{x} \)
Pisagor özdeşliğini kullanalım.
\( = 1^2 - 2\sin^2{x}\cos^2{x} \)
\( = 1 - \dfrac{1}{2}(2\sin{x}\cos{x})^2 \)
Sinüs iki kat açı formülünü kullanalım.
\( \sin^4{x} + \cos^4{x} = 1 - \dfrac{1}{2}\sin^2(2x) \)
Sinüs fonksiyonu \( [-1, 1] \) aralığında değer alır.
\( -1 \le \sin(2x) \le 1 \)
Eşitsizliğin taraflarının karesini alalım.
\( 0 \le \sin^2(2x) \le 1 \)
Eşitsizliğin taraflarını 2'ye bölelim.
\( 0 \le \dfrac{1}{2}\sin^2(2x) \le \dfrac{1}{2} \)
Eşitsizliğin taraflarını -1 ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile çarpılırsa eşitsizlik yön değiştirir.
\( -\dfrac{1}{2} \le -\dfrac{1}{2}\sin^2(2x) \le 0 \)
Eşitsizliğin taraflarına 1 ekleyelim.
\( \dfrac{1}{2} \le 1 - \dfrac{1}{2}\sin^2(2x) \le 1 \)
Ortadaki ifade en küçük değeri sorulan ifadeye eşittir.
\( \dfrac{1}{2} \le \sin^4{x} + \cos^4{x} \le 1 \)
Buna göre verilen ifadenin alabileceği en küçük değer \( \frac{1}{2} \) olarak bulunur.
\( \dfrac{\pi}{2} \le x \lt \pi \) olmak üzere,
\( 3\sin{x} - 4\cos{x} = 5 \) olduğuna göre, \( \tan{x} \) değerini bulunuz.
Çözümü GösterEşitliğin taraflarını katsayıların kareleri toplamı 1 olacak şekilde 5'e bölelim.
\( \sin{x} \cdot \dfrac{3}{5} - \cos{x} \cdot \dfrac{4}{5} = 1 \)
Sinüs fark formülü aşağıdaki gibidir.
\( \sin(x - y) = \sin{x}\cos{y} - \cos{x}\sin{y} \)
İfadeyi sinüs fark formülünün açılımına benzetmek için aşağıdaki trigonometrik değerlere sahip bir \( y \) açısı tanımlayalım. Değerlerin kareleri toplamı 1 olduğu için böyle bir açı olduğundan emin olabiliriz.
\( \cos{y} = \frac{3}{5}, \quad \sin{y} = \frac{4}{5} \) olmak üzere,
\( (\frac{3}{5})^2 + (\frac{4}{5})^2 = 1^2 \)
\( \sin(x - y) = \sin{x}\cos{y} - \cos{x}\sin{y} \)
\( \sin(x - y) = 1 \)
Sinüs değeri 1 olan açı \( \frac{\pi}{2} \)'dir.
\( x - y = \dfrac{\pi}{2} \)
\( x = \dfrac{\pi}{2} + y \)
\( x \) açısının tanjant değerini bulalım.
Tanjant II. bölgede negatiftir.
\( \tan{x} = \tan\left( \frac{\pi}{2} + y \right) = -\cot{y} \)
Sinüs değeri \( \frac{4}{5} \) olan \( y \) açısının karşı kenarına \( 4k \), hipotenüse \( 5k \) dersek komşu kenar \( 3k \) ve kotanjant değeri \( \frac{3k}{4k} = \frac{3}{4} \) olur.
\( = -\dfrac{3}{4} \) bulunur.
\( x + y = \dfrac{\pi}{4} \) olduğuna göre,
\( \dfrac{(1 + \tan{x})(1 + \tan{y})}{\tan(x + y)} \)
ifadesinin en sade halini bulunuz.
Çözümü Göster\( x \) ve \( y \) açıları için tanjant toplam formülünü yazalım.
\( \tan(x + y) = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
\( x + y = \dfrac{\pi}{4} \) olarak veriliyor.
\( \tan{\dfrac{\pi}{4}} = 1 = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
\( 1 - \tan{x}\tan{y} = \tan{x} + \tan{y} \)
\( \tan{x} + \tan{y} + \tan{x}\tan{y} = 1 \)
Soruda verilen ifadede payın açılımını yazalım.
\( \dfrac{(1 + \tan{x})(1 + \tan{y})}{\tan(x + y)} \)
\( = \dfrac{1 + \tan{x} + \tan{y} + \tan{x}\tan{y}}{1} \)
Paydaki trigonometrik ifadenin değerini yukarıda 1 olarak bulmuştuk.
\( = 1 + 1 = 2 \) olarak bulunur.
Yukarıdaki şekilde merkezleri ortak olan iki kare verilmiştir. Büyük kare, içteki kare ve dört eş üçgenden oluşmaktadır.
Üçgenlerden her birinin alanı, büyük karenin alanının onikide biri olduğuna göre, \( x \) kaç derecedir?
Çözümü Göster\( a \le b \) olmak üzere, üçgenin dik kenarlarına \( a \) ve \( b \), üçgenin hipotenüsüne \( c \) diyelim.
Eş üçgenlerin her birinin alanının içteki karenin alanına oranını bulalım.
Üçgenlerden her birinin alanı büyük karenin alanının onikide biri olduğuna göre, üçgenlerin toplam alanı büyük karenin alanının \( 4 \cdot \frac{1}{12} = \frac{1}{3} \)'ü olur.
Dolayısıyla, içteki karenin alanı büyük karenin alanının \( 1 - \frac{1}{3} = \frac{2}{3} \)'ü olur.
\( \dfrac{\frac{1}{12}}{\frac{2}{3}} = \dfrac{1 \cdot 3}{12 \cdot 2} = \dfrac{1}{8} \)
Buna göre, eş üçgenlerin her birinin alanı içteki karenin alanının sekizde biridir.
Bir üçgenin alanı \( \frac{ab}{2} \), içteki karenin alanı \( c^2 \) ile hesaplanır.
\( \dfrac{\frac{ab}{2}}{c^2} = \dfrac{1}{8} \)
\( c^2 = 4ab \)
\( a \) ve \( b \) uzunluklarını \( x \) cinsinden yazalım.
\( a = c\sin{x} \)
\( b = c\cos{x} \)
Bu değerleri denklemde yerine yazalım.
\( c^2 = 4(c\sin{x})(c\cos{x}) \)
\( c^2 = 4c^2\sin{x}\cos{x} \)
\( 1 = 4\sin{x}\cos{x} \)
Sinüs iki kat açı formülünü kullanalım.
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( 1 = 2\sin(2x) \)
\( \sin(2x) = \dfrac{1}{2} \)
\( a \le b \) olarak kabul ettiğimiz için \( 2x \) dar açıdır.
\( 2x = 30° \)
\( x = 15° \) bulunur.
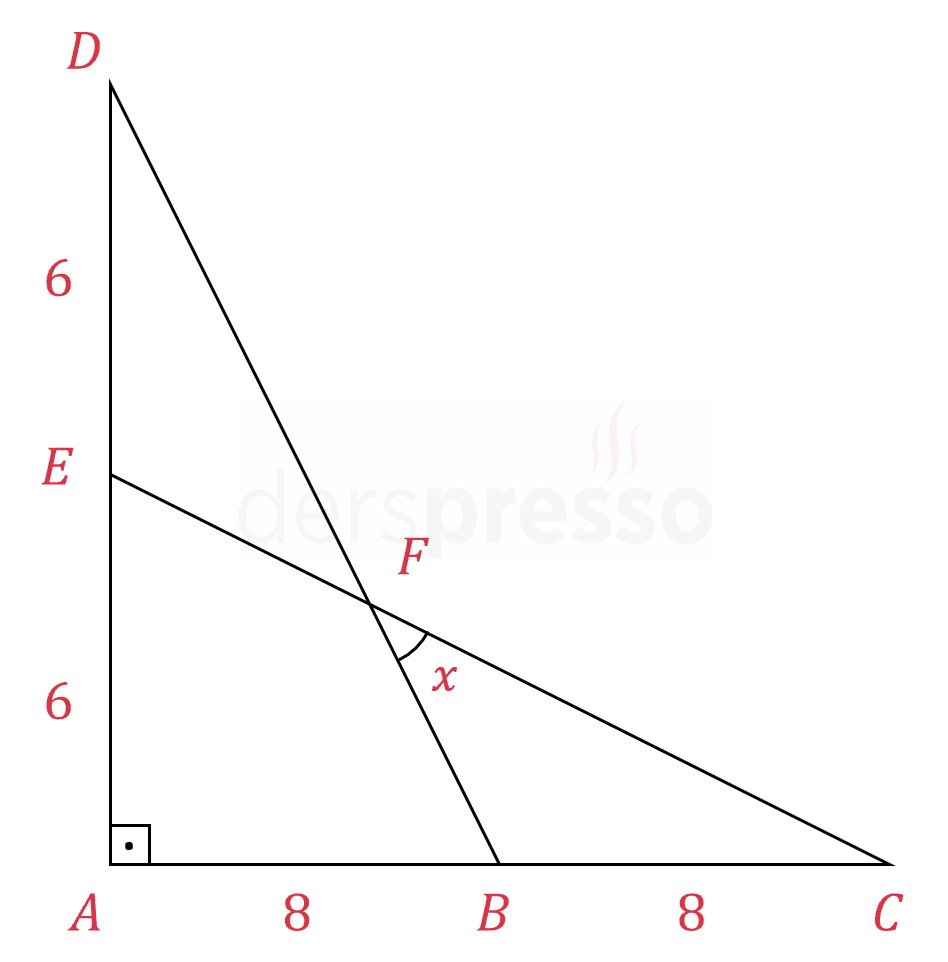
\( [BD] \cap [EC] = {F} \)
\( \abs{AE} = \abs{ED} = 6 \)
\( \abs{AB} = \abs{BC} = 8 \)
\( m(\widehat{BFC}) = x \)
Verilenlere göre \( \tan{x} \) kaçtır?
Çözümü Göster
\( m(\widehat{BCF}) = y \) diyelim.
\( \tan{y} = \dfrac{6}{8 + 8} = \dfrac{3}{8} \)
\( \widehat{ABD} \) açısı \( BCF \) üçgeninin bir dış açısıdır.
\( m(\widehat{ABD}) = x + y \)
\( \tan(x + y) = \dfrac{6 + 6}{8} = \dfrac{3}{2} \)
Tanjant toplam formülünü yazalım.
\( \tan{(x + y)} = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
\( \dfrac{3}{2} = \dfrac{\tan{x} + \frac{3}{8}}{1 - \tan{x} \cdot \frac{3}{8}} \)
\( \dfrac{3}{2} = \dfrac{8\tan{x} + 3}{8 - 3\tan{x}} \)
İçler - dışlar çarpımı yapalım.
\( 24 - 9\tan{x} = 16\tan{x} + 6 \)
\( 25\tan{x} = 18 \)
\( \tan{x} = \dfrac{18}{25} \) bulunur.
\( ABC \) bir dik üçgendir.
\( m(\widehat{BAD}) = x \)
\( m(\widehat{DAC}) = y \)
\( m(\widehat{BCA}) = z \)
olduğuna göre,
\( \tan{x}\tan{y} + \tan{x}\tan{z} + \tan{y}\tan{z} \) işleminin sonucunu bulunuz.
Çözümü Göster\( x + y + z = 90° \)
\( x + y = 90° - z \)
Bir açının tanjantı ile kotanjantının çarpımı 1'dir.
\( \tan(x + y)\cot(x + y) = 1 \)
\( \tan(x + y)\cot(90° - z) = 1 \)
Tümler açıların tanjant ve kotanjant değerleri birbirine eşittir.
\( \tan(x + y)\tan{z} = 1 \)
Tanjant toplam formülünü yazalım.
\( \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \cdot \tan{z} = 1 \)
\( \tan{x}\tan{z} + \tan{y}\tan{z} = 1 - \tan{x}\tan{y} \)
\( \tan{x}\tan{y} + \tan{x}\tan{z} + \tan{y}\tan{z} = 1 \) bulunur.
\( f(x) = \sin{x} - \cos{x} + 4 \)
olduğuna göre, \( f^{-1}(x) \) fonksiyonunu bulunuz.
Çözümü GösterFonksiyon tanımını tek bir trigonometrik fonksiyon cinsinden yazabilirsek fonksiyonun tersini kolaylıkla bulabiliriz.
\( \sin{x} \)'in katsayısı olan 1 yerine \( \tan{\frac{\pi}{4}} \) yazalım.
\( f(x) = \tan{\dfrac{\pi}{4}}\sin{x} - \cos{x} + 4 \)
\( = \dfrac{\sin{\frac{\pi}{4}}\sin{x}}{\cos{\frac{\pi}{4}}} - \cos{x} + 4 \)
\( = \dfrac{\sin{\frac{\pi}{4}}\sin{x} - \cos{\frac{\pi}{4}}\cos{x}}{\cos{\frac{\pi}{4}}} + 4 \)
Paydaki ifade kosinüs toplam formülünün açılımıdır.
\( = \dfrac{-\cos(\frac{\pi}{4} + x)}{\frac{1}{\sqrt{2}}} + 4 \)
\( = 4 - \sqrt{2}\cos\left( \dfrac{\pi}{4} + x \right) \)
Bu fonksiyonun tersini almak için \( x \)'i yalnız bırakalım.
\( y = 4 - \sqrt{2}\cos\left( \dfrac{\pi}{4} + x \right) \)
\( \sqrt{2}\cos\left( \dfrac{\pi}{4} + x \right) = 4 - y \)
\( \cos\left( \dfrac{\pi}{4} + x \right) = \dfrac{\sqrt{2}(4 - y)}{2} \)
\( \dfrac{\pi}{4} + x = \arccos\left( \dfrac{\sqrt{2}(4 - y)}{2} \right) \)
\( x = \arccos\left( \dfrac{\sqrt{2}(4 - y)}{2} \right) - \dfrac{\pi}{4} \)
\( x \) ve \( y \) değişkenlerini aralarında yer değiştirdiğimizde \( y = f^{-1}(x) \) fonksiyonunu buluruz.
\( y = f^{-1}(x) = \arccos\left( \dfrac{\sqrt{2}(4 - y)}{2} \right) - \dfrac{\pi}{4} \)
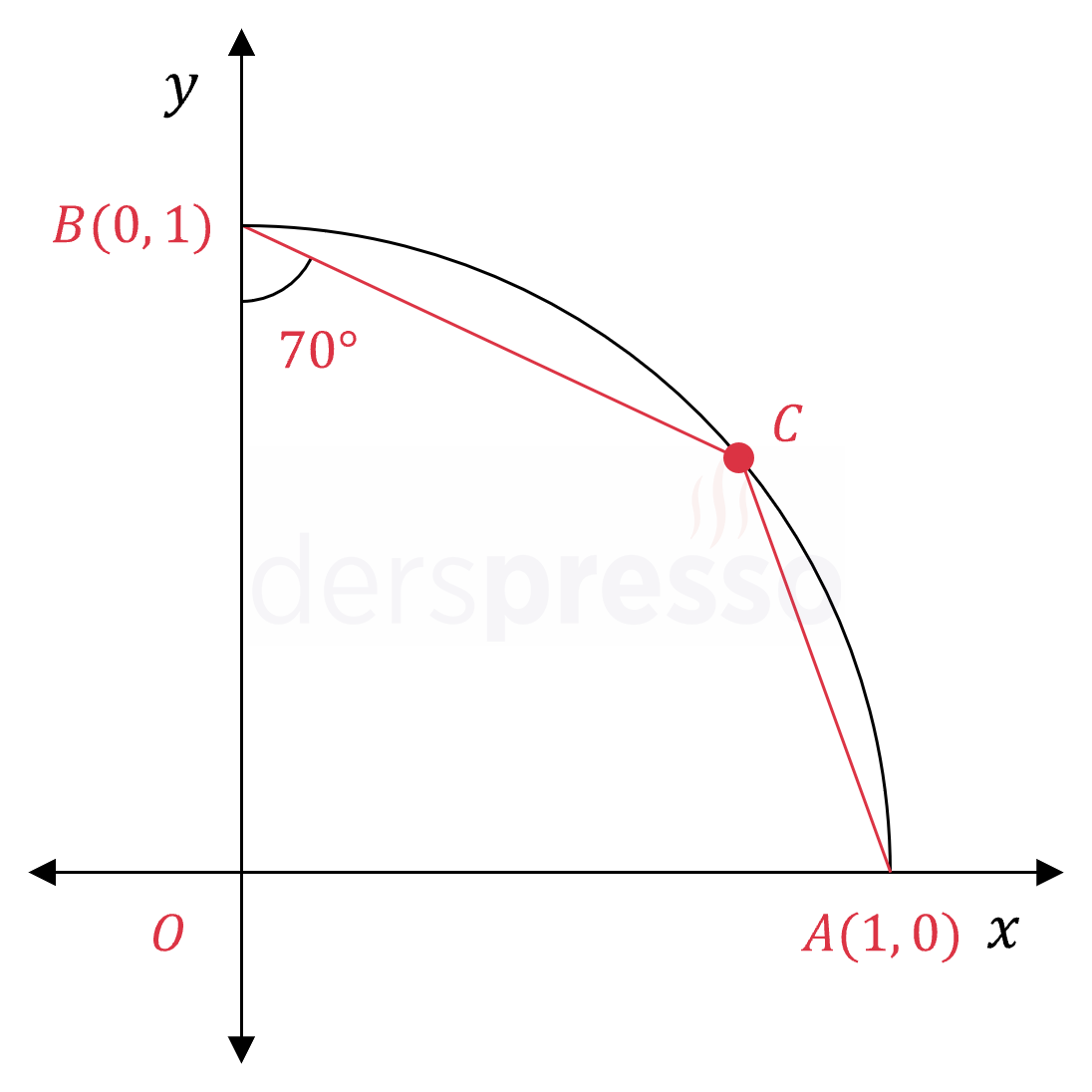
Yukarıda \( O \) merkezli çeyrek birim çember verilmiştir.
\( \sin{25°} = a \) olduğuna göre, \( \abs{AC} \) uzunluğunu \( a \) cinsinden bulunuz.
Çözümü Göster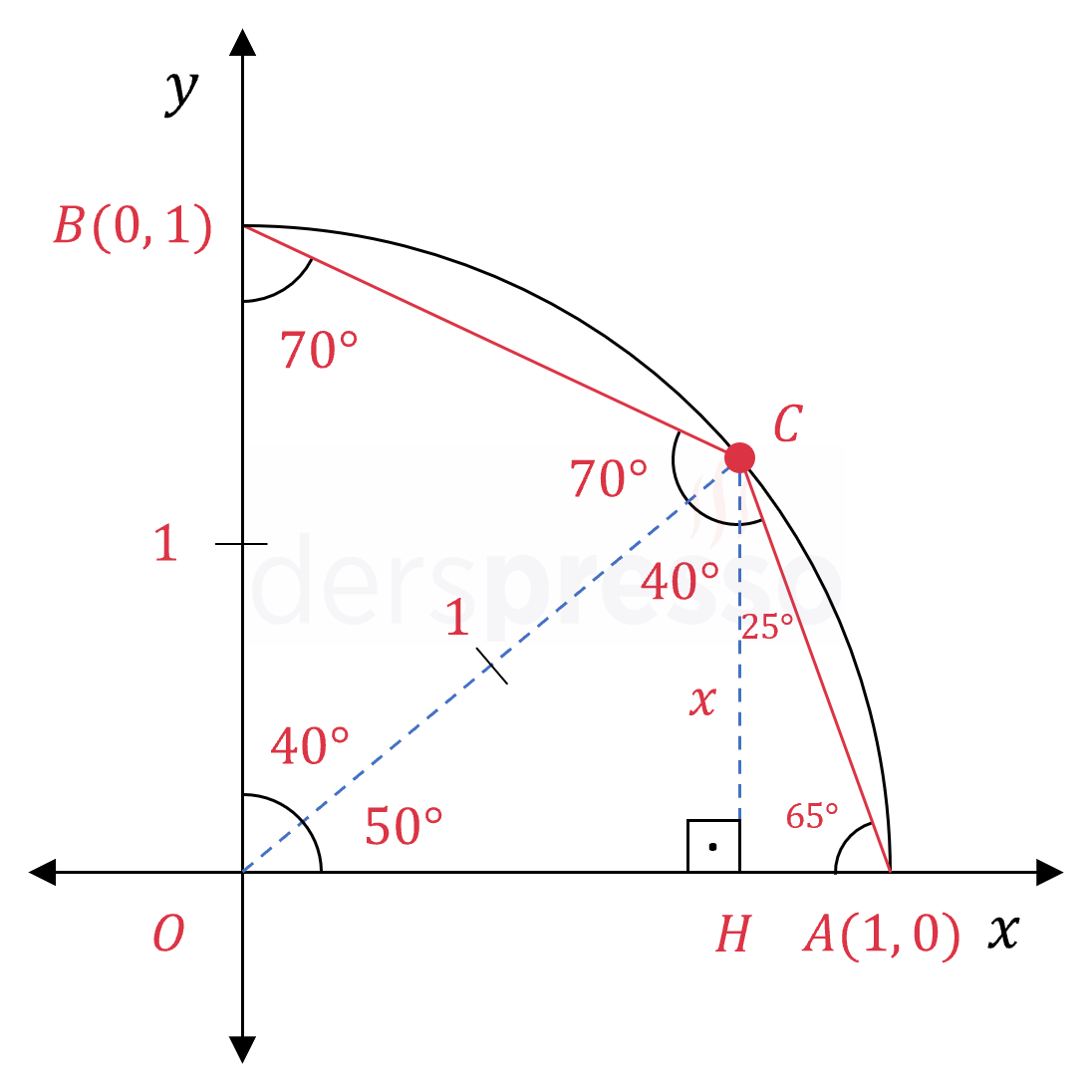
Orijin ile \( C \) noktasını birleştirelim. \( [OC] \) birim çemberin yarıçapıdır.
\( \abs{OC} = \abs{OB} = \abs{OA} = 1 \)
\( BOC \) ve \( COA \) ikizkenar üçgenlerdir.
\( m(\widehat{OCB}) = m(\widehat{OBC}) = 70° \)
\( m(\widehat{BOC}) = 180° - 140° = 40° \)
\( \widehat{BOC} \) ve \( \widehat{COA} \) tümler açılardır.
\( m(\widehat{COA}) = 50° \)
\( m(\widehat{OAC}) = m(\widehat{OCA}) = 65° \)
\( m(\widehat{HCA}) = 25° \)
\( \abs{CH} = x \) diyelim.
\( COH \) üçgeninde \( \sin{50°} = \frac{x}{1} \) yazabiliriz.
\( x = \sin{50°} \)
\( CHA \) üçgeninde \( \cos{25°} = \frac{x}{\abs{AC}} \) yazabiliriz.
\( \abs{AC} = \dfrac{x}{\cos{25°}} \)
\( = \dfrac{\sin{50°}}{\cos{25°}} \)
Sinüs iki kat açı formülünü kullanalım.
\( = \dfrac{2\sin{25°}\cos{25°}}{\cos{25°}} \)
\( = 2\sin{25°} = 2a \) bulunur.