Üçgenin Açı Özellikleri
Üçgenin iç açıları toplamı \( 180° \)'dir.

\( x + y + z = 180° \)
İSPATI GÖSTER
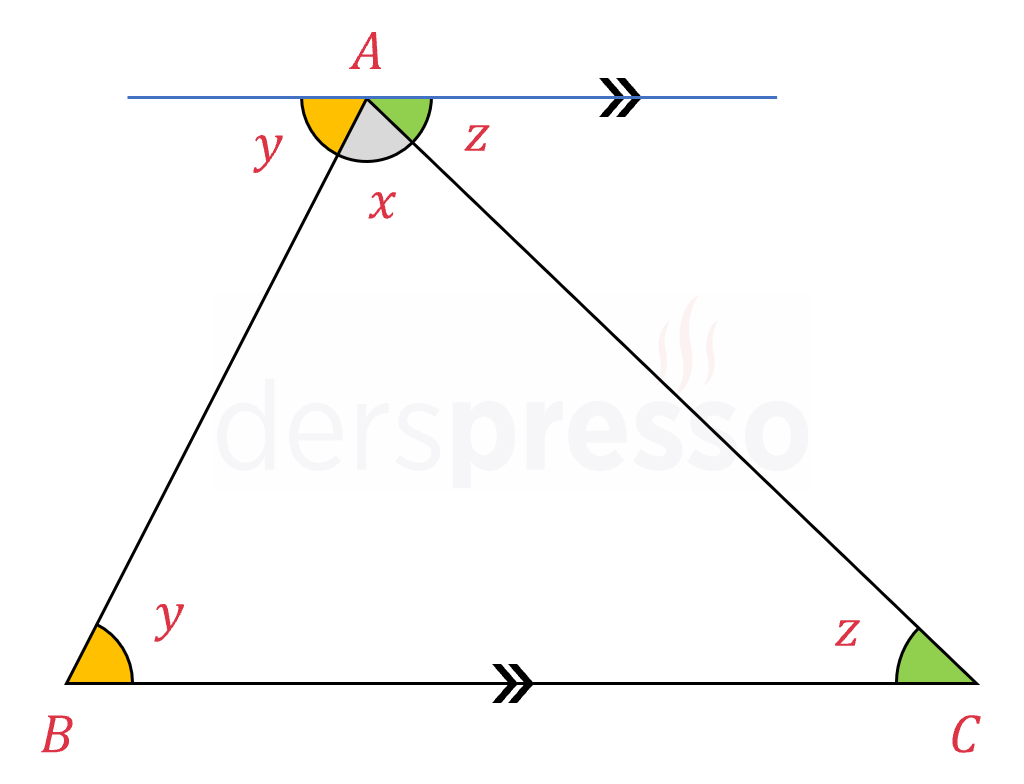
\( A \) köşesinden geçen ve \( a \) kenarına paralel bir doğru çizelim.
Z kuralına göre \( \hat{A} \) iç açısına komşu iki açı, üçgenin taban iç açıları ile iç ters açılardır.
Dolayısıyla \( x \), \( y \) ve \( z \) açıları bütünler açılardır ve toplamları \( 180° \) olur.
Üçgenin dış açıları toplamı \( 360° \)'dir.

\( x' + y' + z' = 360° \)
İSPATI GÖSTER
Üçgenin iç açıları toplamı \( 180° \)'dir.
\( x + y + z = 180° \)
Üçgenin dış açılarını iç açılar cinsinden yazalım.
\( x' = 180° - x, \quad y' = 180° - y, \) \( \quad z' = 180° - z \)
\( x' + y' + z' = (180° - x) + (180° - y) \) \( + (180° - z) \)
\( x' + y' + z' = 540° - (x + y + z) \) \( = 360° \)
Bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( x' = y + z \)
\( y' = x + z \)
\( z' = x + y \)
İSPATI GÖSTER
İspat 1:

\( A \) noktasından geçen ve \( [BC] \) kenarına paralel bir doğru çizelim (mavi doğru).
Bu doğru parçası \( x' \) açısını iki farklı açıya ayırır ve oluşan açılar \( y \) açısının yöndeş açısı ve \( z \) açısının iç ters açısı olur.
Buna göre \( x' \) açısını bu iki açının toplamı şeklinde aşağıdaki şekilde yazabiliriz.
\( x' = y + z \)
İspat 2:
Üçgenin iç açıları toplamı \( 180° \)'dir.
\( x + y + z = 180° \)
\( x = 180° - (y + z) \)
Bir dış açıyı iç açı cinsinden yazalım.
\( x' = 180° - x \)
Bu denklemde \( x \) yerine bir önceki denklemdeki eşitini yazalım.
\( x' = 180° - (180° - (y + z)) = y + z \)
Dış açı eşitsizliğine göre, bir üçgenin herhangi bir dış açısının ölçüsü kendisine komşu olmayan iki iç açının her birinin ölçüsünden daha büyüktür.
\( y' \gt x \)
\( y' \gt z \)
İSPATI GÖSTER

Bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( y' = x + z \)
\( x = y' - z \)
\( z = y' - x \)
\( x \) açısı sıfırdan büyüktür.
\( x \gt 0 \)
\( y' - z \gt 0 \)
\( y' \gt z \)
\( z \) açısı sıfırdan büyüktür.
\( z \gt 0 \)
\( y' - x \gt 0 \)
\( y' \gt x \)
İki iç açıortayın kesişmesiyle oluşan açının formülü aşağıdaki gibidir ve bu açı her zaman bir geniş açıdır.
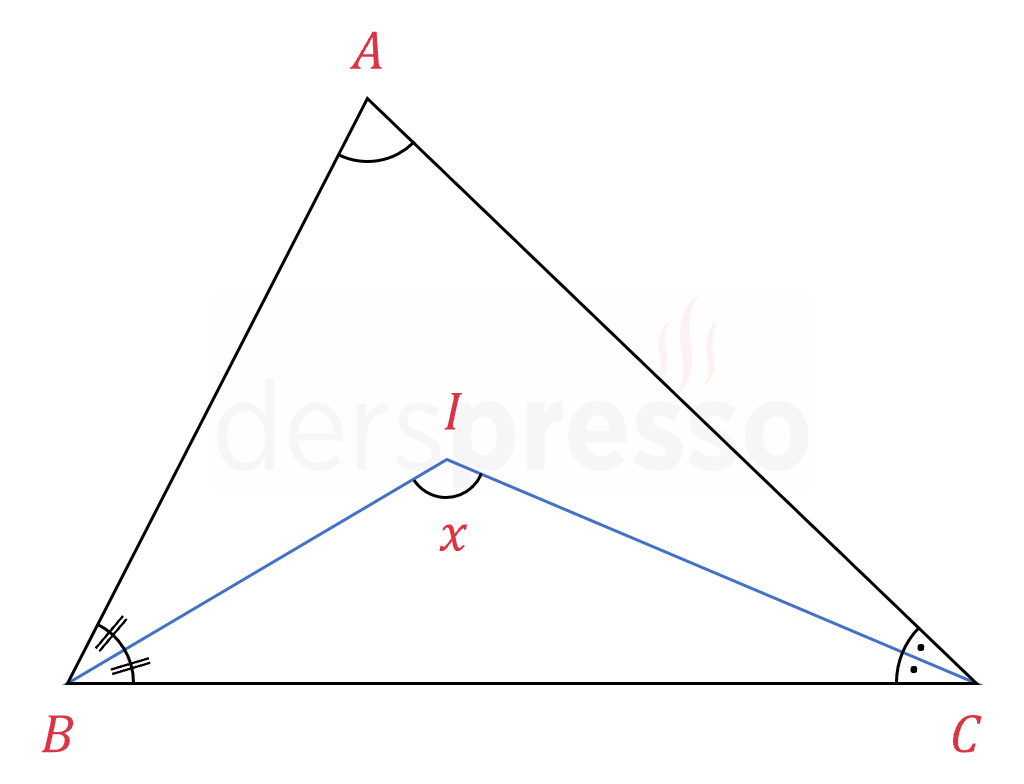
\( I \): İç açıortayların kesişim noktası
\( x = 90° + \dfrac{m(\hat{A})}{2} \)
İSPATI GÖSTER
Büyük üçgenin iç açıları toplamı:
\( m(\hat{A}) + m(\hat{B}) + m(\hat{C}) = 180° \)
\( m(\hat{B}) + m(\hat{C}) = 180° - m(\hat{A}) \)
Küçük üçgenin iç açıları toplamı:
\( x + \dfrac{m(\hat{B})}{2} + \dfrac{m(\hat{C})}{2} = 180° \)
\( x + \dfrac{m(\hat{B}) + m(\hat{C})}{2} = 180° \)
\( m(\hat{B}) + m(\hat{C}) \) yerine yukarıda bulduğumuz eşitini yazalım.
\( x + \dfrac{180° - m(\hat{A})}{2} = 180° \)
\( x + 90° - \dfrac{m(\hat{A})}{2} = 180° \)
\( x = 90° + \dfrac{m(\hat{A})}{2} \)
İki dış açıortayın kesişmesiyle oluşan açının formülü aşağıdaki gibidir ve bu açı her zaman bir dar açıdır.
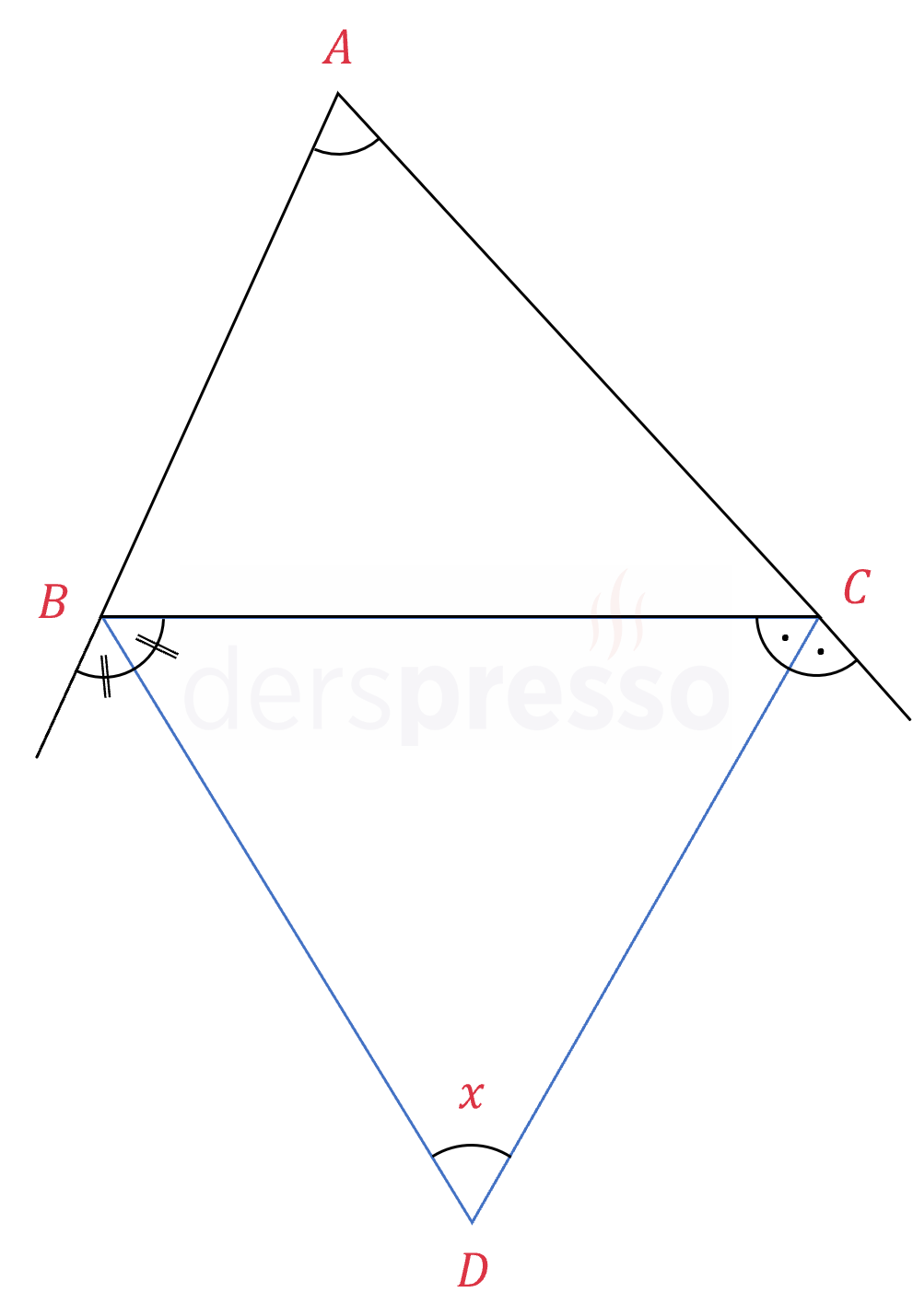
\( D \): İki dış açıortayın kesişim noktası
\( x = 90° - \dfrac{m(\hat{A})}{2} \)
İSPATI GÖSTER
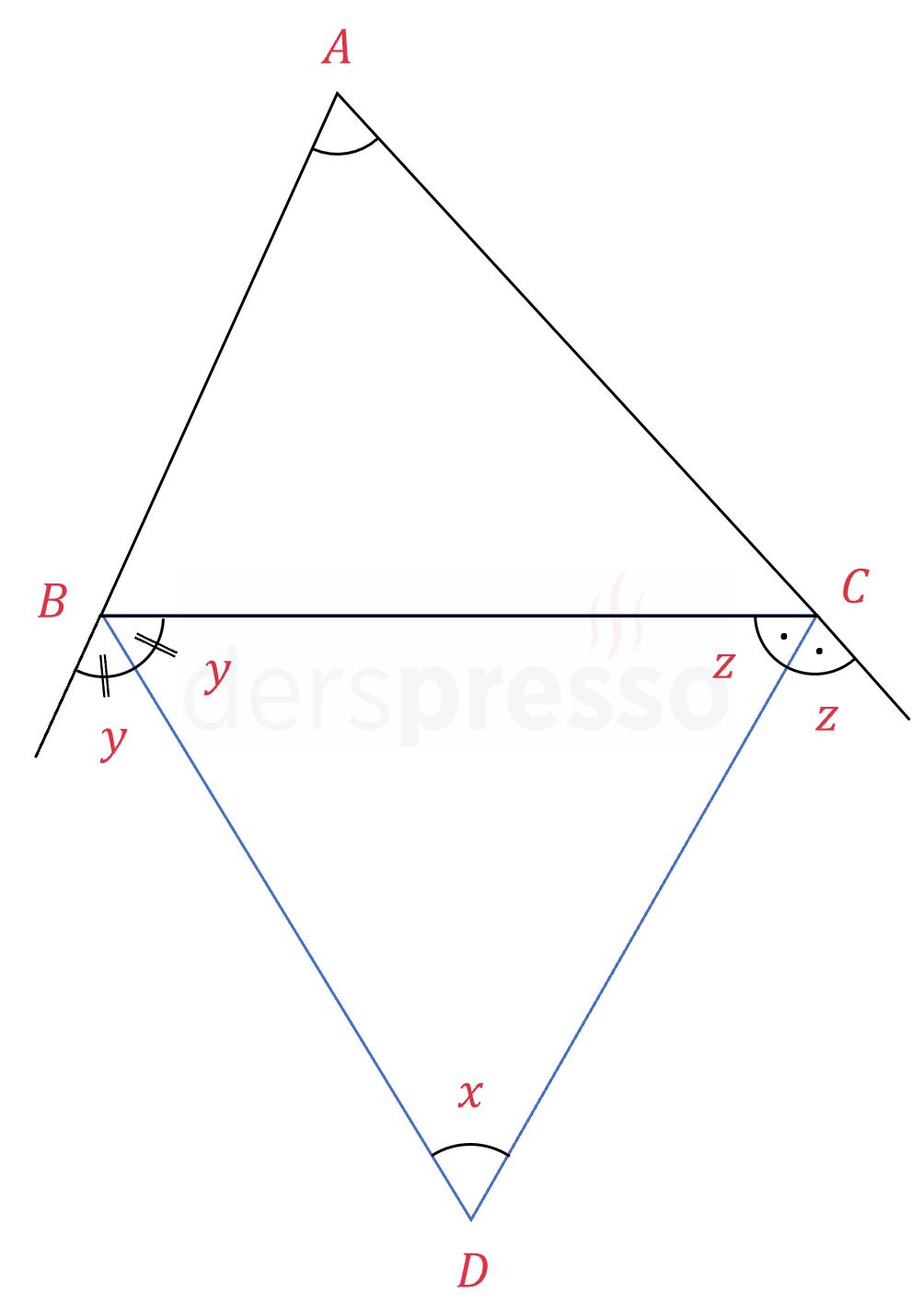
\( B \) ve \( C \) köşelerinin dış açı ölçülerine sırasıyla \( 2y \) ve \( 2z \) diyelim.
\( \widehat{ABC} \) üçgeninin iç açıları toplamı:
\( m(\hat{A}) + m(\hat{B}) + m(\hat{C}) = 180° \)
\( \hat{B} \) ve \( \hat{C} \) iç açılarını \( y \) ve \( z \) cinsinden yazalım:
\( m(\hat{B}) + 2y = 180° \)
\( m(\hat{B}) = 180° - 2y \)
\( m(\hat{C}) + 2z = 180° \)
\( m(\hat{C}) = 180° - 2z \)
Bu açıları \( \widehat{ABC} \) iç açı formülünde yerine koyalım:
\( m(\hat{A}) + 180° - 2y + 180° - 2z = 180° \)
\( y + z = 90° + \dfrac{m(\hat{A})}{2} \)
\( \widehat{DBC} \) üçgeninin iç açıları toplamı:
\( x + y + z = 180° \)
\( x = 180° - (y + z) \)
\( x = 180° - (90° + \dfrac{m(\hat{A})}{2}) \)
\( x = 90° - \dfrac{m(\hat{A})}{2} \)
Bir iç açıortay ve bir dış açıortayın kesişmesiyle oluşan açının ölçüsü aşağıdaki formülle bulunur.
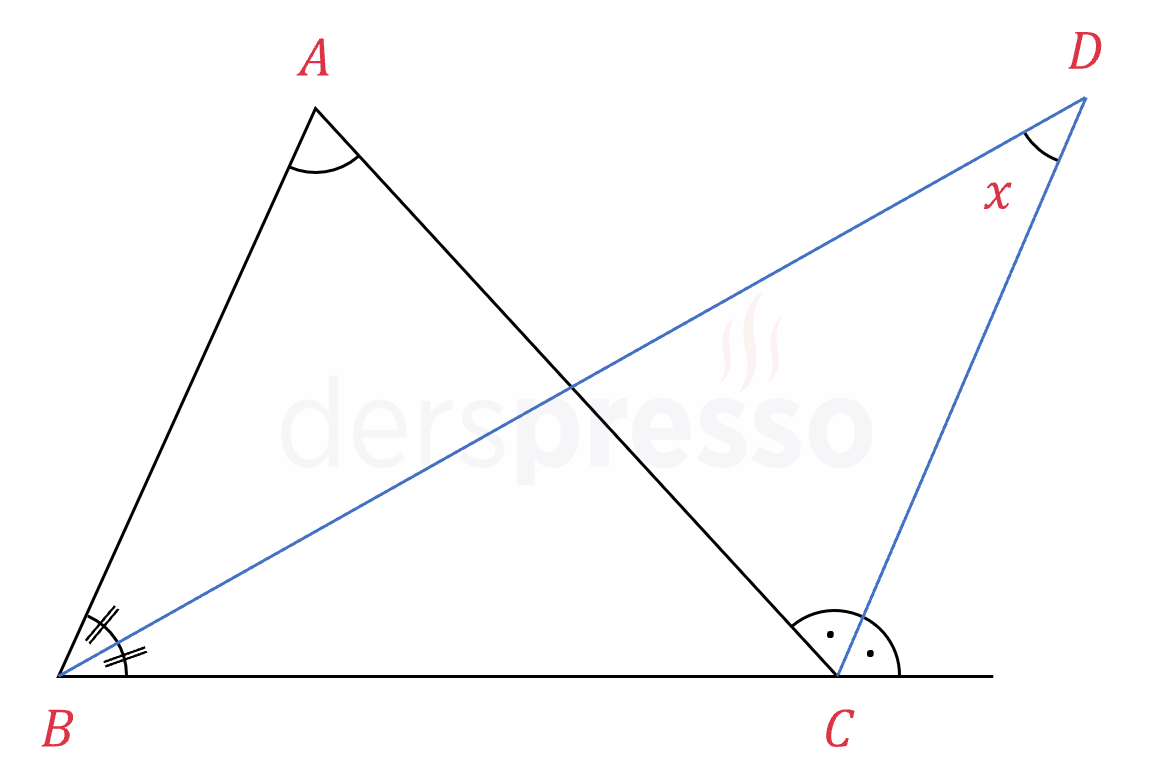
\( D \): Bir iç ve bir dış açıortayın kesişim noktası
\( x = \dfrac{m(\hat{A})}{2} \)
İSPATI GÖSTER

\( \widehat{BCD} \) üçgeni için dış açı formülünü yazalım:
\( x + y = z \)
\( x = z - y \)
\( \widehat{ABC} \) üçgeni için dış açı formülü yazalım:
\( m(\hat{A}) + 2y = 2z \)
\( m(\hat{A}) = 2(z - y) \)
\( z - y \) yerine yukarıda bulduğumuz eşitini yazalım.
\( m(\hat{A}) = 2x \)
\( x = \dfrac{m(\hat{A})}{2} \)
Üçgenin bir kenarı içe büküldüğünde üçgenin dışında oluşan açının ölçüsü aşağıdaki formülle bulunur.

\( x = a + b + c \)
İSPATI GÖSTER

\( [CD] \) doğru parçasını \( [AB] \) kenarını kesecek şekilde uzatalım ve \( \overset{\triangle}{AEC} \) üçgeninde \( \widehat{BED} \) açısı için dış açı formülünü yazalım.
\( y = a + c \)
Şimdi \( \overset{\triangle}{BED} \) üçgeninde \( x \) açısı için dış açı formülünü yazalım.
\( x = b + y \)
Yukarıda bulduğumuz \( y \) değerini yerine koyalım.
\( x = a + b + c \)
Bir köşeye ait iç açıortay ve yükseklik arasında kalan açının ölçüsü aşağıdaki formülle bulunur.

\( h_a \): \( A \) köşesine ait yükseklik
\( n_a \): \( A \) köşesine ait açıortay
\( x = \dfrac{\abs{b - c}}{2} \)
İSPATI GÖSTER
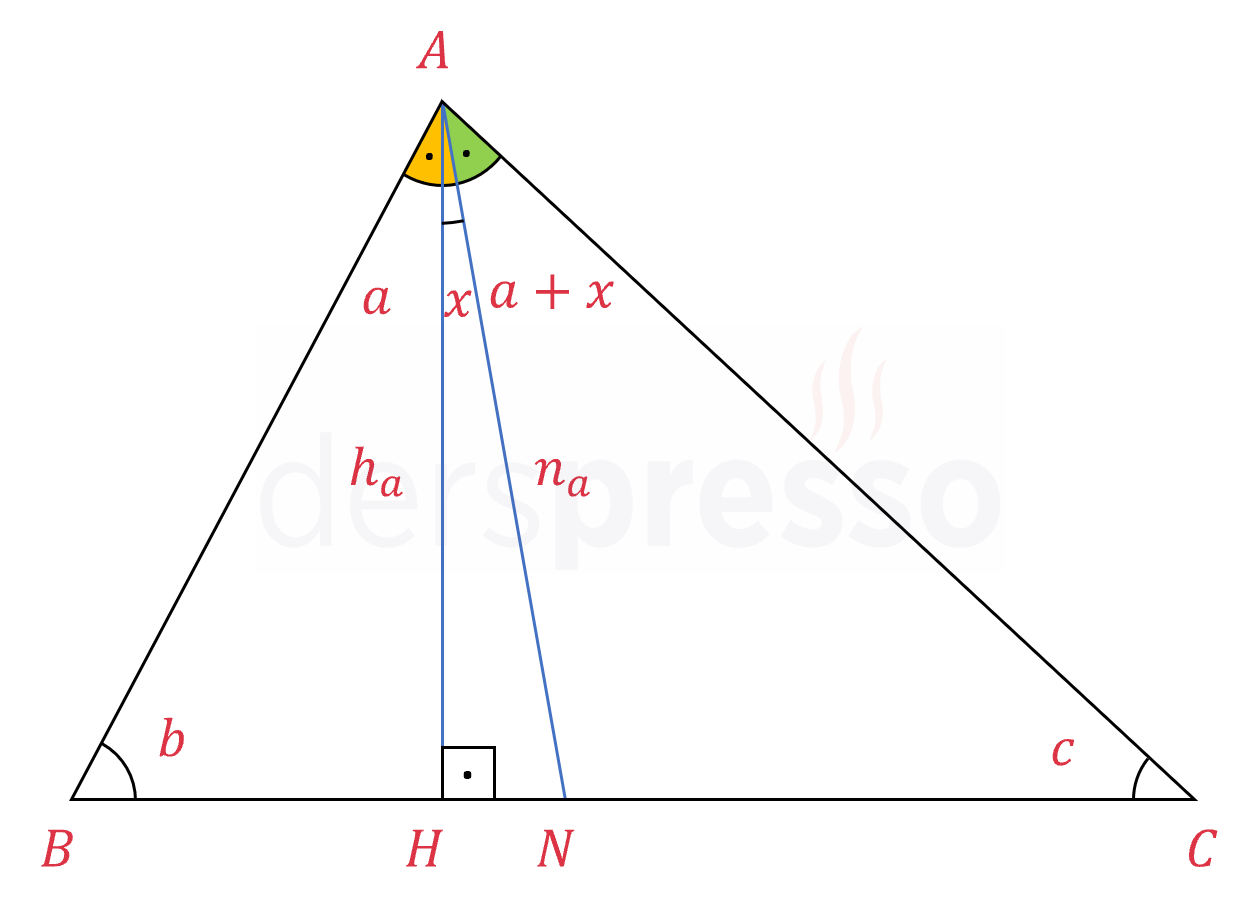
\( m(\widehat{BAH}) = a \) diyelim.
\( [AN] \) açıortay ve \( m(\widehat{BAN}) = m(\widehat{NAC}) \) olduğu için,
\( m(\widehat{NAC}) = a + x \) olur.
\( \overset{\triangle}{BAH} \) ve \( \overset{\triangle}{CAH} \) üçgenleri birer dik üçgen olduğu için dik olmayan açıların toplamı \( 90° \) olur.
\( b + a = 90° \)
\( c + 2x + a = 90° \)
İki denklemi birbirine eşitleyelim.
\( b + a = c + 2x + a \)
\( b = c + 2x \)
\( x \)'i yalnız bırakalım.
\( x = \dfrac{b - c}{2} \)
Bu örnekte yükseklik açıortayın solunda kaldığı için \( b \) açısı \( c \) açısından büyük olur. Yüksekliğin açıortayın sağında kaldığı durumda \( c \) açısı \( b \) açısından büyük olacak ve bu formül negatif sonuç verecektir. Her iki durumda da pozitif sonuç verecek şekilde denklemi açıların farkının mutlak değerini alarak yazabiliriz.
\( x = \dfrac{\abs{b - c}}{2} \)
Açılarına Göre Üçgenler
Üçgenler iç açılarına göre aşağıdaki tiplerde olabilir.
Dar Açılı Üçgenler
Dar açılı üçgenlerin tüm açıları 90°'den küçüktür.

Dik Açılı Üçgenler
Dik açılı üçgenlerin bir açısı 90°'dir. Dik açılı üçgenlerde diğer iki açı dar açıdır.

Geniş Açılı Üçgenler
Geniş açılı üçgenlerin bir açısı 90°'den büyüktür. Geniş açılı üçgenlerde diğer iki açı dar açıdır.


Şekildeki \( \overset{\triangle}{ABC} \) üçgeninin dış açılarının toplamı kaçtır?
Çözümü GösterÜçgenin iç açılarına \( x \), \( y \) ve \( z \) diyelim.

\( A \) köşesinin dış açısı \( = 180° - x \)
\( B \) köşesinin dış açısı \( = 180° - y \)
\( C \) köşesinin dış açısı \( = 180° - z \)
Üçgenin dış açılarının toplamı:
\( = (180 - x) + (180 - y) + (180 - z) \)
\( = 540 - (x + y + z) = 540 - 180 = 360° \)
Buna göre \( \overset{\triangle}{ABC} \) üçgeninin (ve tüm üçgenlerin) dış açılarının toplamı \( 360° \) olur.

\( m(\widehat{ABD}) = m(\widehat{DBC}) \)
\( m(\widehat{ACD}) = m(\widehat{DCB}) \)
\( m(\widehat{BAC}) = 70° \)
olduğuna göre, \( y = m(\widehat{BDC}) \) açısının ölçüsü kaçtır?
Çözümü Göster\( m(\widehat{ABD}) = m(\widehat{DBC}) = a \)
\( m(\widehat{ACD}) = m(\widehat{DCB}) = b \) diyelim.

\( \overset{\triangle}{ABC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 2a+ 2b + 70 = 180 \)
\( 2a + 2b = 110 \)
\( a + b = 55° \)
\( \overset{\triangle}{DBC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( a + b + y = 180 \)
\( 55 + y = 180 \)
\( y = 125° \) bulunur.
Bir üçgenin iç açılarının 3, 4, 5 sayıları ile doğru orantılı olduğu biliniyor.
Buna göre en küçük açının derecesi kaçtır?
Çözümü GösterÜçgenin iç açıları 3, 4, 5 sayıları ile doğru orantılı olduğuna göre bu açılara sırasıyla \( 3k \), \( 4k \) ve \( 5k \) diyebiliriz.
Üçgenin iç açıları toplam formülünü yazalım.
\( 3k + 4k + 5k = 180 \)
\( 12k = 180 \)
\( k = 15 \)
Buna göre en küçük açının ölçüsü \( 3k = 45° \) olur.

\( \abs{AB} = \abs{AD} \)
\( m(\widehat{DAE}) = \beta, m(\widehat{EAC}) = \alpha \)
\( m(\widehat{ACB}) = 30°, \alpha + \beta = 45° \)
olduğuna göre, \( x = m(\widehat{BAD}) \) açısı kaç derecedir?
Çözümü GösterÜçgende bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.

\( m(\widehat{AED}) = \alpha + 30 \)
\( m(\widehat{ADB}) = \alpha + \beta + 30 \)
\( \alpha + \beta = 45 \) olduğu biliniyor.
\( m(\widehat{ADB}) = 30 + 45 = 75° \)
\( \abs{AB} = \abs{AD} \) olduğu için,
\( m(\widehat{ABD}) = 75° \)
\( \overset{\triangle}{ABD} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 2 \cdot 75 + x = 180 \)
\( x = 30° \) bulunur.

\( m(\widehat{ACD}) = 35°, \abs{AB} = \abs{AD} = \abs{DC} \)
olduğuna göre, \( x = m(\widehat{EAB}) \) açısının ölçüsü kaçtır?
Çözümü Göster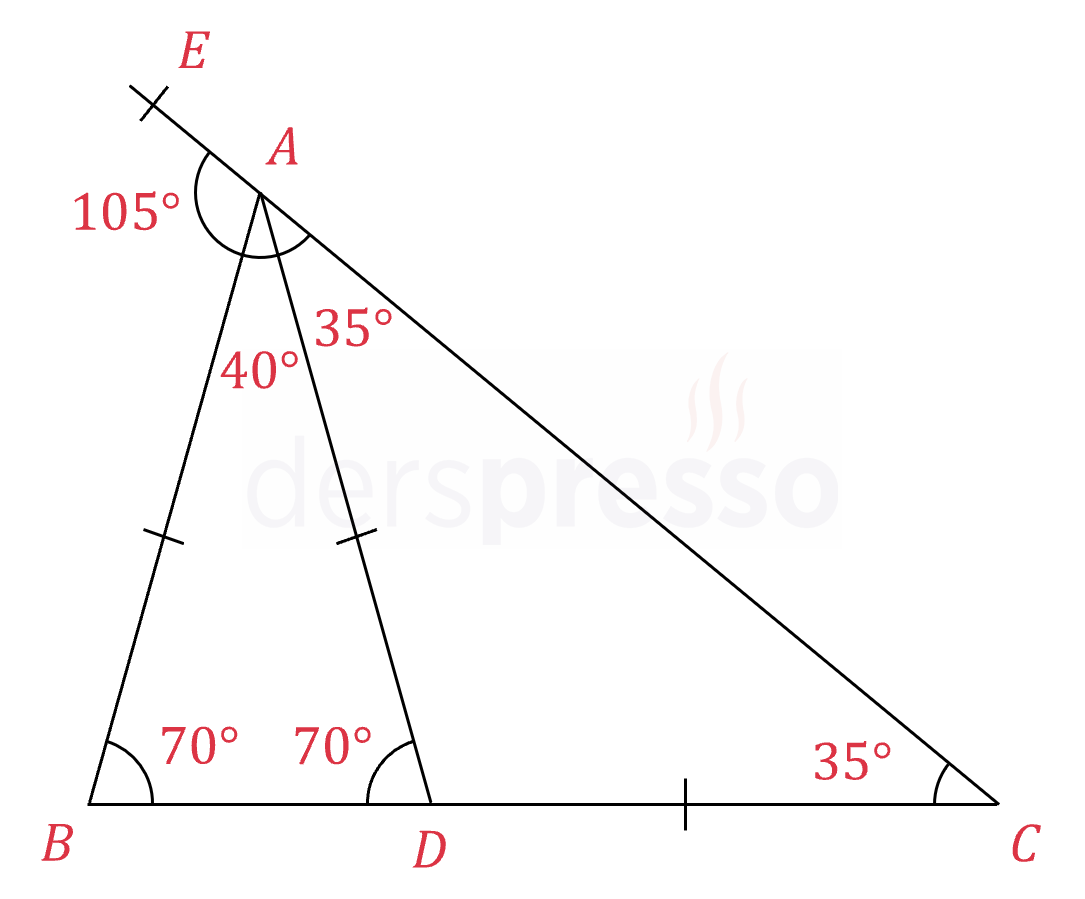
\( m(\widehat{ACD}) = 35 \) ve \( \abs{AD} = \abs{DC} \) olduğu için,
\( m(\widehat{DAC}) = 35° \)
Üçgende bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{ADB}) = m(\widehat{ACD}) + m(\widehat{DAC}) \)
\( = 35 + 35 = 70° \)
\( \abs{AB} = \abs{AD} \) olduğu için,
\( m(\widehat{ABD}) = 70° \)
\( \overset{\triangle}{ABD} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 70 + 70 + m(\widehat{BAD}) = 180 \)
\( m(\widehat{BAD}) = 40° \)
\( A \) noktasındaki açıların toplamı \( 180° \) olur.
\( 40 + 35 + x = 180 \)
\( x = 105° \) bulunur.
Bir üçgenin iki iç açısının ölçüleri arasındaki oran 3:4 şeklindedir.
Açılardan birinin bütünleyeni diğerinin tümlerinin 3 katı olduğuna göre, bu açılardan küçük olanın alabileceği değerlerin toplamı kaçtır?
Çözümü GösterAçıların ölçülerine \( 3x \) ve \( 4x \) diyelim.
Verilen bilgiyi iki şekilde yorumlayabiliriz.
Durum 1: Küçük açının bütünleyeni büyük açının tümlerinin 3 katıdır.
\( 180 - 3x = 3(90 - 4x) \)
\( 180 - 3x = 270 - 12x \)
\( 9x = 90 \)
\( x = 10° \)
Bu durumda küçük açı \( 3x = 30° \), büyük açı \( 4x = 40° \) olur.
Durum 2: Büyük açının bütünleyeni küçük açının tümlerinin 3 katıdır.
\( 180 - 4x = 3(90 - 3x) \)
\( 180 - 4x = 270 - 9x \)
\( 5x = 90 \)
\( x = 18° \)
Bu durumda küçük açı \( 3x = 54° \), büyük açı \( 4x = 72° \) olur.
Her iki durumda da açıların toplamı 180°'den küçük olduğu için açılar bir üçgenin iç açıları olabilir.
Buna göre küçük açının alabileceği değerlerin toplamı \( 30 + 54 = 84° \) olarak bulunur.

\( [DE] \parallel [AC] \)
\( m(\widehat{BDE}) = 80°, m(\widehat{GCB}) = m(\widehat{GCF}) = 35° \)
olduğuna göre, \( x = m(\widehat{BAC}) \) açısının ölçüsü kaçtır?
Çözümü Göster
\( [DE] \parallel [AC] \) olduğu için \( \widehat{BFC} \) ve \( \widehat{BDE} \) yöndeş açılardır ve ölçüleri birbirine eşittir.
\( m(\widehat{BFC}) = 80° \)
Üçgende bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{BGC}) = m(\widehat{GCF}) + m(\widehat{GFC}) \)
\( = 35 + 80 = 115° \)
\( \overset{\triangle}{BGC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 115 + 35 + m(\widehat{GBC}) = 180 \)
\( m(\widehat{GBC}) = 30° \)
\( \overset{\triangle}{ABC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 2 \cdot 30 + 2 \cdot 35 + x = 180 \)
\( x = 50° \) bulunur.

\( \abs{AB} = \abs{BC} = \abs{AD} \)
\( m(\widehat{DAB}) = 60°, m(\widehat{ABC}) = 130° \)
olduğuna göre, \( x = m(\widehat{BCD}) \) açısının ölçüsü kaçtır?
Çözümü Göster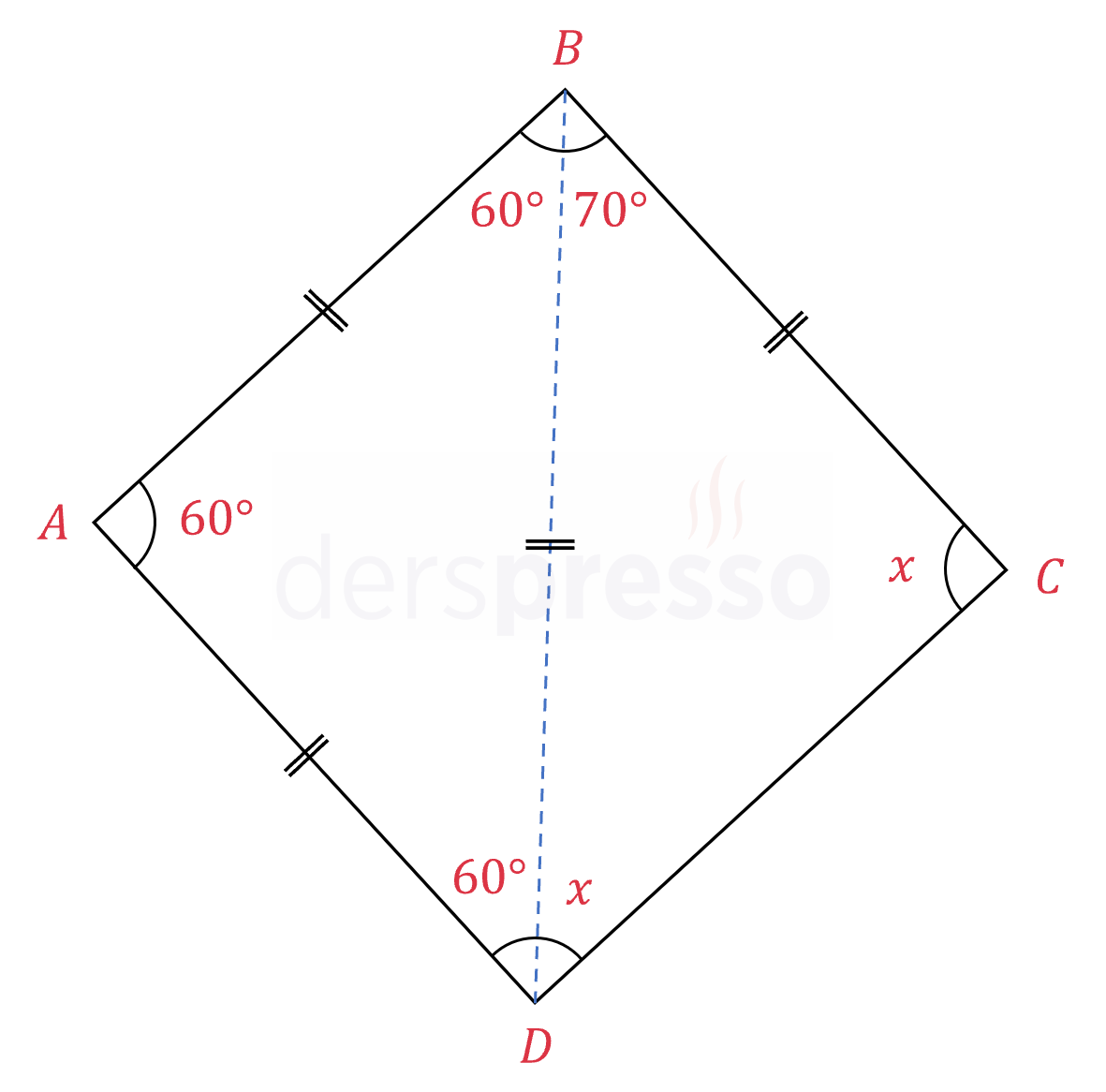
B ve D noktalarını birleştirelim.
\( \abs{AB} = \abs{AD} \) ve \( m(\widehat{DAB}) = 60° \) olduğu için,
\( m(\widehat{ABD}) = m(\widehat{ADB}) = 60° \)
Dolayısıyla \( \overset{\triangle}{ABD} \) üçgeni bir eşkenar üçgendir.
\( \abs{AB} = \abs{AD} = \abs{BD} \)
\( m(\widehat{DBC}) = 130 - 60 = 70° \)
\( \abs{BC} = \abs{BD} \) olduğu için \( m(\widehat{BDC}) = m(\widehat{BCD}) \) olur.
\( \overset{\triangle}{BCD} \) üçgeninin iç açıları toplam formülünü yazalım.
\( x + x + 70 = 180 \)
\( x = 55° \) bulunur.

\( \abs{AC} = \abs{BC}, \abs{DB} = \abs{DC} \)
\( m(\widehat{DCA}) = 30° \)
olduğuna göre, \( x = m(\widehat{DAC}) \) açısının ölçüsü kaçtır?
Çözümü Göster
\( \abs{DB} = \abs{DC} \) olduğu için \( m(\widehat{DBC}) = m(\widehat{DCB}) = x \) olur.
\( \abs{AC} = \abs{BC} \) olduğu için \( m(\widehat{BAC}) = m(\widehat{ABC}) = x \) olur.
\( ABC \) üçgeninin iç açıları toplam formülünü yazalım.
\( 3x + 30 = 180 \)
\( x = 50° \) bulunur.

\( m(\widehat{ABD}) = m(\widehat{DBC}) \)
\( m(\widehat{ACD}) = m(\widehat{DCE}) \)
\( m(\widehat{BAC}) = 80° \)
olduğuna göre, \( x = m(\widehat{BDC}) \) açısının ölçüsü kaçtır?
Çözümü GösterEşit açıların ölçülerine \( y \) ve \( z \) diyelim.

Üçgende bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{DCE}) = m(\widehat{BDC}) + m(\widehat{DBC}) \)
\( z = x + y \)
\( x = z - y \)
\( m(\widehat{ACE}) = m(\widehat{ABC}) + m(\widehat{BAC}) \)
\( 2z = 2y + 80 \)
\( 2(z - y) = 80 \)
\( z - y \) yerine yukarıda bulduğumuz eşitini yazalım.
\( 2x = 80 \)
\( x = 40° \) bulunur.

\( \abs{AB} = \abs{AC}, \abs{AD} = \abs{BD} \)
\( m(\widehat{DAC}) = 75° \)
olduğuna göre, \( x = m(\widehat{BAD}) \) açısının ölçüsü kaçtır?
Çözümü Göster
\( \abs{AD} = \abs{BD} \) olduğu için \( m(\widehat{ABD}) = x \) olur.
\( \abs{AB} = \abs{AC} \) olduğu için \( m(\widehat{ACD}) = x \) olur.
\( \overset{\triangle}{ABC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 3x + 75 = 180 \)
\( 3x = 105° \)
\( x = 35° \) bulunur.

\( [ED] \perp [AB], \abs{AB} = \abs{BC} \)
\( [ED] \) doğru parçası \( \widehat{BEA} \) açısının açıortayıdır.
\( m(\widehat{BAE}) = 50° \)
olduğuna göre, \( x = m(\widehat{EAC}) \) açısının ölçüsü kaçtır?
Çözümü Göster
\( \abs{AB} = \abs{BC} \) olduğu için,
\( m(\widehat{BAC}) = m(\widehat{ACB}) = 50 + x \)
\( \overset{\triangle}{ADE} \) dik üçgen olduğu için dik olmayan açılar tümlerdir.
\( m(\widehat{AED}) = 90 - 50 = 40° \)
\( m(\widehat{BED}) = m(\widehat{AED}) = 40° \)
\( \overset{\triangle}{BED} \) dik üçgen olduğu için dik olmayan açılar tümlerdir.
\( m(\widehat{DBE}) = 90 - 40 = 50° \)
\( \overset{\triangle}{ABC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 2(x + 50) + 50 = 180 \)
\( x = 15° \) bulunur.

\( m(\widehat{FAB}) = m(\widehat{BAC}) \)
\( m(\widehat{CAD}) = m(\widehat{DAE}) \)
\( m(\widehat{ABC}) = 50° \)
olduğuna göre, \( x = m(\widehat{ADE}) \) açısının ölçüsü kaçtır?
Çözümü Göster
Eşit açıların ölçülerine \( a \) ve \( b \) diyelim.
\( 2a + 2b = 180° \)
\( a + b = m(\widehat{BAD}) = 90° \)
\( \overset{\triangle}{BAD} \) dik üçgen olduğu için dik olmayan açılar tümlerdir.
\( m(\widehat{ADB}) = 90 - 50 = 40° \)
\( \widehat{ADB} \) ve \( x \) açıları bütünler açılardır.
\( x = 180 - 40 = 140° \) bulunur.

\( \abs{AB} = \abs{BE} \)
\( m(\widehat{DAC}) = m(\widehat{EBD}) = x \)
\( m(\widehat{ABE}) = 70° \)
olduğuna göre, \( y = m(\widehat{ACD}) \) açısının ölçüsü kaçtır?
Çözümü Göster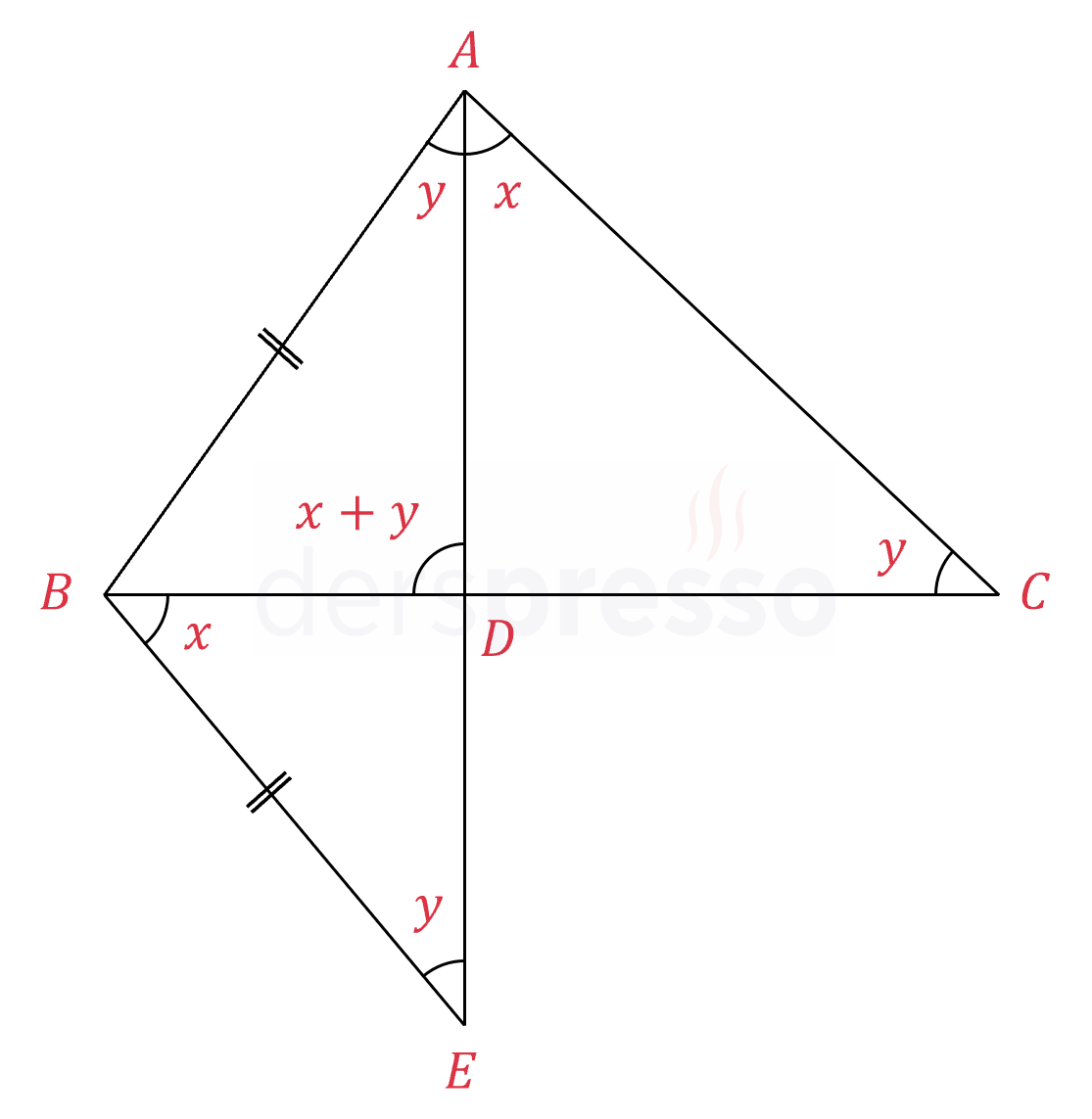
Üçgende bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{ADB}) = m(\widehat{DAC}) + m(\widehat{DCA}) \)
\( = x + y \)
Buna göre \( \overset{\triangle}{BED} \) üçgeninin bir dış açısının ölçüsü \( x + y \) olur.
\( m(\widehat{DBE}) = x \) olduğu için \( m(\widehat{BED}) = y \) olur.
\( \abs{AB} = \abs{BE} \) olduğu için \( m(\widehat{BAE}) = y \) olur.
\( \overset{\triangle}{ABE} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 70 + 2y = 180 \)
\( y = 55° \) bulunur.
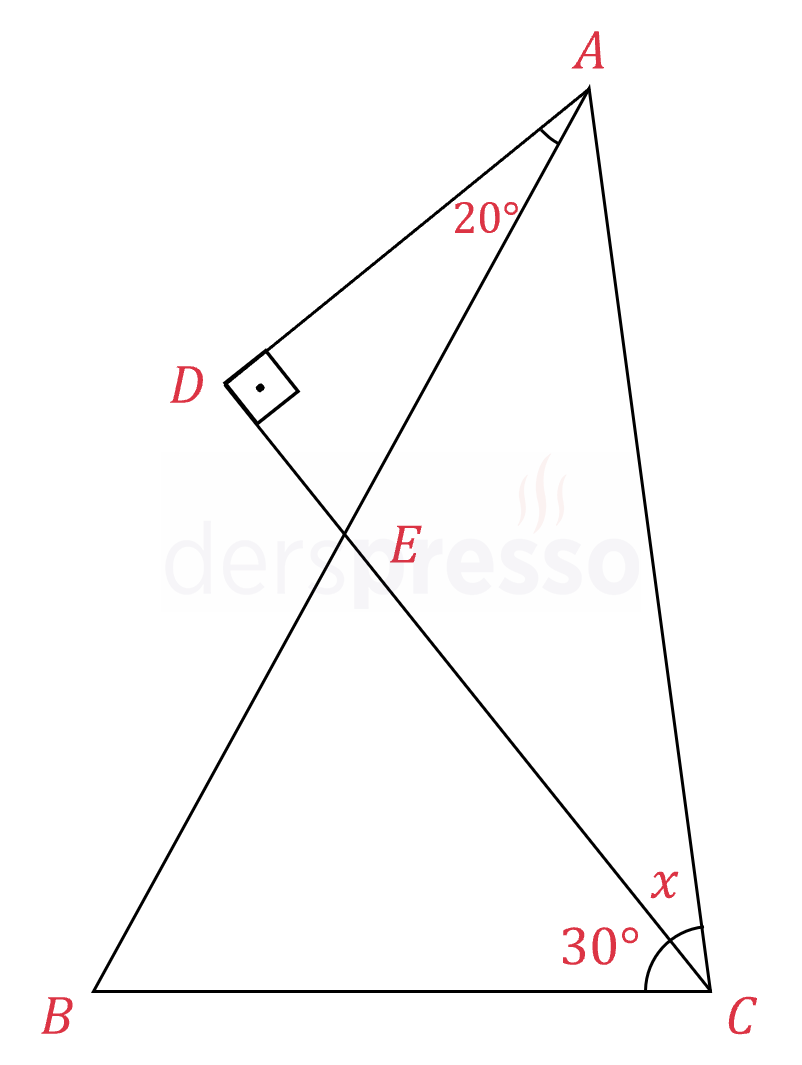
\( [AD] \perp [DC], \abs{AB} = \abs{AC} \)
\( m(\widehat{DAE}) = 20° \)
\( m(\widehat{DCB}) = 30° \)
olduğuna göre, \( x = m(\widehat{ACD}) \) açısının ölçüsü kaçtır?
Çözümü Göster
\( \overset{\triangle}{ADE} \) dik üçgen olduğu için dik olmayan açılar tümlerdir.
\( m(\widehat{DEA}) = 90 - 20 = 70° \)
\( \widehat{DEA} \) ve \( \widehat{BEC} \) ters açılar oldukları için ölçüleri birbirine eşittir.
\( m(\widehat{DEA}) = m(\widehat{BEC}) = 70° \)
\( \overset{\triangle}{BEC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 30 + 70 + m(\widehat{EBC}) = 180 \)
\( m(\widehat{EBC}) = 80° \)
\( \abs{AB} = \abs{AC} \) olduğu için \( m(\widehat{ABC}) = m(\widehat{ACB}) \) olur.
\( x + 30 = 80 \)
\( x = 50° \) bulunur.

\( \abs{AD} = \abs{AE} = \abs{BE} \)
\( m(\widehat{EAC}) = m(\widehat{DEB}) \)
\( m(\widehat{ACE}) = 65° \)
olduğuna göre, \( x = m(\widehat{DAE}) \) açısının ölçüsü kaçtır?
Çözümü Göster
\( \abs{AE} = \abs{BE} \) olduğu için,
\( m(\widehat{DBE}) = m(\widehat{DAE}) = x \)
\( m(\widehat{EAC}) = m(\widehat{DEB}) = y \) diyelim.
Üçgende bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{BEA}) = y + 65 \)
Buna göre \( m(\widehat{DEA}) = 65° \) olur.
\( \abs{AD} = \abs{AE} \) olduğu için,
\( m(\widehat{ADE}) = m(\widehat{AED}) = 65° \)
\( \overset{\triangle}{ADE} \) üçgeninin iç açıları toplam formülünü yazalım.
\( x + 65 + 65 = 180 \)
\( x = 50° \) bulunur.

\( \abs{AD} = \abs{DC}, \abs{AB} = \abs{AC} \)
\( m(\widehat{DCB}) = 33° \)
olduğuna göre, \( x = m(\widehat{ADC}) \) açısının ölçüsü kaçtır?
Çözümü Göster
Eşit uzunluktaki kenarları gören açıların ölçüleri eşittir.
\( m(\widehat{DAC}) = m(\widehat{DCA}) = a \)
\( \abs{AB} = \abs{AC} \) olduğu için,
\( m(\widehat{ABC}) = m(\widehat{ACB}) = a + 33° \)
\( \overset{\triangle}{ABC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( a + 33 + a + 33 + a = 180 \)
\( 3a + 66 = 180 \)
\( a = 38° \)
\( \overset{\triangle}{ADC} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 2a + x = 180 \)
\( 2 \cdot 38 + x = 180 \)
\( x = 104° \) bulunur.

\( \abs{AC} = \abs{AL}, \quad \abs{BC} = \abs{BK} \)
\( m(\widehat{KCL}) = 51° \) olduğuna göre,
\( m(\widehat{ACB}) \) kaç derecedir?
Çözümü Göster\( m(\widehat{ACK}) = x \) ve \( m(\widehat{BCL}) = y \) diyelim.
\( m(\widehat{ACB}) = x + y + 51 \)
\( \abs{AC} = \abs{AL} \) olduğu için \( m(\widehat{ACL}) = m(\widehat{ALC}) = x + 51 \) olur.
\( \abs{BC} = \abs{BK} \) olduğu için \( m(\widehat{BCK}) = m(\widehat{BKC}) = y + 51 \) olur.
\( KCL \) üçgeninin iç açıları toplam formülünü yazalım.
\( 51 + (y + 51) + (x + 51) = 180 \)
\( x + y = 27 \)
\( m(\widehat{ACB}) = x + y + 51 \)
\( = 27 + 51 = 78° \) bulunur.

Yukarıda verilen şekle göre \( a \) kaçtır?
Çözümü Göster\( \widehat{BDF} \) ve \( \widehat{DFG} \) açılarının ölçüleri eşit olduğuna göre bu açılar iç ters açılardır.
Buna göre \( [BD] \) ve \( [FG] \) paraleldir.
\( [BD] \) ve \( [FG] \) paralel ise \( \widehat{BCA} \) ve \( \widehat{FGC} \) açılarının ölçüleri eşit olur.
\( \widehat{BCA} = \widehat{FGE} = 70° \)
\( ABC \) üçgeninin iç açılarının toplamını yazalım.
\( a + 60 + 70 = 180 \)
\( a = 50° \) bulunur.
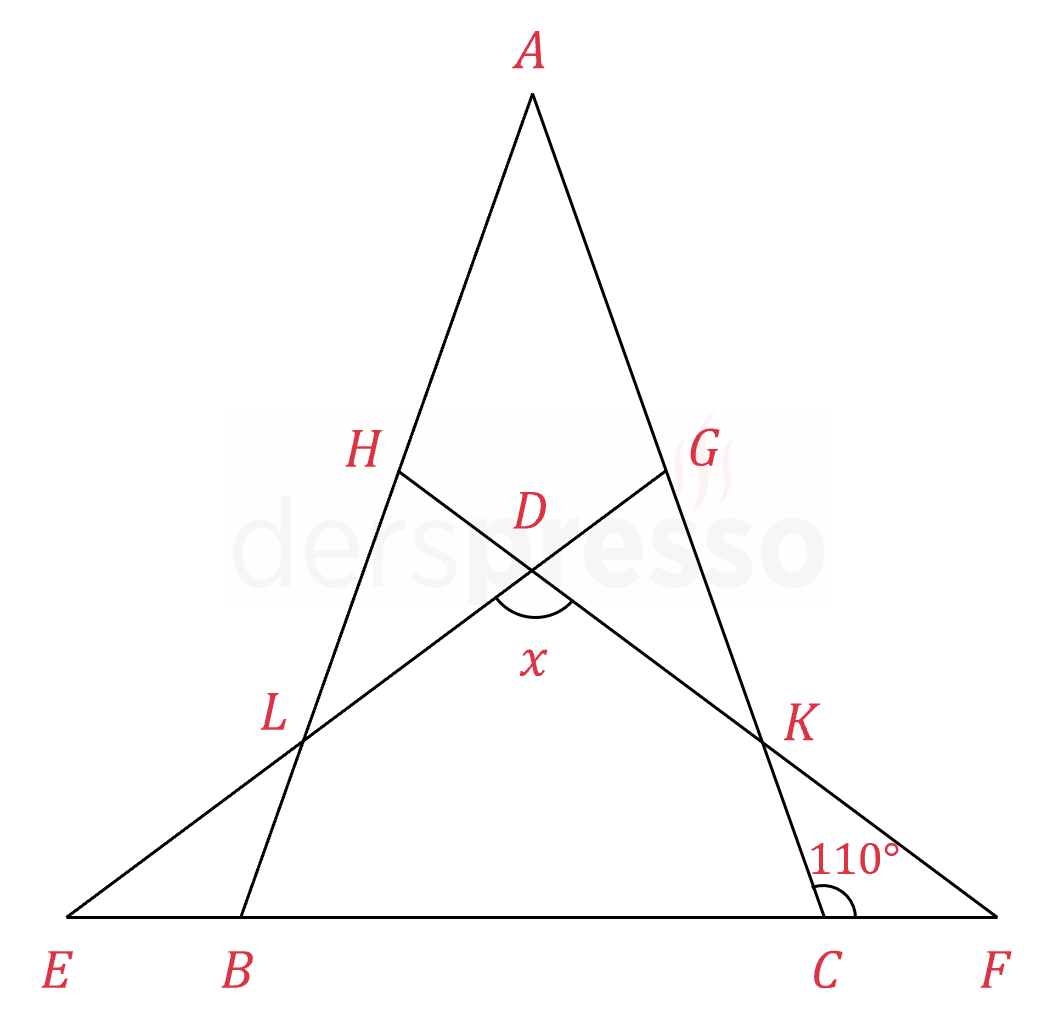
\( \abs{AB} = \abs{AC}, \abs{EG} = \abs{EC}, \abs{FH} = \abs{FB} \)
\( m(\widehat{KCF}) = 110° \)
olduğuna göre, \( x = m(\widehat{EDF}) \) açısının ölçüsü kaçtır?
Çözümü Göster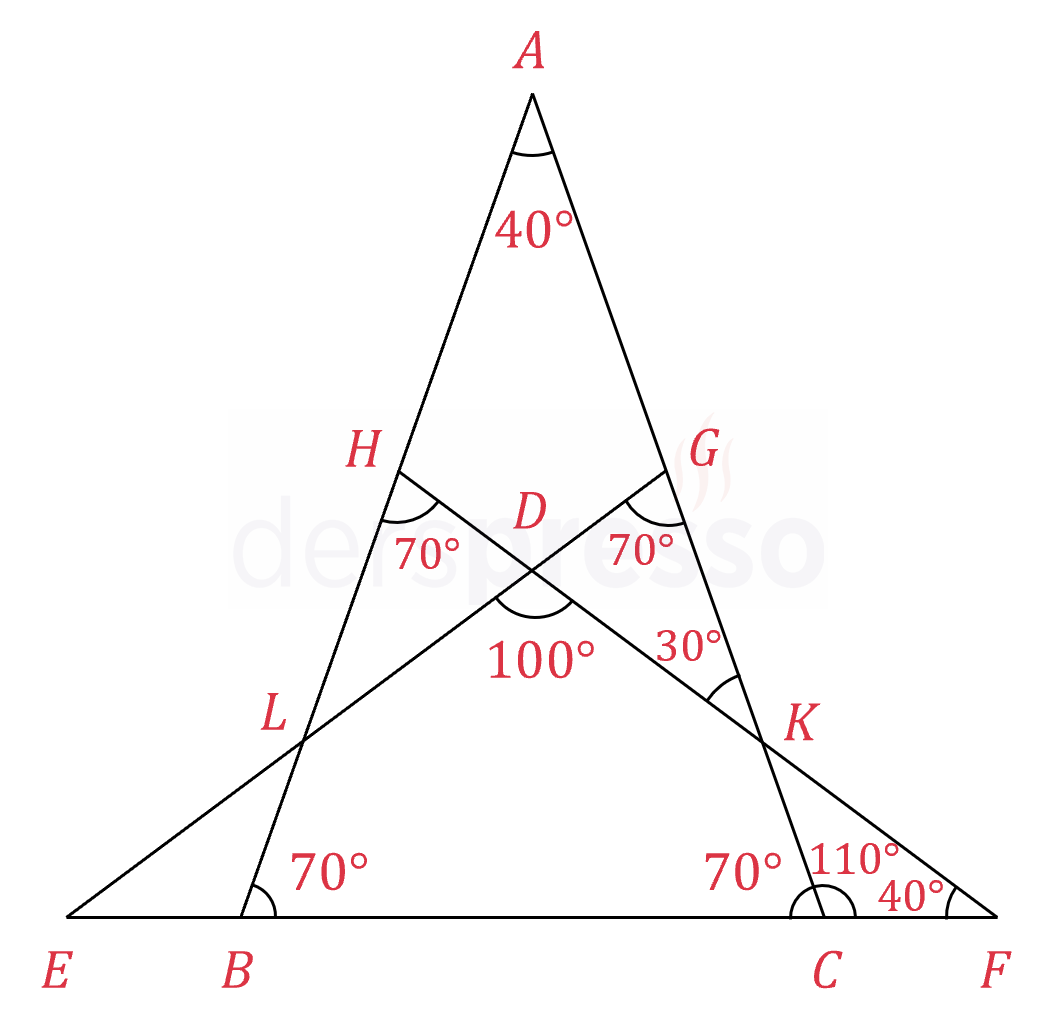
\( \widehat{ACB} \) açısı \( \widehat{KCF} \) açısının bütünler açısıdır.
\( m(\widehat{ACB}) = 180 - 110 = 70° \)
\( \abs{AB} = \abs{AC} \) olduğu için,
\( m(\widehat{ABC}) = 70° \)
\( \abs{FH} = \abs{FB} \) olduğu için,
\( m(\widehat{BHF}) = 70° \)
\( \abs{EG} = \abs{EC} \) olduğu için,
\( m(\widehat{CGE}) = 70° \)
\( \overset{\triangle}{HBF} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 2 \cdot 70 + m(\widehat{BFH}) = 180 \)
\( m(\widehat{BFH}) = 40° \)
\( \overset{\triangle}{CFK} \) üçgeninin iç açıları toplam formülünü yazalım.
\( 110 + 40 + m(\widehat{CKF}) = 180 \)
\( m(\widehat{CKF}) = 30° \)
\( \widehat{CKF} \) ve \( \widehat{DKG} \) ters açılar oldukları için ölçüleri birbirine eşittir.
\( m(\widehat{DKG}) = 30° \)
Üçgende bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( x = m(\widehat{EDF}) = 70 + 30 \)
\( = 100° \) bulunur.

Şekildeki \( \hat{O} \) açısı 20 derecedir.
Buna göre, \( \hat{K}, \hat{L}, \hat{M}, \hat{N} \) iç açılarının toplamı kaçtır?
Çözümü Göster\( \abs{KN} \) kenarının \( \abs{OM} \) ve \( \abs{OL} \) kenarları ile kesiştiği noktalara \( A \) ve \( B \), bu noktalardaki açılara \( a \) ve \( b \), şeklin diğer iç açılarına \( k, l, m, n \) diyelim.

\( AKM \) üçgeninde bir dış açı kendisine komşu olmayan iki iç açının toplamına eşittir.
\( a = k + m \)
Benzer şekilde, \( BLN \) üçgeninde bir dış açı kendisine komşu olmayan iki iç açının toplamına eşittir.
\( b = l + n \)
Buna göre, şeklin iç açılarının toplamı üçgenin iç açıları toplamına eşittir.
\( 20 + a + b = 180 \)
\( 20 + k + m + l + n = 180 \)
\( k + l + n + n = 160° \) bulunur.