Açıortay
Üçgenin bir iç açısını iki eş parçaya bölen ve karşı kenarı kesen doğru parçasına açıortay ya da iç açıortay denir. \( A \), \( B \) ve \( C \) köşelerine ait açıortaylar sırasıyla \( n_a \), \( n_b \) ve \( n_c \) ile gösterilir.
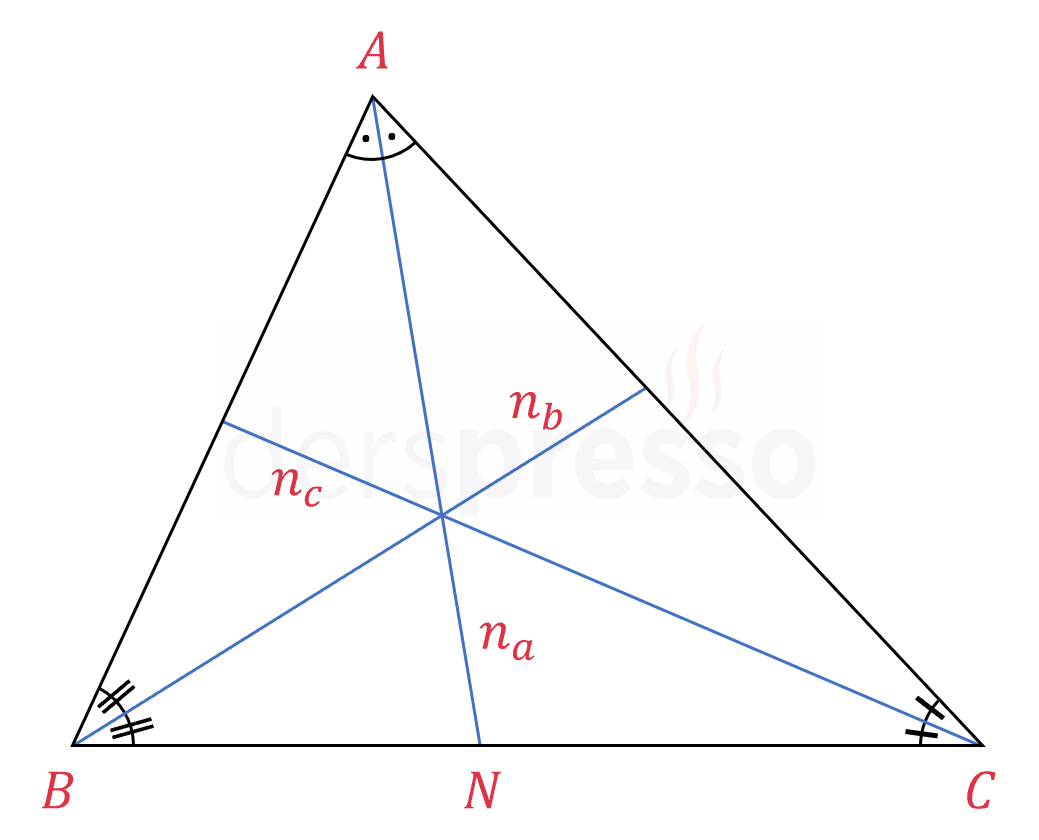
Bir üçgenin iç açıortayları her zaman tek bir noktada ve üçgenin içinde kesişir. İki açıortayın kesiştiği nokta biliniyorsa üçüncü açıortay da bu noktadan geçmek zorundadır. Bu nokta aynı zamanda üçgenin \( r \) yarıçaplı iç teğet çemberinin merkezidir.
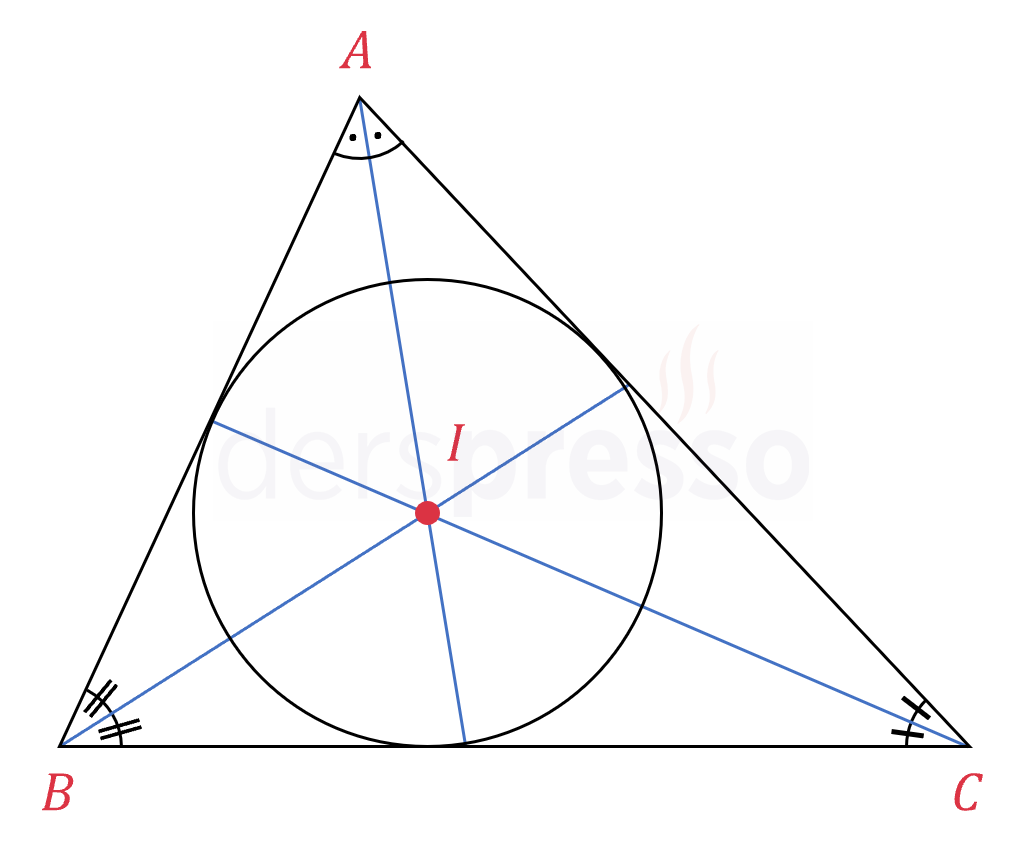
Bir açıortayın herhangi bir noktasından açıortayın kollarına indirilen dikmelerin uzunlukları birbirine eşittir. Aynı zamanda bu dikmelerin açıortayın kollarını kestiği noktalardan açıortayın köşesine olan uzunluklar da eşittir.
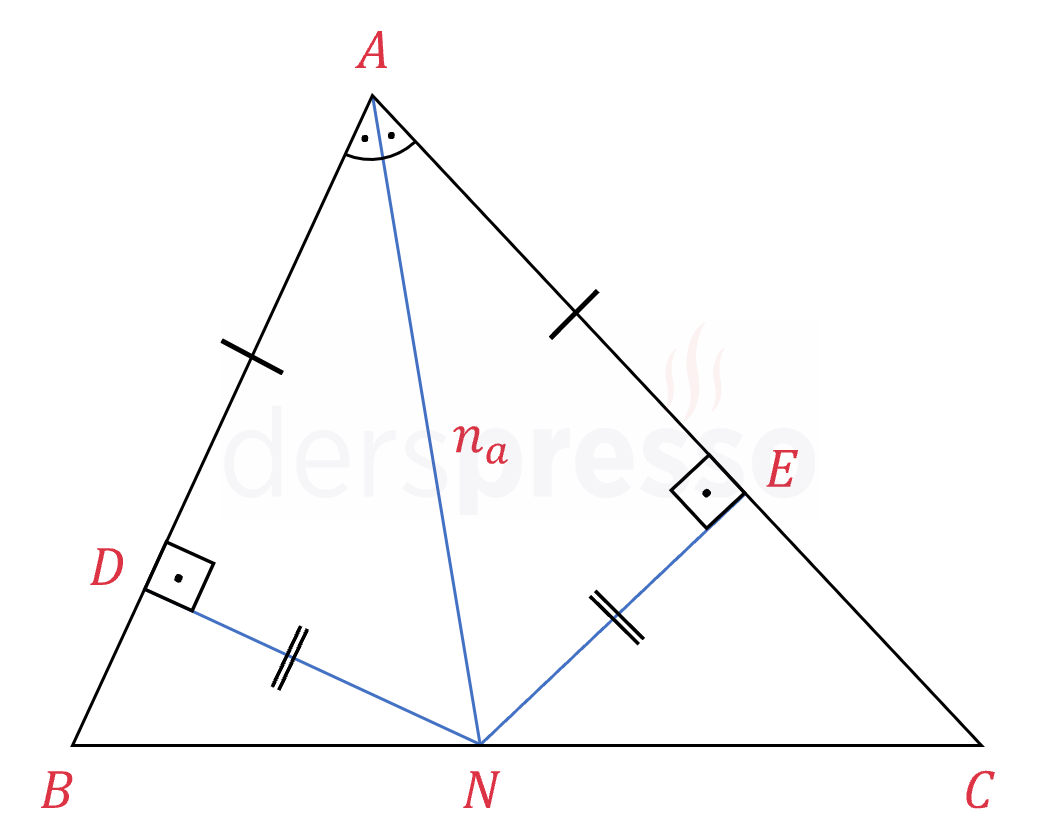
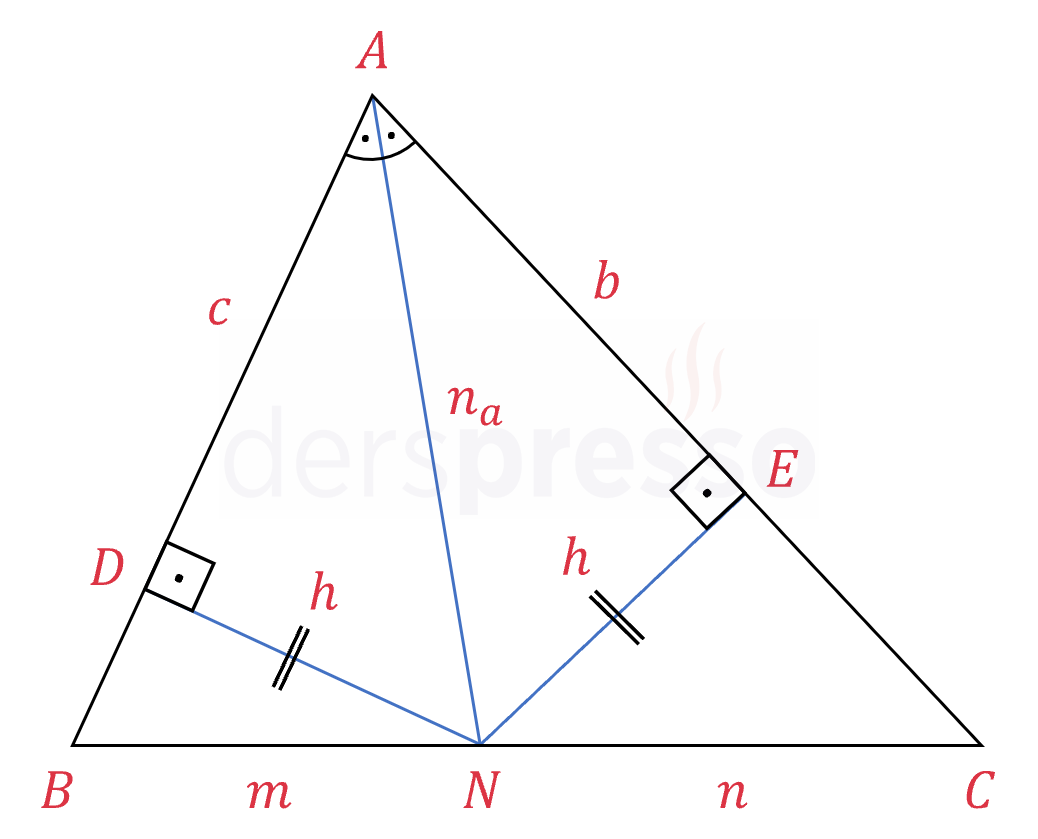
\( [AN] \), \( A \) köşesine ait iç açıortay,
\( [DN] \perp [AB] \) ve \( [NE] \perp [AC] \) olmak üzere,
\( [DN] = [EN] \)
\( [AD] = [AE] \)
İSPATI GÖSTER

Açıortay üzerindeki bir \( C \) noktasından açının kollarına indirilen dikmelerin ve açının kolları üzerinde oluşan doğru parçalarının uzunluklarının eşit olduğunu ve oluşan iki üçgenin eş üçgenler olduğunu gösterelim.
\( m(\widehat{AOC}) = m(\widehat{EOC}) \)
\( m(\widehat{OAC}) = m(\widehat{OEC}) = 90° \)
\( AOC \) ve \( EOC \) üçgenlerinin ikişer açısı eşit olduğu için, üçüncü açıları da eşittir, dolayısıyla iki üçgen benzerdir.
\( [OC] \) kenarı bu iki üçgen için ortak kenar olduğu için, üçgenlerin benzerlik oranı 1'dir, dolayısıyla bu iki üçgen aynı zamanda eş üçgenlerdir. Buna göre, aşağıdaki kenar uzunlukları da eşittir.
\( \abs{CA} = \abs{CE} \)
\( \abs{OA} = \abs{OE} \)
Bir üçgenin en uzun açıortayı üçgenin en kısa kenarına aittir.
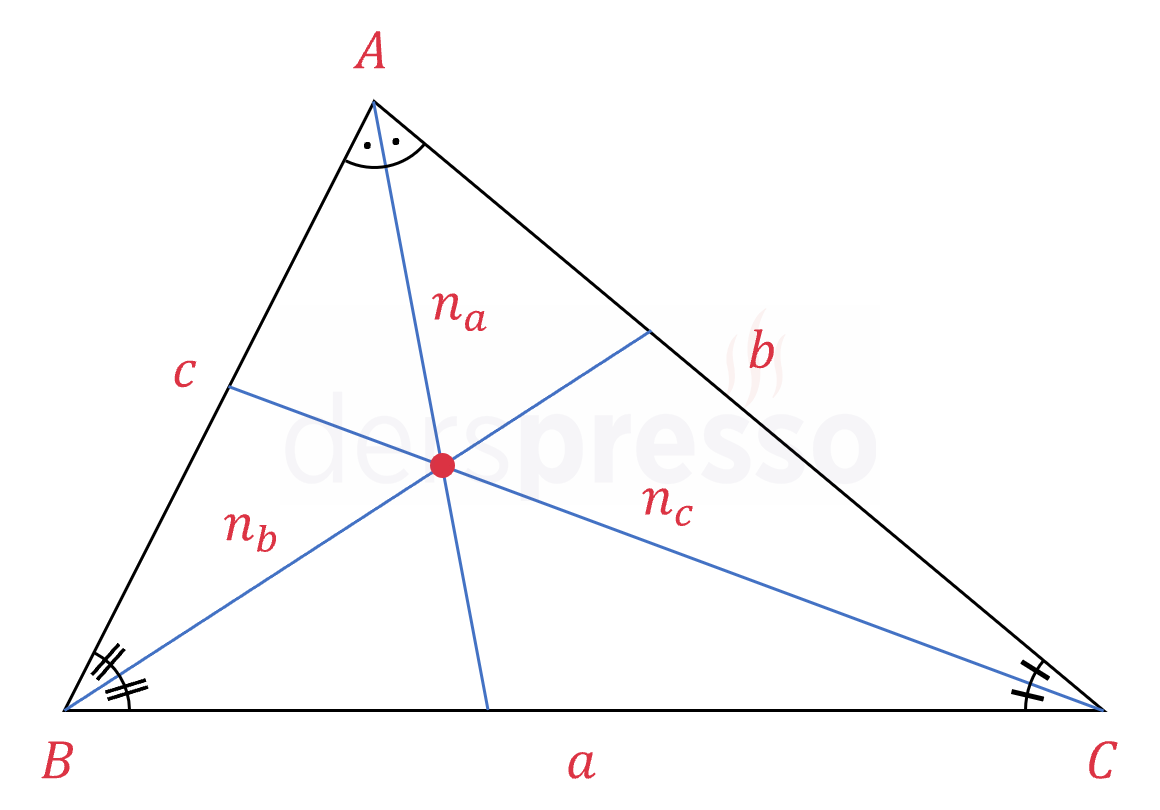
\( a \ge b \ge c \) ise,
\( n_a \le n_b \le n_c \)
Bir üçgenin iç teğet çemberinin merkezi ile üçgenin köşelerini birleştiren doğru parçalarının oluşturduğu alanlar, her alanın komşu olduğu kenar uzunluğu ile doğru orantılıdır.
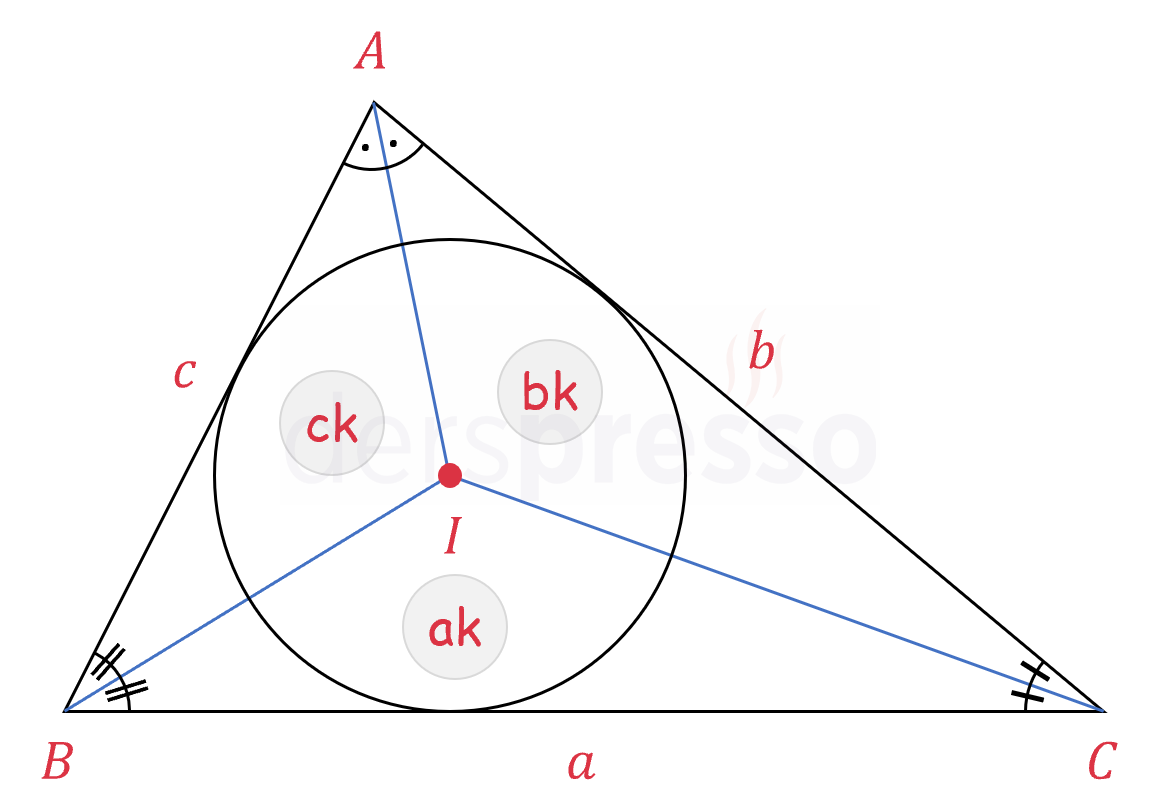
\( I \) üçgenin iç teğet çemberinin merkezi olmak üzere,
\( \dfrac{A(BIC)}{a} = \dfrac{A(CIA)}{b} = \dfrac{A(AIB)}{c} = k \)
İSPATI GÖSTER
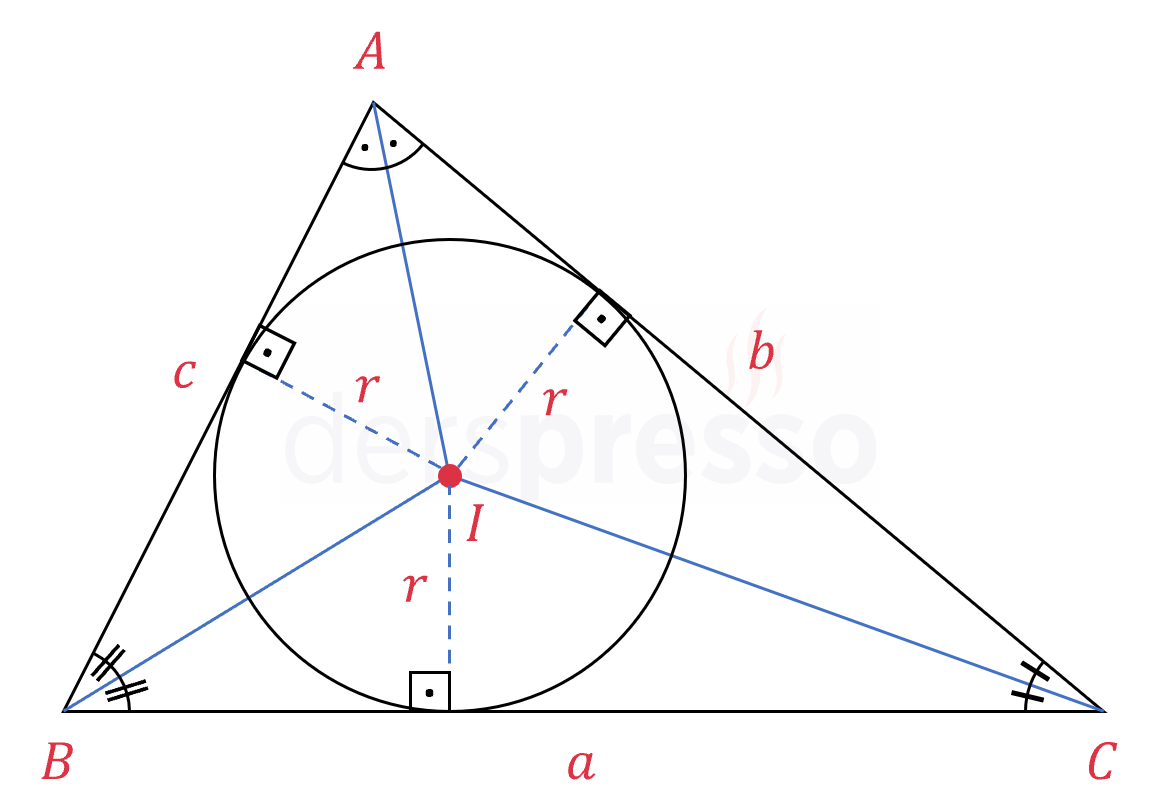
İç teğet çemberin merkezi olan \( I \) noktasından üçgenin kenarlarına birer dikme çizelim.
Bu dikmeler aynı zamanda iç teğet çemberin birer yarıçapıdır.
İç teğet çemberin yarıçapı \( ABC \) üçgeninin kenarlarına teğet olduğu için yarıçap üç kenarı da dik keser, dolayısıyla aynı zamanda üç üçgenin de yüksekliğidir.
Buna göre üçgenlerin alanlarını aşağıdaki gibi yazabiliriz.
\( A(ABI) = \dfrac{c \cdot r}{2} \)
\( A(BCI) = \dfrac{a \cdot r}{2} \)
\( A(CAI) = \dfrac{b \cdot r}{2} \)
Her eşitlikte kenar uzunluklarını eşitliğin sol tarafına aldığımızda ilgili alanların kenar uzunluklarına oranının sabit olduğunu görürüz.
\( \dfrac{A(ABI)}{c} = \dfrac{r}{2} \)
\( \dfrac{A(BCI)}{a} = \dfrac{r}{2} \)
\( \dfrac{A(CAI)}{b} = \dfrac{r}{2} \)
\( \dfrac{A(BIC)}{a} = \dfrac{A(CIA)}{b} = \dfrac{A(AIB)}{c} = \dfrac{r}{2} = k \)
İç Açıortay Teoremi
Üçgenin bir köşesinden karşı kenara çizilen iç açıortayın iki yanındaki kenarların uzunluk oranı, açıortayın karşı kenarda böldüğü parçaların uzunluk oranına eşittir. Yükseklikleri aynı iki üçgenin alanlarının oranı taban uzunlukları ile orantılı olduğu için, bu orantıya açıortayın ayırdığı iki üçgenin alanlarının oranını da ekleyebiliriz.
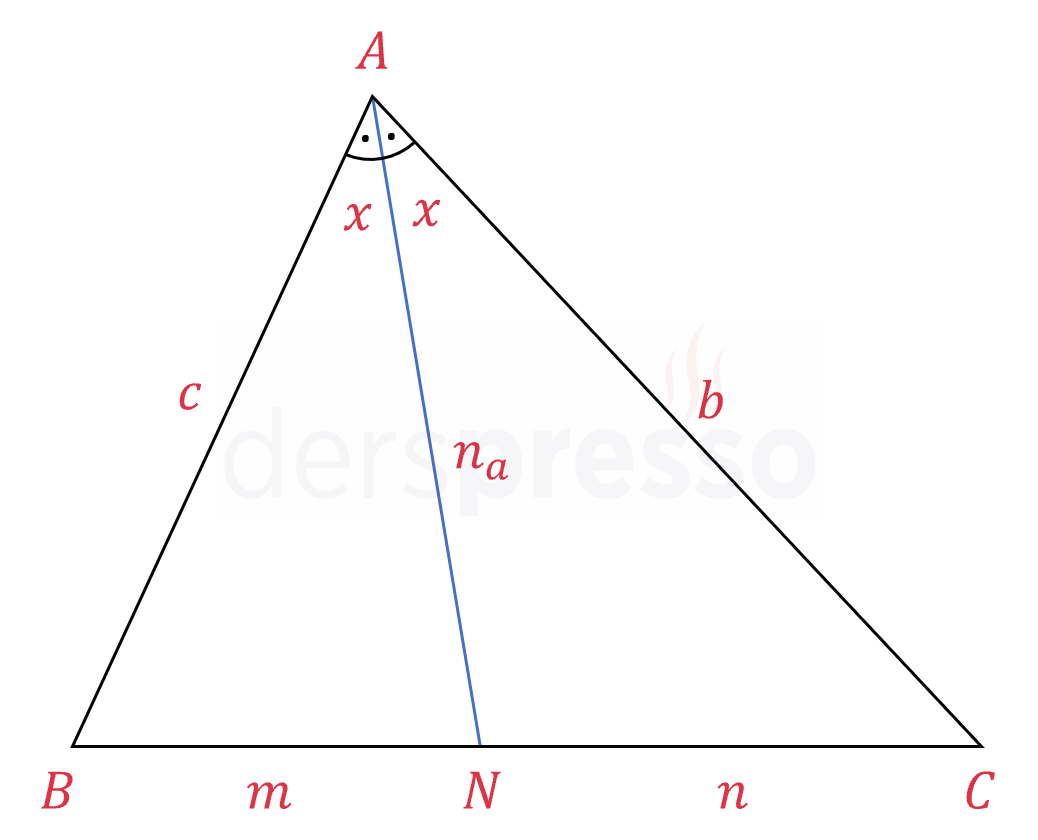
\( [AN] \), \( A \) köşesine ait iç açıortay olmak üzere,
\( \dfrac{c}{b} = \dfrac{m}{n} = \dfrac{A(ABN)}{A(ANC)} \)
İSPATI GÖSTER
İspat 1:
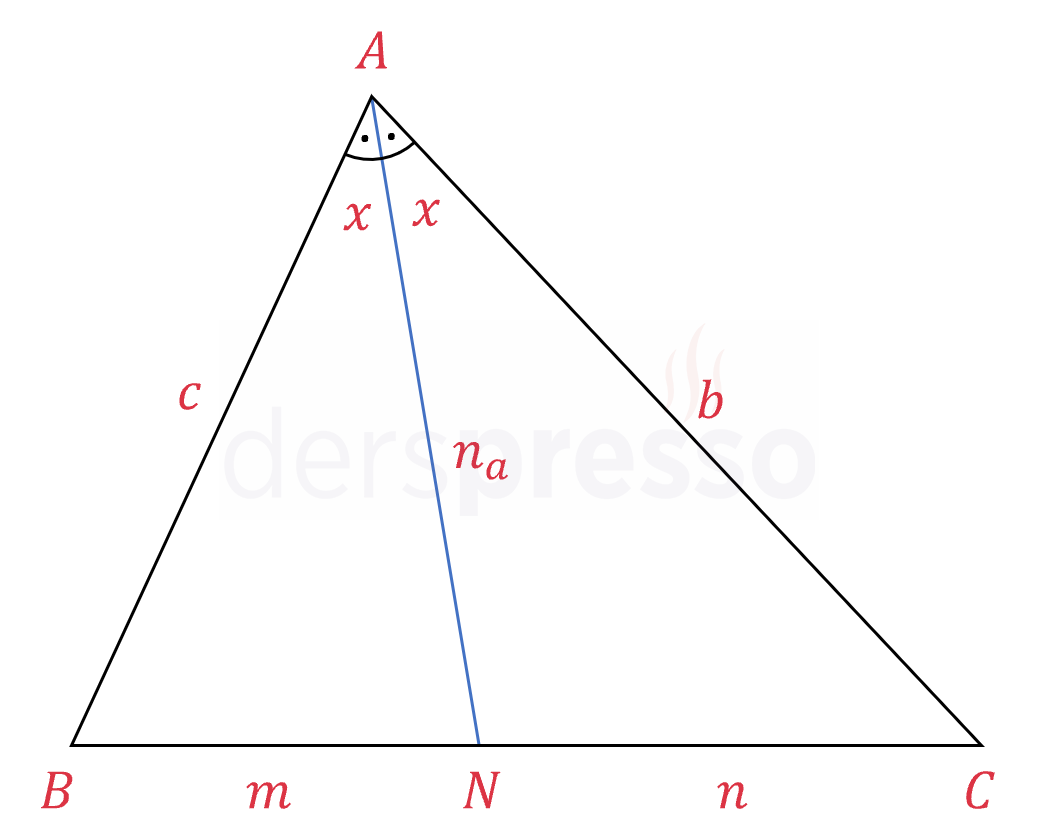
\( \overset{\triangle}{ABN} \) ve \( \overset{\triangle}{ANC} \) üçgenlerinin alanlarını sinüs alan formülünü kullanarak yazalım.
\( A(\overset{\triangle}{ABN}) = \dfrac{1}{2} \cdot n_a \cdot c \cdot \sin{x} \)
\( A(\overset{\triangle}{ANC}) = \dfrac{1}{2} \cdot n_a \cdot b \cdot \sin{x} \)
Bu iki üçgenin tabanları aynı doğru üzerinde ve tepe noktaları aynı nokta olduğu için, yükseklikleri eşittir, dolayısıyla alanlarının oranı taban uzunluklarının oranına eşittir.
\( \dfrac{A(\overset{\triangle}{ABN})}{A(\overset{\triangle}{ANC})} = \dfrac{m}{n} \)
Alan formüllerini yerine koyalım.
\( \dfrac{\frac{1}{2} \cdot n_a \cdot c \cdot \sin{x}}{\frac{1}{2} \cdot n_a \cdot b \cdot \sin{x}} = \dfrac{m}{n} \)
Pay ve paydadaki ortak çarpanları sadeleştirirsek, iç açıortay teoremi formülünü elde ederiz.
\( \dfrac{c}{b} = \dfrac{m}{n} = \dfrac{A(\overset{\triangle}{ABN})}{A(\overset{\triangle}{ANC})} \)
İspat 2:
Açıortayın karşı kenarı kestiği noktadan yan kenarlara birer dikme indirelim. Yukarıda bu dikmelerin uzunluklarının birbirine eşit olduğunu görmüştük.
\( \overset{\triangle}{ABN} \) ve \( \overset{\triangle}{ANC} \) üçgenlerinin alanlarını yan kenarları taban olarak alarak yazalım.
\( A(\overset{\triangle}{ABN}) = \dfrac{c \cdot h}{2} \)
\( A(\overset{\triangle}{ANC}) = \dfrac{b \cdot h}{2} \)
Bu iki üçgenin alanlarının oranının \( m \) ve \( n \) uzunluklarının oranına eşit olduğunu göstermiştik.
\( \dfrac{A(\overset{\triangle}{ABN})}{A(\overset{\triangle}{ANC})} = \dfrac{m}{n} \)
Alan formüllerini yerine koyalım.
\( \dfrac{\frac{c \cdot h}{2}}{\frac{b \cdot h}{2}} = \dfrac{m}{n} \)
Pay ve paydadaki ortak çarpanları sadeleştirirsek, iç açıortay teoremi formülünü elde ederiz.
\( \dfrac{c}{b} = \dfrac{m}{n} = \dfrac{A(\overset{\triangle}{ABN})}{A(\overset{\triangle}{ANC})} \)
Bir iç açıortayın uzunluğu aşağıdaki formülle bulunabilir.
\( n_a = \sqrt{c \cdot b - m \cdot n} \)
İSPATI GÖSTER

\( \overset{\triangle}{ABN} \) üçgenine Kosinüs Teoremi'ni uygulayalım ve kosinüs ifadesini yalnız bırakalım.
\( m^2 = {n_a}^2 + c^2 - 2 \cdot n_a \cdot c \cdot \cos{x} \)
\( \cos{x} = \dfrac{{n_a}^2 + c^2 - m^2}{2 \cdot n_a \cdot c} \)
\( \overset{\triangle}{ANC} \) üçgenine Kosinüs Teoremi'ni uygulayalım ve kosinüs ifadesini yalnız bırakalım.
\( n^2 = {n_a}^2 + b^2 - 2 \cdot n_a \cdot b \cdot \cos{x} \)
\( \cos{x} = \dfrac{{n_a}^2 + b^2 - n^2}{2 \cdot n_a \cdot b} \)
İki kosinüs ifadesini birbirine eşitleyelim ve paydalardaki ortak çarpanları sadeleştirelim.
\( \dfrac{{n_a}^2 + c^2 - m^2}{2 \cdot n_a \cdot c} = \dfrac{{n_a}^2 + b^2 - n^2}{2 \cdot n_a \cdot b} \)
\( \dfrac{{n_a}^2 + c^2 - m^2}{c} = \dfrac{{n_a}^2 + b^2 - n^2}{b} \)
İçler-dışlar çarpımı yapalım.
\( b \cdot {n_a}^2 + b \cdot c^2 - b \cdot m^2 = c \cdot {n_a}^2 + c \cdot b^2 - c \cdot n^2 \)
Açıortay uzunluğunu yalnız bırakalım.
\( b \cdot {n_a}^2 - c \cdot {n_a}^2 = b \cdot m^2 - b \cdot c^2 + c \cdot b^2 - c \cdot n^2 \)
\( {n_a}^2 \cdot (b - c) = (c \cdot b^2 - b \cdot c^2) - (c \cdot n^2 - b \cdot m^2) \)
Yukarıdaki Açıortay Teoremi'nde elde ettiğimiz orantıyı aşağıdaki şekilde de yazabiliriz.
\( \dfrac{c}{b} = \dfrac{m}{n} \Longrightarrow c \cdot n = b \cdot m \)
Bu eşitliği elimizdeki eşitlikte yerine koyalım.
\( {n_a}^2 \cdot (b - c) = c \cdot b \cdot (b - c) - (\underbrace{c \cdot n}_{b \cdot m} \cdot n - \underbrace{b \cdot m}_{c \cdot n} \cdot m) \)
\( {n_a}^2 \cdot (b - c) = c \cdot b \cdot (b - c) - (b \cdot m \cdot n - c \cdot n \cdot m) \)
\( {n_a}^2 \cdot (b - c) = c \cdot b \cdot (b - c) - m \cdot n \cdot (b - c) \)
İki taraftaki \( (b - c) \) çarpanını sadeleştirelim.
\( {n_a}^2 = c \cdot b - m \cdot n \)
\( n_a = \sqrt{c \cdot b - m \cdot n} \)
Dış Açıortay Teoremi
Üçgenin bir köşesinden çizilen dış açıortay için aşağıdaki orantı geçerlidir.
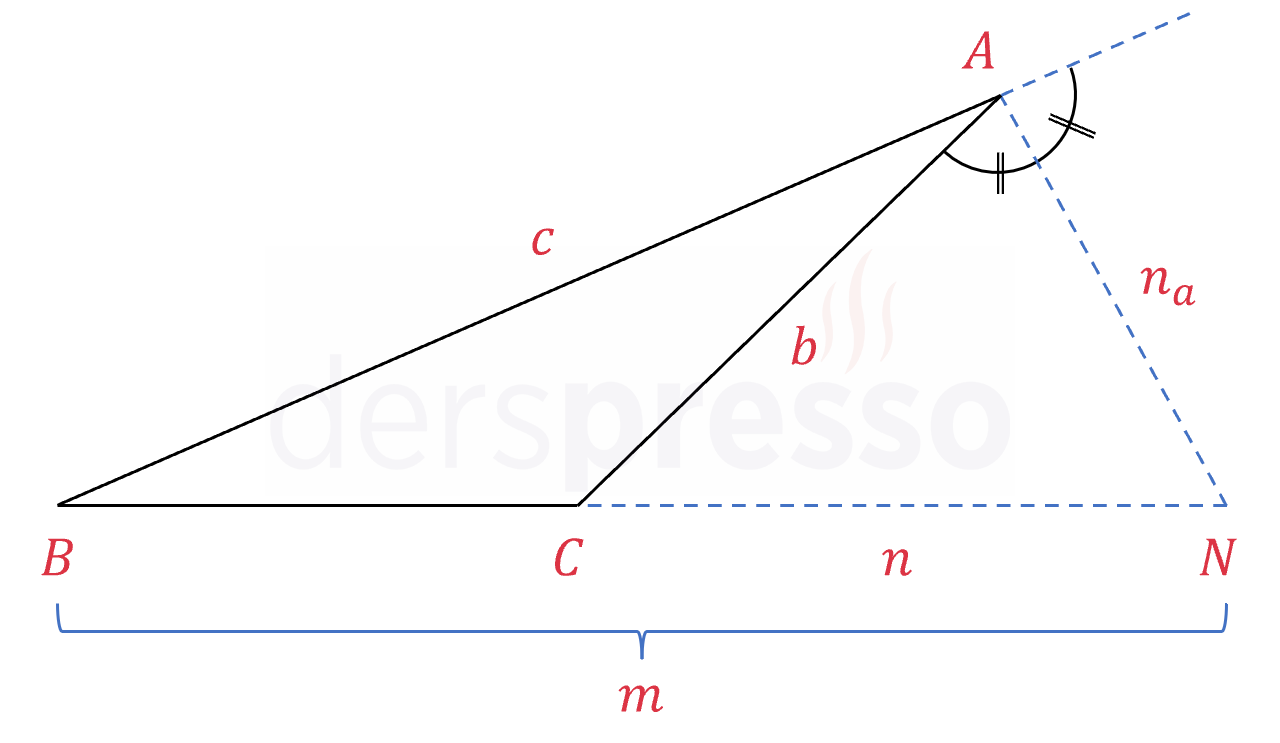
\( [AN] \), \( A \) köşesine ait bir dış açıortay olmak üzere,
\( \dfrac{c}{b} = \dfrac{m}{n} \)
İSPATI GÖSTER

\( C \) noktasından geçen ve \( [AB] \) kenarına paralel bir doğru çizelim ve bu doğrunun dış açıortayı kestiği noktaya \( D \) diyelim.
\( \widehat{ADC} \) ve \( \widehat{EAD} \) açıları iç ters açılar oldukları için, ölçüleri eşittir.
\( m(\widehat{ADC}) = m(\widehat{EAD}) \)
Bu durumda \( \overset{\triangle}{ACD} \) ikizkenar bir üçgendir.
\( \abs{CA} = \abs{CD} = b \)
\( \overset{\triangle}{NAB} \) üçgenine Temel Orantı Teoremi'ni uygularsak Dış Açıortay Teoremi formülünü elde ederiz.
\( \dfrac{\abs{BA}}{\abs{CD}} = \dfrac{\abs{NB}}{\abs{NC}} \)
\( \dfrac{c}{b} = \dfrac{m}{n} \)
Bir dış açıortayın uzunluğu aşağıdaki formülle bulunabilir.
\( n_a = \sqrt{m \cdot n - c \cdot b} \)
İSPATI GÖSTER
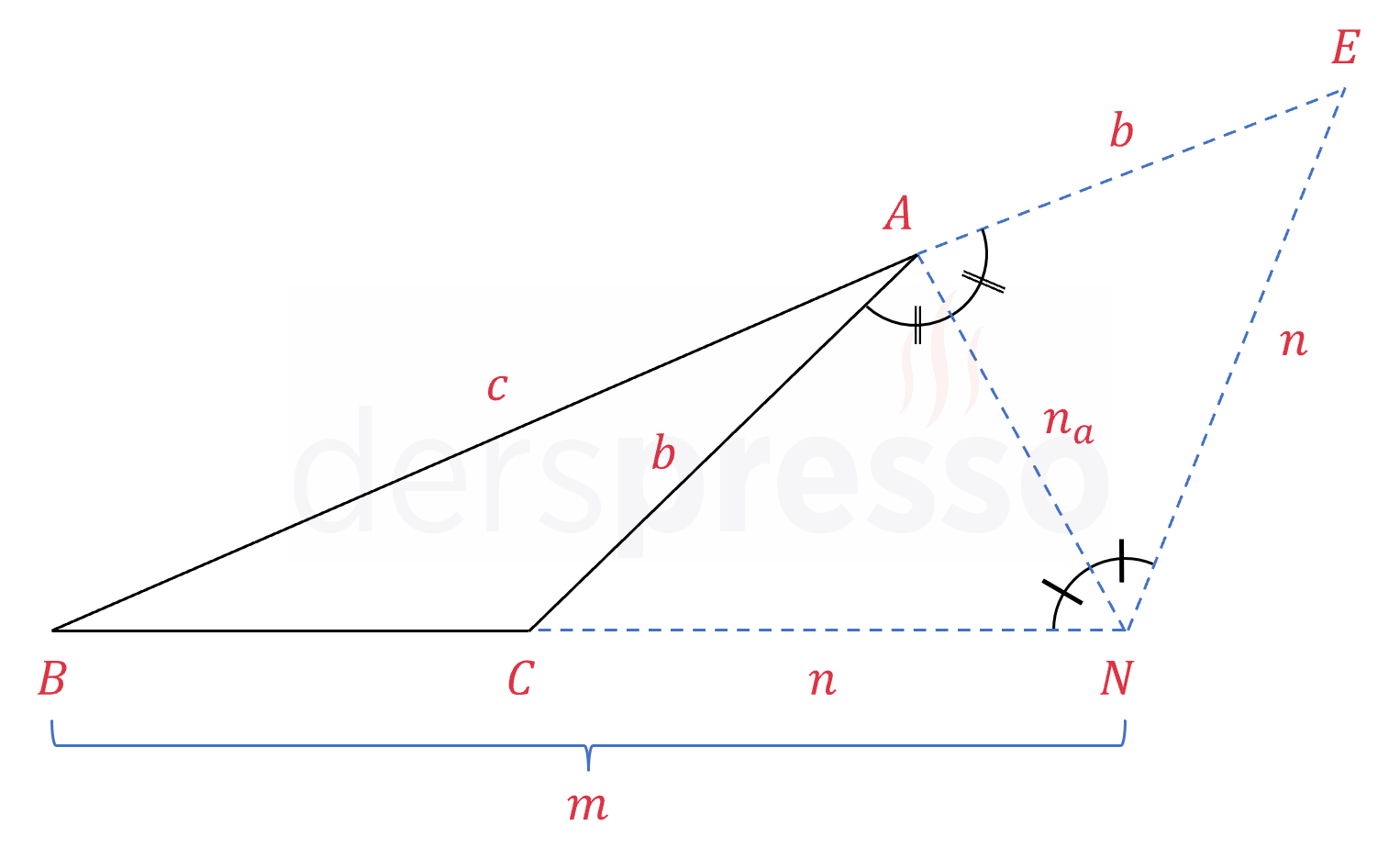
\( A \) köşesinin dış açıortayının \( [BC] \) kenarının uzantısını kestiği nokta \( N \)'dir.
\( N \) noktasından \( m(\widehat{ANC}) = m(\widehat{ANE}) \) olacak şekilde bir doğru çizelim. Bu doğrunun \( [BA] \) kenarının uzantısını kestiği noktaya \( E \) diyelim.
\( \overset{\triangle}{NAC} \) ve \( \overset{\triangle}{NAE} \) üçgenlerinin ikişer açısı eşit olduğu için, üçüncü açıları da eşittir, dolayısıyla bu üçgenler benzerdir. Üçgenlerin \( [NA] \) kenarı ortak olduğu için, bu iki üçgen aynı zamanda eş üçgenlerdir. Buna göre aşağıdaki kenar uzunlukları da birbirine eşittir.
\( \abs{AC} = \abs{AE} = b \)
\( \abs{NC} = \abs{NE} = n \)
\( \overset{\triangle}{ABC} \) üçgeninde \( A \) köşesinin bir dış açıortayı olan \( n_a \), aynı zamanda büyük \( \overset{\triangle}{EBN} \) üçgeninde \( N \) köşesinin bir iç açıortayı olmaktadır. Dolayısıyla, bu açıortaya \( \overset{\triangle}{EBN} \) üçgeni için iç açıortay teoremini uygularsak dış açıortay uzunluk formülünü elde ederiz.
\( n_a = \sqrt{m \cdot n - c \cdot b} \)
Bir köşeden çizilen iç ve dış açıortaylar bütünler iki açıyı iki eşit açıya böldükleri için iç ve dış açıortayların arasında oluşan açı \( 90° \) olur.

\( x + y = 90° \)
Dış Teğet Çember
Bir üçgenin iki dış açıortayı ile bir iç açıortayı üçgenin dışında bir noktada kesişir. Bu nokta üçgenin dış teğet çemberlerinden birinin merkezidir. Dış teğet çember üçgenin bir kenarına ve diğer iki kenarın üçgenin dışındaki uzantılarına teğettir.

Bir üçgenin her biri bir kenara dıştan teğet olmak üzere toplam üç farklı dış teğet çemberi vardır.

\( [AD] \) doğru parçası \( A \) köşesinin açıortayıdır.
\( \abs{AB} = 8 , \abs{AC} = 12, \abs{BC} = 10 \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü Göster\( \abs{BC} = 10 \) olduğu için \( \abs{DC} = 10 - x \) diyelim.
İç açıortay teoremini kullanalım.
\( \dfrac{\abs{AB}}{\abs{AC}} = \dfrac{\abs{BD}}{\abs{DC}} \)
\( \dfrac{8}{12} = \dfrac{x}{10 - x} \)
İçler - dışlar çarpımı yapalım.
\( 80 - 8x = 12x \)
\( 20x = 80 \)
\( x = 4 \) bulunur.

\( [AB] \perp [BC] \) ve \( [AD] \) doğru parçası \( A \) köşesinin açıortayıdır.
\( \abs{AB} = 6, \abs{AC} = 10 \)
olduğuna göre, \( \abs{AD} = x \) kaçtır?
Çözümü Göster
Pisagor teoremini kullanarak \( \abs{BC} \) uzunluğunu bulalım.
\( \abs{AC}^2 = \abs{AB}^2 + \abs{BC}^2 \)
\( \abs{BC} = \sqrt{10^2 - 6^2} \)
\( \abs{BC} = 8 \)
İç açıortay teoremini kullanalım.
\( \abs{BD} = y, \abs{DC} = 8 - y \) diyelim.
\( \dfrac{\abs{AB}}{\abs{AC}} = \dfrac{\abs{BD}}{\abs{DC}} \)
\( \dfrac{6}{10} = \dfrac{y}{8 - y} \)
İçler - dışlar çarpımı yapalım.
\( 10y = 48 - 6y \)
\( 16y = 48 \)
\( y = 3 \)
\( ABD \) dik üçgeninin iki kenar uzunluğunu bildiğimiz için Pisagor teoremi ile dik kenar uzunluğunu bulabiliriz.
\( \abs{AD}^2 = \abs{AB}^2 + \abs{BD}^2 \)
\( x = \abs{AD} = \sqrt{6^2 + 3^2} \)
\( = \sqrt{45}= 3\sqrt{5} \) bulunur.

\( [CD] \) doğru parçası \( C \) köşesinin açıortayıdır.
\( \abs{BC} = 6, \abs{BD} = 4, \abs{AD} + \abs{AC} = 15 \)
olduğuna göre, \( \abs{AD} = x \) kaçtır?
Çözümü Göster
\( \abs{AD} + \abs{AC} = 15 \) olduğu için \( \abs{AC} = 15 - x \) diyelim.
İç açıortay teoremini kullanalım.
\( \dfrac{\abs{CB}}{\abs{DB}} = \dfrac{\abs{CA}}{\abs{DA}} \)
\( \dfrac{6}{4} = \dfrac{15 - x}{x} \)
İçler - dışlar çarpımı yapalım.
\( 6x = 60 - 4x \)
\( 10x = 60 \)
\( x = 6 \) bulunur.

\( [AC] \) doğrusu \( A \) köşesinin açıortayıdır.
\( \abs{CD} = x + 4, \abs{CB} = 2x - 4, \abs{AB} = 6 \)
olduğuna göre, \( \abs{AC} \) kaçtır?
Çözümü GösterBir açıortayın herhangi bir noktasından açıortayın kollarına indirilen dikmelerin uzunlukları birbirine eşittir.
\( 2x - 4 = x + 4 \)
\( x = 8 \)
\( \abs{CB} \) uzunluğunu bulalım.
\( \abs{CB} = 2x - 4 = 12 \)
\( CBA \) dik üçgeninde Pisagor teoremini kullanalım.
\( \abs{AC}^2 = \abs{CB}^2 + \abs{BA}^2 \)
\( \abs{AC} = \sqrt{12^2 + 6^2} \)
\( = 6\sqrt{5} \) bulunur.

\( ADC \) üçgeninde \( [AB] \) doğru parçası \( A \) köşesinin dış açıortayıdır.
\( \abs{AC} = 12, \abs{AD} = 4, \abs{DC} = 6 \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü Göster\( ADC \) üçgeni için dış açıortay teoremini kullanalım.
\( \dfrac{\abs{AD}}{\abs{AC}} = \dfrac{\abs{BD}}{\abs{BC}} \)
\( \dfrac{4}{12} = \dfrac{x}{6 + x} \)
İçler - dışlar çarpımı yapalım.
\( 12x = 24 + 4x \)
\( 8x = 24 \)
\( x = 3 \) bulunur.

\( [AD] \) doğru parçası \( A \) köşesinin açıortayıdır.
\( [AB] \perp [BC], m(\widehat{ACB}) = 45° \)
\( \abs{DC} = 3\sqrt{2} \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü Göster
\( D \) noktasından \( [AC] \) kenarına bir dik indirelim.
\( [AD] \) açıortayından açıortayın kollarına indirilen diklerin uzunlukları eşit olur.
\( \abs{BD} = \abs{DE} = x \)
\( DEC \) dik üçgeni 45-45-90° üçgeni olduğu için ikizkenar üçgendir.
45-45-90° üçgeninde dik açının gördüğü kenar 45°'lik açının gördüğü kenarın \( \sqrt{2} \) katıdır.
\( \abs{ED} = x = 3 \) bulunur.

\( ABC \) üçgeninin çevresi 30 birim olup \( [AD] \) doğru parçası \( A \) köşesinin açıortayıdır.
\( \abs{AB} = 14, \abs{AC} = 6 \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü Göster
İç açıortay teoremini kullanarak \( [BD] \) ve \( [DC] \) kenar uzunluklarının oranını bulalım.
\( \dfrac{\abs{AB}}{\abs{AC}} = \dfrac{\abs{BD}}{\abs{DC}} \)
\( \dfrac{14}{6} = \dfrac{\abs{BD}}{\abs{DC}} \)
\(\abs{BD} = 7k, \abs{DC} = 3k \) diyelim.
\( ABC \) üçgenin çevresi 30 birimdir.
\( 14 + 6 + 7k + 3k = 30 \)
\( 20 + 10k = 30 \)
\( k = 1 \)
\( \abs{BD} = x = 7k = 7 \) bulunur.

\( ABC \) üçgeninde \( [BK] \) ve \( [CK] \) doğru parçaları sırasıyla \( B \) ve \( C \) köşelerinin açıortaylarıdır.
\( \abs{BC} = 19, \abs{CE} = 7, \abs{KE} = 5 \)
olduğuna göre, \( \abs{BK} = x \) kaçtır?
Çözümü Göster\( K \) noktasından \( [BC] \) kenarına bir dik indirelim.
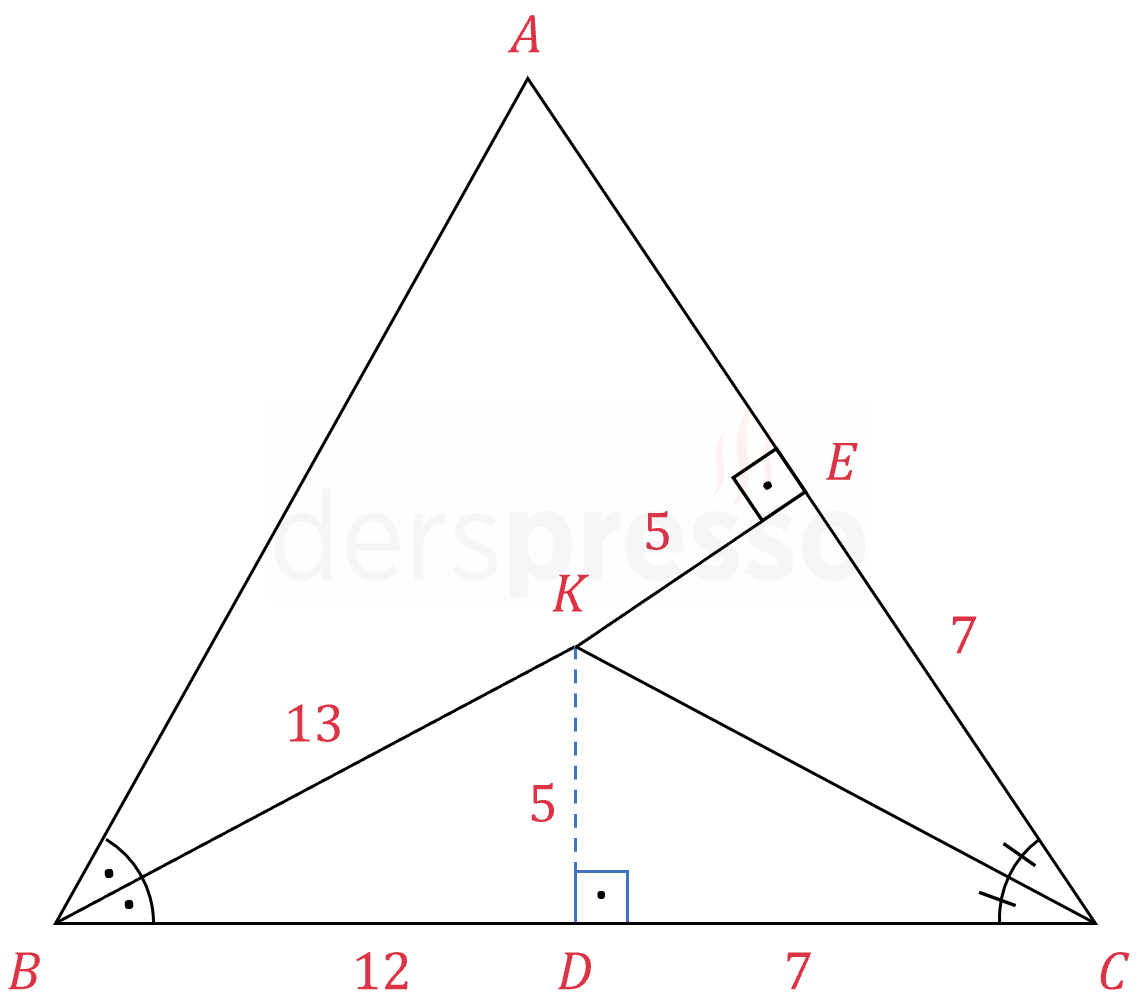
\( [KD] \perp [BC] \)
Bir açıortay üzerindeki bir noktadan açıortayın kollarına indirilen dikmelerin uzunlukları birbirine eşittir.
\( \abs{KD} = \abs{KE} = 5 \)
Bu dikmelerin açıortayın kollarını kestiği noktalardan açıortayın köşesine olan uzunluklar da eşittir.
\( \abs{CD} = \abs{CE} = 7 \)
Bu durumda \( \abs{BD} = 12 \) olur.
Oluşan \( BDK \) üçgeni 5-12-13 özel üçgenidir.
\( \abs{BK} = x = 13 \) bulunur.
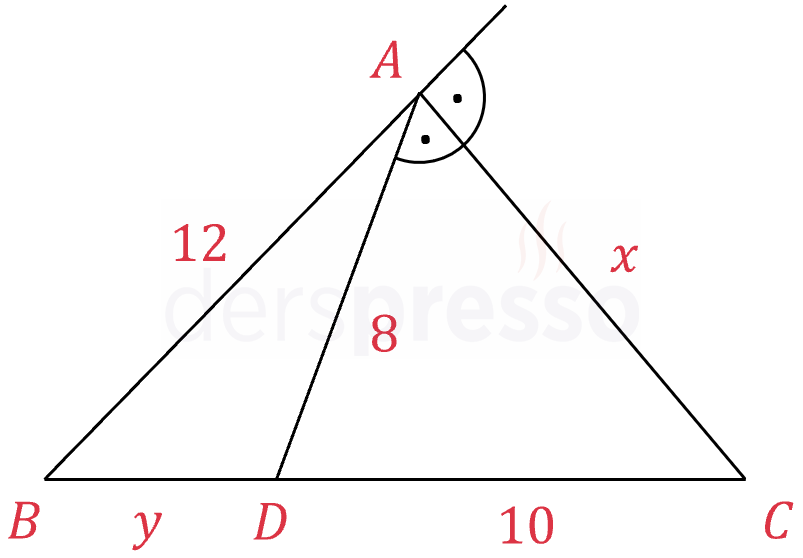
\( [AC] \) doğru parçası \( A \) köşesinin dış açıortayıdır.
\( \abs{AB} = 12, \abs{AD} = 8, \abs{DC} = 10 \)
olduğuna göre, \( \abs{AC} = x \) kaçtır?
Çözümü GösterÖnce dış açıortay teoremini kullanarak \( y \) uzunluğunu bulalım.
\( \dfrac{\abs{AD}}{\abs{AB}} = \dfrac{\abs{CD}}{\abs{CB}} \)
\( \dfrac{8}{12} = \dfrac{10}{10 + y} \)
İçler - dışlar çarpımı yapalım.
\( 120 = 80 + 8y \)
\( 8y = 40 \)
\( y = 5 \)
\( x \) uzunluğunu bulmak için dış açıortay uzunluk formülünü kullanalım.
\( x = \sqrt{\abs{CB} \cdot \abs{CD} - \abs{AB} \cdot \abs{AD}} \)
\( = \sqrt{15 \cdot 10 - 12 \cdot 8} \)
\( = \sqrt{54} = 3\sqrt{6} \) bulunur.
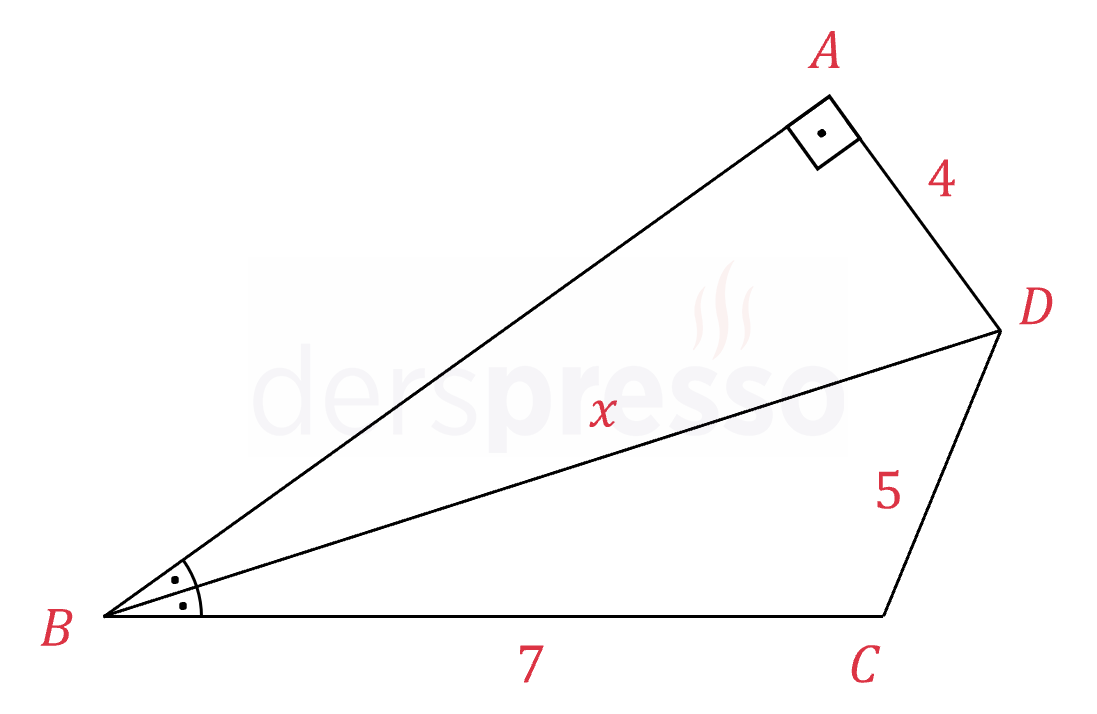
\( [BD] \) doğrusu \( B \) köşesinin açıortayıdır.
\( [BA] \perp [AD], \abs{DA} = 4 \)
\( \abs{BC} = 7, \abs{CD} = 5 \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü GösterAçıortaydan açıortayın bir koluna indirilen dikin benzerini açıortayın diğer koluna da indirelim.
\( [DE] \perp [BE] \)

Bir açıortayın herhangi bir noktasından açıortayın kollarına indirilen dikmelerin uzunlukları birbirine eşittir.
\( \abs{AD} = \abs{DE} = 4 \)
Oluşan \( DEC \) üçgeni 3-4-5 özel üçgenidir.
\( \abs{CE} = 3 \)
\( [BE] = 7 + 3 = 10 \)
\( BED \) üçgeninde Pisagor teoremini kullanarak \( \abs{BD} \) uzunluğunu bulalım.
\( x^2 = \abs{BE}^2 + \abs{DE}^2 \)
\( x = \sqrt{10^2 + 4^2} \)
\( = 2\sqrt{29} \) bulunur.

\( [AD] \) doğru parçası \( A \) köşesinin açıortayıdır.
\( m(\widehat{ABC}) = 30°, m(\widehat{ACB}) = 45° \)
\( \abs{BD} = 6 \)
olduğuna göre, \( \abs{DC} = x \) kaçtır?
Çözümü Göster\( D \) noktasından açıortayın kollarına dikler indirelim.
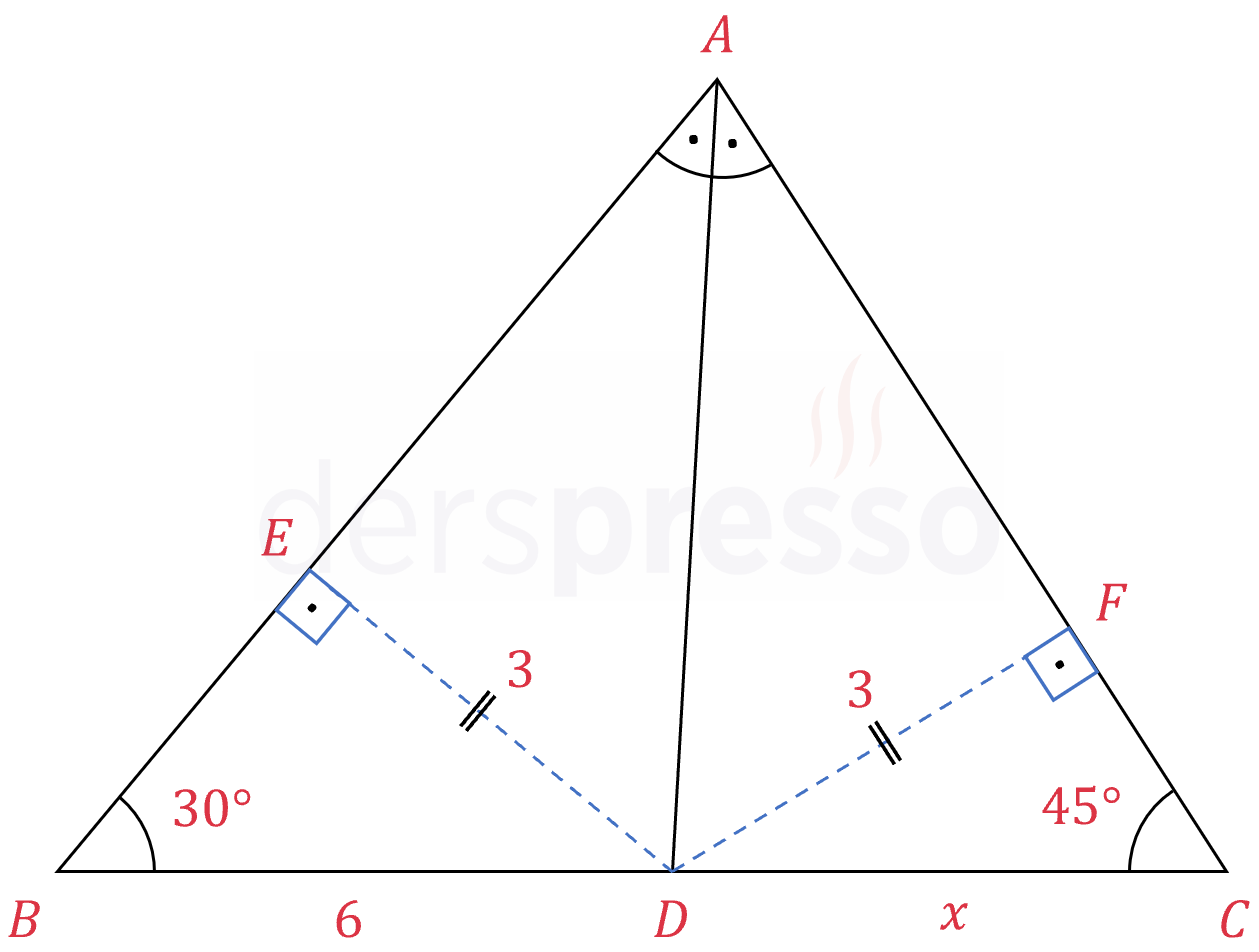
\([DE] \perp [AB], [DF] \perp [AC] \)
\( BED \) üçgeni 30-60-90° üçgenidir ve 30°'lik açının gördüğü kenarın uzunluğu dik açının gördüğü kenarın uzunluğunun yarısına eşittir.
\(\abs{BD} = 6 \Longrightarrow \abs{ED} = 3 \)
Bir açıortay üzerindeki bir noktadan açıortayın kollarına indirilen dikmelerin uzunlukları birbirine eşittir.
\( \abs{DF} = \abs{ED} = 3 \)
\( DFC \) üçgeni 45-45-90° üçgenidir ve dik açının gördüğü kenarın uzunluğu 45°'lik açının açının gördüğü kenarın uzunluğunun \( \sqrt{2} \) katıdır.
\( \abs{DC} = x = 3\sqrt{2} \) bulunur.