Eşkenar Üçgen
Üç kenar uzunluğu birbirine eşit olan üçgene eşkenar üçgen denir.
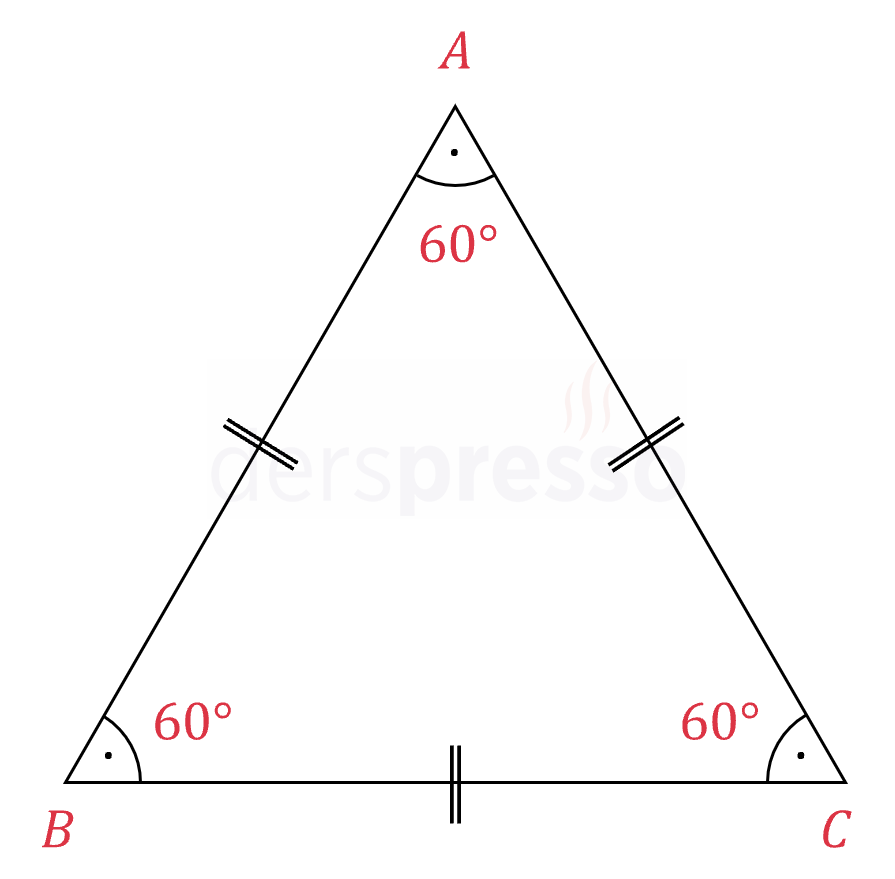
Eşkenar üçgenlerin tüm iç açıları birbirine eşit ve 60°'dir. Bunun karşıtı da doğrudur, yani tüm iç açıları birbirine eşit olan üçgen eşkenardır.
\( \abs{AB} = \abs{BC} = \abs{AC} \Longleftrightarrow \) \( m(\widehat{A}) = m(\widehat{B}) = m(\widehat{C}) = 60° \)
Eşkenar üçgen ikizkenar üçgenin tüm özelliklerini taşır.
Eşkenar üçgende tüm kenarlara ait yüksekliklerin uzunlukları eşittir. Bir kenara ait yükseklik, aynı zamanda o kenara ait açıortay, kenarortay ve orta dikmedir.
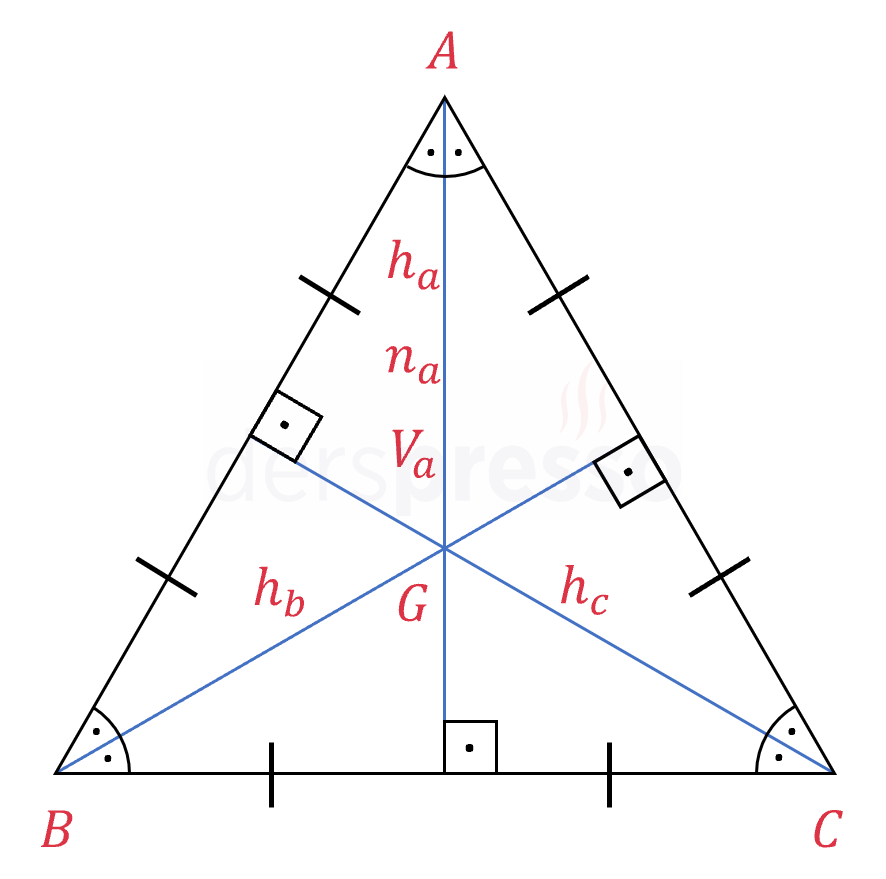
\( h_a = h_b = h_c \)
\( h_a = n_a = V_a \)
Eşkenar üçgenin tüm merkezleri (diklik merkezi, iç teğet çemberin merkezi, ağırlık merkezi, çevrel çemberin merkezi) aynı noktadadır.
Eşkenar üçgenin yüksekliği kenar uzunluğu cinsinden aşağıdaki şekilde ifade edilebilir.
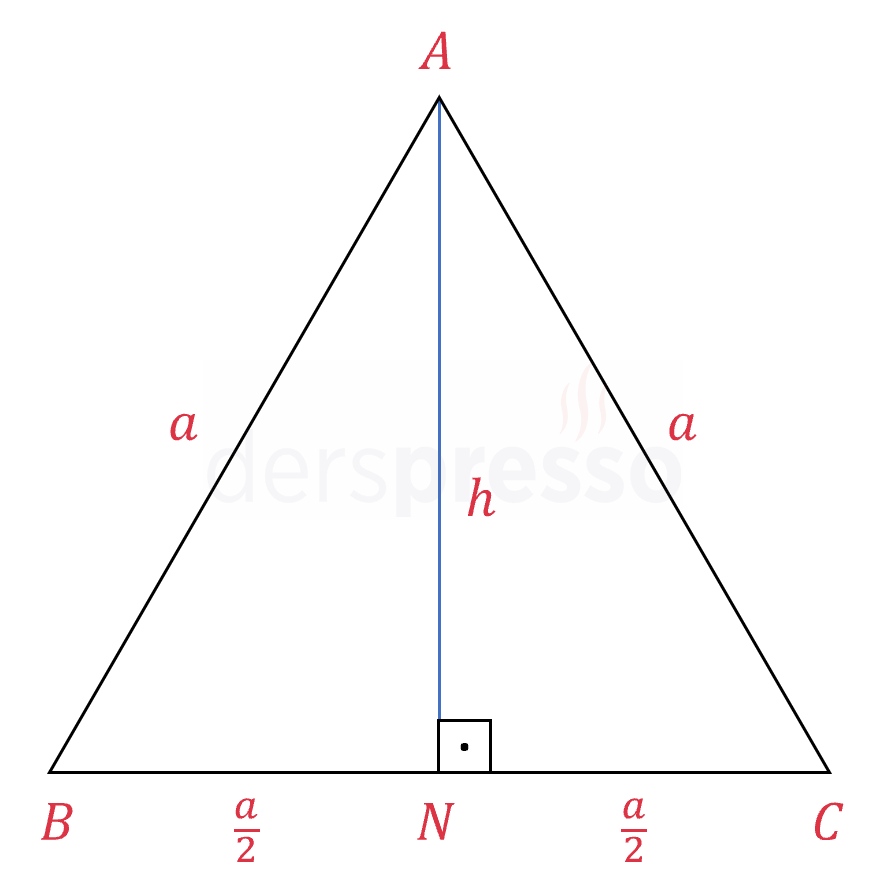
\( h = \dfrac{a\sqrt{3}}{2} \)
İSPATI GÖSTER
\( ANC \) dik üçgenine Pisagor teoremini uygulayalım.
\( a^2 = h^2 + \left( \dfrac{a}{2} \right)^2 \)
\( h^2 \)'yi yalnız bırakalım.
\( h^2 = a^2 - \dfrac{a^2}{4} = \dfrac{3a^2}{4} \)
\( h = \dfrac{a\sqrt{3}}{2} \)
Eşkenar üçgenin alanı bu yükseklik değeri kullanılarak aşağıdaki şekilde ifade edilebilir.
\( A = \dfrac{a^2\sqrt{3}}{4} \)
İSPATI GÖSTER
Üçgenin alan formülünü yazalım.
\( A = \dfrac{a \cdot h}{2} \)
İspatıyla birlikte verdiğimiz eşkenar üçgen yükseklik formülünü kullanalım.
\( h = \dfrac{a\sqrt{3}}{2} \)
\( A = \dfrac{a \cdot \frac{a\sqrt{3}}{2}}{2} \)
\( = \dfrac{a^2\sqrt{3}}{4} \)
Eşkenar üçgenin içinden alınan herhangi bir noktadan kenarlara çizilen paralel doğruların uzunluklarının toplamı, eşkenar üçgenin bir kenar uzunluğuna eşittir.
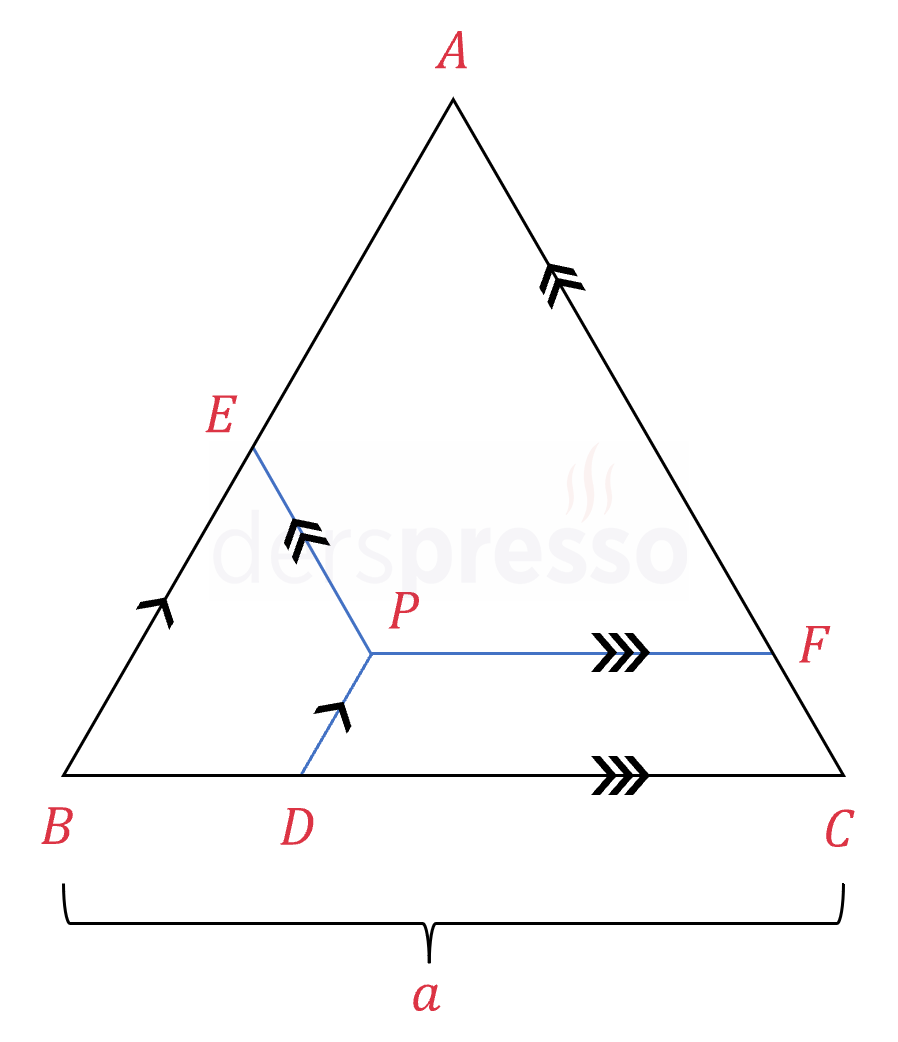
\( P \) üçgenin içinde bir nokta,
\( [PD] \parallel [AB] \), \( [PE] \parallel [AC] \) ve \( [PF] \parallel [BC] \) olmak üzere,
\( \abs{PD} + \abs{PE} + \abs{PF} = a \)
İSPATI GÖSTER
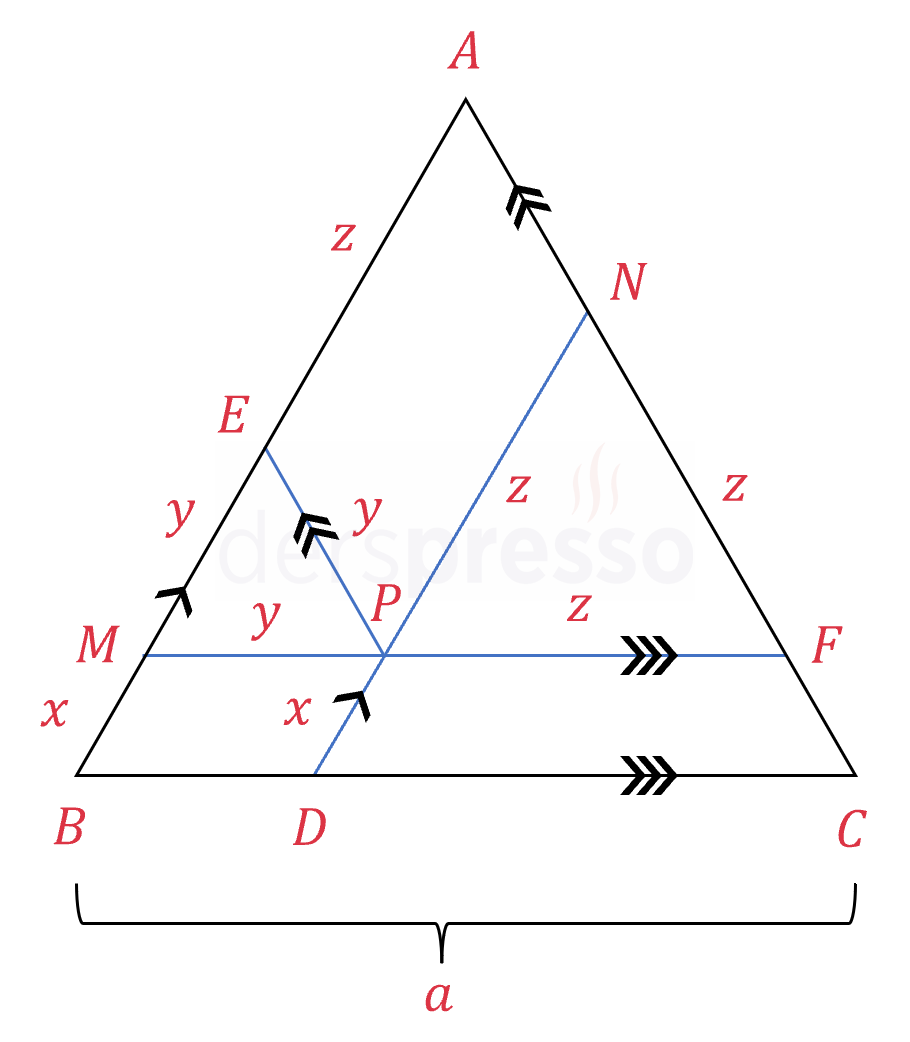
\( [FP] \) doğru parçasını uzatalım ve \( [AB] \) kenarını kestiği noktaya \( M \) diyelim.
\( [DP] \) doğru parçasını uzatalım ve \( [AC] \) kenarını kestiği noktaya \( N \) diyelim.
\( \abs{PD} = x \)
\( \abs{PE} = y \)
\( \abs{PF} = z \) diyelim.
\( BDPM \) bir paralelkenar olduğu için:
\( \abs{MB} = \abs{PD} = x \)
\( \widehat{ABC} \) ve \( \widehat{EMP} \) yöndeş açılar olduğu için ölçüleri birbirine eşittir ve 60°'dir.
\( \widehat{BAC} \) ve \( \widehat{MEP} \) yöndeş açılar olduğu için ölçüleri birbirine eşittir ve 60°'dir.
Buna göre, iki açısı 60° olan \( EMP \) üçgeninin üçüncü açısı da 60°'dir ve üçgen bir eşkenar üçgendir.
\( \abs{ME} = \abs{PE} = y \)
\( \widehat{ACB} \) ve \( \widehat{NFP} \) yöndeş açılar olduğu için ölçüleri birbirine eşittir ve 60°'dir.
\( \widehat{BAC} \) ve \( \widehat{PNF} \) yöndeş açılar olduğu için ölçüleri birbirine eşittir ve 60°'dir.
Buna göre, iki açısı 60° olan \( NFP \) üçgeninin üçüncü açısı da 60°'dir ve üçgen bir eşkenar üçgendir.
\( \abs{PN} = \abs{PF} = z \)
\( AEPN \) bir paralelkenar olduğu için karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{AE} = \abs{NP} = z \)
Buna göre \( [AB] \) kenar uzunluğunu bileşenleri cinsinden aşağıdaki gibi yazabiliriz.
\( a = x + y + z \)
\( a = \abs{PD} + \abs{PE} + \abs{PF} \)
Eşkenar üçgenin üzerinden ya da içinden alınan herhangi bir noktadan kenarlara çizilen dikmelerin uzunlukları toplamı, eşkenar üçgenin yüksekliğine eşittir.
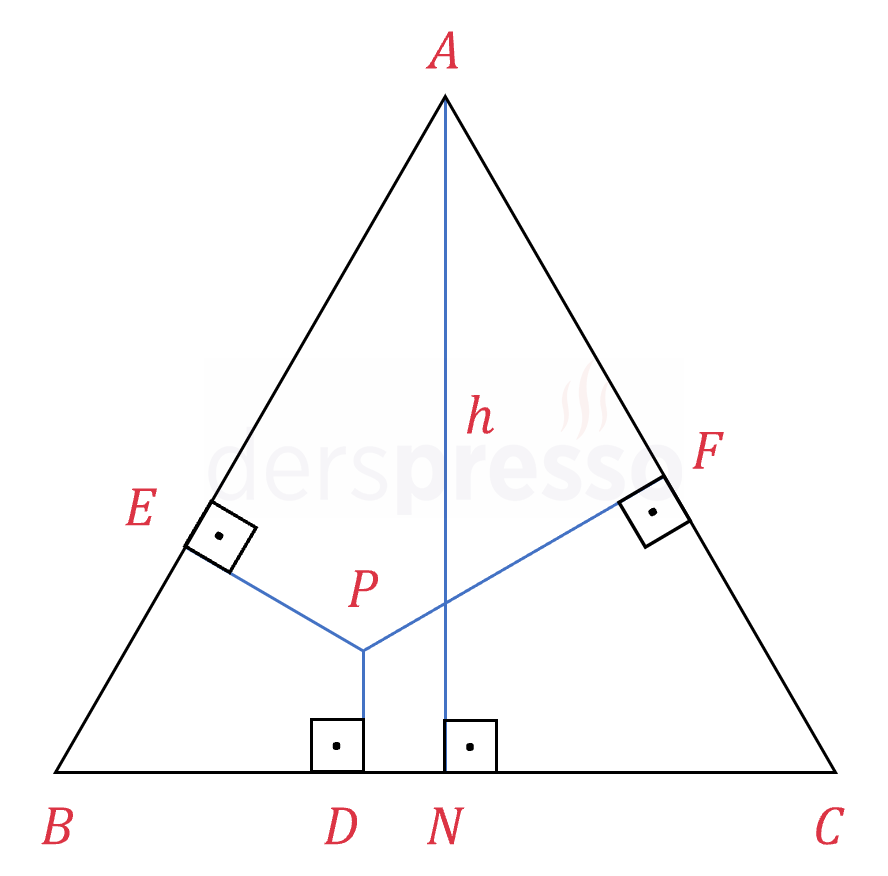
\( P \) üçgenin üzerinde ya da içinde bir nokta,
\( [PD] \perp [BC] \), \( [PE] \perp [AB] \) ve \( [PF] \perp [AC] \) olmak üzere,
\( \abs{PD} + \abs{PE} + \abs{PF} = \abs{AN} = h \)
İSPATI GÖSTER
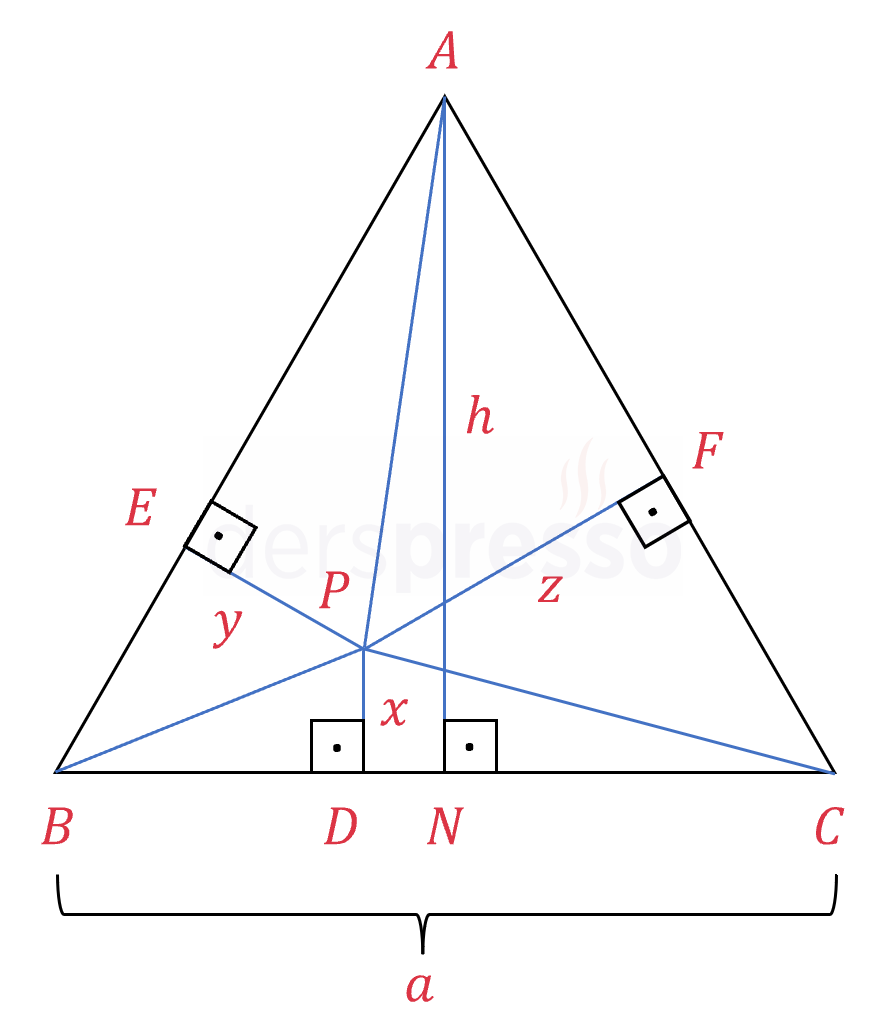
\( P \) noktasından üçgenin köşelerine birer doğru parçası çizelim.
\( ABC \) üçgeninin alanı \( BCP \), \( ABP \) ve \( CAP \) üçgenlerinin alanları toplamına eşittir.
\( A(ABC) = \dfrac{a \cdot h}{2} \)
\( A(BCP) = \dfrac{a \cdot x}{2} \)
\( A(ABP) = \dfrac{a \cdot y}{2} \)
\( A(CAP) = \dfrac{a \cdot z}{2} \)
\( A(ABC) = A(BCP) + A(ABP) + A(CAP) \)
\( \dfrac{a \cdot h}{2} = \dfrac{a \cdot x}{2} + \dfrac{a \cdot y}{2} + \dfrac{a \cdot z}{2} \)
\( a \cdot h = a \cdot (x + y + z) \)
\( h = x + y + z \)
\( \abs{PD} + \abs{PE} + \abs{PF} = h \)
Eşkenar üçgenin dışından alınan herhangi bir noktadan kenarlara çizilen dikmelerden, dıştaki dikmelerin uzunlukları toplamının diğer iki dikmenin arasında kalan dikmenin uzunluğundan farkı eşkenar üçgenin yüksekliğine eşittir.
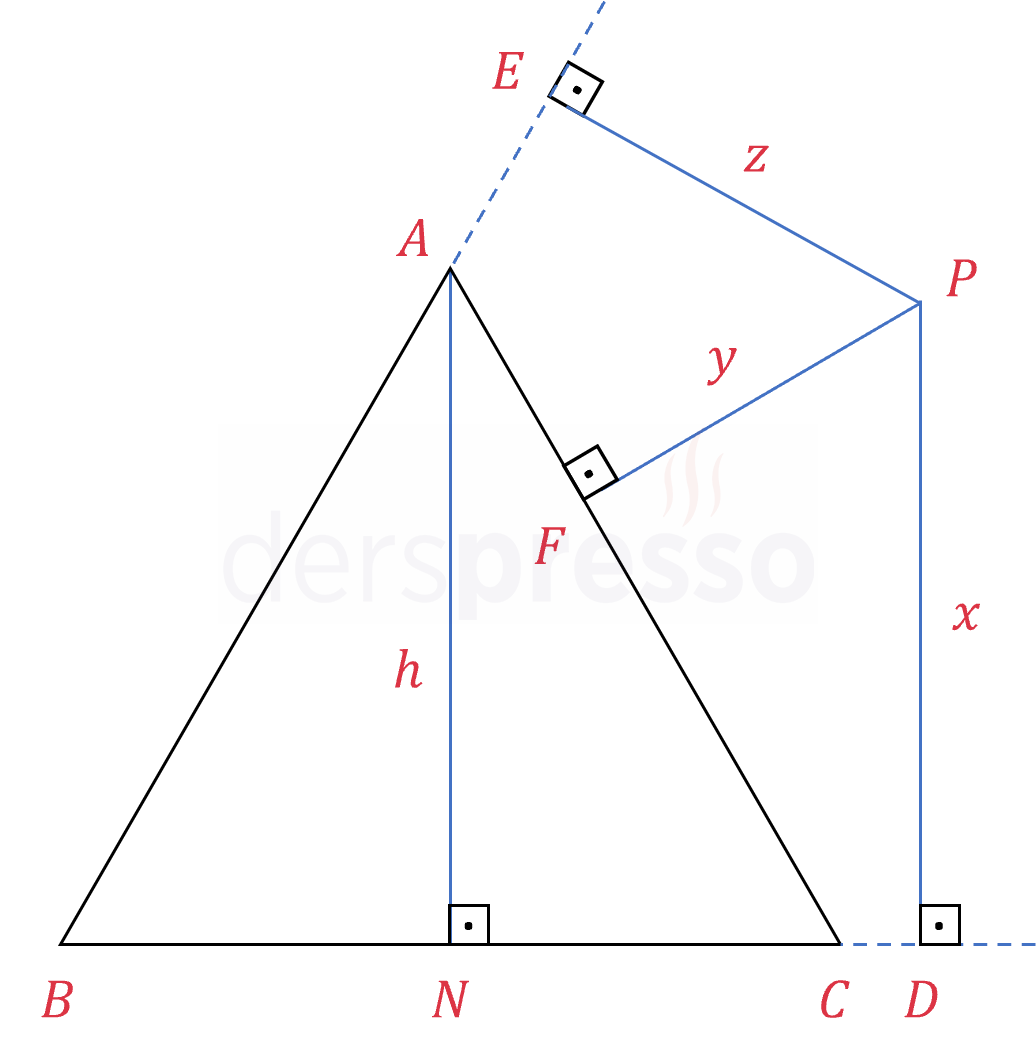
\( P \) üçgenin dışında bir nokta,
\( [PD] \perp [BC] \), \( [PE] \perp [AB] \) ve \( [PF] \perp [AC] \) olmak üzere,
\( \abs{PD} + \abs{PE} - \abs{PF} = \abs{AN} \)
\( x + z - y = h \)
İSPATI GÖSTER
\( P \) noktasından üçgenin üç köşesine birer doğru parçası çizelim (kırmızı çizgiler).
\( ABC \) eşkenar üçgeninin bir kenar uzunluğuna \( a \) diyelim.
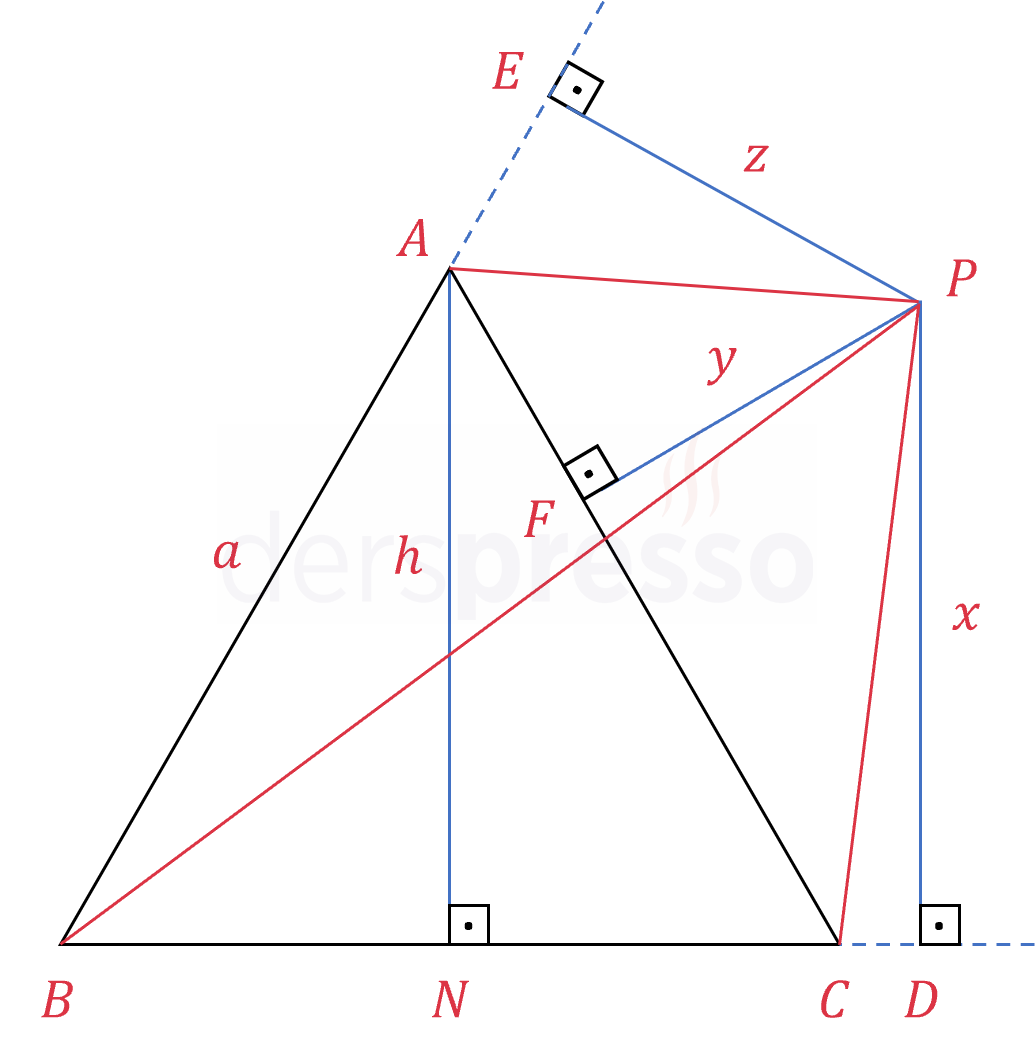
Oluşan \( APCB \) dörtgeninin alanını iki üçgenin alanları toplamı olarak iki farklı şekilde yazabiliriz.
\( A(CPB) + A(APB) = A(APC) + A(ABC) \)
Bu dört üçgenin alan formüllerini yazalım.
\( \dfrac{ax}{2} + \dfrac{az}{2} = \dfrac{ay}{2} + \dfrac{ah}{2} \)
Eşitliğin iki tarafındaki ortak çarpanları sadeleştirelim.
\( x + z = y + h \)
\( y \) uzunluğunu eşitliğin sol tarafına alalım.
\( x + z - y = h \)
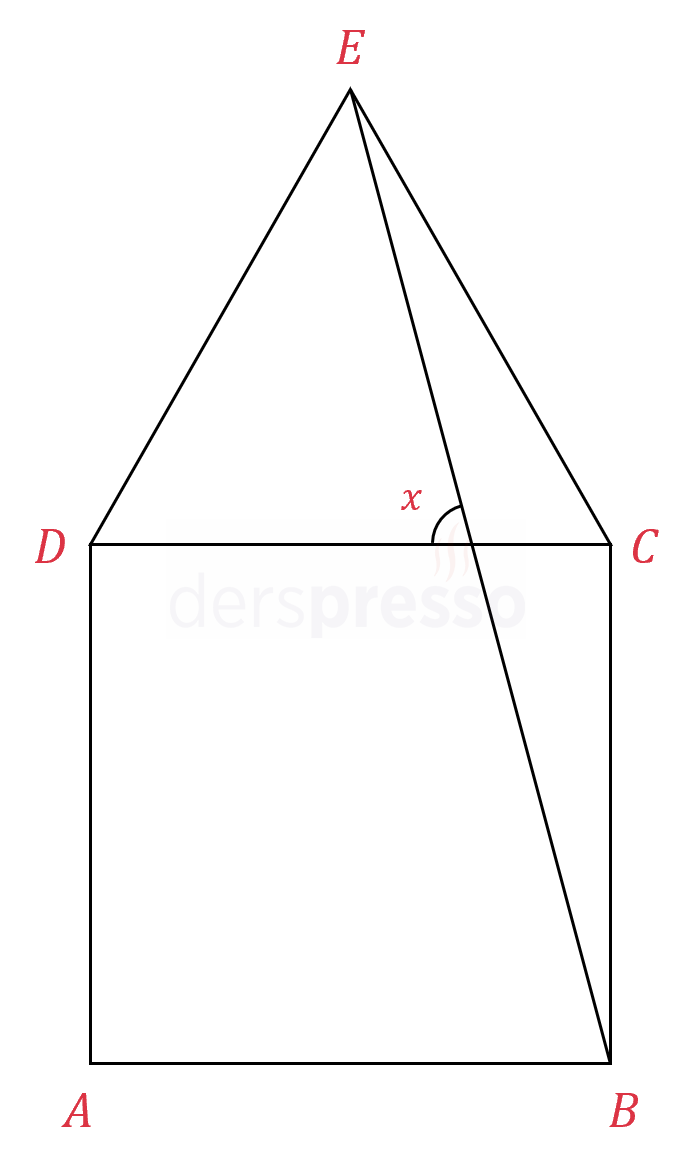
Yukarıdaki şekil birer kenarı ortak bir kare ve eşkenar üçgenden oluşmaktadır.
Buna göre \( x \) açısının ölçüsü kaç derecedir?
Çözümü Göster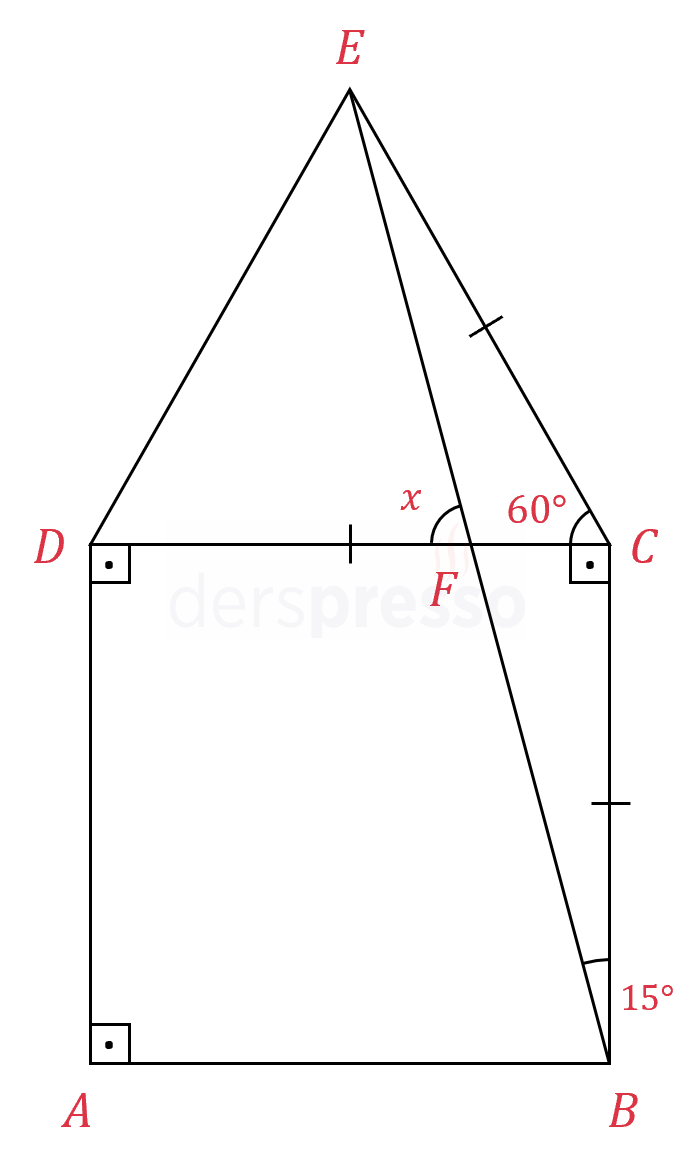
\( m(ECB) = 90 + 60 = 150° \)
Kare ve eşkenar üçgenin birer kenarı ortak olduğu için \( ECB \) üçgeni ikizkenar üçgendir.
\( m(CBF) = \dfrac{180 - 150}{2} = 15° \)
\( m(BFC) = 90 - 15 = 75° \)
\( x \) ve \( BFC \) açıları ters açılar olduğu için ölçüleri eşittir.
\( x = 75° \) bulunur.

Yukarıdaki şekilde bir kare ve bir eşkenar üçgen verilmiştir.
Karenin bir kenar uzunluğu 20 cm olduğuna göre, eşkenar üçgenin bir kenar uzunluğu kaç cm'dir?
Çözümü Göster\( x, y, z \) uzunluklarını aşağıdaki şekildeki gibi tanımlayalım.
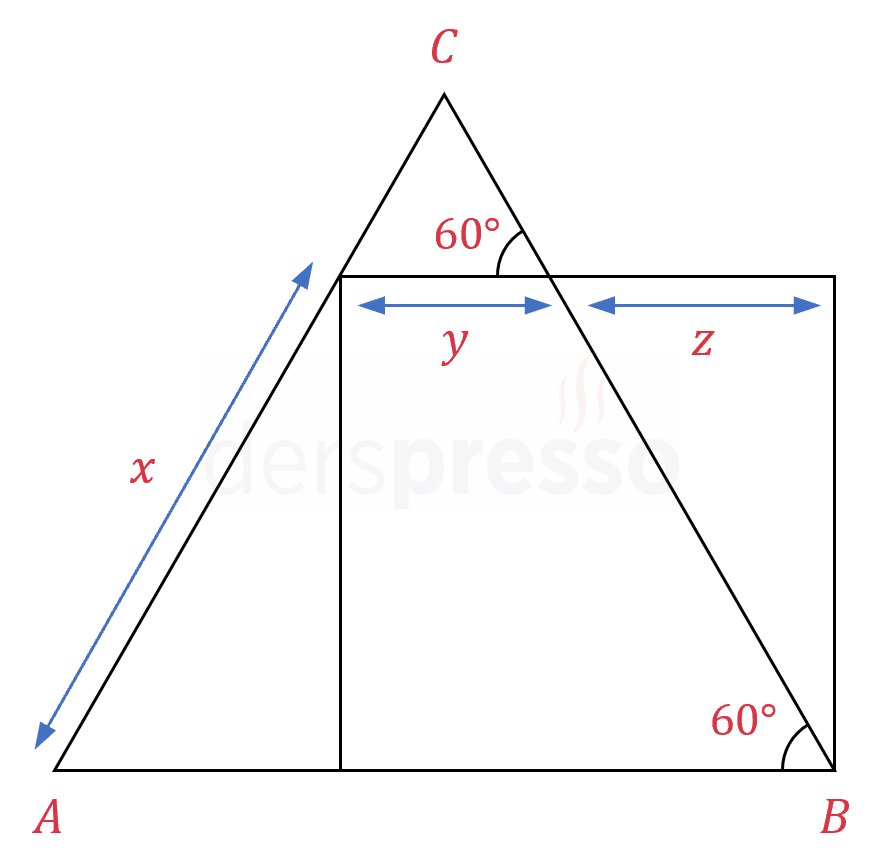
En üstte oluşan küçük üçgen de bir eşkenar üçgen olduğu için tüm kenar uzunlukları \( y \) olur.
Dolayısıyla, büyük eşkenar üçgenin bir kenar uzunluğu \( x + y \) olur.
Trigonometrik oranları kullanarak \( x, y, z \) uzunluklarını bulalım.
\( x = \dfrac{20}{\sin{60°}} = \dfrac{20}{\frac{\sqrt{3}}{2}} \)
\( = \dfrac{40\sqrt{3}}{3} \)
\( z = \dfrac{20}{\tan{60°}} = \dfrac{20}{\sqrt{3}} \)
\( = \dfrac{20\sqrt{3}}{3} \)
\( y = 20 - z = 20 - \dfrac{20\sqrt{3}}{3} \)
\( = \dfrac{60 - 20\sqrt{3}}{3} \)
Eşkenar üçgenin bir kenar uzunluğu \( x + y \) toplamına eşittir.
\( x + y = \dfrac{40\sqrt{3}}{3} + \dfrac{60 - 20\sqrt{3}}{3} \)
\( = \dfrac{60 + 20\sqrt{3}}{3} \) cm bulunur.
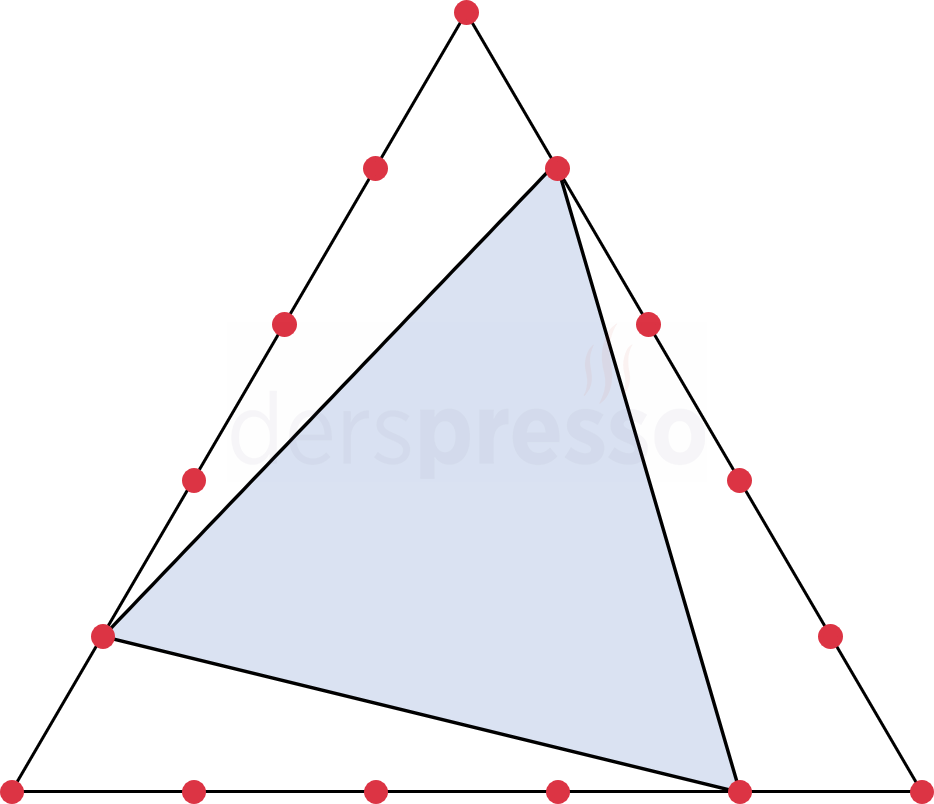
Bir eşkenar üçgenin kenarları, bölen noktalar da bir üçgen oluşturacak şekilde 4'e 1 oranında iki parçaya bölünüyor.
İçteki üçgenin alanının büyük eşkenar üçgenin alanına oranı nedir?
Çözümü GösterBüyük eşkenar üçgenin alanına \( A \), oluşan üç küçük üçgenden her birinin alanına \( a \) diyelim.
Oluşan üç küçük üçgenin alanının büyük eşkenar üçgenin alanının kaçta kaçı olduğunu bulalım.
Küçük üçgenlerden birinin taban uzunluğu, büyük eşkenar üçgenin taban uzunluğunun beşte dördüdür.
Küçük üçgenlerden birinin yüksekliği, büyük eşkenar üçgenin yüksekliğinin beşte biridir.
\( a = A \cdot \dfrac{1}{5} \cdot \dfrac{4}{5} = \dfrac{4A}{25} \)
Üç küçük üçgenin toplam alanını bulalım.
\( 3a = 3 \cdot \dfrac{4A}{25} = \dfrac{12A}{25} \)
Bulduğumuz oranı 1'den çıkararak içteki renkli üçgenin alanının büyük eşkenar üçgenin alanına oranını bulalım.
\( \dfrac{A - \frac{12A}{25}}{A} = \dfrac{13}{25} \) bulunur.