Birinci Dereceden İki Bilinmeyenli Denklemler
Birinci dereceden iki bilinmeyenli denklemler, dereceleri bir olan iki bilinmeyenden oluşan denklemlerdir.
\( a, b, c \in \mathbb{R}, \quad a \ne 0, \quad b \ne 0 \) olmak üzere,
\( ax + by + c = 0 \)
Yukarıdaki denklemde \( x \) ve \( y \) denklemin bilinmeyenleri, \( a \), \( b \) ve \( c \) denklemin katsayılarıdır. \( c \) katsayısı aynı zamanda denklemin sabit terimidir.
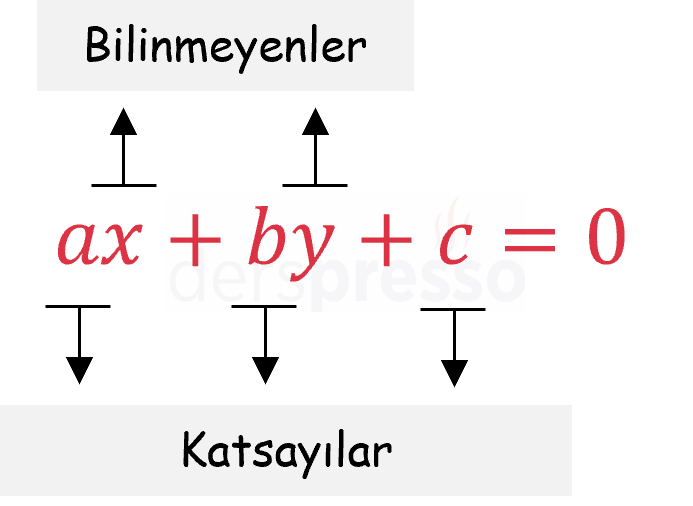
Birinci dereceden iki bilinmeyenli denklemler farklı formlarda olabilir. Aşağıdaki denklemlerin tümünde terimleri düzenlediğimizde ilk satırdaki \( ax + by + c = 0 \) formundaki \( 2x - y + 4 = 0 \) denklemi elde edilebilir.
\( 2x - y + 4 = 0 \)
\( 2x - y = -4 \)
\( y = 2x + 4 \)
\( \dfrac{y}{4} - \dfrac{x}{2} = 1 \)
Birinci Dereceden İki Bilinmeyenli Denklemlerin Çözüm Kümesi
Birinci dereceden iki bilinmeyenli bir denklemin sonsuz sayıda çözümü vardır ve çözüm kümesi koordinat düzleminde bir doğruya karşılık gelir. Bu doğru üzerindeki her nokta ve karşılık geldiği \( (x, y) \) sıralı ikilisi denklemin bir çözümüdür.
\( 3x + 2y - 24 = 0 \) denkleminin çözüm kümesini bulalım.
Verilen denklemin analitik düzlemde grafiğini çizelim.

Bu doğru üzerindeki tüm noktalar denklemin birer çözümüdür, yani doğru üzerindeki herhangi bir noktanın karşılık geldiği \( (x, y) \) değerleri denklemde yerine konduğunda denklemi sağlar. Benzer şekilde doğru üzerinde olmayan bir noktanın karşılık geldiği \( (x, y) \) değerleri denklemde yerine konduğunda denklemi sağlamaz.
| Nokta | \( 3x + 2y - 24 = 0 \) |
|---|---|
| \( (-3, 3) \) | \( 3 \cdot (-3) + 2 \cdot 3 - 24 = -27 \ne 0 \) |
| \( (8, 9) \) | \( 3 \cdot 8 + 2 \cdot 9 - 24 = 18 \ne 0 \) |
| \( (0, 12) \) | \( 3 \cdot 0 + 2 \cdot 12 - 24 = 0 \) |
| \( (2, 9) \) | \( 3 \cdot 2 + 2 \cdot 9 - 24 = 0 \) |
| \( (4, 6) \) | \( 3 \cdot 4 + 2 \cdot 6 - 24 = 0 \) |
| \( (6, 3) \) | \( 3 \cdot 6 + 2 \cdot 3 - 24 = 0 \) |
| \( (8, 0) \) | \( 3 \cdot 8 + 2 \cdot 0 - 24 = 0 \) |
Bu örnek bize birinci dereceden iki bilinmeyenli denklemlerin çözüm kümesinin sonsuz elemanlı olduğunu ve çözüm kümesinin koordinat düzleminde bir doğruya karşılık geldiğini göstermektedir.
\( mx + 8 = -2y \)
\( 6x - 4y = -n \)
denklem sisteminin çözüm kümesi sonsuz elemanlı olduğuna göre, \( m + n \) kaçtır?
Çözümü Göster\( mx + 2y + 8 = 0 \)
\( 6x - 4y + n = 0 \)
Birinci dereceden iki bilinmeyenli iki denklemden oluşan denklem sisteminin çözüm kümesi sonsuz elemanlı ise bu denklemlerin temsil ettiği doğrular çakışıktır, dolayısıyla katsayılarının oranları birbirine eşittir.
\( a_1x + b_1y + c_1 = 0 \)
\( a_2x + b_2y + c_2 = 0 \)
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} \)
Verilen denklemlerin katsayılarına bu eşitliği uygulayalım.
\( \dfrac{m}{6} = \dfrac{2}{-4} = \dfrac{8}{n} \)
\( m = -3, \quad n = -16 \)
\( m + n = -3 + (-16) = -19 \) bulunur.
\( 3x + 1 = -ay \)
\( ax + 12y = -2 \)
denklem sisteminin çözüm kümesi boş küme olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( 3x + ay + 1 = 0 \)
\( ax + 12y + 2 = 0 \)
Birinci dereceden iki bilinmeyenli iki denklemden oluşan denklem sisteminin çözüm kümesi boş küme ise bu denklemlerin temsil ettiği doğrular paraleldir, dolayısıyla \( x \) ve \( y \) katsayılarının oranları birbirine eşitken sabit terimlerinin oranları farklıdır.
\( a_1x + b_1y + c_1 = 0 \)
\( a_2x + b_2y + c_2 = 0 \)
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \ne \dfrac{c_1}{c_2} \)
Verilen denklemlerin katsayılarına bu eşitliği/eşitsizliği uygulayalım.
\( \dfrac{3}{a} = \dfrac{a}{12} \ne \dfrac{1}{2} \)
\( a^2 = 36 \Longrightarrow a = \pm 6 \)
\( \dfrac{a}{12} \ne \dfrac{1}{2} \Longrightarrow a \ne 6 \)
\( a = -6 \) bulunur.
\( (k - 2)x + 4y - \dfrac{2}{7} = 0 \)
\( (4k - 10)x + 8y + \dfrac{23}{5} = 0 \)
denklem sisteminin çözüm kümesi tek elemanlı olduğuna göre, \( k \) kaç olamaz?
Çözümü GösterBirinci dereceden iki bilinmeyenli iki denklemden oluşan denklem sisteminin çözüm kümesi tek elemanlı ise bu denklemlerin temsil ettiği doğrular çakışık ya da paralel olamaz, dolayısıyla \( x \) ve \( y \) katsayılarının oranları birbirinden farklıdır.
\( a_1x + b_1y + c_1 = 0 \)
\( a_2x + b_2y + c_2 = 0 \)
\( \dfrac{a_1}{a_2} \ne \dfrac{b_1}{b_2} \)
Verilen denklemlerin katsayılarına bu eşitsizliği uygulayalım.
\( \dfrac{k - 2}{4k - 10} \ne \dfrac{4}{8} \)
\( \dfrac{k - 2}{4k - 10} \ne \dfrac{1}{2} \)
\( 2k - 4 \ne 4k - 10 \)
\( 2k \ne 6 \)
\( k \ne 3 \) bulunur.
\( y = kx + 6 \)
\( 4y = t + 8x \)
denklemlerinin çözüm kümeleri ortak olduğuna göre, \( \frac{t}{k} \) ifadesi kaça eşittir?
Çözümü GösterBirinci dereceden iki bilinmeyenli denklemlerin grafikleri birer doğrudur.
İki doğrunun çözüm kümelerinin aynı olması için bu doğrular çakışık olmalıdır.
İki doğrunun çakışık olması için katsayılarının ve sabit terimlerinin oranları birbirine eşit olmalıdır.
\( kx - y + 6 = 0 \)
\( 8x - 4y + t = 0 \)
\( \dfrac{k}{8} = \dfrac{-1}{-4} = \dfrac{6}{t} \)
Birinci ve ikinci eşitlikler arası içler - dışlar çarpımı yaparak \( k \) değeri bulalım.
\( -4k = -8 \Longrightarrow k = 2 \)
İkinci ve üçüncü eşitlikler arası içler - dışlar çarpımı yaparak \( t \) değeri bulalım.
\( -1 \cdot t = -4 \cdot 6 \)
\( t = 24 \)
Buna göre \( \frac{t}{k} = \frac{24}{2} = 12 \) bulunur.
\( (7m - 3n - 15)x + (3m + n - 11)y = 0 \)
eşitliği her \( x \) ve \( y \) reel sayısı için sağlandığına göre, \( m \cdot n \) çarpımı kaçtır?
Çözümü GösterVerilen eşitliğin her \( x \) ve \( y \) reel sayısı için sağlanması için parantez içindeki ifadeler sıfıra eşit olmalıdır. Bu şekilde \( x \) ve \( y \) değişkenleri hangi değerleri alırlarsa alsınlar \( 0 = 0 \) eşitliği elde edilir.
\( 7m - 3n - 15 = 0 \)
\( 3m + n - 11 = 0 \)
Aksi durumda örneğin aşağıdaki gibi bir eşitlik her \( x \) ve \( y \) sayısı için sağlanmaz.
\( 2x + 3y = 0 \)
Denklemlerde sabit terimleri eşitliğin sağ tarafına alalım.
\( 7m - 3n = 15 \)
\( 3m + n = 11 \)
İkinci denklemin taraflarını 3 ile çarpalım.
\( 7m - 3n = 15 \)
\( 9m + 3n = 33 \)
Denklemleri taraf tarafa toplayalım.
\( 16m = 48 \)
\( m = 3 \)
\( m \) değerini ilk denklemde yerine yazarak \( n \) değerini bulalım.
\( 7(3) - 3n = 15 \)
\( n = 2 \)
\( m \cdot n = 3 \cdot 2 = 6 \) bulunur.