İkinci Dereceden Dizi
Genel terimi ikinci dereceden polinom olan dizilere ikinci dereceden dizi denir.
\( a, b, c \in \mathbb{R}, a \ne 0 \) olmak üzere,
\( (a_n) = an^2 + bn + c \)
\( (a_n) = n^2 \)
\( (b_n) = 3n^2 + 4n \)
\( (c_n) = 2n^2 - 5 \)
\( (d_n) = n^2 + 2n - 1 \)
Örnek bir ikinci dereceden dizinin terimlerini bulalım.
\( (a_n) = 2n^2 + 3n - 1 \)
\( a_1 = 2(1)^2 + 3(1) - 1 = 4 \)
\( a_2 = 2(2)^2 + 3(2) - 1 = 13 \)
\( a_3 = 2(3)^2 + 3(3) - 1 = 26 \)
\( a_4 = 2(4)^2 + 3(4) - 1 = 43 \)
\( a_5 = 2(5)^2 + 3(5) - 1 = 64 \)
\( a_6 = 2(6)^2 + 3(6) - 1 = 89 \)
\( (a_n) = (4, 13, 26, 43, 64, 89, \ldots) \)
Bir dizinin ardışık terimleri arasındaki farklara 1. farklar, ardışık 1. farklar arasındaki farklara da 2. farklar diyelim. İkinci dereceden dizilerin ortak özelliği 1. farkların aritmetik dizi oluşturması, dolayısıyla 2. farkların dizi boyunca sabit olmasıdır.
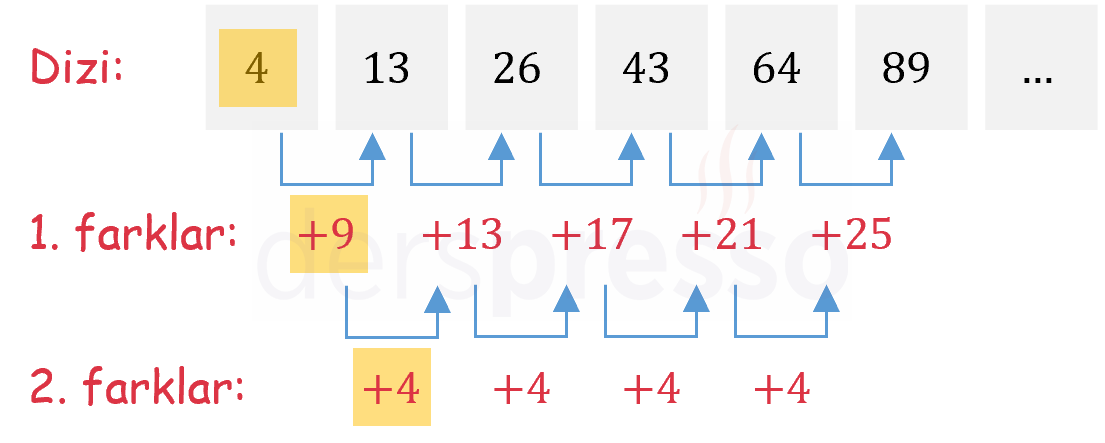
Genel Terimin Bulunması
Terimleri verilen ikinci dereceden bir dizinin genel terimi iki yöntemle bulunabilir.
Lineer Denklem Sistemi Çözümü
Bu yöntemde dizinin herhangi üç terimi seçilir ve \( (a_n) = an^2 + bn + c \) formundaki genel terimde yerine konur. Elde edilen üç bilinmeyenli üç denklem, birinci dereceden denklem sistemleri bölümünde incelediğimiz çözüm yöntemlerinden biriyle çözülür ve \( a \), \( b \), \( c \) katsayıları bulunur.
\( (a_n) = (5, 12, 25, 44, 69, 100, \ldots) \)
İlk 6 terimi yukarıda verilen ikinci dereceden dizinin genel terimini bulalım.
Dizinin genel terimini yazalım.
\( (a_n) = an^2 + bn + c \)
Dizinin ilk 3 terimini bu genel terimde yerine koyalım.
\( a_1 = a(1)^2 + b(1) + c = 5 \)
\( a_2 = a(2)^2 + b(2) + c = 12 \)
\( a_3 = a(3)^2 + b(3) + c = 25 \)
Buna göre aşağıdaki üç bilinmeyenli üç denklemi elde ederiz.
\( a + b + c = 5 \)
\( 4a + 2b + c = 12 \)
\( 9a + 3b + c = 25 \)
Bu lineer denklem sistemini çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 3, \quad b = -2, \quad c = 4 \)
\( (a_n) = 3n^2 - 2n + 4 \)
Formül Çözümü
Pratik bir yöntem olarak aşağıdaki üç formül kullanılarak da genel terimin \( a \), \( b \) ve \( c \) katsayıları bulunabilir.
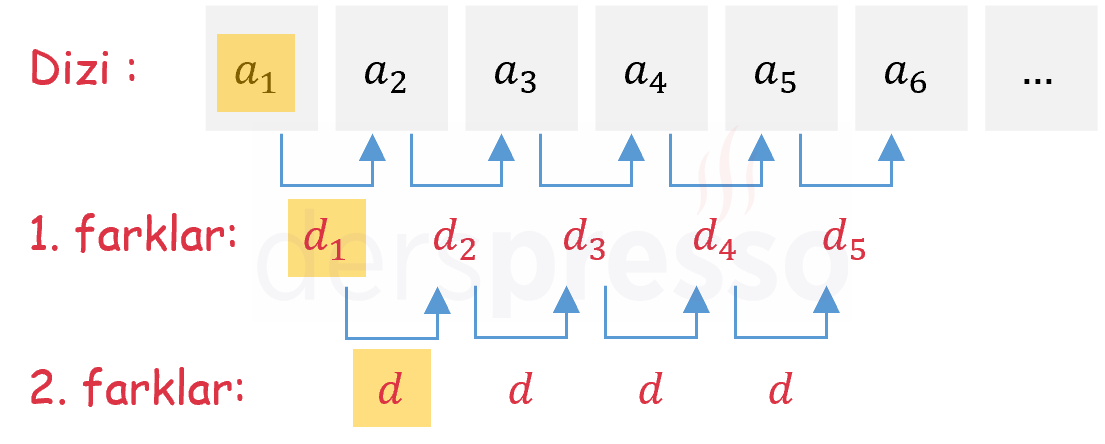
\( (a_n) = an^2 + bn + c \) ikinci dereceden dizi,
\( (d1_n) = (d_1, d_2, d_3, \ldots) \) 1. farkların oluşturduğu aritmetik dizi,
\( (d2_n) = (d, d, d, \ldots) \) 2. farkların oluşturduğu sabit dizi olmak üzere,
\( a \), \( b \) ve \( c \) katsayıları aşağıdaki üç formülle bulunabilir.
\( 2a = d \)
\( 3a + b = d_1 \)
\( a + b + c = a_1 \)
İSPATI GÖSTER
Aşağıdaki şekilde bir ikinci dereceden dizi tanımlayalım.
\( (a_n) = an^2 + bn + c \)
Bu dizinin ilk 5 terimini bulalım.
\( a_1 = a(1)^2 + b(1) + c \)
\( = a + b + c \)
\( a_2 = a(2)^2 + b(2) + c \)
\( = 4a + 2b + c \)
\( a_3 = a(3)^2 + b(3) + c \)
\( = 9a + 3b + c \)
\( a_4 = a(4)^2 + b(4) + c \)
\( = 16a + 4b + c \)
\( a_5 = a(5)^2 + b(5) + c \)
\( = 25a + 5b + c \)
\( (a_n) \) dizisinin 1. farklarından oluşan \( (d1_n) \) dizisini tanımlayalım.
\( d1_1 = a_2 - a_1 \)
\( = 4a + 2b + c - (a + b + c) \)
\( = 3a + b \)
\( d1_2 = a_3 - a_2 \)
\( = 9a + 3b + c - (4a + 2b + c) \)
\( = 5a + b \)
\( d1_3 = a_4 - a_3 \)
\( = 16a + 4b + c - (9a + 3b + c) \)
\( = 7a + b \)
\( d1_4 = a_5 - a_4 \)
\( = 25a + 5b + c - (16a + 4b + c) \)
\( = 9a + b \)
\( (a_n) \) dizisinin 2. farklarından oluşan \( (d2_n) \) dizisini tanımlayalım.
\( d2_1 = d1_2 - d1_1 \)
\( = 5a + b - (3a + b) \)
\( = 2a \)
\( d2_2 = d1_3 - d1_2 \)
\( = 7a + b - (5a + b) \)
\( = 2a \)
\( d2_3 = d1_4 - d1_3 \)
\( = 9a + b - (7a + b) \)
\( = 2a \)
Elde ettiğimiz dizileri ve terimleri kullanarak üç formülü türetelim.
\( a \) katsayısının iki katı 2. farkların sabit terimine eşittir.
\( 2a = d2_1 = d2_2 = d2_3 = \ldots \)
\( 3a + b \) değeri 1. farkların ilk terimine eşittir.
\( 3a + b = d1_1 \)
Dizinin katsayılar toplamı dizinin ilk terimine eşittir.
\( a + b + c = a_1 \)
Bu formüllerin kullanımını bir örnek üzerinden gösterelim.
\( (a_n) = (4, 13, 26, 43, 64, 89, \ldots) \)
İlk 6 terimi yukarıda verilen ikinci dereceden dizinin genel terimini bulalım.
Dizinin 1. ve 2. farklarını bulalım.
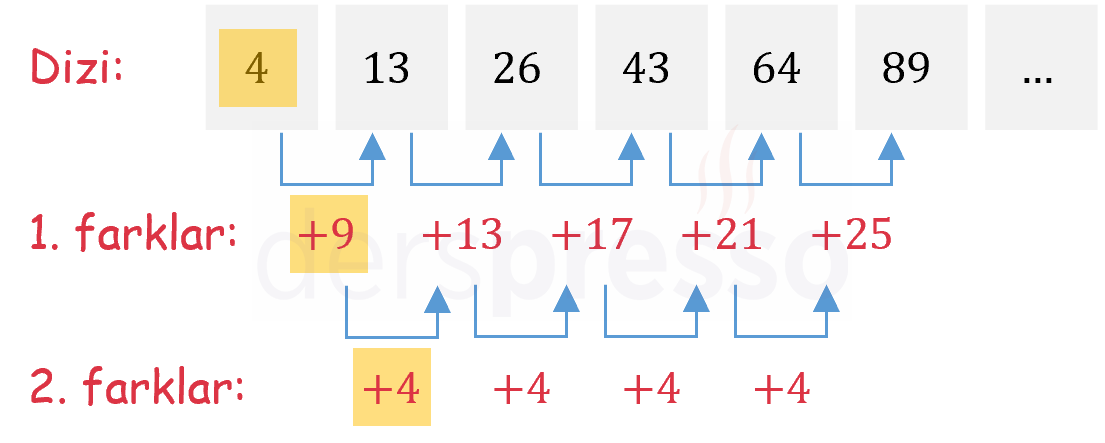
\( a \) katsayısının iki katı 2. farkların sabit terimine eşittir.
\( 2a = 4 \)
\( a = 2 \)
\( 3a + b \) değeri 1. farkların ilk terimine eşittir.
\( 3a + b = 9 \)
\( 3(2) + b = 9 \)
\( b = 3 \)
Dizinin katsayılar toplamı dizinin ilk terimine eşittir.
\( a + b + c = 4 \)
\( 2 + 3 + c = 4 \)
\( c = -1 \)
Buna göre dizinin genel terimini aşağıdaki gibi buluruz.
\( (a_n) = 2n^2 + 3n - 1 \)
Sabit ivmeyle hızlanan bir aracın hareketinin her saniyesinde metre cinsinden aldığı yollar aşağıdaki gibi bir dizi oluşturuyor.
\( 8, 22, 42, 68, \ldots \)
Buna göre bu araç hareketinin 13. saniyesinde kaç metre yol alır?
Çözümü GösterAracın her saniyede aldığı yollar arasındaki artış miktarını inceleyelim.
\( 8\overset{+14}{\longrightarrow}22\overset{+20}{\longrightarrow}42\overset{+26}{\longrightarrow}68, \ldots \)
Artış miktarlarının aritmetik dizi oluşturduğunu görüyoruz.
Bu durumda genel terim ikinci dereceden bir denklemle ifade edilebilir.
\( (a_n) = an^2 + bn + c \)
\( n \)'ye farklı değerler vererek üç farklı denklem elde edelim.
\( n = 1 \) verelim.
\( a + b + c = 8 \)
\( n = 2 \) verelim.
\( 4a + 2b + c = 22 \)
\( n = 3 \) verelim.
\( 9a + 3b + c = 42 \)
Elde ettiğimiz üç denklemden oluşan denklem sistemini çözelim.
\( a + b + c = 8 \implies b + c = 8 - a \)
Bu ifadeyi ikinci denklemde yerine koyalım.
\( 4a + b + (b + c) = 22 \)
\( 4a + b + 8 - a = 22 \)
\( 3a + b = 14 \)
Bu ifadeyi üçüncü denklemde yerine koyalım.
\( 3(3a + b) + c = 42 \)
\( 42 + c = 42 \)
\( c = 0 \implies b = 8 - a \)
\( 3a + (8 - a) = 14 \)
\( 2a + 8 = 14 \)
\( a = 3 \)
\( b = 8 - 3 = 5 \)
Buna göre dizinin genel terimi aşağıdaki gibi olur.
\( (a_n) = 3n^2 + 5n \)
Aracın 13. saniyede aldığı yolu hesaplayalım.
\( a_{13} = 3 (13)^2 + 5(13) = 572 \) bulunur.
Doğal sayılar kümesinin elemanları aşağıdaki şekilde farklı kümelere bölünüyor.
\( P_1 = \{1\} \)
\( P_2 = \{2, 3\} \)
\( P_3 = \{4, 5, 6\} \)
\( P_4 = \{7, 8, 9, 10\} \)
Buna göre \( P_{25} \) kümesinin elemanlarının toplamı kaçtır?
Çözümü Göster\( P_n \) şeklindeki kümelerin ilk terimlerini veren bir \( (a_n) \) dizisi tanımlayalım.
\( (a_n) = (1, 2, 4, 7, \ldots) \)
Dizinin 1. farkları aritmetik, 2. farkları da sabit bir dizi oluşturduğu için dizi ikinci dereceden bir dizidir.
\( (d1_n) = (1, 2, 3, \ldots) \)
\( (d2_n) = (1, 1, 1 \ldots) \)
İkinci dereceden dizinin genel terimini bulma formüllerini kullanalım.
\( (a_n) = an^2 + bn + c \) dizisinin 1. farkları \( \{d_1, d_2, d_3, \ldots\} \) ve 2. farkı \( d \) olmak üzere,
\( a \) katsayısının iki katı 2. farkların sabit terimine eşittir.
\( 2a = 1 \)
\( a = \dfrac{1}{2} \)
\( 3a + b \) değeri 1. farkların ilk terimine eşittir.
\( 3a + b = 1 \)
\( b = -\dfrac{1}{2} \)
Dizinin katsayılar toplamı dizinin ilk terimine eşittir.
\( a + b + c = 1 \)
\( c = 1 \)
Buna göre dizinin genel terimini aşağıdaki gibi buluruz.
\( (a_n) = \dfrac{1}{2}n^2 - \dfrac{1}{2}n + 1 \)
\( = \dfrac{n^2 - n + 2}{2} \)
Bu genel terimi kullanarak \( P_{25} \) kümesinin ilk ve son elemanlarını bulalım.
\( P_{25} \) kümesinin ilk elemanı \( a_{25} \) değerine eşittir.
\( a_{25} = \dfrac{25^2 - 25 + 2}{2} = 301 \)
\( P_{25} \) kümesinin son elemanını bulmak için \( P_{26} \) kümesinin ilk elemanını veren \( a_{26} \) değerinden 1 çıkaralım.
\( a_{26} = \dfrac{26^2 - 26 + 2}{2} = 326 \)
Buna göre \( P_{25} \) kümesinin ilk elemanı 301, son elemanı 325'tir.
Ardışık sayılarda terimler toplamı formülü ile 301'den 325'e kadarki ardışık sayıların toplamını bulalım.
\( \text{Terimler toplamı} = \dfrac{\text{İlk terim} + \text{Son terim}}{2} \cdot \text{Terim sayısı} \)
\( P_{25} \) kümesinin 25 elemanı vardır.
\( = \dfrac{301 + 325}{2} \cdot 25 \)
\( = 7825 \) bulunur.