İki Kümenin Farkı
\( A \) kümesinde olup \( B \) kümesinde olmayan elemanların kümesine \( A \) fark \( B \) kümesi denir ve \( A - B \) ya da \( A \setminus B \) şeklinde gösterilir.
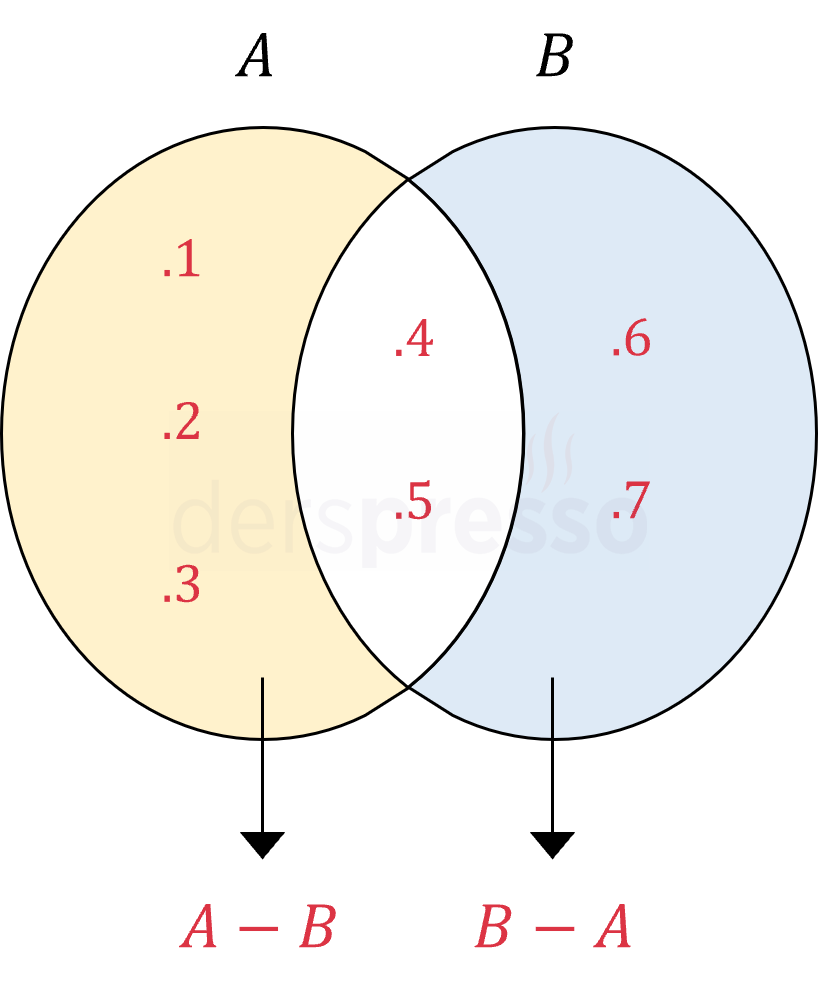
\( A - B = \{ x \mid x \in A \land x \notin B \} \)
\( B - A = \{ x \mid x \in B \land x \notin A \} \)
\( A = \{ 1, 2, 3, \textcolor{red}{4}, \textcolor{red}{5} \} \)
\( B = \{ \textcolor{red}{4}, \textcolor{red}{5}, 6, 7 \} \)
\( A - B = \{ 1, 2, 3 \} \)
\( B - A = \{ 6, 7 \} \)
İki kümenin birbirinden farklarının birleşimi (renkli alanların toplamı), kümelerin birleşim kümesinin kesişim kümesinden farkı olarak da ifade edilebilir.
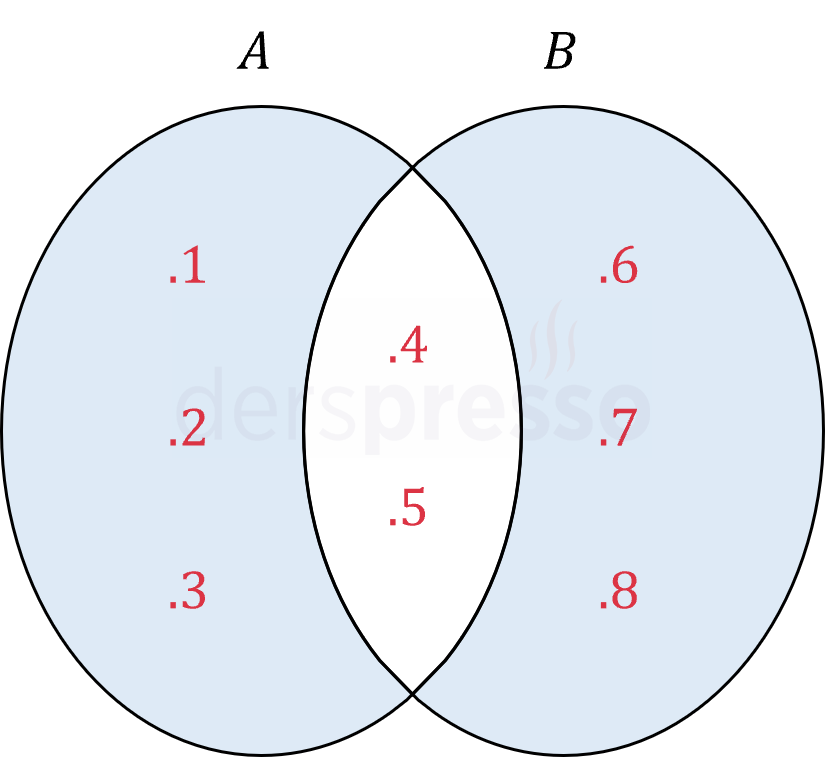
\( (A - B) \cup (B - A) \) \( = (A \cup B) - (A \cap B) \)
İki kümenin birleşimi; bu birleşimi oluşturan üç bölgenin, yani kümelerin birbirinden farkları ile kesişimlerinin birleşimi şeklinde de ifade edilebilir.
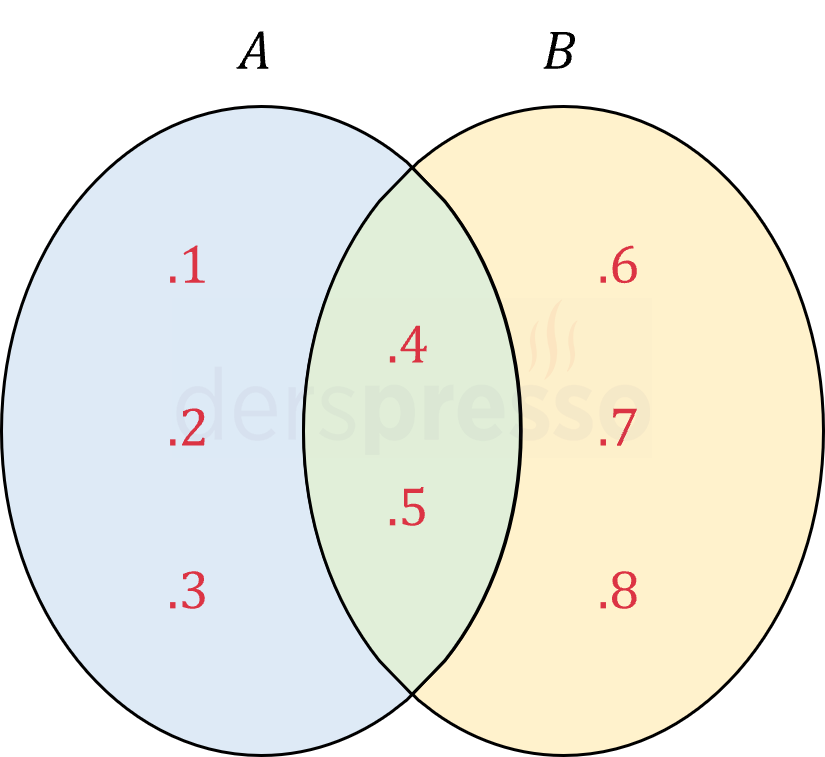
\( A \cup B = (A - B) \cup (B - A) \cup (A \cap B) \)
Bir küme, bir diğer kümeden farkı ile onunla kesişiminin birleşimi şeklinde de tanımlanabilir.

\( A = (A - B) \cup (A \cap B) \)
\( A \) kümesinin \( B \) kümesinden farkı, \( A \) ve \( B' \) kümelerinin kesişimine eşittir.
\( A - B = A \cap B' \)
Simetrik Fark
İki kümenin simetrik farkı, kümelerin birleşim kümesinde olup kesişim kümesinde olmayan elemanlardan oluşur. İki kümenin simetrik farkı \( A \triangle B \) şeklinde gösterilir.
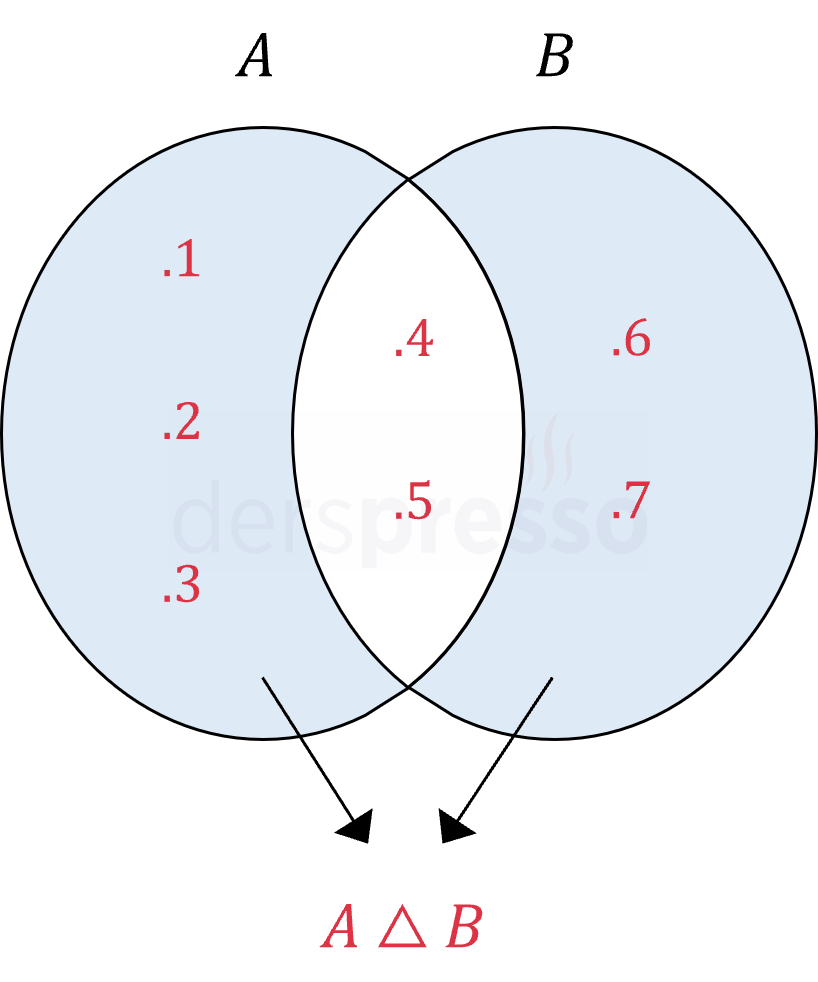
\( A \triangle B = \{ x \mid x \in A \veebar x \in B \} \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7, 8 \} \)
\( A \triangle B = \{ 1, 2, 3, 6, 7, 8 \} \)
İki kümenin simetrik farkı, kümelerin ayrı ayrı birbirlerinden farklarının birleşimi şeklinde de ifade edilebilir.
\( A \triangle B = (A - B) \cup (B - A) \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7, 8 \} \)
\( A - B = \{ 1, 2, 3 \} \)
\( B - A = \{ 6, 7, 8 \} \)
\( A \triangle B = (A - B) \cup (B - A) \)
\( = \{ 1, 2, 3, 6, 7, 8 \} \)
Alternatif olarak; iki kümenin simetrik farkı, kümelerin birleşiminin kesişimlerinden farkı şeklinde de ifade edilebilir.
\( A \triangle B = (A \cup B) - (A \cap B) \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7, 8 \} \)
\( A \cup B = \{ 1, 2, 3, 4, 5, 6, 7, 8 \} \)
\( A \cap B = \{ 4, 5 \} \)
\( A \triangle B = (A \cup B) - (A \cap B) \)
\( = \{ 1, 2, 3, 6, 7, 8 \} \)
\( K = \{ 13, 14, 15, 16 \} \)
\( L = \{ 14, 18, 21, 30 \} \)
\( M = \{ 13, 16, 21, 30 \} \)
\( N = \{ 16, 23, 27, 32 \} \)
olduğuna göre, \( (K \triangle L) \triangle (M \triangle N) \) işleminin sonucu kaç elemanlıdır?
Çözümü Göster\( \triangle \) sembolü simetrik fark işlemi için kullanılır.
İki kümenin simetrik farkı, kümelerin birleşim kümesinde olup kesişim kümesinde olmayan elemanlardan oluşur.
\( K \triangle L = \{13, 15, 16, 18, 21, 30\} \)
\( M \triangle N = \{13, 21, 23, 27, 30, 32\} \)
\( (K \triangle L) \triangle (M \triangle N) = \{15, 16, 18, 23, 27, 32\} \)
Buna göre verilen işlemin sonucu 6 elemanlıdır.
Fark İşlem Özellikleri
Fark işleminin değişme özelliği yoktur.
\( A - B \ne B - A \)
\( A = \{ 1, 2, 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7 \} \)
\( A - B = \{ 1, 2, 3 \} \)
\( B - A = \{ 6, 7 \} \)
Simetrik fark işleminin değişme özelliği vardır.
\( A \triangle B = B \triangle A \)
Fark İşlem Kuralları
Bir kümenin boş kümeden farkı kendisine eşittir.
\( A - \emptyset = A \)
İSPATI GÖSTER
\( A - \emptyset \) ve \( A \) kümelerinin eşitliğini göstermek için iki kümenin birbirinin alt kümesi olduğunu gösterelim.
(1) \( A - \emptyset \subseteq A \) olduğunu gösterelim.
Bir kümenin diğer bir kümeden farkı kendisinin alt kümesidir.
\( A - B \subseteq A \)
Buna göre \( A - \emptyset \) kümesi \( A \) kümesinin alt kümesidir.
(2) \( A \subseteq A - \emptyset \) olduğunu gösterelim.
\( x \in A \) olsun.
Boş küme tanımına göre, her \( x \) için \( x \notin \emptyset \) olur.
\( x \notin \emptyset \)
\( p \) ve \( q \) doğru ise \( p \land q \) doğru olur.
\( x \in A \land x \notin \emptyset \)
Bu ifade fark kümesinin tanımıdır.
\( \equiv x \in A - \emptyset \)
Buna göre \( A \) kümesi \( A - \emptyset \) kümesinin alt kümesidir.
\( A - \emptyset \) ve \( A \) kümeleri birbirinin alt kümesi olduğuna göre bu iki küme eşittir.
\( A - \emptyset = A \)
Bir kümenin bir üst kümesinden farkı boş kümedir.
\( A \subseteq B \) ise,
\( A - B = \emptyset \)
İSPATI GÖSTER
\( A \subseteq B \Rightarrow A - B = \emptyset \) olduğunu gösterelim.
\( A \subseteq B \) olduğunu kabul edelim.
Alt küme tanımına göre, bir küme diğer bir kümenin alt kümesi ise birinci kümenin her elemanı ikinci kümenin de elemanıdır.
\( \forall x, x \in A \Rightarrow x \in B \)
"İse" ifadesini "veya" ifadesi şeklinde yazalım.
\( \forall x, x \notin A \lor x \in B \)
Niceleyicinin yüklemine De Morgan kuralını uygulayalım.
\( \forall x, (x \in A \land x \notin B)' \)
Parantez içindeki ifade \( A - B \) kümesinin tanımıdır.
\( \forall x, (x \in A - B)' \)
Değil işlemini niceleyicinin dışına alalım.
\( (\exists x, x \in A - B)' \)
Elde ettiğimiz ifade \( A - B \) kümesi için boş küme tanımıdır.
\( A - B = \emptyset \)
Bir kümenin kendisinden ve evrensel kümeden farkı boş kümedir.
\( A - A = \emptyset \)
\( A - E = \emptyset \)
Evrensel kümenin bir kümeden farkı o kümenin tümleyenidir.
\( E - A = A' \)
Bir kümenin diğer bir kümeden farkı kendisinin alt kümesidir.
\( A - B \subseteq A \)
İSPATI GÖSTER
\( A - B \subseteq A \) olduğunu göstermek için, \( A - B \) kümesinin her elemanının \( A \) kümesinin de elemanı olduğunu gösterelim.
\( x \in A - B \) olsun.
Fark kümesi tanımına göre, \( A - B \) kümesi \( A \) kümesinde olup \( B \) kümesinde olmayan elemanlardan oluşur.
\( x \in A \land x \notin B \)
\( p \land q \) doğru ise \( p \) ve \( q \) doğrudur.
\( x \in A \)
\( A - B \subseteq A \) olduğunu göstermiş olduk.
Bir kümenin diğer bir kümeden farkı kümenin kendisine eşitse bu kümeler ayrık kümelerdir (kesişimleri boş kümedir). Aynı şekilde, iki küme ayrık ise kümelerden birinin diğerinden farkı kümenin kendisine eşittir.

\( A - B = A \iff A \cap B = \emptyset \)
\( B - A = B \iff A \cap B = \emptyset \)
Bir küme diğer bir kümenin alt kümesi ise alt kümenin kapsayan kümeden farkı boş kümedir.

\( B \subseteq A \Longrightarrow B - A = \emptyset \)
Bir kümenin diğer iki kümenin birleşiminden farkı, bu kümenin diğer iki küme ile ayrı ayrı farklarının kesişimine eşittir.

\( A - (B \cup C) = (A - B) \cap (A - C) \)
İSPATI GÖSTER
Fark kümesi tanımına göre, \( A - (B \cup C) \) kümesi \( A \) kümesinde olup \( B \cup C \) kümesinde olmayan elemanlardan oluşur.
\( A - (B \cup C) = \{x \mid x \in A \land x \notin B \cup C\} \)
\( = \{x \mid x \in A \land (x \in B \cup C)'\} \)
Birleşim kümesi tanımına göre, \( B \cup C \) kümesi \( B \) veya \( C \) kümesinde bulunan elemanlardan oluşur.
\( = \{x \mid x \in A \land (x \in B \lor x \in C)'\} \)
De Morgan kuralını uygulayalım.
\( = \{x \mid x \in A \land x \notin B \land x \notin C\} \)
\( p \equiv p \land p \) olduğu için yukarıdaki önermeye \( x \in A \) önermesini ekleyebiliriz.
\( = \{x \mid (x \in A \land x \notin B) \land (x \in A \land x \notin C)\} \)
Parantez içindeki ifadeler fark kümesinin tanımıdır.
\( = \{x \mid (x \in A - B) \land (x \in A - C)\} \)
Bu ifade kesişim kümesinin tanımıdır.
\( = \{x \mid x \in (A - B) \cap (A - C)\} \)
\( = (A - B) \cap (A - C) \)
Bir kümenin diğer iki kümenin kesişiminden farkı, bu kümenin diğer iki küme ile ayrı ayrı farklarının birleşimine eşittir.

\( A - (B \cap C) = (A - B) \cup (A - C) \)
\( s(A \cup B) = 8 \) ve \( s(B - A) = 5 \) olduğuna göre, \( A \) kümesinin eleman sayısı kaçtır?
Çözümü Göster
\( A \) ve \( B - A \) ayrık kümelerdir ve birleşimleri \( A \) ve \( B \) kümelerinin birleşimini verir.
\( s(A) + s(B - A) = s(A \cup B) \)
\( s(A) + 5 = 8 \)
\( s(A) = 3 \) bulunur.
\( s(A - B) = 4, \quad s(B - A) = 2 \)
\( A \cup B \) kümesinin öz alt küme sayısı 511 olduğuna göre, \( s(A) \) kaçtır?
Çözümü Göster\( n \) elemanlı bir kümenin öz alt kümelerinin sayısı \( 2^n - 1 \) formülü ile bulunur.
\( 2^n - 1 = 511 \)
\( n = s(A \cup B) = 9 \)
İki kümenin birleşim kümesini, kümelerin birbirinden farkı ve kesişimleri cinsinden aşağıdaki şekilde yazabiliriz.
\( s(A \cup B) = s(A - B) + s(B - A) + s(A \cap B) \)
\( 9 = 4 + 2 + s(A \cap B) \)
\( s(A \cap B) = 3 \)

\( s(A) = s(A - B) + s(A \cap B) \)
\( = 4 + 3 = 7 \) olarak bulunur.
\( B \not\subset A \) ve \( s(A - B) = 5 \) olmak üzere,
\( A \) kümesinin alt kümelerinin sayısı 128 olduğuna göre, \( B \) kümesinin alt kümelerinin sayısı en az kaç olabilir?
Çözümü Göster\( n \) elemanlı bir kümenin alt küme sayısı \( 2^n \) formülü ile bulunur.
\( 2^n = 128 \)
\( n = s(A) = 7 \)

\( B \not\subset A \) olduğu için \( x \gt 0 \) olmalıdır.
\( x = 1 \) için \( s(B) = 3 \) olur.
Buna göre, \( B \) kümesinin alt küme sayısı en az \( 2^3 = 8 \) olabilir.

Yukarıdaki şemadaki taralı bölgeyi \( A \), \( B \) ve \( C \) kümeleri cinsinden yazınız.
Çözümü GösterTaralı bölge \( A \) ve \( B \) kümelerinin kesişiminin \( C \) kümesinden farkıdır.
\( (A \cap B) - C \)
\( (A - \emptyset) \cap (\emptyset - A) \) ifadesinin en sade hali nedir?
Çözümü GösterBir kümenin boş kümeden farkı kendisi, boş kümenin bir kümeden farkı boş kümedir.
\( (A - \emptyset) \cap (\emptyset - A) \)
\( = A \cap \emptyset \)
Bir kümenin boş küme ile kesişimi boş kümedir.
\( = \emptyset \) bulunur.
\( A \cup B \) kümesinin öz alt kümelerinin sayısı 63,
\( s(A) = s(B) - 3, \quad s(A \cap B) = 1 \)
olduğuna göre, \( B - A \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( n \) elemanlı bir kümenin öz alt küme sayısı \( 2^n - 1 \) formülü ile bulunur.
\( 2^n - 1 = 63 \)
\( n = s(A \cup B) = 6 \)
İki kümenin birleşim kümesinin eleman sayısı formülünü yazalım.
\( \underbrace{s(A \cup B)}_{6} = \underbrace{s(A)}_{s(B) - 3} + s(B) - \underbrace{s(A \cap B)}_{1} \)
\( 6 = 2s(B) - 4 \)
\( s(B) = 5 \)
\( s(A) = s(B) - 3 = 2 \)

\( s(B - A) = 4 \) bulunur.
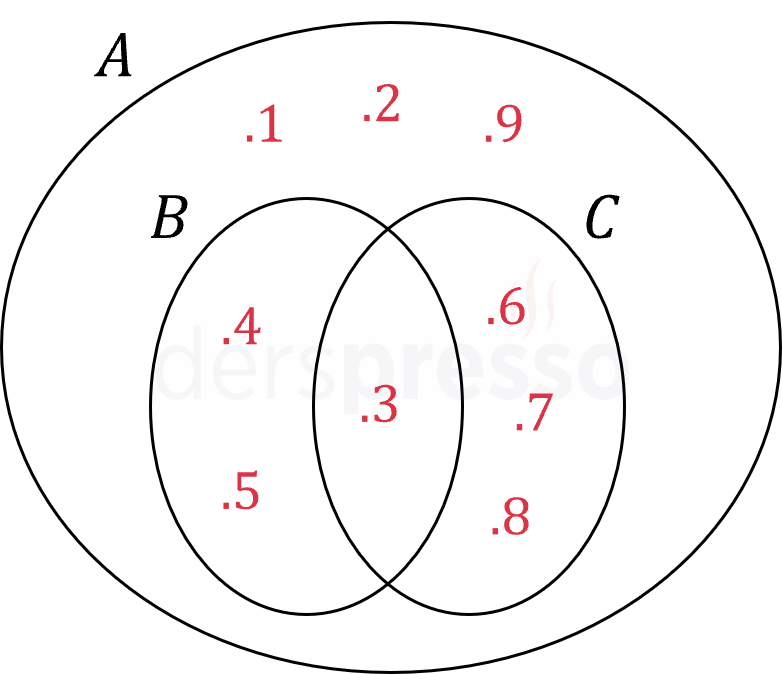
Yukarıdaki şekilde \( A \), \( B \) ve \( C \) kümeleri verilmiştir.
\( ((A - B) \cap C)' \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( A - B = \{ 1, 2, 6, 7, 8, 9 \} \)
\( (A - B) \cap C = \{ 6, 7, 8 \} \)
\( ((A - B) \cap C)' = \{ 1, 2, 3, 4, 5, 9 \} \)
\( s(((A - B) \cap C)') = 6 \) bulunur.
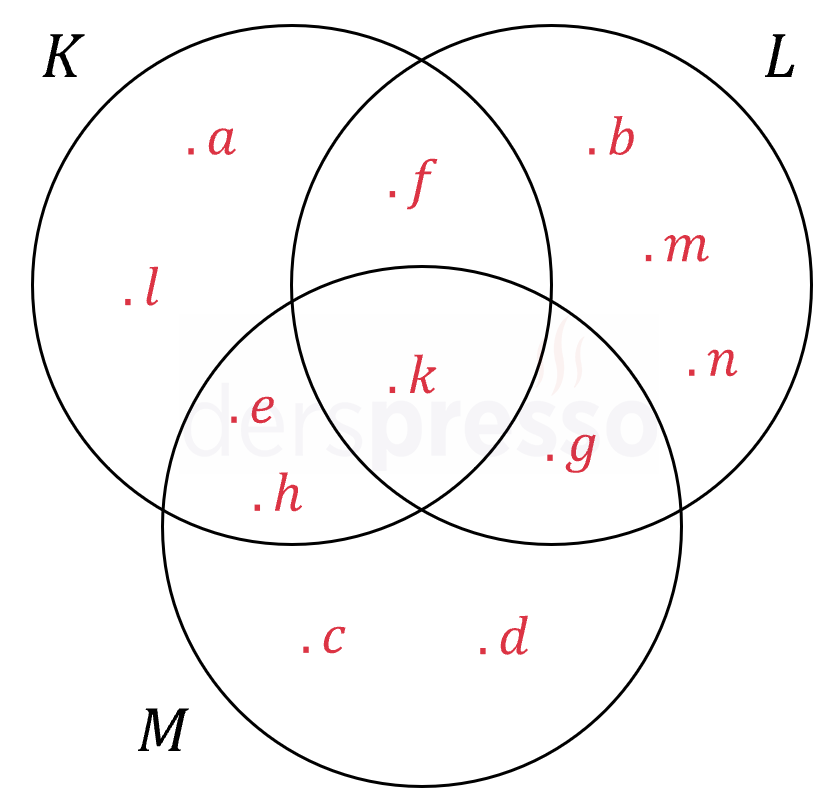
Yukarıdaki Venn şemasındaki \( K \), \( L \) ve \( M \) kümeleri için aşağıdakilerden hangisi yanlıştır?
I. \( K - L = \{ a, e, h, l \} \)
II. \( M - L = \{ c, d \} \)
III. \( (K \cap M) - L = \{ e, h \} \)
IV. \( (K \cap L) - (L \cap M) = \{ f, k \} \)
Çözümü Göster\( M - L = \{ c, d, e, h \} \) olduğu için II. öncül yanlıştır.
\( (K \cap L) - (L \cap M) = \{ f \} \) olduğu için IV. öncül yanlıştır.
Buna göre I. ve III. öncüller doğrudur.
\( A \) ve \( B \) aynı evrensel kümenin iki alt kümesidir.
\( (A \cup B) \cap (B' - A)' \) ifadesinin en sade hali nedir?
Çözümü Göster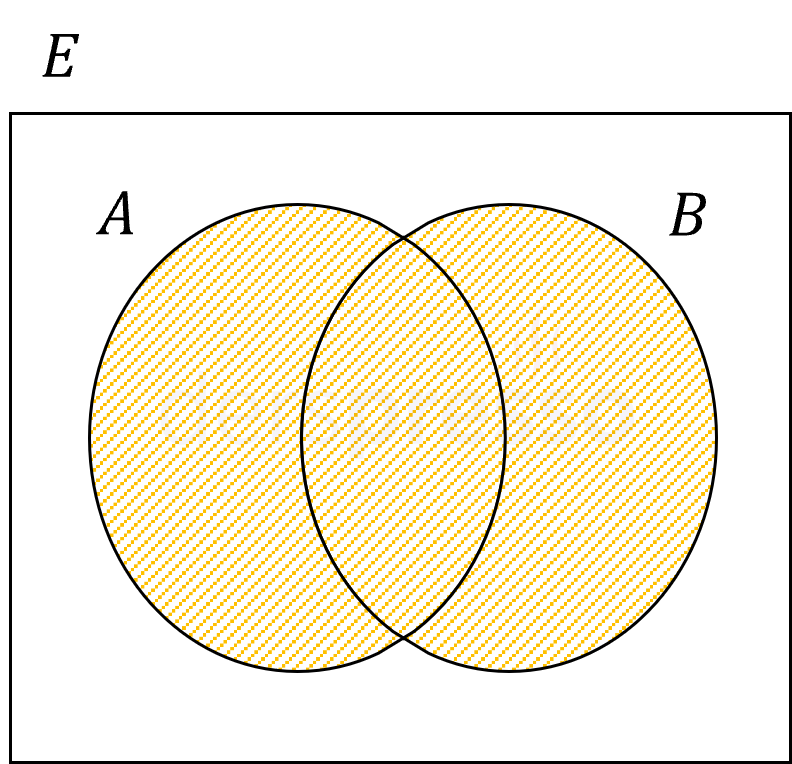
\( B' - A \) kümesi evrensel kümede bulunup \( A \) ve \( B \) kümelerinde bulunmayan elemanlardan oluşur (beyaz alan).
Bu ifadenin tümleyeni \( A \cup B \) kümesidir.
\( (B' - A)' = A \cup B \)
Sorudaki ifade düzenlendiğinde, \( (A \cup B) \cap (A \cup B) \) ifadesi elde edilir.
Bir kümenin kendisiyle kesişimi kendisine eşittir.
\( (A \cup B) \cap (A \cup B) = A \cup B \)
\( A \) ve \( B \) kümeleri \( E \) evrensel kümesinin iki alt kümesidir.
\( (A' \cap B)' \cup (B - A) \) ifadesinin en sade hali nedir?
Çözümü Göster\( (A' \cap B)' \cup (B - A) \)
Fark işlemini kesişim işlemi şeklinde yazalım.
\( = (A' \cap B)' \cup (B \cap A') \)
Kesişim işleminin değişme özelliği vardır.
\( = (A' \cap B)' \cup (A' \cap B) \)
İşlemin iki tarafında parantez içindeki ifadeler aynıdır. Bir kümenin tümleyeni ile birleşimi evrensel kümeye eşittir.
\( = E \) bulunur.
\( U = \{ x \mid 0 \le x \le 20, x \in \mathbb{Z} \} \)
\( A \) kümesi \( U \) kümesindeki tek sayı elemanlardan, \( B \) kümesi \( A \) kümesindeki asal sayı elemanlardan, \( C \) kümesi de \( U \) kümesindeki 4'e tam bölünen elemanlardan oluşmaktadır.
Buna göre \( U - (A \cup B \cup C) \) kümesinin elemanlarının toplamı nedir?
Çözümü Göster\( U = \{ 0, 1, 2, 3, \ldots, 20 \} \)
\( A \), \( B \) ve \( C \) kümelerinin elemanlarını listeleyelim.
\( A = \{ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 \} \)
\( B = \{ 3, 5, 7, 11, 13, 17, 19 \} \)
\( C = \{ 0, 4, 8, 12, 16, 20 \} \)
Bu üç kümenin birleşim kümesini bulalım.
\( A \cup B \cup C = \{ 0, 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20 \} \)
\( U \) kümesinin birleşim kümesinden farkını bulalım.
\( U - (A \cup B \cup C) = \{ 2, 6, 10, 14, 18 \} \)
Bu kümenin elemanlarının toplamını bulalım.
\( 2 + 6 + 10 + 14 + 18 = 50 \) bulunur.
\( A \) ve \( B \) aynı evrensel kümenin iki alt kümesidir.
\( s(A') = 7 \) ve \( s(B') = 11 \) olduğuna göre, \( s(A) - s(B) \) değeri kaçtır?
Çözümü Göster\( A \), \( B \) ve evrensel kümeleri Venn şeması şeklinde çizelim ve her bölgenin eleman sayısına birer değişken atayalım.

\( s(A') = c + d = 7 \)
\( s(B') = a + d = 11 \)
İkinci eşitlikten birinciyi taraf tarafa çıkaralım.
\( (a + d) - (c + d) = 11 - 7 \)
\( a - c = 4 \)
\( s(A) = a + b \)
\( s(B) = b + c \)
Birinci eşitlikten ikinciyi taraf tarafa çıkaralım.
\( s(A) - s(B) = (a + b) - (b + c) \)
\( a - c = 4 \) bulunur.
\( A \) ve \( B \) boş kümeden farklı iki kümedir.
\( s(B - A) = 3s(A - B) \)
\( s(A) + 2s(B) = 42 \)
olduğuna göre, \( A \cup B \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( s(A - B) = a \) diyelim.
\( s(B - A) = 3s(A - B) = 3a \)
\( s(A \cap B) = b \) diyelim.

\( s(A) + 2s(B) = 42 \) veriliyor.
\( (a + b) + 2(b + 3a) = 42 \)
\( 7a + 3b = 42 \)
Kümelerin boş olmadığı bilindiğine göre ve eleman sayılarının tam sayı olması gerektiği için bu eşitlik sadece aşağıdaki değerlerde sağlanır.
\( a = 3, \quad b = 7 \)
\( s(A \cup B) = 4a + b \)
\( = 4(3) + 7 = 19 \) bulunur.
\( s(A - B) = 4 \)
\( s(A' \cap B') = 3 \)
\( s(A' \cup B') = 12 \)
olduğuna göre, \( B - A \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( s(A' \cap B') \) ifadesi \( A \) ve \( B \) kümelerinin elemanı olmayıp yalnızca evrensel kümenin elemanı olan elemanları belirtir.

\( s(A' \cup B') \) ifadesi \( A \cap B \) dışında kalan elemanları belirtir.
\( s(A' \cup B') = 4 + a + 3 = 12 \)
\( a = 5 \)
\( s(B - A) = a = 5 \) bulunur.
\( A \) ve \( B \) aynı evrensel kümede bulunan boş kümeden farklı iki kümedir.
\( 3s(A - B) = 4s(A - B') = 5s(B - A) \)
olduğuna göre, evrensel kümenin eleman sayısı en az kaçtır?
Çözümü GösterVerilen eşitliği bir orantı sabitine eşitleyelim.
\( EKOK(3, 4, 5) = 60 \)
\( 3s(A - B) = 4s(A - B') = 5s(B - A) = 60k \)
Kümelerin eleman sayılarını \( k \) cinsinden yazalım.
\( s(A - B) = 20k \)
\( s(A - B') = s(A \cap B) = 15k \)
\( s(B - A) = 12k \)
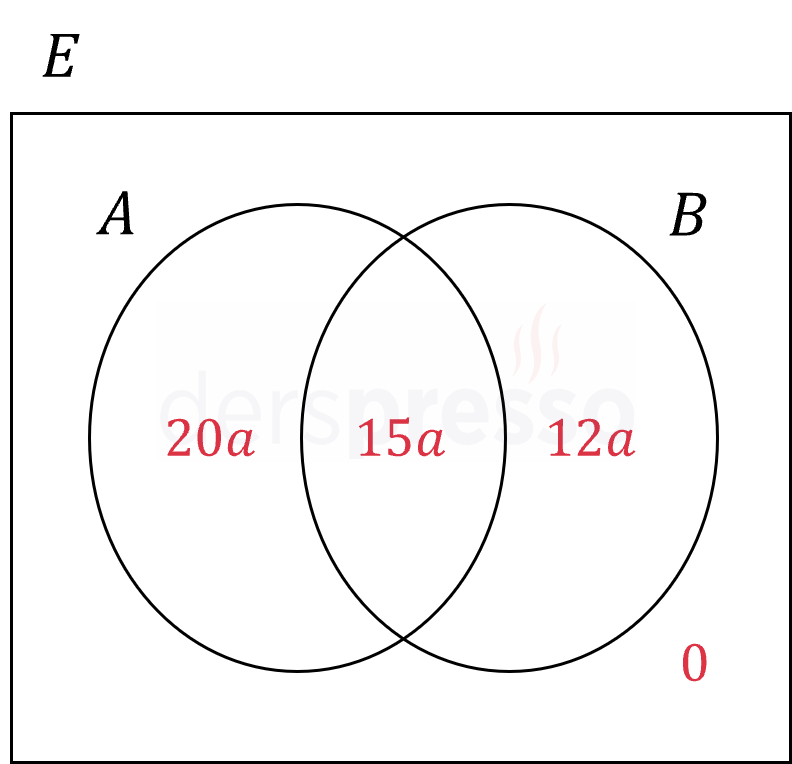
\( s(A \cup B) = 47k \)
Kümelerin eleman sayıları tam sayı olacağı için en az eleman sayısını elde etmek için \( k = 1 \) verelim.
\( = 47(1) = 47 \)
Evrensel kümenin eleman sayısının en az olması için yalnız evrensel kümede bulunan eleman sayısını 0 alalım.
\( s((A \cup B)') = 0 \)
\( s(E) = 47 + 0 = 47 \) bulunur.
\( \dfrac{s(K - L)}{3} = \dfrac{s(L - K)}{5} = \dfrac{s(K \cap L)}{2} \)
\( s(K \cup L) = 90 \)
olduğuna göre, \( s(K) \) kaçtır?
Çözümü GösterVerilen orantıyı bir orantı sabitine eşitleyelim.
\( \dfrac{s(K - L)}{3} = \dfrac{s(L - K)}{5} = \dfrac{s(K \cap L)}{2} = k \)
Kümelerin eleman sayılarını orantı sabiti cinsinden yazalım.
\( s(K - L) = 3k \)
\( s(L - K) = 5k \)
\( s(K \cap L) = 2k \)
Verileri Venn şemasında gösterelim.

\( s(K \cup L) = 3k + 2k + 5k = 10k = 90 \)
\( k = 9 \)
\( s(K) = 5k = 45 \) bulunur.
\( A_p = \{ x \mid (-1)^p \lt \dfrac{x}{p} \lt 4, x \in \mathbb{R} \} \) olduğuna göre,
\( A_1 - A_2 \) kümesi nedir?
Çözümü Göster\( p = 1 \) için:
\( A_1 = \{ x \mid (-1)^1 \lt \dfrac{x}{1} \lt 4 \} \)
\( = (-1, 4) \)
\( p = 2 \) için:
\( A_2 = \{ x \mid (-1)^2 \lt \dfrac{x}{2} \lt 4 \} \)
\( = (2, 8) \)
\( A_1 \) kümesinin \( A_2 \) kümesinden farkı olan aralığı bulalım.
\( A_1 - A_2 = (-1, 4) - (2, 8) \)
Yukarıdaki işlemde "\( - \)" sembolünün çıkarma değil, kümelerde fark işlemi olduğuna dikkat edilmelidir.
\( = (-1, 2] \) bulunur.
\( A = \{ \text{Sınıftaki kız öğrenciler} \} \)
\( B = \{ \text{Sınıftaki takdir alan öğrenciler} \} \)
\( C = \{ \text{Sınıftaki mavi gözlü öğrenciler} \} \)
\( D = \{ \text{Sınıftaki sarışın öğrenciler} \} \)
olduğuna göre, aşağıdaki ifade hangi öğrencileri ifade eder?
\( [(A \cap C) - D] \cup B' \)
Çözümü GösterVerilen küme sınıftaki mavi gözlü kız öğrenciler içinde sarışın olmayanlar ile sınıftaki tüm öğrenciler içinde takdir almamış olanların birleşimini ifade eder.

Aşağıdaki ifadelerin yukarıdaki şekildeki \( p, q, r, s, t \) bölgelerinden hangisine karşılık geldiğini belirtin.
(a) \( (A \cap B) \cap C \)
(b) \( (A \cap B) - C \)
(c) \( (A \cap C) - B \)
(d) \( A - (B \cup C) \)
(e) \( C - A \)
Çözümü Göster(a) seçeneği \( p \) bölgesini ifade eder.
(b) seçeneği \( q \) bölgesini ifade eder.
(c) seçeneği \( t \) bölgesini ifade eder.
(d) seçeneği \( r \) bölgesini ifade eder.
(e) seçeneği \( s \) bölgesini ifade eder.
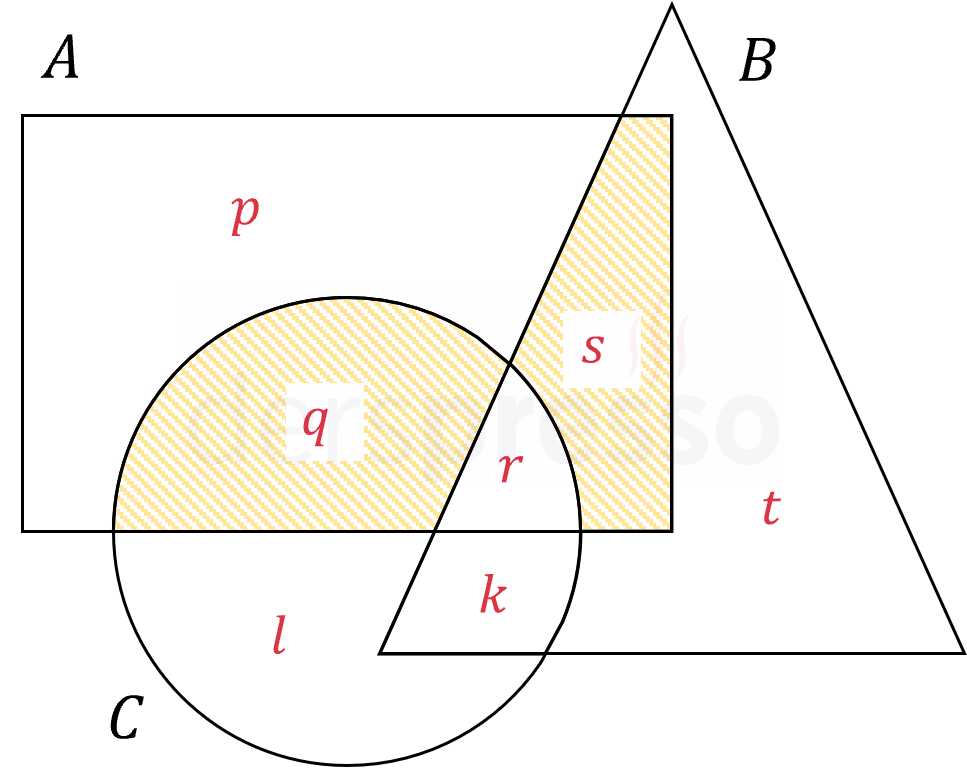
Aşağıdaki ifadelerin yukarıdaki şekildeki \( p, q, r, s, t, k, l \) bölgelerinden hangisine ya da hangilerine karşılık geldiğini belirtin.
(a) \( A - (B \cup C) \)
(b) \( C - (A \cup B) \)
(c) \( B - (A \cup C) \)
(d) \( [A \cap (B \cap C)] \cup [(C \cap B) - A] \)
(e) \( [(A \cap C) - B] \cup [(A \cap B) - C] \)
Çözümü Göster(a) seçeneği \( p \) bölgesini ifade eder.
(b) seçeneği \( l \) bölgesini ifade eder.
(c) seçeneği \( t \) bölgesini ifade eder.
(d) seçeneği \( r \) ve \( k \) bölgelerinin birleşimini ifade eder.
(e) seçeneği \( q \) ve \( s \) bölgelerinin birleşimini ifade eder.

Aşağıdaki ifadelerin yukarıdaki şekildeki \( p, q, r, s, t, k, l, a, b, c, d \) bölgelerinden hangisine ya da hangilerine karşılık geldiğini belirtin.
(a) \( A \cap B \cap C \)
(b) \( (A - C) - (B - C) \)
(c) \( C - (A \cup B) \)
(d) \( (A \cap C) - (B \cap C) \)
(e) \( (A \cap B) - C \)
Çözümü Göster(a) seçeneği \( l \) bölgesini ifade eder.
(b) seçeneği \( p \) ve \( r \) bölgelerinin birleşimini ifade eder.
(c) seçeneği \( c \) ve \( d \) bölgelerinin birleşimini ifade eder.
(d) seçeneği \( q \) bölgesini ifade eder.
(e) seçeneği \( a \) ve \( b \) bölgelerinin birleşimini ifade eder.
Buna göre doğru cevap (c) seçeneğidir.

Aşağıdaki ifadelerden hangisi şekildeki taralı bölgeyi ifade etmez?
(a) \( (C \cap A) - B \)
(b) \( (A - B) \cap C \)
(c) \( (A \cap B') \cap C \)
(d) \( (C - A) \cap B \)
(e) \( (C - B) \cap A \)
Çözümü Göster(a), (b), (c) ve (e) seçenekleri taralı bölgeyi ifade eder.
\( (C - A) \cap B = \emptyset \) olduğu için (d) seçeneği taralı bölgeyi ifade etmez.
\( A \cap B = \{ 2, 3, 6, 9, 13, 14, 18 \} \)
\( B \cap C = \{ 2, 6, 8, 10, 14 \} \)
olduğuna göre, \( A - C \) kümesinin eleman sayısı en az kaçtır?
Çözümü GösterVerilen iki kesişim kümesinin kesişimini bulalım.
\( (A \cap B) \cap (B \cap C) = \{ 2, 6, 14 \} \)
Kümelerde kesişim işleminin birleşme özelliği vardır.
\( = A \cap (B \cap B) \cap C \)
Bir kümenin kendisiyle kesişimi yine kendisine eşittir.
\( = A \cap B \cap C \)
Bilinen elemanları bir Venn şeması üzerinde gösterelim.
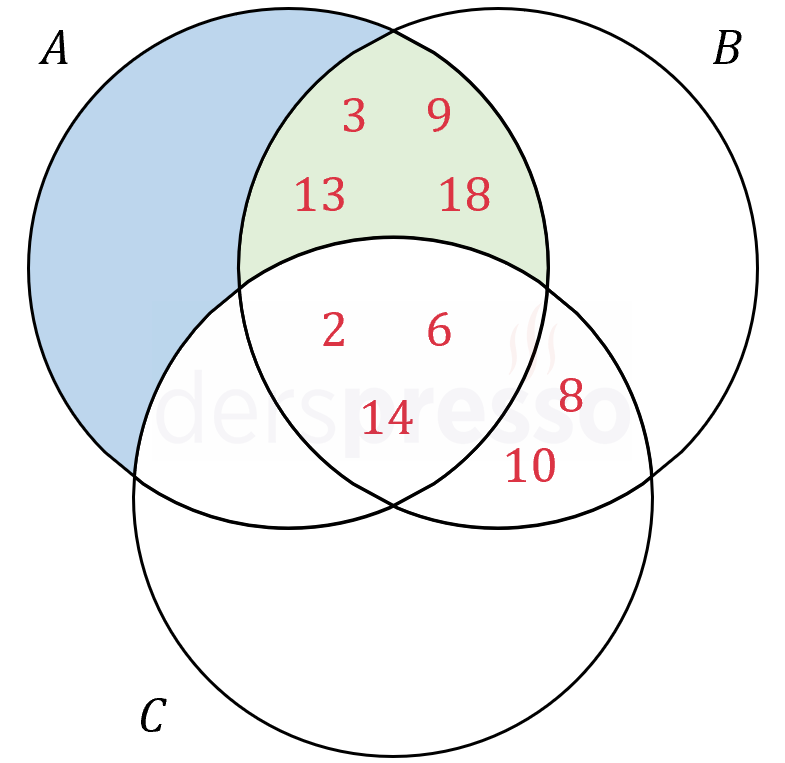
\( A - C \) kümesinin eleman sayısının en az olması için, mavi ile işaretli bölgede eleman bulunmamalı ve fark kümesi sadece yeşil bölgedeki elemanlardan oluşmalıdır.
\( A - C = \{ 3, 9, 13, 18 \} \)
\( s(A - C) = 4 \) bulunur.
\( s(A - B') = x - 1 \)
\( s[B - (A \cap B)] = 2x + 3 \)
\( s(B) = 11 \)
olduğuna göre \( s(A \cap B) \) kaçtır?
Çözümü Göster\( A \) kümesinin \( B \) kümesinin tümleyeninden farkı iki kümenin kesişimidir.
\( A - B' = A \cap B \)
\( B \) kümesinin \( A \) kümesi ile kesişiminden farkı \( A \) kümesinden farkına eşittir.
\( B - (A \cap B) = B - A \)
\( A \cap B \) ve \( B - A \) kümelerinin birleşimi \( B \) kümesine eşittir.
\( (A \cap B) \cup (B - A) = B \)
\( A \cap B \) ve \( B - A \) kümeleri ayrık kümeler olduğu için eleman sayıları toplamı \( B \) kümesinin eleman sayısına eşittir.
\( s(A \cap B) + s(B - A) = s(B) \)
\( (x - 1) + (2x + 3) = 11 \)
\( x = 3 \)
\( s(A \cap B) = x - 1 = 2 \) bulunur.
Aşağıdaki ifadelerden hangileri tek başına sağlandığında 3 sayısı kesinlikle \( A \) kümesinin elemanı olur?
I. \( \{ 3 \} \cup A = A \)
II. \( \{ 3 \} - A = \emptyset \)
III. \( s(A \cap \{ 3 \}) = 1 \)
IV. \( A - \{ 3 \} = \emptyset \)
Çözümü GösterI. öncül: Birleşim kümesinin \( A \) kümesine eşit olması için 3 sayısı \( A \) kümesinin bir elemanı olmalıdır.
II. öncül: 3 sayısının \( A \) kümesinden farkının boş küme olması için 3 sayısı \( A \) kümesinin bir elemanı olmalıdır.
III. öncül: \( A \) kümesi ile 3 sayısının kesişiminin tek elemanlı olması için 3 sayısı \( A \) kümesinin bir elemanı olmalıdır.
IV. öncül: \( A \) kümesinin 3 sayısından farklı bir elemanı yoktur, ancak \( A \) kümesi boş küme de olabileceği için 3 sayısı \( A \) kümesinin bir elemanı olmayabilir.
Buna göre I., II. ve III. öncüller tek başına sağlandığında 3 sayısı kesinlikle \( A \) kümesinin elemanı olur.

Yukarıdaki şekildeki kümeler aşağıdaki şekilde tanımlanıyor.
\( A \): E harfi ile başlayan kelimeler kümesi
\( B \): K harfi ile biten kelimeler kümesi
\( C \): 4 harfli kelimeler kümesi
Buna göre,
\( K = \) {İrmik, Erik, Ece, Ecem, İnek, Elma, Kek, Uzak, Buse, Kedi}
kümesinin elemanlarından kaç tanesi şekildeki taralı bölgelerin elemanıdır?
Çözümü GösterŞekildeki taralı bölge \( C \cap [(A - B) \cup (B - A)] \) ile ifade edilir.
Buna göre bu bölgenin elemanları, 4 harfli VE (E harfi ile başlayan, ama K harfi ile bitmeyen VEYA K harfi ile biten, ama E harfi ile başlamayan) kelimelerdir.
\( K \) kümesinin elemanlarından Ecem, İnek, Elma ve Uzak kelimeleri bu koşulları sağlar.
Buna göre \( K \) kümesinin 4 elemanı taralı bölgeye aittir.