Kartezyen Çarpımının Grafik Gösterimi
Önceki bölümde kartezyen çarpımının sıralı ikililerden oluşan bir kümeye karşılık geldiğini ve analitik düzlemde bir noktayı ifade etmek için kullanılan \( (x, y) \) gösteriminin de aslında bir sıralı ikili olduğunu belirtmiştik.
Kartezyen çarpımı alınan iki kümenin elemanları sırasıyla bir noktanın \( x \) ve \( y \) koordinatları olarak kabul edilirse, kartezyen çarpımı sonucu elde edilen sıralı ikililer analitik düzlemde birer nokta olarak işaretlenerek kartezyen çarpımının grafiksel gösterimi elde edilebilir.
Aşağıdaki iki kümenin kartezyen çarpımlarını liste yöntemi ile ve grafik olarak gösterelim.
\( A = \{ 1, 2, 3, 4 \} \)
\( B = \{ 2, 3, 4 \} \)
İki kümenin kartezyen çarpımı aşağıdaki gibidir.
\( A \times B = \{ \)
\( \quad (1, 2), (1, 3), (1, 4), \)
\( \quad (2, 2), (2, 3), (2, 4), \)
\( \quad (3, 2), (3, 3), (3, 4), \)
\( \quad (4, 2), (4, 3), (4, 4) \)
\( \} \)
Kartezyen çarpımının elemanı olan sıralı ikilileri kartezyen düzleminde birer nokta olarak işaretleyelim.

Aralıkların Kartezyen Çarpımı
Kümeler sonlu sayıda elemandan oluşabildikleri gibi sonsuz sayıda elemandan da oluşabilir. Örneğin reel sayılar kümesinde birer aralık olarak tanımlanmış iki kümenin de kartezyen çarpımı alınabilir ve bu çarpım bir grafik olarak gösterilebilir.
Aşağıdaki iki kümenin kartezyen çarpımlarını ortak özellik yöntemi ile ve grafik olarak gösterelim.
\( A = \{ x \mid -1 \le x \lt 3, x \in \mathbb{R} \} \)
\( B = \{ y \mid 1 \lt y \le 4, y \in \mathbb{R} \} \)
\( A \) kümesi sayı doğrusu üzerinde \( [-1, 3) \) yarı açık aralığını, \( B \) kümesi \( (1, 4] \) yarı açık aralığını ifade etmektedir.
İki kümenin kartezyen çarpımı aşağıdaki gibidir.
\( A \times B = \{ (x, y) \mid -1 \le x \lt 3, \) \( 1 \lt y \le 4 \} \)
Kartezyen çarpımının elemanı olan sonsuz sayıdaki sıralı ikililerin karşılık geldiği aralıkları kartezyen düzleminde işaretleyelim.
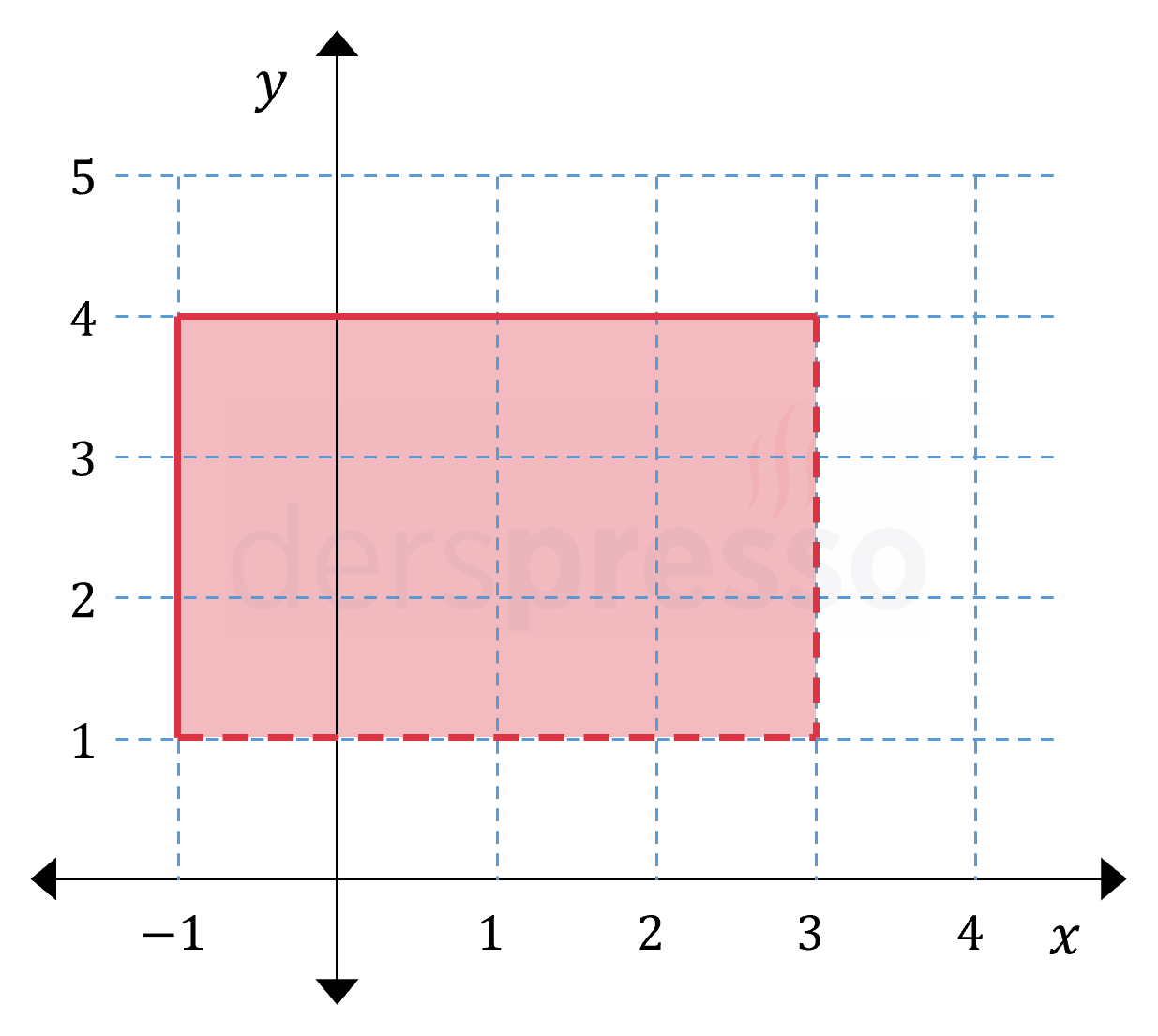
Bu grafikle ilgili birkaç noktayı vurgulamamız önem taşımaktadır.
- Bu grafik bir önceki örnekteki grafikten farklı olarak; sadece belirli noktaları değil, bu noktalar arasındaki sonsuz sayıda noktayı da içermektedir.
- Küme tanımlarındaki aralıklardaki açık sınır değerleri grafikte kesikli doğrularla gösterilmiştir ve bu doğrular üzerindeki noktalar grafiğe dahil değildir.
- Küme tanımlarındaki aralıklardaki kapalı sınır değerleri grafikte sürekli doğrularla gösterilmiştir ve bu doğrular üzerindeki noktalar grafiğe dahildir.
- Köşe noktalarında görülebileceği gibi, bir noktanın grafiğe dahil olabilmesi için o noktanın hem \( x \) hem de \( y \) bileşeni ilgili kümelerde tanımlı olmalıdır.
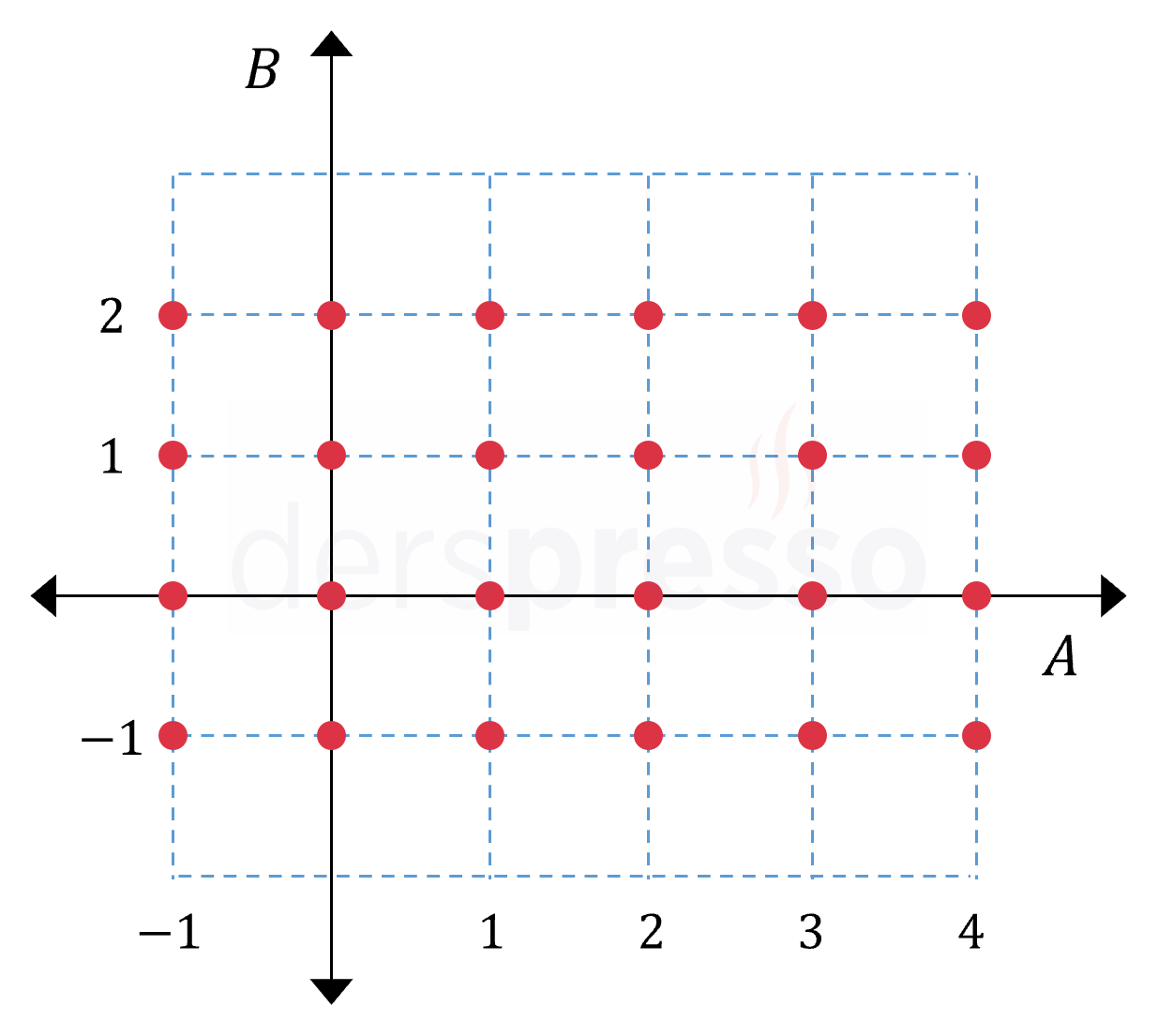
Yukarıda \( A \times B \) kümesinin elemanları gösterilmiştir. Buna göre \( A - B \) kümesinin kaç alt kümesi vardır?
Çözümü GösterGrafikteki noktaların \( A \) ekseni üzerindeki izdüşümlerinin karşılık geldiği değerler \( A \) kümesinin elemanlarıdır.
\( A = \{ -1, 0, 1, 2, 3, 4 \}\)
Grafikteki noktaların \( B \) ekseni üzerindeki izdüşümlerinin karşılık geldiği değerler \( B \) kümesinin elemanlarıdır.
\( B = \{ -1, 0, 1, 2 \}\)
\( A - B = \{ 3, 4 \} \)
\( n \) elemanlı bir kümenin alt küme sayısı \( 2^n \) formülü ile bulunur.
Buna göre \( A - B \) kümesinin alt küme sayısı \( 2^2 = 4 \) olur.
\( A = \{ x \mid -2 \lt x \le 1, x \in \mathbb{R} \} \)
\( B = \{ x \mid -1 \le x \lt 3, x \in \mathbb{Z} \} \)
olduğuna göre, \( A \times B \) kartezyen çarpım kümesinin grafiği nedir?
Çözümü Göster\( A \) kümesi reel sayılarda tanımlı olduğu için verilen aralıktaki tüm reel sayıları kapsar ve bir doğru parçasına karşılık gelir.
Bu yarı kapalı doğru parçasına -2 dahil değil, 1 dahildir.
\( B \) kümesi tam sayılarda tanımlı olduğu için sadece aralıktaki tam sayıları kapsar ve belirli noktalara karşılık gelir.
Bu noktalara -1 dahil, 3 dahil değildir.
Bu iki kümenin kartezyen çarpımlarının grafiği aşağıdaki gibi olur.
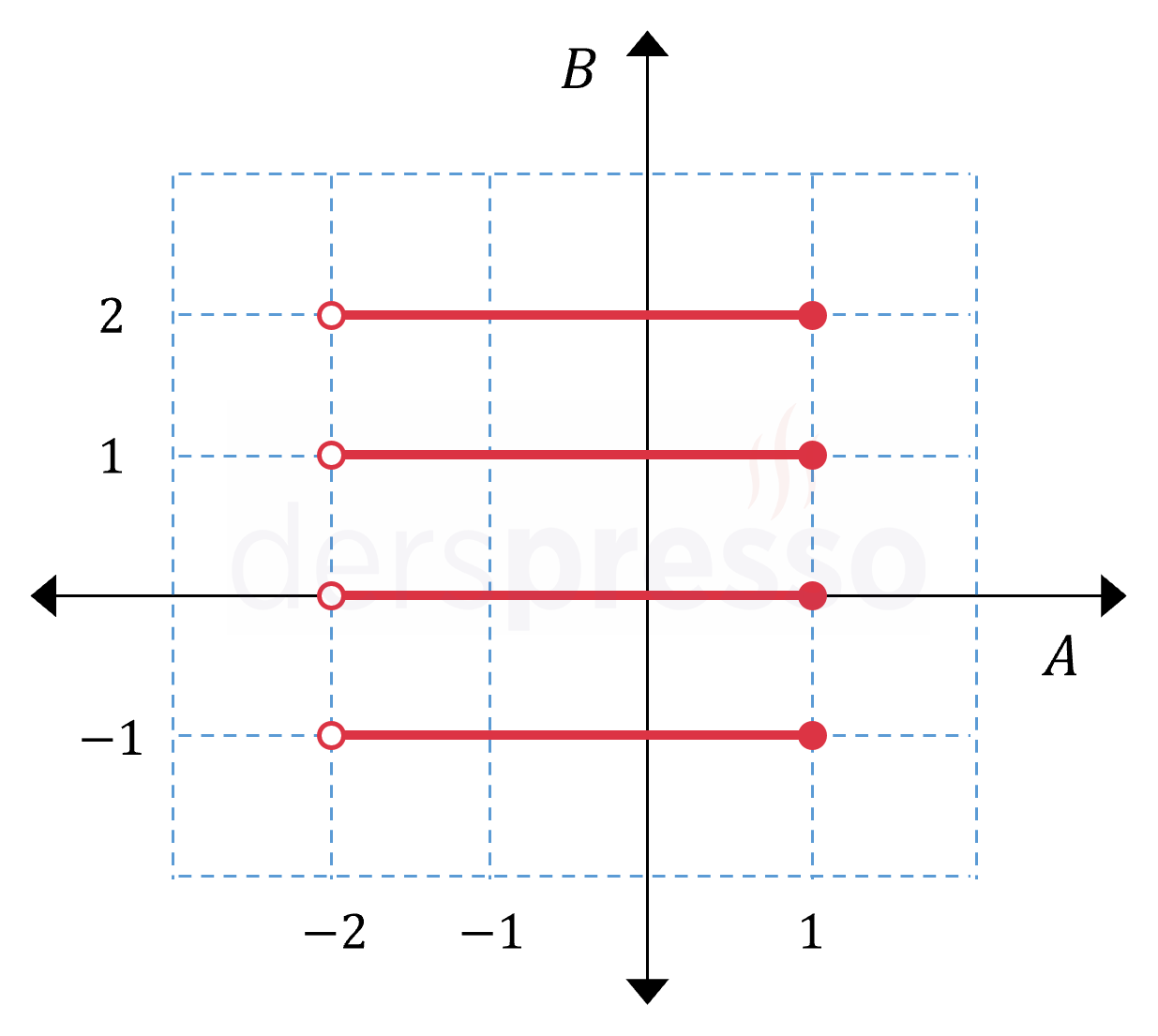
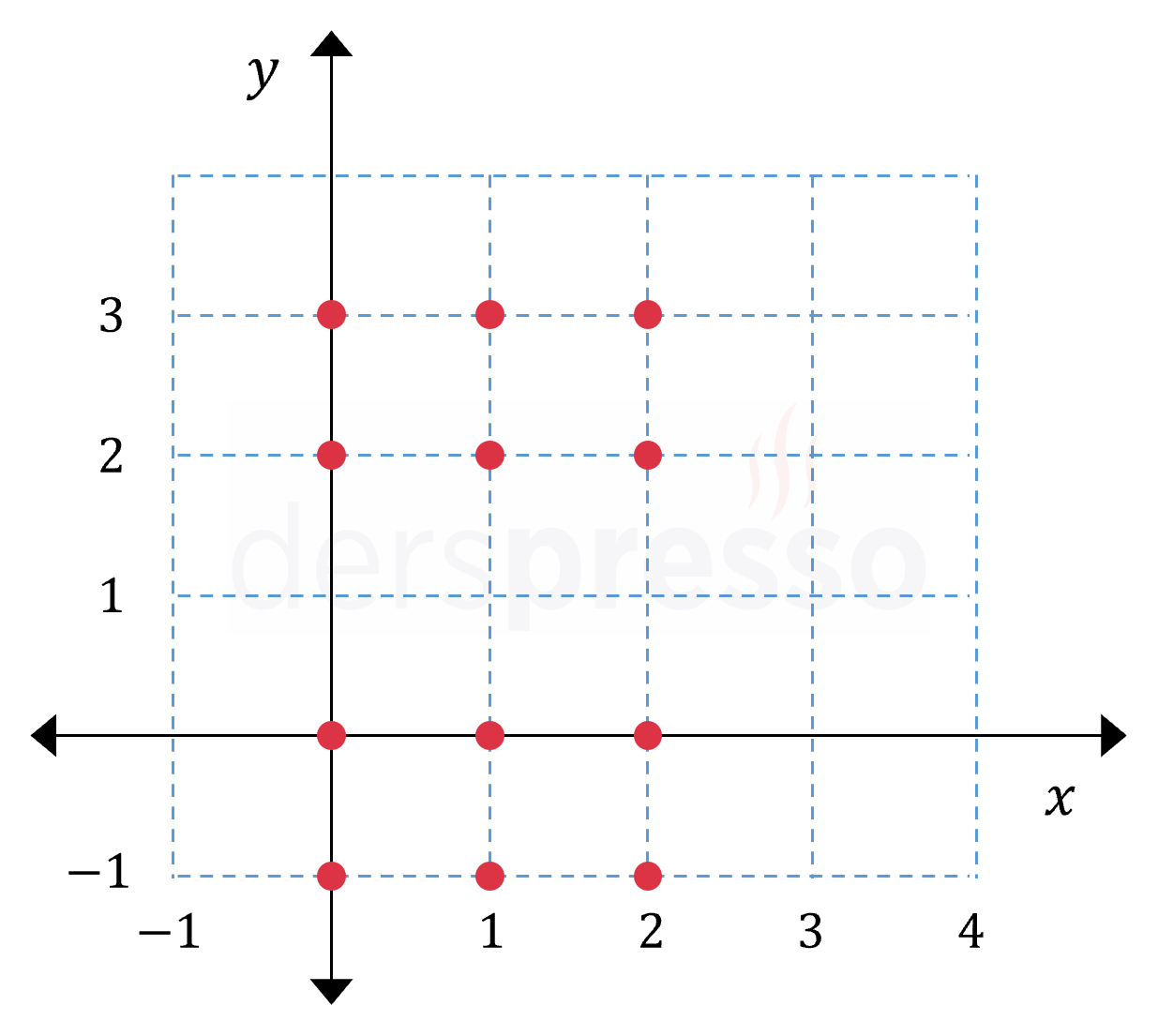
Yukarıda \( A \times B \) kartezyen çarpımının koordinat düzleminde grafiği verilmiştir.
Buna göre, aynı düzleme \( B \times A \) kartezyen çarpımının grafiği çizilirse kaç nokta iki kez işaretlenmiş olur?
Çözümü GösterGrafikteki noktaların \( A \) ekseni üzerindeki izdüşümlerinin karşılık geldiği değerler \( A \) kümesinin elemanlarıdır.
\( A = \{ 0, 1, 2 \} \)
Grafikteki noktaların \( B \) ekseni üzerindeki izdüşümlerinin karşılık geldiği değerler \( B \) kümesinin elemanlarıdır.
\( B = \{ -1, 0, 2, 3 \} \)
\( B \times A \) kartezyen çarpımında da bulunacak elemanlar iki kümenin ortak elemanları arasındaki kartezyen çarpımına eşittir.
\( A \cap B = \{ 0, 2 \} \)
Buna göre aşağıdaki 4 nokta iki grafikte de ortaktır ve iki kez işaretlenir.
\( (A \cap B) \times (A \cap B) = \{ (0, 0), (0, 2), (2, 0), (2, 2) \} \)
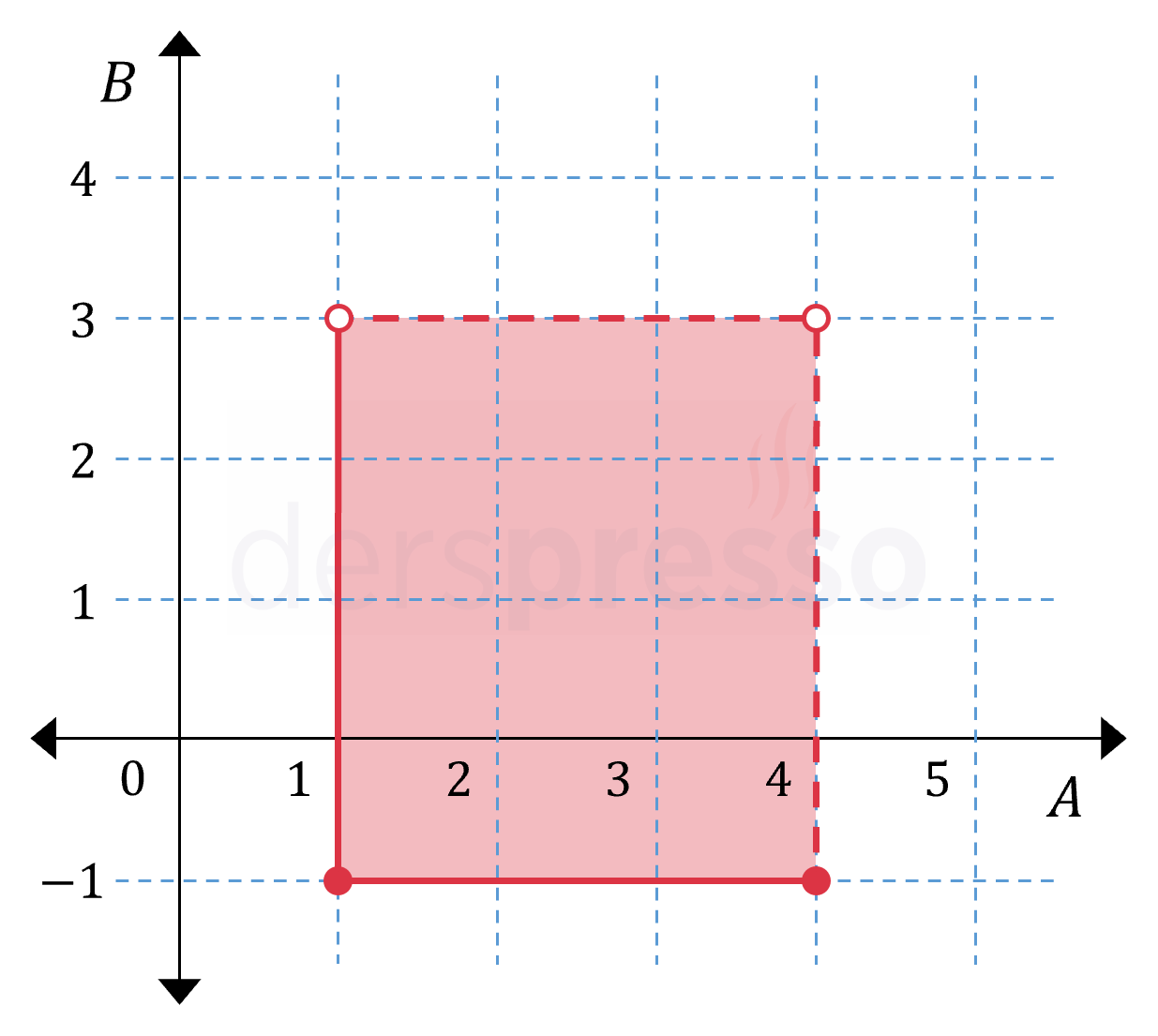
Şekilde \( A \times B \) kartezyen çarpımının grafiği verilmiştir.
Buna göre, \( B \cap A' \) kümesi nedir?
Çözümü GösterGrafikteki noktaların \( A \) ekseni üzerindeki izdüşümlerinin karşılık geldiği değerler \( A \) kümesinin elemanlarıdır.
\( A = [1, 4] \)
Grafikteki noktaların \( B \) ekseni üzerindeki izdüşümlerinin karşılık geldiği değerler \( B \) kümesinin elemanlarıdır.
\( B = [-1, 3) \)
İki kümeyi sayı doğrusu üzerinde gösterelim.
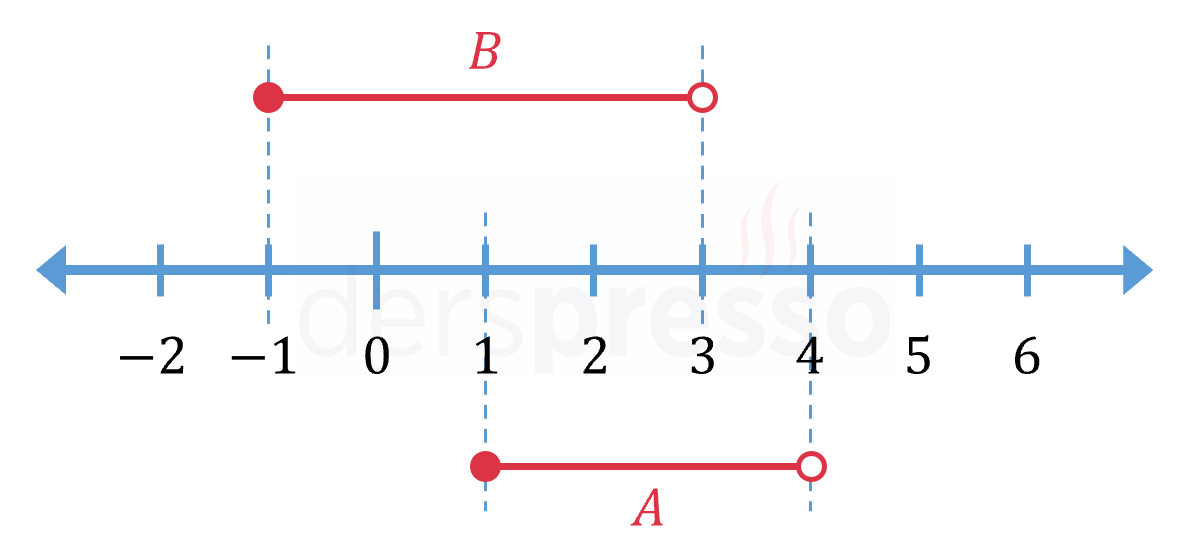
\( B \cap A' = [-1, 3) \cap [(-\infty, 1) \cup (4, \infty)] \)
\( = [-1, 1) \) bulunur.
\( A \), \( B \) ve \( K \) kümeleri aşağıdaki şekilde tanımlanıyor.
\( A = \{ x \mid 2 \le x \le 3, x \in \mathbb{R} \} \)
\( B = \{ x \mid 1 \le x \le 5, x \in \mathbb{R} \} \)
\( K = B - A \)
Buna göre, \( K \times K \) kartezyen çarpım kümesinin grafiği nedir?
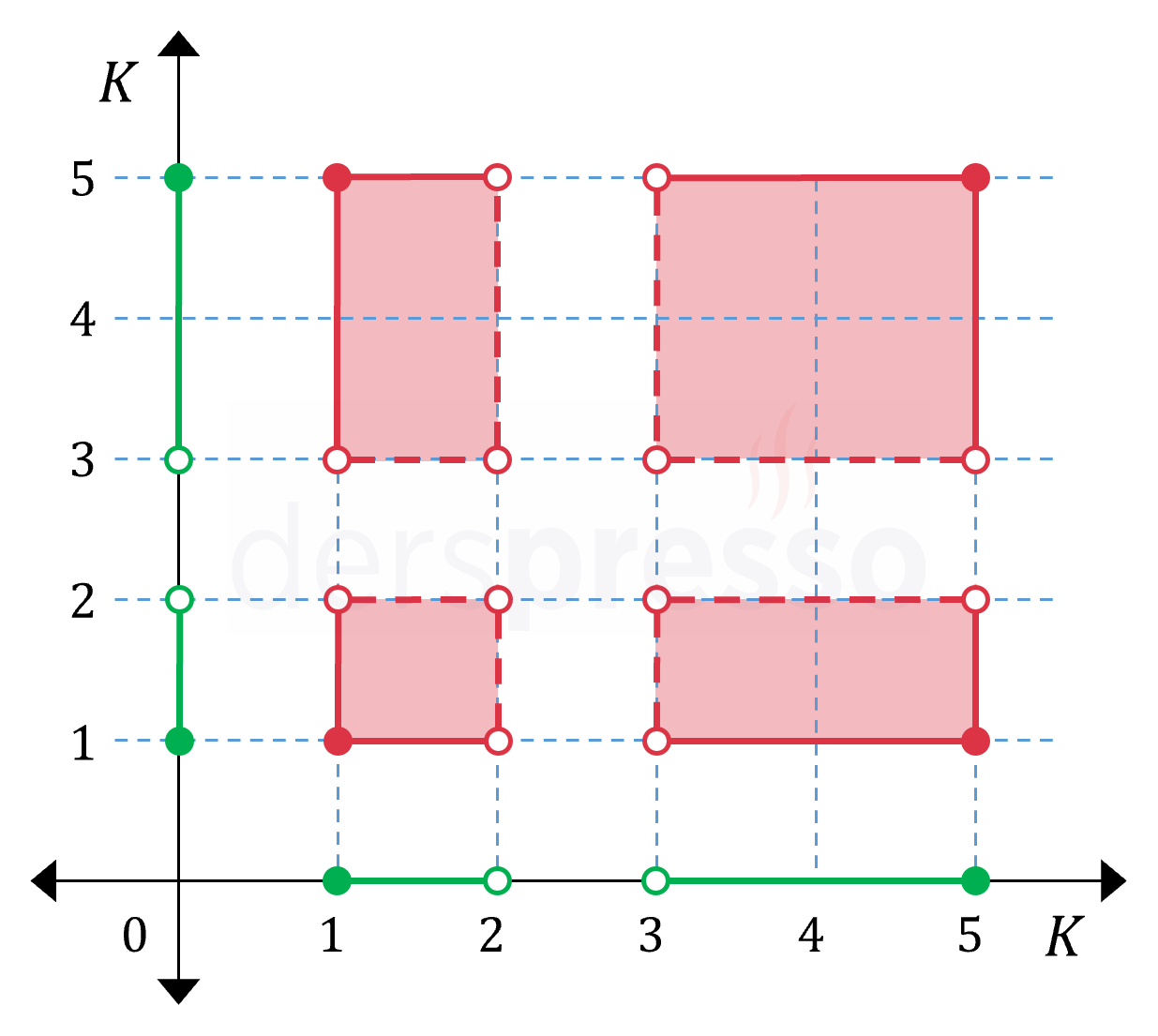
Çözümü Göster\( K = B - A \) olduğu için iki kümenin farkı \( [1, 2) \) ve \( (3, 5] \) yarı açık aralıklarının birleşimi olur.
\( K = [1, 2) \cup (3, 5] \)
O halde \( K \times K \) kartezyen çarpımının grafiği aşağıdaki gibi olur.
Eksenler üzerinde işaretli yeşil aralıklar grafiğin parçası olmayıp kartezyen çarpım grafiğinin nasıl oluştuğunu göstermek için bilgi amaçlı verilmiştir.