Kartezyen Çarpımı
\( A \) ve \( B \) kümelerinin kartezyen çarpımı, birinci bileşeni \( A \) kümesinin, ikinci bileşeni \( B \) kümesinin elemanı olmak üzere yazılabilecek tüm sıralı ikililerin kümesidir. \( A \) ve \( B \) kümelerinin kartezyen çarpımı \( A \times B \) şeklinde gösterilir.
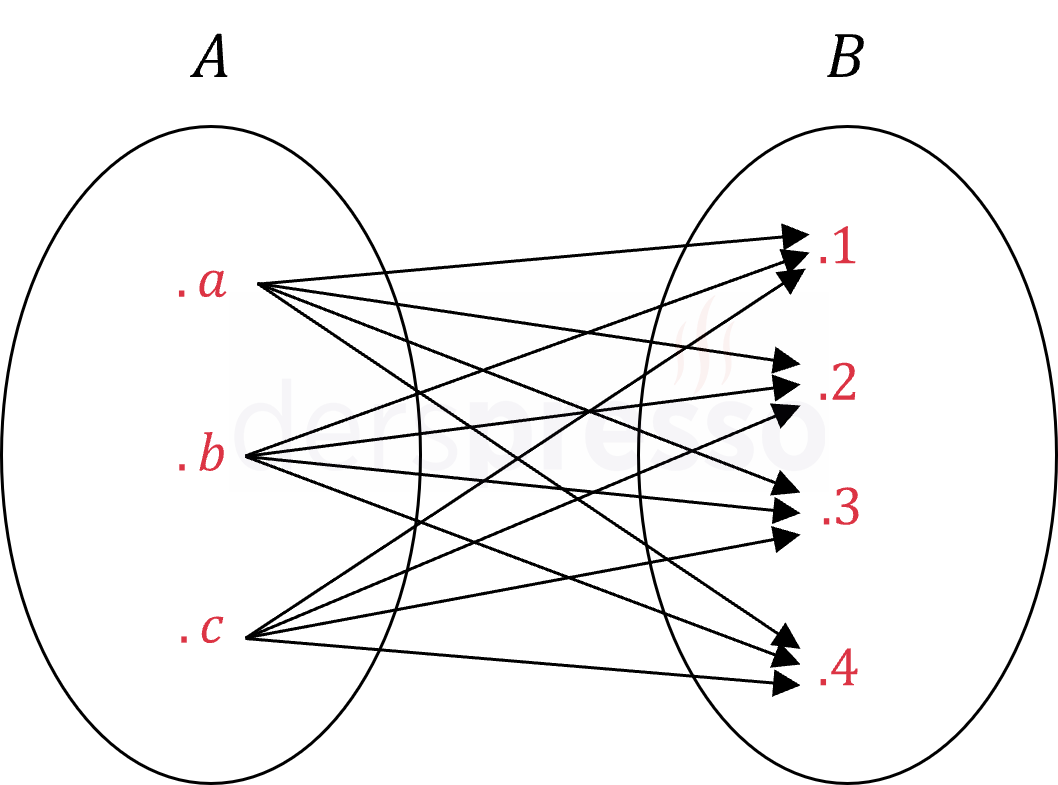
\( A \times B = \{ (a, b) \mid a \in A \land b \in B \} \)
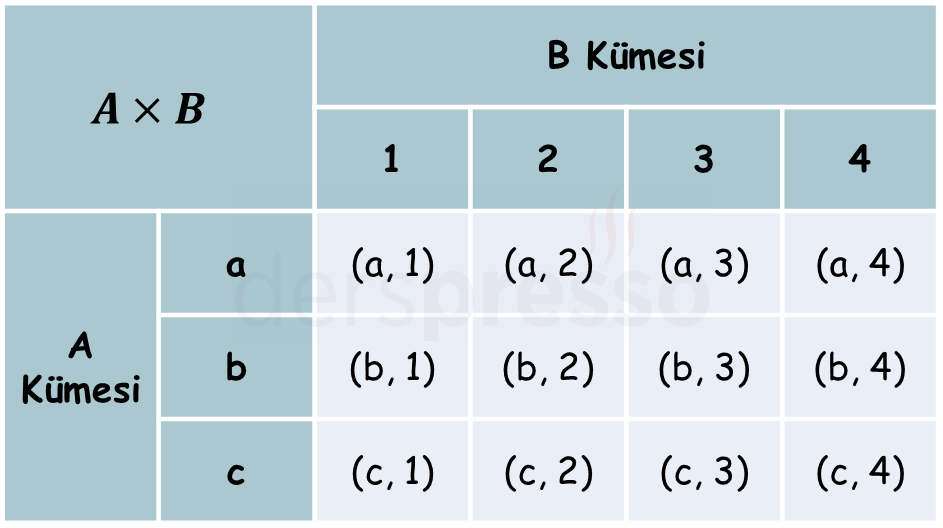
\( A = \{a, b, c \} \)
\( B = \{1, 2, 3, 4 \} \)
\( A \times B = \{ (a, 1), (a, 2), (a, 3), (a, 4), \)
\( \quad (b, 1), (b, 2), (b, 3), (b, 4), \)
\( \quad (c, 1), (c, 2), (c, 3), (c, 4) \} \)
İki kümenin kartezyen çarpımı da bir kümedir ve elemanları sıralı ikililerdir (sıralı ikililerin parantez içindeki bileşenleri değildir). Kartezyen çarpım kümesinin elemanı olan her bir sıralı ikili, yukarıdaki Venn şemasındaki bir oka karşılık gelir.
\( A = \{a, b \} \)
\( B = \{1, 2, 3 \} \)
\( A \times B = \{(a, 1), (a, 2), \) \( (a, 3), (b, 1), \) \( (b, 2), (b, 3) \} \)
\( (a, 2) \in A \times B \)
\( a \notin A \times B \)
\( A \) ve \( B \) kümelerinin kartezyen çarpım kümesinin eleman sayısı, iki kümenin eleman sayılarının çarpımına eşittir.
\( s(A \times B) = s(A) \cdot s(B) \)
Bir kümenin kendisiyle kartezyen çarpımı üslü ifade şeklinde de gösterilebilir.
\( A^2 = A \times A \)
Buna göre, her noktanın koordinatlarının birer sıralı ikili (sıralı üçlü) olarak ifade edildiği iki (üç) boyutlu kartezyen koordinat sistemi aşağıdaki şekilde de ifade edilebilir.
\( \mathbb{R}^2 = \mathbb{R} \times \mathbb{R} \)
\( \mathbb{R}^3 = \mathbb{R} \times \mathbb{R} \times \mathbb{R} \)
Kartezyen Çarpımı İşlem Özellikleri
Kartezyen çarpım kümesinin elemanları olan sıralı ikililerde bileşenlerin sırası önemli olduğu için kartezyen çarpımının değişme özelliği yoktur.
\( A \ne \emptyset, \quad B \ne \emptyset \) olmak üzere,
\( A \times B \ne B \times A \)
\( A = \{ a, b \} \)
\( B = \{ 1, 2, 3 \} \)
\( A \times B = \{ (a, 1), (a, 2), \) \( (a, 3), (b, 1), \) \( (b, 2), (b, 3) \} \)
\( B \times A = \{ (1, a), (1, b), \) \( (2, a), (2, b), \) \( (3, a), (3, b) \} \)
Kartezyen çarpımının kesişim işlemi üzerinde dağılma özelliği vardır.
\( A \times (B \cap C) = (A \times B) \cap (A \times C) \)
\( A = \{ a, b, c \} \)
\( B = \{ 1, 2 \} \)
\( C = \{ 1, 3 \} \)
\( A \times (B \cap C) = A \times \{ 1 \} \)
\( = \{ (a, 1), (b, 1), (c, 1) \} \)
\( (A \times B) \cap (A \times C) = \)
\( \{ (a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2) \} \cap \)
\( \{ (a, 1), (a, 3), (b, 1), \) \( (b, 3), (c, 1), (c, 3) \} \)
\( = \{ (a, 1), (b, 1), (c, 1) \} \)
İSPATI GÖSTER
İlk olarak \( A \times ( B \cap C) \subseteq (A \times B) \cap (A \times C) \) olduğunu gösterelim.
\( (x, y) \in A \times (B \cap C) \) alalım.
Bu durumda \( x \in A \) ve \( y \in (B \cap C) \) olur.
\( y \in (B \cap C) \) ise \( y \) her iki kümenin de elemanıdır.
\( x \in A \land (y \in B \land y \in C) \)
"Ve" bileşik önermesinin birleşme özelliği vardır.
\( \equiv (x \in A \land y \in B) \land (x \in A \land y \in C) \)
\( \equiv (x, y) \in (A \times B) \land (x, y) \in (A \times C) \)
\( \equiv (x, y) \in (A \times B) \cap (A \times C) \) olur. \( \textcolor{red}{(1)} \)
Şimdi \( (A \times B) \cap (A \times C) \subseteq A \times (B \cap C) \) olduğunu gösterelim.
\( (x, y) \in (A \times B) \cap (A \times C) \) alalım.
Bu durumda \( (x, y) \in (A \times B) \land (x, y) \in (A \times C) \) olur.
\( (x, y) \in A \times B \Rightarrow x \in A \land y \in B \)
\( (x, y) \in A \times C \Rightarrow x \in A \land y \in C \)
\( x \in A \land (y \in B \land y \in C) \)
\( \equiv x \in A \land y \in (B \cap C) \)
\( \equiv (x, y) \in A \times (B \cap C) \) olur. \( \textcolor{red}{(2)} \)
Yukarıda kırmızı ile işaretlediğimiz \( (1) \) ve \( (2) \)'den \( A \times (B \cap C) = (A \times B) \cap (A \times C) \) olur.
Kartezyen çarpımının birleşim işlemi üzerinde dağılma özelliği vardır.
\( A \times (B \cup C) = (A \times B) \cup (A \times C) \)
Yukarıdaki örnekteki kümeleri kullanalım.
\( A \times (B \cup C) = A \times \{ 1, 2, 3 \} \)
\( = \{ (a, 1), (a, 2), (a, 3), \) \( (b, 1), (b, 2), (b, 3), \) \( (c, 1), (c, 2), (c, 3) \} \)
\( (A \times B) \cup (A \times C) = \)
\( \{ (a, 1), (a, 2), (b, 1), \) \( (b, 2), (c, 1), (c, 2) \} \cup \)
\( \{ (a, 1), (a, 3), (b, 1), \) \( (b, 3), (c, 1), (c, 3) \} \)
\( = \{ (a, 1), (a, 2), (a, 3), \) \( (b, 1), (b, 2), (b, 3), \) \( (c, 1), (c, 2), (c, 3) \} \)
İSPATI GÖSTER
İlk olarak \( A \times (B \cup C) \subseteq (A \times B) \cup (A \times C) \) olduğunu gösterelim.
\( (x, y) \in A \times (B \cup C) \) alalım.
Bu durumda \( x \in A \) ve \( y \in (B \cup C) \) olur.
Buradan \( x \in A \land (y \in B \lor y \in C) \) elde edilir.
\( x \in A \land (y \in B \lor y \in C) \)
"Ve" işleminin "veya" işlemi üzerinde soldan ve sağdan dağılma özelliği vardır.
\( (x \in A \land y \in B) \lor (x \in A \lor y \in C) \)
\( (x, y) \in (A \times B) \lor (x, y) \in (A \times C) \)
\( (x, y) \in (A \times B) \cup (A \times C) \) olur. \( \textcolor{red}{(1)} \)
Şimdi \( (A \times B) \cup (A \times C) \subseteq A \times (B \cup C) \) olduğunu gösterelim.
\( (x, y) \in (A \times B) \cup (A \times C) \) alalım.
Bu durumda \( (x, y) \in (A \times B) \lor (x, y) \in (A \times C) \) olur.
\( (x, y) \in (A \times B) \Rightarrow x \in A \land y \in B \)
\( (x, y) \in (A \times C) \Rightarrow x \in A \land y \in C \)
\( x \in A \land (y \in B \lor y \in C) \)
\( \equiv x \in A \land y \in (B \cup C) \)
\( \equiv (x, y) \in A \times (B \cup C) \) olur. \( \textcolor{red}{(2)} \)
Yukarıda kırmızı ile işaretlediğimiz \( (1) \) ve \( (2) \)'den \( A \times (B \cup C) = (A \times B) \cup (A \times C) \) olur.
Kartezyen çarpımının fark işlemi üzerinde dağılma özelliği vardır.
\( A \times (B - C) = (A \times B) - (A \times C) \)
Yukarıdaki örnekteki kümeleri kullanalım.
\( A \times (B - C) = A \times \{ 2 \} \)
\( = \{ (a, 2), (b, 2), (c, 2) \} \)
\( (A \times B) - (A \times C) = \)
\( \{ (a, 1), (a, 2), (b, 1), \) \( (b, 2), (c, 1), (c, 2) \} - \)
\( \{ (a, 1), (a, 3), (b, 1), \) \( (b, 3), (c, 1), (c, 3) \} \)
\( = \{ (a, 2), (b, 2), (c, 2) \} \)
İSPATI GÖSTER
İlk olarak \( A \times (B - C) \subseteq (A \times B) - (A \times C) \) olduğunu gösterelim.
\( (x, y) \in A \times (B - C) \) alalım.
Bu durumda \( x \in A \) ve \( y \in (B - C) \) olur.
\( y \in (B - C) \Rightarrow y \in B \land y \notin C \)
\( x \in A \land (y \in B \land y \notin C) \) olur.
\( \equiv (x \in A \land y \in B) \land (x \in A \land y \notin C) \)
\( \equiv (x, y) \in (A \times B) \land (x, y) \notin (A \times C) \)
\( \equiv (x, y) \in (A \times B) - (A \times C) \) olur. \( \textcolor{red}{(1)} \)
Şimdi \( (A \times B) - (A \times C) \subseteq A \times (B - C) \) olduğunu gösterelim.
\( (x, y) \in (A \times B) - (A \times C) \) alalım.
Bu durumda \( (x, y) \in (A \times B) \land (x, y) \notin (A \times C) \) olur.
\( (x, y) \in (A \times B) \Rightarrow x \in A \land y \in B \)
\( x \in A \) olduğunu yukarıda bulduğumuz için \( y \notin C \) olur.
\( (x, y) \notin (A \times C) \Rightarrow x \in A \land y \not\in C \)
\( x \in A \land (y \in B \land y \notin C) \)
\( \equiv x \in A \land y \in (B - C) \)
\( \equiv (x, y) \in A \times (B - C) \) olur. \( \textcolor{red}{(2)} \)
Yukarıda kırmızı ile işaretlediğimiz \( (1) \) ve \( (2) \)'den \( A \times (B - C) = (A \times B) - (A \times C) \) olur.
Kartezyen Çarpımı İşlem Kuralları
Bir kümenin boş küme ile kartezyen çarpımı yine boş kümedir.
\( A \times \emptyset = \emptyset \times A = \emptyset \)
\( A \) ve \( B \) kümelerinin birer alt kümesi olan iki kümenin kartezyen çarpımı, \( A \) ve \( B \) kümelerinin kartezyen çarpımının alt kümesidir.
\( C \subseteq A \) ve \( D \subseteq B \) olmak üzere,
\( C \times D \subseteq A \times B \)
İSPATI GÖSTER
\( (c, d) \in C \times D \) olsun.
Bu durumda \( c \in C \) ve \( d \in D \) olur.
\( C \subseteq A \) ve \( D \subseteq B \) olduğu için \( c \) ve \( d \) sırasıyla \( A \) ve \( B \)'nin de birer elemanı olur.
\( c \in A \) ve \( d \in B \) olur.
Bunun bir sonucu olarak \( (c, d) \) sıralı ikilisi \( A \times B \) kartezyen çarpımının da bir elemanı olur.
\( (c, d) \in A \times B \)
\( C \times D \) çarpımının elemanı olan her sıralı ikilinin \( A \times B \) kartezyen çarpımının da bir elemanı olduğunu göstermiş olduk. Buna göre \( C \times D \) kartezyen çarpımı \( A \times B \) çarpımının bir alt kümesidir.
\( C \times D \subseteq A \times B\)
Aşağıdaki gibi dört kümenin kesişim kümelerinin kartezyen çarpımı, kartezyen çarpımlarının kesişim kümesine eşittir.
\( (A_1 \cap A_2) \times (B_1 \cap B_2) \) \( = (A_1 \times B_1) \) \( \cap (A_2 \times B_2) \)
İSPATI GÖSTER
\( (A_1 \cap A_2) \times (B_1 \cap B_2) = (A_1 \times B_1) \cap (A_2 \times B_2) \)
\( (a, b) \) sıralı ikilisi \( A_1 \cap A_2 \) ve \( B_1 \cap B_2 \) kümelerinin kartezyen çarpım kümesinin bir elemanı olsun.
\( (a, b) \in (A_1 \cap A_2) \times (B_1 \cap B_2) \)
Bu ifadeyi sıralı ikilinin birinci bileşeni olan \( a \)'nın \( A_1 \) ve \( A_2 \) kümelerinin ortak elemanı, ikinci bileşeni olan \( b \)'nin de \( B_1 \) ve \( B_2 \) kümelerinin ortak elemanı olduğunu gösteren bir bileşik önerme şeklinde yazabiliriz.
\( (a \in A_1 \land a \in A_2) \land (b \in B_1 \land b \in B_2) \)
"Ve" bağlacının birleşme ve değişme özellikleri olduğu için önermelerin sırasını değiştirebiliriz.
\( (a \in A_1 \land b \in B_1) \land (a \in A_2 \land b \in B_2) \)
\( a \in A_1 \) ve \( b \in B_1 \) olduğuna göre, kartezyen çarpım tanımı gereği \( (a, b) \in A_1 \times B_1 \) olacaktır. Aynı şekilde, \( a \in A_2 \) ve \( b \in B_2 \) olduğuna göre, \( (a, b) \in A_2 \times B_2 \) olacaktır.
\( ((a, b) \in A_1 \times B_1) \land ((a, b) \in A_2 \times B_2) \)
\( (a, b) \) hem \( A_1 \times B_1 \) hem de \( A_2 \times B_2 \) kartezyen çarpım kümelerinin elemanı ise, bu iki kartezyen çarpım kümesinin kesişiminin de elemanıdır.
\( (a, b) \in (A_1 \times B_1) \cap (A_2 \times B_2) \)
Buna göre, takip ettiğimiz adımlar gereği ispatın en başında \( (a, b) \) sıralı ikilisinin elemanı olduğunu söylediğimiz küme, ispatın sonunda elde ettiğimiz kümeye eşittir.
\( (A_1 \cap A_2) \times (B_1 \cap B_2) = (A_1 \times B_1) \cap (A_2 \times B_2) \)
Üç Kümenin Kartezyen Çarpımı
\( A \), \( B \) ve \( C \) kümelerinin kartezyen çarpımı, birinci bileşeni \( A \) kümesinden, ikinci bileşeni \( B \) kümesinden, üçüncü bileşeni \( C \) kümesinden alınmak üzere, yazılabilecek tüm \( (a, b, c) \) sıralı üçlülerinin kümesidir. \( A \), \( B \) ve \( C \) kümelerinin kartezyen çarpımı \( A \times B \times C \) ile gösterilir.
\( A = \{a, b, c\} \)
\( B = \{1, 2\} \)
\( C = \{x, y\} \)
\( A \times B \times C = \{ \)
\( \quad (a, 1, x), (a, 1, y), (a, 2, x), (a, 2, y), \)
\( \quad (b, 1, x), (b, 1, y), (b, 2, x), (b, 2, y), \)
\( \quad (c, 1, x), (c, 1, y), (c, 2, x), (c, 2, y) \)
\( \} \)
\( A \), \( B \) ve \( C \) kümelerinin kartezyen çarpım kümesinin eleman sayısı üç kümenin eleman sayılarının çarpımına eşittir.
\( s(A \times B \times C) = s(A) \cdot s(B) \cdot s(C) \)
Yukarıdaki örnek için:
\( s(A \times B \times C) = s(A) \cdot s(B) \cdot s(C) \)
\( = 3 \cdot 2 \cdot 2 = 12 \)
\( K = \{ 1, 2, 3, 4 \} \)
\( L = \{ 2, 3, 4 \} \)
\( M = \{ 3, 4, 5 \} \)
olduğuna göre, \( (K \cap L) \times (L - M) \) kümesi nedir?
Çözümü Göster\( K \cap L = \{ 2, 3, 4 \} \)
\( L - M = \{ 2 \} \)
\( (K \cap L) \times (L - M) = \{ (2, 2), (3, 2), (4, 2) \} \)
\( K \times L = \{ (a, 1), (b, 1), \) \( (c, 1), (a, 2), \) \( (b, 2), (c, 2) \} \)
\( M \times N = \{ (4, x), (5, x), \) \( (4, y), (5, y), \) \( (4, z), (5, z) \} \)
olduğuna göre, \( M \times L \) kümesi nedir?
Çözümü Göster\( K \times L \) kümesinin sıralı ikililerinin ikinci bileşenleri \( L \) kümesini oluşturur.
\( L = \{ 1, 2 \} \)
\( M \times N \) kümesinin sıralı ikililerinin birinci bileşenleri \( M \) kümesini oluşturur.
\( M = \{ 4, 5 \} \)
\( M \times L = \{ (4, 1), (4, 2), (5, 1), (5, 2 ) \} \)
\( A = \{-2, -1, 0, 1, 2, 4\} \) olduğuna göre,
\( A \times A \) kartezyen çarpım kümesinin elemanlarının kaçında ikinci bileşen birinci bileşenin karesine eşittir?
Çözümü GösterBir sayının karesi negatif olamayacağı için ikinci bileşen negatif olamaz.
İkinci bileşenin her olası değeri için koşulu sağlayan sıralı ikilileri listeleyelim.
\( (x, 0) \) için \( \{(0, 0)\} \)
\( (x, 1) \) için \( \{(1, 1), (-1, 1)\} \)
\( (x, 2) \) için \( \emptyset \)
\( (x, 4) \) için \( \{(2, 4), (-2, 4)\} \)
Buna göre istenen koşulu sağlayan sıralı ikili sayısı 5'tir.
\( A = \{ x \mid -2 \le x \le 2, x \in \mathbb{Z} \} \)
\( s[(A \times B) \cup (A \times C)] = 45 \)
olduğuna göre, \( s(B \cup C) \) kaçtır?
Çözümü GösterKartezyen çarpımının kesişim, birleşim ve fark işlemleri üzerinde dağılma özelliği vardır.
\( (A \times B) \cup (A \times C) = A \times (B \cup C) \)
\( A = \{ -2, -1, 0, 1, 2 \} \)
\( s(A) = 5 \)
İki kümenin kartezyen çarpımının eleman sayısı, kümelerin eleman sayılarının çarpımına eşittir.
\( s[A \times (B \cup C)] = s(A) \cdot s(B \cup C) = 45 \)
Buna göre \( s(B \cup C) = 9 \) bulunur.
\( s(A - B) = 4 \)
\( s(A \cap B) = 2 \)
\( s[(B \times A) \cup (A \times A)] = 48 \)
olduğuna göre, \( s(B - A) \) kaçtır?
Çözümü Göster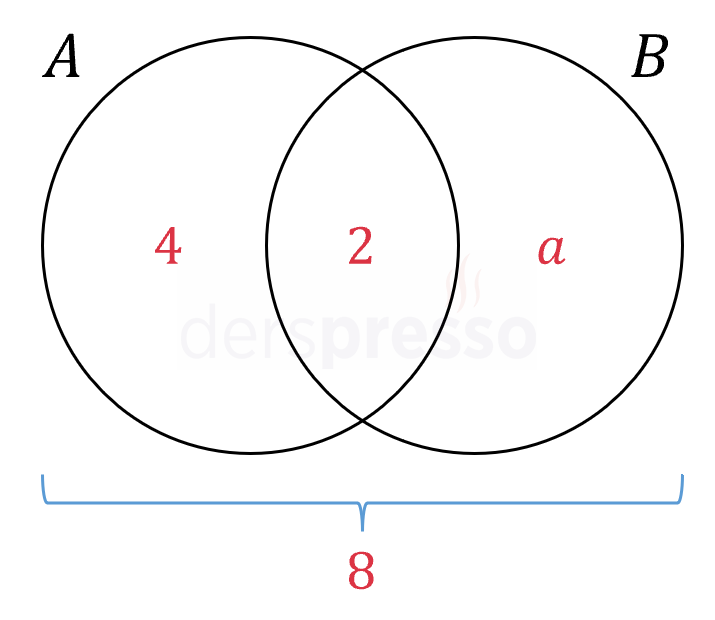
Ayrık \( A - B \) ve \( A \cap B \) kümelerinin birleşimi \( A \) kümesine eşittir.
\( s(A) = 4 + 2 = 6 \)
Kartezyen çarpımının kesişim, birleşim ve fark işlemleri üzerinde dağılma özelliği vardır.
\( (B \times A) \cup (A \times A) = (B \cup A) \times A \)
İki kümenin kartezyen çarpımının eleman sayısı, kümelerin eleman sayılarının çarpımına eşittir.
\( s[(B \cup A) \times A] = s(B \cup A) \cdot s(A) = 48 \)
Buna göre \( s(B \cup A) = 8 \) olur.
\( s(B - A) = s(B \cup A) - s(A) = a \)
\( = 8 - 6 = 2 \) bulunur.
\( A = \{ 1, 2, 3, 6 \} \)
\( B = \{ 6, 1 \} \) olduğuna göre,
\( A \times B \) kartezyen çarpım kümesinin alt kümelerinden kaç tanesinde \( (2, 6) \) ikilisi vardır?
Çözümü Göster\( A \times B \) kümesi \( 4 \cdot 2 = 8 \) elemanlıdır ve bu elemanlardan biri \( (2, 6) \) sıralı ikilisidir.
\( A \times B \) kümesinin \( (2, 6) \) dışındaki 7 elemanı ile \( 2^7 = 128 \) alt küme oluşturulabilir.
Bu 128 alt kümeye sonradan \( (2, 6) \) elemanını ekleyebileceğimizi düşünürsek \( A \times B \) kümesinin 128 alt kümesinde \( (2, 6) \) elemanı bulunur.
\( A \) ve \( B \) birer kümedir.
\( s(A \times B) = 28 \)
\( s(B \times B) = 49 \)
olduğuna göre, \( s(A \times A) \) kaçtır?
Çözümü Gösterİki kümenin kartezyen çarpımının eleman sayısı, kümelerin eleman çarpımlarının sayısına eşittir.
\( s(B \times B) = s(B) \cdot s(B) = 49 \)
\( s(B) = 7 \)
\( s(A \times B) = s(A) \cdot s(B) = 28 \)
\( s(A) \cdot 7 = 28 \)
\( s(A) = 4 \)
Buna göre \( s(A \times A) = s(A) \cdot s(A) = 16 \) bulunur.
\( K \), \( L \) ve \( M \) birer kümedir.
\( s(K \times L) = 11, s(K \times M) = 19 \)
olduğuna göre, \( s(L \times M) \) kaçtır?
Çözümü Gösterİki kümenin kartezyen çarpımının eleman sayısı, kümelerin eleman çarpımlarının sayısına eşittir.
\( s(K \times L) = s(K) \cdot s(L) = 11 \)
11 asal sayı olduğu için pozitif tam sayı çarpanları sadece 1 ve 11 olabilir.
\( s(K \times M) = s(K) \cdot s(M) = 19 \)
19 asal sayı olduğu için pozitif tam sayı çarpanları sadece 1 ve 19 olabilir.
Yukarıdaki iki eşitlikte ortak çarpan \( s(K) \) olduğu için \( s(K) = 1 \) olmalıdır.
Buna göre \( s(L) = 11 \) ve \( s(M) = 19 \) olur.
\( s(L \times M) = s(L) \cdot s(M) = 11 \cdot 19 = 209 \) bulunur.
\( K = \{a, b, c, d\} \)
\( L = \{\{1\}, 2, 4, 5\} \)
\( M = \{x, \{y\}, \{\{t\}\}\} \)
kümeleri için aşağıdakilerin hangileri yanlıştır?
I. \( (a, b) \) ikilisi \( K \times K \) kümesinin bir elemanıdır.
II. \( (b, 1) \) ikilisi \( K \times L \) kümesinin bir elemanıdır.
III. \( (\{1\}, \{y\}) \) ikilisi \( L \times M \) kümesinin bir elemanıdır.
IV. \( (c, x) \) ikilisi \( M \times K \) kümesinin bir elemanıdır.
V. \( (a, a) \) ikilisi \( K \times K \) kümesinin bir elemanıdır.
VI. \( (\{t\}, 4) \) ikilisi \( M \times L \) kümesinin bir elemanıdır.
Çözümü Göster\( a, b \in K \) olduğu için \( (a, b) \in K \times K \) olur. I. öncül doğrudur.
\( 1 \notin L \) ve \( \{1\} \in L \) olduğu için \( (b, 1) \notin K \times L \) olur. II. öncül yanlıştır.
\( \{1\} \in L \) ve \( \{y\} \in M \) olduğu için \( (\{1\}, \{y\}) \in L \times M \) olur. III. öncül doğrudur.
\( c \in K \) ve \( x \in M \) olduğu için \( (c, x) \notin M \times K \) ve \( (c, x) \in K \times M \) olur. IV. öncül yanlıştır.
\( a \in K \) olduğu için \( (a, a) \in K \times K \) olur. V. öncül doğrudur.
\( \{t\} \notin M \) ve \( \{\{t\}\} \in M \) olduğu için \( (\{t\}, 4) \notin M \times L \) olur. VI. öncül yanlıştır.
Buna göre II., IV. ve VI. öncüller yanlıştır.
\( K \) ve \( L \) birer kümedir.
\( s(K \times K) - s(L \times L) = 31 \)
olduğuna göre, \( s(K \cup L) \) en az kaçtır?
Çözümü Göster\( s(K \times K) - s(L \times L) = 31 \)
İki kümenin kartezyen çarpımının eleman sayısı, kümelerin eleman çarpımlarının sayısına eşittir.
\( s(K) \cdot s(K) - s(L) \cdot s(L) = 31 \)
\( [s(K)]^2 - [s(L)]^2 = 31 \)
İki kare farkı özdeşliğini kullanalım.
\( (s(K) - s(L))(s(K) + s(L)) = 31 \)
31 asal sayı olduğu için pozitif tam sayı çarpanları sadece 1 ve 31 olabilir.
Buna göre iki kümenin eleman sayılarının toplamı 31, farkı 1 olur.
\( s(K) + s(L) = 31 \)
\( s(K) - s(L) = 1 \)
Buradan \( s(K) = 16 \) ve \( s(L) = 15 \) bulunur.
\( s(K \cup L) \) kümesinin en düşük değeri \( L \subset K \) olduğunda oluşur.
O halde \( L \subset K \) için \( s(K \cup L) = 16 \) bulunur.
\( A = \{a, b, c, d, e, f\} \)
\( A \) kümesinin birer alt kümesi olan \( B \) ve \( C \) kümeleri için \( \{a, b\} \subseteq B \) ve \( \{f\} \subseteq C \) veriliyor.
Buna göre, yazılabilecek farklı \( B \) ve \( C \) kümelerinin kartezyen çarpımlarının kaçında eleman sayısı bir tam kare sayı olur?
Çözümü GösterFarklı eleman sayılarında kaç farklı \( B \) ve \( C \) kümesi yazılabileceğini bulalım.
\( \{a, b\} \subseteq B \subseteq A \)
Buna göre \( B \) kümesi \( \{c, d, e, f\} \) kümesinin elemanlarını içerip içermemesine göre \( 2^4 = 16 \) farklı şekilde olabilir.
\( C(4, 0) = 1 \) farklı 2 elemanlı \( B \) kümesi yazılabilir.
\( C(4, 1) = 4 \) farklı 3 elemanlı \( B \) kümesi yazılabilir.
\( C(4, 2) = 6 \) farklı 4 elemanlı \( B \) kümesi yazılabilir.
\( C(4, 3) = 4 \) farklı 5 elemanlı \( B \) kümesi yazılabilir.
\( C(4, 4) = 1 \) farklı 6 elemanlı \( B \) kümesi yazılabilir.
\( \{f\} \subseteq C \subseteq A \)
Buna göre \( C \) kümesi \( \{a, b, c, d, e\} \) kümesinin elemanlarını içerip içermemesine göre \( 2^5 = 32 \) farklı şekilde olabilir.
\( C(5, 0) = 1 \) farklı 1 elemanlı \( C \) kümesi yazılabilir.
\( C(5, 1) = 5 \) farklı 2 elemanlı \( C \) kümesi yazılabilir.
\( C(5, 2) = 10 \) farklı 3 elemanlı \( C \) kümesi yazılabilir.
\( C(5, 3) = 10 \) farklı 4 elemanlı \( C \) kümesi yazılabilir.
\( C(5, 4) = 5 \) farklı 5 elemanlı \( C \) kümesi yazılabilir.
\( C(5, 5) = 1 \) farklı 6 elemanlı \( C \) kümesi yazılabilir.
\( B \times C \) kartezyen çarpım kümesinin eleman sayısı aşağıdaki durumlarda bir tam kare sayı olur.
Durum 1: \( s(B) = 2, s(C) = 2 \)
\( s(B \times C) = s(B) \cdot s(C) = 4 \)
Bu şekilde \( 1 \cdot 5 = 5 \) farklı kartezyen çarpım kümesi yazılabilir.
Durum 2: \( s(B) = 3, s(C) = 3 \)
\( s(B \times C) = s(B) \cdot s(C) = 9 \)
Bu şekilde \( 4 \cdot 10 = 40 \) farklı kartezyen çarpım kümesi yazılabilir.
Durum 3: \( s(B) = 4, s(C) = 4 \)
\( s(B \times C) = s(B) \cdot s(C) = 16 \)
Bu şekilde \( 6 \cdot 10 = 60 \) farklı kartezyen çarpım kümesi yazılabilir.
Durum 4: \( s(B) = 5, s(C) = 5 \)
\( s(B \times C) = s(B) \cdot s(C) = 25 \)
Bu şekilde \( 4 \cdot 5 = 20 \) farklı kartezyen çarpım kümesi yazılabilir.
Durum 5: \( s(B) = 6, s(C) = 6 \)
\( s(B \times C) = s(B) \cdot s(C) = 36 \)
Bu şekilde \( 1 \cdot 1 = 1 \) farklı kartezyen çarpım kümesi yazılabilir.
Durum 6: \( s(B) = 4, s(C) = 1 \)
\( s(B \times C) = s(B) \cdot s(C) = 4 \)
Bu şekilde \( 6 \cdot 1 = 6 \) farklı kartezyen çarpım kümesi yazılabilir.
Tüm durumların toplamını alalım.
\( = 5 + 40 + 60 + 20 + 1 + 6 \)
\( = 132 \) bulunur.