Determinant
Determinant kare matrisler için hesaplanan reel sayı bir değerdir ve matrislerin tersinin bulunmasında ve lineer denklem sistemlerinin çözümünde kullanılır.
Bir matrisin determinantı \( det(A) \) veya \( \abs{A} \) şeklinde gösterilir. Determinant \( \abs{A} \) şeklinde gösterildiği durumlarda mutlak değer ile karıştırılmamalıdır. Ayrıca determinant mutlak değerden farklı olarak negatif değer alabilen bir büyüklüktür.
Determinant Hesaplama
Bir matrisinin determinantını hesaplamak oldukça fazla işlem gerektirebilir. \( 3 \times 3 \) ve daha küçük boyutlu matrislerin determinantı için hatırlaması kolay formül ve yöntemler mevcuttur. Daha büyük matrislerin determinantı için kullanabileceğimiz yöntemlerden önümüzdeki bölümlerde bahsedeceğiz.
\( 1 \times 1 \) Matrisin Determinantı
\( 1 \times 1 \) bir matrisin determinantı matrisin tek elemanına eşittir.
\( A = \begin{bmatrix} a \end{bmatrix} \) olmak üzere,
\( det(A) = a \)
\( A = \begin{bmatrix} 3 \end{bmatrix} \) olmak üzere,
\( det(A) = 3 \)
\( 2 \times 2 \) Matrisin Determinantı
\( 2 \times 2 \) bir matrisin determinantı aşağıdaki şekilde yeşil ok üzerindeki iki elemanın çarpımı ile kırmızı ok üzerindeki iki elemanın çarpımının farkına eşittir.

\( det(A) = ad - cb \)
\( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \) olmak üzere,
\( det(A) = 1 \cdot 4 - 3 \cdot 2 = -2 \)
\( 3 \times 3 \) Matrisin Determinantı
Sarrus kuralı olarak bilinen yönteme göre, \( 3 \times 3 \) bir matrisin determinantını bulmak için önce ilk iki sütundaki elemanlar matrisin sağına \( 3 \times 5 \) bir matris oluşturacak şekilde kopyalanır. Matrisin determinantı yeşil oklar üzerindeki elemanların çarpımlarının toplamı ile kırmızı oklar üzerindeki elemanların çarpımlarının toplamının farkına eşittir.
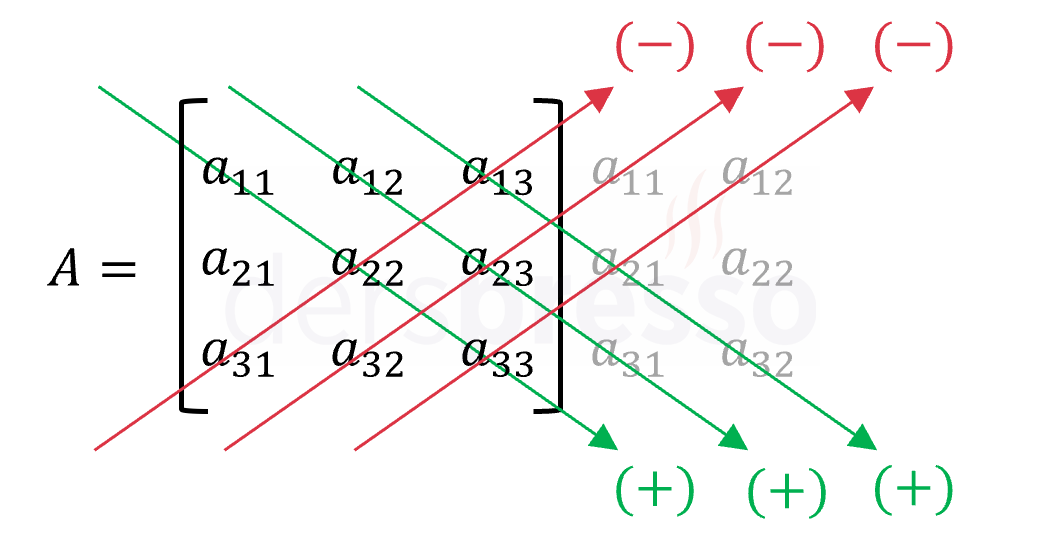
\( det(A) = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} \) \( + a_{13}a_{21}a_{32} \) \( - (a_{31}a_{22}a_{13} \) \( + a_{32}a_{23}a_{11} \) \( + a_{33}a_{21}a_{12}) \)
\( A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \) olmak üzere,
\( det(A) = 1 \cdot 5 \cdot 9 + 2 \cdot 6 \cdot 7 \) \( + 3 \cdot 4 \cdot 8 \) \( - (7 \cdot 5 \cdot 3 \) \( + 8 \cdot 6 \cdot 1 \) \( + 9 \cdot 4 \cdot 2) \)
\( = 45 + 84 + 96 - 105 - 48 - 72 \)
\( = 0 \)
Determinantın Özellikleri
Determinantın bazı özellikleri aşağıdaki gibidir.
Birim matrislerin determinantı 1'dir.
\( det(I_m) = 1 \)
\( I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \)
\( det(I_3) = 1 \cdot 1 \cdot 1 + 0 \cdot 0 \cdot 0 \) \( + 0 \cdot 0 \cdot 0 \) \( - (0 \cdot 1 \cdot 0 \) \( + 0 \cdot 0 \cdot 1 \) \( + 1 \cdot 0 \cdot 0) \)
\( = 1 \)
\( m \times m \) bir matrisin bir \( k \) reel sayısı ile skaler çarpımının determinantı, matrisin determinantının \( k^m \) katına eşittir.
\( det(kA) = k^m \cdot det(A) \)
\( 4I_3 = \begin{bmatrix} 4 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 4 \end{bmatrix} \)
\( det(4I_3) = 4 \cdot 4 \cdot 4 + 0 \cdot 0 \cdot 0 \) \( + 0 \cdot 0 \cdot 0 \) \( - (0 \cdot 4 \cdot 0 \) \( + 0 \cdot 0 \cdot 4 \) \( + 4 \cdot 0 \cdot 0) \)
\( = 4^3 = 64 \)
İki matrisin çarpımlarının determinantı matrislerin determinantlarının çarpımına eşittir.
\( det(AB) = det(A) \cdot det(B) \)
\( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)
\( det(A) = 1 \cdot 4 - 3 \cdot 2 = -2 \)
\( B = \begin{bmatrix} 2 & 4 \\ -3 & -1 \end{bmatrix} \)
\( det(B) = 2 \cdot (-1) - (-3) \cdot 4 = 10 \)
\( AB = \begin{bmatrix} 1 \cdot 2 + 2 \cdot (-3) & 1 \cdot 4 + 2 \cdot (-1) \\ 3 \cdot 2 + 4 \cdot (-3) & 3 \cdot 4 + 4 \cdot (-1) \end{bmatrix} \)
\( = \begin{bmatrix} -4 & 2 \\ -6 & 8 \end{bmatrix} \)
\( det(AB) = -4 \cdot 8 - (-6) \cdot 2 = -20 \)
Bir matrisin kuvvetinin determinantı matrisin determinantının kuvvetine eşittir.
\( det(A^n) = [det(A)]^n \)
Bir matrisin ve transpozunun determinantları birbirine eşittir.
\( det(A^T) = det(A) \)
Bir matrisin tersinin determinantı o matrisin determinantının çarpmaya göre tersine eşittir.
\( det(A) \ne 0 \) olmak üzere,
\( det(A^{-1}) = \dfrac{1}{det(A)} \)
Bir (üst ya da alt) üçgen matrisin determinantı ana köşegeni üzerindeki elemanların çarpımına eşittir.
\( A = \begin{bmatrix} \textcolor{red}{3} & 0 & 0 \\ 5 & \textcolor{red}{-2} & 0 \\ 2 & -4 & \textcolor{red}{6} \end{bmatrix} \)
\( det(A) = 3 \cdot (-2) \cdot 6 = -36 \)
Tüm elemanları sıfır olan bir satır (ya da sütun) içeren matrisin determinantı sıfırdır.
\( A = \begin{bmatrix} a & b & c \\ \textcolor{red}{0} & \textcolor{red}{0} & \textcolor{red}{0} \\ d & e & f \end{bmatrix} \)
\( det(A) = 0 \)
İki satırının (ya da sütununun) tüm elemanları arasında sabit bir orantı olan matrisin determinantı sıfırdır.
\( A = \begin{bmatrix} a & b & c \\ d & e & f \\ \textcolor{red}{2a} & \textcolor{red}{2b} & \textcolor{red}{2c} \end{bmatrix} \)
\( det(A) = 0 \)
Orantı sabitinin 1 olduğu durum için, birbirinin aynısı iki satırı (ya da sütunu) olan matrisin determinantı sıfırdır.
\( A = \begin{bmatrix} a & b & c \\ d & e & f \\ \textcolor{red}{a} & \textcolor{red}{b} & \textcolor{red}{c} \end{bmatrix} \)
\( det(A) = 0 \)