Matris Tanımı

Sayıların bir tablo oluşturacak şekilde satır ve sütunlar halinde düzenlenmiş haline matris denir.

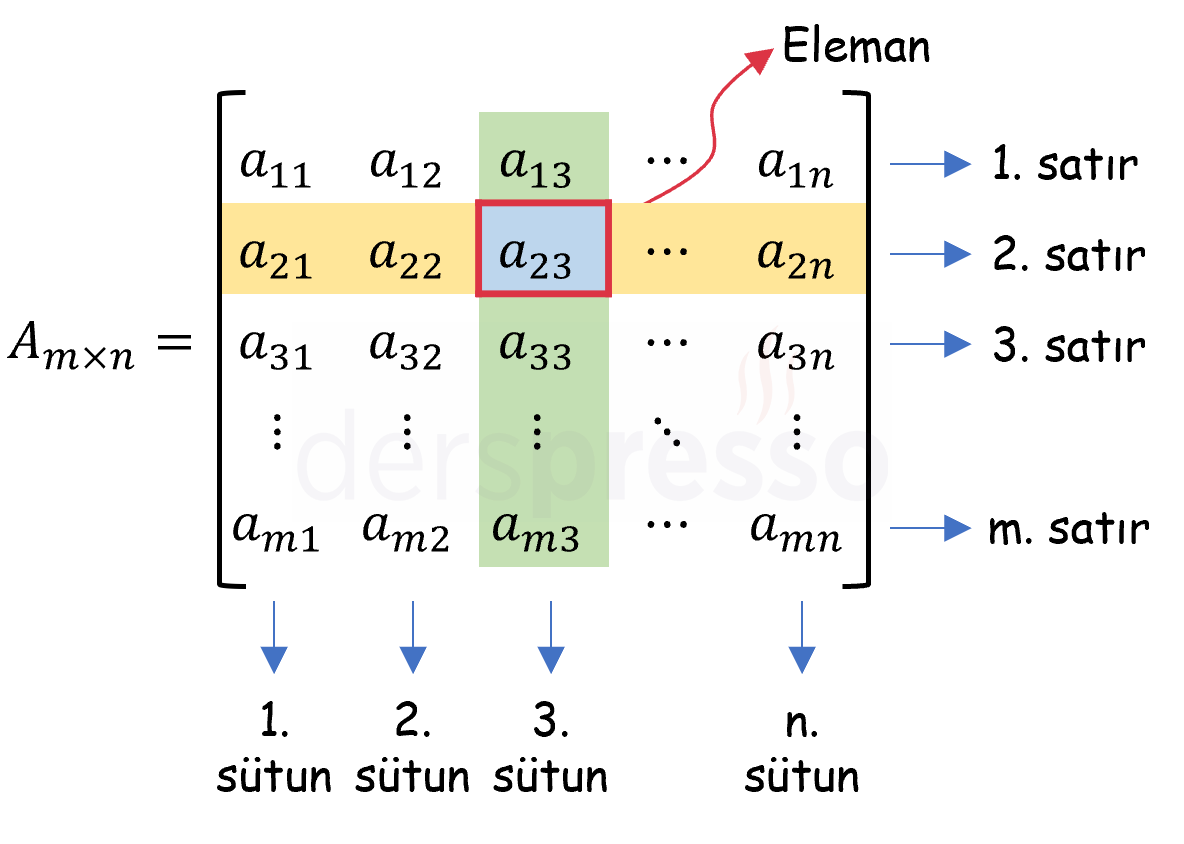
Yukarıdaki örnek üzerinden matrisleri daha detaylı şekilde aşağıdaki gibi tanımlayabiliriz.

• Matrisler genellikle büyük harf ile gösterilirler (\( A, B, C, \ldots \)).
• Matrisin satır ve sütunlarını dolduran sayı, sembol ya da nesnelere matrisin elemanları ya da öğeleri denir.
• Bir matrisin elemanlarını listelemek için genellikle [köşeli] ya da (yuvarlak) parantez kullanılır.
• Bir matriste yatay doğrultuda aynı hizada yer alan elemanların kümesine satır, dikey doğrultuda aynı hizada yer alan elemanların kümesine sütun ya da kolon denir.
• Bir matrisin satırları yukarıdan aşağı doğru, sütunları da soldan sağa doğru 1'den başlayarak numaralandırılır (programlama dillerinde bu numaralandırma 0'dan da başlayabilir).
• Bir matrisin satır ve sütun sayısı o matrisin boyutlarıdır. Matrisler boyutlarına göre isimlendirilirler. Örneğin \( m \) satır ve \( n \) sütundan oluşan bir matris \( m \times n \) bir matristir.
• Bir \( A \) matrisinin \( i \). satırı ve \( j \). sütununun kesişiminde yer alan eleman \( a_{ij} \) ya da \( a_{i,j} \) şeklinde gösterilir.
• \( m \times n \) bir matrisin toplamda \( m \cdot n \) elemanı vardır.

Matrisler reel ya da karmaşık sayı elemanlardan oluşabilir. Biz bu konu anlatımında elemanları reel sayı olan matrisleri inceleyeceğiz.

Ana Köşegen

Bir matrisin \( a_{11} \) elemanı ile başlayarak \( a_{ii} \) şeklindeki, aynı satır ve sütun numaralı elemanlarına matrisin ana köşegeni, asal köşegeni ya da birincil köşegeni denir.

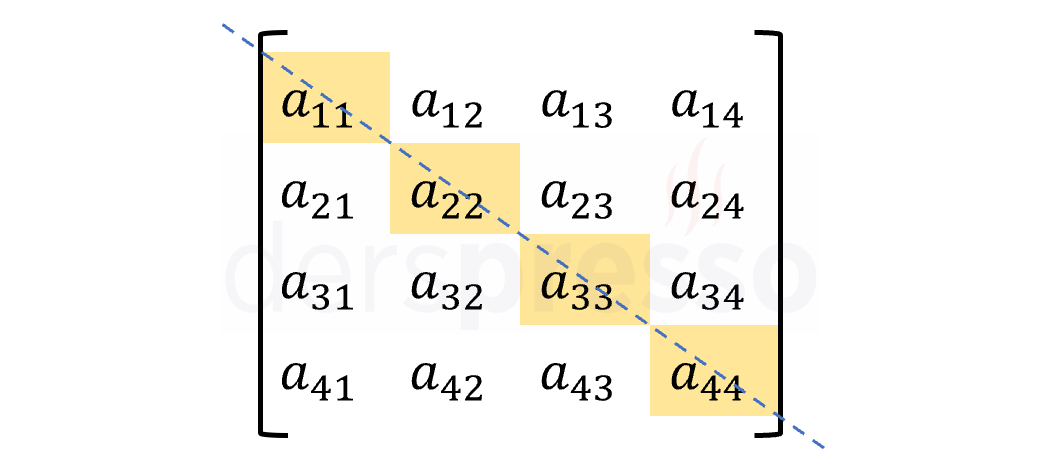
Aşağıdaki matrislerde ana köşegen üzerindeki elemanlar kırmızı ile işaretlenmiştir.

Örnek Bir Matris

Aşağıda örnek bir matris ve bazı özellikleri verilmiştir.