Satır İşlemleri ile Ters Matris Bulma
Konu tekrarı için: Temel Satır İşlemleri | Gauss Eliminasyon Yöntemi | Gauss - Jordan Eliminasyon Yöntemi
Tersi olan kare matrisler aynı boyuttaki birim matrisle satırca denktir. Bir diğer ifadeyle, birim matrisle satırca denk olan matrislerin tersi vardır.
\( A \) matrisi tersi alınabilir bir matris ise,
\( A \sim I \sim A^{-1} \)
Bir \( A \) matrisini birim matrise dönüştürmek için uygulanacak temel satır işlemleri aynı sırada birim matrise uygulandığında \( A^{-1} \) matrisi elde edilir.
Buna göre bir \( A \) matrisinin tersini temel satır işlemleri ile bulmak için aşağıdaki adımlar takip edilir.
- \( A \) matrisi ile aynı boyuttaki birim matris \( A \) matrisi ile yan yana yazılarak \( [\ A\ |\ I\ ] \) şeklinde bir artırılmış matris elde edilir.
- Artırılmış matrisin sol tarafı Gauss - Jordan eliminasyon yöntemi ile birim matris formuna getirilir. Her işlem matrisin sağ tarafındaki ilgili satıra da uygulanır.
- Artırılmış matrisin sol tarafı birim matrise eşit olduğunda matris \( [\ I\ |\ A^{-1}\ ] \) formuna gelmiş olur, yani matrisin sağ tarafı \( A \) matrisinin tersine eşit olur.
Bu yönteme göre artırılmış matrisin sol tarafında birim matris elde edilemiyorsa \( A \) matrisinin tersi yoktur.
Şimdi bu yöntemi kullanarak aşağıdaki matrisin ters matrisini bulalım.
\( A = \begin{bmatrix} 1 & 5 & 0 \\ 2 & 8 & 1 \\ -1 & 0 & -3 \end{bmatrix} \)
| İşlem | Matris |
|---|---|
|
Verilen matrisin sağına aynı boyuttaki birim matrisi ekleyelim. \( [\ A\ |\ I\ ] \) |

|
|
Satır 1:
1. satırın pivotu \( a_{11} = 1 \) elemanıdır. Belirlediğimiz pivotla aynı sütunda bulunan sıfırdan farklı elemanları toplama satır işlemleri ile sıfıra eşitleyelim. \( -2R_1 + R_2 \rightarrow R_2 \) \( R_1 + R_3 \rightarrow R_3 \) |

|
|
Satır 2:
2. satırın pivotu \( a_{22} = -2 \) elemanıdır. Belirlediğimiz pivotla aynı sütunda bulunan sıfırdan farklı elemanları toplama satır işlemleri ile sıfıra eşitleyelim. \( \dfrac{5}{2}R_2 + R_1 \rightarrow R_1 \) \( \dfrac{5}{2}R_2 + R_3 \rightarrow R_3 \) |

|
|
Satır 3:
3. satırın pivotu \( a_{33} = -\frac{1}{2} \) elemanıdır. Belirlediğimiz pivotla aynı sütunda bulunan sıfırdan farklı elemanları toplama satır işlemleri ile sıfıra eşitleyelim. \( 5R_3 + R_1 \rightarrow R_1 \) \( 2R_3 + R_2 \rightarrow R_2 \) |

|
|
Matris köşegen matris formundadır. Matrisi birim matrise dönüştürmek için 2. ve 3. satırın pivotlarını çarpma satır işlemi ile 1'e eşitleyelim. \( -\dfrac{1}{2}R_2 \rightarrow R_2 \) \( -2R_3 \rightarrow R_3 \) Bu işlemler sonucunda matrisin sol tarafı birim matrise eşit olur. Bu noktada matrisin sağ tarafı da \( A \) matrisinin tersini verir. |
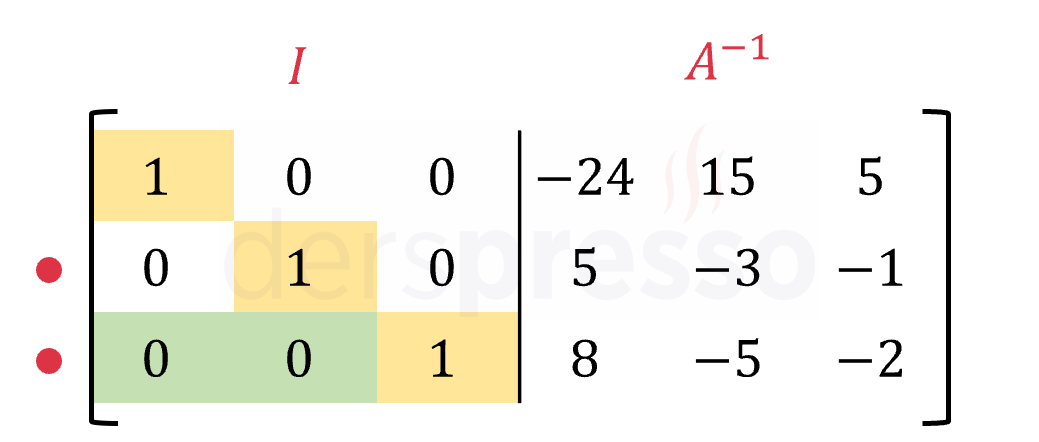
|
Bu yöntemi şu şekilde özetleyebiliriz. Bir \( A \) matrisi tersi olan bir matris ise \( A \) matrisini birim matrise dönüştürmek için uygulanması gereken satır işlemleri aynı sırada birim matrise uygulandığında \( A^{-1} \) matrisi elde edilir.