Limitin Epsilon-Delta Tanımı
Epsilon-delta (\( \varepsilon-\delta \)) tanımı limitin standart ve en doğru tanımı olarak kabul edilir ve önümüzdeki bölümlerde göreceğimiz limit kural ve özelliklerinin ispatlarının temelini teşkil eder.
Bu tanımın anlaşılması ve problemlere uygulanması pek çok öğrenci için hemen mümkün olmayabilir. Özellikle lise seviyesindeki problemlerde ihtiyaç duyulan bir tanım olmadığı düşünülürse, limit konusunun başlarında bu tanımın tam anlaşılmaması bir eksiklik olarak görülmemelidir.
Limitin epsilon-delta tanımı aşağıdaki gibidir.
\( f: A \to \mathbb{R}, \quad a, L \in \mathbb{R} \),
\( A \) reel sayılar kümesinde tanımlı, \( a \) noktasını içeren ya da içermeyen açık bir aralık olmak üzere,
\( \lim\limits_{x \to a} f(x) = L \) limiti,
her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
Her \( x \in A \) değeri için,
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
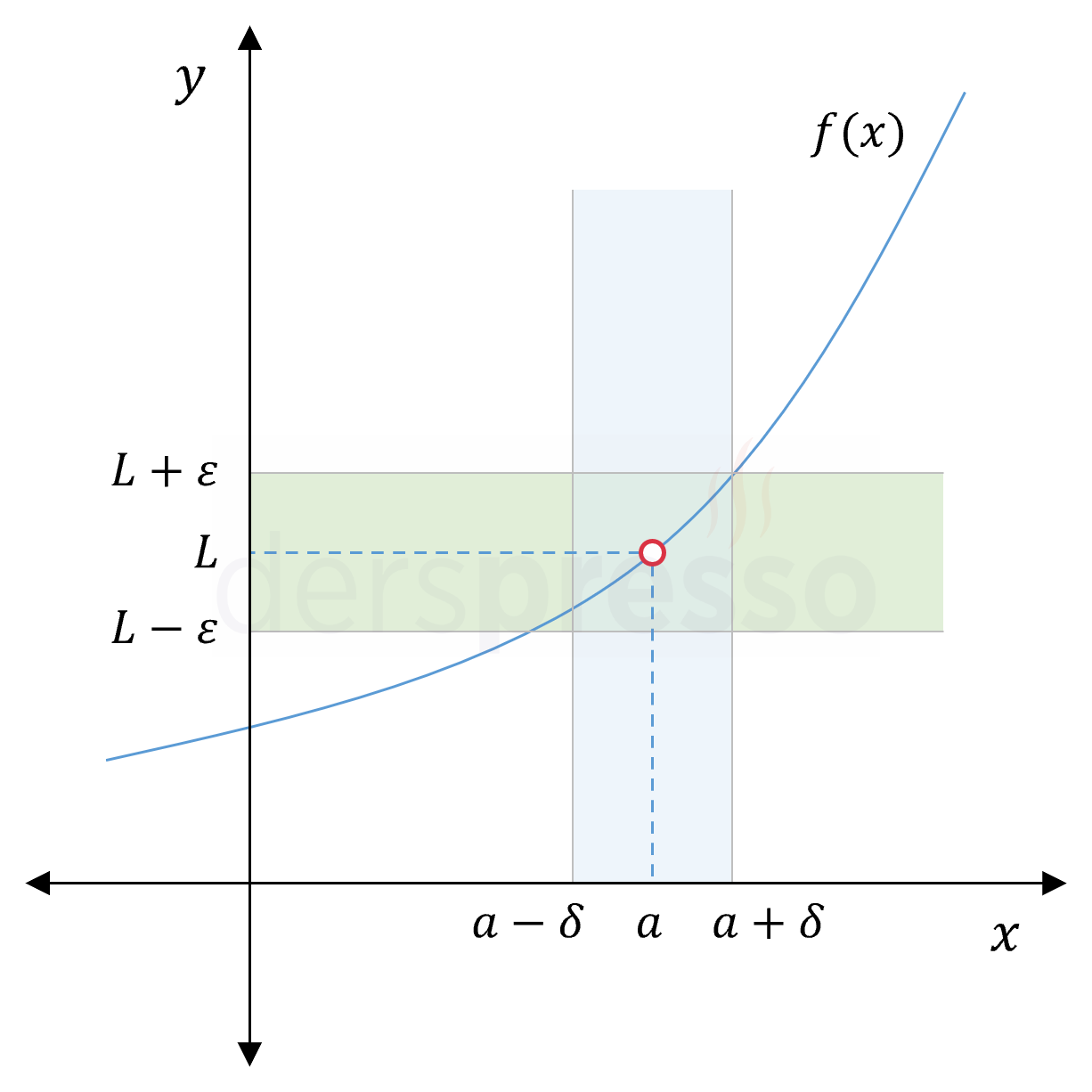
Bu tanımdaki \( \delta \) değeri \( \varepsilon \) değerine bağlı olan ve \( \varepsilon \) cinsinden ifade edilen bir değişkendir, bu yüzden soru ve ispatlarda \( \delta = \delta(\varepsilon) \) şeklinde de ifade edilebilir.
\( \lim\limits_{x \to 3} (4x - 2) = 10 \) limitinin doğruluğunu epsilon-delta tanımını kullanarak gösterelim.
Adım 1: Tanım
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Bu tanımı kullanarak aşağıdaki limitin doğruluğunu gösterelim.
\( \lim\limits_{x \to 3} (4x - 2) = 10 \)
Bu limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - 3} \lt \delta \Longrightarrow \abs{(4x - 2) - 10} \lt \varepsilon \)
Adım 2: \( \delta \) Değerini Bulma
Bu önermeyi her \( \varepsilon \gt 0 \) için sağlayan bir \( \delta = \delta(\varepsilon) \gt 0 \) ifadesi bulmaya çalışalım.
\( \abs{(4x - 2) - 10} \lt \varepsilon \)
\( \abs{4x - 12} \lt \varepsilon \)
\( \abs{4(x - 3)} \lt \varepsilon \)
\( 4\abs{x - 3} \lt \varepsilon \)
\( \abs{x - 3} \lt \delta \) olduğu için, \( 4\abs{x - 3} \) ifadesinin üst sınır değerini \( \delta \) cinsinden \( 4\delta \) şeklinde ifade edebiliriz.
\( 4\abs{x - 3} \lt 4\delta \le \varepsilon \)
Bu durumda her \( \varepsilon \gt 0 \) için önermeyi sağlayacak \( \delta \) değerini aşağıdaki şekilde seçebiliriz.
\( 0 \le \delta \le \dfrac{\varepsilon}{4} \)
Adım 3: İspat
Herhangi bir \( \varepsilon \gt 0 \) verilmiş olsun.
\( \delta = \frac{\varepsilon}{4} \) olarak seçelim ve bu \( \delta \) değeri için aşağıdaki önermenin sağlandığını gösterelim.
\( 0 \lt \abs{x - 3} \lt \delta \Longrightarrow \abs{(4x - 2) - 10} \lt \varepsilon \)
\( 0 \lt \abs{x - 3} \lt \delta \) olarak kabul edelim.
\( \abs{(4x - 2) - 10} = \abs{4x - 12} = 4\abs{x - 3} \)
\( \abs{x - 3} \) ifadesi için üst sınır değeri olarak \( \delta \) kullanabiliriz.
\( 4\abs{x - 3} \lt 4\delta \)
\( \delta = \frac{\varepsilon}{4} \) yazalım.
\( 4\abs{x - 3} \lt 4 \cdot \dfrac{\varepsilon}{4} = \varepsilon \)
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.
\( \lim\limits_{x \to 2} (3x^2 + 7) = 19 \) limitinin doğruluğunu epsilon-delta tanımını kullanarak gösterelim.
Adım 1: Tanım
\( \lim\limits_{x \to a} {f(x)} = L \)
Yukarıdaki limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Bu tanımı kullanarak aşağıdaki limitin doğruluğunu gösterelim.
\( \lim\limits_{x \to 2} (3x^2 + 7) = 19 \)
Bu limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - 2} \lt \delta \Longrightarrow \abs{(3x^2 + 7) - 19} \lt \varepsilon \)
Adım 2: \( \delta \) Değerini Bulma
Bu önermeyi her \( \varepsilon \gt 0 \) için sağlayan bir \( \delta = \delta(\varepsilon) \gt 0 \) ifadesi bulmaya çalışalım.
\( \abs{(3x^2 + 7) - 19} \lt \varepsilon \)
\( \abs{3x^2 - 12} \lt \varepsilon \)
\( \abs{3(x - 2)(x + 2)} \lt \varepsilon \)
\( 3\abs{x - 2}\abs{x + 2} \lt \varepsilon \)
\( \abs{x - 2} \lt \delta \) olduğu için, \( 3\abs{x - 2} \) ifadesinin üst sınır değerini \( \delta \) cinsinden \( 3\delta \) şeklinde ifade edebiliriz.
\( \abs{x + 2} \) ifadesi için bir üst sınır değeri bulabilmek için \( \delta \le 1 \) şeklinde bir üst sınır değeri belirleyelim ve bu doğrultuda oluşan \( \abs{x - 2} \lt \delta = 1 \) aralığı için \( \abs{x + 2} \) ifadesinin en büyük değerini bulalım.
\( \abs{x - 2} \lt 1 \)
\( -1 \lt x - 2 \lt 1 \)
\( 3 \lt x + 2 \lt 5 \)
\( 3 \lt \abs{x + 2} \lt 5 \)
Buna göre \( \abs{x + 2} \) ifadesinin üst sınır değeri 5 olur.
Bulduğumuz üst sınır değerlerini yerine koyalım.
\( 3\abs{x - 2}\abs{x + 2} \lt \varepsilon \)
\( 3\abs{x - 2}\abs{x + 2} \lt 3\delta \cdot 5 \lt \varepsilon \)
\( 3\abs{x - 2}\abs{x + 2} \lt 15\delta \lt \varepsilon \)
Bu durumda her \( \varepsilon \gt 0 \) için önermeyi sağlayacak \( \delta \) değerini aşağıdaki şekilde seçebiliriz.
\( 0 \le \delta \le \min\{1, \frac{\varepsilon}{15}\} \)
Adım 3: İspat
Herhangi bir \( \varepsilon \gt 0 \) verilmiş olsun.
\( \delta \le \min\{1, \frac{\varepsilon}{15}\} \) olarak seçelim ve bu \( \delta \) değeri için aşağıdaki önermenin sağlandığını gösterelim.
\( 0 \lt \abs{x - 2} \lt \delta \Longrightarrow \abs{(3x^2 + 7) - 19} \lt \varepsilon \)
\( 0 \lt \abs{x - 2} \lt \delta \) olarak kabul edelim.
\( \abs{(3x^2 + 7) - 19} = \abs{3x^2 - 12} \)
\( = \abs{3(x - 2)(x + 2)} = 3\abs{x - 2}\abs{x + 2} \)
\( \abs{x - 2} \) ifadesi için üst sınır değeri olarak \( \delta \), \( \abs{x + 2} \) ifadesi için üst sınır değeri olarak \( 5 \) kullanabiliriz.
\( 3\abs{x - 2}\abs{x + 2} \lt 3\delta \cdot 5 \)
\( \delta = \frac{\varepsilon}{15} \) yazalım.
\( 3\abs{x - 2}\abs{x + 2} \lt 3 \cdot \dfrac{\varepsilon}{15} \cdot 5 = \varepsilon \)
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.
Tek Taraflı Limit
Limitin epsilon-delta tanımı tek taraflı limite küçük değişikliklerle aşağıdaki şekilde uyarlanabilir.
Sağdan Limit
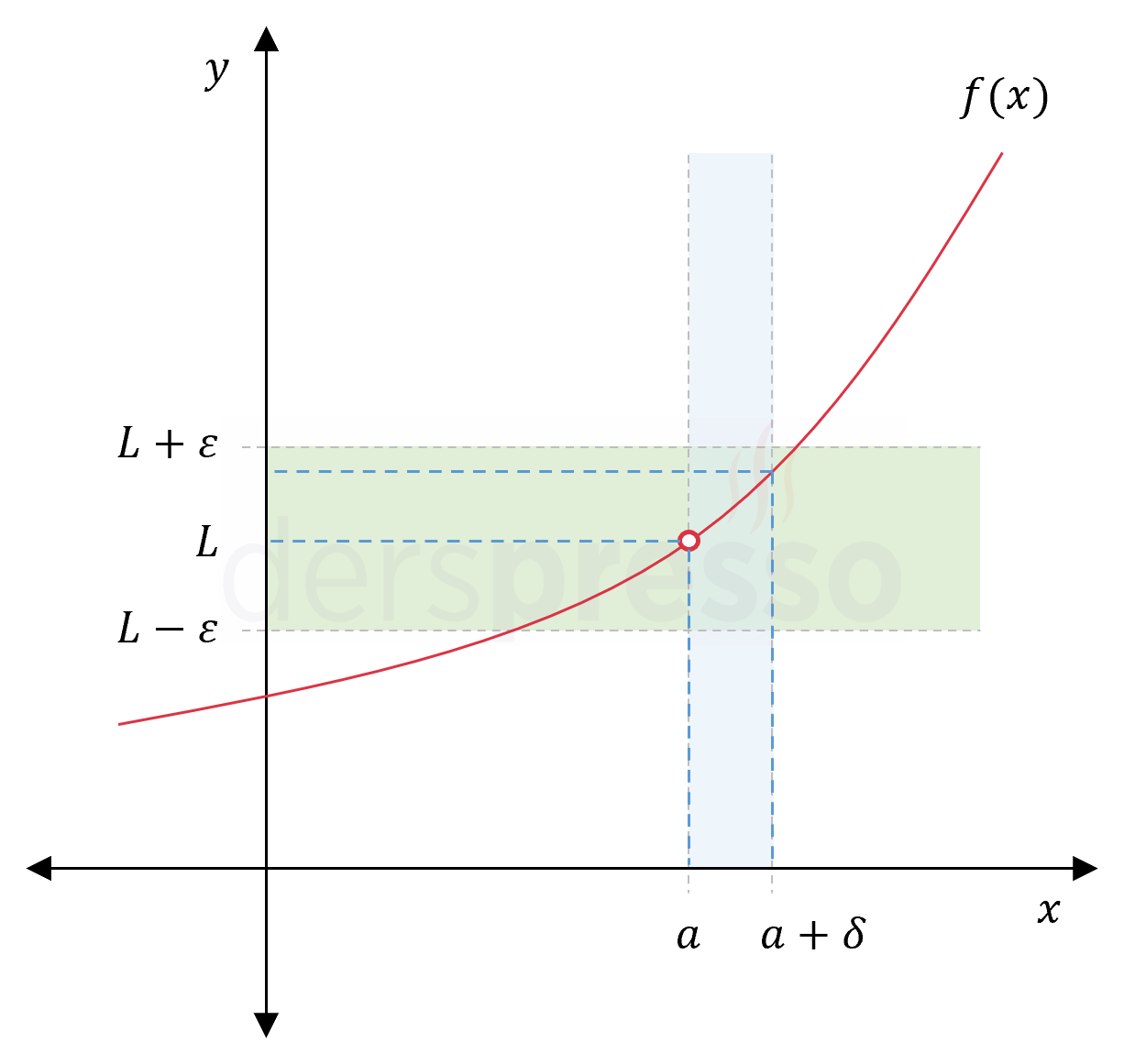
Sağdan limitin epsilon-delta tanımında, \( x \) \( a \)'ya sağdan yaklaştığı için \( 0 \lt \abs{x - a} \lt \delta \) eşitsizliği yerine \( a \lt x \lt a + \delta \) kullanılır.
Yukarıda tanımını yaptığımız \( f \) fonksiyonu için,
\( \lim\limits_{x \to a^+} f(x) = L \) limiti,
her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
Her \( x \in A \) değeri için,
\( a \lt x \lt a + \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Soldan Limit
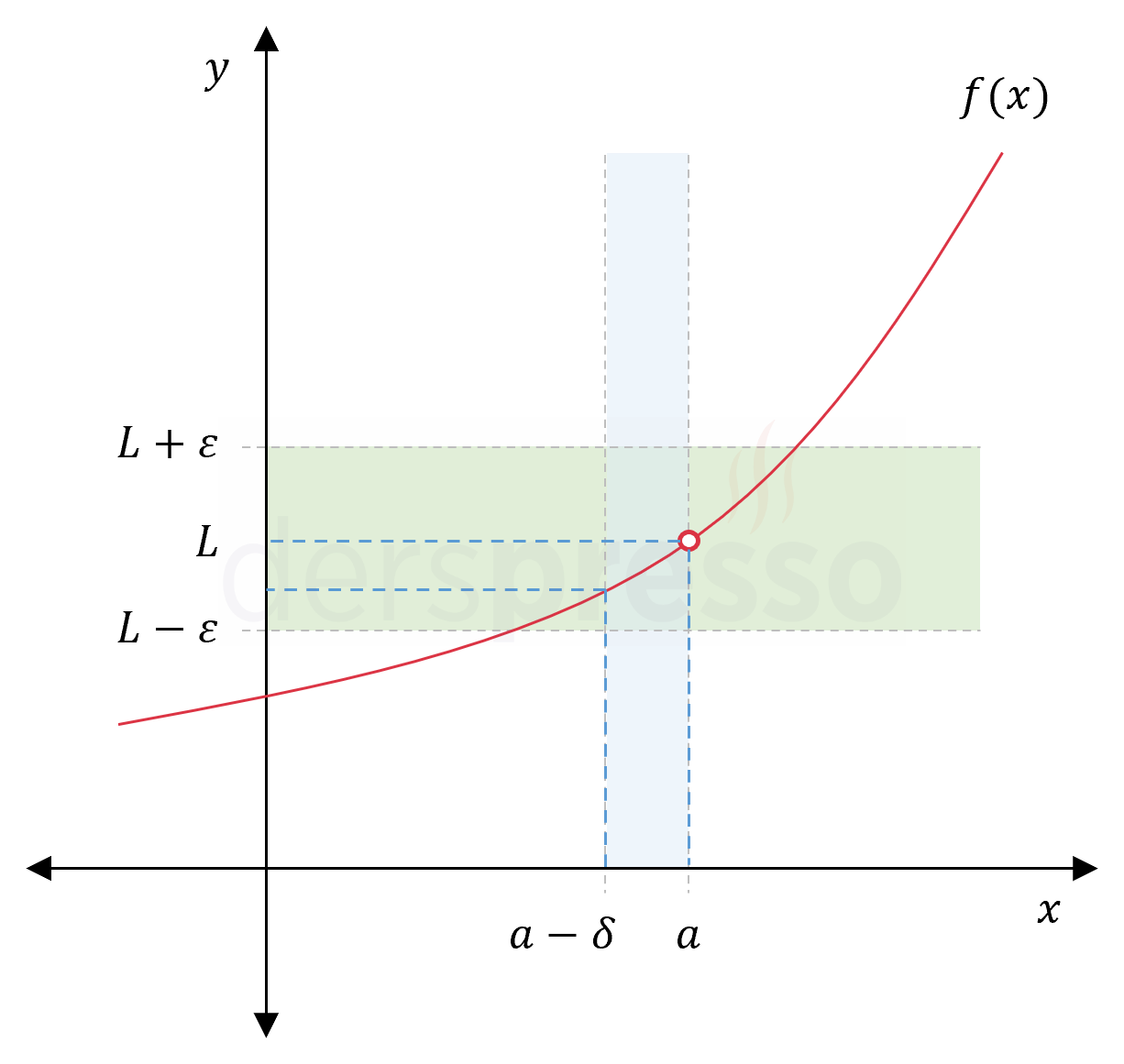
Soldan limitin epsilon-delta tanımında, \( x \) \( a \)'ya soldan yaklaştığı için \( 0 \lt \abs{x - a} \lt \delta \) eşitsizliği yerine \( a - \delta \lt x \lt a \) kullanılır.
Yukarıda tanımını yaptığımız \( f \) fonksiyonu için,
\( \lim\limits_{x \to a^-} f(x) = L \) limiti,
her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
Her \( x \in A \) değeri için,
\( a - \delta \lt x \lt a \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Sonsuz Limit
İleriki bölümlerde detaylı inceleyeceğimiz üzere, bir \( f \) fonksiyonunun \( x = a \) noktasındaki soldan, sağdan ve/veya iki taraflı limiti pozitif ya da negatif sonsuz ise bu limite sonsuz limit denir.
Sonsuz limitin epsilon-delta tanımı aşağıdaki gibidir.
\( f: A \to \mathbb{R}, \quad a, M \in \mathbb{R} \),
\( A \) reel sayılar kümesinde tanımlı, \( a \) noktasını içeren ya da içermeyen açık bir aralık olmak üzere,
\( \lim\limits_{x \to a} f(x) = +\infty \) limiti,
her \( M \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur.
Her \( x \in A \) değeri için,
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow f(x) \gt M \)

Sonsuz limitin tanımı tek taraflı limitler ve fonksiyonun negatif sonsuza gittiği durum için de benzer şekilde yapılabilir.
Sonsuzda Limit
İleriki bölümlerde detaylı inceleyeceğimiz üzere, bir \( f \) fonksiyonunda \( x \) değişkeni pozitif ya da negatif yönde gitgide artan çok büyük değerler aldığında \( f(x) \)'in yaklaştığı değere, \( f \) fonksiyonunun pozitif ya da negatif sonsuzdaki limiti denir.
Sonsuzda limitin epsilon-delta tanımı aşağıdaki gibidir.
\( f: \mathbb{R} \to \mathbb{R}, \quad N, L \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to \infty} f(x) = L \) limiti,
her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( N \gt 0 \) değeri bulunabiliyorsa mevcuttur ve \( L \) değerine eşittir.
Her \( x \in A \) değeri için,
\( x \gt N \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
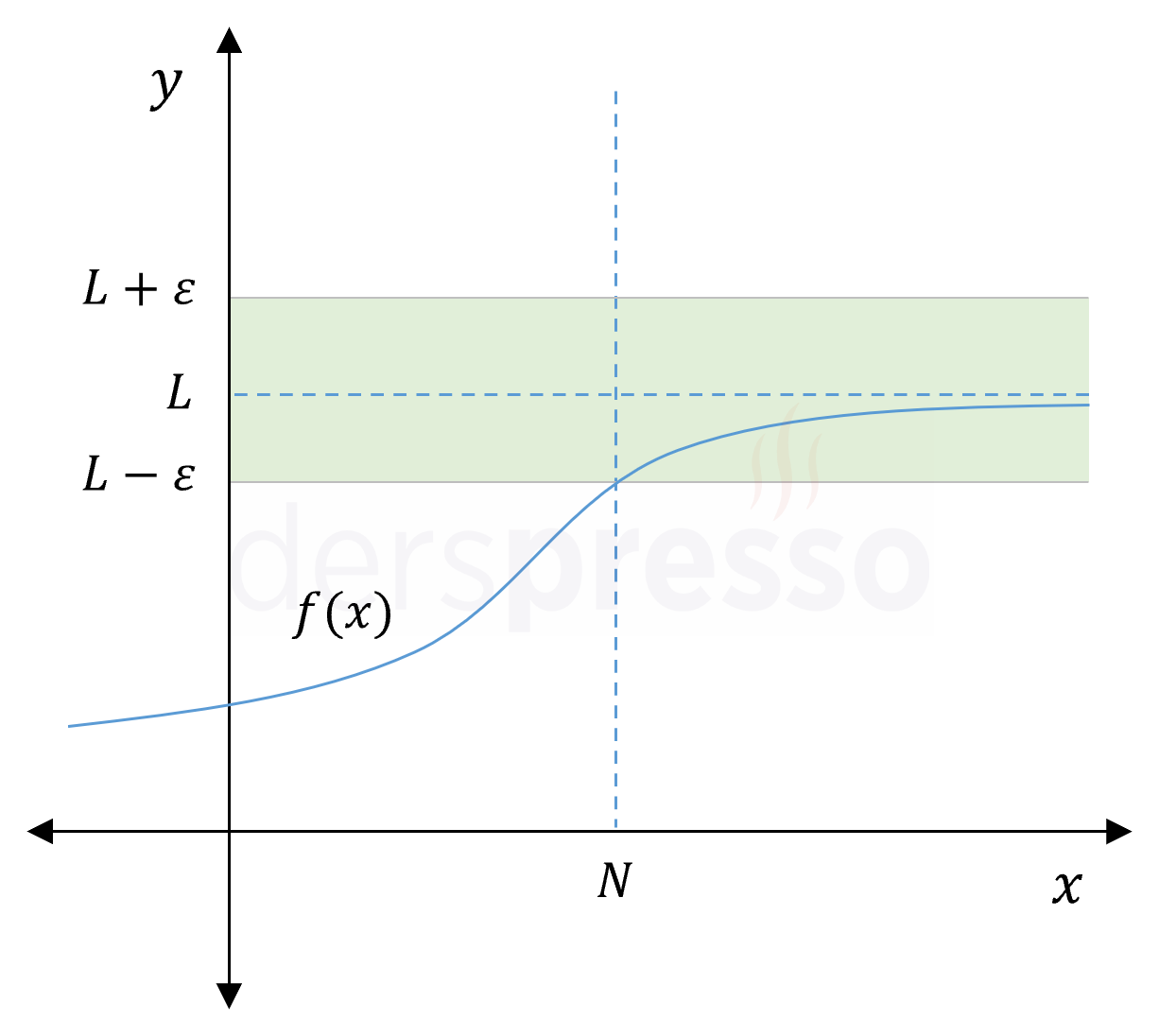
Sonsuzda limitin tanımı \( x \)'in negatif sonsuza gittiği durum için de benzer şekilde yapılabilir.
\( \lim\limits_{x \to 0} x^2 = 0 \) limitinin doğruluğunu epsilon-delta tanımını kullanarak gösterin.
Çözümü GösterAdım 1: Tanım
Verilen limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - 0} \lt \delta \Longrightarrow \abs{x^2 - 0} \lt \varepsilon \)
Adım 2: \( \delta \) Değerini Bulma
Bu önermeyi her \( \varepsilon \gt 0 \) için sağlayan bir \( \delta = \delta(\varepsilon) \gt 0 \) ifadesi bulmaya çalışalım.
\( \abs{x^2} \lt \varepsilon \)
\( \abs{x}^2 \lt \varepsilon \)
\( \abs{x} \lt \delta \) olduğu için, \( \abs{x}^2 \) ifadesinin üst sınır değerini \( \delta \) cinsinden \( \delta^2 \) şeklinde ifade edebiliriz.
\( \abs{x} \lt \delta^2 \le \varepsilon \)
Bu durumda her \( \varepsilon \gt 0 \) için önermeyi sağlayacak \( \delta \) değerini aşağıdaki şekilde seçebiliriz.
\( 0 \le \delta \le \sqrt{\varepsilon} \)
Adım 3: İspat
Herhangi bir \( \varepsilon \gt 0 \) verilmiş olsun.
\( \delta = \sqrt{\varepsilon} \) olarak seçelim ve bu \( \delta \) değeri için aşağıdaki önermenin sağlandığını gösterelim.
\( 0 \lt \abs{x - 0} \lt \delta \Longrightarrow \abs{x^2 - 0} \lt \varepsilon \)
\( 0 \lt \abs{x} \lt \delta \) olarak kabul edelim.
\( \abs{x^2 - 0} = \abs{x}^2 \)
\( \abs{x} \) ifadesi için üst sınır değeri olarak \( \delta \) kullanabiliriz.
\( \abs{x}^2 \lt \delta^2 \)
\( \delta = \sqrt{\varepsilon} \) yazalım.
\( \abs{x}^2 \lt \sqrt{\varepsilon}^2 = \varepsilon \)
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.
\( \lim\limits_{x \to 2} \dfrac{x^2 + x - 6}{x - 2} = 5 \) limitinin doğruluğunu epsilon-delta tanımını kullanarak gösterin.
Çözümü GösterAdım 1: Tanım
Verilen limit, her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa mevcuttur.
\( 0 \lt \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - L} \lt \varepsilon \)
Limit ifadesindeki bilgileri önermede yerine koyalım.
\( 0 \lt \abs{x - 2} \lt \delta \Longrightarrow \abs{\dfrac{x^2 + x - 6}{x - 2} - 5} \lt \varepsilon \)
Adım 2: \( \delta \) Değerini Bulma
Bu önermeyi her \( \varepsilon \gt 0 \) için sağlayan bir \( \delta = \delta(\varepsilon) \gt 0 \) ifadesi bulmaya çalışalım.
\( \abs{\dfrac{x^2 + x - 6}{x - 2} - 5} \lt \varepsilon \)
\( \abs{\dfrac{x^2 + x - 6 - 5(x - 2)}{x - 2}} \lt \varepsilon \)
\( \abs{\dfrac{x^2 + x - 6 - 5x + 10)}{x - 2}} \lt \varepsilon \)
\( \abs{\dfrac{x^2 - 4x + 4}{x - 2}} \lt \varepsilon \)
\( \abs{\dfrac{(x - 2)^2}{x - 2}} \lt \varepsilon \)
\( \abs{x - 2} \lt \varepsilon \)
\( \abs{x - 2} \lt \delta \) olduğu için, \( \abs{x - 2} \) ifadesinin üst sınır değerini \( \delta \) cinsinden \( \delta \) şeklinde ifade edebiliriz.
\( \abs{x - 2} \lt \delta \le \varepsilon \)
Bu durumda her \( \varepsilon \gt 0 \) için önermeyi sağlayacak \( \delta \) değerini aşağıdaki şekilde seçebiliriz.
\( 0 \le \delta \le \varepsilon \)
Adım 3: İspat
Herhangi bir \( \varepsilon \gt 0 \) verilmiş olsun.
\( \delta = \varepsilon \) olarak seçelim ve bu \( \delta \) değeri için aşağıdaki önermenin sağlandığını gösterelim.
\( 0 \lt \abs{x - 2} \lt \delta \Longrightarrow \abs{\dfrac{x^2 + x - 6}{x - 2} - 5} \lt \varepsilon \)
\( 0 \lt \abs{x - 2} \lt \delta \) olarak kabul edelim.
\( \abs{\dfrac{x^2 + x - 6}{x - 2} - 5} = \abs{\dfrac{x^2 + x - 6 - 5(x - 2)}{x - 2}} \)
\( = \abs{\dfrac{x^2 - 4x + 4}{x - 2}} = \abs{\dfrac{(x - 2)^2}{x - 2}} \)
\( = \abs{x - 2} \)
\( \abs{x - 2} \) ifadesi için üst sınır değeri olarak \( \delta \) kullanabiliriz.
\( \abs{x - 2} \lt \delta \)
\( \delta = \varepsilon \) yazalım.
\( \abs{x - 2} \lt \varepsilon \)
Verilen limitin doğruluğunu epsilon-delta tanımını kullanarak göstermiş olduk.