Sonsuzda Limit
Şu ana kadar fonksiyonların \( x \) bir reel sayı değere yaklaşırkenki limitini hesapladık. Bu bölümde \( x \) pozitif ya da negatif sonsuza giderkenki limit değerinden bahsedeceğiz.
Bir \( f \) fonksiyonunda \( x \) değişkeni pozitif ya da negatif yönde gitgide artan çok büyük değerler alırken fonksiyonun yaklaştığı değere, \( f \) fonksiyonunun pozitif ya da negatif sonsuzdaki limiti denir.
\( x \) pozitif sonsuza giderken limit:
\( \lim\limits_{x \to \infty} {f(x)} \)
\( x \) negatif sonsuza giderken limit:
\( \lim\limits_{x \to -\infty} {f(x)} \)
Bir fonksiyonun sonsuzdaki limiti bir reel sayı olabilir, pozitif ya da negatif sonsuz olabilir ya da tanımsız olabilir.
| Grafik | Açıklama |
|---|---|

|
Reel sayı limit: \( f(x) = \dfrac{2x}{\sqrt{x^2 + 1}} + 1 \) olmak üzere, \( \lim\limits_{x \to \infty} {f(x)} = 3 \) \( \lim\limits_{x \to -\infty} {f(x)} = -1 \) |

|
Sonsuz limit: \( f \) üçüncü dereceden pozitif başkatsayılı bir polinom fonksiyonu olmak üzere, \( \lim\limits_{x \to \infty} {f(x)} = \infty \) \( \lim\limits_{x \to -\infty} {f(x)} = -\infty \) |
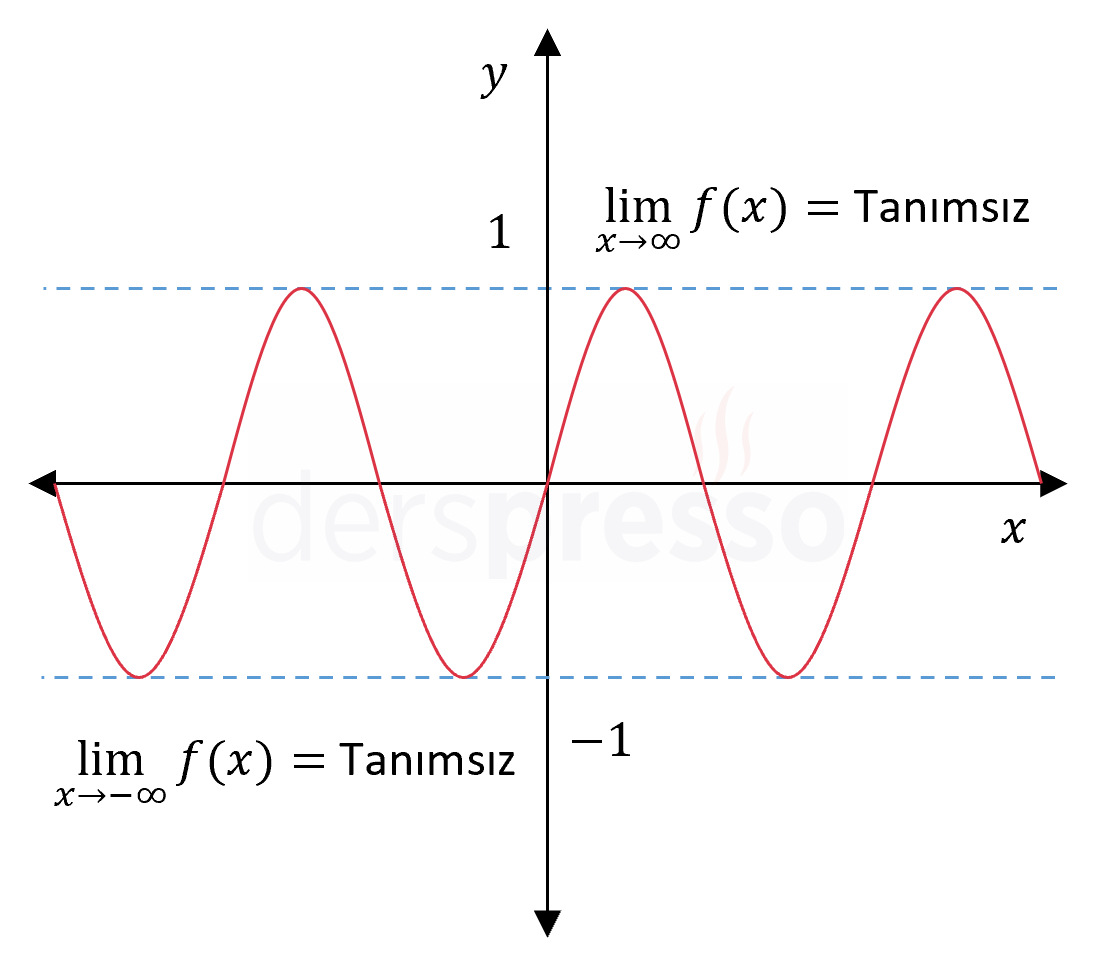
|
Tanımsız limit: \( f(x) = \sin{x} \) olmak üzere, \( \lim\limits_{x \to \infty} {f(x)} = \) Tanımsız \( \lim\limits_{x \to -\infty} {f(x)} = \) Tanımsız |
Bazı Fonksiyonların Sonsuzda Limiti
Sabit Fonksiyon
Sabit fonksiyonun sonsuzdaki limiti fonksiyonun sabit değerine eşittir.

\( c \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to \infty} {c} = c \)
\( \lim\limits_{x \to -\infty} {c} = c \)
Polinom Fonksiyonu
Tek dereceli polinom fonksiyonlarının sonsuzdaki limiti başkatsayının işaretine göre aşağıdaki gibidir.
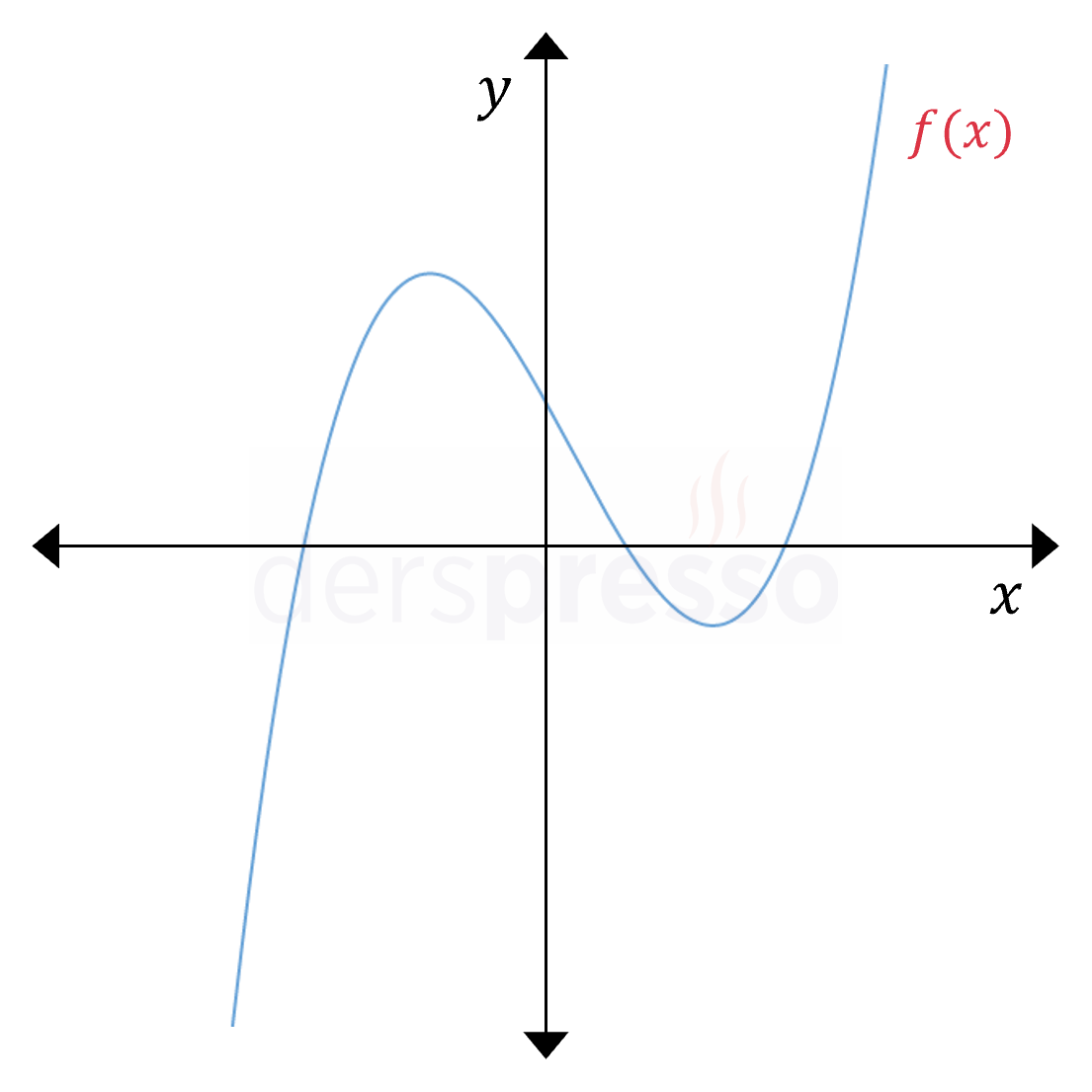
\( n \in \mathbb{Z^+} \) olmak üzere,
\( f(x) = ax^{2n-1} + \ldots \)
\( a \gt 0 \) ise,
\( \lim\limits_{x \to \infty} {f(x)} = \infty \)
\( \lim\limits_{x \to -\infty} {f(x)} = -\infty \)
\( a \lt 0 \) ise,
\( \lim\limits_{x \to \infty} {f(x)} = -\infty \)
\( \lim\limits_{x \to -\infty} {f(x)} = \infty \)
\( \lim\limits_{x \to -\infty} (3x + \ldots) = -\infty \)
\( \lim\limits_{x \to \infty} (-2x^3 + \ldots) = -\infty \)
Sabit fonksiyon hariç, çift dereceli polinom fonksiyonlarının sonsuzdaki limiti başkatsayının işaretine göre aşağıdaki gibidir.
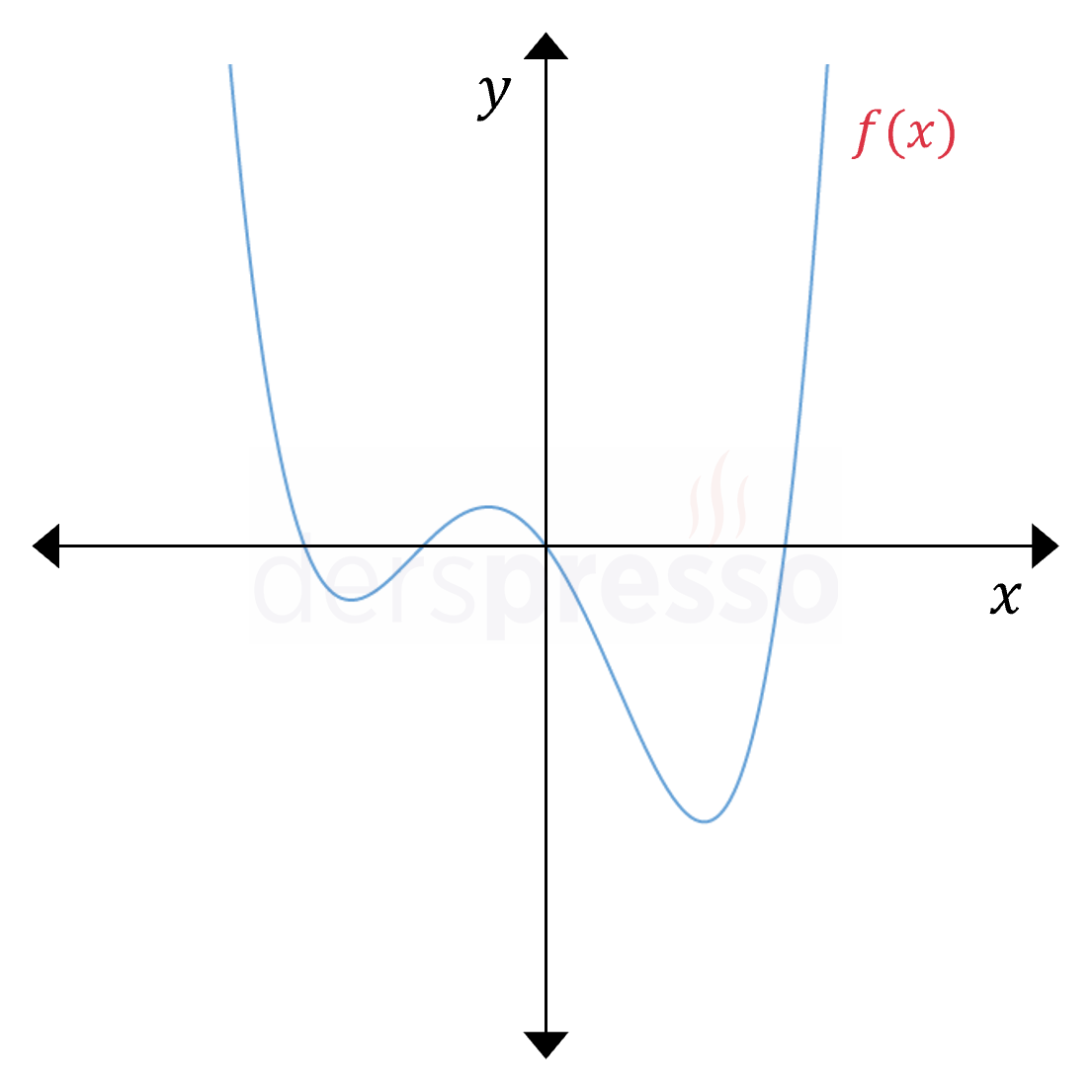
\( n \in \mathbb{Z^+} \) olmak üzere,
\( f(x) = ax^{2n} + \ldots \)
\( a \gt 0 \) ise,
\( \lim\limits_{x \to \infty} {f(x)} = \infty \)
\( \lim\limits_{x \to -\infty} {f(x)} = \infty \)
\( a \lt 0 \) ise,
\( \lim\limits_{x \to \infty} {f(x)} = -\infty \)
\( \lim\limits_{x \to -\infty} {f(x)} = -\infty \)
\( \lim\limits_{x \to -\infty} (-2x^2 + \ldots) = -\infty \)
\( \lim\limits_{x \to \infty} (x^4 + \ldots) = \infty \)
Yukarıdaki iki kuralda görülebileceği üzere, polinom fonksiyonlarının sonsuzdaki davranışını fonksiyonun derecesi ve başkatsayının işareti belirler, diğer terimlerin sonsuzdaki davranışa bir etkisi yoktur.
Üstel Fonksiyon
Üstel fonksiyonun sonsuzdaki limiti tabanın değerine göre aşağıdaki gibidir.
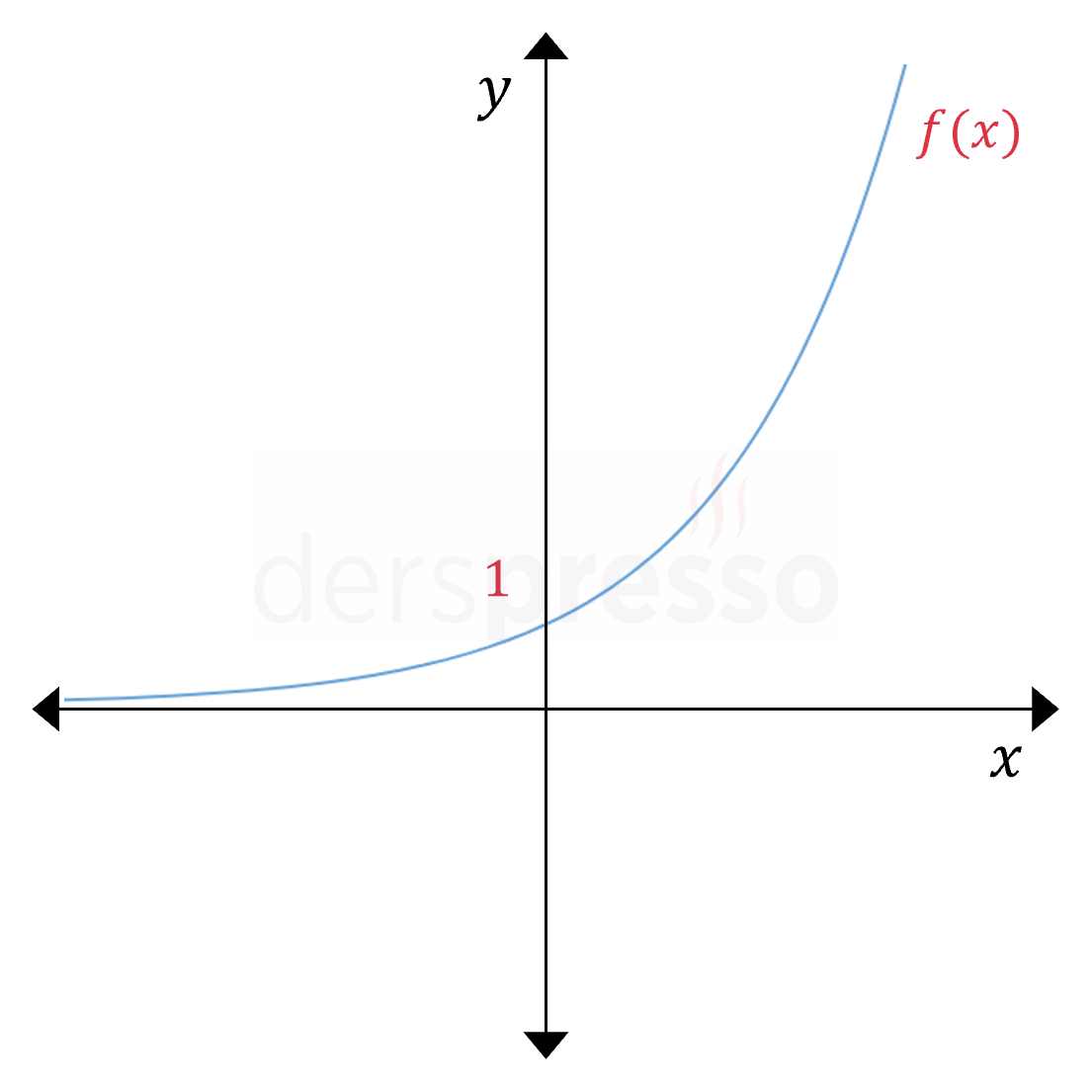
\( a \gt 1 \) ise,
\( \lim\limits_{x \to \infty} {a^x} = \infty \)
\( \lim\limits_{x \to -\infty} {a^x} = 0^+ \)
\( 0 \lt a \lt 1 \) ise,
\( \lim\limits_{x \to \infty} {a^x} = 0^+ \)
\( \lim\limits_{x \to -\infty} {a^x} = \infty \)
\( \lim\limits_{x \to -\infty} {e^{x}} = 0 \)
\( \lim\limits_{x \to \infty} (\frac{1}{2})^x = 0 \)
Logaritma Fonksiyonu
Logaritma fonksiyonunun sonsuzdaki limiti tabanın değerine göre aşağıdaki gibidir.
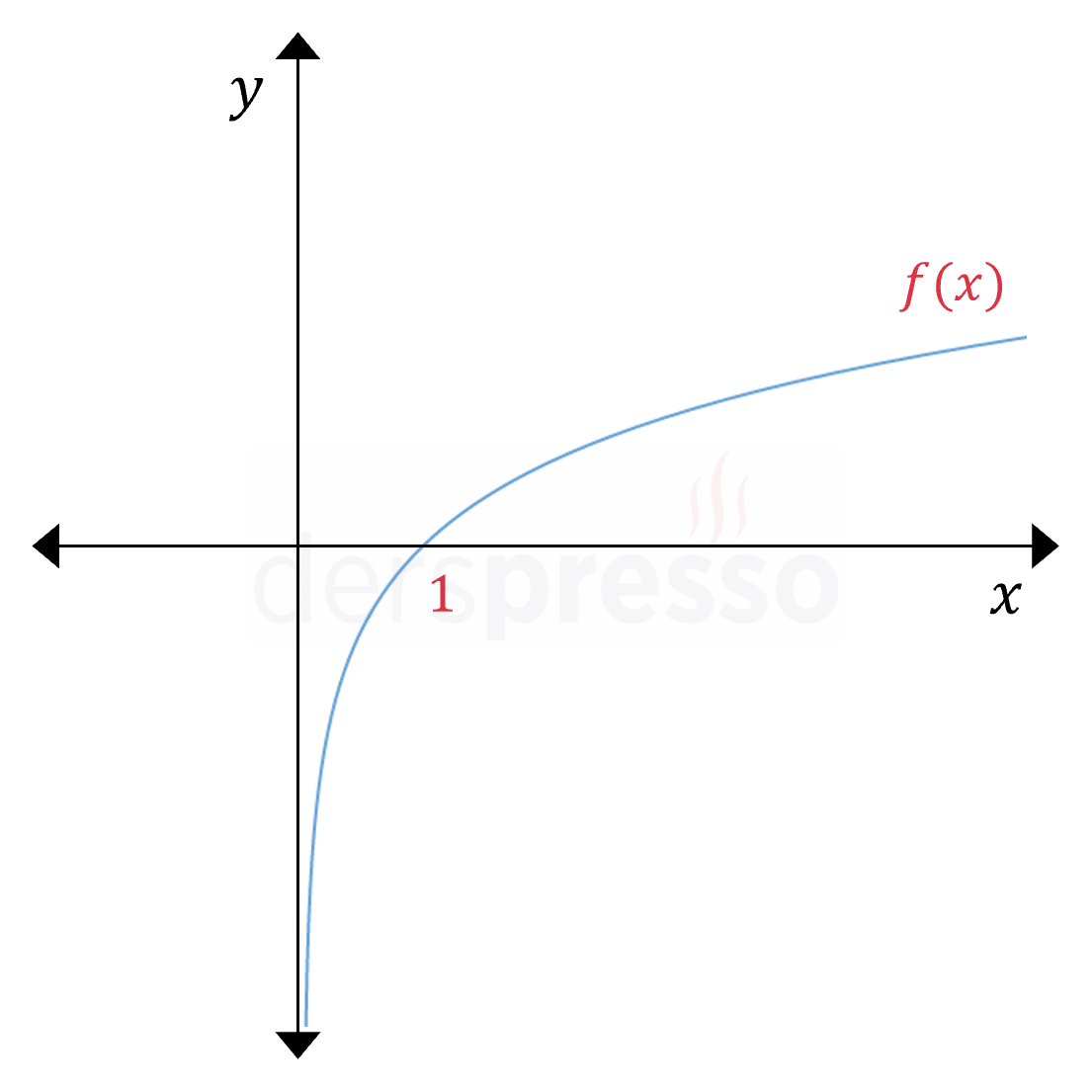
\( a \gt 1 \) ise,
\( \lim\limits_{x \to \infty} {\log_a{x}} = \infty \)
\( 0 \lt a \lt 1 \) ise,
\( \lim\limits_{x \to \infty} {\log_a{x}} = -\infty \)
Negatif Üslü Kuvvet Fonksiyonu
Üssü negatif reel sayı olan kuvvet fonksiyonlarının sonsuzdaki limiti aşağıdaki gibidir.
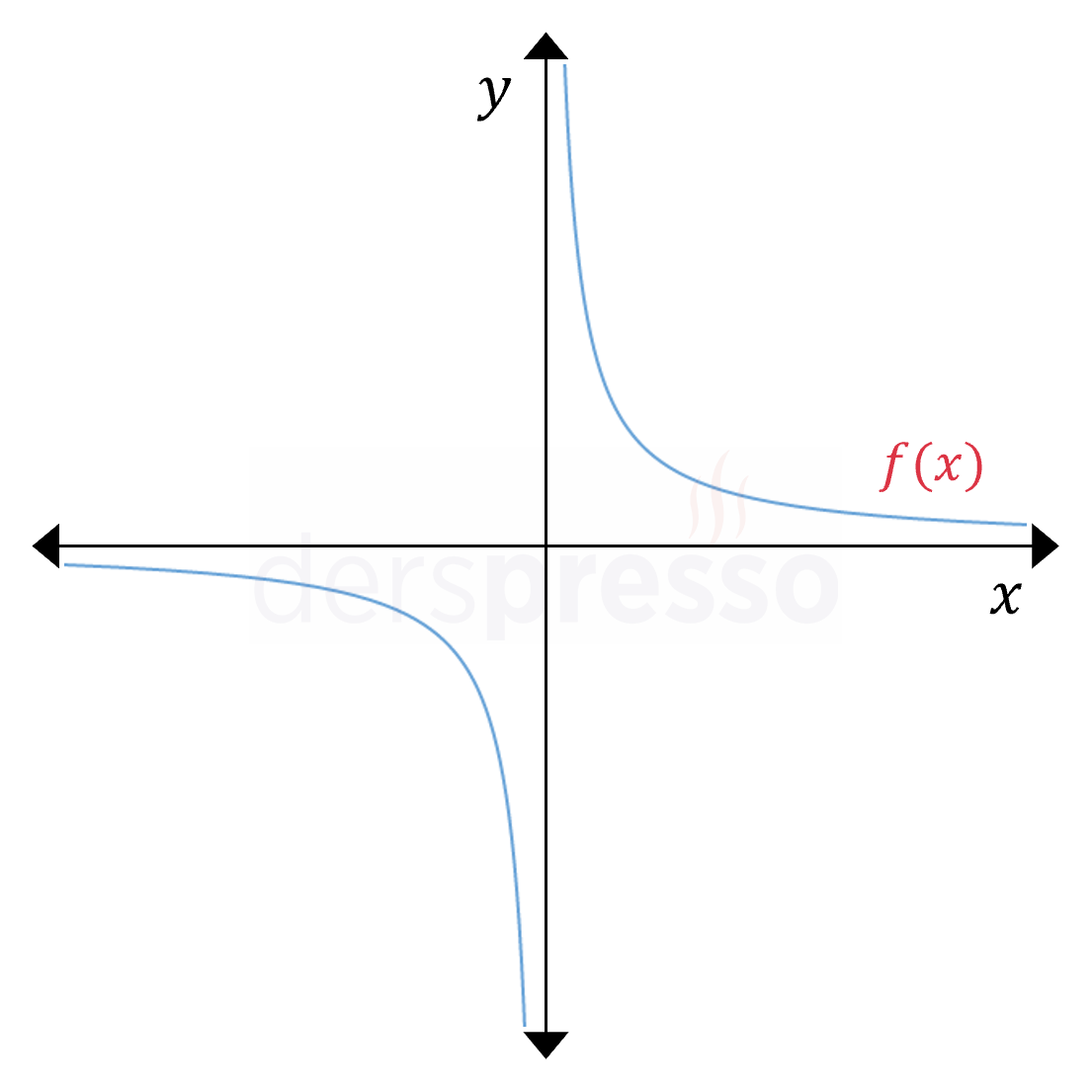
\( n \in \mathbb{R^+} \) olmak üzere,
\( \lim\limits_{x \to \infty} {\dfrac{1}{x^n}} = 0^+ \)
\( n \) pozitif tek sayı ise,
\( \lim\limits_{x \to -\infty} {\dfrac{1}{x^n}} = 0^- \)
\( n \) pozitif çift sayı ise,
\( \lim\limits_{x \to -\infty} {\dfrac{1}{x^n}} = 0^+ \)
\( \lim\limits_{x \to \infty} {\dfrac{1}{x}} = 0^+ \)
\( \lim\limits_{x \to -\infty} {\dfrac{1}{x}} = 0^- \)
\( \lim\limits_{x \to \infty} {\dfrac{1}{x^2}} = 0^+ \)
\( \lim\limits_{x \to -\infty} {\dfrac{1}{x^2}} = 0^+ \)
Rasyonel Fonksiyon
\( p(x) \) ve \( q(x) \) birer polinom fonksiyonu olmak üzere, \( \frac{p(x)}{q(x)} \) formundaki rasyonel fonksiyonların sonsuzdaki limitini bulmak için pay ve paydadaki tüm terimler \( x \)'in paydadaki en yüksek dereceli üssüne bölünür ve elde edilen ifadenin yukarıdaki kurallar kullanılarak limiti bulunur.
\( \lim\limits_{x \to \infty} {\dfrac{3x^2 - 4x + 1}{5x^3 + 2x^2 - 4x - 7}} \) limitini bulalım.
Pay ve paydadaki terimleri \( x \)'in paydadaki en yüksek dereceli üssüne (\( x^3 \)) bölelim.
\( \lim\limits_{x \to \infty} {\dfrac{\frac{3}{x} - \frac{4}{x^2} + \frac{1}{x^3}}{5 + \frac{2}{x} - \frac{4}{x^2} - \frac{7}{x^3}}} \)
Limit işlemini önce bölme kuralı ile paya ve paydaya, daha sonra toplama kuralı ile terimlere dağıtalım.
\( = \dfrac{\lim\limits_{x \to \infty} {\frac{3}{x}} - \lim\limits_{x \to \infty} {\frac{4}{x^2}} + \lim\limits_{x \to \infty} {\frac{1}{x^3}}}{\lim\limits_{x \to \infty} {5} + \lim\limits_{x \to \infty} {\frac{2}{x}} - \lim\limits_{x \to \infty} {\frac{4}{x^2}} - \lim\limits_{x \to \infty} {\frac{7}{x^3}}} \)
\( x \to \infty \) iken \( \frac{1}{x^n} \to 0 \) olur.
\( = \dfrac{0 - 0 + 0}{5 + 0 - 0 - 0} \)
\( = \dfrac{0}{5} = 0 \)
Fonksiyonun pozitif sonsuzda sıfıra yaklaştığı aşağıda grafik üzerinde gösterilmiştir. Negatif sonsuzdaki limit hesaplandığında fonksiyonun yine sıfıra yaklaştığı görülebilir.
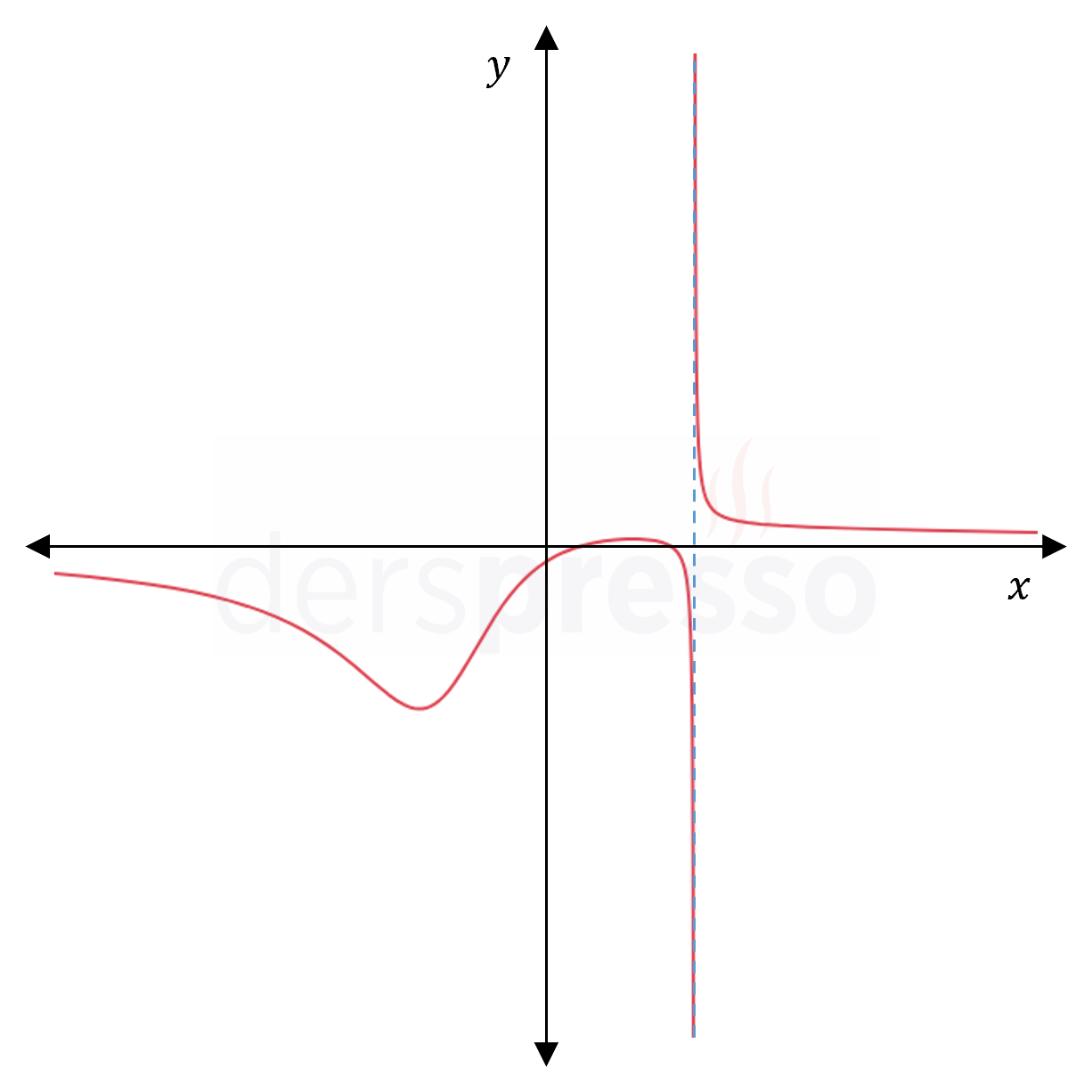
\( \lim\limits_{x \to -\infty} {\dfrac{-5x^4 + 4x^2 - 6}{7x^4 - 5x^2 - 2x}} \) limitini bulalım.
Pay ve paydadaki terimleri \( x \)'in paydadaki en yüksek dereceli üssüne (\( x^4 \)) bölelim.
\( \lim\limits_{x \to -\infty} {\dfrac{-5 + \frac{4}{x^2} - \frac{6}{x^4}}{7 - \frac{5}{x^2} - \frac{2}{x^3}}} \)
Limit işlemini önce bölme kuralı ile paya ve paydaya, daha sonra toplama kuralı ile terimlere dağıtalım.
\( = \dfrac{\lim\limits_{x \to -\infty} {-5} + \lim\limits_{x \to -\infty} {\frac{4}{x^2}} - \lim\limits_{x \to -\infty} {\frac{6}{x^4}}}{\lim\limits_{x \to -\infty} {7} - \lim\limits_{x \to -\infty} {\frac{5}{x^2}} - \lim\limits_{x \to -\infty} {\frac{2}{x^3}}} \)
\( x \to -\infty \) iken \( \frac{1}{x^n} \to 0 \) olur.
\( = \dfrac{-5 + 0 - 0}{7 - 0 - 0} \)
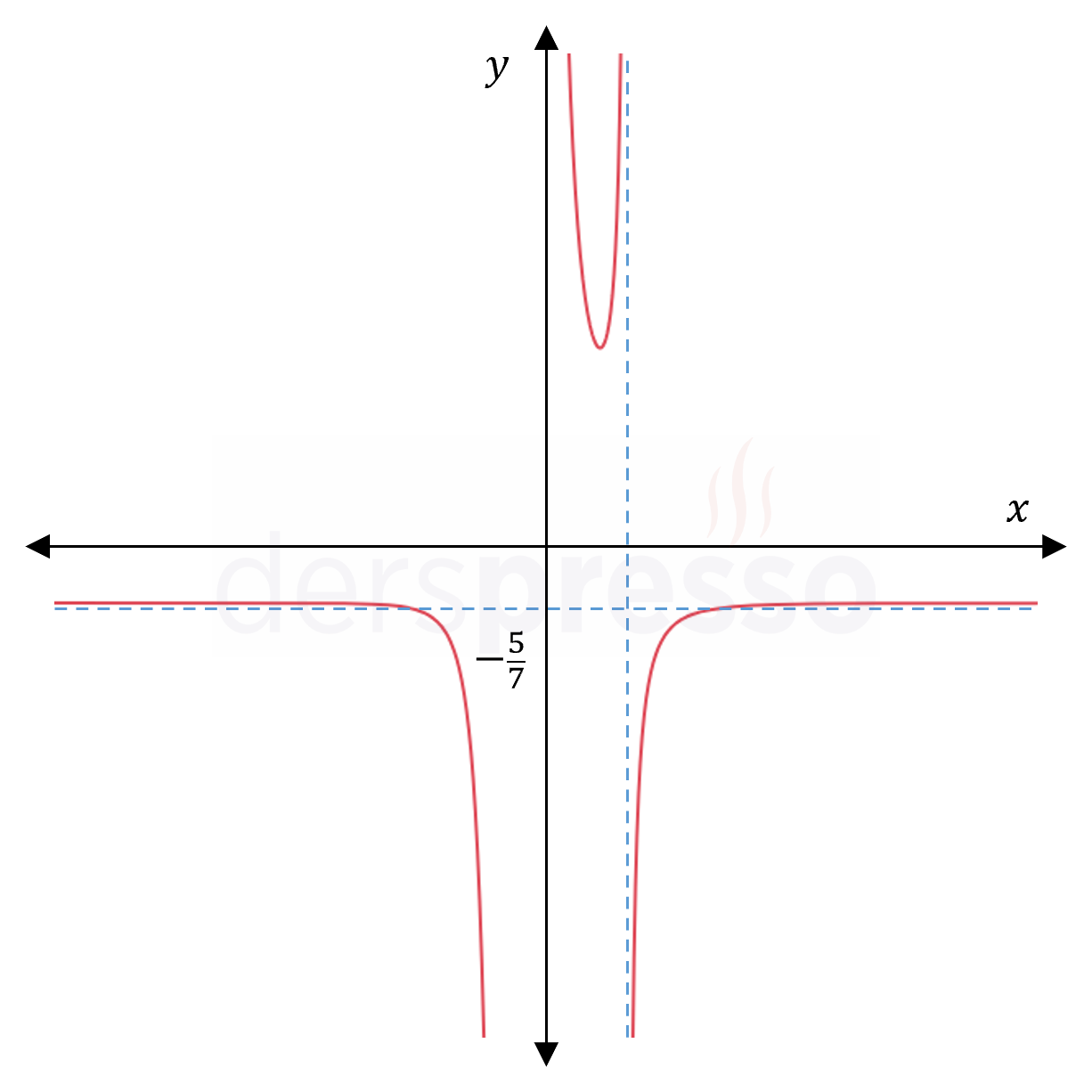
\( = -\dfrac{5}{7} \)
Fonksiyonun negatif sonsuzda \( y = -\frac{5}{7} \) doğrusuna yaklaştığı aşağıda grafik üzerinde gösterilmiştir. Pozitif sonsuzdaki limit hesaplandığında fonksiyonun aynı doğruya yaklaştığı görülebilir.
\( \lim\limits_{x \to -\infty} {\dfrac{2x^5 - 3x^4 + 7x^2 + 4}{9x^4 + 5x^3 - 8}} \) limitini bulalım.
Pay ve paydadaki terimleri \( x \)'in paydadaki en yüksek dereceli üssüne (\( x^4 \)) bölelim.
\( \lim\limits_{x \to -\infty} {\dfrac{2x - 3 + \frac{7}{x^2} + \frac{4}{x^4}}{9 + \frac{5}{x} - \frac{8}{x^4}}} \)
Limit işlemini önce bölme kuralı ile paya ve paydaya, daha sonra toplama kuralı ile terimlere dağıtalım.
\( = \dfrac{\lim\limits_{x \to -\infty} (2x) - \lim\limits_{x \to -\infty} {3} + \lim\limits_{x \to -\infty} {\frac{7}{x^2}} + \lim\limits_{x \to -\infty} {\frac{4}{x^4}}}{\lim\limits_{x \to -\infty} {9} + \lim\limits_{x \to -\infty} {\frac{5}{x}} - \lim\limits_{x \to -\infty} {\frac{8}{x^4}}} \)
\( x \to -\infty \) iken \( \frac{1}{x^n} \to 0 \) olur.
\( x \to -\infty \) iken \( (2x) \to -\infty \) olur.
\( = \dfrac{-\infty - 3 + 0 + 0}{9 + 0 - 0} \)
\( = -\infty \)
Fonksiyonun negatif sonsuzda negatif sonsuza gittiği aşağıda grafik üzerinde gösterilmiştir. Pozitif sonsuzdaki limit hesaplandığında fonksiyonun bu sefer pozitif sonsuza gittiği görülebilir.

Rasyonel fonksiyonların pay ve paydasındaki tüm terimler \( x \)'in paydadaki değil de paydaki en yüksek dereceli üssüne bölündüğünde yanlış sonuç elde edilebilir. Örneğin yukarıdaki üçüncü örnekte işlem bu şekilde yapıldığında sonuç negatif sonsuz yerine pozitif sonsuz olarak bulunur.
Yukarıdaki üç örnekte incelediğimiz üç farklı durum için aşağıdaki kısayol kurallar kullanılabilir.
- Paydasının derecesi payının derecesinden daha büyük olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti sıfıra eşittir.
- Pay ve paydasının dereceleri eşit olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti pay ve paydadaki polinomların başkatsayılarının oranına eşittir.
- Payının derecesi paydasının derecesinden daha büyük olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti pay ve paydadaki en yüksek dereceli terimlerin birbirine bölümünün limitine eşittir.
Buna göre, bir rasyonel fonksiyonun sonsuzdaki limiti pay ve paydadaki en yüksek dereceli terimler dışındaki terimler silindiğinde elde edilen ifadenin sonsuzdaki limitine eşittir.
\( \lim\limits_{x \to \infty} {\dfrac{9x^{99} - 7x^{49} + 8}{-3x^{98} + 6x^{37} - 8x^{14} + 1}} \) limitini bulalım.
Bir rasyonel fonksiyonun sonsuzdaki limiti, pay ve paydadaki en yüksek dereceli terimler dışındaki terimler silindiğinde elde edilen ifadenin sonsuzdaki limitine eşittir.
\( \lim\limits_{x \to \infty} {\dfrac{9x^{99} - 7x^{49} + 8}{-3x^{98} + 6x^{37} - 8x^{14} + 1}} = \lim\limits_{x \to \infty} {\dfrac{9x^{99}}{-3x^{98}}} \)
\( = \lim\limits_{x \to \infty} (-3x) \)
\( x \to \infty \) iken \( -3x \to -\infty \) olur.
\( = -\infty \)
Köklü Rasyonel İfadeler
Köklü ifade içeren rasyonel ifadelerin sonsuzdaki limitini bulurken, (rasyonel fonksiyonlarda kullandığımız yönteme benzer şekilde) pay ve paydadaki tüm terimler \( x \)'in paydadaki en yüksek dereceli üssüne bölünür ve elde edilen ifadenin limiti bulunur.
\( \lim\limits_{x \to -\infty} {\dfrac{\sqrt{4x^2 - x + 3}}{3x - 4}} \) limitini bulalım.
Pay ve paydadaki terimleri \( x \)'in paydadaki en yüksek dereceli üssüne bölelim.
\( \lim\limits_{x \to -\infty} {\dfrac{\frac{\sqrt{4x^2 - x + 3}}{x}}{3 - \frac{4}{x}}} \)
\( x \) ifadesini kök içine alalım.
\( x \to -\infty \) iken \( x = -\sqrt{x^2} \) olur.
\( = \lim\limits_{x \to -\infty} {\dfrac{-\sqrt{\frac{4x^2 - x + 3}{x^2}}}{3 - \frac{4}{x}}} \)
\( = \lim\limits_{x \to -\infty} {\dfrac{-\sqrt{4 - \frac{1}{x} + \frac{3}{x^2}}}{3 - \frac{4}{x}}} \)
Limit işlemini önce bölme kuralı ile paya ve paydaya, daha sonra bileşke fonksiyon kuralı ile payda kök içine ve toplama kuralı ile paydadaki terimlere dağıtalım.
\( = \dfrac{-\sqrt{\lim\limits_{x \to -\infty} {4} - \lim\limits_{x \to -\infty} {\frac{1}{x}} + \lim\limits_{x \to -\infty} {\frac{3}{x^2}}}}{\lim\limits_{x \to -\infty} {3} - \lim\limits_{x \to -\infty} {\frac{4}{x}}} \)
\( x \to -\infty \) iken \( \frac{1}{x^n} \to 0 \) olur.
\( = \dfrac{-\sqrt{4 - 0 + 0}}{3 - 0} \)
\( = -\dfrac{2}{3} \)
Trigonometrik Fonksiyon
Trigonometrik fonksiyonlar (sinüs, kosinüs, tanjant, kotanjant, sekant, kosekant) periyodik oldukları için grafikleri periyotları dahilinde tekrar eder, dolayısıyla pozitif ve negatif sonsuzdaki limitleri tanımlı değildir.
Ters sinüs ve ters kosinüs fonksiyonlarının tanım kümeleri \( [-1, 1] \) aralığı olduğu için sonsuzdaki limitleri tanımlı değildir.
Ters tanjant fonksiyonunun \( y = -\frac{\pi}{2} \) ve \( y = \frac{\pi}{2} \) olmak üzere iki yatay asimptotu vardır.

\( \lim\limits_{x \to \infty} {\arctan{x}} = \dfrac{\pi}{2} \)
\( \lim\limits_{x \to -\infty} {\arctan{x}} = -\dfrac{\pi}{2} \)
Ters kotanjant fonksiyonunun \( y = 0 \) ve \( y = \pi \) olmak üzere iki yatay asimptotu vardır.
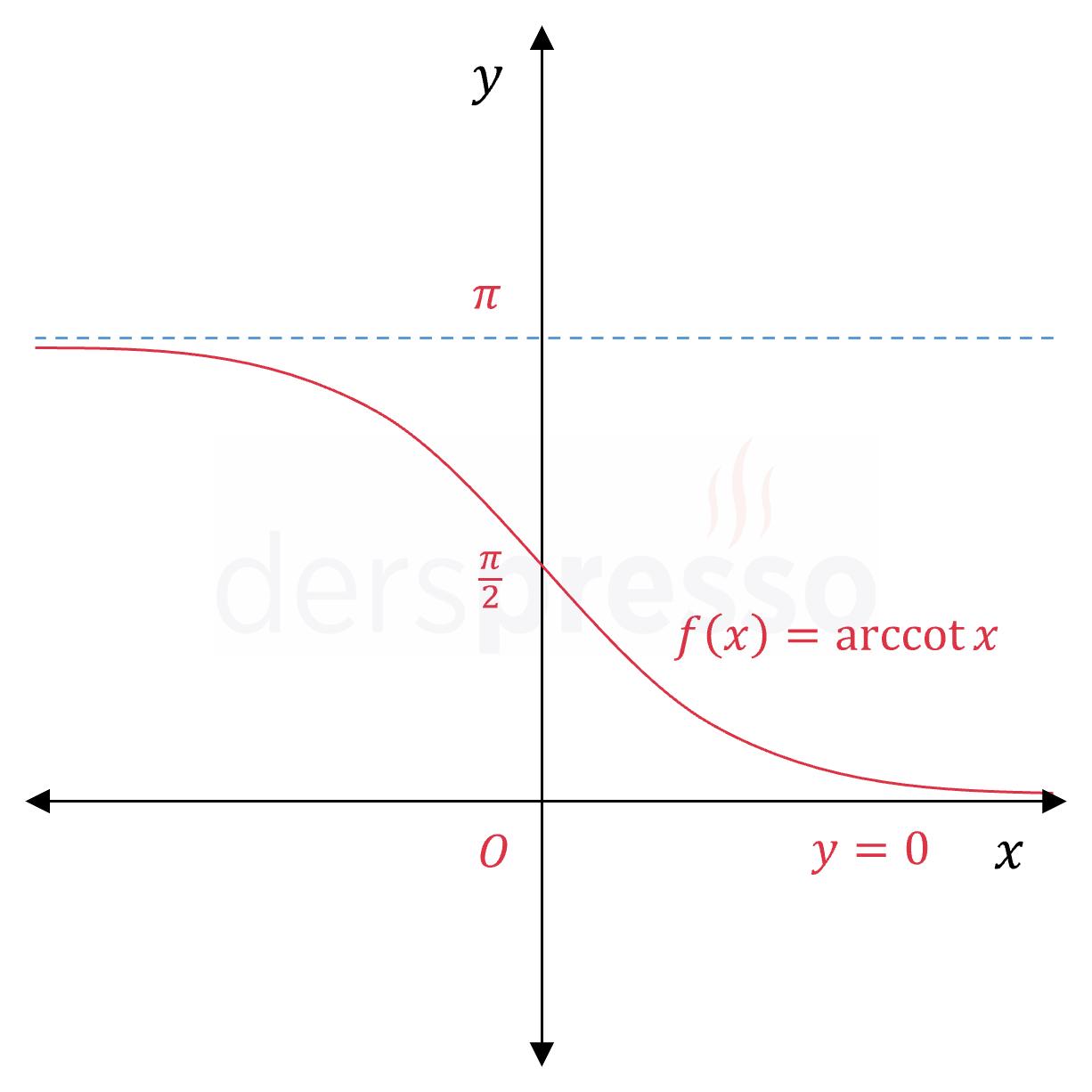
\( \lim\limits_{x \to \infty} {\arccot{x}} = 0 \)
\( \lim\limits_{x \to -\infty} {\arccot{x}} = \pi \)
Fonksiyonların Büyüme Hızı
\( \frac{f(x)}{g(x)} \) formundaki bir rasyonel ifadenin payı ve paydası polinom fonksiyonu değilse ifadenin sonsuzdaki limiti pay ve paydadaki fonksiyonların büyüme hızları karşılaştırılarak belirlenebilir.
\( x \) pozitif sonsuza giderken \( f \) ve \( g \) fonksiyonlarının pozitif sonsuza gittiğini varsayalım.
\( f \) fonksiyonunun büyüme hızı \( g \) fonksiyonunkinden büyükse limit sonsuzdur.
\( \lim\limits_{x \to \infty} \dfrac{f(x)}{g(x)} = \infty \)
\( g \) fonksiyonunun büyüme hızı \( f \) fonksiyonunkinden büyükse limit sıfırdır.
\( \lim\limits_{x \to \infty} \dfrac{f(x)}{g(x)} = 0 \)
\( f \) ve \( g \) fonksiyonlarının büyüme hızları eşitse limit sıfırdan farklı bir reel sayıdır.
\( \lim\limits_{x \to a} \dfrac{f(x)}{g(x)} = L \ne 0 \)
Farklı tipteki fonksiyonların büyüme hızlarını karşılaştırırken aşağıdaki sıralama kullanılabilir. Buradaki küçüklük/büyüklük ilişkisi \( x \)'in çok büyük değerleri için geçerlidir.
\( n \in \mathbb{Z}, n \gt 1 \) ve
\( a \in \mathbb{R}, a \gt 1 \) olmak üzere,
\( \text{Sabit} \lt \text{Logaritma} \lt \text{Kök} \lt \text{Birim} \lt \text{Kuvvet} \lt \text{Üstel} \lt \text{Faktöriyel} \lt x^x \)
\( a \lt \log_a{x} \lt \sqrt[n]{x} \lt x \lt x^n \lt a^x \lt x! \lt x^x \)
Kuvvet ve üstel fonksiyonlarda \( a \)'nın daha büyük değerleri daha küçük değerlerine göre daha hızlı büyüme gösterir. Köklü fonksiyonlarda \( a \)'nın daha küçük değerleri daha büyük değerlerine göre daha hızlı büyüme gösterir.
Kuvvet fonksiyonları:
\( x^2 \lt x^3 \lt x^4 \lt \ldots \)
Üstel fonksiyonlar:
\( 2^x \lt e^x \lt 3^x \lt \ldots \)
Kök fonksiyonları:
\( \ldots \lt \sqrt[4]{x} \lt \sqrt[3]{x} \lt \sqrt{x} \)
Farklı tabanlardaki iki logaritma fonksiyonu arasında benzer bir karşılaştırma yapamayız, çünkü iki fonksiyonun oranı taban değiştirme formülü ile sabit bir sayıya eşittir.
\( \lim\limits_{x \to \infty} {\dfrac{\log_4{x}}{\log_2{x}}} = \lim\limits_{x \to \infty} {\log_2{4}} = 2 \)
Büyüme hızları farklı terimlerden oluşan bir rasyonel ifadenin sonsuzdaki limitini, sadece pay ve paydadaki büyüme hızı en büyük olan terimleri dikkate alarak bulabiliriz.
\( \lim\limits_{x \to \infty} {\dfrac{x^{100} + \sqrt{x} + 1000}{\ln{x} + e^x + x}} \) limitini bulalım.
\( \lim\limits_{x \to \infty} {\dfrac{x^{100} + \sqrt{x} + 1000}{\ln{x} + e^x + x}} \)
Verilen rasyonel ifadede büyüme hızı en büyük terimler payda \( x^{100} \), paydada ise \( e^x \) olur.
Buna göre sonsuzdaki limiti sadece pay ve paydadaki büyüme hızı en büyük olan terimleri dikkate alarak bulabiliriz.
\( = \lim\limits_{x \to \infty} {\dfrac{x^{100}}{e^x}} \)
Üstel fonksiyonların büyüme hızı kuvvet fonksiyonlarının büyüme hızından büyük olduğu için ifadenin sonsuzdaki limiti sıfıra eşittir.
\( = 0 \)
Yatay Asimptot
Bir \( f \) fonksiyonunun pozitif veya negatif sonsuzdaki limiti bir \( L \) reel sayısı olarak tanımlı ise fonksiyonun bir yatay asimptotu vardır ve denklemi \( y = L \) doğrusudur.
\( L \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to \infty} {f(x)} = L \) veya
\( \lim\limits_{x \to -\infty} {f(x)} = L \) ise,
\( y = L \) doğrusu \( f \) fonksiyonunun bir yatay asimptotudur.
Aşağıdaki grafikte fonksiyonun pozitif sonsuzdaki limiti \( 5 \), negatif sonsuzdaki limiti \( -2 \) olduğu için, \( y = 5 \) ve \( y = -2 \) doğruları fonksiyonun yatay asimptotlarıdır.
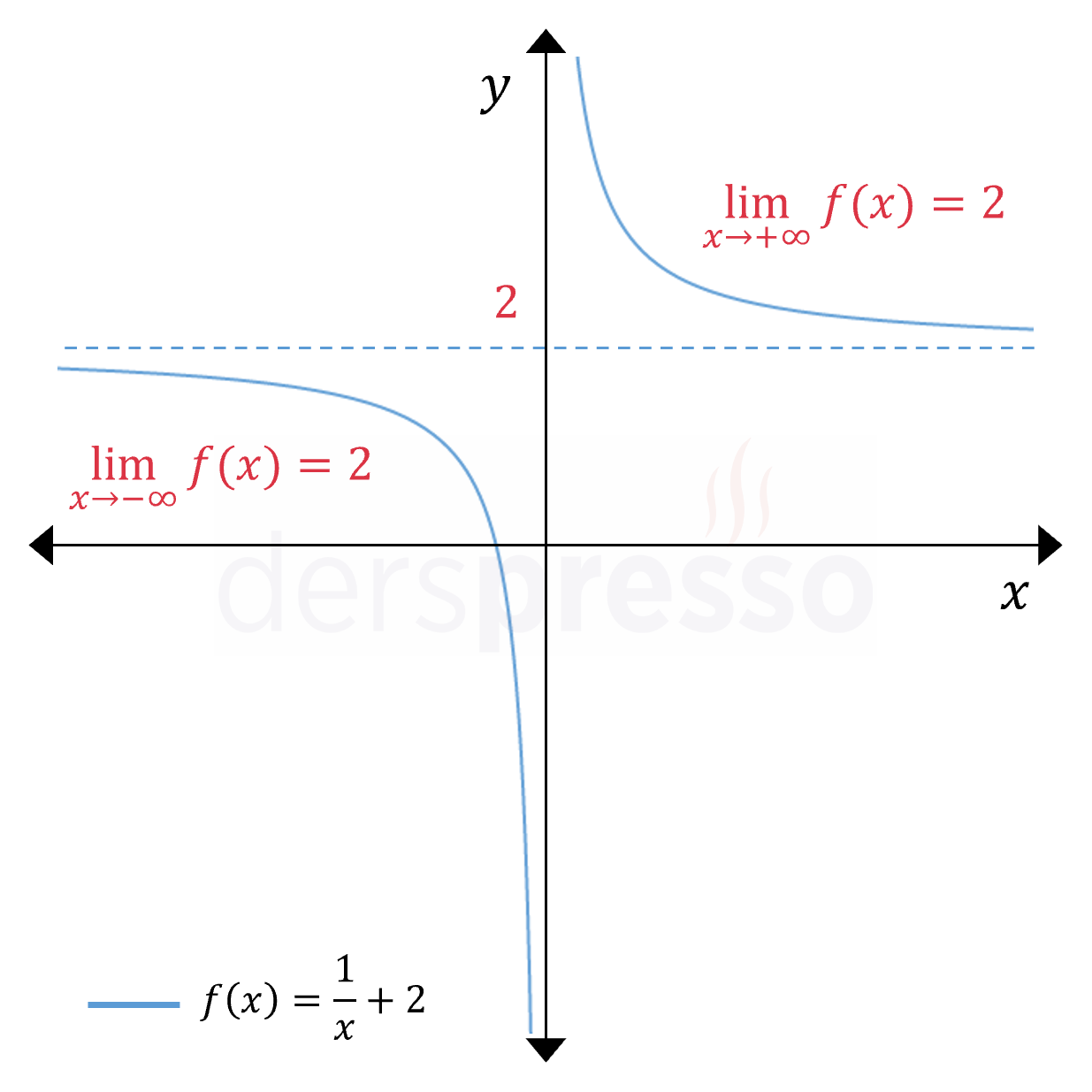
\( \lim\limits_{x \to \infty} {f(x)} = 5 \)
\( \lim\limits_{x \to -\infty} {f(x)} = -2 \)
Yatay asimptotlar sadece \( x \) pozitif ya da negatif sonsuza giderken oluşabilir ve bir fonksiyonun bu iki durumla sınırlı olmak üzere en fazla iki yatay asimptotu olabilir.
Yatay asimptotlar fonksiyon grafiğinin bir parçası olmayıp fonksiyonun sonsuzdaki davranışının daha kolay anlaşılmasını sağlamak için çizilir.
Yukarıda bazı örneklerini verdiğimiz üzere, yatay asimptotların oluştuğu durumlardan bazıları şunlardır.
- Üstel fonksiyonların \( y = 0 \) şeklinde tek bir yatay asimptotu vardır.
- Negatif üslü kuvvet fonksiyonlarının \( y = 0 \) şeklinde tek bir yatay asimptotu vardır.
- Payın derecesi paydanın derecesinden küçük olan rasyonel fonksiyonların \( y = 0 \) şeklinde tek bir yatay asimptotu vardır.
- Payın ve paydanın başkatsayıları sırasıyla \( a \) ve \( b \) olmak üzere, payın derecesi paydanın derecesine eşit olan rasyonel fonksiyonların \( y = \frac{a}{b} \) şeklinde tek bir yatay asimptotu vardır.
- Ters tanjant fonksiyonunun \( y = -\frac{\pi}{2} \) ve \( y = \frac{\pi}{2} \) olmak üzere iki yatay asimptotu vardır.
- Ters kotanjant fonksiyonunun \( y = 0 \) ve \( y = \pi \) olmak üzere iki yatay asimptotu vardır.
Bir fonksiyonun bir ya da iki yatay asimptotu olabilir ya da hiç asimptotu olmayabilir.
Dikey asimptotlardan farklı olarak, bir fonksiyon grafiği yatay asimptotu kesebilir.
\( f(x) = \dfrac{2x + 3}{x + 1} \) fonksiyonunun yatay asimptotlarını bulalım.
Fonksiyonun negatif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to -\infty} \dfrac{2x + 3}{x + 1} = 2 \)
Fonksiyonun pozitif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to \infty} \dfrac{2x + 3}{x + 1} = 2 \)
Buna göre fonksiyonun \( y = 2 \) doğrusu olmak üzere tek bir yatay asimptotu vardır ve \( x \) hem pozitif hem negatif sonsuza giderken fonksiyon grafiği bu doğruya yaklaşır.
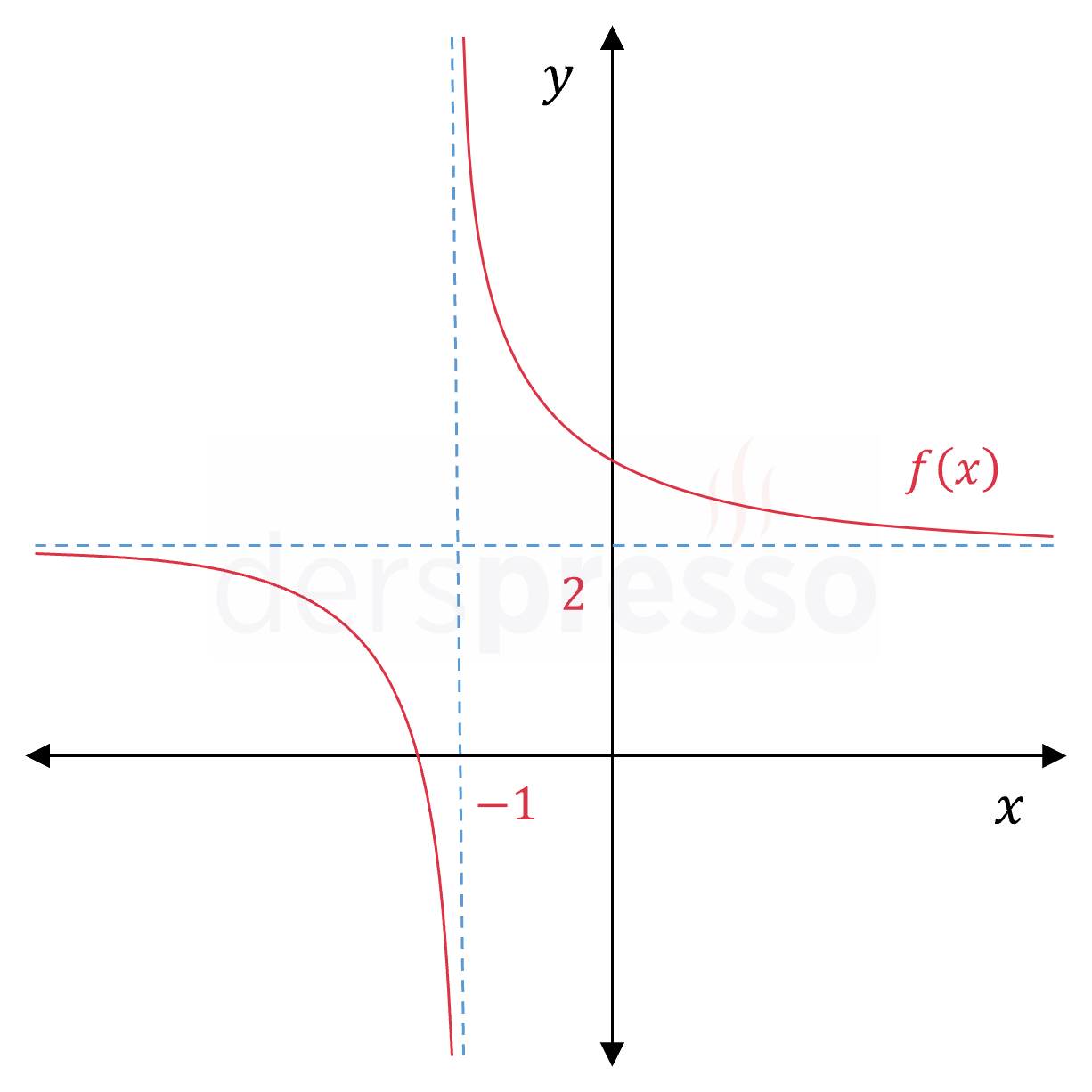
Grafikte görebileceğimiz gibi, \( x \) negatif sonsuza giderken grafik \( y = 2 \) doğrusuna aşağıdan, \( x \) pozitif sonsuza giderken yukarıdan yaklaşmaktadır.
Eğik Asimptot
\( x \) pozitif ya da negatif sonsuza giderken fonksiyon grafiğinin yaklaştığı asimptot \( y = a \) şeklinde sabit bir fonksiyon değil, \( y = mx + c \) şeklinde bir doğru ise bu doğruya eğik asimptot ya da eğimli asimptot denir. Buna göre yatay asimptotlar eğimi sıfır olan eğik asimptot olarak da düşünülebilir.
\( m \ne 0 \) olmak üzere,
\( \lim\limits_{x \to \infty} [f(x) - (mx + b)] = 0 \) veya
\( \lim\limits_{x \to -\infty} [f(x) - (mx + b)] = 0 \) ise,
\( y = mx + b \) doğrusu \( f \) fonksiyonunun bir eğik asimptotudur.
Aşağıdaki grafikte mavi kesikli çizgi ile gösterilen \( y = x + 2 \) doğrusu \( f(x) = \frac{x^2 - 9}{\sqrt{x - 2}} \) fonksiyonunun eğik asimptotudur.
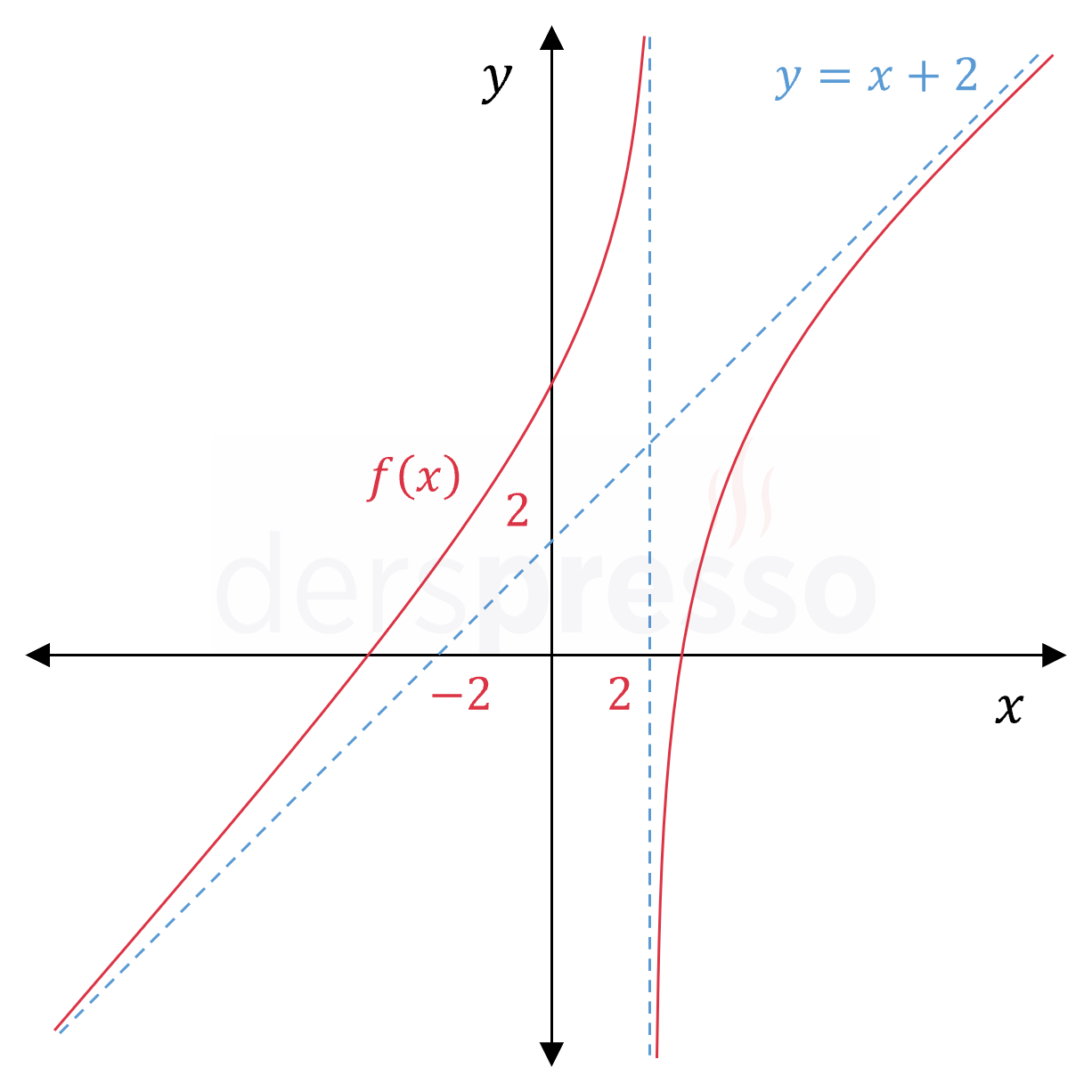
Eğri Asimptot
Asimptotlar sadece doğrusal değil, ikinci ya da daha yüksek dereceden birer polinom fonksiyonu da olabilir. Bu tip doğrusal olmayan asimptotlara eğri asimptot denir.
Aşağıdaki grafikte mavi kesikli çizgi ile gösterilen \( y = x^2 - 2x + 1 \) eğrisi \( f(x) = \frac{x^3 - 2x^2 + x - 1}{x} \) fonksiyonunun eğri asimptotudur.
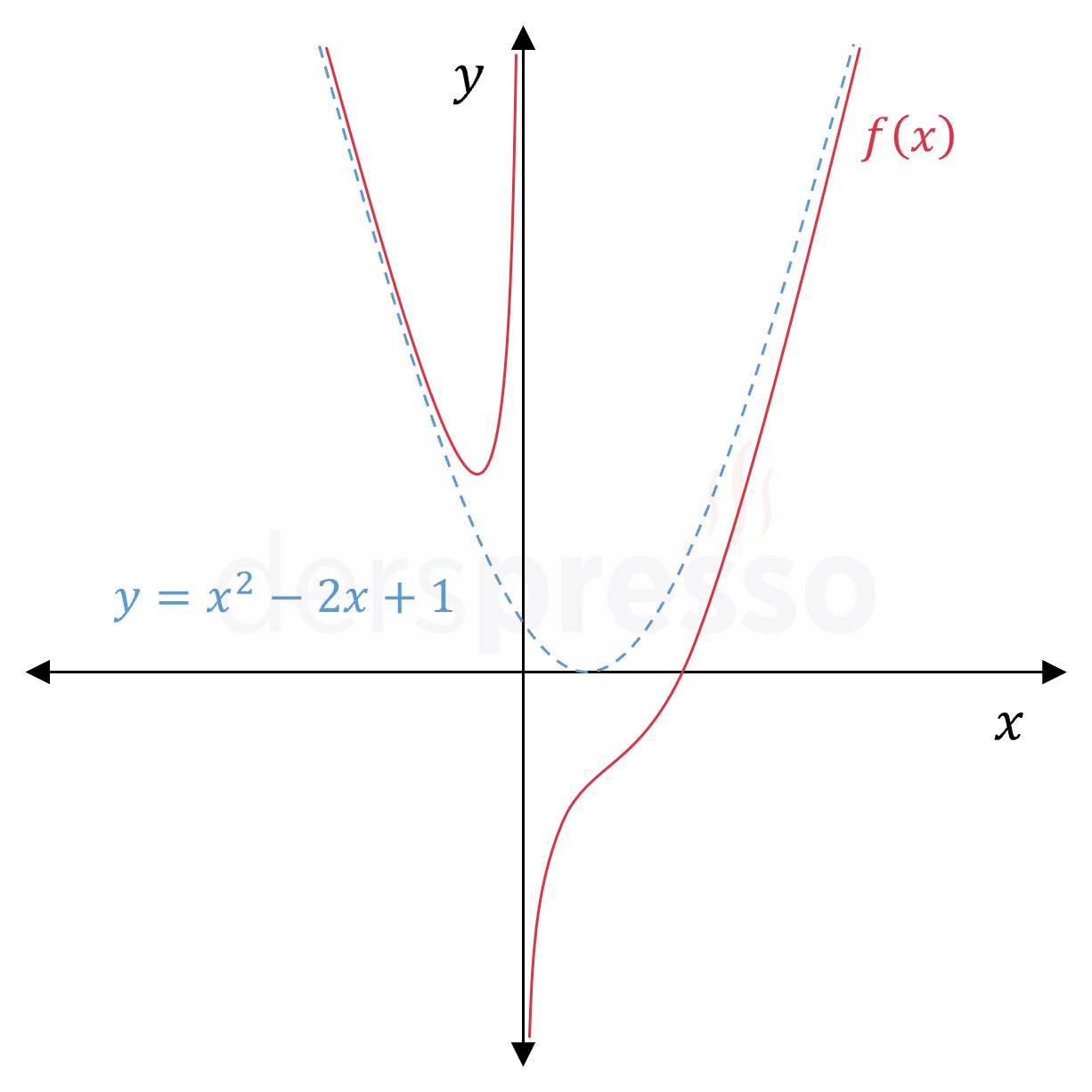
Yatay/Eğik/Eğri Asimptotun Bulunması
Bir fonksiyon yatay, eğik ve eğri asimptot tiplerinden sadece birine sahip olabilir. Rasyonel fonksiyonların yatay/eğik/eğri asimptotunun denklemi aşağıdaki yöntemle bulunabilir.
\( p(x), q(x) \) birer polinom ve \( q(x) \ne 0 \) olmak üzere,
\( f(x) = \dfrac{p(x)}{q(x)} = \dfrac{ax^{m} + \ldots}{bx^{n} + \ldots} \)
Paydaki polinom paydadaki polinoma bölündüğünde elde edilen bölüm polinomuna \( b(x) \) diyelim.
\( p(x) = q(x)b(x) + k(x) \)
Bu polinom bölme işleminden elde edilen \( b(x) \) polinomu yatay/eğik/eğri asimptotun denklemini verir. Bölme işleminin sonucu dört farklı şekilde olabilir.
| Payın ve Paydanın Derecesi | Asimptot Denklemi | Örnek |
|---|---|---|
|
Payın derecesi paydanınkinden küçük \( m \lt n \) |
Bu durumda \( b(x) = 0 \) olacağı için asimptot denklemi \( y = 0 \) olur, dolayısıyla \( x \) ekseni ile çakışık yatay bir asimptot oluşur. \( der[b(x)] = 0 \) Asimptot denklemi: \( y = 0 \) |
\( f(x) = \dfrac{1}{x} \) Asimptot denklemi: \( y = 0 \) |
|
Payın derecesi paydanınkine eşit \( m = n \) |
Bu durumda bölüm polinomu sabit fonksiyon, asimptot denklemi de pay ve paydanın başkatsayılarının oranı olur, dolayısıyla yine yatay bir asimptot oluşur. \( der[b(x)] = m - n = 0 \) Asimptot denklemi: \( y = \dfrac{a}{b} \) |
\( f(x) = \dfrac{2x - 1}{x + 1} \) Asimptot denklemi: \( y = \dfrac{2}{1} = 2 \) |
|
Payın derecesi paydanınkinden 1 fazla \( m - n = 1 \) |
Bu durumda bölüm polinomu doğrusal fonksiyon, asimptot denklemi \( y = mx + c \) şeklinde bir doğru olur. \( der[b(x)] = m - n = 1 \) Asimptot denklemi: \( y = mx + c \) |
\( f(x) = \dfrac{x^2 - 9}{x - 2} \) Asimptot denklemi: \( y = x + 2 \) |
|
Payın derecesi paydanınkinden 2+ fazla \( m - n \gt 1 \) |
Bu durumda bölüm polinomunun ve asimptot denkleminin derecesi pay ve paydanın derecelerinin farkına eşit olur, yani ikinci ya da daha yüksek dereceden bir eğri asimptot oluşur. \( der[b(x)] = m - n \gt 1 \) Asimptot denklemi: \( y = ax^{m - n} + \ldots \) |
\( f(x) = \dfrac{x^3 - 2x^2 + x - 1}{x} \) Asimptot denklemi: \( y = x^2 - 2x + 1 \) |
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to \infty} {\dfrac{2x + 7}{x^2 + 1}} \)
(b) \( \lim\limits_{x \to -\infty} {\dfrac{3x^2 + 7x + 12}{2x + 4}} \)
(c) \( \lim\limits_{x \to \infty} {\dfrac{5x^2 + 3x + 6}{3x^2 - 2x + 7}} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to \infty} {\dfrac{2x + 7}{x^2 + 1}} \)
Paydasının derecesi payının derecesinden daha büyük olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti sıfıra eşittir.
\( = 0 \)
(b) seçeneği:
\( \lim\limits_{x \to -\infty} {\dfrac{3x^2 + 7x + 12}{2x + 4}} \)
Payının derecesi paydasının derecesinden daha büyük olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti pay ve paydadaki en yüksek dereceli terimlerin birbirine bölümünün limitine eşittir.
\( = \lim\limits_{x \to -\infty} {\dfrac{3x^2}{2x}} \)
\( = \lim\limits_{x \to -\infty} {\dfrac{3x}{2}} \)
\( = -\infty \)
(c) seçeneği:
\( \lim\limits_{x \to \infty} {\dfrac{5x^2 + 3x + 6}{3x^2 - 2x + 7}} \)
Pay ve paydasının dereceleri eşit olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti pay ve paydadaki polinomların başkatsayılarının oranına eşittir.
\( = \dfrac{5}{3} \)
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to -\infty} {\dfrac{5x^7 - x^4 + 7}{-2x^9 + x^3 - 3}} \)
(b) \( \lim\limits_{x \to -\infty} {\dfrac{7x^5 - 2x^2 + 4}{2x^3 + 3x^2 - x + 9}} \)
(c) \( \lim\limits_{x \to -\infty} {\dfrac{-4x^4 + x^3 - 2x}{2x^4 + x + 7}} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to -\infty} {\dfrac{5x^7 - x^4 + 7}{-2x^9 + x^3 - 3}} \)
Paydasının derecesi payının derecesinden daha büyük olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti sıfıra eşittir.
\( = 0 \)
(b) seçeneği:
\( \lim\limits_{x \to -\infty} {\dfrac{7x^5 - 2x^2 + 4}{2x^3 + 3x^2 - x + 9}} \)
Payının derecesi paydasının derecesinden daha büyük olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti pay ve paydadaki en yüksek dereceli terimlerin birbirine bölümünün limitine eşittir.
\( \lim\limits_{x \to -\infty} {\dfrac{7x^5}{2x^3}} \)
\( \lim\limits_{x \to -\infty} {\dfrac{7x^2}{2}} \)
\( x \to -\infty \) iken \( x^2 \to \infty \) olur.
\( = \infty \)
(c) seçeneği:
\( \lim\limits_{x \to -\infty} {\dfrac{-4x^4 + x^3 - 2x}{2x^4 + x + 7}} \)
Pay ve paydasının dereceleri eşit olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti pay ve paydadaki polinomların başkatsayılarının oranına eşittir.
\( = \dfrac{-4}{2} = -2 \)
Aşağıdakilerden hangisi \( f \) fonksiyonunun bir yatay asimptotunun olduğunu gösterir?
(a) \( \lim\limits_{x \to 4} {f(x)} = 2 \)
(b) \( \lim\limits_{x \to 4} {f(x)} = \infty \)
(c) \( \lim\limits_{x \to \infty} {f(x)} = 2 \)
(d) \( \lim\limits_{x \to \infty} {f(x)} = \infty \)
(e) \( \lim\limits_{x \to \infty} {f(x)} = \) Tanımsız
Çözümü GösterBir fonksiyonda \( x \) pozitif ya da negatif sonsuza giderken fonksiyon değeri belirli bir \( a \) reel sayı değerine yaklaşıyorsa bu \( x \) değerinde fonksiyonun bir yatay asimptotu vardır.
\( \lim\limits_{x \to \pm\infty} {f(x)} = a \)
(c) seçeneğindeki ifade \( y = 2 \) doğrusunun fonksiyonun bir yatay asimptotu olduğunu gösterir.
\( \lim\limits_{x \to \infty} \dfrac{5x + \abs{2 - 5x}}{3 - 4x} \) limitinin sonucunu bulunuz.
Çözümü Göster\( x \to \infty \) iken \( (2 - 5x) \to -\infty \) olduğu için mutlak değer içindeki ifade mutlak değerden negatif işaretli çıkar.
\( \lim\limits_{x \to \infty} \dfrac{5x + \abs{2 - 5x}}{3 - 4x} = \lim\limits_{x \to \infty} \dfrac{5x - 2 + 5x}{3 - 4x} \)
\( = \lim\limits_{x \to \infty} \dfrac{10x - 2}{3 - 4x} \)
Payının derecesi paydasının derecesine eşit olan rasyonel fonksiyonlarda \( x \) pozitif ve negatif sonsuza giderken fonksiyon polinomların başkatsayılarının oranına yaklaşır.
\( = \dfrac{10}{-4} = -\dfrac{5}{2} \) bulunur.
\( \lim\limits_{x \to \infty} {\dfrac{9^x + 6^x}{6^x + 4^x}} \) limitinin sonucu kaçtır?
Çözümü GösterBüyüme hızları farklı terimlerden oluşan bir rasyonel ifadenin sonsuzdaki limitini, sadece pay ve paydadaki büyüme hızı en büyük olan terimleri dikkate alarak bulabiliriz.
\( \lim\limits_{x \to \infty} {\dfrac{9^x + 6^x}{6^x + 4^x}} = \lim\limits_{x \to \infty} {\dfrac{9^x}{6^x}} \)
\( = \lim\limits_{x \to \infty} \left( \dfrac{9}{6} \right)^x \)
\( = \lim\limits_{x \to \infty} \left( \dfrac{3}{2} \right)^x \)
\( x \to \infty \) iken \( (\frac{3}{2})^x \to \infty \) olur.
\( = \infty \)
Aşağıdaki fonksiyonların yatay asimptotlarını bulunuz.
(a) \( f(x) = \dfrac{x - 5}{\abs{x} + 5} \)
(b) \( g(x) = 5^{2x - 3} \)
(c) \( h(x) = \arccot(2x + 1) \)
Çözümü GösterBir fonksiyonda \( x \) pozitif ya da negatif sonsuza giderken fonksiyon değeri belirli bir \( a \) reel sayısına yaklaşıyorsa bu \( y = a \) doğrusu fonksiyonun bir yatay asimptotudur.
(a) seçeneği:
\( f(x) = \dfrac{x - 5}{\abs{x} + 5} \)
Fonksiyonun negatif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to -\infty} {\dfrac{x - 5}{\abs{x} + 5}} \)
\( x \to -\infty \) iken \( \abs{x} = -x \) olur.
\( = \lim\limits_{x \to -\infty} {\dfrac{x - 5}{-x + 5}} \)
Pay ve paydasının dereceleri eşit olan rasyonel fonksiyonların pozitif ve negatif sonsuzdaki limiti pay ve paydadaki polinomların başkatsayılarının oranına eşittir.
\( = -1 \)
\( y = -1 \) doğrusu \( x \) negatif sonsuza giderken fonksiyonun bir yatay asimptotudur.
Fonksiyonun pozitif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to \infty} {\dfrac{x - 5}{\abs{x} + 5}} \)
\( x \to \infty \) iken \( \abs{x} = x \) olur.
\( = \lim\limits_{x \to \infty} {\dfrac{x - 5}{x + 5}} = 1 \)
\( y = 1 \) doğrusu \( x \) pozitif sonsuza giderken fonksiyonun bir yatay asimptotudur.
Buna göre fonksiyonun \( y = -1 \) ve \( y = 1 \) doğruları olmak üzere iki yatay asimptotu vardır.
(b) seçeneği:
\( g(x) = 5^{2x - 3} \)
Fonksiyonun negatif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to -\infty} {5^{2x - 3}} \)
Üstel fonksiyon tüm reel sayılarda tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini üsse alabiliriz.
\( = 5^{\lim\limits_{x \to -\infty} {2x - 3}} \)
\( x \to -\infty \) iken \( 2x - 3 \to -\infty \) olur.
\( = 5^{-\infty} \)
\( x \to -\infty \) iken \( 5^x \to 0 \) olur.
\( = 0 \)
\( y = 0 \) doğrusu \( x \) negatif sonsuza giderken fonksiyonun bir yatay asimptotudur.
Fonksiyonun pozitif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to \infty} {5^{2x - 3}} = \infty \)
\( x \) pozitif sonsuza giderken fonksiyonun bir yatay asimptotu yoktur.
Buna göre fonksiyonun \( y = 0 \) doğrusu olmak üzere tek bir yatay asimptotu vardır.
(c) seçeneği:
\( h(x) = \arccot(2x + 1) \)
Fonksiyonun negatif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to -\infty} {\arccot(2x + 1)} \)
\( x \to -\infty \) iken \( 2x + 1 \to -\infty \) olur.
\( = \arccot(-\infty) \)
\( x \to -\infty \) iken \( \arccot{x} \to \pi \) olur.
\( = \pi \)
\( y = \pi \) doğrusu \( x \) negatif sonsuza giderken fonksiyonun bir yatay asimptotudur.
Fonksiyonun pozitif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to \infty} {\arccot(2x + 1)} \)
\( x \to \infty \) iken \( 2x + 1 \to \infty \) olur.
\( = \arccot{\infty} \)
\( x \to \infty \) iken \( \arccot{x} \to 0 \) olur.
\( = 0 \)
\( y = 0 \) doğrusu \( x \) pozitif sonsuza giderken fonksiyonun bir yatay asimptotudur.
Buna göre fonksiyonun \( y = \pi \) ve \( y = 0 \) doğruları olmak üzere iki yatay asimptotu vardır.
\( f(x) = \dfrac{5x + 4}{\sqrt{x^2 + 2x - 3}} \) fonksiyonunun yatay asimptotlarını bulunuz.
Çözümü GösterFonksiyonun negatif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to -\infty} \dfrac{5x + 4}{\sqrt{x^2 + 2x - 3}} \)
Pay ve paydadaki terimleri \( x \)'in paydadaki en yüksek dereceli üssü olan \( \abs{x} \) ifadesine bölelim.
\( x \to -\infty \) iken \( \abs{x} = -x = \sqrt{x^2} \) olur.
\( = \lim\limits_{x \to -\infty} \dfrac{-5 - \frac{4}{x}}{\frac{\sqrt{x^2 + 2x - 3}}{-x}} \)
\( x \) ifadesini kök içine alalım.
\( = \lim\limits_{x \to -\infty} \dfrac{-5 - \frac{4}{x}}{\sqrt{\frac{x^2 + 2x - 3}{x^2}}} \)
\( = \lim\limits_{x \to -\infty} \dfrac{-5 - \frac{4}{x}}{\sqrt{1 + \frac{2}{x} - \frac{3}{x^2}}} \)
Limit işlemini önce bölme kuralı ile paya ve paydaya, daha sonra bileşke fonksiyon kuralı ile payda kök içine ve toplama kuralı ile paydadaki terimlere dağıtalım.
\( = \dfrac{-\lim\limits_{x \to -\infty} {5} - \lim\limits_{x \to -\infty} {\frac{4}{x}}}{\sqrt{\lim\limits_{x \to -\infty} {1} + \lim\limits_{x \to -\infty} {\frac{2}{x}} - \lim\limits_{x \to -\infty} \frac{3}{x^2}}} \)
\( x \to -\infty \) iken \( \frac{1}{x^n} \to 0 \) olur.
\( = \dfrac{-5 - 0}{\sqrt{1 + 0 - 0}} \)
\( = -5 \)
Buna göre \( y = -5 \) doğrusu \( x \) negatif sonsuza giderken \( f \) fonksiyonunun yatay asimptotudur.
Fonksiyonun pozitif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to \infty} \dfrac{5x + 4}{\sqrt{x^2 + 2x - 3}} \)
Pay ve paydadaki terimleri \( x \)'in paydadaki en yüksek dereceli üssü olan \( \abs{x} \) ifadesine bölelim.
\( x \to \infty \) iken \( \abs{x} = x = \sqrt{x^2} \) olur.
\( = \lim\limits_{x \to \infty} \dfrac{5 + \frac{4}{x}}{\frac{\sqrt{x^2 + 2x - 3}}{x}} \)
\( x \) ifadesini kök içine alalım.
\( = \lim\limits_{x \to \infty} \dfrac{5 + \frac{4}{x}}{\sqrt{\frac{x^2 + 2x - 3}{x^2}}} \)
\( = \lim\limits_{x \to \infty} \dfrac{5 + \frac{4}{x}}{\sqrt{1 + \frac{2}{x} - \frac{3}{x^2}}} \)
Limit işlemini önce bölme kuralı ile paya ve paydaya, daha sonra bileşke fonksiyon kuralı ile payda kök içine ve toplama kuralı ile paydadaki terimlere dağıtalım.
\( = \dfrac{\lim\limits_{x \to \infty} {5} + \lim\limits_{x \to \infty} {\frac{4}{x}}}{\sqrt{\lim\limits_{x \to \infty} {1} + \lim\limits_{x \to \infty} {\frac{2}{x}} - \lim\limits_{x \to \infty} \frac{3}{x^2}}} \)
\( x \to \infty \) iken \( \frac{1}{x^n} \to 0 \) olur.
\( = \dfrac{5 + 0}{\sqrt{1 + 0 - 0}} \)
\( = 5 \)
Buna göre \( y = 5 \) doğrusu \( x \) pozitif sonsuza giderken \( f \) fonksiyonunun yatay asimptotudur.
\( f(x) = \sqrt{2x + 1} - \sqrt{2x} \) fonksiyonunun yatay asimptotlarını bulunuz.
Çözümü Göster\( f \) fonksiyonu sadece \( x \ge 0 \) için tanımlı olduğu için sadece pozitif sonsuzdaki yatay asimptotu inceleyebiliriz.
Fonksiyonun pozitif sonsuzdaki limitini bulalım.
\( \lim\limits_{x \to \infty} \sqrt{2x + 1} = \infty \)
\( \lim\limits_{x \to \infty} \sqrt{2x} = \infty \)
Buna göre verilen limit ifadesinde \( \infty - \infty \) belirsizliği vardır.
Belirsizliği gidermek için payı ve paydayı paydaki ifadenin eşleniği ile çarpalım.
\( \lim\limits_{x \to \infty} \dfrac{(\sqrt{2x + 1} - \sqrt{2x})(\sqrt{2x + 1} + \sqrt{2x})}{\sqrt{2x + 1} + \sqrt{2x}} \)
\( = \lim\limits_{x \to \infty} \dfrac{(\sqrt{2x + 1})^2 - (\sqrt{2x})^2}{\sqrt{2x + 1} + \sqrt{2x}} \)
\( = \lim\limits_{x \to \infty} \dfrac{2x + 1 - 2x}{\sqrt{2x + 1} + \sqrt{2x}} \)
\( = \lim\limits_{x \to \infty} \dfrac{1}{\sqrt{2x + 1} + \sqrt{2x}} \)
\( x \to \infty \) iken paydadaki ifade pozitif sonsuza gider.
\( = 0 \)
Buna göre \( y = 0 \) doğrusu \( x \) pozitif sonsuza giderken \( f \) fonksiyonunun yatay asimptotudur.