Parabolün Denkleminin Bulunması
Bir parabolün denklemini yazabilmek için aşağıdakilerden biri bilinmelidir.
- Parabolün tepe noktası ve ikinci bir nokta
- Parabol \( x \) eksenini iki noktada kesiyorsa bu iki nokta ve üçüncü bir nokta
- Parabol \( x \) eksenini tek bir noktada (teğet) kesiyorsa bu nokta ve ikinci bir nokta
- Parabolün geçtiği herhangi farklı üç nokta
Tepe Noktası Bilinen Parabolün Denklemi
İnteraktif uygulama: Tepe Noktası Bilinen Parabolün Denklemi
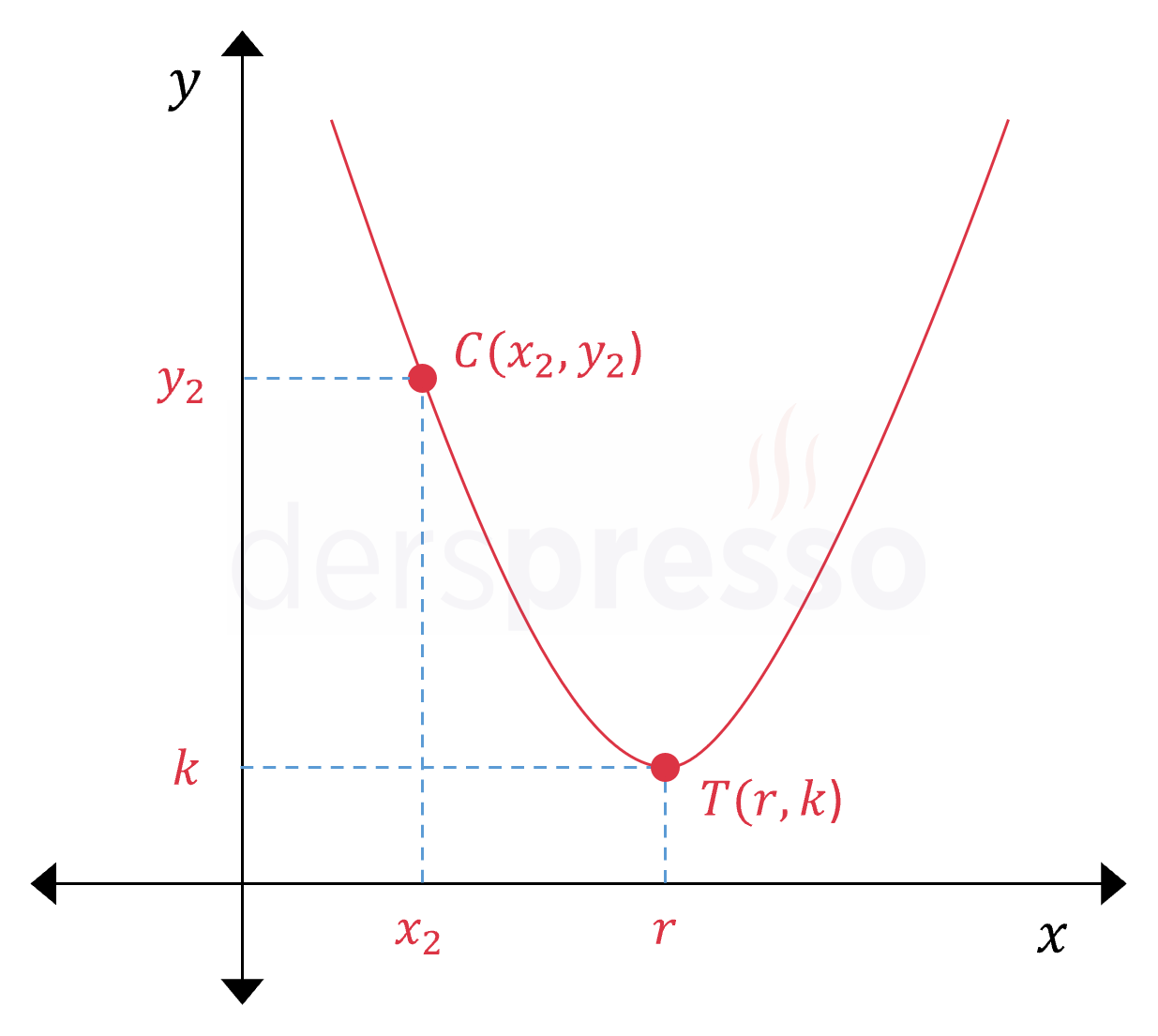
Tepe noktası ve ikinci bir noktası bilinen parabolün denklemi aşağıdaki formülle bulunabilir.
Tepe noktası \( T(r, k) \), ikinci noktanın koordinatları \( C(x_2, y_2) \) olmak üzere,
\( y = a(x - r)^2 + k \)
Bu formülde önce tepe noktasının koordinatları denklemde yerine konur. Sonra ikinci noktanın koordinatları denklemde \( x \) ve \( y \) yerine konarak \( a \) başkatsayısı hesaplanır.
İkinci nokta parabolün \( y \) eksenini kestiği nokta olmak zorunda değildir, parabol üzerindeki herhangi bir nokta olabilir.
Tepe noktası \( T(1, 3) \) olan ve \( C(-1, 11) \) noktasından geçen parabolün denklemi:
\( y = a(x - r)^2 + k \)
Tepe noktasının koordinatlarını denklemde yerine koyalım.
\( y = a(x - 1)^2 + 3 \)
İkinci noktanın koordinatlarını denklemde yerine koyarak başkatsayıyı bulalım.
\( 11 = a(-1 - 1)^2 + 3 \)
\( a = 2 \)
Parabolün denklemi aşağıdaki gibi bulunur.
\( y = 2(x - 1)^2 + 3 \)
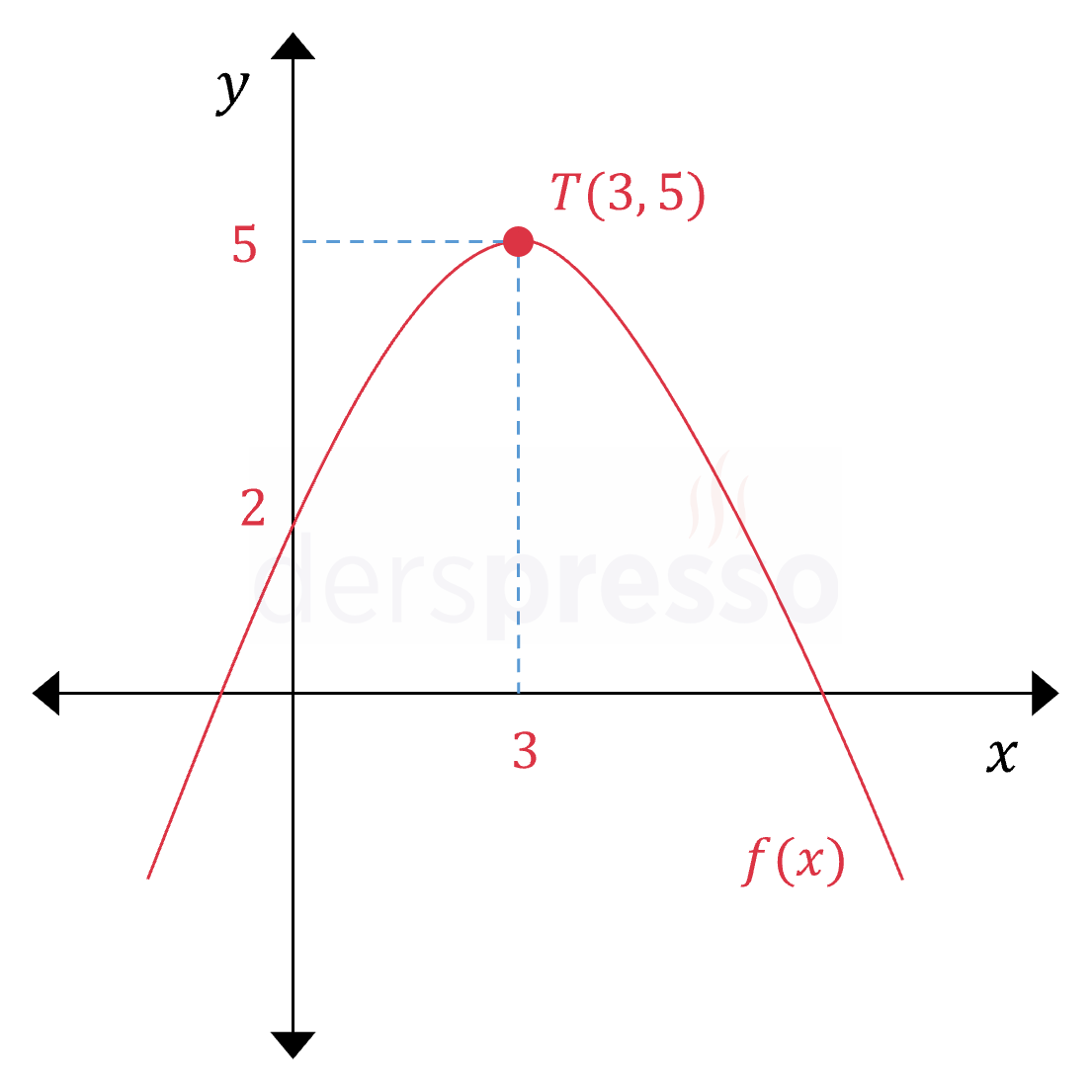
Yukarıda grafiği verilen parabolün denklemini bulunuz.
Çözümü GösterParabolün tepe noktası \( T(3, 5) \) olduğundan tepe noktası bilinen parabolün denklemi formülünü kullanalım.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( f(x) = a(x - r)^2 + k \)
\( f(x) = a(x - 3)^2 + 5 \)
Parabolün \( y \) eksenini kestiği \( (0, 2) \) noktasını denklemde yerine koyarak \( a \) katsayısını bulalım.
\( 2 = a(0 - 3)^2 + 5 \)
\( 2 = 9a + 5 \)
\( a = -\dfrac{1}{3} \)
Buna göre parabolün denklemi aşağıdaki gibi bulunur.
\( f(x) = -\dfrac{1}{3}(x - 3)^2 + 5 \)
x Eksenini Kestiği İki Nokta Bilinen Parabolün Denklemi
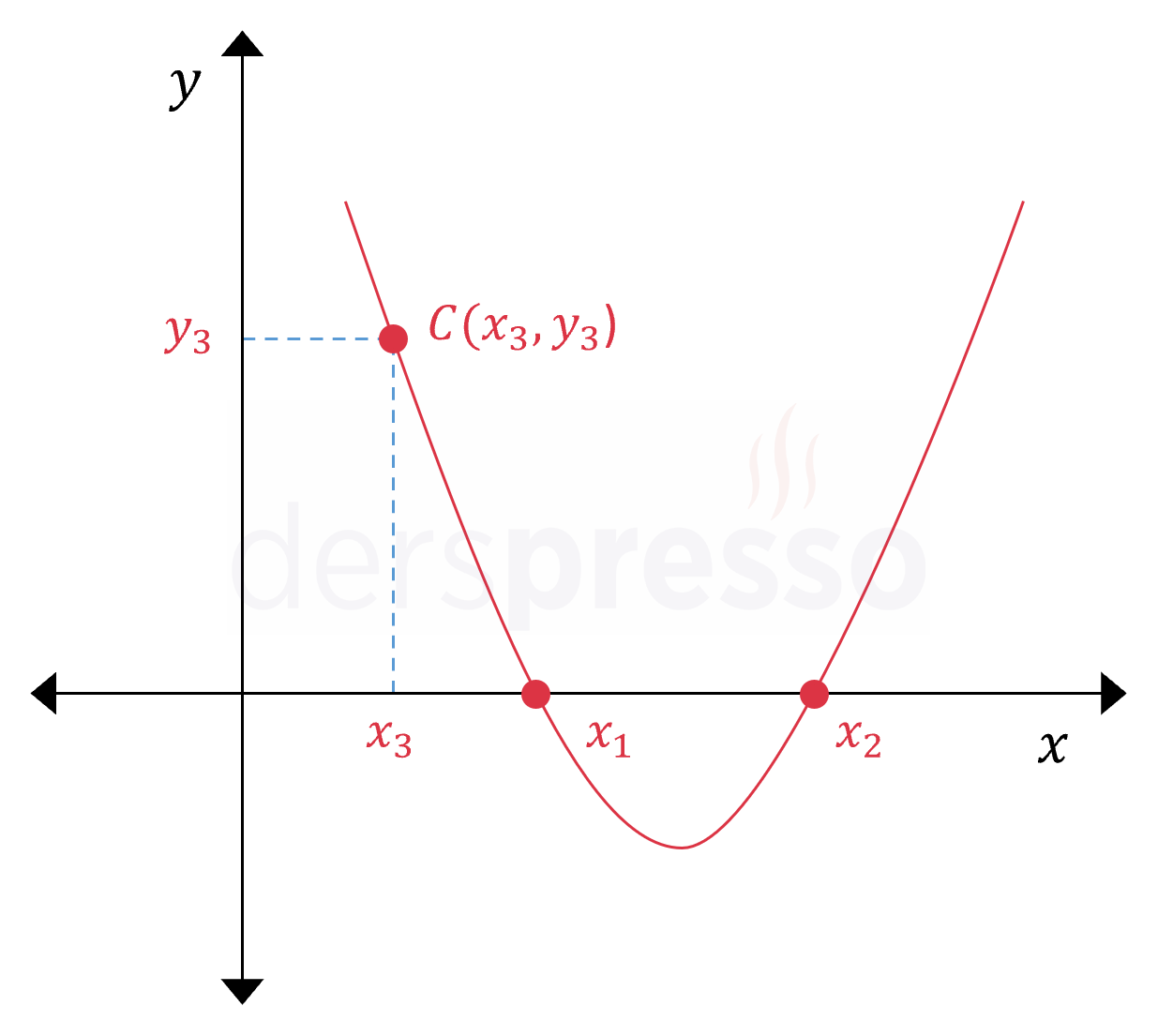
\( x \) eksenini kestiği iki nokta ve üçüncü bir noktası bilinen parabolün denklemi aşağıdaki formülle bulunabilir.
\( x \) eksenini kestiği noktaların apsisleri \( x_1 \) ve \( x_2 \), üçüncü noktanın koordinatları \( C(x_3, y_3) \) olmak üzere,
\( y = a(x - x_1)(x - x_2) \)
Bu formülde önce parabolün \( x \) eksenini kestiği noktaların apsis değerleri denklemde yerine konur. Sonra üçüncü noktanın koordinatları denklemde \( x \) ve \( y \) yerine konarak \( a \) başkatsayısı hesaplanır.
Üçüncü nokta parabolün \( y \) eksenini kestiği nokta olmak zorunda değildir, parabol üzerindeki herhangi bir nokta olabilir.
\( x \) eksenini \( -3 \) ve \( 2 \) noktalarında kesen ve \( C(-2, 12) \) noktasından geçen parabolün denklemi:
\( y = a(x - x_1)(x - x_2) \)
\( x \) eksenini kestiği noktaların apsis değerlerini denklemde \( x_1 \) ve \( x_2 \) yerine koyalım.
\( y = a(x - (-3))(x - 2) \)
Üçüncü noktanın koordinatlarını denklemde yerine koyarak başkatsayıyı bulalım.
\( 12 = a(-2 + 3)(-2 - 2) \)
\( a = -3 \)
Parabolün denklemi aşağıdaki gibi bulunur.
\( y = -3(x + 3)(x - 2) \)
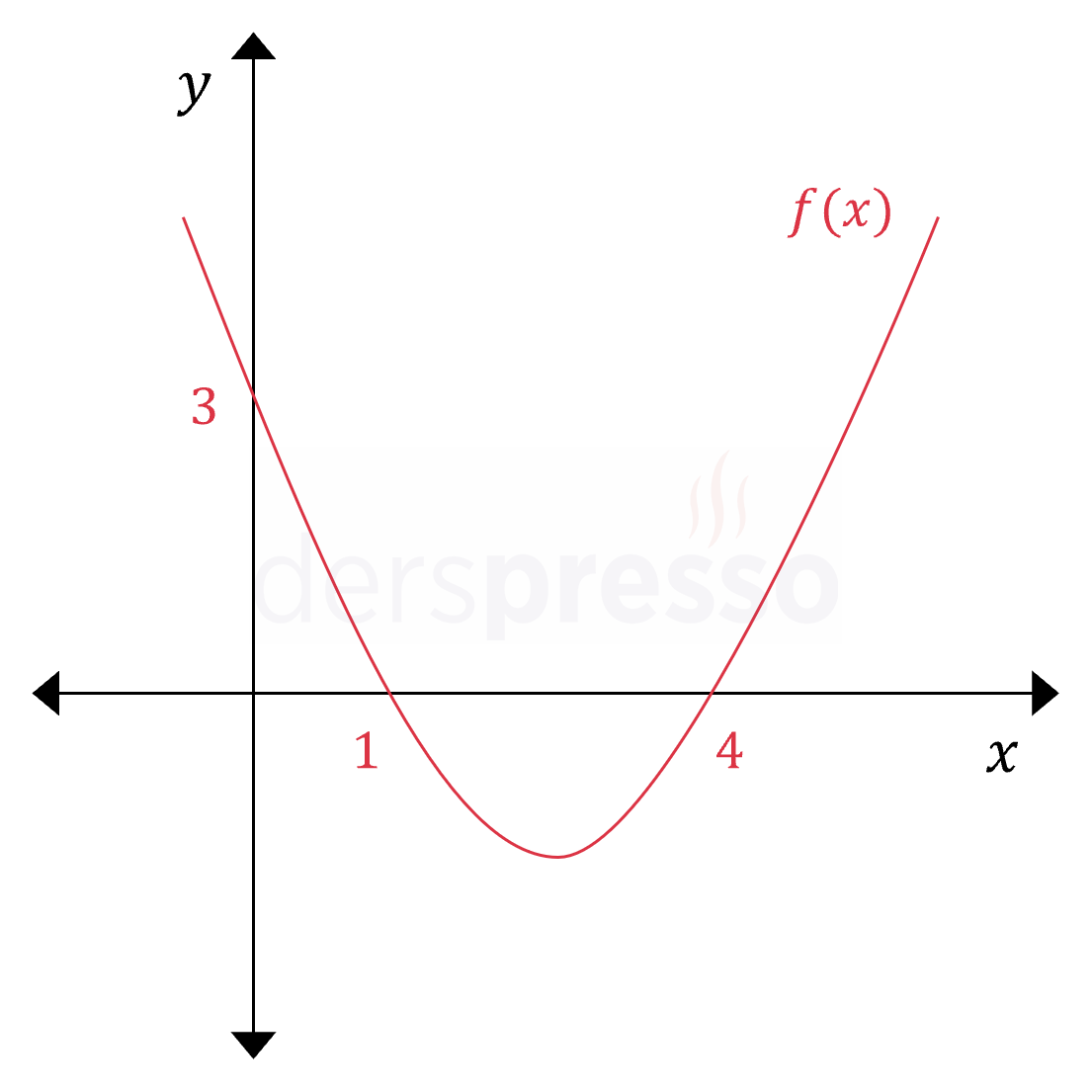
Yukarıda grafiği verilen parabolün denklemini bulunuz.
Çözümü GösterParabolün \( x \) eksenini kestiği noktalar verildiği için \( x \) eksenini kestiği iki nokta bilinen parabolün denklemi formülünü kullanalım.
\( f(x) = a(x - x_1)(x - x_2) \)
\( f(x) = a(x - 1)(x - 4) \)
Parabolün geçtiği \( (0, 3) \) noktasını denklemde yerine koyarak \( a \) katsayısını bulalım.
\( 3 = a(0 - 1)(0 - 4) \)
\( a = \dfrac{3}{4} \)
Buna göre parabolün denklemi aşağıdaki gibi bulunur.
\( f(x) = \dfrac{3}{4}(x - 1)(x - 4) \)
x Eksenini Teğet Kestiği Nokta Bilinen Parabolün Denklemi
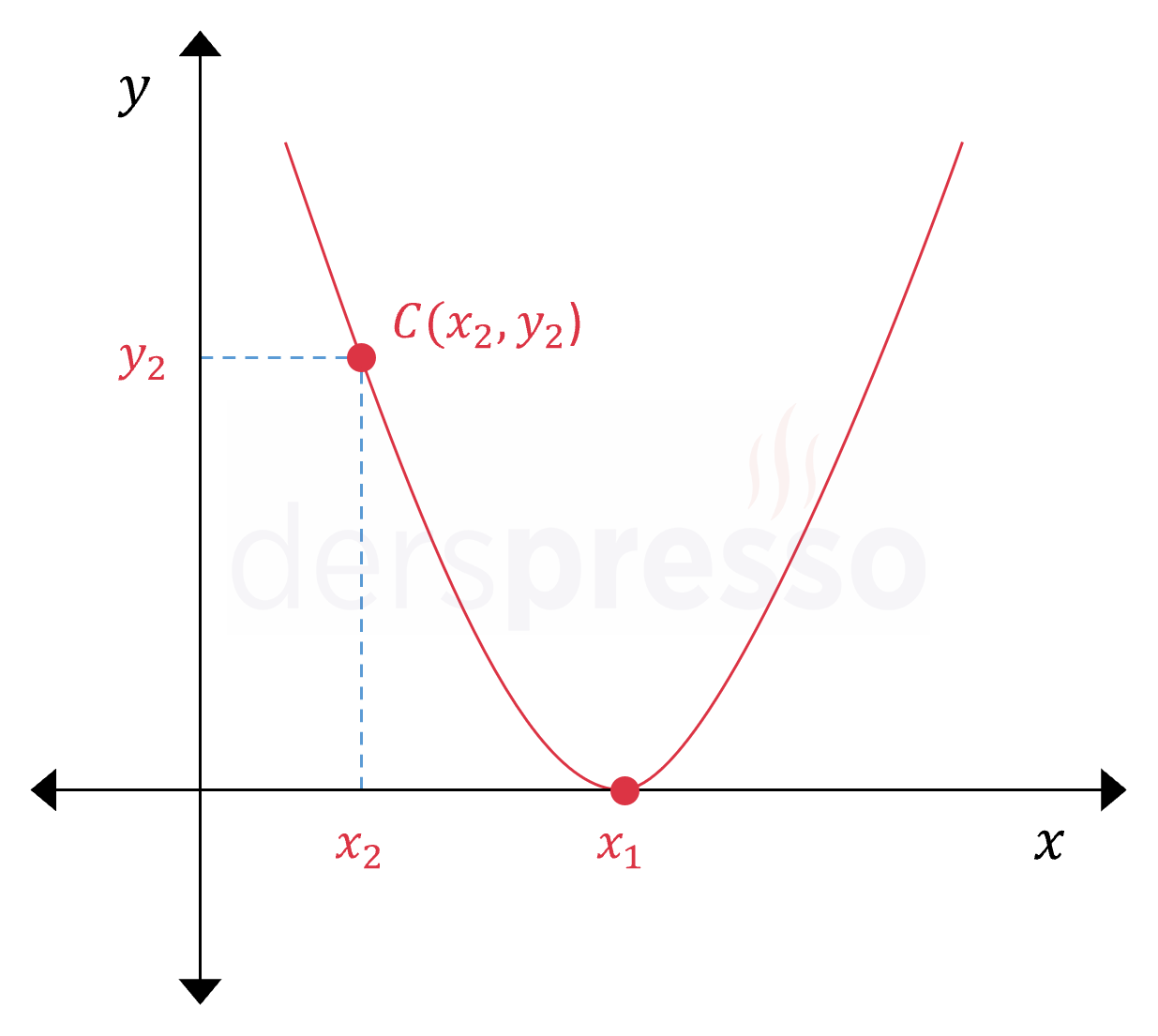
\( x \) eksenini teğet kestiği tek nokta ve ikinci bir noktası bilinen parabolün denklemi aşağıdaki formülle bulunabilir.
\( x \) eksenini kestiği noktanın apsisi \( x_1 \), ikinci noktanın koordinatları \( C(x_2, y_2) \) olmak üzere,
\( y = a(x - x_1)^2 \)
Bu formülde önce parabolün \( x \) eksenini teğet kestiği noktanın apsis değeri denklemde yerine konur. Sonra ikinci noktanın koordinatları denklemde \( x \) ve \( y \) yerine konarak \( a \) başkatsayısı hesaplanır.
İkinci nokta parabolün \( y \) eksenini kestiği nokta olmak zorunda değildir, parabol üzerindeki herhangi bir nokta olabilir.
\( x \) eksenini \( 2 \) noktasında teğet kesen ve \( C(0, -4) \) noktasından geçen parabolün denklemi:
\( y = a(x - x_1)^2 \)
\( x \) eksenini kestiği noktanın apsis değerini denklemde \( x_1 \) yerine koyalım.
\( y = a(x - 2)^2 \)
İkinci noktanın koordinatlarını denklemde yerine koyarak başkatsayıyı bulalım.
\( -4 = a(0 - 2)^2 \)
\( a = -1 \)
Parabolün denklemi aşağıdaki gibi bulunur.
\( y = -(x - 2)^2 \)
Herhangi Üç Noktası Bilinen Parabolün Denklemi
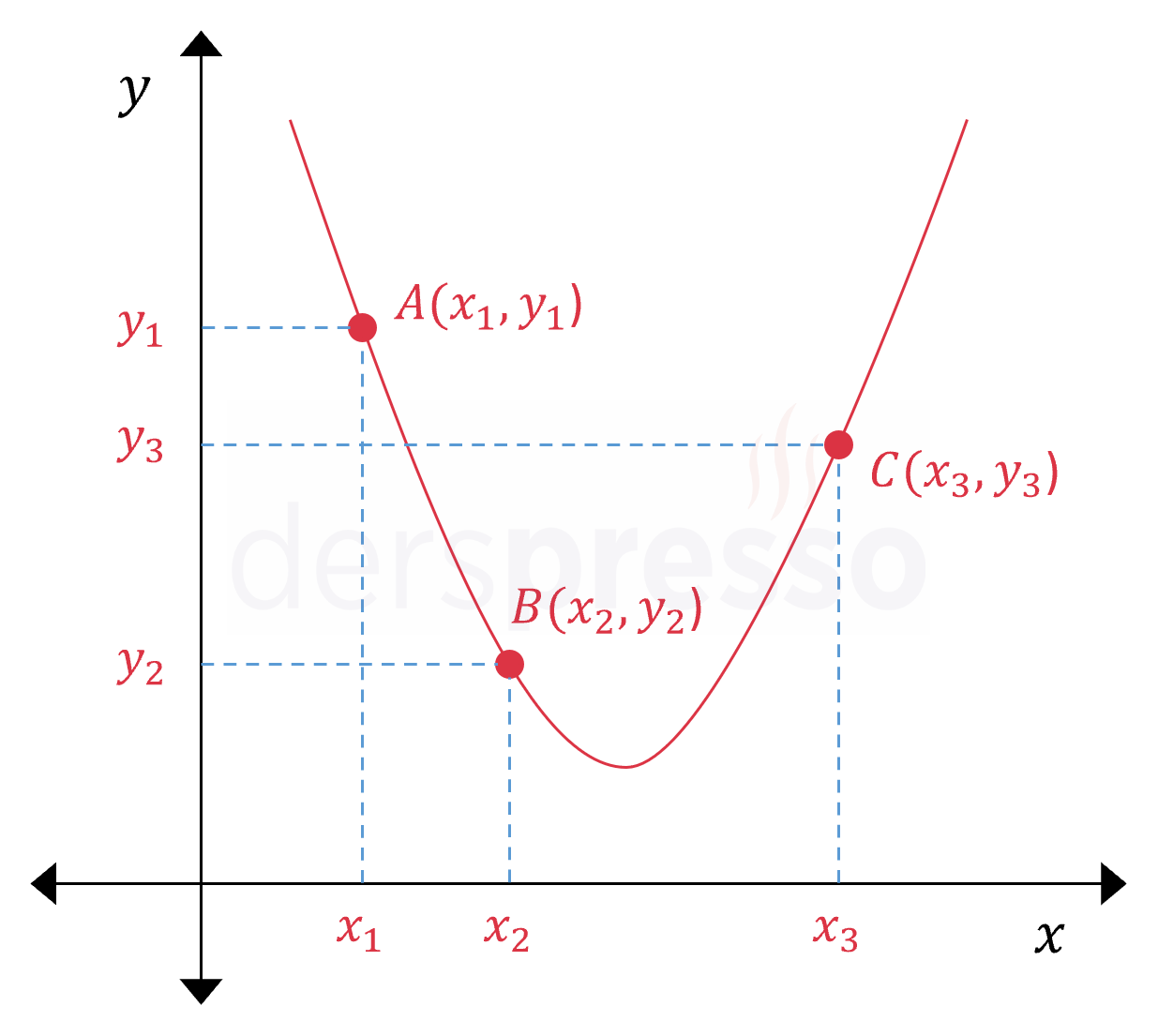
Herhangi üç noktası bilinen parabolün denklemini bulmak için; bu üç noktanın koordinatları parabol denkleminde yerlerine konur, bilinmeyenleri \( a \), \( b \) ve \( c \) olan üç bilinmeyenli üç lineer denklem elde edilir ve bu denklem sistemi çözülür. Daha sonra bulunan \( a \), \( b \) ve \( c \) katsayı değerleri denklemde yerine yazılarak parabol denklemi elde edilir.
Parabolün geçtiği noktalar \( A(x_1, y_1) \), \( B(x_2, y_2) \), \( C(x_3, y_3) \) olmak üzere,
\( y = ax^2 + bx + c \)
Noktaların koordinatları denklemde yerine konduğunda elde edilen lineer denklemler:
\( y_1 = ax_1^2 + bx_1 + c \)
\( y_2 = ax_2^2 + bx_2 + c \)
\( y_3 = ax_3^2 + bx_3 + c \)
\( A(-1, 6) \), \( B(1, 2) \) ve \( C(4, 11) \) noktalarından geçen parabolün denklemi:
\( y = ax^2 + bx + c \)
Üç noktayı denklemde yerine koyarak üç bilinmeyenli üç lineer denklem elde edelim.
\( 6 = a(-1)^2 + b(-1) + c \)
\( 2 = a(1)^2 + b(1) + c \)
\( 11 = a(4)^2 + b(4) + c \)
Denklemleri düzenleyelim.
\( a - b + c = 6 \)
\( a + b + c = 2 \)
\( 16a + 4b + c = 11 \)
Bu lineer denklem sistemini çözdüğümüzde \( a \), \( b \) ve \( c \) için aşağıdaki değerleri buluruz.
\( a = 1, \quad b = -2, \quad c = 3 \)
Parabolün denklemi aşağıdaki gibi bulunur.
\( y = x^2 - 2x + 3 \)
Birinci dereceden denklem sistemlerinin çözüm yöntemleri için birinci dereceden denklem sistemleri sayfasını inceleyebilirsiniz.
\( f(x) = ax^2 + bx + c \) parabolünün grafiğinin eksenleri kestiği bölümler aşağıda verilmiştir.

Buna göre \( a + b + c \) toplamı kaçtır?
Çözümü GösterVerilen grafiklere göre parabol \( x \) eksenini tek bir \( x = -4 \) noktasında, \( y \) eksenini de \( y = -32 \) noktasında kesmektedir.
Buna göre parabolün tepe noktası \( x \) eksenine teğet olduğu \( T(-4, 0) \) noktasıdır.
Tepe noktası \( T(r, k) \) olan parabolün denklemi formülünü kullanalım.
\( f(x) = a(x - r)^2 + k \)
\( f(x) = a(x + 4)^2 + 0 \)
Parabolün \( y \) eksenini kestiği \( (0, -32) \) noktasının koordinatlarını denklemde yerine koyalım.
\( f(0) = a(0 + 4)^2 = -32 \)
\( a = -2 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = -2(x + 4)^2 \)
Parantez içindeki ifadenin açılımını yazalım.
\( f(x) = -2(x^2 + 8x + 16) \)
\( = -2x^2 - 16x - 32 \)
Buna göre \( a + b + c = -2 - 16 - 32 = -50 \) bulunur.
\( f(x) = a(x - 2 + b)^2 + b - 7 \) parabolünün tepe noktasının koordinatları toplamı kaçtır?
Çözümü GösterDenklemi \( f(x) = a(x - r)^2 + k \) formunda verilen bir parabolün tepe noktası \( T(r, k) \) olur.
Verilen parabol denklemini düzenleyelim.
\( f(x) = a(x - (2 - b))^2 + b - 7 \)
Buna göre tepe noktasının koordinatları aşağıdaki gibi olur.
\( r = 2 - b, \quad k = b - 7 \)
Tepe noktasının koordinatları toplamı \( r + k = 2 - b + b - 7 = -5 \) olarak bulunur.

Yukarıdaki grafiği verilen parabolün alabileceği en küçük değer kaçtır?
Çözümü GösterParabol \( x \) eksenini -3 ve 1 noktalarında kestiği için denklemini aşağıdaki şekilde yazabiliriz.
\( f(x) = a(x + 3)(x - 1) \)
Parabolün başkatsayısını bulmak için \( y \) eksenini kestiği \( (0, -3) \) noktasının koordinatlarını denklemde yerine koyalım.
\( f(0) = a(0 + 3)(0 - 1) = -3 \)
\( a = 1 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = (x + 3)(x - 1) = x^2 + 2x - 3 \)
Kolları yukarı yönlü olan bir parabol en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{2}{2(1)} = -1 \)
Parabolün tepe noktasındaki değerini bulalım.
\( k = f(r) = f(-1) \)
\( = (-1)^2 + 2(-1) - 3 = -4 \) bulunur.
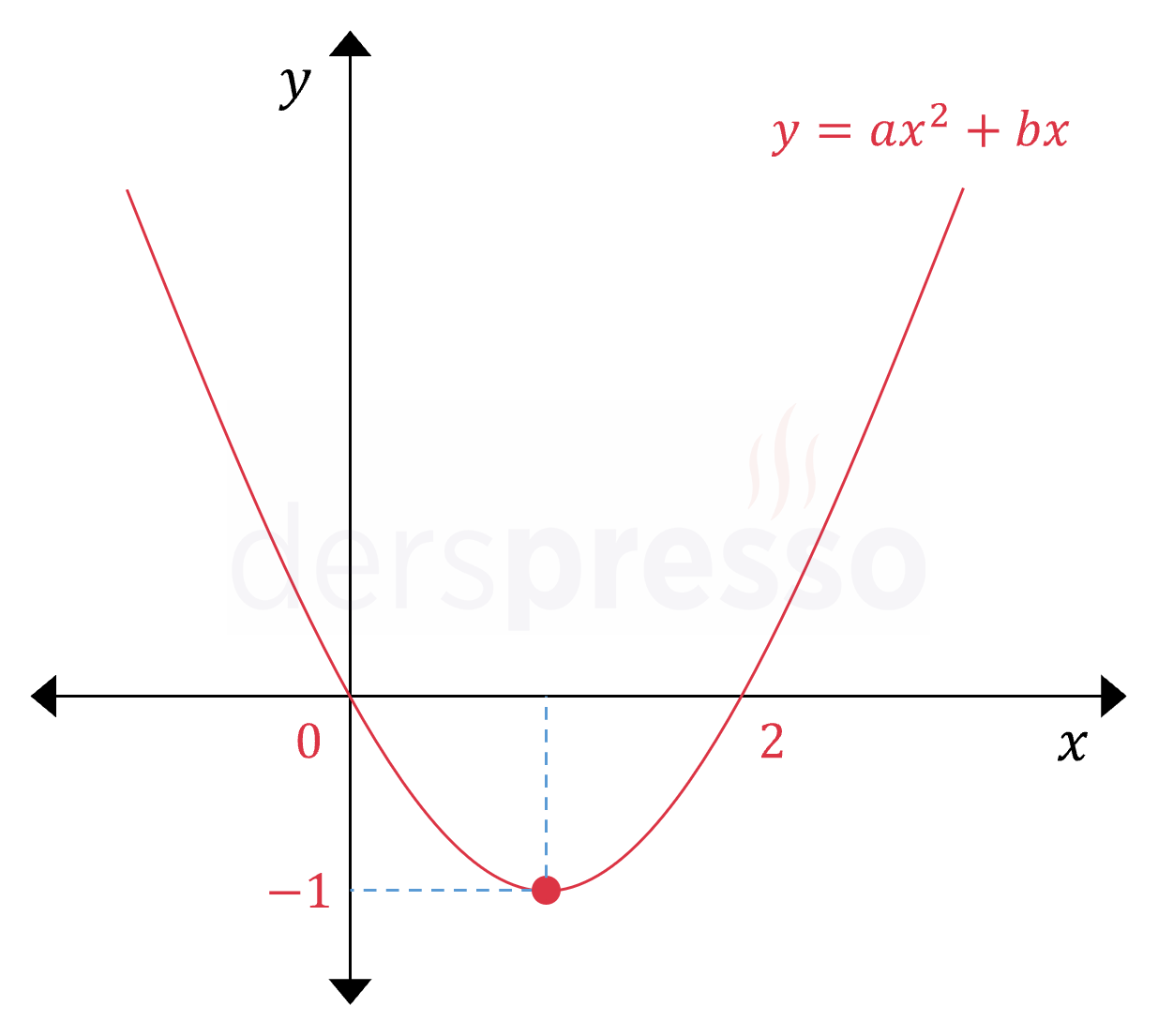
Yukarıda grafiği verilen parabolün tepe noktasının ordinatı \( -1 \) olduğuna göre, katsayılar toplamı kaçtır?
Çözümü GösterParabolün genel denklemini yazalım.
\( y = ax^2 + bx + c \)
Parabol \( x \) eksenini \( x = 0 \) ve \( x = 2 \) noktalarında kesmektedir.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Tepe noktasının apsis değeri köklerin apsis değerlerinin ortalamasıdır.
\( r = \dfrac{0 + 2}{2} = 1 \)
\( r = -\dfrac{b}{2a} = 1 \)
\( b = -2a \)
Parabol orijinden geçtiği için denkleminin sabit terimi 0'dır.
\( c = 0 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( y = ax^2 - 2ax \)
Tepe noktasının koordinatlarını denklemde yerine koyarak \( a \) değerini bulalım.
\( f(1) = a(1)^2 - 2a(1) = -1 \)
\( a - 2a = -1 \)
\( a = 1 \)
\( b = -2a = -2 \) bulunur.
Parabolün denklemi aşağıdaki gibi olur.
\( y = x^2 - 2x \)
Denklemin katsayılar toplamını bulalım.
\( a + b + c = 1 + (-2) + 0 = -1 \) bulunur.
\( f(x) \) parabolü \( x \) eksenini \( -5 \) ve \( 1 \) noktalarında kestiğine göre,
\( \dfrac{f(-6) \cdot f(4)}{f(2) \cdot f(-2)} \) oranı kaçtır?
Çözümü Göster\( x \) eksenini kestiği noktaların apsisleri \( x_1 \) ve \( x_2 \) olan parabolün denklemini yazalım.
\( f(x) = a(x - x_1)(x - x_2) \)
\( = a(x - (-5))(x - 1) \)
\( = a(x + 5)(x - 1) \)
Soruda verilen fonksiyon değerlerini bulalım.
\( f(-6) = a(-6 + 5)(-6 - 1) \)
\( = a(-1)(-7) = 7a \)
\( f(4) = a(4 + 5)(4 - 1) \)
\( = a(9)(3) = 27a \)
\( f(2) = a(2 + 5)(2 - 1) \)
\( = a(7)(1) = 7a \)
\( f(-2) = a(-2 + 5)(-2 - 1) \)
\( = a(3)(-3) = -9a \)
Bulduğumuz değerleri yerine koyalım.
\( \dfrac{f(-6) \cdot f(4)}{f(2) \cdot f(-2)} = \dfrac{7a \cdot 27a}{7a \cdot (-9a)} \)
\( = -3 \) bulunur.
Aşağıda grafiği verilen parabolün başkatsayısı 8'dir. Orijinden geçen parabolün tepe noktası \( T \) noktasıdır.
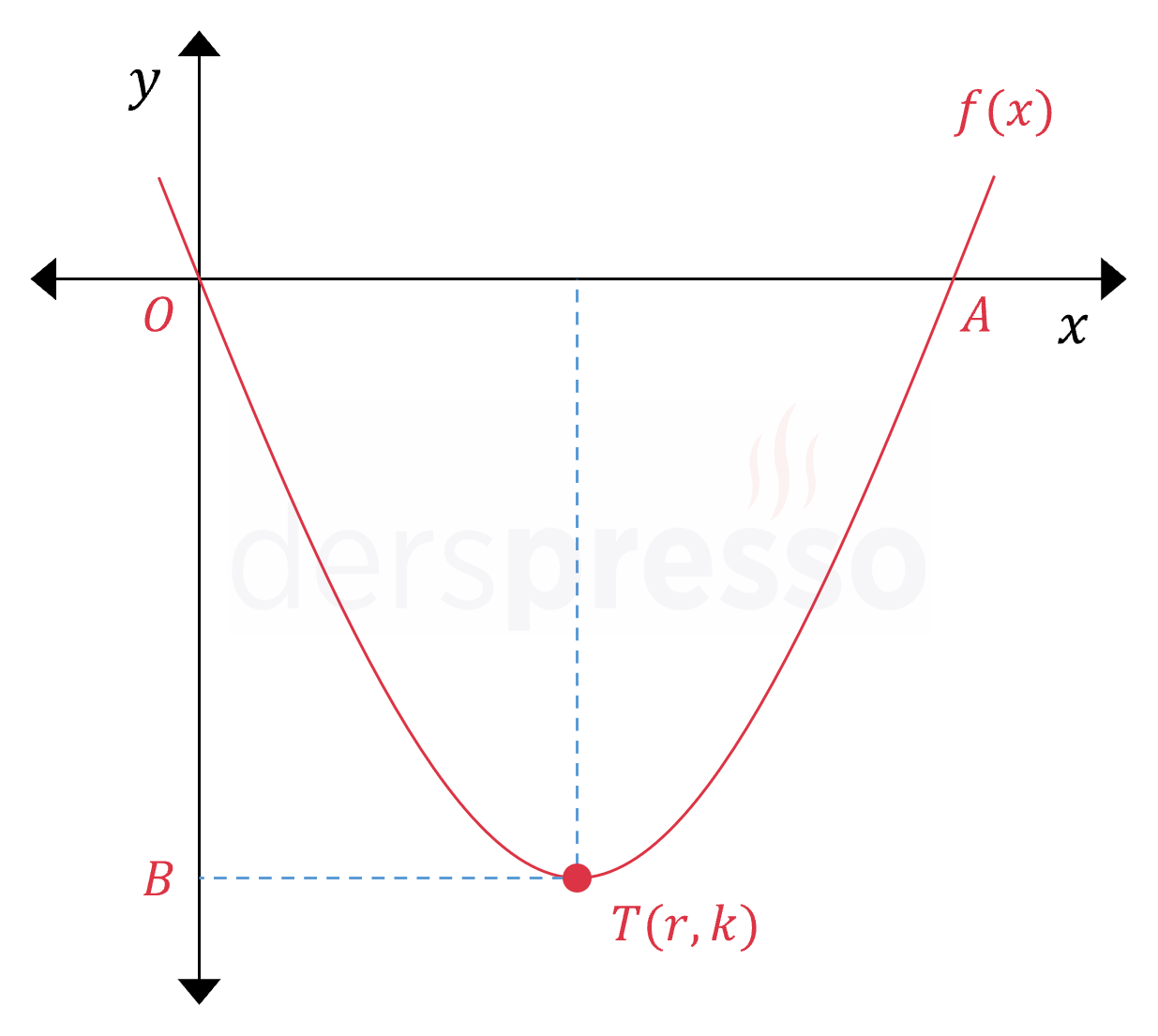
\( \abs{OA} = \abs{OB} \) olduğuna göre, \( f(\frac{3}{2}) \) kaçtır?
Çözümü GösterTepe noktası \( T(r, k) \) olan parabolün denklemi aşağıdaki gibidir.
\( f(x) = 8(x - r)^2 + k \)
Tepe noktasının apsisi köklerin apsis değerlerinin aritmetik ortalamasına eşittir.
Buna göre \( A \) noktasının koordinatları \( A(2r, 0) \) olur.
\( \abs{OA} = \abs{OB} \) olduğu için \( B \) noktasının koordinatları \( B(0, -2r) \) olur.
Dolayısıyla tepe noktasının koordinatları \( T(r, -2r) \) olur.
Tepe noktasının koordinatlarını denklemde yerine koyalım.
\( f(x) = 8(x - r)^2 - 2r \)
\( A(2r, 0) \) noktasının koordinatlarını denklemde yerine koyarak \( r \) değerini bulalım.
\( f(2r) = 8(2r - r)^2 - 2r = 0 \)
\( 8r^2 - 2r = 0 \)
\( 2r(4r - 1) = 0 \)
\( r \gt 0 \) olduğu için \( r = \frac{1}{4} \) olur.
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = 8(x - \frac{1}{4})^2 - \frac{1}{2} \)
\( f(\frac{3}{2}) \) değerini bulmak için denklemde \( x = \frac{3}{2} \) yazalım.
\( f(\frac{3}{2}) = 8(\frac{3}{2} - \frac{1}{4})^2 - \frac{1}{2} \)
\( = 12 \) bulunur.
\( y = f(x) \) parabolünün simetri ekseni \( x = 2 \) doğrusudur.
\( f \) fonksiyonunun \( y \) eksenini kestiği noktanın ordinatı \( -3 \) ve aldığı en büyük değer \( -1 \)'dir.
Buna göre \( f(1) \) kaçtır?
Çözümü GösterDenklemi \( f(x) = a(x - r)^2 + k \) formunda verilen parabolün tepe noktası \( T(r, k) \) noktasıdır.
Parabolün simetri ekseni \( x = 2 \) ise tepe noktasının apsis değeri \( r = 2 \) olur.
Bir parabolün aldığı en büyük değer varsa başkatsayı negatiftir, parabolün kolları aşağı yönlüdür ve parabol en büyük değerini tepe noktasında alır.
Buna göre tepe noktasının ordinat değeri \( k = -1 \) olur.
Parabolün denklemini aşağıdaki şekilde yazabiliriz.
\( f(x) = a(x - 2)^2 - 1 \)
Parabol \( y \) eksenini \( (0, -3) \) noktasında kesiyor.
Bu noktanın koordinatlarını denklemde yerine koyarak \( a \) değerini bulalım.
\( f(0) = -3 \)
\( f(0) = a(0 - 2)^2 - 1 = -3 \)
\( 4a - 1 = -3 \)
\( a = -\dfrac{1}{2} \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = -\frac{1}{2}(x - 2)^2 - 1 \)
\( f(1) \) değerini bulmak için \( x = 1 \) yazalım.
\( f(1) = -\frac{1}{2}(1 - 2)^2 - 1 = -\frac{3}{2} \) bulunur.
Genişliği 60 metre olan bir yük gemisi yüksekliği 40 metre ve su yüzeyindeki genişliği 80 metre olan parabol şeklindeki bir köprünün altından zorlukla geçebiliyor. Buna göre bu yük gemisinin su yüzeyinin üstünde kalan yüksekliği kaç metredir?
Çözümü GösterKöprüyü koordinat düzleminde tepe noktası \( y \) ekseni üzerinde olan bir parabol olarak düşünelim.
Buna göre parabol \( x \) eksenini aşağıdaki şekildeki gibi \( (-40, 0) \) ve \( (40, 0) \) noktalarında, \( y \) eksenini de \( (0, 40) \) noktasında keser.
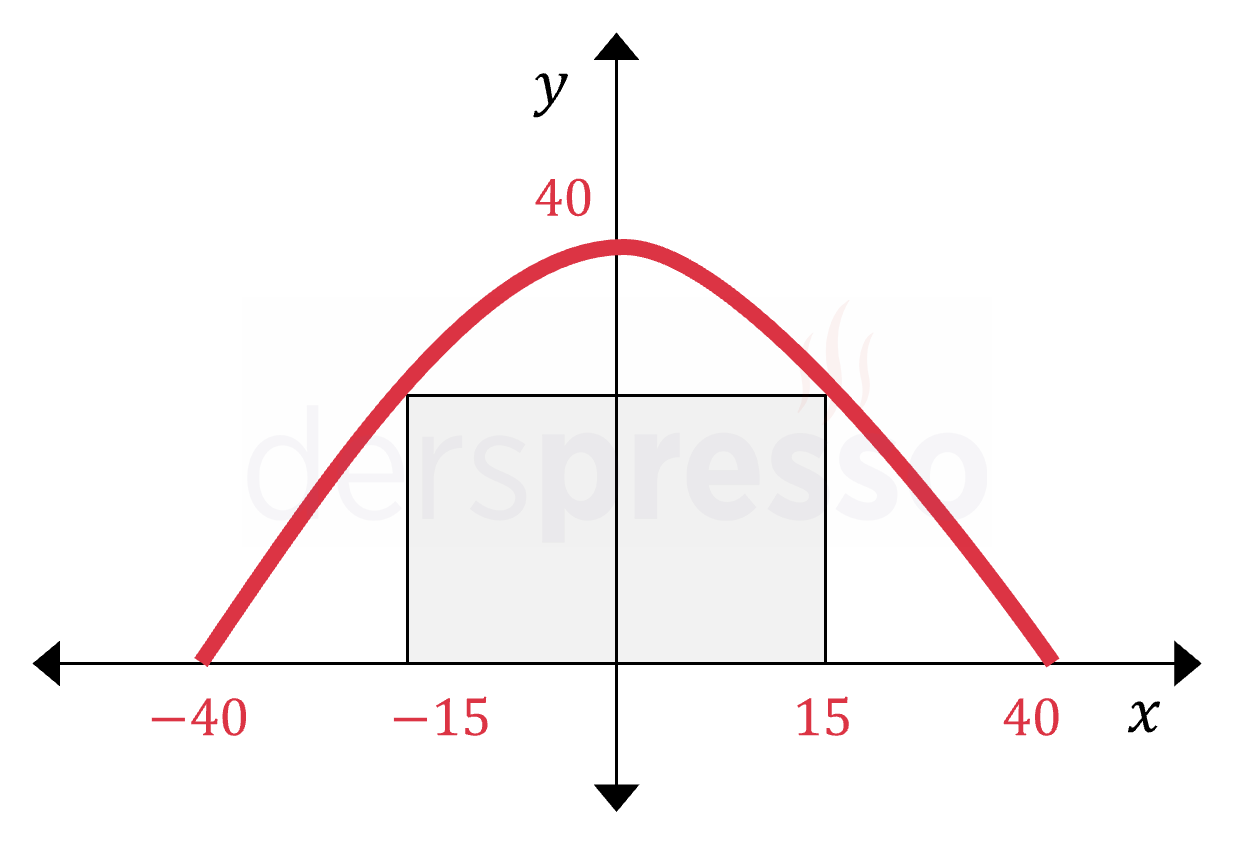
Köprü için \( x \) eksenini kestiği noktalar bilinen parabol denklemini yazalım.
\( y = a(x - 40)(x + 40) \)
\( (0, 40) \) noktası parabolün üzerinde olduğu için koordinatları denklemi sağlamalıdır.
\( 40 = a(0 - 40)(0 + 40) \)
\( a = -\dfrac{1}{40} \)
Geminin yüksekliği \( x = 30 \) ve \( x = -30 \) değerlerinde parabolün değerine eşit olur.
\( y = -\dfrac{1}{40}(30 - 40)(30 + 40) \)
\( = 17,5 \) metre bulunur.