Parabolün Tepe Noktası
Kolları yukarı yönlü parabollerin en küçük, aşağı yönlü parabollerin en büyük değerini aldığı noktaya parabolün tepe noktası denir ve genellikle \( T(r, k) \) ile gösterilir.
Tepe noktası \( y \) değeri açısından bir parabolün dönüm noktasıdır. Kolları yukarı yönlü parabollerde \( y \) değeri tepe noktasına kadar azalırken tepe noktasından itibaren artmaya başlar.
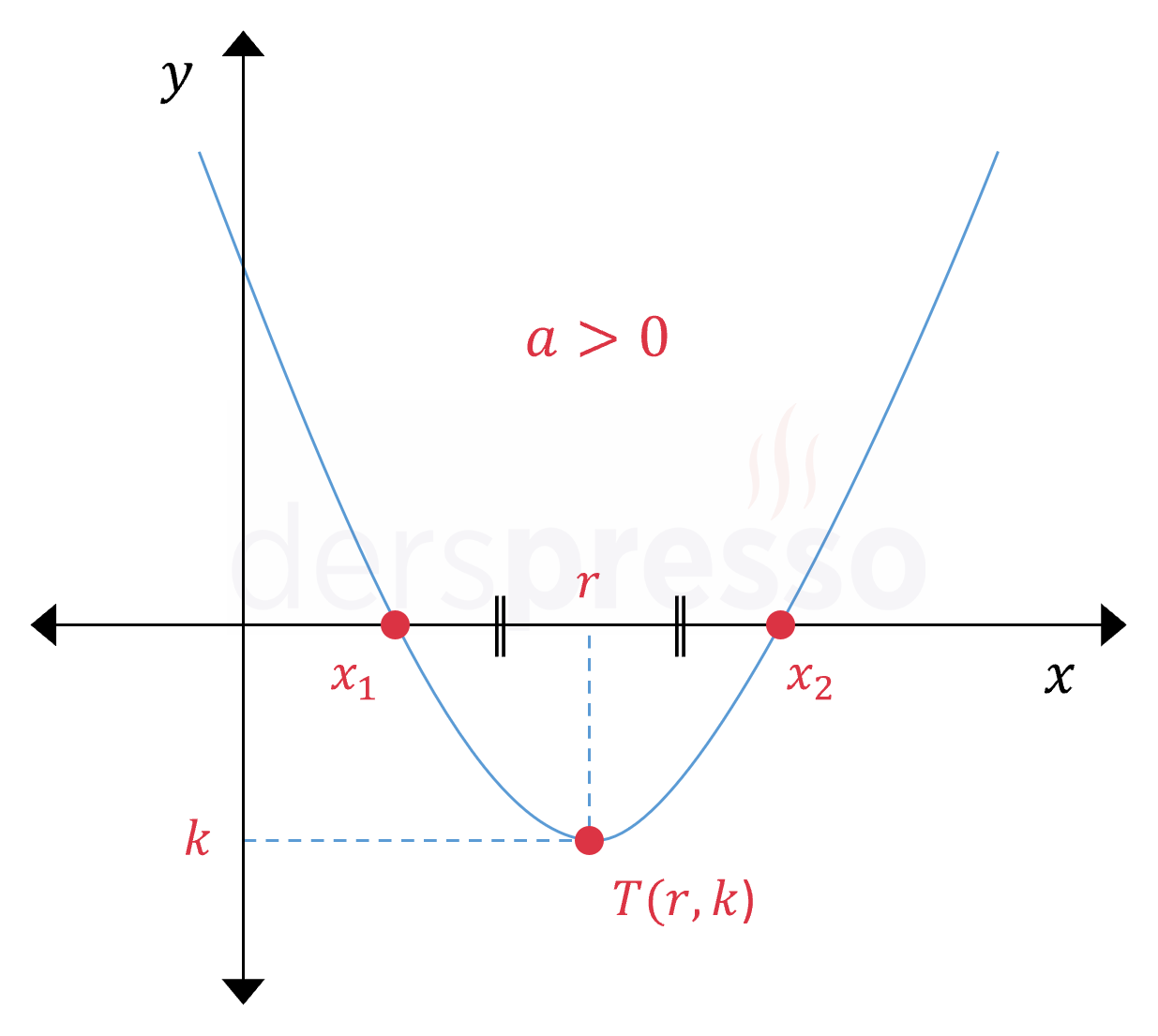
Kolları aşağı yönlü parabollerde ise \( y \) değeri tepe noktasına kadar artarken tepe noktasından itibaren azalmaya başlar.
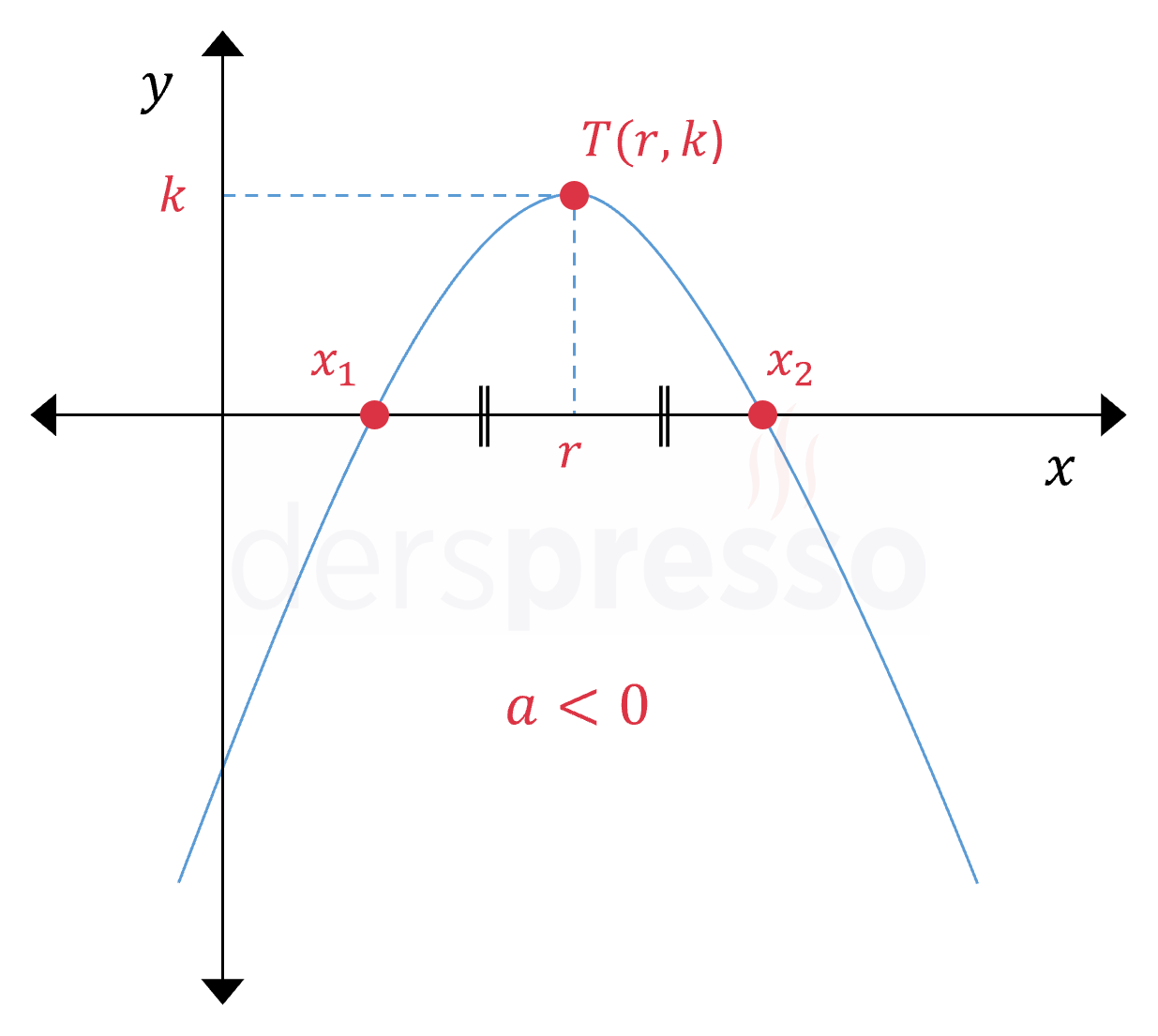
Bir parabolün tepe noktasının apsis ve ordinat değerleri aşağıdaki formüllerle bulunur.
\( f(x) = ax^2 + bx + c \)
\( T(r, k) \) parabolün tepe noktası olmak üzere,
\( r = -\dfrac{b}{2a} \)
\( k = f(r) = \dfrac{4ac - b^2}{4a} \)
\( f(x) = x^2 - 4x - 2 \)
\( r = -\dfrac{-4}{2 \cdot 1} = 2 \)
\( k = f(2) = 2^2 - 4(2) - 2 = -6 \)
Parabolün tepe noktası \( T(2, -6) \) noktasıdır.
İSPATI GÖSTER
Bir parabolün tepe noktasının apsis değeri, parabolün simetrisi gereği grafiğin \( x \) eksenini kestiği noktaların orta noktasıdır. Dolayısıyla, ikinci dereceden denklemlerde gördüğümüz kökler toplamı formülünü kullanarak tepe noktasının apsis değerini bulabiliriz.
Kökler toplamı: \( x_1 + x_2 = -\dfrac{b}{a} \)
\( r = \dfrac{x_1 + x_2}{2} = -\dfrac{b}{2a} \)
\( r \) değerini parabol denkleminde yerine koyarak tepe noktasının ordinat değerini (\( k \)) bulalım.
\( y = ax^2 + bx + c \)
\( k = a\left( -\dfrac{b}{2a} \right)^2 + b\left( -\dfrac{b}{2a} \right) + c \)
\( = \dfrac{ab^2}{4a^2} - \dfrac{b^2}{2a} + c \)
\( = \dfrac{b^2}{4a} - \dfrac{2b^2}{4a} + \dfrac{4ac}{4a} \)
\( = \dfrac{4ac - b^2}{4a} \)
Tepe noktasının konumu \( y \) eksenine göre üç şekilde olabilir.
| Grafik | Tepe Noktasının Konumu |
|---|---|
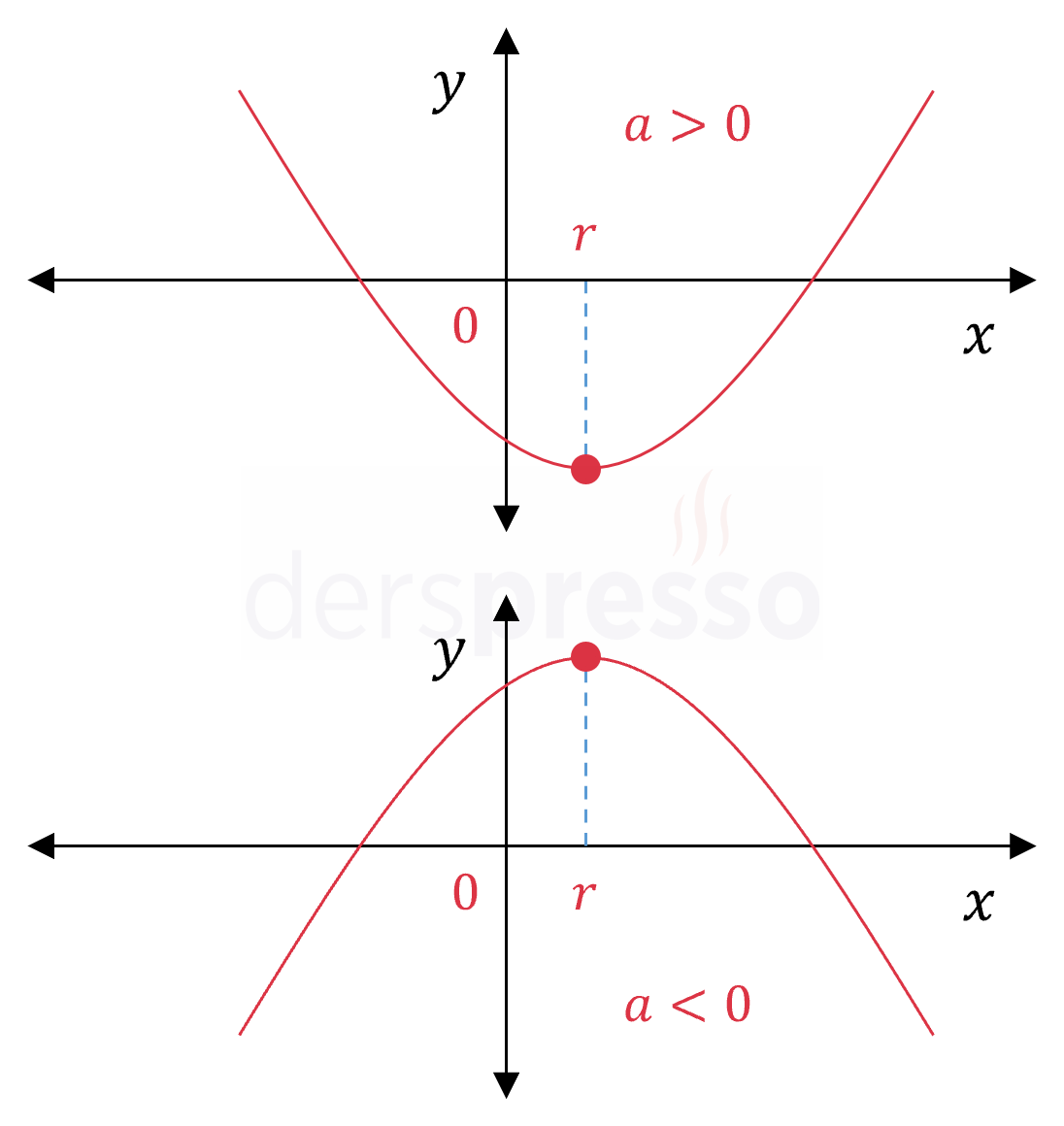
|
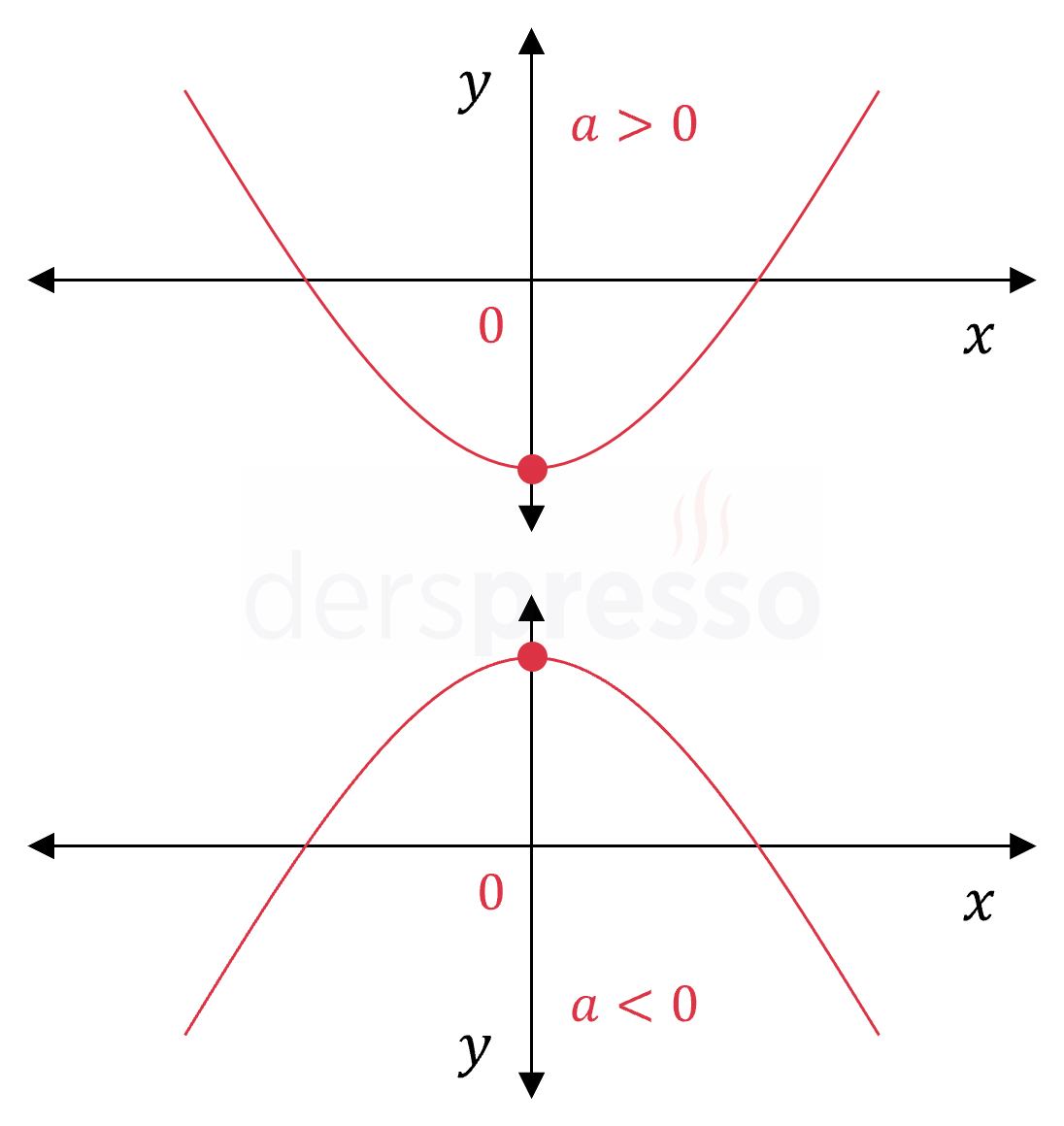
Tepe noktası \( y \) ekseninin sağında: Bu durumda tepe noktasının apsis değeri pozitif olur. \( r = -\dfrac{b}{2a} \gt 0 \) Bunun bir sonucu olarak \( a \) ve \( b \) katsayıları ters işaretli olur, yani parabolün kolları yukarı yönlü ise \( b \lt 0 \), aşağı yönlü ise \( b \gt 0 \) olur. |
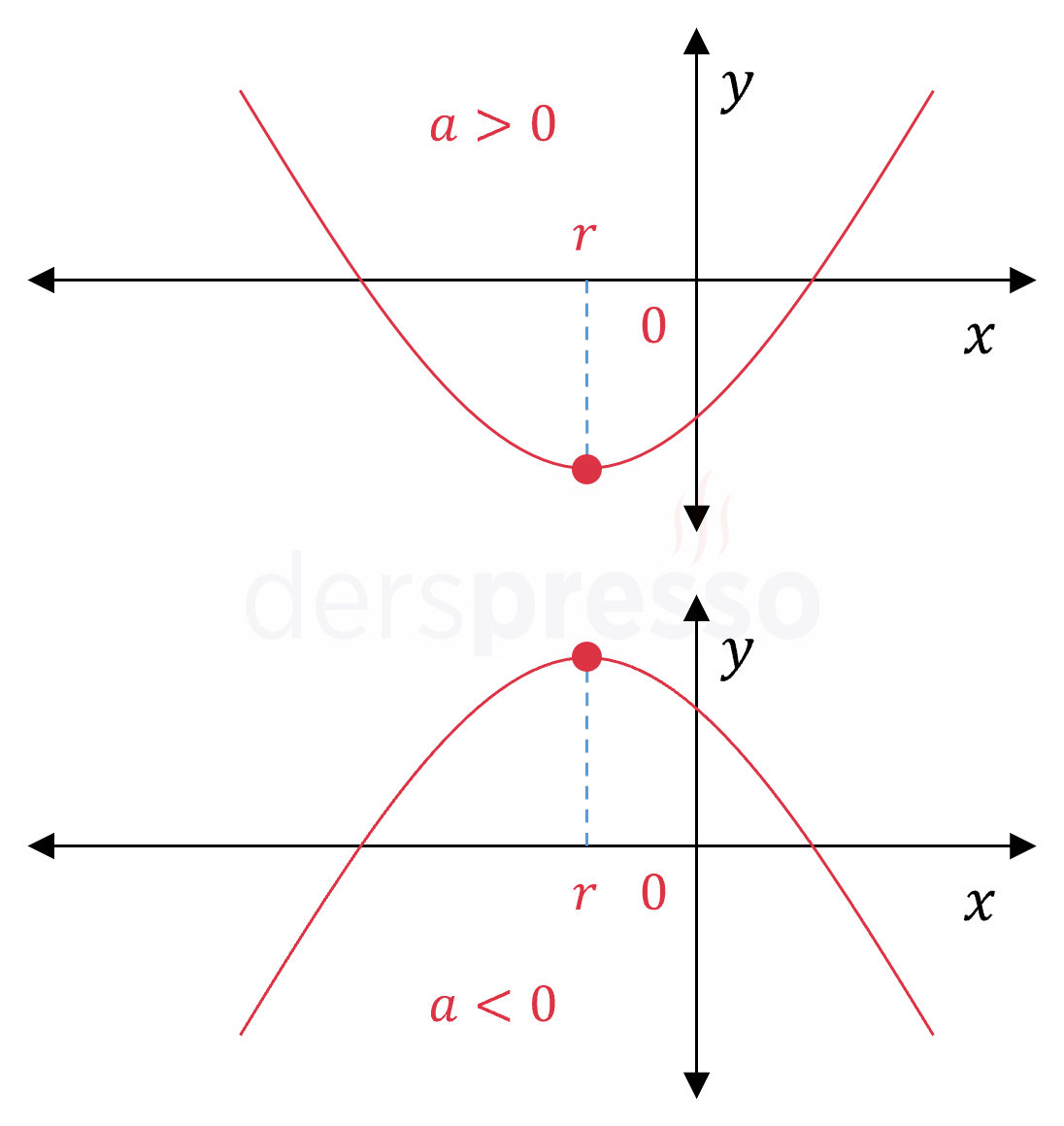
|
Tepe noktası \( y \) ekseninin solunda: Bu durumda tepe noktasının apsis değeri negatif olur. \( r = -\dfrac{b}{2a} \lt 0 \) Bunun bir sonucu olarak \( a \) ve \( b \) katsayıları aynı işaretli olur, yani parabolün kolları yukarı yönlü ise \( b \gt 0 \), aşağı yönlü ise \( b \lt 0 \) olur. |
|
Tepe noktası \( y \) ekseninin üzerinde: Bu durumda tepe noktasının apsis değeri sıfır olur. \( r = -\dfrac{b}{2a} = 0 \) Bunun bir sonucu olarak \( b = 0 \) olur. |
Parabolün tepe noktasının \( y \) ekseni üzerinde olması; parabolün \( y \) eksenine göre simetrik olması (parabolün simetri ekseninin \( y \) ekseni olması), dolayısıyla parabolün bir çift fonksiyon olması anlamına da gelir.
Aşağıdaki parabollerin tepe noktalarının koordinatlarını bulunuz.
(a) \( f(x) = 3x^2 + 6x + 7 \)
(b) \( g(x) = -2x^2 + 2x - 5 \)
(c) \( h(x) = -4x^2 - 5 \)
Çözümü GösterDenklemi \( f(x) = ax^2 + bx + c \) ve tepe noktası \( T(r, k) \) olan bir parabolün tepe noktasının koordinatları aşağıdaki formüllerle bulunur.
\( r = -\dfrac{b}{2a} \)
\( k = f(r) \)
Bu formülleri kullanarak verilen parabollerin tepe noktalarını bulalım.
(a) seçeneği:
\( y = 3x^2 + 6x + 7 \)
Tepe noktasının apsisini bulalım.
\( r = -\dfrac{6}{2(3)} = -1 \)
Tepe noktasının ordinatını bulalım.
\( k = f(-1) \)
\( = 3(-1)^2 + 6(-1) + 7 = 4 \)
\( T(r, k) = T(-1, 4) \)
(b) seçeneği:
\( y = -2x^2 + 2x - 5 \)
Tepe noktasının apsisini bulalım.
\( r = -\dfrac{2}{2(-2)} = \dfrac{1}{2} \)
Tepe noktasının ordinatını bulalım.
\( k = g(\dfrac{1}{2}) \)
\( = -2(\dfrac{1}{2})^2 + 2(\dfrac{1}{2}) - 5 = -\dfrac{9}{2} \)
\( T(r, k) = T(\dfrac{1}{2}, -\dfrac{9}{2}) \)
(c) seçeneği:
\( y = -4x^2 - 5 = -4x^2 + 0x - 5 \)
Tepe noktasının apsisini bulalım.
\( r = -\dfrac{0}{2(-4)} = 0 \)
Parabolün \( x \)'li terimi olmadığından tepe noktasının apsisi \( x = 0 \) olur, dolayısıyla parabol \( y \) eksenine göre simetriktir.
Tepe noktasının ordinatını bulalım.
\( k = h(0) \)
\( = -4(0)^2 - 5 = -5 \)
\( T(r, k) = T(0, -5) \)
\( f(x) = 4x^2 + mx - 3 \) parabolü \( A(-1, 9) \) noktasından geçtiğine göre, tepe noktasının koordinatları nedir?
Çözümü GösterParabol \( A \) noktasından geçtiğine göre, koordinatları parabol denklemini sağlar.
\( f(-1) = 9 \)
\( 4(-1)^2 + m(-1) - 3 = 9 \)
\( m = -8 \)
Buna göre fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = 4x^2 - 8x - 3 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-8}{2(4)} = 1 \)
Tepe noktasının apsisini fonksiyonda yerine koyarak ordinatını bulalım.
\( k = f(1) = 4(1)^2 - 8(1) - 3 = -7 \)
\( T(r, k) = T(1, -7) \) bulunur.
\( y = (k + 1)x^2 + (2k - 3)x - 6 \)
parabolünün tepe noktası \( x = 1 \) doğrusu üzerinde ise \( k \) değerini bulunuz.
Çözümü GösterParabolün katsayılarını yazalım.
\( a = k + 1, \quad b = 2k - 3, \quad c = -6 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Tepe noktası \( x = 1 \) doğrusu üzerinde ise \( r = 1 \) olur.
\( r = -\dfrac{b}{2a} = 1 \)
\( -\dfrac{2k - 3}{2(k + 1)} = 1 \)
\( 3 - 2k = 2k + 2 \)
\( k = \dfrac{1}{4} \) bulunur.
\( f(x) = x^2 - mx + n - 5 \) parabolünün tepe noktası \( T(3, -5) \) olduğuna göre, \( m + n \) toplamı kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -m, \quad c = n - 5 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-m}{2(1)} = 3 \)
\( m = 6 \)
\( f(x) = x^2 - 6x + n - 5 \)
Tepe noktasının koordinatlarını fonksiyonda yerine koyalım.
\( f(3) = -5 \)
\( 3^2 - 6(3) + n - 5 = -5 \)
\( n = 9 \)
\( m + n = 6 + 9 = 15 \) bulunur.
İkinci dereceden bir \( f(x) \) fonksiyonu en küçük değerine \( x = -2 \) noktasında ulaşıyor ve \( -3 \) değerini alıyor.
Bu fonksiyonun grafiği \( y \) eksenini \( y = 5 \) noktasında kestiğine göre, \( f(3) \) kaçtır?
Çözümü Gösterİkinci dereceden bir fonksiyonun grafiği paraboldür.
Bir parabolün en küçük değeri varsa başkatsayısı pozitiftir, parabolün kolları yukarı yönlüdür ve parabol en küçük değerini tepe noktasında alır.
Buna göre parabolün tepe noktası \( T(-2, -3) \) noktasıdır.
Tepe noktası bilinen parabolün denklemini yazalım.
\( f(x) = a(x + 2)^2 - 3 \)
Parabolün \( y \) eksenini kestiği \( (0, 5) \) noktasının koordinatlarını denklemde yerine koyarak \( a \) değerini bulalım.
\( 5 = a(0 + 2)^2 - 3 \)
\( a = 2 \)
Parabolün denklemi aşağıdaki gibi olur.
\( f(x) = 2(x + 2)^2 - 3 \)
\( f(3) \) değerini bulalım.
\( f(3) = 2(3 + 2)^2 - 3 \)
\( = 47 \) bulunur.
\( f(x) = 2(3x - 9)^2 + 6 \) parabolünün tepe noktasının koordinatları toplamı kaçtır?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
Tepe noktası \( T(r, k) \) olan parabolün denklemi aşağıdaki şekilde ifade edilebilir.
\( f(x) = a(x - r)^2 + k \)
Verilen denklemde \( x \)'in katsayısı 3 olduğu için yukarıdaki genel formül tepe noktasının koordinatlarını vermez.
Buna göre sorudaki denklemi \( a(x - r)^2 + k \) formuna getirelim.
\( f(x) = 2(3x - 9)^2 + 6 \)
\( = 2[3(x - 3)]^2 + 6 \)
\( = 18(x - 3)^2 + 6 \)
Bu denkleme göre parabolün tepe noktası aşağıdaki gibi bulunur.
\( T(r, k) = T(3, 6) \)
Parabolün tepe noktasının koordinatları toplamı \( 3 + 6 = 9 \) bulunur.
\( f(x) = x^2 + 4x + 2m - 3 \) parabolünün alabileceği en küçük değer \( -1 \) olduğuna göre, \( m \) kaçtır?
Çözümü GösterBaşkatsayısı pozitif (kolları yukarı yönlü) olan bir parabol en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{4}{2(1)} = -2 \)
Tepe noktasının apsisini fonksiyonda yerine koyarak tepe noktasının ordinat değerine eşitleyelim.
\( f(r) = k \)
\( f(-2) = -1 \)
\( (-2)^2 + 4(-2) + 2m - 3 = -1 \)
\( 4 - 8 + 2m - 3 = -1 \)
\( m = 3 \) bulunur.
\( y = x^2 + (m + 1)x - m + 2 \) parabolünün en küçük değeri \( -12 \) olduğuna göre, \( m \)'nin alabileceği değerlerin toplamı kaçtır?
Çözümü GösterPozitif başkatsayılı (kolları yukarı yönlü olan) bir parabol en küçük değerini tepe noktasında alır, dolayısıyla bu en küçük değer tepe noktasının ordinat değerine eşittir.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( k = \dfrac{4ac - b^2}{4a} = -12 \)
Parabolün katsayılarını yazalım.
\( a = 1, \quad b = m + 1, \quad c = -m + 2 \)
\( \dfrac{4(1)(-m + 2) - (m + 1)^2}{4(1)} = -12 \)
\( -4m + 8 - m^2 - 2m - 1 = -48 \)
\( m^2 + 6m - 55 = 0 \)
\( (m + 11)(m - 5) = 0 \)
\( m = -11 \) ya da \( m = 5 \)
\( m \)'nin alabileceği değerler toplamı \( -11 + 5 = -6 \) olarak bulunur.
Alternatif olarak, bulduğumuz denklemin deltası sıfırdan büyük olduğu için (denklemin iki farklı reel kökü olduğu için), \( m \)'nin alabileceği değerler toplamını kökler toplamı formülü ile de bulabiliriz.
\( \Delta = b^2 - 4ac \)
\( = 6^2 - 4(1)(-55) = 256 \gt 0 \)
\( m_1 + m_2 = -\dfrac{b}{a} = -6 \)
\( y = x^2 - 6x + 7 \) parabolünün tepe noktasının orijine olan uzaklığı nedir?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-6}{2(1)} = 3 \)
\( k = f(3) = 3^2 - 6(3) + 7 = -2 \)
\( T(3, -2) \)
Tepe noktasının koordinatları \( O(0, 0) \) olan orijine olan uzaklığını bulalım.
\( \abs{TO} = \sqrt{3^2 + (-2)^2} \)
\( = \sqrt{13} \) bulunur.
\( y = x^2 - 2x + m \) parabolünün tepe noktasının \( x \) eksenine olan uzaklığı 3 birimdir.
Buna göre \( m \)'nin alabileceği değerlerin çarpımı kaçtır?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-2}{2(1)} = 1 \)
Tepe noktasının \( x \) eksenine uzaklığı 3 birim ise tepe noktasının koordinatları \( T(1, 3) \) ya da \( T(1, -3) \) olur.
Her iki durum için \( m \) değerini bulalım.
\( T(1, 3) \) için:
\( f(1) = 3 \)
\( 1^2 - 2(1) + m = 3 \)
\( m = 4 \)
\( T(1, -3) \) için:
\( f(1) = -3 \)
\( 1^2 - 2(1) + m = -3 \)
\( m = -2 \)
Buna göre \( m \)'nin alabileceği değerlerin çarpımı \( 4 \cdot (-2) = -8 \) olarak bulunur.
\( f(x) = x^2 - 2mx + m + 6 \) parabolünün tepe noktası IV. bölgede olduğuna göre, \( m \)'nin alabileceği en küçük tam sayı değer nedir?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
Tepe noktası IV. bölgede ise \( r \gt 0 \) ve \( k \lt 0 \) olmalıdır.
\( r = -\dfrac{b}{2a} = -\dfrac{-2m}{2(1)} = m \)
\( r \gt 0 \Longrightarrow m \gt 0 \)
\( f(r) = f(m) = m^2 - 2m^2 + m + 6 \)
\( -m^2 + m + 6 \lt 0 \)
\( m^2 - m - 6 \gt 0 \)
\( (m + 2)(m - 3) \gt 0 \)
\( m \lt -2 \) ya da \( m \gt 3 \)
\( m \) için bulduğumuz iki aralığın kesişim kümesi \( m \)'nin en geniş değer aralığını verir.
\( m \gt 3 \)
Buna göre \( m \)'nin alabileceği en küçük tam sayı değer 4 olarak bulunur.
\( x \in \mathbb{R} \) olmak üzere,
\( A = 2x^2 + 12 \), \( B = 18x - x^2 \) olduğuna göre, \( A - B \) farkı en az kaçtır?
Çözümü Göster\( A - B \) farkını bulalım.
\( A - B = (2x^2 + 12) - (18x - x^2) \)
\( = 3x^2 - 18x + 12 \)
Pozitif başkatsayılı bu ikinci dereceden denklemin grafiği kolları yukarı yönlü bir paraboldür ve en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-18}{2(3)} = 3 \)
Tepe noktasının apsisini fonksiyonda yerine koyarak ordinatını bulalım.
\( k = f(3) = 3(3)^2 - 18(3) + 12 = -15 \)
Buna göre \( A - B \) farkının en küçük değeri -15'tir.
\( m \in \mathbb{R} \) olmak üzere,
\( A = (2 - m)(m - 4) \) olduğuna göre, \( A \)'nın en büyük değeri kaçtır?
Çözümü Göster\( A = (2 - m)(m - 4) = -m^2 + 6m - 8 \)
Bu ikinci dereceden ifadenin grafiği bir paraboldür. Negatif başkatsayılı (kolları aşağı yönlü olan) bir parabol en büyük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{6}{2(-1)} = 3 \)
Tepe noktasının apsisini fonksiyonda yerine koyarak ordinatını bulalım.
\( k = f(3) = -3^2 + 6(3) - 8 = 1 \)
Buna göre \( A \)'nın en büyük değeri 1'dir.
\( m \in \mathbb{R} \) olmak üzere,
\( f(x) = (x + 4)(m - x) \) fonksiyonunun en büyük değerinin 9'dan küçük olması için \( m \) hangi aralıkta olmalıdır?
Çözümü Göster\( f(x) = (x + 4)(m - x) \)
\( = -(x + 4)(x - m) \)
\( f \) fonksiyonu negatif başkatsayılı ve kökleri \( x = m \) ve \( x = -4 \) olan bir paraboldür.
Pozitif başkatsayılı bir parabol en küçük değerini, negatif başkatsayılı bir parabol en büyük değerini tepe noktasında alır.
Ayrıca parabollerin tepe noktasının apsisi köklerin orta noktasıdır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = \dfrac{m + (-4)}{2} \)
Bu değeri fonksiyonda yerine koyup fonksiyonun aldığı en küçük değeri bulalım.
\( f(\dfrac{m - 4}{2}) = (m - \dfrac{m - 4}{2})(\dfrac{m - 4}{2} + 4) \)
\( = \dfrac{m + 4}{2} \cdot \dfrac{m + 4}{2} \)
\( = \dfrac{(m + 4)^2}{4} \)
Bu ifadenin değerinin 9'dan küçük olmasını istiyoruz.
\( \dfrac{(m + 4)^2}{4} \lt 9 \)
\( (m + 4)^2 \lt 36 \)
\( -6 \lt m + 4 \lt 6 \)
\( -10 \lt m \lt 2 \) bulunur.
\( f(x) = a - 4 + 4x - x^2 \)
\( g(x) = 4 - 2a - 2ax + x^2 \) fonksiyonları veriliyor.
\( f \) fonksiyonunun en büyük değeri \( g \) fonksiyonunun en küçük değerinden küçük olduğuna göre, \( a \)'nın alabileceği en büyük tam sayı değer kaçtır?
Çözümü GösterHer iki fonksiyon da birer paraboldür.
Pozitif başkatsayılı bir parabol en küçük değerini, negatif başkatsayılı bir parabol en büyük değerini tepe noktasında alır.
\( f(x) \) fonksiyonunu tam kareye tamamlayalım.
\( f(x) = a - (x^2 - 4x + 4) \)
\( = a - (x - 2)^2 \)
Parantez içindeki tam kare ifadenin en küçük değeri sıfır olduğu için \( f \) fonksiyonunun en büyük değeri \( a \) olur.
\( g(x) \) fonksiyonunu tam kareye tamamlayalım.
\( g(x) = (x - a)^2 - 2a + 4 - a^2 \)
Parantez içindeki tam kare ifadenin en küçük değeri sıfır olduğu için \( g \) fonksiyonunun en küçük değeri \( -2a + 4 - a^2 \) olur.
\( f(x) \) fonksiyonunun en büyük değeri \( g(x) \) fonksiyonunun en küçük değerinden küçüktür.
\( a \lt -2a + 4 - a^2 \)
\( a^2 + 3a - 4 \lt 0 \)
\( (a + 4)(a - 1) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için eşitsizliğin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
\( a \in (-4, 1) \)
\( a \)'nın en büyük tam sayı değeri 0 olarak bulunur.
\( y = x^2 + 5 \) ve \( y = -x^2 + 3x + 2 \) parabolleri arasındaki en kısa dikey mesafe kaç birimdir?
Çözümü GösterHerhangi bir \( x \) değeri için paraboller arasındaki dikey mesafe iki denklemin farkının mutlak değerine eşittir.
\( \abs{x^2 + 5 - (-x^2 + 3x + 2)} = \abs{2x^2 - 3x + 3} \)
\( 2x^2 - 3x + 3 \) ifadesi başkatsayısı pozitif ve deltası negatif olan bir paraboldür.
Parabolün katsayılarını yazalım.
\( a = 2, \quad b = -3, \quad c = 3 \)
\( \Delta = (-3)^2 - 4(2)(3) = -15 \lt 0 \)
Delta negatif olduğu için iki parabol arasındaki dikey mesafeyi veren parabol \( x \) eksenini kesmez, dolayısıyla tüm reel sayılarda pozitiftir ve en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-3}{2(2)} = \dfrac{3}{4} \)
İki parabol arasındaki en kısa mesafeyi bulmak için fark fonksiyonunda \( x = \frac{3}{4} \) koyalım.
\( 2x^2 - 3x + 3 = 2(\dfrac{3}{4})^2 - 3(\dfrac{3}{4}) + 3 \)
\( = \dfrac{15}{8} \) bulunur.
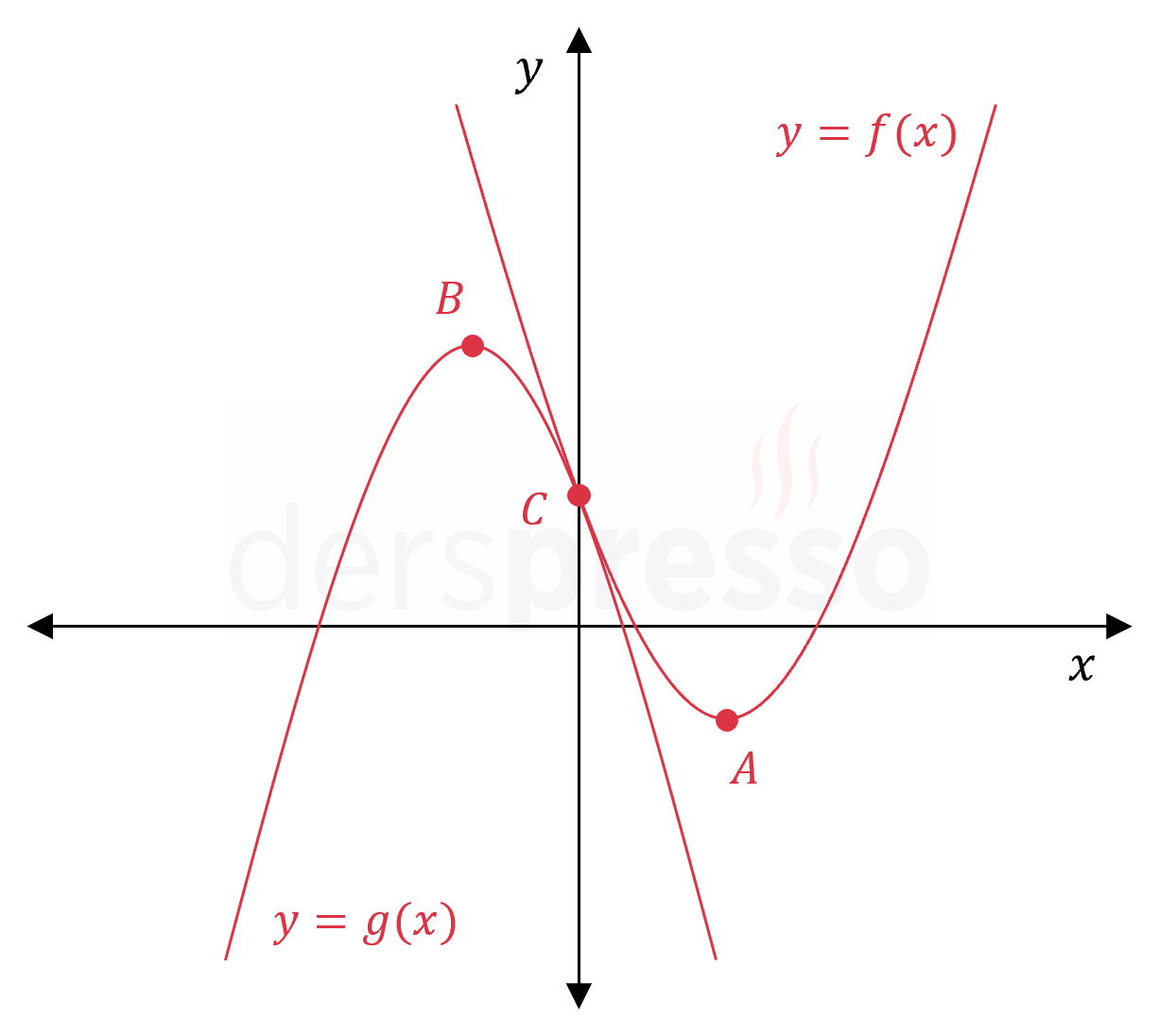
Şekildeki \( f(x) \) ve \( g(x) \) parabolleri \( y \) ekseni üzerindeki \( C \) noktasında kesişmektedir.
\( f(x) = x^2 -(k + 3)x + 2k + 1 \)
\( g(x) = -x^2 -(3k + 1)x + 5k - 2 \)
Buna göre parabollerin tepe noktaları arasındaki \( \abs{AB} \) uzaklığı kaçtır?
Çözümü Göster\( f(x) \) ve \( g(x) \) parabolleri \( y \) eksenini aynı noktada kestiğine göre sabit terimleri eşittir.
\( 2k + 1 = 5k - 2 \)
\( k = 1 \)
\( f(x) = x^2 -4x + 3 \)
\( g(x) = -x^2 -4x + 3 \)
\( f(x) \) parabolünün tepe noktasının koordinatlarını bulalım.
\( A(r_1, k_1) \)
\( r_1 = -\dfrac{-4}{2(1)} = 2 \)
\( k_1 = f(2) = 2^2 -4(2) + 3 = -1 \)
\( g(x) \) parabolünün tepe noktasının koordinatlarını bulalım.
\( A(2, -1) \)
\( B(r_2, k_2) \)
\( r_2 = -\dfrac{-4}{2(-1)} = -2 \)
\( k_2 = g(-2) = -(-2)^2 -4(-2) + 3 = 7 \)
\( B(-2, 7) \)
\( \abs{AB} \) uzaklığını bulalım.
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( = \sqrt{(-2 - 2)^2 + (7 - (-1))^2} \)
\( = \sqrt{80} = 4\sqrt{5} \) bulunur.
Parabolün Simetri Ekseni
Tüm parabol grafikleri parabolün tepe noktasından geçen ve \( y \) eksenine paralel bir doğruya göre simetriktir. Bu doğruya parabolün simetri ekseni denir.
Parabolün simetri ekseninin denklemi:
\( x = r = -\dfrac{b}{2a} \)
\( f(x) = -2x^2 + 12x - 7 \)
\( r = -\dfrac{12}{2 \cdot (-2)} = 3 \)
Parabolün simetri ekseni \( x = 3 \) doğrusudur.
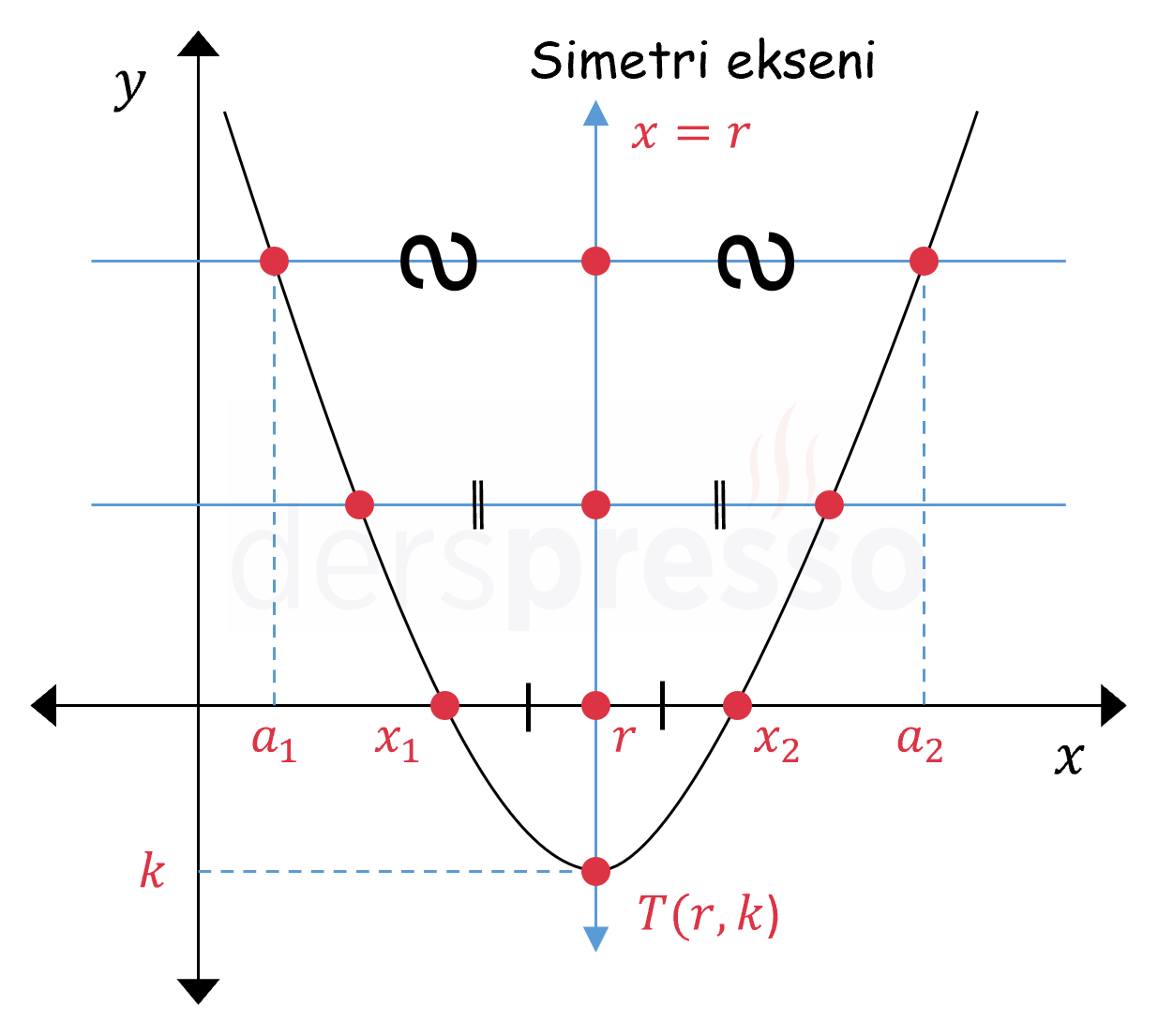
Parabolün simetrisi gereği, grafik üzerinde çizilen \( x \) eksenine paralel doğruların parabolü kestiği noktaların orta noktaları her zaman simetri ekseni üzerinde olur, bir diğer ifadeyle bu noktaların apsis değerlerinin aritmetik ortalaması \( r \)'ye eşit olur.
\( r = \dfrac{x_1 + x_2}{2} = \dfrac{a_1 + a_2}{2} \)
Bir parabol üzerindeki simetri eksenine göre simetrik iki noktanın fonksiyon değerleri birbirine eşittir. Bunun karşıtı da doğrudur, yani bir parabol üzerindeki iki farklı noktanın fonksiyon değerleri birbirine eşitse bu iki nokta simetri eksenine göre simetriktir.
Bunun bir sonucu olarak, tepe noktasının apsis değerine belirli bir reel sayı eklenip çıkarıldığında elde edilen fonksiyon değerleri birbirine eşit olur.
\( m \in \mathbb{R} \) olmak üzere,
\( f(r + m) = f(r - m) \)
\( f(x_1) = f(x_2) = 0 \)
\( f \) parabolünün tepe noktası \( T(8, k) \) ise,
\( f(8 + 1000) = f(8 - 1000) \)
\( f(x) = 4x^2 - (2m + 1)x - 3 \) parabolünün simetri ekseni \( x = -1 \) doğrusu olduğuna göre, \( m \) kaçtır?
Çözümü GösterBir parabolün simetri ekseni \( x = r = -\frac{b}{2a} \) doğrusudur.
\( r = -\dfrac{b}{2a} \)
\( -\dfrac{-(2m + 1)}{2(4)} = -1 \)
\( 2m + 1 = -8 \)
\( m = -\dfrac{9}{2} \) bulunur.
\( f(x) \) parabolü için \( f(\frac{1}{7}) = f(\frac{20}{7}) \) eşitliği sağlandığına göre, parabolün simetri ekseninin denklemi nedir?
Çözümü GösterBir parabol üzerindeki simetri eksenine göre simetrik iki noktanın fonksiyon değerleri birbirine eşittir.
Benzer şekilde, bir parabol üzerindeki iki farklı noktanın fonksiyon değerleri birbirine eşitse bu iki nokta simetri eksenine göre simetriktir.
Verilen iki noktanın fonksiyon değerleri birbirine eşit olduğu için bu iki nokta simetri eksenine göre simetrik noktalardır. Buna göre simetri ekseni bu iki noktanın orta noktasından geçer.
Parabolün simetri ekseni \( x = r \) olmak üzere,
\( r = \dfrac{\frac{1}{7} + \frac{20}{7}}{2} \)
\( = \dfrac{3}{2} \) bulunur.
Buna göre parabolün simetri ekseni \( x = \frac{3}{2} \) doğrusudur.
\( y = x^2 + mx + n \) parabolünün simetri ekseni \( x = 2 \) doğrusudur.
Parabolün en küçük değeri 6 olduğuna göre, parabol \( y \) eksenini hangi noktada keser?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
Bir parabolün simetri ekseni \( x = r = -\frac{b}{2a} \) doğrusudur.
\( r = -\dfrac{b}{2a} \)
\( -\dfrac{m}{2(1)} = 2 \)
\( m = -4 \)
Simetri ekseni tepe noktasından geçtiği için tepe noktasının apsisi \( x = 2 \) olur.
Tepe noktası: \( T(2, k) \)
Pozitif başkatsayılı bir parabol en küçük değerini tepe noktasında alır. Buna göre tepe noktasının ordinatı \( k = 6 \) olur.
Tepe noktası: \( T(2, 6) \)
Tepe noktasının koordinatlarını parabol denkleminde yerine koyarak \( n \) değerini bulalım.
\( f(2) = 6 \)
\( 2^2 - 4(2) + n = 6 \)
\( n = 10 \)
Parabolün denklemi aşağıdaki gibi olur.
\( y = x^2 - 4x + 10 \)
Parabolün \( y \) eksenini kestiği noktayı bulmak için denklemde \( x = 0 \) koyalım.
\( y = 0^2 - 4(0) + 10 = 10 \) bulunur.
Buna göre parabol \( y \) eksenini \( (0, 10) \) noktasında keser.
\( f(x) = x^2 - 3mx + 2m - 3 \) parabolünün simetri ekseni \( x = 6 \) doğrusudur.
Buna göre \( f \) parabolünün \( y \) eksenini kestiği noktanın ordinatı kaçtır?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
Parabolün katsayılarını yazalım.
\( a = 1, \quad b = -3m, \quad c = 2m - 3 \)
Parabolün simetri ekseni tepe noktasından geçen \( x = r \) doğrusudur.
\( r = -\dfrac{b}{2a} = -\dfrac{-3m}{2(1)} = 6 \)
\( m = 4 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = x^2 - 3(4)x + 2(4) - 3 \)
\( = x^2 - 12x + 5 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı \( f(0) \) değerine yani parabol denkleminin sabit terimine eşittir.
\( f(0) = 5 \) bulunur.
\( f(x) = x^2 - 6x + 13 \) parabolünde,
\( f(m - 5) = f(3m + 7) \)
\( f(8 - n) = f(4 - 2n) \)
olduğuna göre, \( mn \) çarpımının en büyük değeri kaçtır?
Çözümü Göster\( f(x) \) parabolünün tepe noktasına \( T(r, k) \) diyelim.
\( a = 1, \quad b = -6, \quad c = 13 \)
\( r = -\dfrac{b}{2a} = -\dfrac{-6}{2(1)} = 3 \)
Buna göre \( f(x) \) parabolünün simetri ekseni \( x = r = 3 \) doğrusudur.
Bir parabol üzerindeki simetri eksenine göre simetrik iki noktanın fonksiyon değerleri birbirine eşittir.
Benzer şekilde, bir parabolde \( f(a) = f(b) \) ise ya \( a = b \) olur ya da \( x = a \) ve \( x = b \) noktaları simetri eksenine göre simetriktir.
Verilen iki eşitlik için bu iki durumu ayrı ayrı inceleyelim.
\( f(m - 5) = f(3m + 7) \)
Durum 1:
\( m - 5 = 3m + 7 \)
\( m = -6 \)
Durum 2:
\( \dfrac{m - 5 + 3m + 7}{2} = 3 \)
\( m = 1 \)
\( f(8 - n) = f(4 - 2n) \)
Durum 1:
\( 8 - n = 4 - 2n \)
\( n = -4 \)
Durum 2:
\( \dfrac{8 - n + 4 - 2n}{2} = 3 \)
\( n = 2 \)
Bulduğumuz farklı \( m \) ve \( n \) değerlerinin çarpımının en büyük değerini bulalım.
\( mn = -6 \cdot (-4) = 24 \) bulunur.
\( f(x) = -x^2 + 8x - 5 \) olduğuna göre,
\( \dfrac{f(-1) - f(\sqrt{2} - 3)}{f(11 - \sqrt{2}) - f(9)} \) ifadesinin değeri kaçtır?
Çözümü GösterVerilen parabolün tepe noktasının apsis değerini bulalım.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{8}{2(-1)} = 4 \)
Buna göre parabol grafiğinde \( x = 4 \) simetri eksenine göre simetrik olan noktaların fonksiyon değerleri birbirine eşit olur.
\( x = -1 \) ve \( x = 9 \) noktaları simetri eksenine göre simetrik olduğu için fonksiyon değerleri birbirine eşittir.
\( \dfrac{-1 + 9}{2} = r = 4 \)
\( f(-1) = f(9) = a \)
Benzer şekilde, \( x = \sqrt{2} - 3 \) ve \( x = 11 - \sqrt{2} \) noktaları simetri eksenine göre simetrik olduğu için fonksiyon değerleri birbirine eşittir.
\( \dfrac{\sqrt{2} - 3 + 11 - \sqrt{2}}{2} = r = 4 \)
\( f(\sqrt{2} - 3) = f(11 - \sqrt{2}) = b \)
Bu değerleri sorudaki ifadede yerine koyalım.
\( \dfrac{f(-1) - f(\sqrt{2} - 3)}{f(11 - \sqrt{2}) - f(9)} \)
\( = \dfrac{a - b}{b - a} = -1 \) bulunur.
\( m \in \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - (2m + 4)x + 4m + 7 \) fonksiyonu için \( f(-2) = f(8) \) eşitliği sağlanmaktadır.
Buna göre \( f(0) \) kaçtır?
Çözümü GösterBir parabol üzerindeki simetri eksenine göre simetrik iki noktanın fonksiyon değerleri birbirine eşittir.
Benzer şekilde, bir parabol üzerindeki iki farklı noktanın fonksiyon değerleri birbirine eşitse bu iki nokta simetri eksenine göre simetriktir.
Verilen iki noktanın fonksiyon değerleri birbirine eşit olduğu için bu iki nokta simetri eksenine göre simetrik noktalardır. Buna göre simetri ekseni bu iki noktanın orta noktasından geçer.
Parabolün simetri ekseni \( x = r \) olmak üzere,
\( r = \dfrac{-2 + 8}{2} = 3 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-(2m + 4)}{2(1)} \)
\( r = m + 2 = 3 \)
\( m = 1 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = x^2 - 6x + 11 \)
\( f(0) = 11 \) bulunur.
\( a \ne 33 \) olmak üzere,
\( f(x) = 2x^2 - 8x + 7 \) parabolünde \( f(33) = f(a) \) olduğuna göre, \( a \) kaçtır?
Çözümü GösterBir parabolün tepe noktası \( T(r, k) \) olmak üzere, \( x = r \) doğrusu parabolün simetri eksenidir.
Simetri eksenine eşit uzaklıktaki noktaların ordinatları birbirine eşittir.
Parabolün tepe noktasının apsisini bulalım.
\( r = -\dfrac{b}{2a} \)
\( = -\dfrac{-8}{2(2)} = 2 \)
Buna göre parabolün simetri ekseni \( x = 2 \) doğrusudur.
\( f(33) = f(a) \) olduğuna göre, \( x = 33 \) ve \( x = a \) doğruları simetri eksenine eşit uzaklıktadır.
\( x = 33 \) doğrusunun \( x = 2 \) doğrusuna olan uzaklığını bulalım.
\( \abs{33 - 2} = 31 \)
Buna göre \( x = a \) doğrusu simetri eksenine eksenin diğer tarafında 31 birim uzaklıkta olmalıdır.
\( a = 2 - 31 = -29 \) bulunur.
\( f(x) = ax^2 + bx + c \) fonksiyonunda \( f(-2) = f(6) = 10 \) eşitliği veriliyor.
\( b \ne 0 \) olduğuna göre, \( \dfrac{a}{b} \) kaçtır?
Çözümü GösterParabolün simetri eksenine eşit uzaklıktaki iki noktadaki fonksiyon değerleri birbirine eşittir.
\( f(-2) = f(6) \) olduğuna göre, \( x = -2 \) ve \( x = 6 \) doğruları simetri eksenine eşit uzaklıktadır, dolayısıyla simetri ekseni bu iki noktanın ortasından geçer.
Simetri ekseninin denklemini bulalım.
\( x = \dfrac{-2 + 6}{2} = 2 \)
Tepe noktasına \( T(r, k) \) diyelim.
Tepe noktası simetri ekseninden geçtiği için apsis değeri simetri ekseninin sabit apsis değerine eşittir.
\( r = 2 \)
\( f(x) = ax^2 + bx + c \) şeklindeki parabol denkleminde tepe noktasının apsisi aşağıdaki formülle bulunur.
\( r = -\dfrac{b}{2a} \)
\( 2 = -\dfrac{b}{2a} \)
\( \dfrac{a}{b} = -\dfrac{1}{4} \) bulunur.
\( f(x) = -x^2 + bx + c \) parabolünde her \( m \) reel sayısı için \( f(-m + 3) = f(m + 3) \) eşitliği sağlanmaktadır.
Buna göre \( f(-1) \), \( f(2) \) ve \( f(5) \) değerlerini küçükten büyüğe sıralayın.
Çözümü GösterTepe noktası \( T(r, k) \) olan bir parabolde her \( m \) reel sayısı için \( f(r - m) = f(r + m) \) eşitliği sağlanır. Bunun sebebi parabolün \( x = r \) simetri eksenine göre simetrik olması ve simetri ekseninden eşit uzaklıktaki noktaların fonksiyon değerlerinin aynı olmasıdır.
Verilen eşitliği düzenleyelim.
\( f(-m + 3) = f(m + 3) \)
\( f(3 - m) = f(3 + m) \)
Bir parabolde her \( m \) sayısı için \( f(3 - m) = f(3 + m) \) eşitliği sağlanıyorsa parabolün tepe noktasının apsis değeri \( x = 3 \) olur.
Verilen parabolün başkatsayısı negatif olduğu için kolları aşağı yönlüdür. Parabol en büyük değerini tepe noktasında alır ve parabol üzerindeki bir noktanın apsis değeri \( x = 3 \) noktasından uzaklaştıkça fonksiyon değeri küçülür.
\( x = -1 \) noktası \( x = 3 \) noktasından en uzak, \( x = 2 \) noktası en yakındır. Buna göre istenen fonksiyon değerlerinin küçükten büyüğe sıralaması aşağıdaki gibi olur.
\( f(-1) \lt f(5) \lt f(2) \)
Bu noktalar aşağıdaki örnek negatif başkatsayılı parabolün grafiği üzerinde gösterilmiştir. Gerçek parabol grafiğinin eksenlere göre konumu ve kollarının açıklığı farklı olabilecek olsa da bu noktaların fonksiyon değerleri arasındaki sıralama değişmeyecektir.
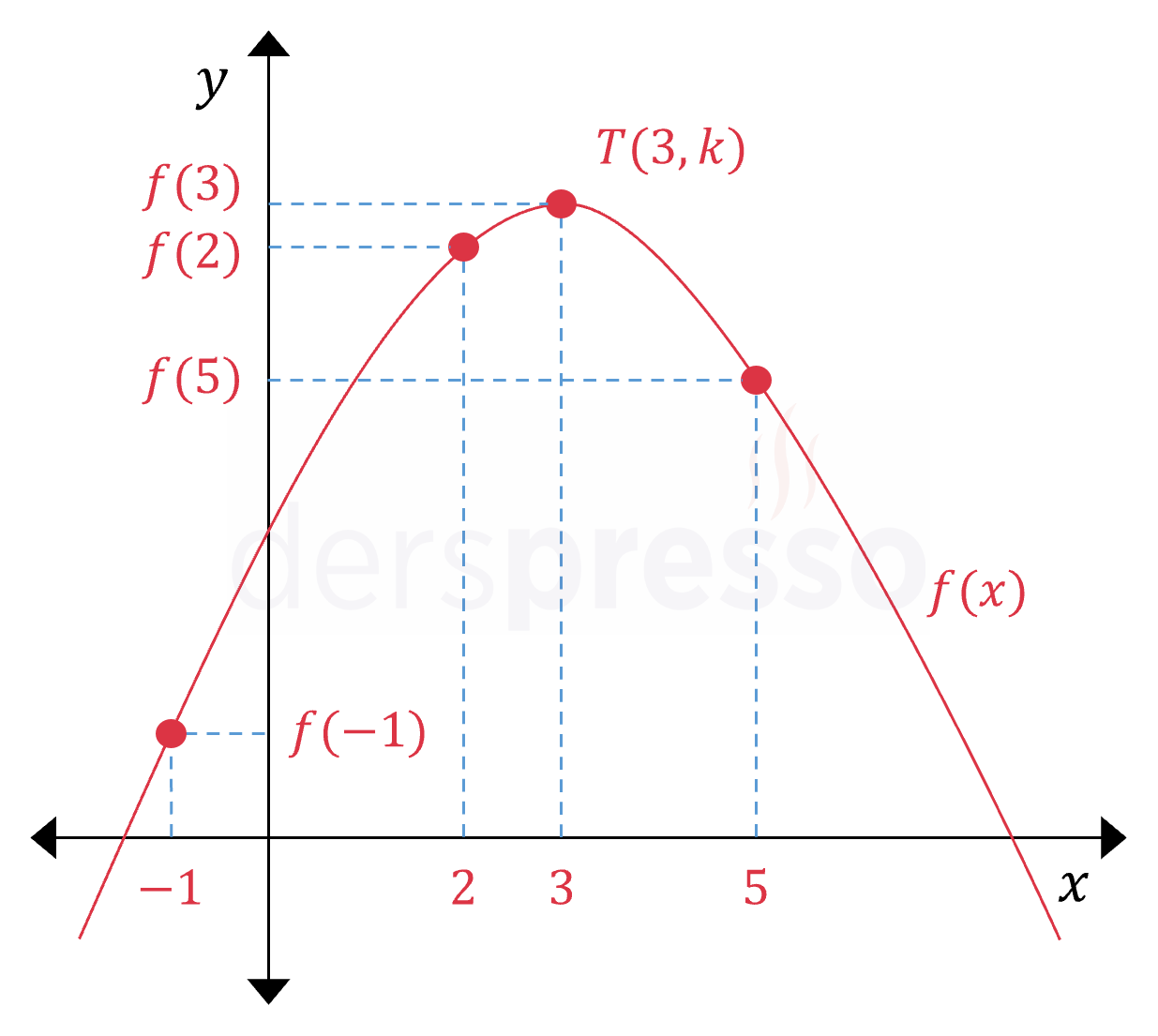
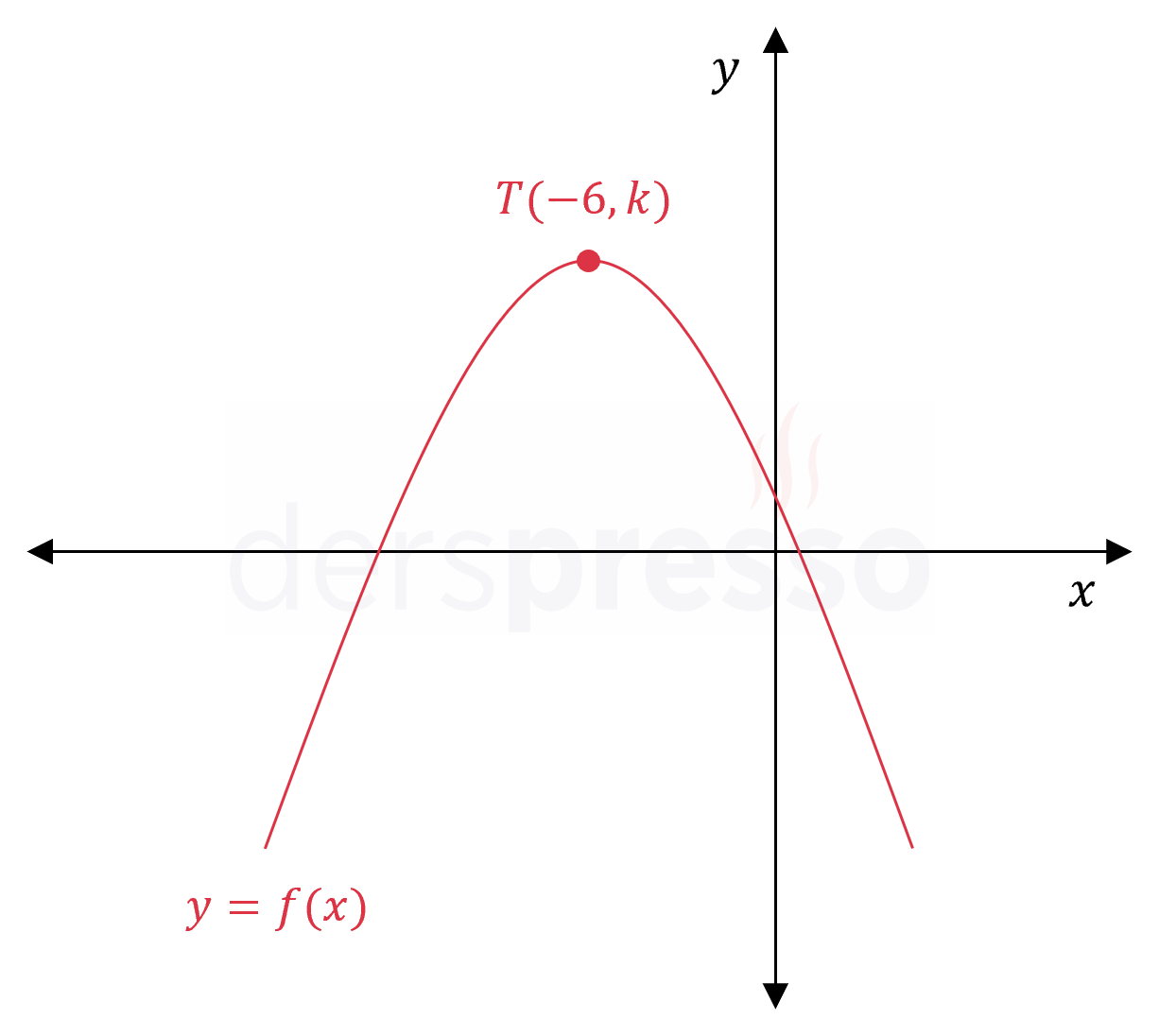
Yukarıdaki şekilde tepe noktası \( T(-6, k) \) olan \( f(x) \) parabolü verilmiştir.
Buna göre \( \dfrac{f(44) + f(2)}{f(-56) + f(-14)} \) oranı kaçtır?
Çözümü GösterParabolün tepe noktası parabolün simetri ekseni üzerinde bulunur.
Buna göre parabol grafiğinde \( x = -6 \) simetri eksenine göre simetrik olan noktaların fonksiyon değerleri birbirine eşit olur.
\( \dfrac{44 + (-56)}{2} = r = -6 \)
Buna göre \( x = 44 \) ve \( x = -56 \) apsisli noktalar simetri eksenine göre simetriktir. Bu değere \( a \) diyelim.
\( f(44) = f(-56) = a \)
\( \dfrac{2 + (-14)}{2} = r = -6 \)
Buna göre \( x = 2 \) ve \( x = -14 \) apsisli noktalar simetri eksenine göre simetriktir. Bu değere \( b \) diyelim.
\( f(2) = f(-14) = b \)
Bu değerleri sorudaki ifadede yerine koyalım.
\( \dfrac{f(44) + f(2)}{f(-56) + f(-14)} \)
\( = \dfrac{a + b}{a + b} = 1 \) bulunur.