Parabolün Tanım ve Görüntü Kümeleri
Tüm polinom fonksiyonlarında olduğu gibi, parabol fonksiyonunu tanımsız yapan bir \( x \) değeri bulunmadığı için parabolün en geniş tanım kümesi tüm reel sayılardır.
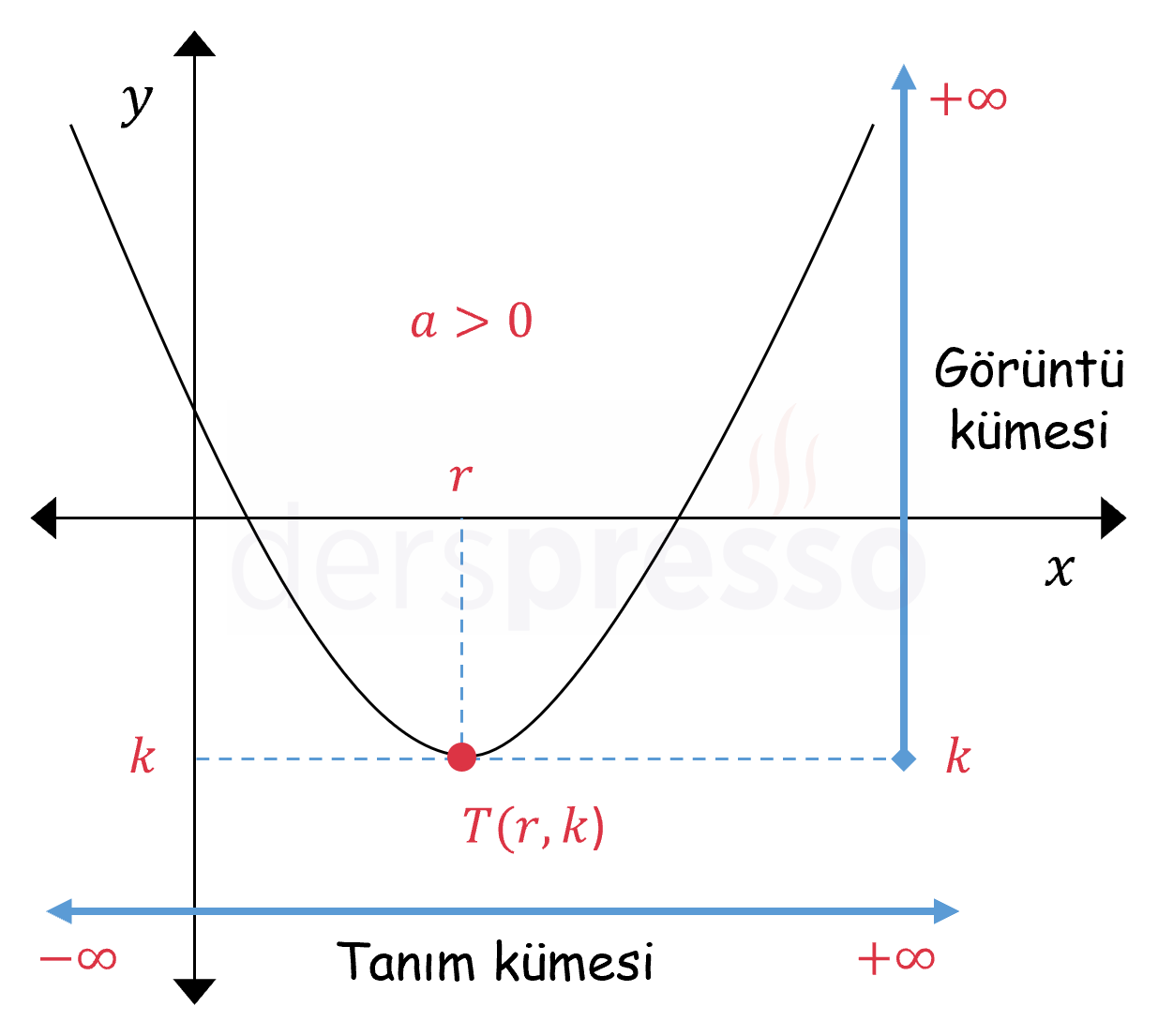
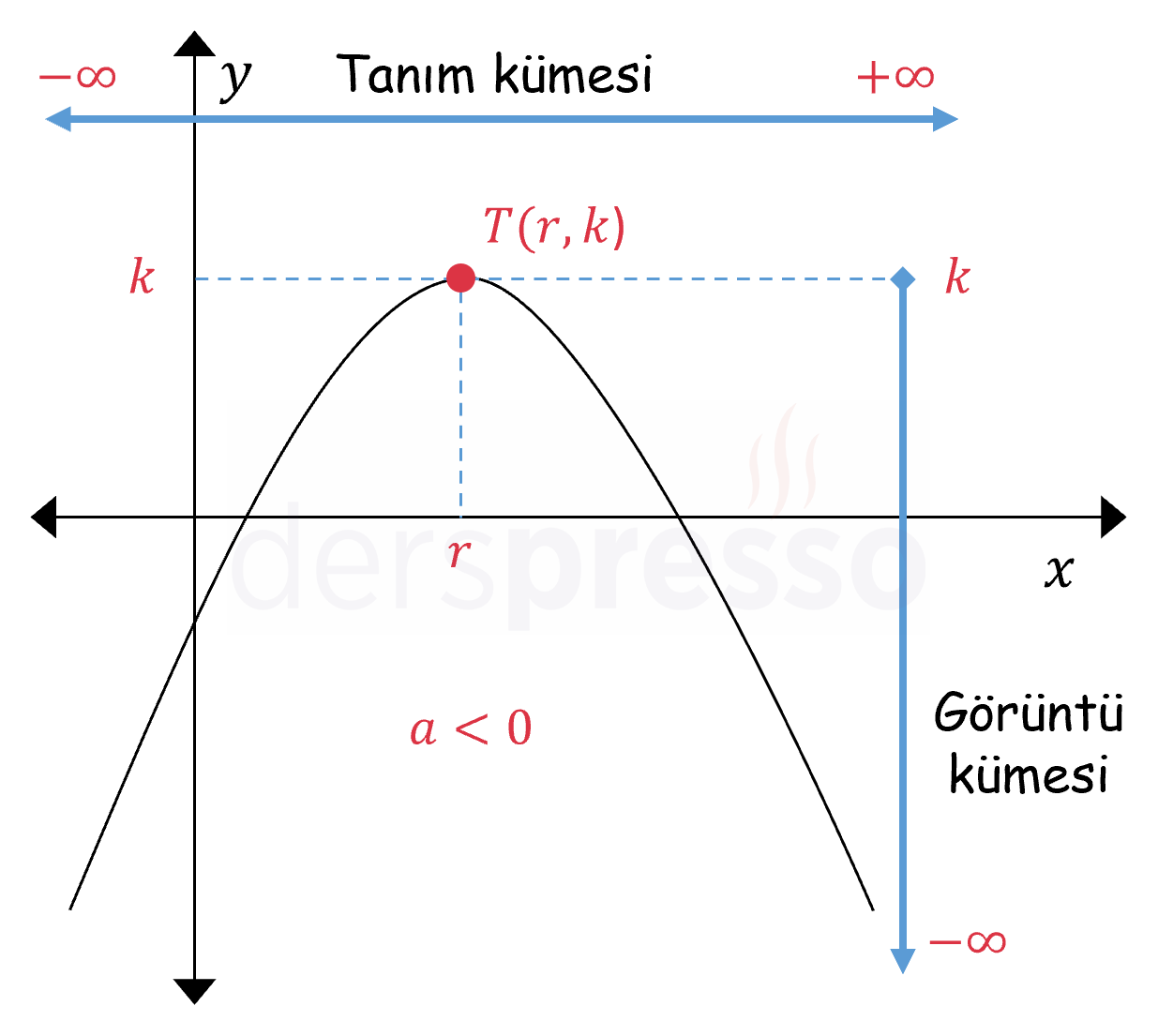
Parabolün görüntü kümesi ise başkatsayısı pozitif (\( a \gt 0 \)) olan paraboller için tepe noktasının (\( T(r, k) \)) ordinat değerinden pozitif sonsuza, başkatsayısı negatif (\( a \lt 0 \)) olan paraboller için tepe noktasının ordinat değerinden negatif sonsuza kadar olan aralıktır.
| Başkatsayı | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( a \gt 0 \) | \( \mathbb{R} \) | \( [k, \infty) \) |
| \( a \lt 0 \) | \( \mathbb{R} \) | \( (-\infty, k] \) |
Aşağıda \( a \gt 0 \) ve \( a \lt 0 \) için örnek parabol grafikleri verilmiş ve en geniş tanım ve görüntü kümeleri grafik üzerinde işaretlenmiştir.
Bir parabolün değerinin her \( x \) değeri için pozitif/negatif/sıfır olduğu biliniyorsa başkatsayısı ve deltası ile ilgili olarak aşağıdaki çıkarımlar yapılabilir.
| Grafik | Parabolün Değeri |
|---|---|
|
Parabol değeri her zaman pozitif ise: \( f(x) \gt 0 \) Bu durumda başkatsayı pozitif, delta sıfırdan küçük olmalıdır. \( a \gt 0 \) \( \Delta \lt 0 \) |

|
Parabol değeri her zaman sıfır ya da pozitif ise: \( f(x) \ge 0 \) Bu durumda başkatsayı pozitif, delta sıfıra eşit ya da sıfırdan küçük olmalıdır. \( a \gt 0 \) \( \Delta \le 0 \) |

|
Parabol değeri her zaman negatif ise: \( f(x) \lt 0 \) Bu durumda başkatsayı negatif, delta sıfırdan küçük olmalıdır. \( a \lt 0 \) \( \Delta \lt 0 \) |

|
Parabol değeri her zaman sıfır ya da negatif ise: \( f(x) \le 0 \) Bu durumda başkatsayı negatif, delta sıfıra eşit ya da sıfırdan küçük olmalıdır. \( a \lt 0 \) \( \Delta \le 0 \) |
\( f: [-2, 8] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 4x - 2 \) ifadesinin görüntü kümesini bulunuz.
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -4, \quad c = -2 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-4}{2(1)} = 2 \)
Buna göre tepe noktası fonksiyonun tanım kümesi içindedir.
Parabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür. Tepe noktası fonksiyonun tanım kümesi içinde olduğu için parabol en küçük değerini tepe noktasında, en büyük değerini tanım kümesinin sınır değerlerinden birinde alır.
Bu üç noktadaki fonksiyon değerlerini bulalım.
\( f(2) = 2^2 - 4(2) - 2 = -6 \)
\( f(-2) = (-2)^2 - 4(-2) - 2 = 10 \)
\( f(8) = 8^2 - 4(8) - 2 = 30 \)
Buna göre parabolün \( [-2, 8] \) aralığında aldığı en küçük değer \( -6 \), en büyük değer \( 30 \)'dur.
Görüntü kümesi: \( f(x) \in [-6, 30] \)
\( f(x) = (k + 2)x^2 - 2kx + k - 3 \) fonksiyonunun grafiği daima \( x \) ekseninin altında kaldığına göre, \( k \)'nın değer aralığını bulunuz.
Çözümü GösterParabolün katsayılarını yazalım.
\( a = k + 2, \quad b = -2k, \quad c = k - 3 \)
Parabolün grafiği daima \( x \) ekseninin altında kalıyorsa iki koşul sağlanmalıdır.
Koşul 1: Parabolün kolları aşağı yönlüdür (başkatsayısı negatiftir).
\( k + 2 \lt 0 \)
\( k \lt -2 \)
Koşul 2: Parabol \( x \) eksenini hiçbir noktada kesmez (deltası sıfırdan küçüktür).
\( \Delta \lt 0 \)
\( b^2 - 4ac \lt 0 \)
\( (-2k)^2 - 4(k + 2)(k - 3) \lt 0 \)
\( 4k^2 - 4(k^2 - k - 6) \lt 0 \)
\( 4k^2 - 4k^2 + 4k + 24 \lt 0 \)
\( 4k \lt -24 \)
\( k \lt -6 \)
Bulduğumuz iki aralığın kesişim kümesi \( k \) değer aralığını verir.
\( k \lt -6 \) bulunur.
\( f(x) = (2n + 2)x^2 - 4nx + 2n + 1 \)
fonksiyonunun grafiği daima \( x \) ekseninin üstünde olduğuna göre, \( n \)'nin değer aralığı nedir?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 2n + 2, \quad b = -4n, \quad c = 2n + 1 \)
Parabol \( x \) ekseninin daima üstünde kalıyorsa iki koşul sağlanmalıdır.
Koşul 1:
Parabolün kolları yukarı yönlü, yani başkatsayısı pozitif olmalıdır.
\( 2n + 2 \gt 0 \)
\( n \gt -1 \)
Koşul 2:
Parabol \( x \) eksenini hiçbir noktada kesmemelidir, yani deltası sıfırdan küçük olmalıdır.
\( \Delta = b^2 - 4ac \lt 0 \)
\( (-4n)^2 - 4(2n + 2)(2n + 1) \lt 0 \)
\( 16n^2 - 4(4n^2 + 6n + 2) \lt 0 \)
\( 16n^2 - 16n^2 - 24n - 8 \lt 0 \)
\( -24n \lt 8 \)
\( n \gt -\dfrac{1}{3} \)
Bulunan iki aralığın kesişim kümesi \( n \)'nin değer aralığını verir.
\( n \in (-\dfrac{1}{3}, \infty) \) bulunur.
\( f(x) = (2x - 9)^2 + (7 - 2x)^2 \) parabolünün en küçük değeri nedir?
Çözümü GösterParantez içindeki ifadelerin açılımını yazalım.
\( f(x) = 4x^2 - 36x + 81 + 49 - 28x + 4x^2 \)
\( = 8x^2 - 64x + 130 \)
Parabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür, dolayısıyla parabol en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Parabolün katsayılarını yazalım.
\( a = 8, \quad b = -64, \quad c = 130 \)
\( r = -\dfrac{b}{2a} = -\dfrac{-64}{2(8)} = 4 \)
Parabolün tepe noktasındaki değerini bulalım.
\( k = f(4) = 8(4)^2 - 64(4) + 130 \)
\( = 2 \) bulunur.
\( f: [0, 3] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 4x + 5 \) fonksiyonunun alabileceği en küçük ve en büyük değerlerin toplamı kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -4, \quad c = 5 \)
Parabolün tepe noktasının fonksiyonun tanım aralığında olup olmadığını kontrol edelim.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-4}{2(1)} = 2 \)
Parabolün tepe noktası parabolün tanım aralığındadır ve parabolün başkatsayısı pozitif ve kolları yukarı yönlüdür, dolayısıyla parabol verilen aralıkta en küçük değerini tepe noktasında, en büyük değerini tanım kümesinin sınır noktalarından birinde alır.
Parabolün bu üç noktadaki değerlerini bulalım.
\( f(0) = 0^2 - 4(0) + 5 = 5 \)
\( f(2) = 2^2 - 4(2) + 5 = 1 \)
\( f(3) = 3^2 - 4(3) + 5 = 2 \)
Buna göre parabolün verilen aralıkta en küçük değeri \( f(2) = 1 \), en büyük değeri \( f(0) = 5 \) olur.
Bu iki değerin toplamı \( 5 + 1 = 6 \) olarak bulunur.
\( x \in \mathbb{R} \) olmak üzere
\( (10 - x)(x - 2) \) çarpımın sonucu aşağıdakilerden hangisi olamaz?
(a) 12
(b) 14
(c) 15
(d) 16
(e) 18
Çözümü GösterVerilen çarpımın açılımı bir parabol denklemi ifade eder.
\( f(x) = -x^2 + 12x - 20 \)
\( f \) parabolünün başkatsayısı negatif olduğu için parabol en büyük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} \)
\( = -\dfrac{12}{2(-1)} = 6 \)
Parabolün en büyük değerini bulmak için denklemde \( x = 6 \) yazalım.
\( k = f(6) \)
\( = -6^2 + 12(6) - 20 = 16 \)
Buna göre parabol \( (-\infty, 16] \) aralığında tüm reel sayı değerlerini alır.
\( f(x) \le 16 \)
Buna göre parabol 18 değerini alamaz. Doğru cevap (e) seçeneğidir.
\( x \in [-8, 1] \) olmak üzere,
\( f(x) = -\dfrac{1}{2}x^2 - 4x + 10 \) parabolünün alabileceği en büyük ve en küçük tam sayı değerler arasındaki fark kaçtır?
Çözümü GösterParabolün başkatsayısı negatif olduğu için kolları aşağı yönlüdür.
Kolları aşağı yönlü bir parabol en büyük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} \)
\( = -\dfrac{-4}{2 \cdot (-\frac{1}{2})} = -4 \)
Tepe noktasının apsisi \( [-8, 1] \) tanım aralığında olduğu için parabol verilen aralıktaki en büyük değerini tepe noktasında alır.
Parabolün tepe noktasındaki değerini bulalım.
\( k = f(-4) \)
\( = -\dfrac{1}{2}(-4)^2 - 4(-4) + 10 = 18 \)
Buna göre parabolün en büyük tam sayı değeri 18'dir.
Parabolün en küçük değeri için verilen sınır değerlerini inceleyelim.
\( x = -8 \) için:
\( f(-8) = -\dfrac{1}{2}(-8)^2 - 4(-8) + 10 \)
\( = -32 + 32 + 10 = 10 \)
\( x = 1 \) için:
\( f(1) = -\dfrac{1}{2}(1)^2 - 4(1) + 10 \)
\( = -\dfrac{1}{2} - 4 + 10 = \dfrac{11}{2} \)
Parabolün kolları aşağı yönlü olduğu için parabolün verilen aralıktaki en küçük tam sayı değeri 6 olur.
Parabolün verilen aralıkta alabileceği en büyük ve en küçük tam sayı değerlerin farkı \( 18 - 6 = 12 \) olarak bulunur.
\( f(x) = -x^2 + 6x + 16 \) parabolünün koordinatları pozitif tam sayılar olan kaç noktası vardır?
Çözümü GösterParabol denkleminde \( x \) değeri parabol üzerindeki bir noktanın apsis değerine, \( -x^2 + 6x + 16 \) ifadesi de bu noktanın ordinat değerine karşılık gelir.
Koordinatları pozitif tam sayılar olan noktaları bulmak için önce ordinatı pozitif olan noktaları bulalım.
\( y = f(x) \gt 0 \)
\( -x^2 + 6x + 16 \gt 0 \)
Eşitsizliğin taraflarını \( -1 \) ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile ile çarpıldığında eşitsizlik yön değiştirir.
\( x^2 - 6x - 16 \lt 0 \)
\( (x + 2)(x - 8) \lt 0 \)
Bu eşitsizlik her bir çarpanı sıfır yapan \( x = -2 \) ve \( x = 8 \) değerlerinin arasındaki aralıkta sağlanır.
\( -2 \lt x \lt 8 \)
Buna göre bu aralıktaki \( x \) değerlerinde parabolün ordinatı pozitif olur.
\( x \)'in bu aralıktaki pozitif tam sayı değerlerini bulalım.
\( x \in \{ 1, 2, 3, 4, 5, 6, 7 \} \)
Parabolün katsayıları tam sayı olduğu için, \( x \)'in tam sayı değerlerinde \( y \) de tam sayı olur.
Buna göre verilen parabolün koordinatları pozitif tam sayılar olan 7 noktası vardır.
\( f:(-4, 9] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 6x + 16 \) fonksiyonunun alabileceği kaç farklı tam sayı değeri vardır?
Çözümü Göster1. yöntem:
Parabolün katsayılarını yazalım.
\( a = 1, \quad b = -6, \quad c = 16 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-6}{2(1)} = 3 \)
Buna göre tepe noktası fonksiyonun tanım kümesi içindedir.
Parabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür. Tepe noktası fonksiyonun tanım kümesi içinde olduğu için parabol en küçük değerini tepe noktasında, en büyük değerini tanım kümesinin sınır değerlerinden birinde alır.
Bu üç noktadaki fonksiyon değerlerini bulalım.
\( f(3) = 3^2 - 6(3) + 16 = 7 \)
\( f(-4) = (-4)^2 - 6(-4) + 16 = 56 \)
\( f(9) = 9^2 - 6(9) + 16 = 43 \)
\( x = -4 \) noktası tanım kümesine dahil olmadığı için fonksiyon \( f(-4) = 56 \) değerini almaz.
Buna göre parabolün tanım kümesi içinde alabileceği en küçük tam sayı değeri 7, en büyük tamsayı değeri 55 olur.
\( f \) fonksiyonunun tanım kümesi içinde alabileceği \( 55 - 7 + 1 = 49 \) farklı tamsayı değeri vardır.
2. yöntem:
\( f(x) = x^2 - 6x + 16 \)
\( = x^2 - 6x + 9 + 7 \)
\( = (x - 3)^2 + 7 \)
Fonksiyonun tanım aralığını \( f(x) \) formuna getirelim.
\( -4 \lt x \le 9 \)
\( -7 \lt x - 3 \le 6 \)
Eşitsizliğin taraflarının karesini alalım.
Verilen aralık sıfır değerini içerdiği için tarafların karesini aldığımızda alt sınır değeri sıfır olur, üst sınır değeri eşitsizlikteki sınır değerlerinden mutlak değerce büyük olanın karesi olur.
\( 0 \le (x - 3)^2 \lt 49 \)
\( 7 \le (x - 3)^2 + 7 \lt 56 \)
\( 7 \le f(x) \lt 56 \)
\( f \) fonksiyonunun tanım kümesi içinde alabileceği \( 55 - 7 + 1 = 49 \) farklı tamsayı değeri vardır.
\( f:(2, 10] \to \mathbb{R} \) olmak üzere,
\( f(x) = -2x^2 + 4x - 7 \) fonksiyonunun alabileceği kaç farklı tam sayı değeri vardır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = -2, \quad b = 4, \quad c = -7 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{4}{2(-2)} = 1 \)
Tepe noktasının apsisi \( x = r = 1 \) olduğu için tanım kümesi içinde yer almaz.
Fonksiyonun alabileceği en küçük/en büyük değerler için, fonksiyonun tanım kümesinin sınır değerlerindeki değerlerini bulalım.
\( f(2) = -2(2)^2 + 4(2) - 7 = -7 \)
\( f(10) = -2(10)^2 + 4(10) - 7 = -167 \)
\( x = 2 \) noktası tanım kümesine dahil olmadığı için fonksiyon \( f(2) = -7 \) değerini almaz.
Buna göre parabolün tanım kümesi içinde alabileceği en küçük tam sayı değeri -167, en büyük tamsayı değeri -8 olur.
\( f \) fonksiyonunun tanım kümesi içinde alabileceği \( -8 - (-167) + 1 = 160 \) farklı tamsayı değeri vardır.
\( f: [1, \infty) \to \mathbb{R} \) olmak üzere,
\( f(x) = (x - 3)^2 + 2 \)
fonksiyonunun grafiğini çizerek görüntü kümesini bulunuz.
Çözümü GösterParabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür.
\( f(x) = (x - r)^2 + k \) formundaki bir parabolün tepe noktası \( T(r, k) \) noktasıdır.
Buna göre verilen parabolün tepe noktası \( T(3, 2) \) olur.
\( x = 1 \) noktasındaki fonksiyon değerini bulalım.
\( f(1) = (1 - 3)^2 + 2 = 6 \)
Buna göre parabolün \( x \in [1, \infty) \) aralığındaki grafiği aşağıdaki gibidir.
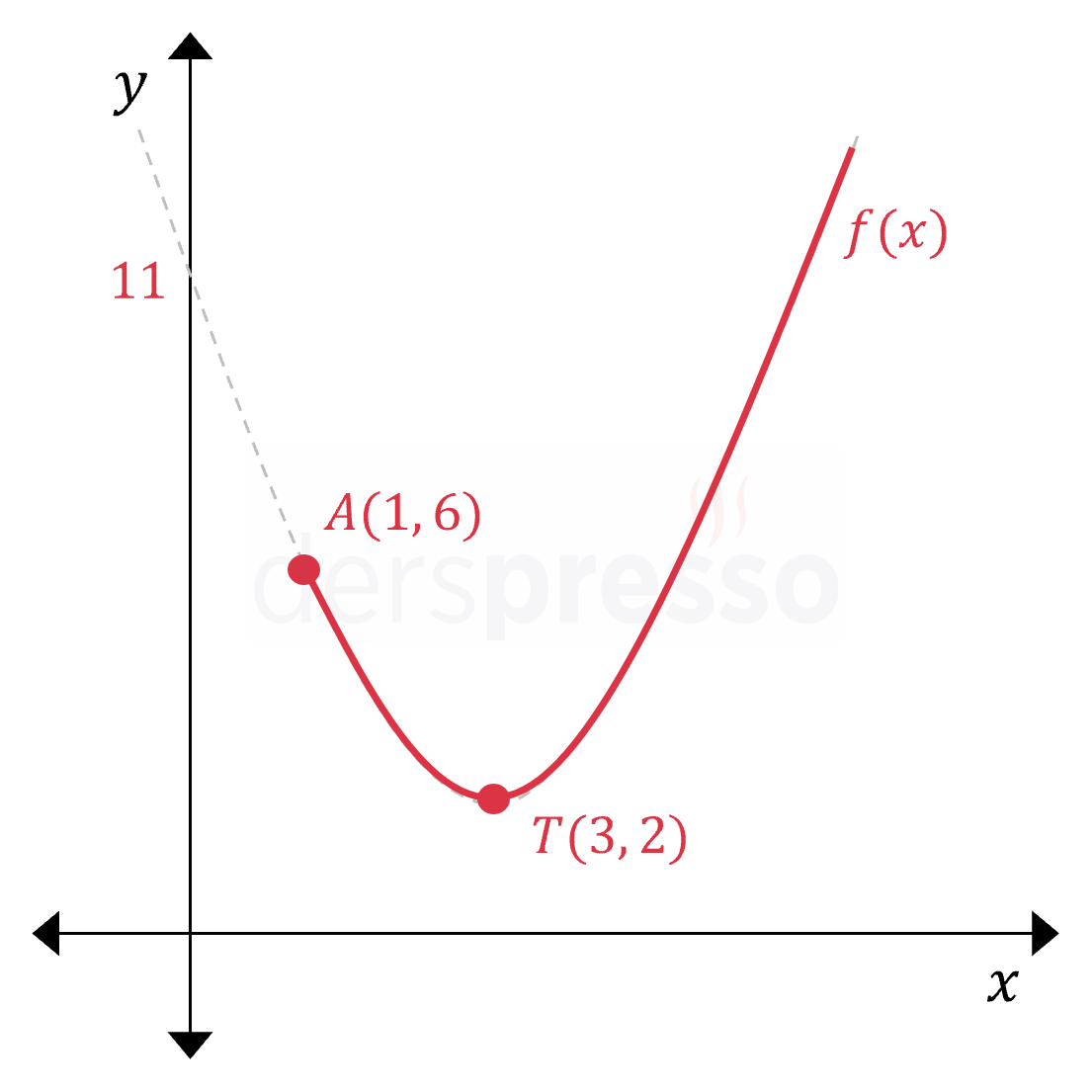
Grafikte görülebileceği üzere, parabolün en küçük değeri tepe noktasındaki \( y = 2 \) değeridir, ayrıca parabol \( x \) sonsuza giderken pozitif sonsuza gider.
Görüntü kümesi: \( f(x) \in [2, \infty) \)
\( f: [2, 8] \to \mathbb{R} \) olmak üzere,
\( f(x) = -\dfrac{1}{2}x^2 + 4x + 3 \)
fonksiyonunun grafiğini çizerek görüntü kümesini bulunuz.
Çözümü GösterParabolün başkatsayısı negatif olduğu için kolları aşağı yönlüdür.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{4}{2(-\frac{1}{2})} = 4 \)
\( k = f(4) \)
\( = -\dfrac{1}{2}(4)^2 + 4(4) + 3 = 11 \)
Buna göre verilen parabolün tepe noktası \( T(4, 11) \) olur.
Fonksiyonun tanım kümesinin uç noktalarındaki değerini bulalım.
\( f(2) = -\dfrac{1}{2}(2)^2 + 4(2) + 3 = 9 \)
\( f(8) = -\dfrac{1}{2}(8)^2 + 4(8) + 3 = 3 \)
Buna göre parabolün \( x \in [2, 8] \) aralığındaki grafiği aşağıdaki gibidir.
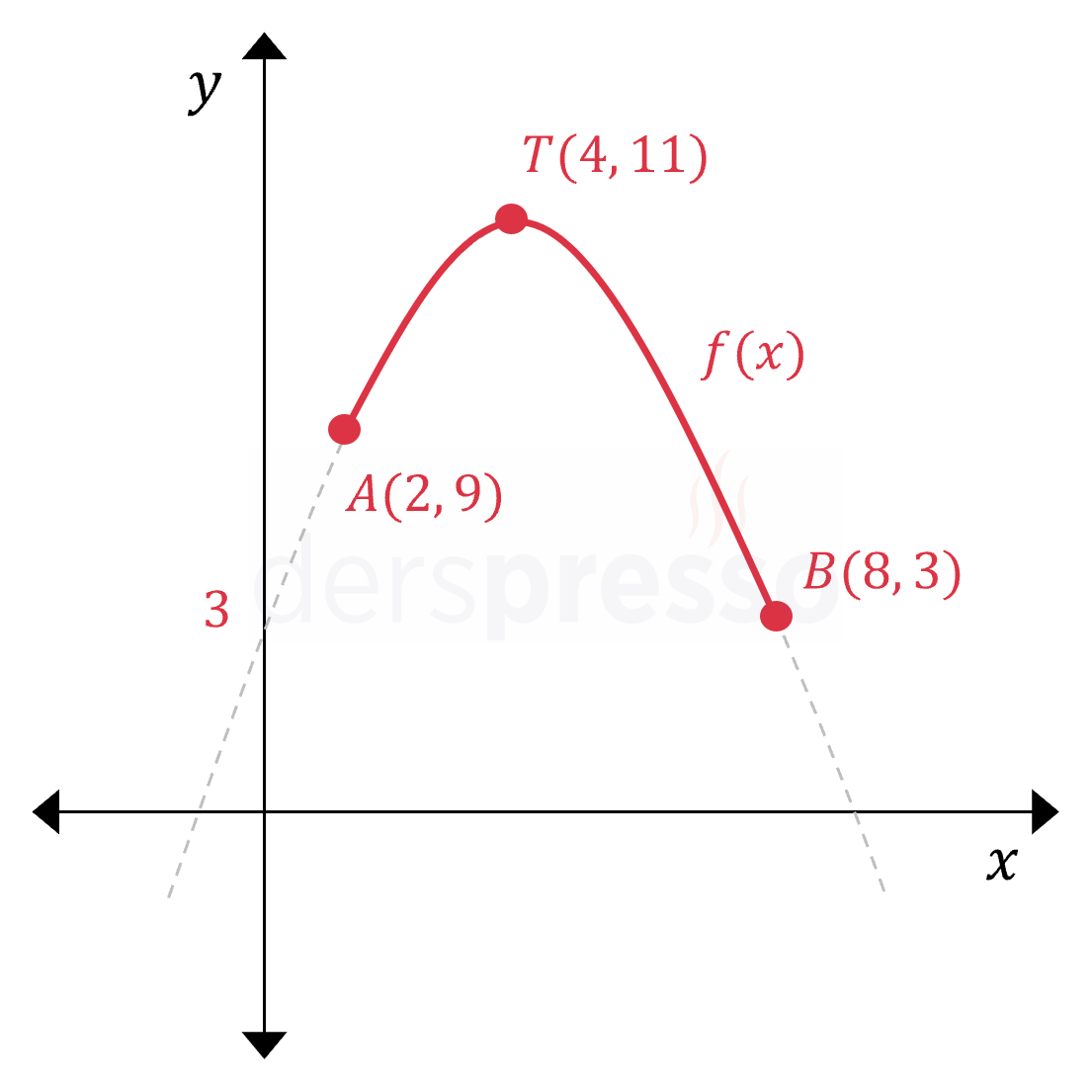
Grafikte görülebileceği üzere, parabolün en küçük değeri \( B \) noktasındaki \( y = 3 \) değeri, en büyük değeri tepe noktasındaki \( y = 11 \) değeridir.
Görüntü kümesi: \( f(x) \in [3, 11] \)
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = x^2 - 7x - 15 \) fonksiyonunun grafiği üzerinden alınacak bir noktanın koordinatları toplamı en az kaç olabilir?
Çözümü GösterParabolün üzerindeki noktaların geometrik yerini aşağıdaki şekilde ifade edebiliriz.
\( (x, f(x)) = (x, x^2 - 7x - 15) \)
Herhangi bir \( x \) değeri için bu noktaların koordinatları toplamını veren fonksiyonun geometrik yerini ise bu noktaların apsis ve ordinat değerlerini toplayarak aşağıdaki şekilde ifade edebiliriz.
\( (x, x + f(x)) = (x, x^2 - 6x - 15) \)
Buna göre bir \( x \) değeri için \( f(x) \) parabolünün koordinatlar toplamını veren fonksiyon aşağıdaki gibi olur.
\( g(x) = x^2 - 6x - 15 \)
Başkatsayısı pozitif olan bu parabolün kolları yukarı yönlüdür, dolayısıyla en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-6}{2(1)} = 3 \)
Buna göre \( x = 3 \) apsisli noktada \( f(x) \) grafiği üzerindeki noktaların koordinatları toplamı en küçük değerini alır.
Bu değeri bulmak için \( g(3) \) değerini hesaplayalım.
\( k = g(3) = 3^2 - 6(3) - 15 \)
\( = -24 \) bulunur.
\( (4x^2 + 11x + 9)^{-1} \) ifadesinin en büyük değeri kaçtır?
Çözümü Göster\( (4x^2 + 11x + 9)^{-1} = \dfrac{1}{4x^2 + 11x + 9} \)
Paydadaki ifadenin deltasını bulalım.
\( \Delta = b^2 - 4ac \)
\( = 11^2 - 4(4)(9) = -23 \lt 0 \)
İfadenin başkatsayısı pozitif ve deltası sıfırdan küçük olduğu için ifade her \( x \) için pozitiftir.
Buna göre verilen ifade her \( x \) için pozitiftir ve ifadenin en büyük değerini alması için payda en küçük değerini almalıdır.
Paydadaki ifade başkatsayısı pozitif olan bir parabol olduğu için en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Parabolün katsayılarını yazalım.
\( a = 4, \quad b = 11, \quad c = 9 \)
\( r = -\dfrac{b}{2a} = -\dfrac{11}{2(4)} = -\dfrac{11}{8} \)
Parabolün tepe noktasındaki değerini bulalım.
\( k = f(-\dfrac{11}{8}) = 4(-\dfrac{11}{8})^2 + 11(-\dfrac{11}{8}) + 9 \)
\( = \dfrac{121}{16} - \dfrac{121}{8} + 9 \)
\( = \dfrac{23}{16} \)
Paydanın en küçük değerini sorudaki ifadede yerine koyalım.
\( \dfrac{1}{\frac{23}{16}} = \dfrac{16}{23} \) bulunur.
\( f \) fonksiyonu bir parabol olup her \( x \) değeri için \( f(x) \ge 0 \) olarak veriliyor.
\( f(1) = 8, \quad f(2) = 2 \)
olduğuna göre, \( f \) fonksiyonunun başkatsayısı hangi aralıktadır?
Çözümü GösterFonksiyonu aşağıdaki şekilde yazabiliriz.
\( f(x) = ax^2 + bx + c \)
Fonksiyonda \( x = 1 \) yazalım.
\( f(1) = a + b + c = 8 \)
Fonksiyonda \( x = 2 \) yazalım.
\( f(2) = 4a + 2b + c = 2 \)
\( b \) ifadesini \( a \) cinsinden bulmak için ikinci denklemden birinci denklemi taraf tarafa çıkaralım.
\( 3a + b = -6 \)
\( b = -6 - 3a \)
\( c \) ifadesini \( a \) cinsinden bulmak için birinci denklemin taraflarını 2 ile çarpıp ikinci denklemden taraf tarafa çıkaralım.
\( 2a - c = -14 \)
\( c = 2a + 14 \)
Her \( x \) değeri için \( f(x) \ge 0 \) sağlandığına göre iki koşul sağlanmalıdır.
Koşul 1: Parabolün kolları yukarı yönlüdür (başkatsayısı pozitiftir).
\( a \gt 0 \)
Koşul 2: Parabol \( x \) eksenini ya tek noktada keser ya da kesmez (deltası sıfıra eşit ya da sıfırdan küçüktür).
\( \Delta = b^2 - 4ac \le 0 \)
\( b \) ve \( c \) ifadelerini \( a \) cinsinden yazalım.
\( (-6 - 3a)^2 - 4a(2a + 14) \le 0 \)
\( 36 + 36a + 9a^2 - 8a^2 - 56a \le 0 \)
\( a^2 - 20a + 36 \le 0 \)
\( (a - 2)(a - 18) \le 0 \)
Bulduğumuz iki aralığın kesişim kümesi \( a \) değer aralığını verir.
\( a \in [2, 18] \) bulunur.
\( x \) liraya üretilen bir mal \( y \) liraya satılmaktadır. \( x \) ile \( y \) arasındaki bağıntı \( y = -x^2 + 17x + 25 \) şeklinde veriliyor.
Bu satıştan elde edilebilecek maksimum kar kaç TL'dir?
Çözümü GösterElde edilen kar, satış ve alış fiyatları arasındaki farka eşittir.
\( y - x = -x^2 + 17x + 25 - x \)
\( = -x^2 + 16x + 25 \)
Buna göre bu ifadenin belirttiği fonksiyonun en büyük değerini bulmalıyız.
Fonksiyon negatif başkatsayılı ve kolları aşağı yönlü bir parabol olduğu için en büyük değerini tepe noktasında alır.
Parabolün katsayılarını yazalım.
\( a = -1, \quad b = 16, \quad c = 25 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{16}{2(-1)} = 8 \)
Buna göre parabol en büyük değerini \( r = 8 \) noktasında alır.
Bu noktadaki fonksiyon değerini bulalım.
\( k = f(8) = -8^2 + 16(8) + 25 \)
\( = 89 \) bulunur.
\( x \) üye sayısı olmak üzere,
Bir spor salonunun bir yılda elde ettiği toplam kâr (bin TL) aşağıdaki fonksiyonla ifade edilmektedir.
\( f(x) = 320x - 2400 - 8x^2 \)
Buna göre aşağıdaki ifadelerden hangileri doğrudur?
I. Kârın en yüksek olması için salonun 20 üyesi olmalıdır.
II. Salonun elde edebileceği en yüksek kâr 600 bin TL'dir.
III. Spor salonu 5 üyesi olduğunda zarar etmektedir.
Çözümü GösterI. öncül:
\( f \) parabolünün kolları aşağı yönlüdür, dolayısıyla fonksiyon en büyük değerini tepe noktasında alır.
Parabolün katsayılarını yazalım.
\( a = -8, \quad b = 320, \quad c = -2400 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} \)
\( = -\dfrac{320}{2(-8)} = 20 \)
\( x \) üye sayısını gösterdiğine göre, kâr üye sayısı 20 olduğunda en yüksek değerine ulaşır.
I. öncül doğrudur.
II. öncül:
\( f \) parabolünün kolları aşağı yönlüdür, dolayısıyla fonksiyon en büyük değerini tepe noktasında alır.
Parabolün tepe noktasındaki değerini bulalım.
\( f(20) = 320(20) - 2400 - 8(20)^2 \)
\( = 6400 - 2400 - 3200 = 800 \)
Salonun elde edebileceği en yüksek kâr 800 bin TL'dir.
II. öncül yanlıştır.
III. öncül:
\( x = 5 \) için fonksiyonun değerini bulalım.
\( f(5) = 320(5) - 2400 - 8(5)^2 \)
\( = 1600 - 2400 - 200 = -1000 \)
\( x = 5 \) için fonksiyonun değeri negatif olduğu için salon 5 üye ile zarar etmektedir.
III. öncül doğrudur.
Buna göre I. ve III. öncüller doğrudur.