Parabol ve Doğrunun Birbirine Göre Durumu
Parabol ile Doğrunun Kesişim Noktaları
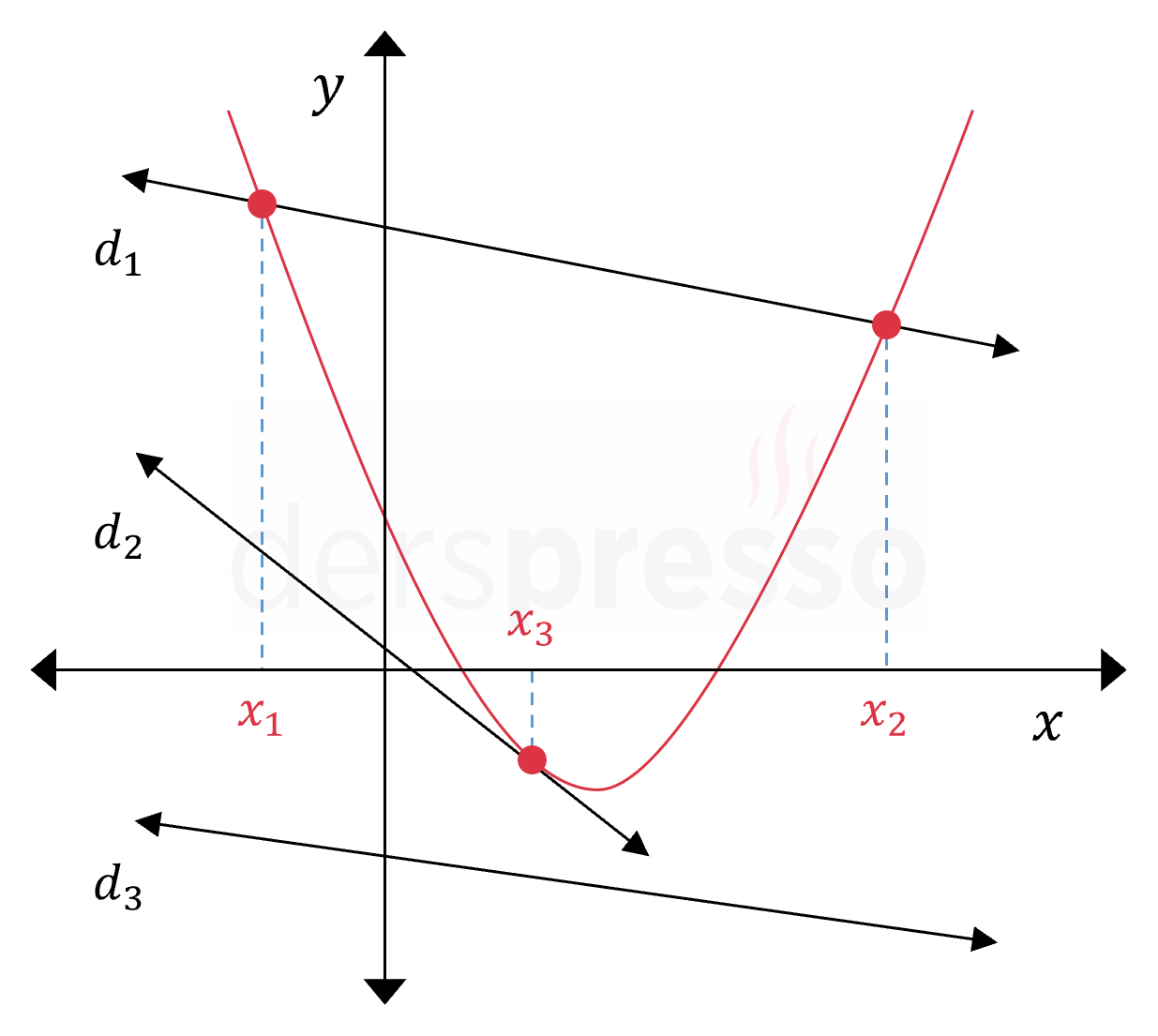
Bir doğru ile bir parabolün birbirine göre durumu, parabolün \( x \) eksenine göre durumuna benzer şekilde üç farklı şekilde olabilir: Doğru parabolü iki noktada kesebilir, tek bir noktada (teğet) kesebilir ya da kesmeyebilir.
Bir doğru ve parabolün birbirine göre durumunu bulmak için iki denklem ortak çözülür ve elde edilen ikinci dereceden denklemin deltası (diskriminantı) incelenir.
\( \Delta = b^2 - 4ac \) ortak çözüm sonucunda elde edilen denklemin deltası olmak üzere,
Doğru parabolü;
- \( \Delta \gt 0 \) ise iki noktada keser,
- \( \Delta = 0 \) ise tek bir noktada (teğet) keser,
- \( \Delta \lt 0 \) ise kesmez.
Ortak çözüm sonucunda elde edilen ikinci dereceden denklemin kökleri doğrunun parabolü kestiği noktaların apsis değerlerini verir. Kesişim noktalarının ordinat değerlerini bulmak için bu apsis değerleri parabol ya da doğru denkleminde yerine konur. Kesişim noktaları parabol ve doğru için ortak olduğu için apsis noktaları her iki denklemde aynı ordinat değerlerini verir.
Burada izlenen yöntem parabolün \( x \) eksenini kestiği noktaları bulmak için kullanılan yöntemle aynıdır. \( x \) ekseni \( y = 0 \) doğrusuna karşılık geldiği için, parabol denklemi sıfıra eşitlendiğinde parabol \( y = 0 \) doğrusu ile ortak çözülmüş olur.
Şimdi bu üç durumla ilgili birer örnek yapalım.
Parabolü İki Noktada Kesen Doğru
Ortak çözümle elde edilen denklemin deltası sıfırdan büyükse doğru parabolü iki noktada keser.
Aşağıda denklemleri verilen parabol ve doğrunun birbirine göre durumlarını inceleyelim.
\( f(x) = x^2 + 2x - 8 \)
\( d_1: y = x + 4 \)
İki denklemi ortak çözelim.
\( x^2 + 2x - 8 = x + 4 \)
Tüm terimleri tek tarafta toplayıp ifadeyi sıfıra eşitleyelim.
\( x^2 + x - 12 = 0 \)
İkinci dereceden denklemin deltasını bulalım.
\( \Delta = b^2 - 4ac \)
\( = 1^2 - 4(1)(-12) = 49 \)
\( \Delta \gt 0 \) olduğuna göre doğru parabolü iki noktada keser.
Bulduğumuz denklemi \( x \) için çözdüğümüzde parabol ile doğrunun kesişim noktalarının apsis değerlerini buluruz.
\( (x + 4)(x - 3) = 0 \)
\( x = -4 \) ve \( x = 3 \)
Bu değerleri doğru (ya da parabol) denkleminde yerine yazdığımızda kesişim noktalarının ordinat değerlerini buluruz.
\( x = -4 \Longrightarrow y = -4 + 4 = 0 \)
\( x = 3 \Longrightarrow y = 3 + 4 = 7 \)
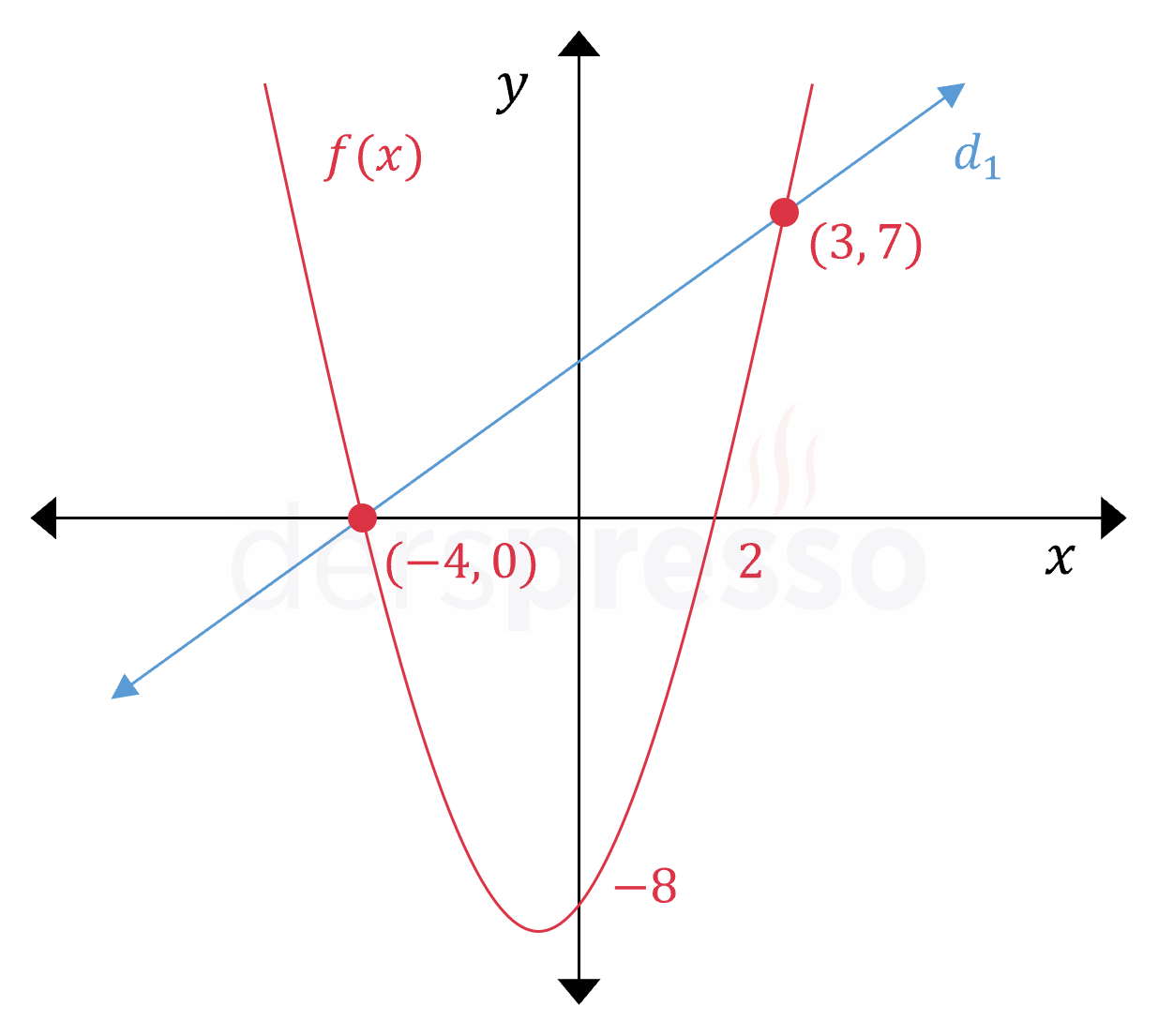
Buna göre parabol ve doğru \( (-4, 0) \) ve \( (3, 7) \) noktalarında kesişir.
Parabolün ve doğrunun grafikleri aşağıda verilmiştir.
Parabolü Tek Noktada (Teğet) Kesen Doğru
Ortak çözümle elde edilen denklemin deltası sıfıra eşitse doğru parabolü tek bir noktada (teğet) keser.
Aşağıda denklemleri verilen parabol ve doğrunun birbirine göre durumlarını inceleyelim.
\( f(x) = \frac{1}{2}x^2 + x - 4 \)
\( d_1: y = 3x - 6 \)
İki denklemi ortak çözelim.
\( \frac{1}{2}x^2 + x - 4 = 3x - 6 \)
Tüm terimleri tek tarafta toplayıp ifadeyi sıfıra eşitleyelim.
\( \frac{1}{2}x^2 - 2x + 2 = 0 \)
\( x^2 - 4x + 4 = 0 \)
İkinci dereceden denklemin deltasını bulalım.
\( \Delta = b^2 - 4ac \)
\( = (-4)^2 - 4(1)(4) = 0 \)
\( \Delta = 0 \) olduğuna göre doğru parabolü tek bir noktada (teğet) keser.
Bulduğumuz denklemi \( x \) için çözdüğümüzde parabol ile doğrunun kesişim noktasının apsis değerini buluruz.
\( (x - 2)^2 = 0 \)
\( x = 2 \)
Bu değeri doğru (ya da parabol) denkleminde yerine yazdığımızda kesişim noktasının ordinat değerini buluruz.
\( x = 2 \Longrightarrow y = 3(2) - 6 = 0 \)
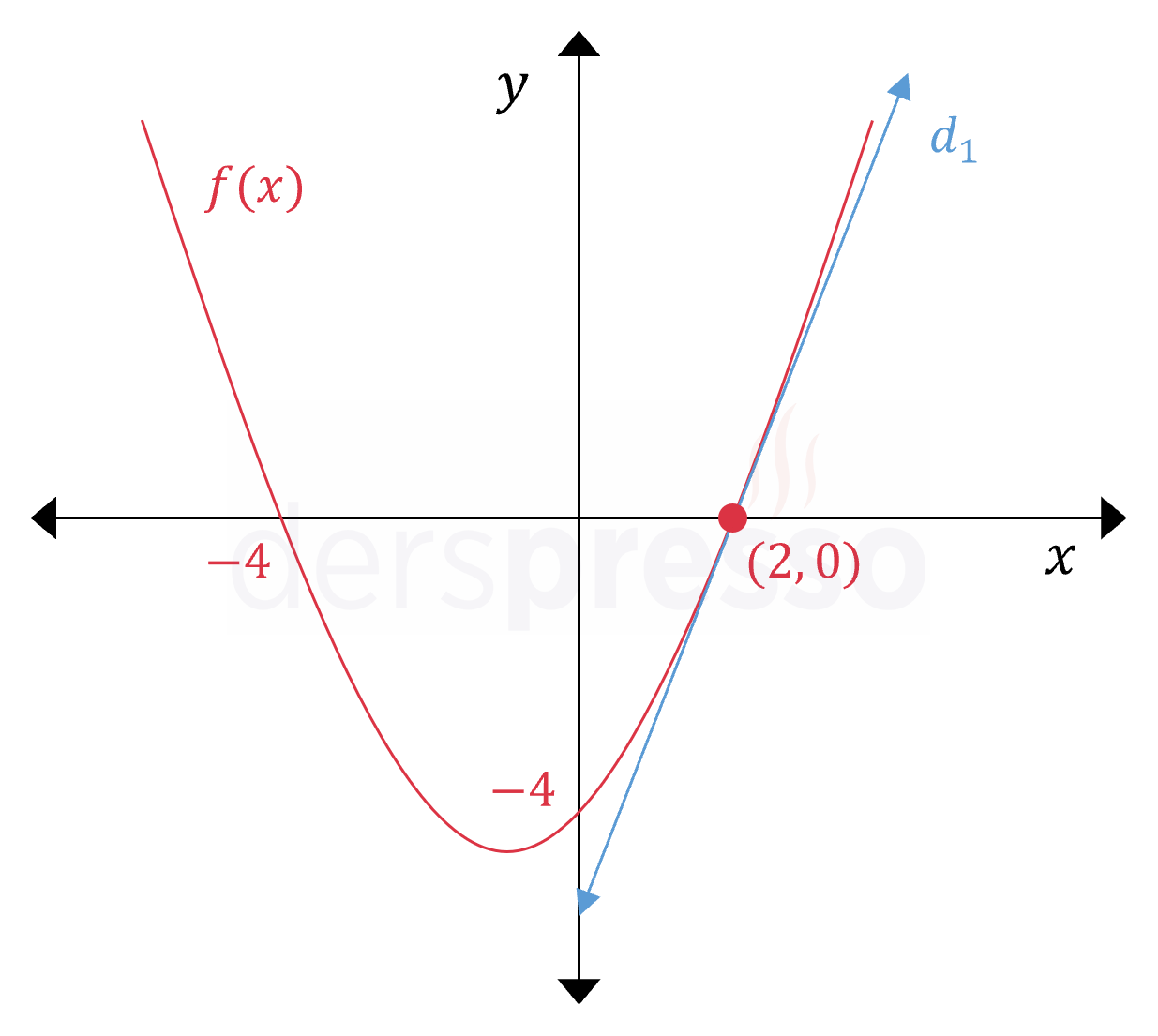
Buna göre parabol ve doğru \( (2, 0) \) noktasında kesişir.
Parabolün ve doğrunun grafikleri aşağıda verilmiştir.
Parabolü Kesmeyen Doğru
Ortak çözümle elde edilen denklemin deltası sıfırdan küçükse doğru parabolü kesmez.
Aşağıda denklemleri verilen parabol ve doğrunun birbirine göre durumlarını inceleyelim.
\( f(x) = -x^2 + 2x + 3 \)
\( d_1: y = x + 4 \)
İki denklemi ortak çözelim.
\( -x^2 + 2x + 3 = x + 4 \)
Tüm terimleri tek tarafta toplayıp ifadeyi sıfıra eşitleyelim.
\( x^2 - x + 1 = 0 \)
İkinci dereceden denklemin deltasını bulalım.
\( \Delta = b^2 - 4ac \)
\( = (-1)^2 - 4(1)(1) = -3 \)
\( \Delta \lt 0 \) olduğuna göre doğru ile parabol kesişmez.
Bu sonuçla tutarlı bir şekilde yukarıda bulduğumuz denklemin reel çarpanlarına ayrılmadığını da görebiliriz.
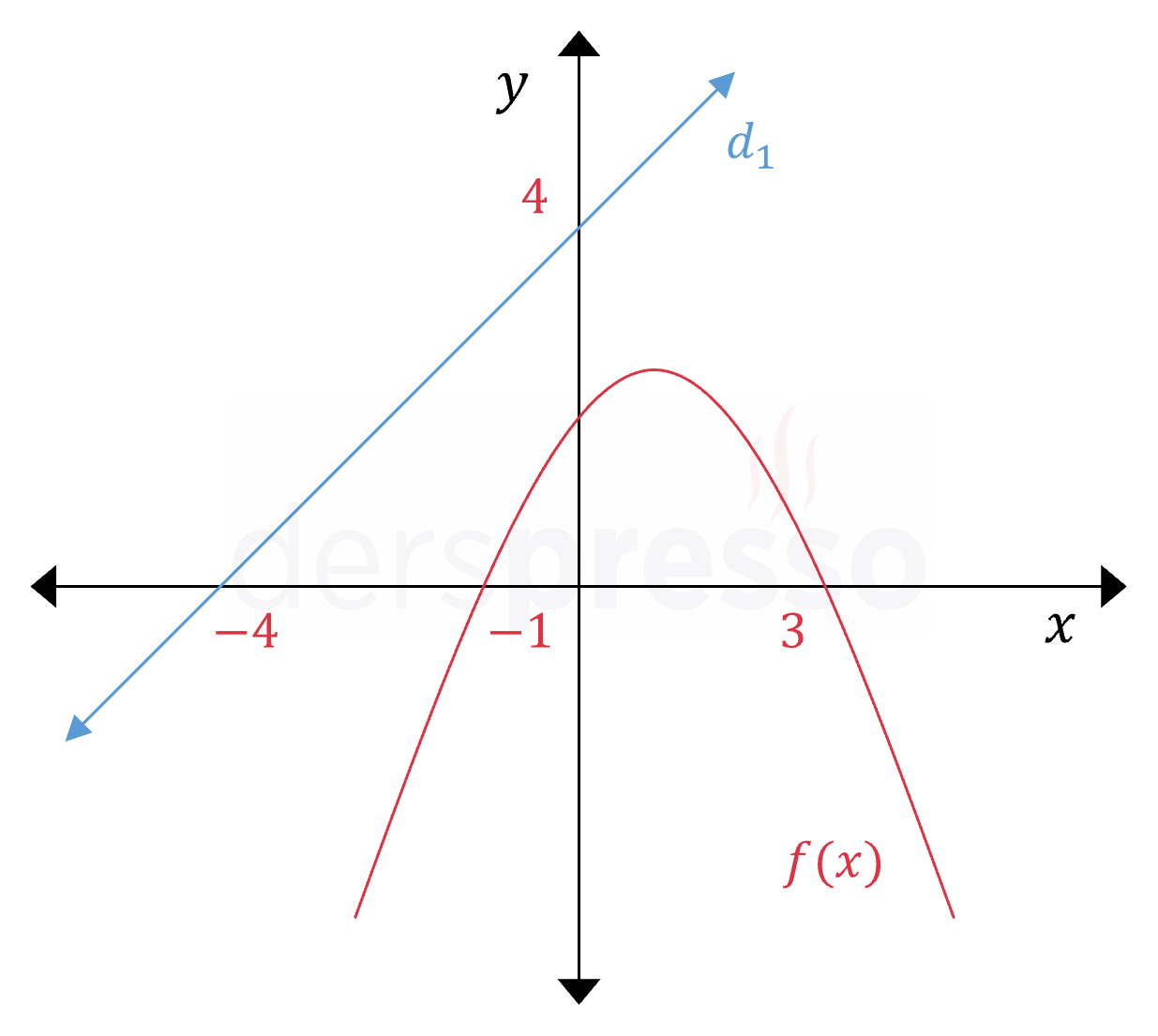
Parabolün ve doğrunun grafikleri aşağıda verilmiştir.
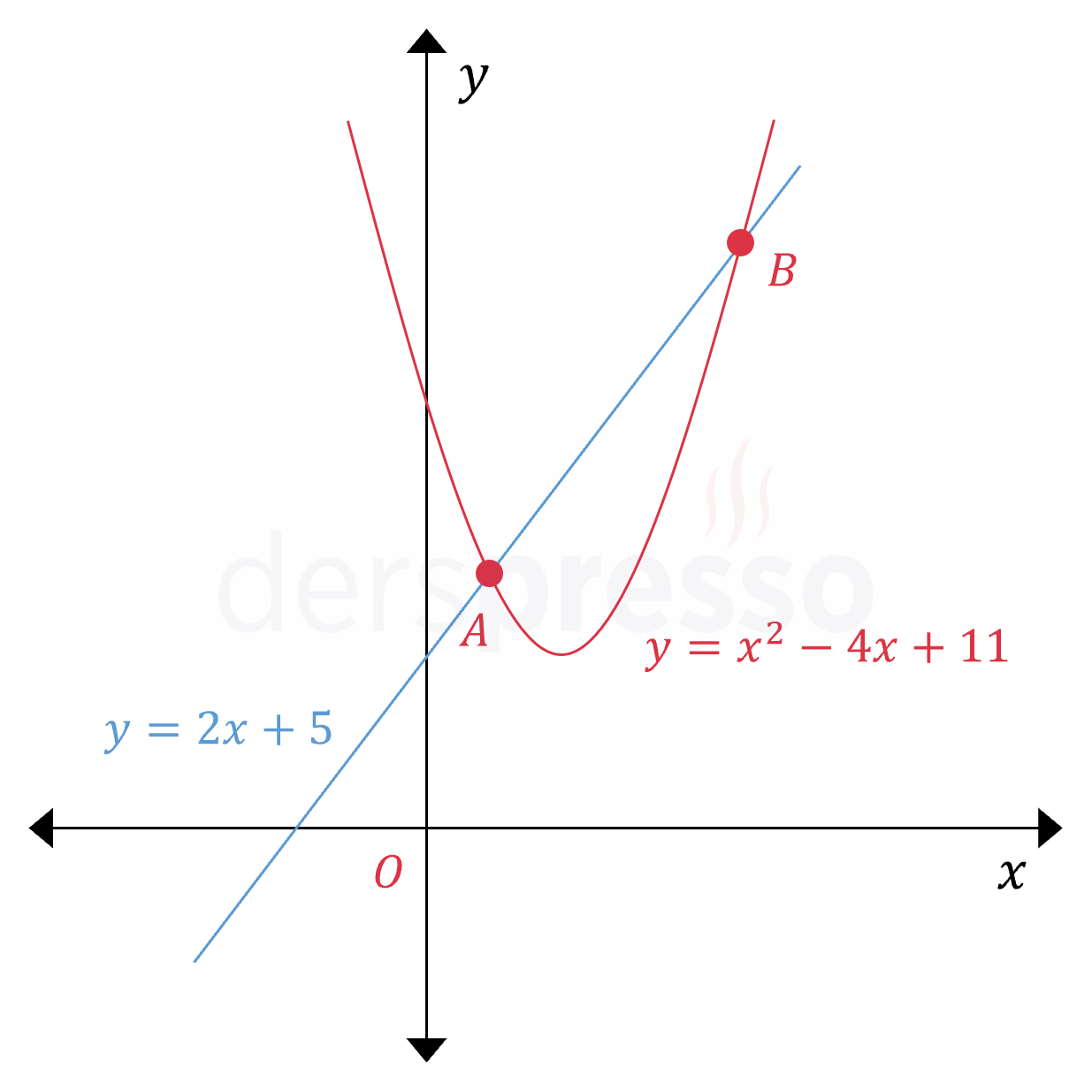
\( y = x^2 - 4x + 11 \) parabolü ile \( y = 2x + 5 \) doğrusu \( A \) ve \( B \) noktalarında kesişmektedir.
\( A \) ve \( B \) noktalarının apsisleri çarpımını bulunuz.
Çözümü Gösterİki denklemi ortak çözdüğümüzde elde edeceğimiz ikinci dereceden denklemin reel kökleri iki grafiğin kesişim noktalarının apsis değerlerini verir.
İki denklemi ortak çözelim.
\( x^2 - 4x + 11 = 2x + 5 \)
\( x^2 - 6x + 6 = 0 \)
Denklemin deltası sıfırdan büyük olduğu için iki reel kökü vardır, dolayısıyla (grafikte de görebileceğimiz gibi) doğru parabolü iki farklı noktada keser.
\( \Delta = b^2 - 4ac \)
\( (-6)^2 - 4(1)(6) \gt 0 \)
Denklemin köklerinin çarpımı için ikinci dereceden denklem kökler çarpımı formülünü kullanalım.
\( x_1 \cdot x_2 = \dfrac{c}{a} = \dfrac{6}{1} = 6 \) bulunur.
\( y = x^2 - 2x + m + 2 \) parabolü ile \( y = x - 1 \) doğrusu birbirine teğet olduğuna göre, \( m \) kaçtır?
Çözümü GösterVerilen parabol ve doğru birbirine teğet olduğuna göre, denklemlerinin ortak çözümünden elde edilen 2. dereceden denklemin tek reel kökü olmalıdır, yani deltası sıfır olmalıdır.
İki denklemi ortak çözelim.
\( x^2 - 2x + m + 2 = x - 1 \)
\( x^2 - 3x + m + 3 = 0 \)
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = 1, \quad b = -3, \quad c = m + 3 \)
\( \Delta = b^2 - 4ac = 0 \)
\( (-3)^2 - 4(1)(m + 3) = 0 \)
\( 9 - 4m - 12 = 0 \)
\( m = -\dfrac{3}{4} \) bulunur.
\( y = x^2 - 4x + 3 \) parabolü ile \( y = x + 1 \) doğrusunun kesişim noktalarının apsisleri toplamı nedir?
Çözümü GösterVerilen parabol ve doğru denklemlerini ortak çözdüğümüzde elde edeceğimiz ikinci dereceden denklemin reel kökleri bu iki grafiğin kesişim noktalarının apsis değerlerini verir.
İki denklemi ortak çözelim.
\( x^2 - 4x + 3 = x + 1 \)
\( x^2 - 5x + 2 = 0 \)
Bu denklemin deltası sıfırdan büyük olduğu için denklemin iki reel kökü vardır, dolayısıyla doğru ve parabol iki farklı noktada kesişir.
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = 1, \quad b = -5, \quad c = 2 \)
\( \Delta = b^2 - 4ac \)
\( (-5)^2 - 4(1)(2) \gt 0 \)
Soruda istenen kesişim noktalarının apsis değerlerinin toplamı bu denklemin kökler toplamına eşittir.
Denklemin kökler toplamını bulalım.
\( x_1 + x_2 = -\dfrac{b}{a} = -\dfrac{-5}{1} = 5 \)
Kesişim noktalarının apsisleri toplamı 5 olarak bulunur.
\( y = x^2 - 5x + 2 \) parabolü ile \( y = 6 - x \) doğrusunun kesişim noktalarını birleştiren doğru parçasının orta noktasının koordinatları nedir?
Çözümü GösterVerilen parabol ve doğru denklemlerini ortak çözdüğümüzde elde edeceğimiz ikinci derecede denklemin reel kökleri bu iki grafiğin kesişim noktalarının apsis değerlerini verir.
İki denklemi ortak çözelim.
\( x^2 - 5x + 2 = 6 - x \)
\( x^2 - 4x - 4 = 0 \)
Parabol ve doğrunun kesişim noktalarına \( A(x_1, y_1) \) ve \( B(x_2, y_2) \), orta noktalarına \( C \) diyelim.
\( C \) noktasının koordinatlarını aşağıdaki orta nokta formülü ile bulabiliriz.
\( C(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}) \)
\( x_1 + x_2 \) toplamını ortak çözüm sonucu elde ettiğimiz ikinci dereceden denklemin kökler toplamı formülü ile bulabiliriz.
\( x_1 + x_2 = -\dfrac{-4}{1} = 4 \)
\( C(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}) = C(2, \dfrac{y_1 + y_2}{2}) \)
\( C \) noktası iki kesişim noktasını birleştiren \( y = 6 - x \) doğrusu üzerinde olduğundan koordinatları doğru denklemini sağlar.
Doğru denkleminde \( x = 2 \) koyalım.
\( y = 6 - x = 6 - 2 = 4 \)
\( C(2, 4) \) bulunur.
\( f(x) = x^2 - 4x - 2 \) parabolü ile \( y = ax + b \) doğrusunun kesişim noktalarını birleştiren doğru parçasının orta noktası \( C(3, 4) \) olduğuna göre, \( b \) kaçtır?
Çözümü GösterVerilen parabol ve doğru denklemlerini ortak çözdüğümüzde elde edeceğimiz ikinci derecede denklemin reel kökleri bu iki grafiğin kesişim noktalarının apsis değerlerini verir.
İki denklemi ortak çözelim.
\( x^2 - 4x - 2 = ax + b \)
\( x^2 - (4 + a)x - 2 - b = 0 \)
Parabol ve doğrunun kesişim noktalarına \( A(x_1, y_1) \) ve \( B(x_2, y_2) \) diyelim.
\( C \) noktasının koordinatlarını aşağıdaki orta nokta formülü ile bulabiliriz.
\( C(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}) = C(3, 4) \)
\( x_1 + x_2 \) toplamını ortak çözüm sonucu elde ettiğimiz ikinci dereceden denklemin kökler toplamı formülü ile bulabiliriz.
\( \dfrac{x_1 + x_2}{2} = \dfrac{-\frac{-(4 + a)}{1}}{2} = 3 \)
\( a = 2 \)
Buna göre doğrunun denklemi aşağıdaki gibi olur.
\( y = 2x + b \)
\( C(3, 4) \) noktası \( A \) ve \( B \) noktalarını birleştiren doğrunun üzerinde olduğu için noktanın koordinatları doğru denklemini sağlar.
\( 4 = 2(3) + b \)
\( b = -2 \) bulunur.
\( m \in \mathbb{R} \) olmak üzere,
\( y = mx - 5 \) doğrusu \( y = (x - 2)^2 \) parabolünü kestiğine göre, \( m \) değer aralığını bulunuz.
Çözümü GösterDoğru ve parabol denklemlerini ortak çözelim.
\( (x - 2)^2 = mx - 5 \)
\( x^2 - 4x + 4 = mx - 5 \)
\( x^2 - (m + 4)x + 9 = 0 \)
Verilen doğrunun parabolü en az bir noktada kesmesi için bu denklemin en az bir reel kökü olmalıdır, dolayısıyla denklemin deltası sıfıra eşit ya da sıfırdan büyük olmalıdır.
Denklemin katsayılarını yazalım.
\( a = 1, \quad b = -(m + 4), \quad c = 9 \)
\( \Delta = b^2 - 4ac \ge 0 \)
\( (-(m + 4))^2 - 4(1)(9) \ge 0 \)
\( (m + 4)^2 \ge 36 \)
\( m + 4 \le -6 \) ya da \( m + 4 \ge 6 \)
\( m \le -10 \) ya da \( m \ge 2 \)
\( m \in (-\infty, -10] \cup [2, \infty) \) bulunur.
\( y \) eksenini \( (0, 5) \) noktasında kesen \( d \) doğrusu, \( y \) eksenini \( (0, -9) \) noktasında kesen reel katsayılı ve başkatsayısı 1 olan bir parabol ile \( A \) ve \( B \) noktalarında kesişiyor.
\( d \) doğrusu parabolün simetri eksenini \( (2, 7) \) noktasında kestiğine göre, \( A \) ve \( B \) noktalarının ordinatları çarpımı kaçtır?
Çözümü Göster\( d \) doğrusunun denklemini aşağıdaki şekilde tanımlayalım.
\( d: y = ax + b \)
\( d \) doğrusu \( y \) eksenini \( (0, 5) \) noktasında kestiği için sabit terimi 5'tir.
\( d: y = ax + 5 \)
\( d \) doğrusu aynı zamanda \( (2, 7) \) noktasından geçtiği için bu noktanın koordinatlarını yazarak \( a \)'yı bulalım.
\( 7 = 2a + 5 \Longrightarrow a = 1 \)
\( d: y = x + 5 \)
Parabolün denklemini aşağıdaki şekilde tanımlayalım.
\( f(x) = x^2 + bx + c \)
Parabol \( y \) eksenini \( (0, -9) \) noktasında kestiği için sabit terimi \( -9 \)'dur.
\( f(x) = x^2 + bx - 9 \)
Parabolün simetri ekseni \( (2, 7) \) noktasından geçtiğine göre, tepe noktasının apsis değeri 2'dir.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{b}{2(1)} = 2 \)
\( b = -4 \)
\( f(x) = x^2 - 4x - 9 \)
\( A \) ve \( B \) noktalarını bulmak için her iki denklemi ortak çözelim.
\( x^2 - 4x - 9 = x + 5 \)
\( x^2 - 5x - 14 = 0 \)
\( (x + 2)(x - 7) = 0 \)
Buna göre parabol ve doğru \( A(-2, m) \) ve \( B(7, n) \) noktalarında kesişir. Bu noktaların ordinat değerlerini bulmak için apsis değerlerini iki denklemden birinde yerine koyalım.
\( y = m = -2 + 5 = 3 \)
\( y = n = 7 + 5 = 12 \)
Buna göre kesişim noktalarının ordinat değerlerinin çarpımı \( 3 \cdot 12 = 36 \) olarak bulunur.
Tepe noktası \( T(-2, 5) \) olan \( f(x) \) parabolü \( y \) eksenini \( (0, 1) \) noktasında kesmektedir.
Apsisleri ordinatlarından 5 birim fazla olan \( A \) ve \( B \) noktaları \( f(x) \) parabolü üzerinde olduğuna göre, \( \abs{AB} \) uzunluğu kaçtır?
Çözümü GösterTepe noktası ve geçtiği bir noktası bilinen parabolün denklemini bulalım.
\( f(x) = a(x - r)^2 + k \)
\( = a(x + 2)^2 + 5 \)
\( (0, 1) \) noktası parabol üzerinde olduğuna göre koordinatları denklemi sağlar.
\( a(0 + 2)^2 + 5 = 1 \)
\( a = -1 \)
\( f(x) = -(x + 2)^2 + 5 \)
Apsisleri ordinatlarından 5 birim fazla olan noktalar \( y = x - 5 \) doğrusu üzerinde yer alır.
\( A \) ve \( B \) noktaları \( y = x - 5 \) doğrusu ile \( f(x) \) parabolü üzerinde yer aldığına göre doğru ve parabol kesişir.
Doğru ile parabolün kesişim noktalarını bulmak için parabol denkleminde \( y = x - 5 \) yazalım.
\( x - 5 = -(x + 2)^2 + 5 \)
\( x - 5 = -x^2 - 4x - 4 + 5 \)
\( x^2 + 5x - 6 = 0 \)
\( (x + 6)(x - 1) = 0 \)
Buna göre doğru ve parabol \( x = -6 \) ve \( x = 1 \) apsisli noktalarda kesişir.
Apsisi -6 olan noktaya \( A \), 1 olan noktaya \( B \) diyelim.
Bu noktaların ordinatlarını bulmak için \( x \) değerlerini doğru denkleminde yerine yazalım.
\( x = -6 \) için: \( y = -6 - 5 = -11 \)
\( A(-6, -11) \)
\( x = 1 \) için: \( y = 1 - 5 = -4 \)
\( B(1, -4) \)
\( \abs{AB} \) uzunluğunu bulalım.
\( \abs{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( = \sqrt{(1 - (-6))^2 + (-4 - (-11))^2} \)
\( = \sqrt{7^2 + 7^2} \)
\( = 7\sqrt{2} \) bulunur.
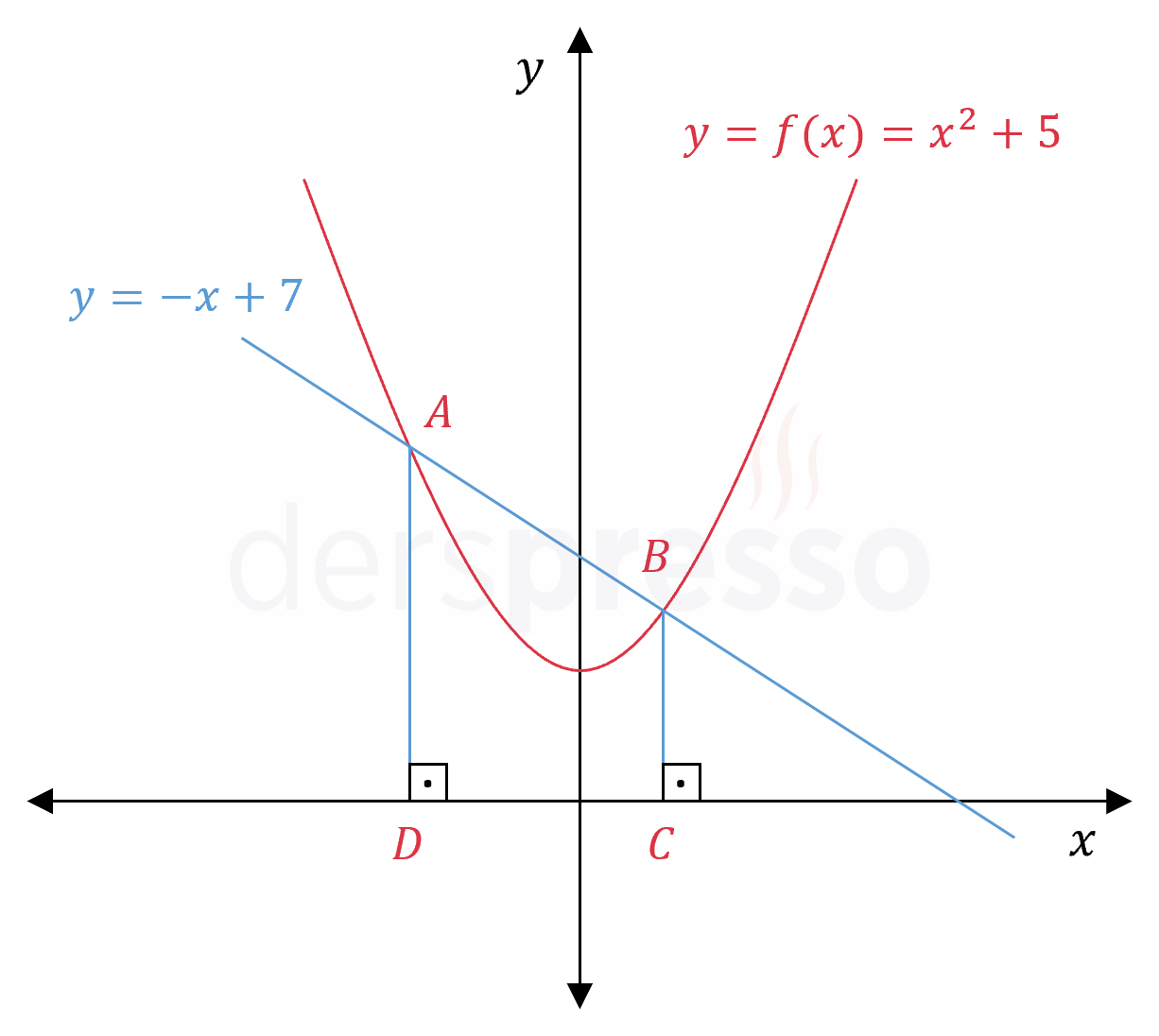
Şekildeki \( y = x^2 + 5 \) parabolü ile \( y = -x + 7 \) doğrusu \( A \) ve \( B \) noktalarında kesişmektedir.
Buna göre \( ABCD \) dik yamuğunun alanı kaçtır?
Çözümü GösterParabol ile doğrunun denklemlerini birbirine eşitleyerek kesişim noktalarının koordinatlarını bulalım.
\( x^2 + 5 = -x + 7 \)
\( x^2 + x - 2 = 0 \)
\( (x + 2)(x - 1) = 0 \)
Buna göre doğru ve parabol \( x = -2 \) ve \( x = 1 \) apsisli noktalarda kesişir.
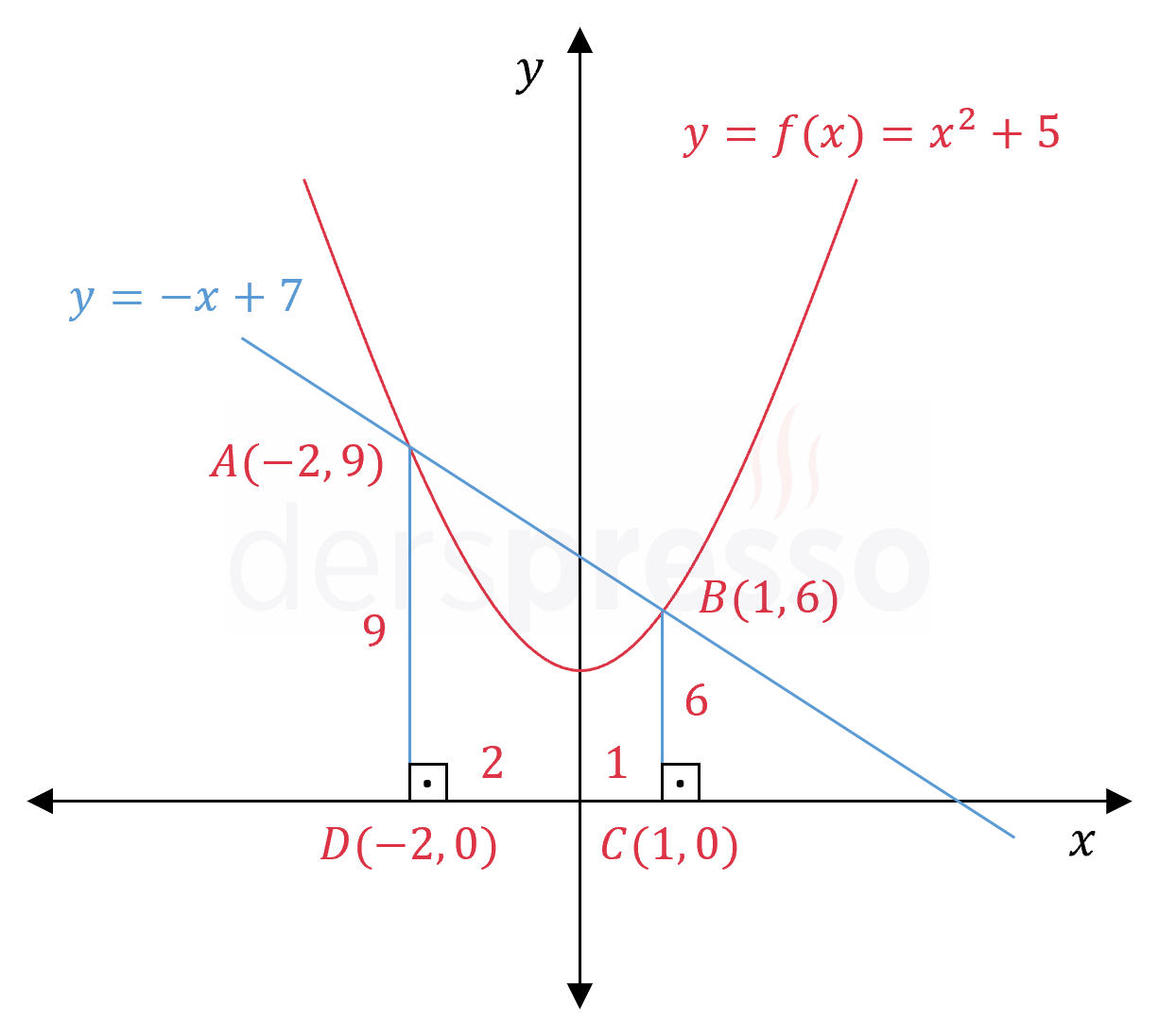
Bu değerleri \( y = -x + 7 \) doğru denkleminde yerine koyarak \( A \) ve \( B \) noktalarının ordinat değerlerini bulalım.
\( x = -2 \) için: \( y = -(-2) + 7 = 9 \)
\( A(-2, 9) \)
\( x = 1 \) için: \( y = -1 + 7 = 6 \)
\( B(1, 6) \)
\( \abs{AD} = 9, \abs{BC} = 6, \abs{DC} = 3 \)
Bu uzunlukları kullanarak \( ABCD \) dik yamuğunun alanını hesaplayalım.
\( A(ABCD) = \dfrac{(\abs{AD} + \abs{BC}) \cdot \abs{CD}}{2} \)
\( = \dfrac{(9 + 6) \cdot 3}{2} \)
\( = \dfrac{45}{2} \) bulunur.
Parabolün Doğruya En Yakın Noktası
Bir \( f(x) \) parabolünün kesişmediği \( d_1 \) doğrusuna en yakın noktası aşağıdaki yöntemle bulunabilir.
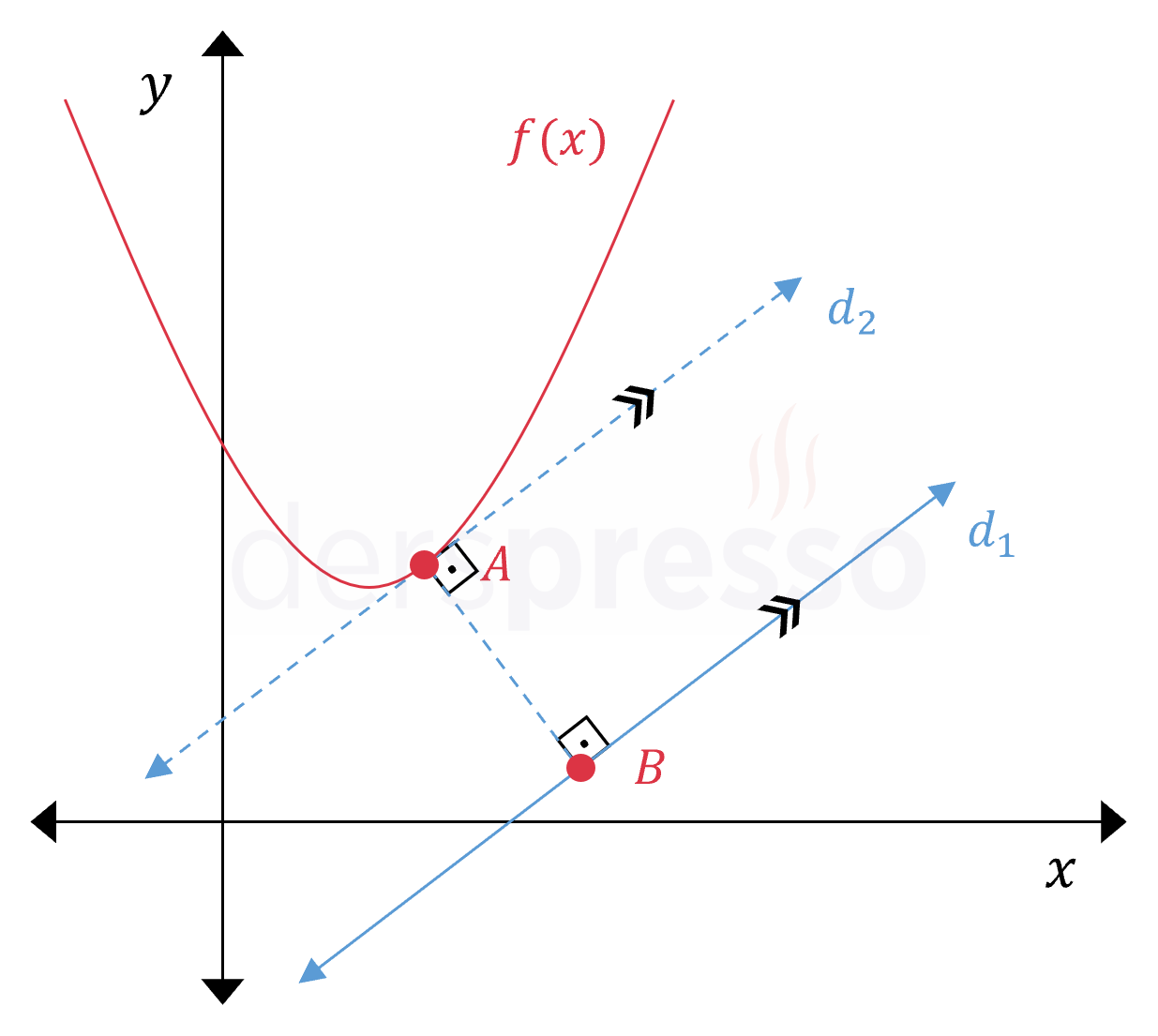
- Parabolün üzerindeki \( d_1 \) doğrusuna en yakın noktaya \( A \) diyelim.
- \( A \) noktası aynı zamanda \( d_1 \) doğrusuna paralel olan ve parabolü teğet kesen \( d_2 \) doğrusunun parabolü kestiği nokta olur.
- \( d_2 \) doğrusunun denklemi için \( d_1 \) ile aynı eğime sahip olan ve parabol denklemi ile ortak çözümünün deltası sıfır olan doğru denklemi bulunur.
- Parabol ve \( d_2 \) doğrusunun ortak çözümü \( A \) noktasının apsis değerini verir.
- Bu apsis değeri parabol ya da \( d_2 \) denkleminde yerine konduğunda \( A \) noktasının ordinat değeri bulunur.
Aşağıda denklemi verilen parabolün \( d_1 \) doğrusun en yakın noktasını bulalım.
\( f(x) = x^2 - \frac{15}{2}x + 15 \)
\( d_1: y = -\frac{3}{2}x + 3 \)
Parabolün üzerindeki \( d_1 \) doğrusuna en yakın noktaya \( A \) diyelim.
\( d_1 \) doğrusuna paralel olan ve parabolü \( A \) noktasında teğet kesen doğruya \( d_2 \) diyelim.
Parabolün ve doğruların grafikleri aşağıda verilmiştir.
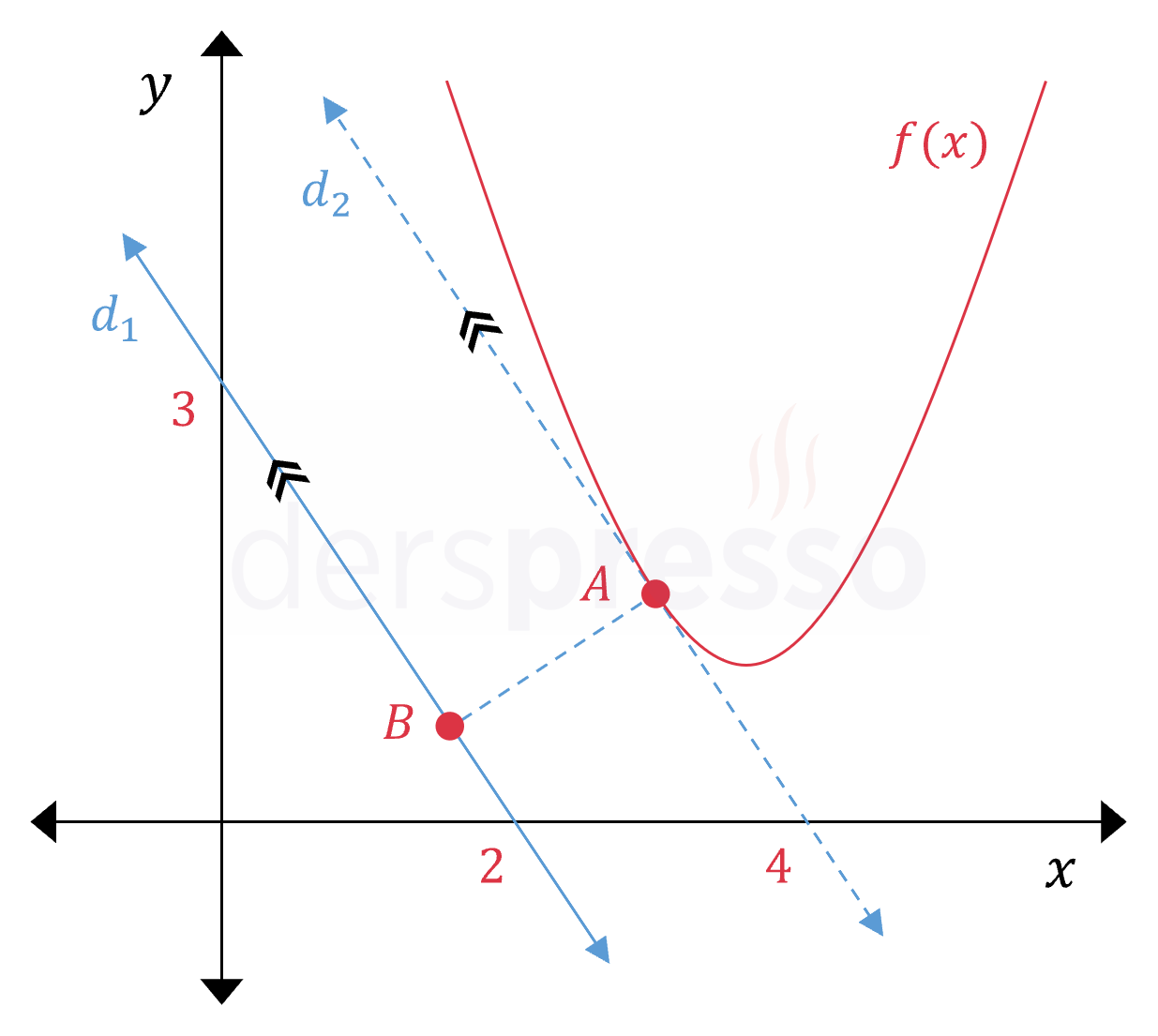
\( d_1 \) ve \( d_2 \) doğruları paralel ve eğimleri aynı olduğu için \( d_2 \) denklemini aşağıdaki şekilde yazabiliriz.
\( d_2: y = -\frac{3}{2}x + c \)
Tek noktada kesişen parabol ve \( d_2 \) denklemlerini ortak çözelim.
\( x^2 - \frac{15}{2}x + 15 = -\frac{3}{2}x + c \)
Tüm terimleri tek tarafta toplayıp ifadeyi sıfıra eşitleyelim.
\( x^2 - 6x + 15 - c = 0 \)
\( d_2 \) doğrusu parabole teğet olduğu için bu denklemin deltası sıfır olur.
\( \Delta = b^2 - 4ac = 0 \)
\( (-6)^2 - 4(1)(15 - c) = 0 \)
\( c = 6 \)
\( d_2 \) denklemi aşağıdaki gibi olur.
\( d_2: y = -\frac{3}{2}x + 6 \)
Buna göre ortak çözümde elde ettiğimiz denklem aşağıdaki gibi olur.
\( x^2 - 6x + 15 - 6 = 0 \)
Bu denklemin çözümü \( d_2 \) doğrusunun parabolü kestiği noktanın apsis değerini verir.
\( (x - 3)^2 = 0 \)
\( x = 3 \)
Bu değeri parabol ya da doğru denkleminde yerine yazdığımızda \( d_2 \) doğrusunun parabolü kestiği noktanın ordinat değerini buluruz.
\( y = -\frac{3}{2}(3) + 6 = \frac{3}{2} \)
Buna göre parabol ve \( d_2 \) doğrusu \( A(3, \frac{3}{2}) \) noktasında kesişir. Bu nokta aynı zamanda parabolün \( d_1 \) doğrusuna en yakın olduğu noktadır.
Doğrunun Parabole En Yakın Noktası
Bir \( d_1 \) doğrusunun kesişmediği \( f(x) \) parabolüne en yakın noktası aşağıdaki yöntemle bulunabilir.
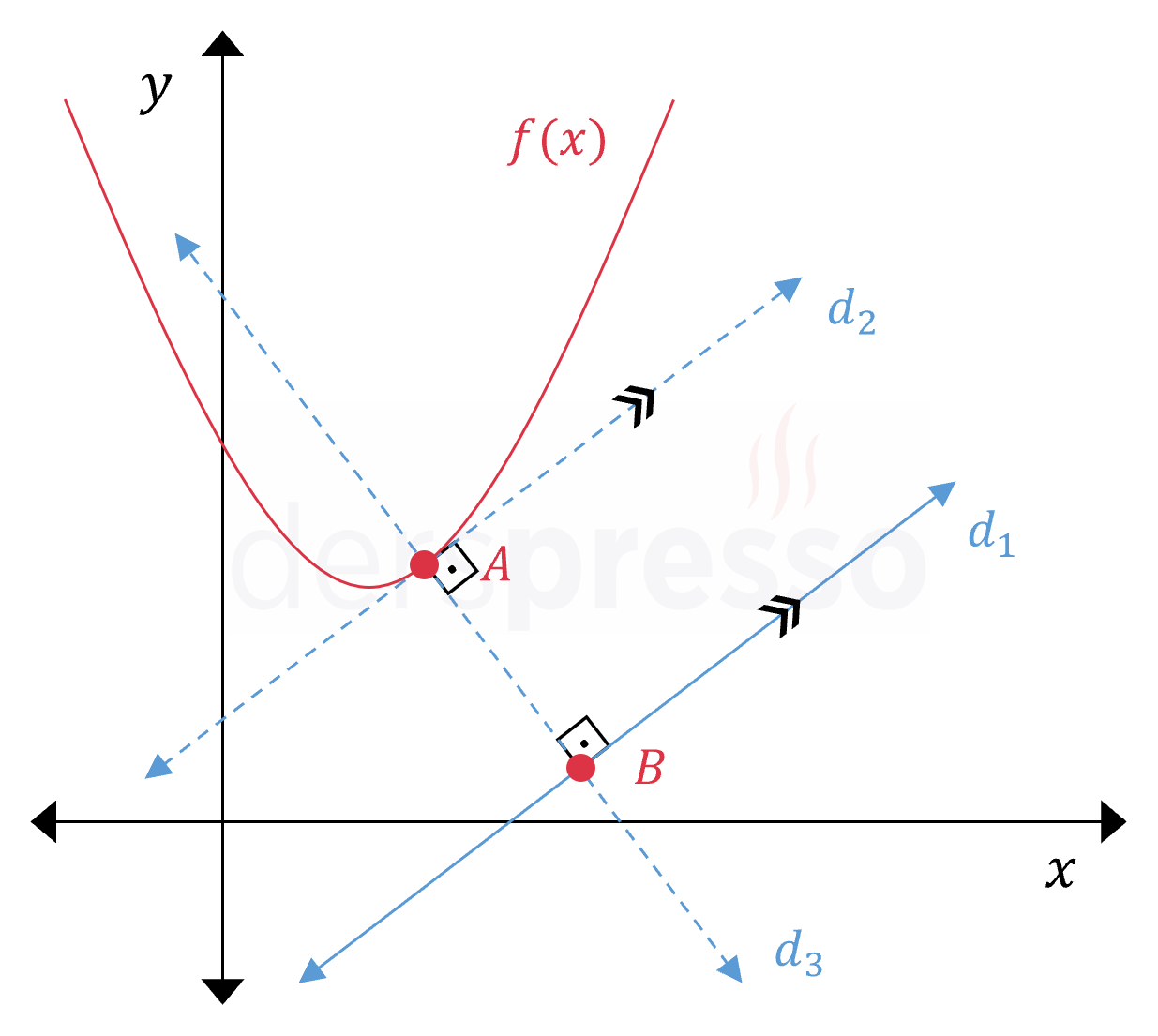
- \( d_1 \) doğrusu üzerinde parabole en yakın olan noktaya \( B \) diyelim.
- Yukarıda "Parabolün Doğruya En Yakın Noktası" bölümünde kullandığımız yöntemle \( d_1 \) doğrusuna paralel olan ve parabolü teğet kesen \( d_2 \) doğrusunun parabolü kestiği \( A \) noktası bulunur.
- \( A \) noktasından geçen ve \( d_2 \) doğrusuna dik olan \( d_3 \) doğrusunun denklemi bulunur.
- \( d_1 \) ve \( d_3 \) doğruları ortak çözülür ve kesişim noktaları olan \( B \) noktası bulunur.
Örnek 4'teki \( d_1 \) doğrusunun \( f(x) \) parabolüne en yakın noktasını bulalım.
\( f(x) = x^2 - \frac{15}{2}x + 15 \)
\( d_1: y = -\frac{3}{2}x + 3 \)
Parabolün üzerindeki \( d_1 \) doğrusuna en yakın noktayı \( A(3, \frac{3}{2}) \) olarak bulmuştuk.
\( A \) noktasından geçen ve \( d_2 \) doğrusuna dik olan doğruya \( d_3 \) diyelim.
Parabolün ve doğruların grafikleri aşağıda verilmiştir.
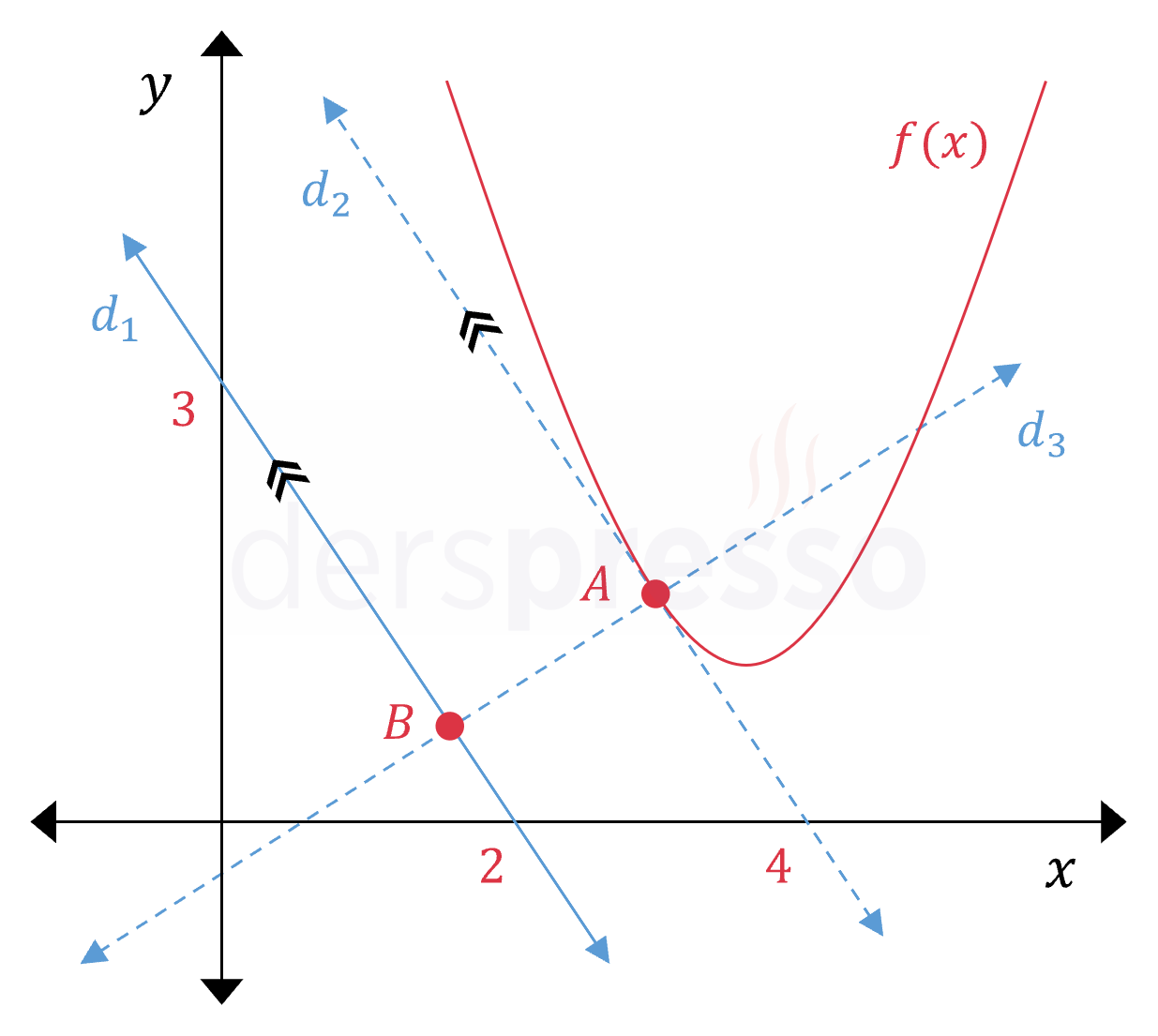
\( d_3 \) doğrusu \( d_2 \) doğrusuna dik olduğu için eğimleri çarpımı \( -1 \) olur.
\( m_2 \cdot m_3 = -1 \)
\( -\frac{3}{2} \cdot m_3 = -1 \)
\( m_3 = \frac{2}{3} \)
\( A \) noktasından geçen ve eğimi \( \frac{2}{3} \) olan doğrunun denklemini yazalım.
\( y - \frac{3}{2} = \frac{2}{3}(x - 3) \)
\( d_3: y = \frac{2}{3}x - \frac{1}{2} \)
\( d_1 \) ve \( d_3 \) doğrularının kesişim noktasını bulmak için iki denklemi ortak çözelim.
\( -\frac{3}{2}x + 3 = \frac{2}{3}x - \frac{1}{2} \)
\( x = \frac{21}{13} \)
Bu değeri doğrulardan birinin denkleminde yerine yazdığımızda kesişim noktalarının ordinat değerini buluruz.
\( y = \frac{2}{3} \cdot \frac{21}{13} - \frac{1}{2} = \frac{15}{26} \)
Buna göre \( d_1 \) ve \( d_3 \) doğruları \( B(\frac{21}{13}, \frac{15}{26}) \) noktasında kesişir. Bu nokta aynı zamanda \( d_1 \) doğrusu üzerinde parabole en yakın olan noktadır.
Doğru ve Parabol Arasındaki En Kısa Uzaklık
Bir \( d_1 \) doğrusu ile kesişmediği \( f(x) \) parabolü arasındaki en kısa uzaklık aşağıdaki yöntemle bulunabilir.
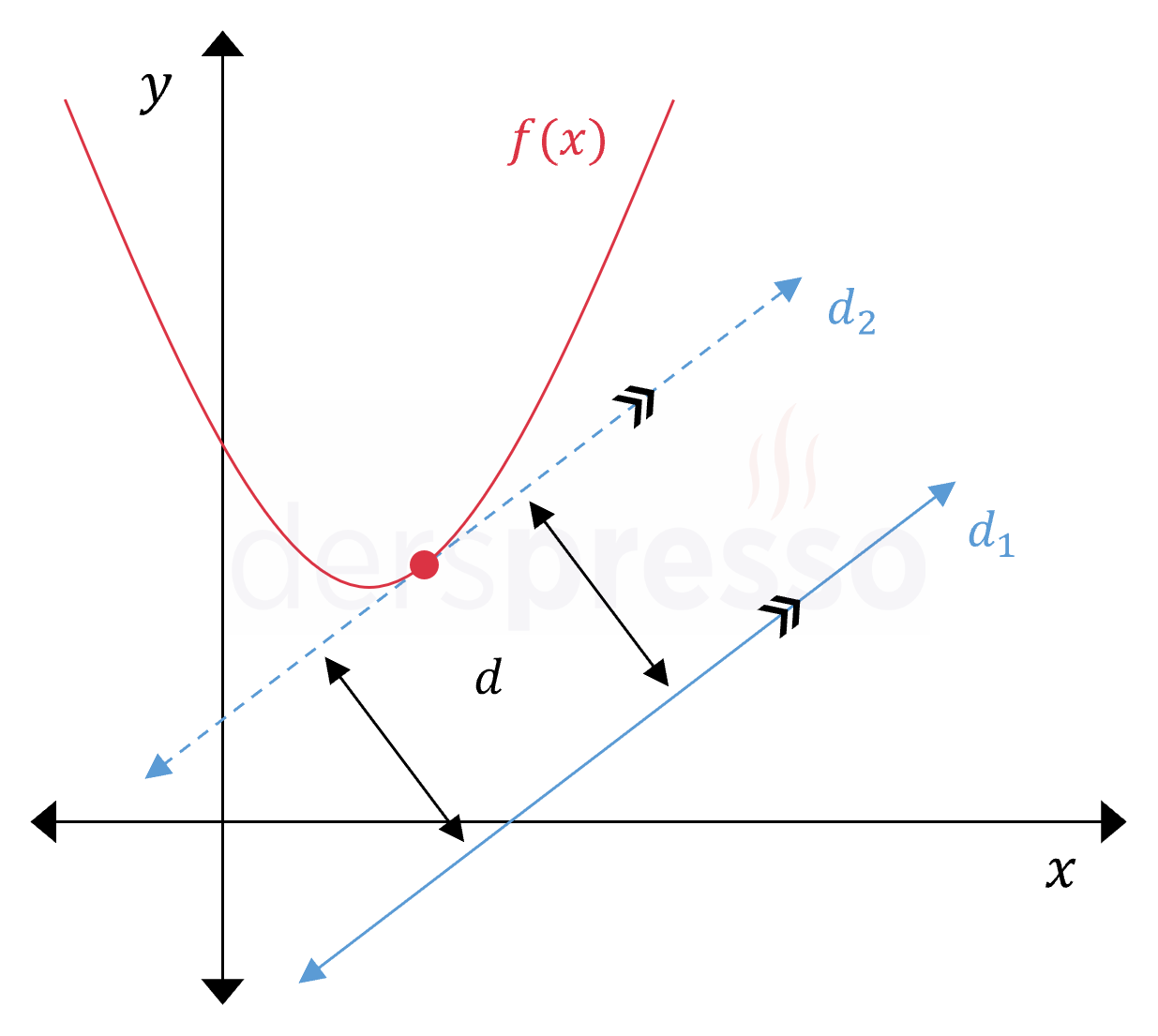
- Yukarıda "Parabolün Doğruya En Yakın Noktası" bölümünde kullandığımız yöntemle \( d_1 \) doğrusuna paralel olan ve parabolü teğet kesen \( d_2 \) doğrusunun denklemi bulunur.
- Doğrunun analitiği konusunda gördüğümüz iki paralel doğru arasındaki uzaklık formülü ile \( d_1 \) ve \( d_2 \) doğruları arasındaki uzaklık bulunur.
Örnek 4'teki \( d_1 \) doğrusu ile \( f(x) \) parabolü arasındaki en kısa uzaklığı bulalım.
\( f(x) = x^2 - \frac{15}{2}x + 15 \)
\( d_1: y = -\frac{3}{2}x + 3 \)
\( d_1 \) doğrusuna paralel olan ve parabolü teğet kesen \( d_2 \) doğrusunun denklemini aşağıdaki şekilde bulmuştuk.
\( d_2: y = -\frac{3}{2}x + 6 \)
Parabolün ve doğruların grafikleri aşağıda verilmiştir.
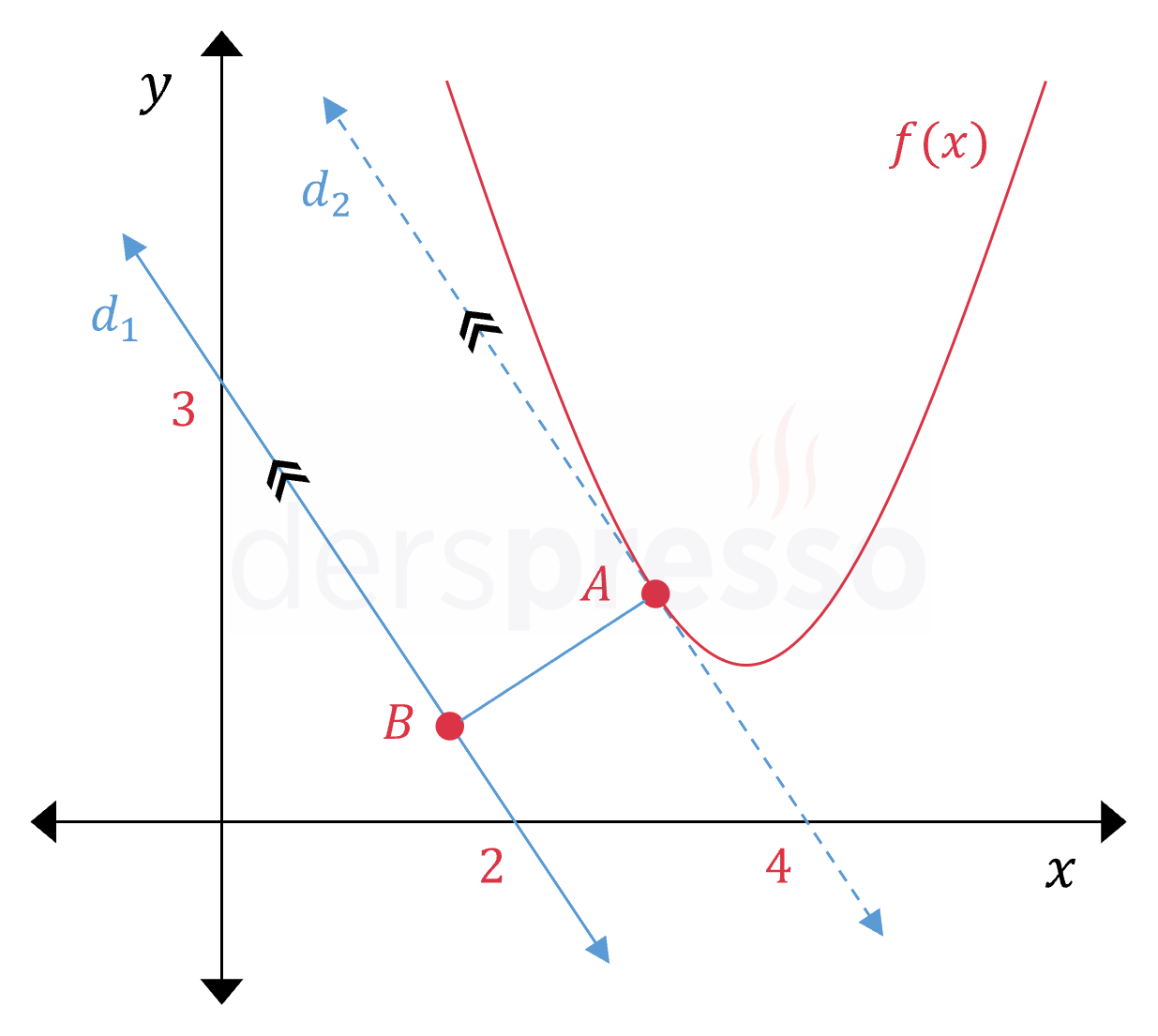
İki doğrunun kapalı denklemlerini yazalım.
\( d_1: \frac{3}{2}x + y - 3 = 0 \)
\( d_2: \frac{3}{2}x + y - 6 = 0 \)
\( d_1 \) ve \( d_2 \) doğruları arasındaki uzaklığı bulmak için iki paralel doğru arasındaki uzaklık formülünü kullanalım.
\( \abs{AB} = \dfrac{\abs{c_2 - c_1}}{\sqrt{a^2 + b^2}} \)
\( = \dfrac{\abs{-6 - (-3)}}{\sqrt{(\frac{3}{2})^2 + 1^2}} \)
\( = \dfrac{3}{\sqrt{\frac{13}{4}}} = \dfrac{6\sqrt{13}}{13} \)
Buna göre \( d_1 \) ve \( d_2 \) doğruları arasındaki uzaklık \( \frac{6\sqrt{13}}{13} \) birimdir. Bu aynı zamanda \( d_1 \) doğrusu ile parabol arasındaki en kısa uzaklıktır.
\( y = 2x^2 - 3x + 1 \) parabolü ile \( y = x + k \) doğrusu analitik düzlemde kesişmediklerine göre, \( k \)'nın alabileceği en büyük tam sayı değeri nedir?
Çözümü GösterVerilen parabol ve doğru kesişmiyorlarsa denklemlerini ortak çözdüğümüzde elde edeceğimiz ikinci dereceden denklemin deltası sıfırdan küçük olur, yani denklemin reel kökü yoktur.
İki denklemi ortak çözelim.
\( 2x^2 - 3x + 1 = x + k \)
\( 2x^2 - 4x + 1 - k = 0 \)
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = 2, \quad b = -4, \quad c = 1 - k \)
\( \Delta = b^2 - 4ac \lt 0 \)
\( (-4)^2 - 4(2)(1 - k) \lt 0 \)
\( 16 - 8 + 8k \lt 0 \)
\( k \lt -1 \)
Buna göre \( k \)'nın alabileceği en büyük tam sayı değeri \( -2 \) olur.
\( y = x^2 - m(x - 1) + 2 \) parabolü ile \( y = mx + 2 \) doğrusu birbirine teğet olduğuna göre, \( m \)'nin alabileceği değerleri bulunuz.
Çözümü GösterVerilen parabol ve doğru birbirine teğet ise tek bir noktada kesişirler, dolayısıyla ortak çözümlerinden elde edeceğimiz ikinci dereceden denklemin deltası sıfır olmalıdır.
İki denklemi ortak çözelim.
\( x^2 - mx + m + 2 = mx + 2 \)
\( x^2 - 2mx + m = 0 \)
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = 1, \quad b = -2m, \quad c = m \)
\( \Delta = b^2 - 4ac = 0 \)
\( (-2m)^2 - 4(1)(m) = 0 \)
\( 4m^2 - 4m = 0 \)
\( 4m(m - 1) = 0 \)
\( m \)'nin alabileceği değerler bu denklemin çarpanlarını sıfır yapan değerlerdir.
\( m \in \{0, 1\} \) bulunur.
\( y = x - 5 \) doğrusu ile \( y = x^2 + mx + 4 \) parabolü kesişmediğine göre, \( m \)'nin alabileceği kaç farklı tam sayı değeri vardır?
Çözümü GösterParabol ve doğru kesişmiyorlarsa iki denklemi ortak çözdüğümüzde elde ettiğimiz ikinci dereceden denklemin deltası sıfırdan küçük olmalıdır.
İki denklemi ortak çözelim.
\( x^2 + mx + 4 = x - 5 \)
\( x^2 + (m - 1)x + 9 = 0 \)
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = 1, \quad b = m - 1, \quad c = 9 \)
\( \Delta = b^2 - 4ac \lt 0 \)
\( (m - 1)^2 - 4(1)(9) \lt 0 \)
\( (m - 1)^2 \lt 36 \)
\( -6 \lt m - 1 \lt 6 \)
\( -5 \lt m \lt 7 \)
Buna göre \( m \)'nin alabileceği \( 6 - (-4) + 1 = 11 \) tam sayı değer vardır.
\( y = -4x^2 + 6x + 3 \) parabolünün \( x - 2y + 5 = 0 \) doğrusuna dik olan teğetinin denklemi nedir?
Çözümü GösterDenklemi \( ax + by + c = 0 \) olan doğrunun eğimi aşağıdaki formülle bulunur.
\( m = -\dfrac{a}{b} \)
Soruda verilen doğrunun eğimini bulalım.
\( m = \dfrac{1}{2} \)
Dik doğruların eğimleri çarpımı \( -1 \) olduğu için bu doğruya dik ve parabole teğet olan doğrunun eğimi \( m = -2 \) olur.
Buna göre parabole teğet olan doğrunun denklemi aşağıdaki gibi olur.
\( y = mx + c = -2x + c \)
Verilen parabol ve doğru birbirine teğet olduğuna göre, bu iki denklemin ortak çözümünden elde edilen ikinci dereceden denklemin tek reel kökü vardır ve denklemin deltası sıfırdır.
İki denklemi ortak çözelim.
\( -4x^2 + 6x + 3 = -2x + c \)
\( -4x^2 + 8x + 3 - c = 0 \)
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = -4, \quad b = 8, \quad c = 3 - c \)
\( \Delta = b^2 - 4ac = 0 \)
\( 8^2 - 4(-4)(3 - c) = 0 \)
\( 64 + 48 - 16c = 0 \)
\( c = 7 \)
Parabole teğet olan doğrunun denklemi \( y = -2x + 7 \) olarak bulunur.
\( f(x) = x^2 - 2x + m \) parabolünün tepe noktası \( y = 2x + 3 \) doğrusu üzerinde olduğuna göre, \( m \) kaçtır?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-2}{2(1)} = 1 \)
Buna göre parabol ve doğru \( x = 1 \) apsisli noktada kesişirler ve bu noktada ordinat değerleri eşittir.
Parabolün \( x = 1 \) apsisli noktadaki değerini bulalım.
\( f(1) = 1^2 - 2(1) + m = m - 1 \)
Doğrunun \( x = 1 \) apsisli noktadaki değerini bulalım.
\( y = 2(1) + 3 = 5 \)
İki ordinat değerini birbirine eşitleyelim.
\( 5 = m - 1 \)
\( m = 6 \) bulunur.
Koordinat düzleminde \( y = x^2 + 5 \) parabolü ile \( y = 6x \) doğrusunun kesişim noktaları arasındaki uzaklık kaç birimdir?
Çözümü GösterParabol ve doğrunun kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( x^2 + 5 = 6x \)
\( x^2 - 6x + 5 = 0 \)
\( (x - 1)(x - 5) = 0 \)
\( x \in \{1, 5\} \)
Buna göre parabol ve doğru bu iki apsis değerli noktalarda kesişir.
Bu iki \( x \) değerini doğru denkleminde yerine koyarak kesişim noktalarını bulalım.
\( y = 6(1) = 6 \)
\( y = 6(5) = 30 \)
Buna göre parabol ve doğrunun kesişim noktaları \( P_1(1, 6) \) ve \( P_2(5, 30) \) olarak bulunur.
İki nokta arasındaki uzaklığı bulalım.
\( \abs{P_1P_2} = \sqrt{(30 - 6)^2 + (5 - 1)^2} \)
\( = \sqrt{592} = 4\sqrt{37} \) birim bulunur.
\( f(x) = mx^2 + 2x + 3 \) parabolü ile \( y = mx + n \) doğrusunun kesişim noktalarının apsisleri toplamı 3 olduğuna göre, \( m \) kaçtır?
Çözümü GösterParabol ve doğru denklemlerini ortak çözdüğümüzde elde edeceğimiz ikinci dereceden denklemin kökleri parabol ve doğrunun kesişim noktalarının apsis değerlerini verir.
Denklemleri ortak çözelim.
\( mx^2 + 2x + 3 = mx + n \)
\( mx^2 + (2 - m)x + 3 - n = 0 \)
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = m, \quad b = 2 - m, \quad c = 3 - n \)
Kesişim noktalarının apsisler toplamının, yani denklemin kökler toplamının 3 olduğunu biliyoruz.
\( x_1 + x_2 = -\dfrac{b}{a} = -\dfrac{2 - m}{m} = 3 \)
\( -2 + m = 3m \)
\( m = -1 \) bulunur.
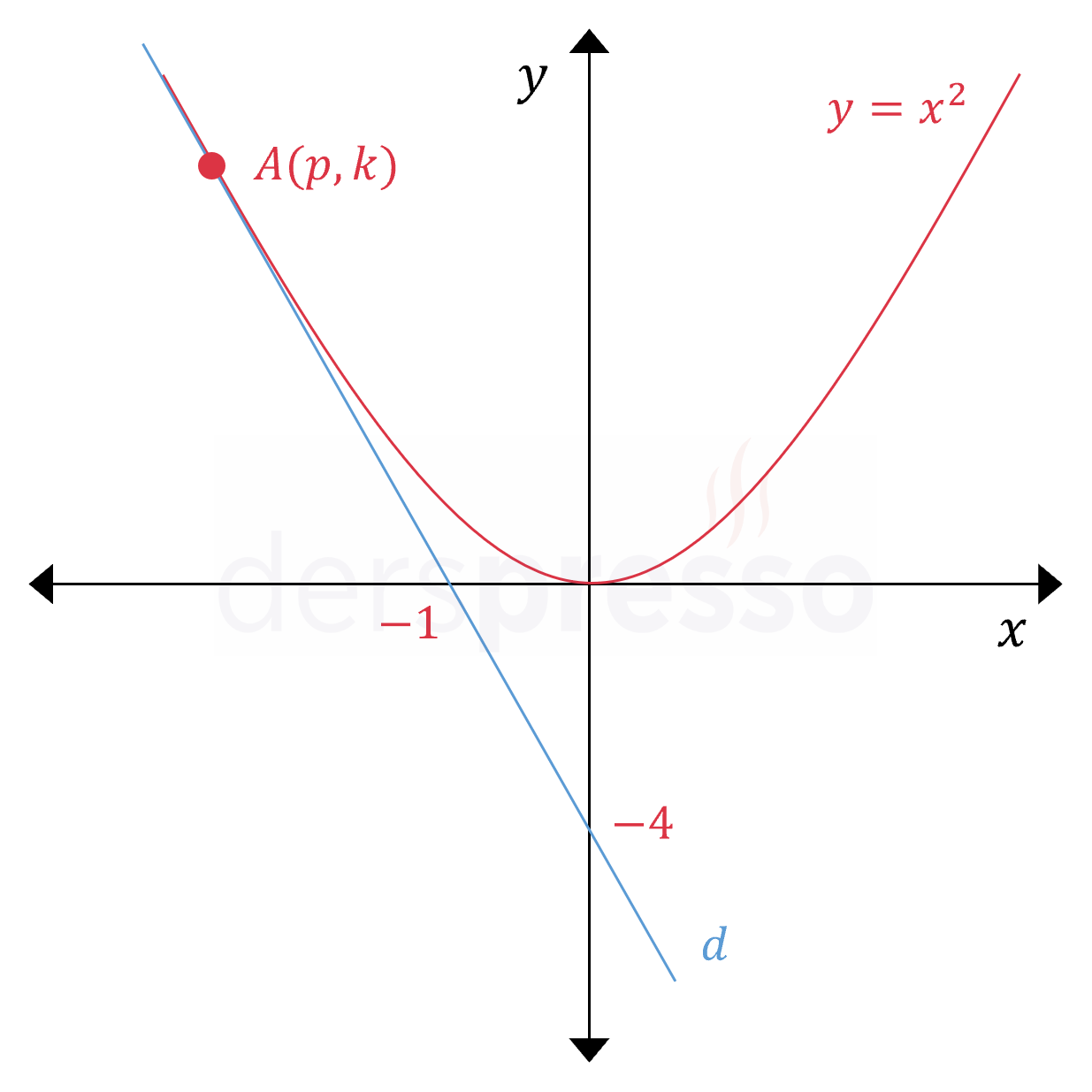
Şekildeki \( d \) doğrusu \( y = x^2 \) parabolüne \( A(p, k) \) noktasında teğettir.
Buna göre \( p + k \) toplamı kaçtır?
Çözümü GösterEksenleri kestiği noktalar bilinen doğrunun denklemi formülünü kullanarak \( d \) doğrusunun denklemini yazalım.
\( \dfrac{x}{-1} + \dfrac{y}{-4} = 1 \)
\( y = -4x - 4 \)
Parabolün ve doğrunun denklemlerinin ortak çözümü, kesişimleri olan \( A(p, k) \) noktasının apsis değerini verir.
\( x^2 = -4x - 4 \)
\( p^2 = -4p - 4 \)
\( p^2 + 4p + 4 = 0 \)
\( (p + 2)^2 = 0 \)
\( p = -2 \)
\( p \) değerini parabol ya da doğru denkleminde yerine koyarak \( A \) noktasının ordinat değerini bulalım.
\( k = -4p - 4 = -4(-2) - 4 = 4 \)
\( A(p, k) = A(-2, 4) \)
Buna göre \( p + k = -2 + 4 = 2 \) bulunur.
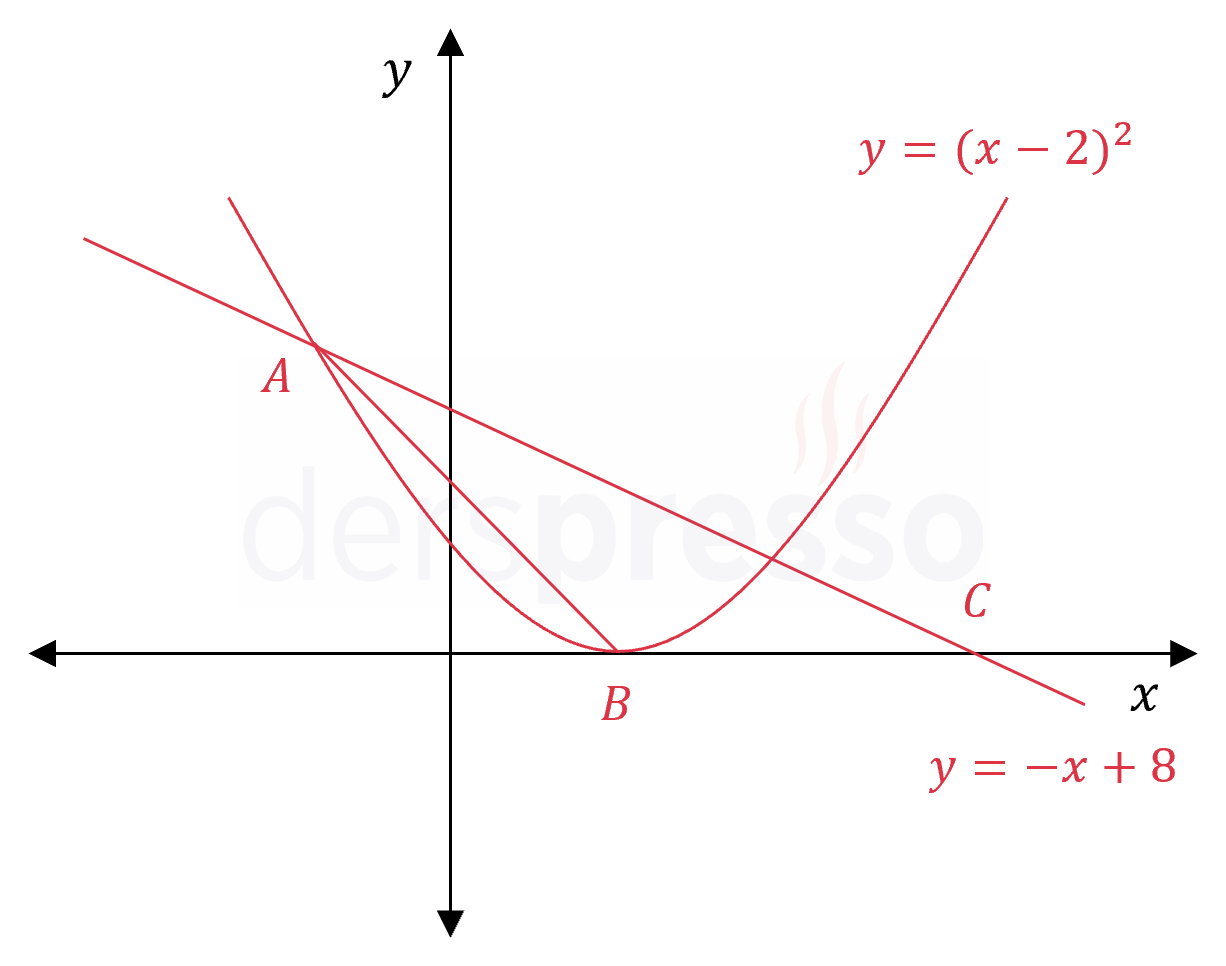
Şekilde \( y = (x - 2)^2 \) parabolü ile \( y = -x + 8 \) doğrusu verilmiştir.
\( B \) noktası parabolün tepe noktası olduğuna göre, \( ABC \) üçgeninin alanı kaçtır?
Çözümü GösterParabol ve doğrunun kesiştikleri \( A \) noktasının koordinatlarını bulalım.
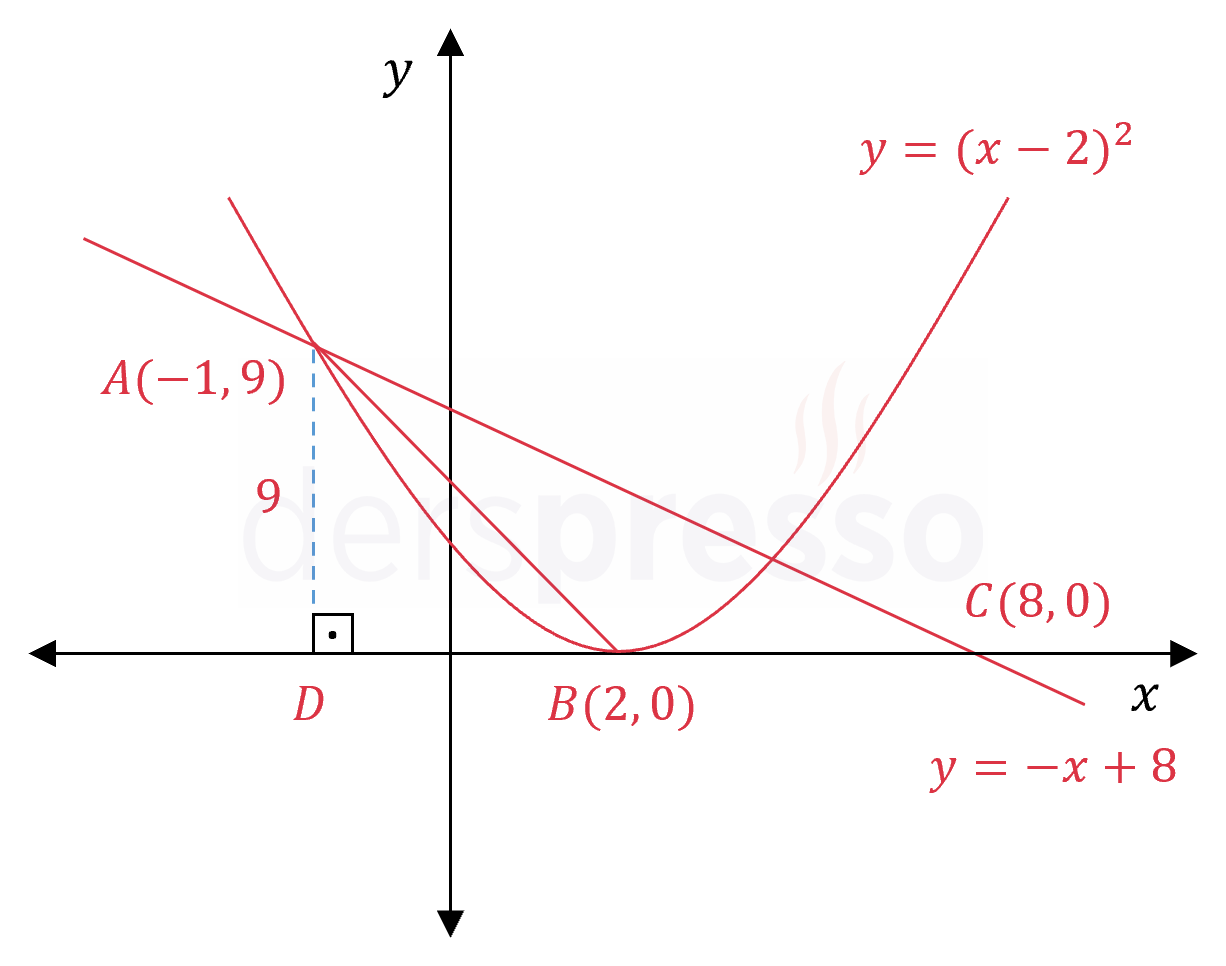
Kesişim noktalarının koordinatlarını bulmak için iki denklemi birbirine eşitleyelim.
\( (x - 2)^2 = -x + 8 \)
\( x^2 - 4x + 4 = -x + 8 \)
\( x^2 - 3x - 4 = 0 \)
\( (x + 1)(x - 4) = 0 \)
Parabol \( x = -1 \) ve \( x = 4 \) apsisli noktalarda kesişirler.
\( A \) noktası II. bölgede yer aldığı için apsisi \( -1 \)' dir.
\( A \) noktasının ordinatını bulmak için iki denklemden birinde \( x = -1 \) yazalım.
\( y = -(-1) + 8 = 9 \)
\( A(-1, 9) \)
\( B \) noktasının koordinatları için parabolün tepe noktasını bulalım.
\( B \) noktasının koordinatlarına \( B(r, k) \) diyelim.
\( y = (x - 2)^2 \)
\( = x^2 - 4x + 4 \)
\( r = -\dfrac{b}{2a} \)
\( = -\dfrac{-4}{2(1)} = 2 \)
\( k = f(2) = 0 \)
\( B(r, k) = B(2, 0) \)
\( C \) noktasının apsisini bulmak için doğru denkleminde \( y = 0 \) koyalım.
\( 0 = -x + 8 \Longrightarrow x = 8 \)
\( C(8, 0) \)
\( ABC \) üçgeninin alanını bulmak için \( [BC] \) kenarını ve bu kenara ait yüksekliği kullanalım.
\( A(ABC) = \dfrac{\abs{BC} \cdot \abs{DA}}{2} \)
\(= \dfrac{(8 - 2) \cdot 9}{2} = 27 \) bulunur.
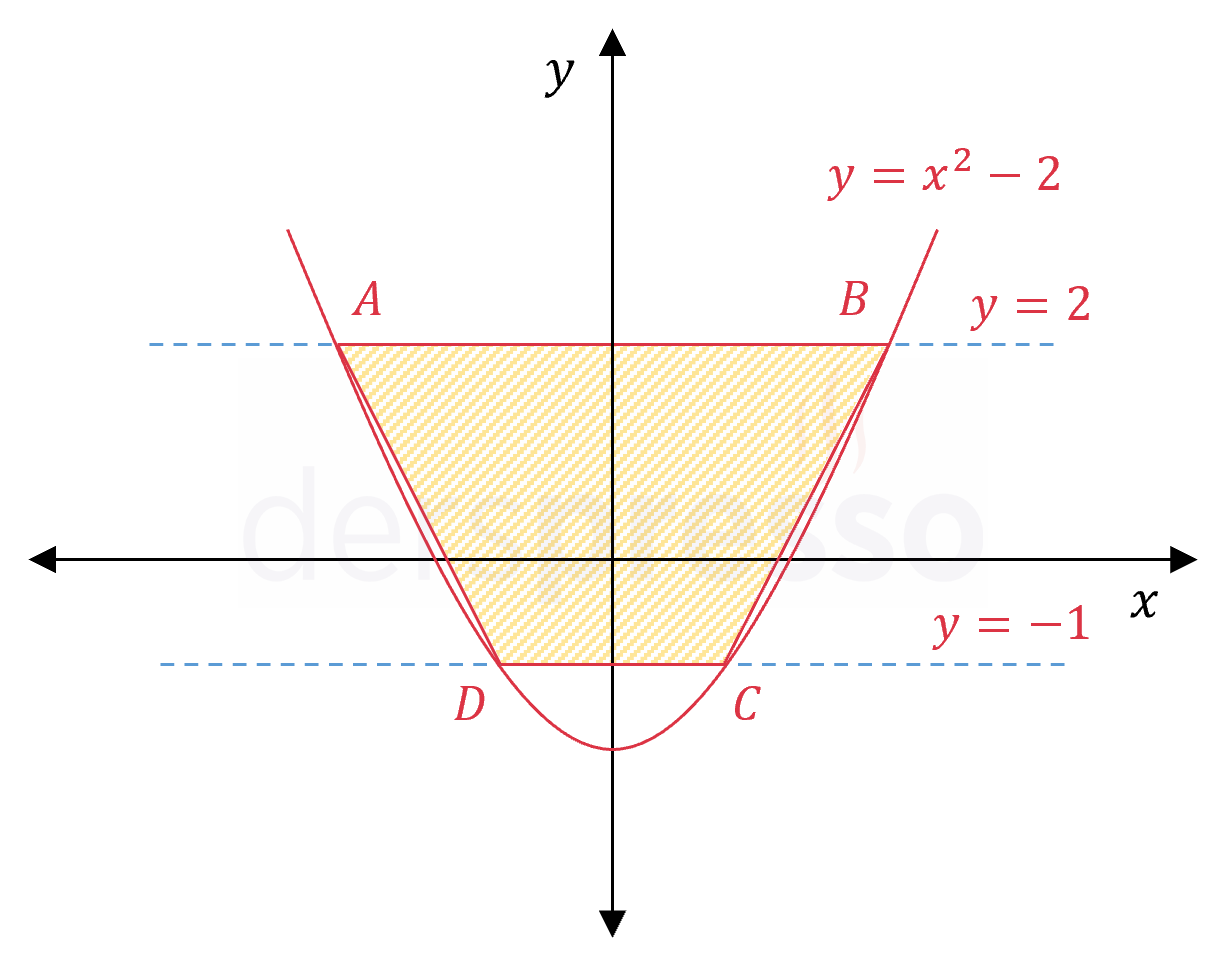
\( ABCD \) yamuğu; \( y = x^2 - 2 \) parabolü, \( y = 2 \) ve \( y = -1 \) doğruları arasına şekildeki gibi yerleştirilmiştir.
Buna göre \( ABCD \) yamuğunun alanı kaçtır?
Çözümü Göster\( y = 2 \) ve \( y = -1 \) doğrularının ordinat değerlerini parabol denkleminde yerine yazarak parabol ve doğruların kesişim noktalarının apsislerini bulalım.
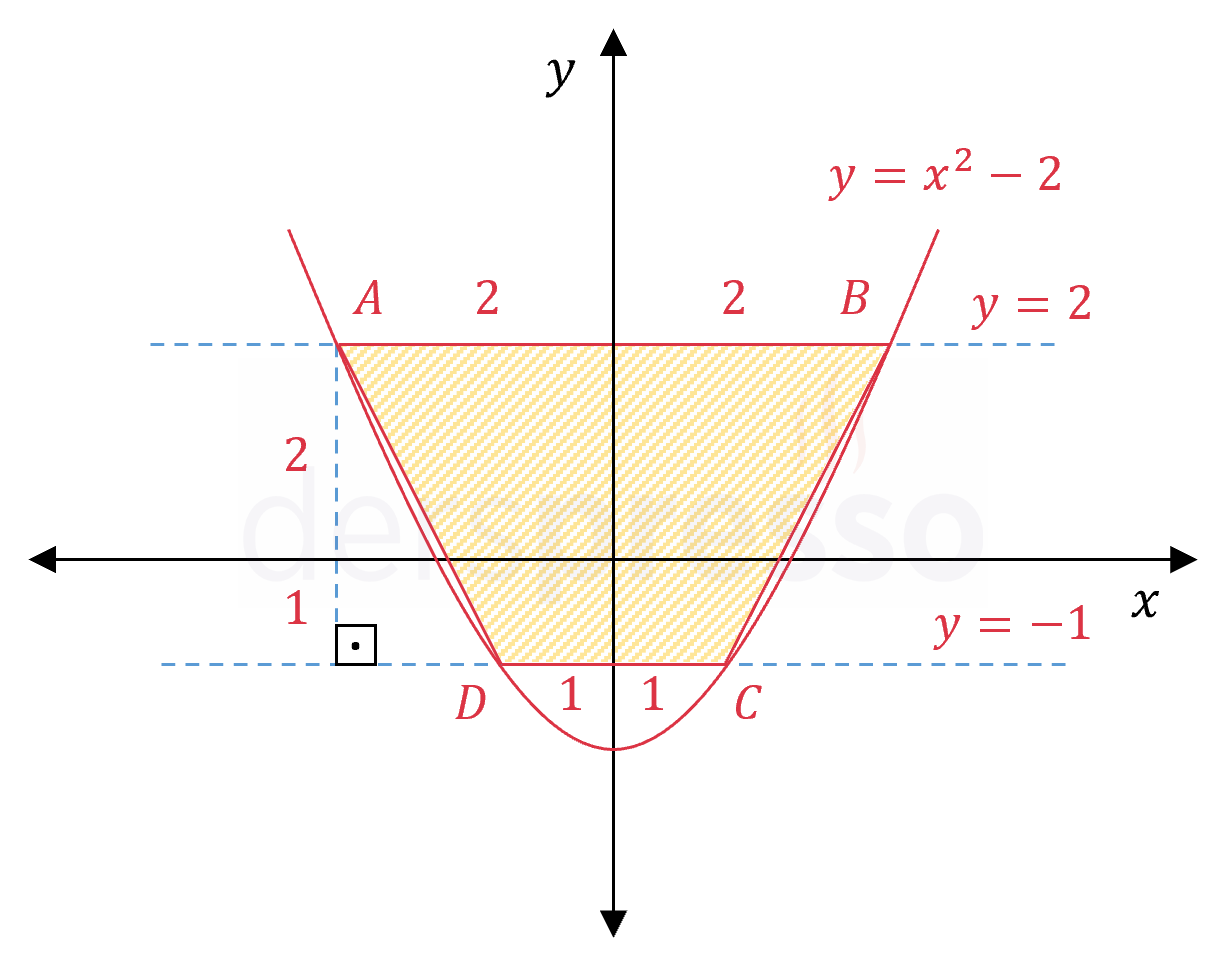
\( A \) ve \( B \) noktalarının apsislerini bulmak için parabol denkleminde \( y = 2 \) yazalım.
\( x^2 - 2 = 2 \)
\( x^2 = 4 \)
\( x = \pm 2 \)
\( A(-2, 2) \)
\( B(2, 2) \)
\( C \) ve \( D \) noktalarının apsislerini bulmak için parabol denkleminde \( y = -1 \) yazalım.
\( x^2 - 2 = -1 \)
\( x^2 = 1 \)
\( x = \pm 1 \)
\( C(1, -1) \)
\( D(-1, -1) \)
\( ABCD \) yamuğunun yüksekliği \( y = 2 \) ve \( y = -1 \) doğruları arasındaki mesafedir.
\( h = 2 - (-1) = 3 \)
\( A(ABCD) = \dfrac{(\abs{AB} + \abs{DC}) \cdot h}{2} \)
\( = \dfrac{(4 + 2) \cdot 3}{2} = 9 \) bulunur.
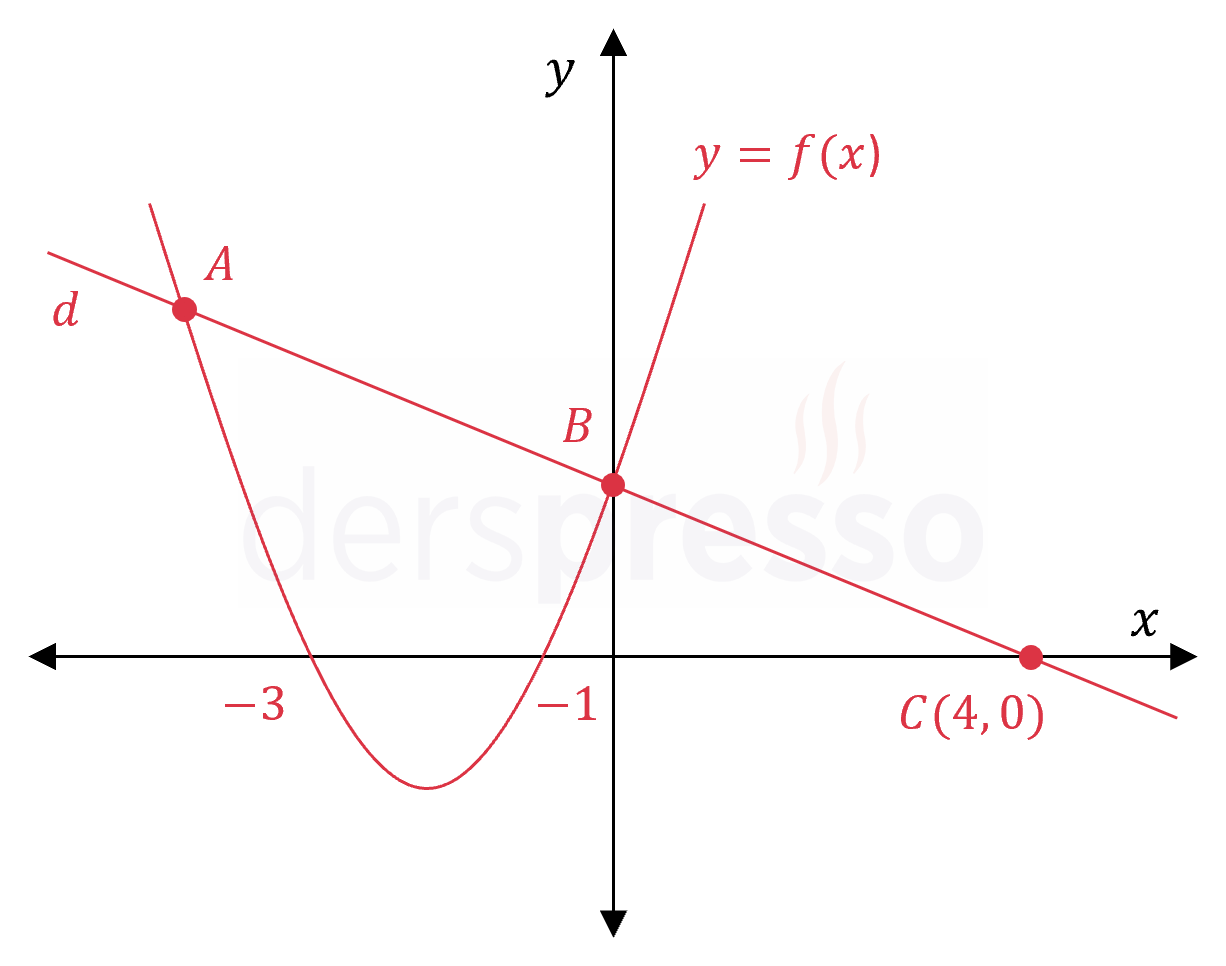
Analitik düzlemde \( d \) doğrusu ve \( f \) parabolü şekildeki gibidir.
Buna göre \( A \) noktasının apsisi kaçtır?
Çözümü Göster\( d \) doğrusunun \( y \) eksenini kestiği noktanın ordinatına \( k \) diyelim.
\( B(0, k) \)
\( d \) doğrusunun ve \( f \) parabolünün denklemlerini bulalım.
\( d \) doğrusunun denklemini bulmak için eksenleri kestiği noktalar bilinen doğru denklemini kullanalım.
\( \dfrac{x}{x_0} + \dfrac{y}{y_0} = 1 \)
\( \dfrac{x}{4} + \dfrac{y}{k} = 1 \)
\( y = -\dfrac{k}{4}x + k \)
\( f \) parabolünün denklemini bulmak için \( x \) eksenini kestiği iki nokta bilinen parabol denklemini kullanalım.
\( f(x) = a(x - x_1)(x - x_2) \)
\( f(x) = a(x + 3)(x + 1) \)
\( f \) parabolü ile \( d \) doğrusunun kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( (1 - \dfrac{x}{4})k = a(x + 1)(x + 3) \)
\( B(0, k) \) noktası bu kesişim noktalarından biri olduğu için koordinatları bu eşitliği sağlar.
\( (1 - \dfrac{0}{4})k = a(0 + 1)(0 + 3) \)
\( k = 3a \)
Bu değeri iki denklemin ortak çözüm denkleminde yerine koyalım.
\( (1 - \dfrac{x}{4})3a = a(x + 1)(x + 3) \)
\( 3 - \dfrac{3x}{4} = x^2 + 4x + 3 \)
\( 12 - 3x = 4x^2 + 16x + 12 \)
\( 4x^2 + 19x = 0 \)
\( x(4x + 19) = 0 \)
\( x = -\dfrac{19}{4} \) ya da \( x = 0 \)
\( f \) parabolü ile \( d \) doğrusu \( x = -\dfrac{19}{4} \) ve \( x = 0 \) apsisli noktalarda kesişir.
\( A \) noktasının apsisi \( -\frac{19}{4} \) olarak bulunur.
\( y = x^2 \) ve \( y = (x - 2)^2 + 1 \) parabollerinin her ikisine de teğet olan doğrunun denklemi nedir?
Çözümü GösterParabollere teğet olan doğrunun denklemini \( y = mx + c \) şeklinde yazalım.
\( y = x^2 \) parabolü ile teğet doğru denklemini ortak çözelim.
\( x^2 = mx + c \)
\( x^2 - mx - c = 0 \)
Doğrunun parabole teğet olabilmesi için bu denklemin deltası sıfır olmalıdır.
\( \Delta = b^2 - 4ac \)
\( (-m)^2 - 4(1)(-c) = 0 \)
\( m^2 + 4c = 0 \)
\( c = -\dfrac{m^2}{4} \)
\( y = (x - 2)^2 + 1 \) parabolü ile teğet doğru denklemini ortak çözelim.
\( (x - 2)^2 + 1 = x^2 - 4x + 5 \)
\( x^2 - 4x + 5 = mx + c \)
\( x^2 - (4 + m)x + 5 - c = 0 \)
Doğrunun parabole teğet olabilmesi için bu denklemin deltası sıfır olmalıdır.
\( \Delta = (-(4 + m))^2 - 4(1)(5 - c) \)
\( 16 + 8m + m^2 - 20 + 4c = 0 \)
\( m^2 + 8m - 4 + 4c = 0 \)
\( y = x^2 \) ve \( y = mx + c \) denklemlerinin ortak çözümünden elde ettiğimiz \( c = -\frac{m^2}{4} \) ifadesini yukarıdaki denklemde yerine yazalım.
\( m^2 + 8m - 4 + 4(-\dfrac{m^2}{4}) = 0 \)
\( m^2 + 8m - 4 - m^2 = 0 \)
\( 8m - 4 = 0 \)
\( m = \dfrac{1}{2} \)
Bu değeri \( c = -\frac{m^2}{4} \) ifadesinde yerine koyalım.
\( c = -\dfrac{{\frac{1}{2}}^2}{4} = -\dfrac{1}{16} \)
İki parabole de teğet olan doğrunun denklemi aşağıdaki şekilde bulunur.
\( y = \dfrac{1}{2}x -\dfrac{1}{16} \)