Asal Çarpanların Küme Gösterimi
Bir sayının asal çarpanlarını küme olarak tanımlayıp Venn şeması şeklinde aşağıdaki gibi gösterebiliriz.
\( 300 = 2^2 \cdot 3^1 \cdot 5^2 \)
\( A = \{ x: 300 \text{ sayısının asal çarpanları} \} \)
\( A = \{ 2, 2, 3, 5, 5 \} \)

NOT: Küme tanımına göre, bir eleman bir kümede sadece bir kez bulunabilir, ancak burada tekrarlayan çarpanları asal çarpanlar kümesine birden fazla kez dahil etmiş olduk. Bu tekrarlayan elemanları "birinci 2 çarpanı, ikinci 2 çarpanı vb." şeklinde birbirinden farklı elemanlar olarak düşünebiliriz.
Benzer şekilde, iki sayının asal çarpanlarını da aşağıdaki gibi gösterebiliriz.
\( 252 = 2^2 \cdot 3^2 \cdot 7^1 \)
\( A = \{ x: 252 \text{ sayısının asal çarpanları} \} \)
\( A = \{ 2, 2, 3, 3, 7 \} \)
\( 120 = 2^3 \cdot 3^1 \cdot 5^1 \)
\( B = \{ x: 120 \text{ sayısının asal çarpanları} \} \)
\( B = \{ 2, 2, 2, 3, 5 \} \)
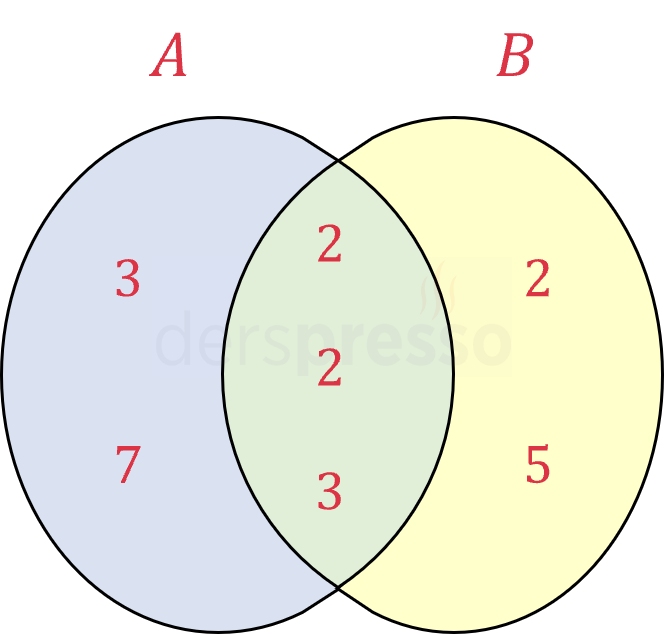
EBOB ve EKOK'un Küme Gösterimi
Yukarıdaki şemada \( A \) kümesi (mavi + yeşil alan) 252'nin asal çarpanlarını, \( B \) kümesi (sarı + yeşil alan) 120'nin asal çarpanlarını içermektedir.
İki kümenin kesişim kümesi (yeşil alan) iki sayıda ortak olan çarpanları içermektedir, bu da iki sayının EBOB'una karşılık gelmektedir. İki kümenin birleşim kümesi ise (mavi + yeşil + sarı alan) iki sayıda ortak olan çarpanlar bir kez sayılacak şekilde tüm çarpanları içermektedir, bu da iki sayının EKOK'una karşılık gelmektedir.
\( A \cap B = \{ 2, 2, 3 \} \)
\( EBOB(252, 120) = 2 \cdot 2 \cdot 3 = 12 \)
\( A \cup B = \{ 2, 2, 2, 3, 3, 5, 7 \} \)
\( EKOK(252, 120) = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 5 \cdot 7 \) \( = 2520 \)
Bu gösterim bize iki sayının EBOB'unun bu sayıların asal çarpanlarının kesişim kümesi olduğunu göstermektedir. Dolayısıyla, iki ya da daha fazla sayının EBOB'unu bulurken aynı zamanda bu sayıların asal çarpanlarının oluşturduğu kümelerin kesişim kümesini buluyor oluruz.
Benzer şekilde, bu gösterim bize iki sayının EKOK'unun bu sayıların asal çarpanlarının birleşim kümesi olduğunu göstermektedir. Dolayısıyla, iki ya da daha fazla sayının EKOK'unu bulurken aynı zamanda bu sayıların asal çarpanlarının oluşturduğu kümelerin birleşim kümesini buluyor oluruz.
Aralarında Asal Sayıların Küme Gösterimi
Aralarında asal sayıların ortak çarpanı olmadığı için küme gösteriminde kesişim kümesi boş küme olur.
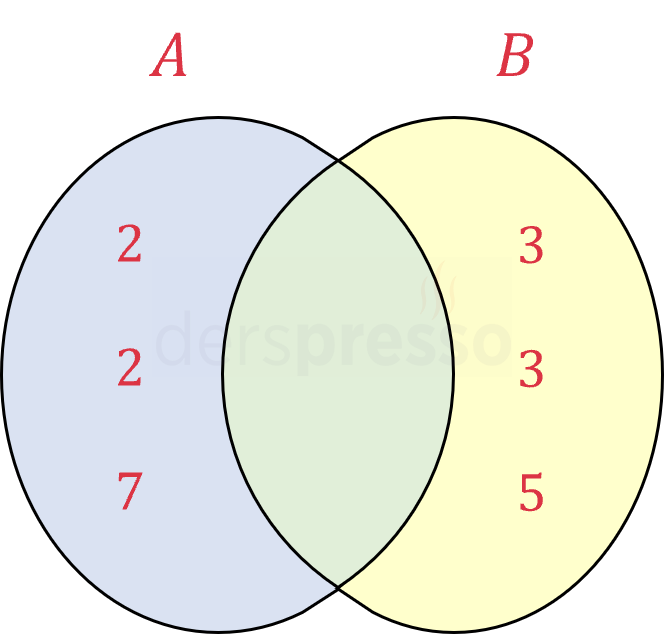
\( 28 = 2^2 \cdot 7^1 \)
\( A = \{ 2, 2, 7 \} \)
\( 45 = 3^2 \cdot 5^1 \)
\( B = \{ 3, 3, 5 \} \)
\( A \cap B = \emptyset \)
\( a \) ve \( b \) birbirinden farklı doğal sayılardır.
\( EKOK(a, b) = 108 \) olduğuna göre, \( a + b \) toplamı en az kaçtır?
Çözümü Göster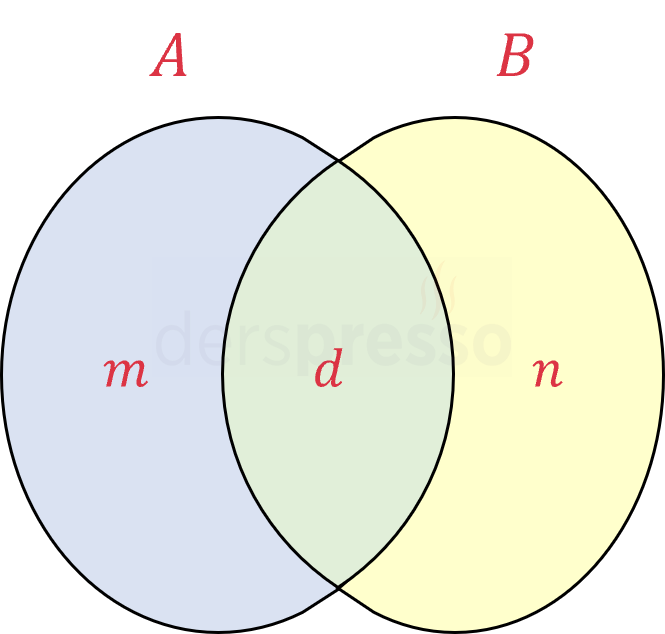
İki sayının asal çarpanlarını Venn şeması şeklinde gösterdiğimizde kesişim kümesindeki çarpanların çarpımı sayıların EBOB'unu, birleşim kümesindeki çarpanların çarpımı da sayıların EKOK'unu verir.
\( EKOK(a, b) = 108 \)
\( d \cdot m \cdot n = 2^2 \cdot 3^3 \)
Sayıların toplamının en küçük değeri için kesişim kümesi boş, yani sayılar aralarında asal olmalıdır.
Bu aşağıdaki iki durumda sağlanır (sayıların aralarında yer değiştirdiği durumları iki kez saymadan).
\( a = 2^2 \cdot 3^3 = 108, \quad b = 1 \)
\( a = 2^2 = 4, \quad b = 3^3 = 27 \)
Sayıların toplamının en küçük olduğu durum ikinci durumdur.
\( a + b = 27 + 4 = 31 \)
\( a \) ve \( b \) aralarında asal sayılar olmak üzere,
\( EKOK(a, b) = 360 \) eşitliğini sağlayan kaç farklı \( (a, b) \) sıralı ikilisi yazılabilir?
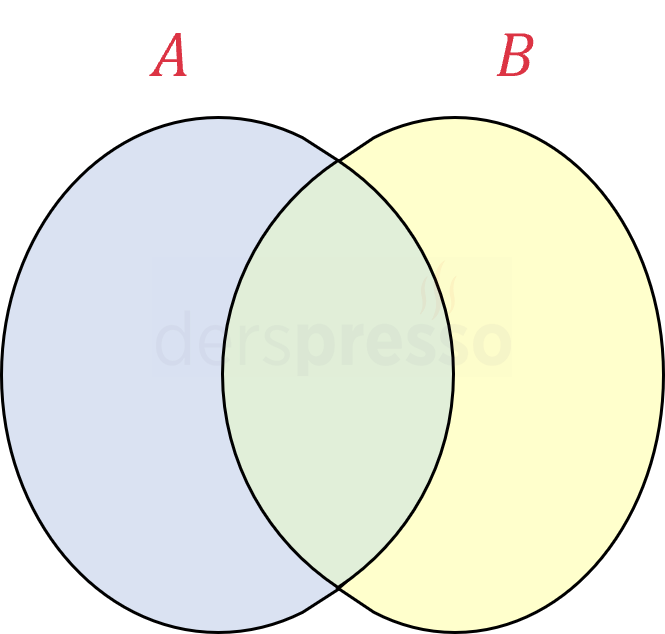
Çözümü GösterAşağıdaki şekilde \( A \) kümesi \( a \) sayısının, \( B \) kümesi de \( b \) sayısının asal çarpanlarını göstermektedir. Kümelerin kesişimi iki sayının ortak asal çarpanlarını (yani EBOB'larını), birleşimi de tekrarsız tüm asal çarpanlarını (yani EKOK'larını) vermektedir.
360'ı asal çarpanlarına ayıralım.
\( EKOK(a, b) = 360 = 2^3 \cdot 3^2 \cdot 5^1 \)
Bu soruda yapmamız gereken, 360'ın asal çarpanlarını yukarıdaki Venn şemasındaki üç bölgeye (mavi, sarı ve yeşil) kaç farklı şekilde dağıtabileceğimizi bulmaktır. Bununla ilgili koşulları şu şekilde sıralayabiliriz.
- Sayıların aralarında asal olduğu belirtildiği için, kesişim kümesi (yeşil bölge) boş küme olmalıdır.
- Bir asal sayının tüm çarpanları aynı bölgede (mavi ya da sarı) olmak zorundadır. Örneğin 3'ün bir asal çarpanı \( a \) sayısının, diğer çarpanı \( b \) sayısının çarpan listesinde yer alırsa bu çarpan iki sayıda ortak olacağı için kesişim kümesinde yer alması gerekecek, bu da sayıların aralarında asallığını bozacaktır.
Dolayısıyla, \( 2^3 \), \( 3^2 \) ve \( 5 \) çarpanlarını bu iki bölgeye kaç farklı şekilde yerleştirebileceğimizi bulmamız gerekmektedir. Bu üç çarpanın her biri için iki seçeneğimiz olduğu için (mavi ve sarı bölgeler), çarpma kuralı gereği sayıları toplamda \( 2^3 = 8 \) farklı şekilde yerleştirebiliriz.
Buna göre sayıların iki bölgeye farklı dağıtımları aşağıdaki gibi olur. Her bir durumda sayıların aralarında asal olduğunu ve çarpımlarının 360 olduğu görebiliriz.
| \( a \) | \( b \) |
|---|---|
| \( 2^3 \cdot 3^2 \cdot 5^1 = 360 \) | \( 2^0 \cdot 3^0 \cdot 5^0 = 1 \) |
| \( 2^3 \cdot 3^2 \cdot 5^0 = 72 \) | \( 2^0 \cdot 3^0 \cdot 5^1 = 5 \) |
| \( 2^3 \cdot 3^0 \cdot 5^1 = 40 \) | \( 2^0 \cdot 3^2 \cdot 5^0 = 9 \) |
| \( 2^3 \cdot 3^0 \cdot 5^0 = 8 \) | \( 2^0 \cdot 3^2 \cdot 5^1 = 45 \) |
| \( 2^0 \cdot 3^2 \cdot 5^1 = 45 \) | \( 2^3 \cdot 3^0 \cdot 5^0 = 8 \) |
| \( 2^0 \cdot 3^2 \cdot 5^0 = 9 \) | \( 2^3 \cdot 3^0 \cdot 5^1 = 40 \) |
| \( 2^0 \cdot 3^0 \cdot 5^1 = 5 \) | \( 2^3 \cdot 3^2 \cdot 5^0 = 72 \) |
| \( 2^0 \cdot 3^0 \cdot 5^0 = 1 \) | \( 2^3 \cdot 3^2 \cdot 5^1 = 360 \) |
Buna göre \( EKOK(a, b) = 360 \) eşitliğini sağlayan 8 farklı \( (a, b) \) sıralı ikilisi yazılabilir.