Bileşke Fonksiyon
\( f \) ve \( g \) fonksiyonlarını \( f \)'nin girdi değerlerini \( g \)'nin çıktı değerleri ile eşleyerek tek bir fonksiyonda birleştiren fonksiyona bileşke fonksiyon denir ve \( g \circ f \) şeklinde gösterilir.
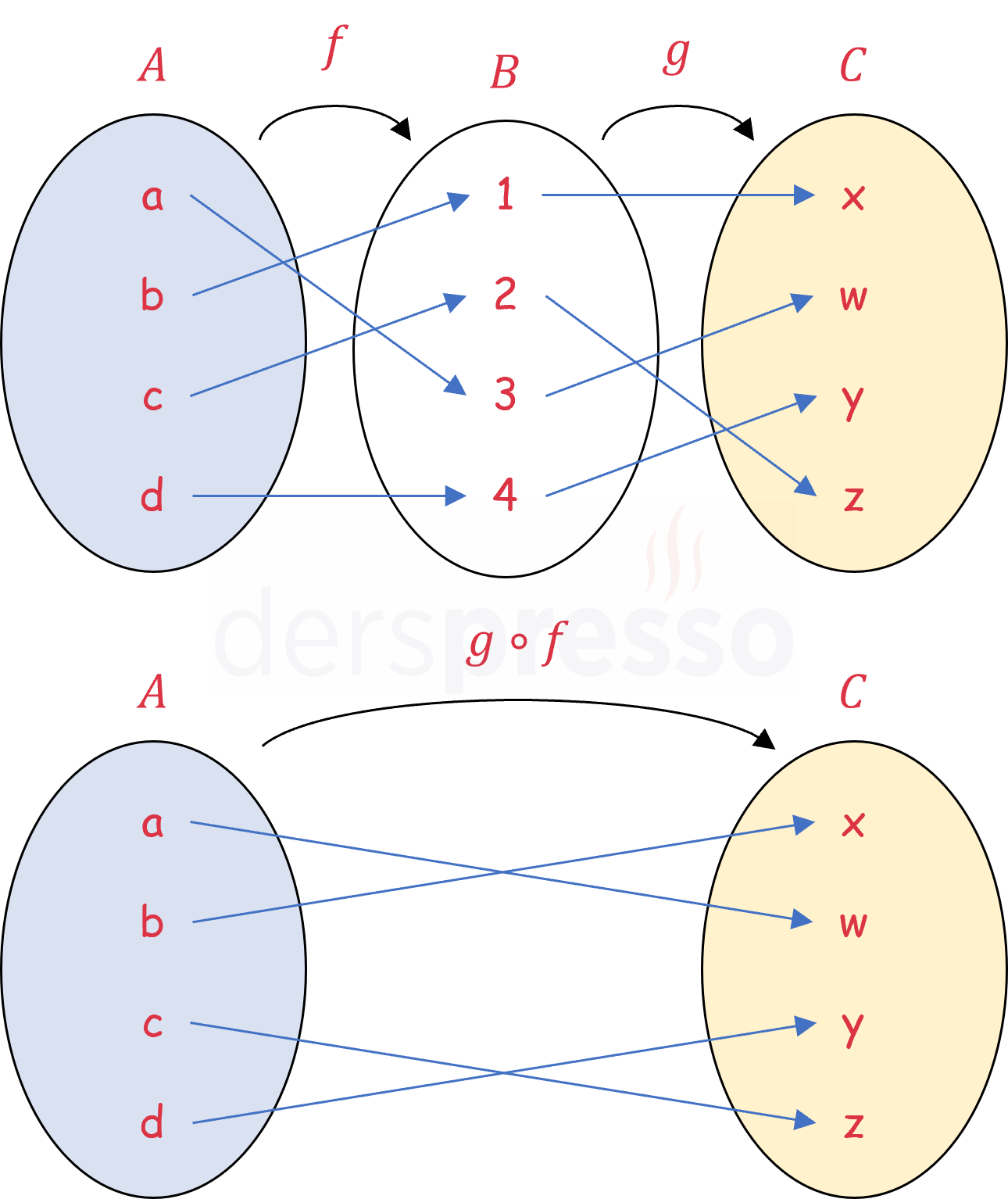
\( f \) fonksiyonunun tanım kümesindeki bir elemanın \( g \circ f \) bileşke fonksiyonuna göre görüntüsü, elemanın \( f \) fonksiyonuna göre görüntüsünün tekrar \( g \) fonksiyonuna göre alınan görüntüsüdür.
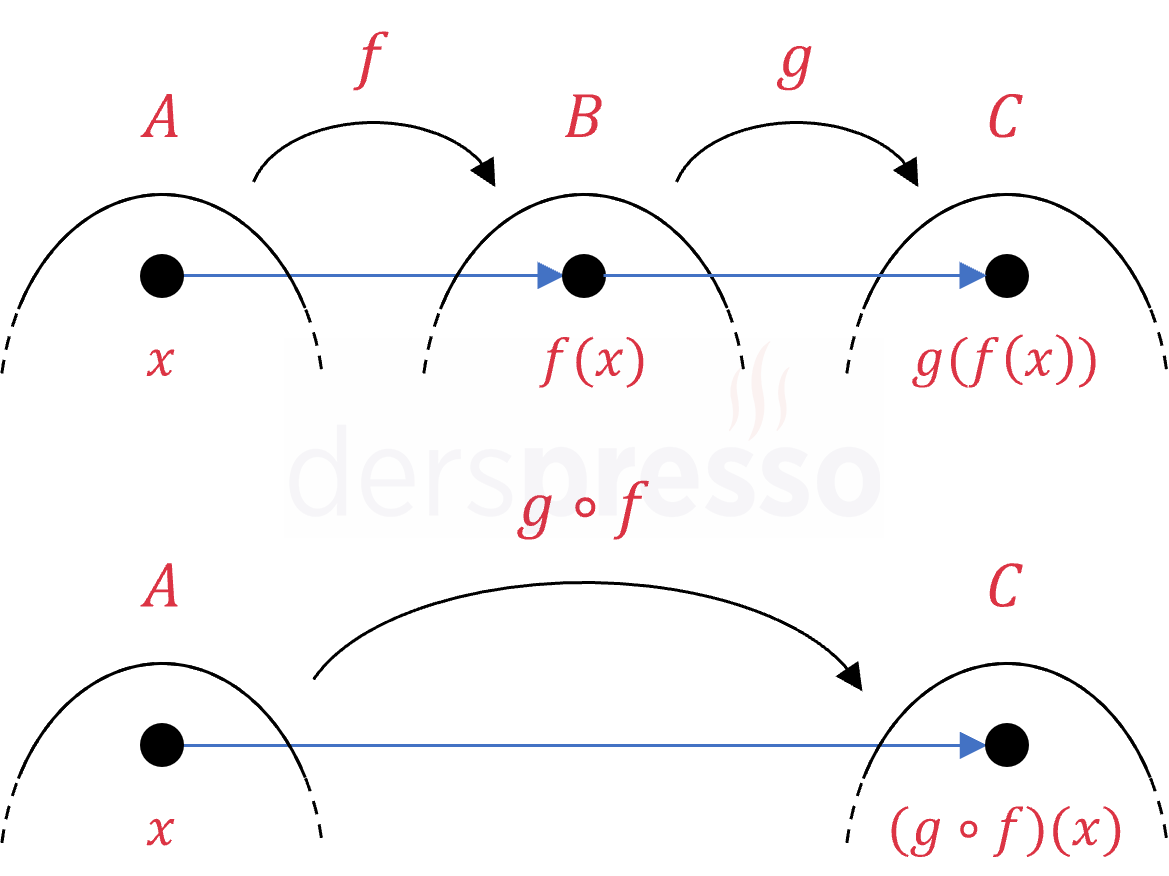
Buna göre bileşke fonksiyonu aşağıdaki şekilde tanımlanabilir.
\( (g \circ f)(x) = g(f(x)) \)
\( f(a) = 3, \quad g(3) = w \) ise,
\( (g \circ f)(a) = g(f(a)) = g(3) = w \)
Dikkat edilirse bileşke fonksiyonlarda fonksiyonların yazılış sırası işlem sırasının tersidir. \( g \circ f \) bileşke fonksiyonunda \( x \) değerinin önce \( f \) fonksiyonuna göre görüntüsü bulunur, daha sonra elde edilen \( f(x) \) değerinin \( g \) fonksiyonuna göre görüntüsü bulunur.
\( (g \circ f)(x) = g(f(x)) \) bileşke fonksiyonunda \( f \) fonksiyonuna "içteki fonksiyon", \( g \) fonksiyonuna "dıştaki fonksiyon" da denir.
Fonksiyon - Makine Benzetmesi
Daha önce yaptığımız fonksiyon - makine benzetmesini bileşke fonksiyona aşağıdaki şekildeki gibi uyarlayabiliriz.

Bu benzetmeyi kullanarak \( f \) fonksiyonunu bir çamaşır makinesi, \( g \) fonksiyonunu da bir kurutma makinesi olarak tanımlarsak \( g \circ f \) bileşke fonksiyonunu yıkama ve kurutma fonksiyonlarını birleştiren tek bir makine olarak düşünebiliriz.
Bileşke Fonksiyonun Bulunması
Tanımları küme liste yöntemi ile verilmiş \( f \) ve \( g \) fonksiyonları arasındaki \( g \circ f \) bileşke fonksiyonu, \( f \)'nin tanım kümesindeki her elemanın \( f \)'ye göre görüntülerinin tekrar \( g \)'ye göre görüntüleri alınarak bulunur.
\( f \): Bir sınıftaki öğrencilerin burçlarını veren fonksiyon
\( f = \) {(Ece, Boğa), (Eda, Yengeç), (Ela, Koç), (Efe, İkizler), ...}
\( g \): Burçların elementlerini veren fonksiyon
\( g = \) {(Koç, Ateş), (Boğa, Toprak), (İkizler, Hava), (Yengeç, Su), (Aslan, Ateş), ...}
\( g \circ f \): Öğrencilerin burçlarının elementlerini veren bileşke fonksiyon
\( g \circ f = \) {(Ece, Toprak), (Eda, Su), (Ela, Ateş), (Efe, Hava), ...}
\( (g \circ f)(\text{Eda}) = g(f(\text{Eda})) = g(\text{Yengeç}) = \text{Su} \)
Tanımları birer formül olarak verilmiş \( f \) ve \( g \) fonksiyonları arasındaki \( g \circ f \) bileşke fonksiyonu aşağıdaki yöntemle bulunur.
- \( (g \circ f)(x) \) fonksiyonu \( g(f(x)) \) şeklinde yazılır.
- \( f(x) \) yerine temsil ettiği fonksiyon tanımı yazılır.
- \( g(x) \) fonksiyonunda her \( x \) yerine \( f(x) \) tanımı yazılır.
\( f(x) = 3x - 1 \)
\( g(x) = 2x^2 + 4x - 5 \) olmak üzere,
\( (g \circ f)(x) = g(\textcolor{red}{f(x)}) = g(\textcolor{red}{3x - 1}) \)
\( = 2(\textcolor{red}{3x - 1})^2 + 4(\textcolor{red}{3x - 1}) - 5 \)
\( f(x) = 5x \)
\( g(x) = x^2 + 2\sqrt{x} - 2^x \)
olduğuna göre, \( (g \circ f)(x) \) kaçtır?
Çözümü Göster\( (g \circ f)(x) = g(f(x)) \)
\( = g(5x) \)
\( g \) fonksiyonunda her \( x \) yerine \( 5x \) yazalım.
\( = (5x)^2 + 2\sqrt{5x} - 2^{5x} \)
\( = 25x^2 + 2\sqrt{5x} - 2^{5x} \)
\( f(x) = 4x \)
\( g(x) = x^2 \)
\( h(x) = \sqrt{3x} \)
fonksiyonları arasındaki tüm ikili bileşke fonksiyonlarını bulunuz.
Çözümü Göster\( f \circ g \) fonksiyonu:
\( (f \circ g)(x) = f(g(x)) = f(x^2) \)
\( = 4x^2 \)
\( g \circ f \) fonksiyonu:
\( (g \circ f)(x) = g(f(x)) = g(4x) \)
\( = (4x)^2 = 16x^2 \)
\( f \circ h \) fonksiyonu:
\( (f \circ h)(x) = f(h(x)) = f(\sqrt{3x}) \)
\( = 4\sqrt{3x} \)
\( h \circ f \) fonksiyonu:
\( (h \circ f)(x) = h(f(x)) = h(4x) \)
\( = \sqrt{3 \cdot 4x} = \sqrt{12x} \)
\( g \circ h \) fonksiyonu:
\( (g \circ h)(x) = g(h(x)) = g(\sqrt{3x}) \)
\( = (\sqrt{3x})^2 = 3x \)
\( h \circ g \) fonksiyonu:
\( (h \circ g)(x) = h(g(x)) = h(x^2) \)
\( = \sqrt{3x^2} = \sqrt{3}x \)
\( f(x) = \dfrac{1}{2}\ln(x + 2) + 1 \)
\( g(x) = e^{2(x - 1)} - 2 \)
olduğuna göre, \( (f \circ g)(x) \) bileşke fonksiyonunun en sade biçimini bulunuz.
Çözümü Göster\( (f \circ g)(x) = f(g(x)) \)
\( = \dfrac{1}{2}\ln(e^{2(x - 1)} - 2 + 2) + 1 \)
\( = \dfrac{1}{2}\ln{e^{2(x - 1)}} + 1 \)
\( \ln{e^x} = x \) kuralını kullanalım.
\( = \dfrac{1}{2}(2(x - 1)) + 1 \)
\( = (x - 1) + 1 \)
\( = x \) bulunur.
\( (f \circ g)(x) = x = I \) olduğuna göre \( f \) ve \( g \) fonksiyonları birbirinin tersidir.
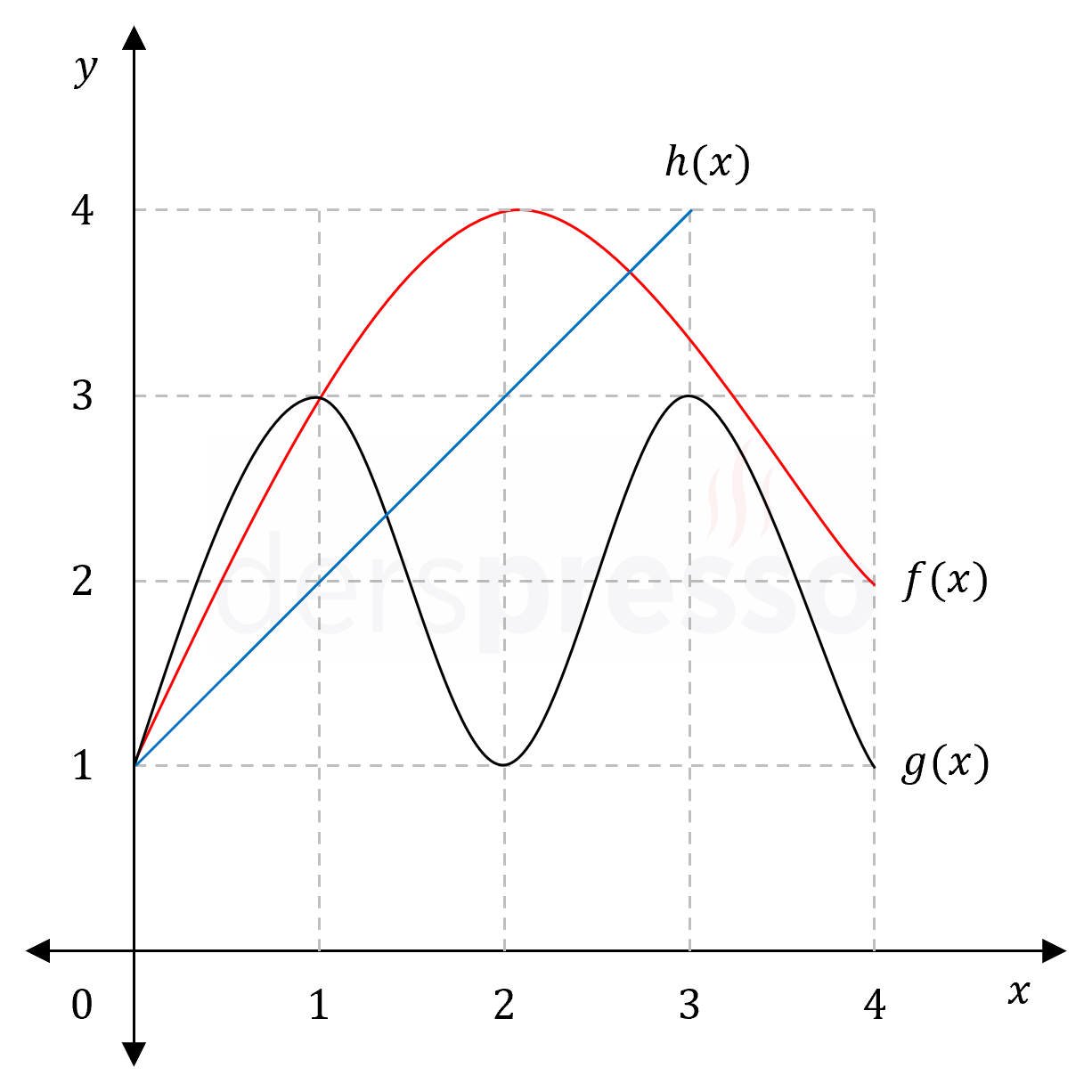
Yukarıdaki grafikte \( f, g \) ve \( h \) fonksiyonlarının grafikleri verilmiştir.
\( a = (f \circ g)(2) \)
\( b = (h \circ f)(1) \)
\( c = (g \circ f)(2) \)
\( d = (f \circ h)(0) \)
\( e = (h \circ g)(4) \)
olduğuna göre, \( a, b, c, d, e \) değerlerini küçükten büyüğe doğru sıralayınız.
Çözümü GösterGrafiği inceleyerek istenen değerleri sırasıyla bulalım.
\( a = (f \circ g)(2) = f(g(2)) \)
\( = f(1) = 3 \)
\( b = (h \circ f)(1) = h(f(1)) \)
\( = h(3) = 4 \)
\( c = (g \circ f)(2) = g(f(2)) \)
\( = g(4) = 1 \)
\( d = (f \circ h)(0) = f(h(0)) \)
\( = f(1) = 3 \)
\( e = (h \circ g)(4) = h(g(4)) \)
\( = h(1) = 2 \)
Bulduğumuz değerleri küçükten büyüğe doğru sıralayalım.
\( c \lt e \lt a = d \lt b \)
Bileşke Fonksiyonun Tanım ve Görüntü Kümesi
Tanım kümesi \( A \) olan bir \( f \) fonksiyonu ile tanım kümesi \( B \) olan bir \( g \) fonksiyonu arasında \( g \circ f \) bileşke fonksiyonu tanımlayalım.
Bir \( x \) değerinin \( g \circ f \) bileşke fonksiyonunun tanım kümesinin elemanı olabilmesi için değer aşağıdaki iki koşulu sağlamalıdır.
- \( A \) kümesinin elemanı olmalıdır (\( x \in A \)).
- \( f \) fonksiyonuna göre görüntüsü \( g \) fonksiyonunun tanım kümesinin elemanı olmalıdır (\( f(x) \in B \)).
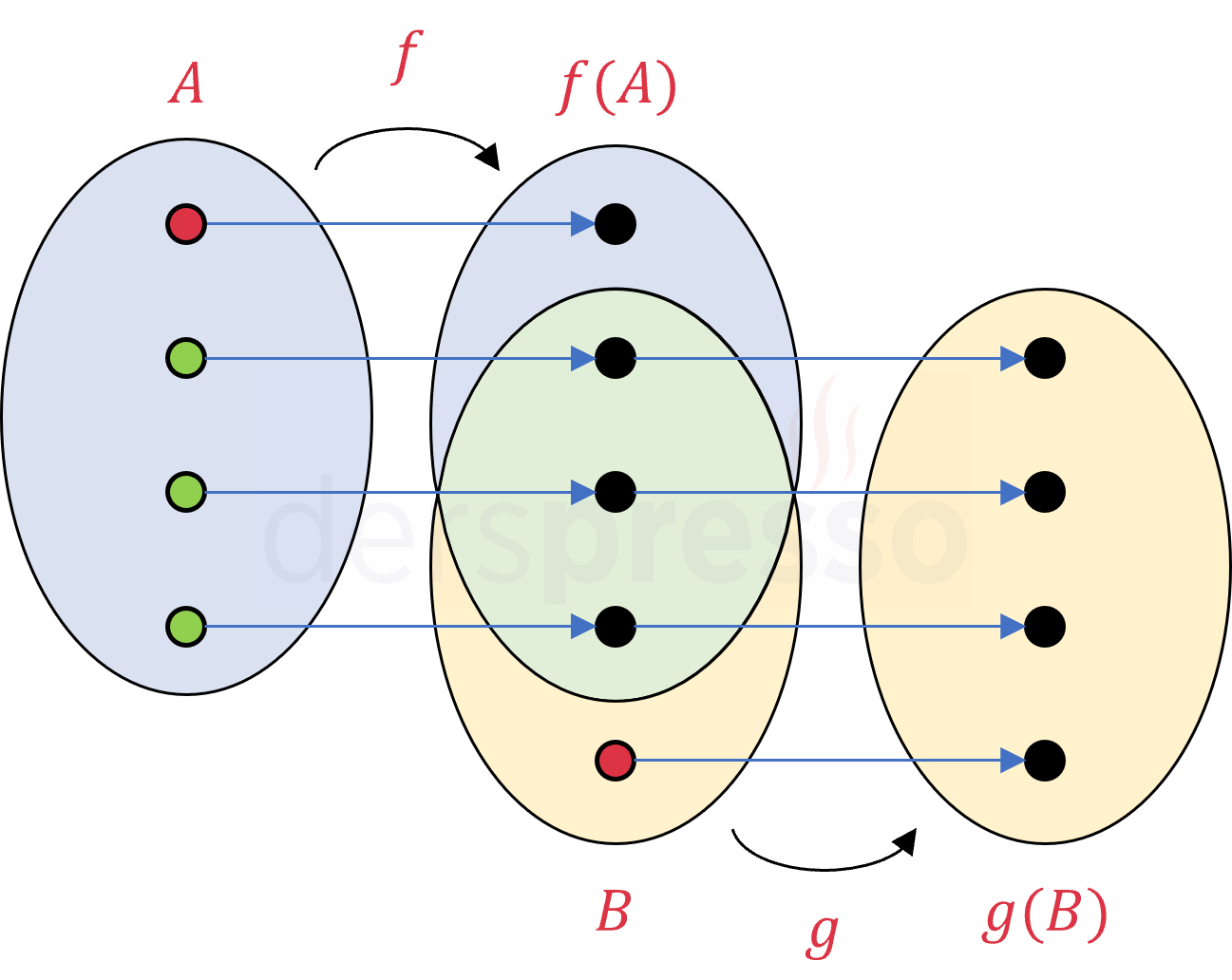
Yukarıdaki şekildeki \( A \) kümesinin yeşil ile işaretlenmiş üç elemanı \( g \circ f \) fonksiyonunun tanım kümesini oluştururlar. \( B \) kümesinde kırmızı ile işaretli eleman birinci koşulu, \( A \) kümesinde kırmızı ile işaretli eleman da ikinci koşulu sağlamadığı için \( g \circ f \) fonksiyonunun tanım kümesine dahil olmazlar.
Buna göre \( g \circ f \) fonksiyonunun tanım kümesi her zaman \( f \) fonksiyonunun tanım kümesine eşittir ya da onun bir alt kümesidir.
\( f(x) = 3x + 1, \quad x \in (-\infty, 3] \)
\( g(x) = x^2 - 1, \quad x \in [1, \infty) \)
\( g \circ f \) fonksiyonunun tanım kümesini bulalım.
\( g \circ f \) fonksiyonunun tanım kümesindeki elemanlar aşağıdaki iki koşulu sağlamalıdır.
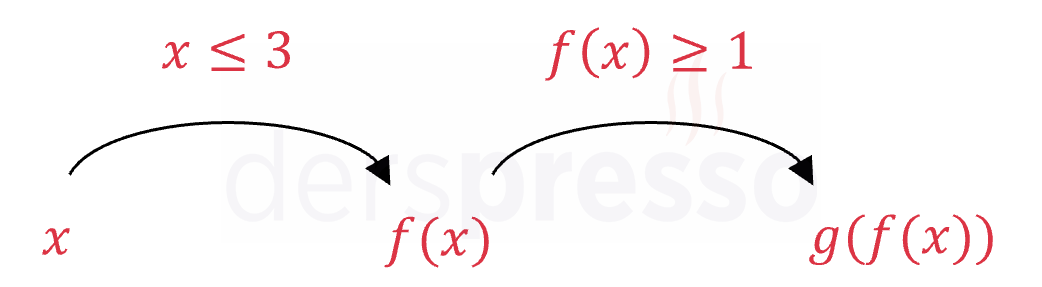
(1) \( f \) fonksiyonunun tanım kümesinde bulunmalıdır.
\( x \le 3 \)
(2) \( f \) fonksiyonuna göre görüntüleri \( g \) fonksiyonunun tanım kümesinde bulunmalıdır.
\( f(x) \ge 1 \)
\( 3x + 1 \ge 1 \)
\( x \ge 0 \)
Bu iki aralığın kesişim kümesi \( g \circ f \) fonksiyonunun tanım kümesini verir.
Tanım kümesi: \( 0 \le x \le 3 \)
\( f(x) = \sqrt{x^2 - 9}, \quad x \in [3, \infty) \)
\( g(x) = 5x + 3, \quad x \in (-\infty, 4) \)
\( g \circ f \) fonksiyonunun tanım kümesini bulalım.
\( g \circ f \) fonksiyonunun tanım kümesindeki elemanlar aşağıdaki iki koşulu sağlamalıdır.
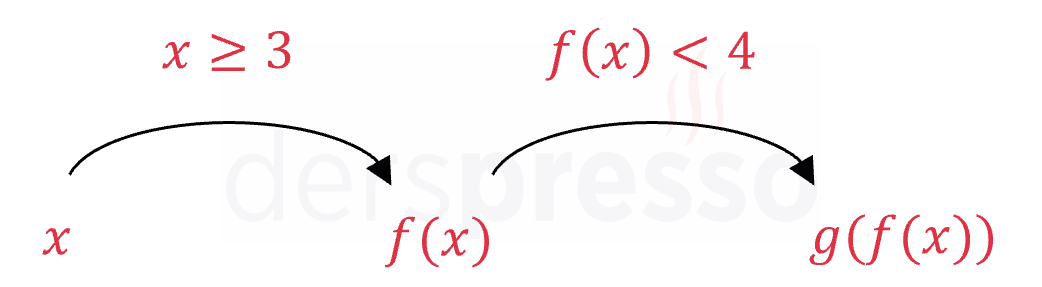
(1) \( f \) fonksiyonunun tanım kümesinde bulunmalıdır.
\( x \ge 3 \)
(2) \( f \) fonksiyonuna göre görüntüleri \( g \) fonksiyonunun tanım kümesinde bulunmalıdır.
\( f(x) \lt 4 \)
\( \sqrt{x^2 - 9} \lt 4 \)
\( x^2 - 9 \lt 16 \)
\( x^2 \lt 25 \)
\( -5 \lt x \lt 5 \)
Bu iki aralığın kesişim kümesi \( g \circ f \) fonksiyonunun tanım kümesini verir.
Tanım kümesi: \( 3 \le x \lt 5 \)
Bir bileşke fonksiyonun tanım kümesini bulduktan sonra görüntü kümesi tanım ve görüntü kümesi bölümünde "Görüntü Kümesinin Bulunması" başlığı altında bahsettiğimiz yöntemlerle bulunabilir.
Tanım kümesine benzer şekilde, \( g \circ f \) fonksiyonunun görüntü kümesi her zaman \( g \) fonksiyonunun görüntü kümesine eşittir ya da onun bir alt kümesidir.
Yukarıda tanım kümesini bulduğumuz bileşke fonksiyonun görüntü kümesini bulalım.
\( f \circ g \) bileşke fonksiyonunu ve tanım kümesini aşağıdaki şekilde bulmuştuk.
\( (f \circ g)(x) = 3x^2 - 2 \)
Tanım kümesi: \( 1 \le x \le 2 \)
Bu fonksiyon tepe noktası \( y \) ekseni üzerinde olan bir paraboldür ve başkatsayısı pozitif olduğu için kolları yukarı yönlüdür.
Tepe noktası \( T(0, k) \) noktasında ve tanım aralığının dışında olduğu için fonksiyonun görüntü kümesi \( f(1) \) ve \( f(2) \) değer aralığı olur.
\( (f \circ g)(1) = 3(1)^2 - 2 = 1 \)
\( (f \circ g)(2) = 3(2)^2 - 2 = 10 \)
Buna göre bileşke fonksiyonun görüntü kümelesi aşağıdaki gibi olur.
Görüntü kümesi: \( 1\le (f \circ g)(x) \le 10 \)
Bileşke Fonksiyonun Grafiği
Bir bileşke fonksiyonun grafiği de bileşke fonksiyon tanımına uygun şekilde bileşeni olan fonksiyonların görüntülerinin bileşkesini verir.
\( f(x) = x - 3 \)
\( g(x) = 2x^2 + 4x \)
fonksiyonlarının grafikleri aşağıdaki gibidir.
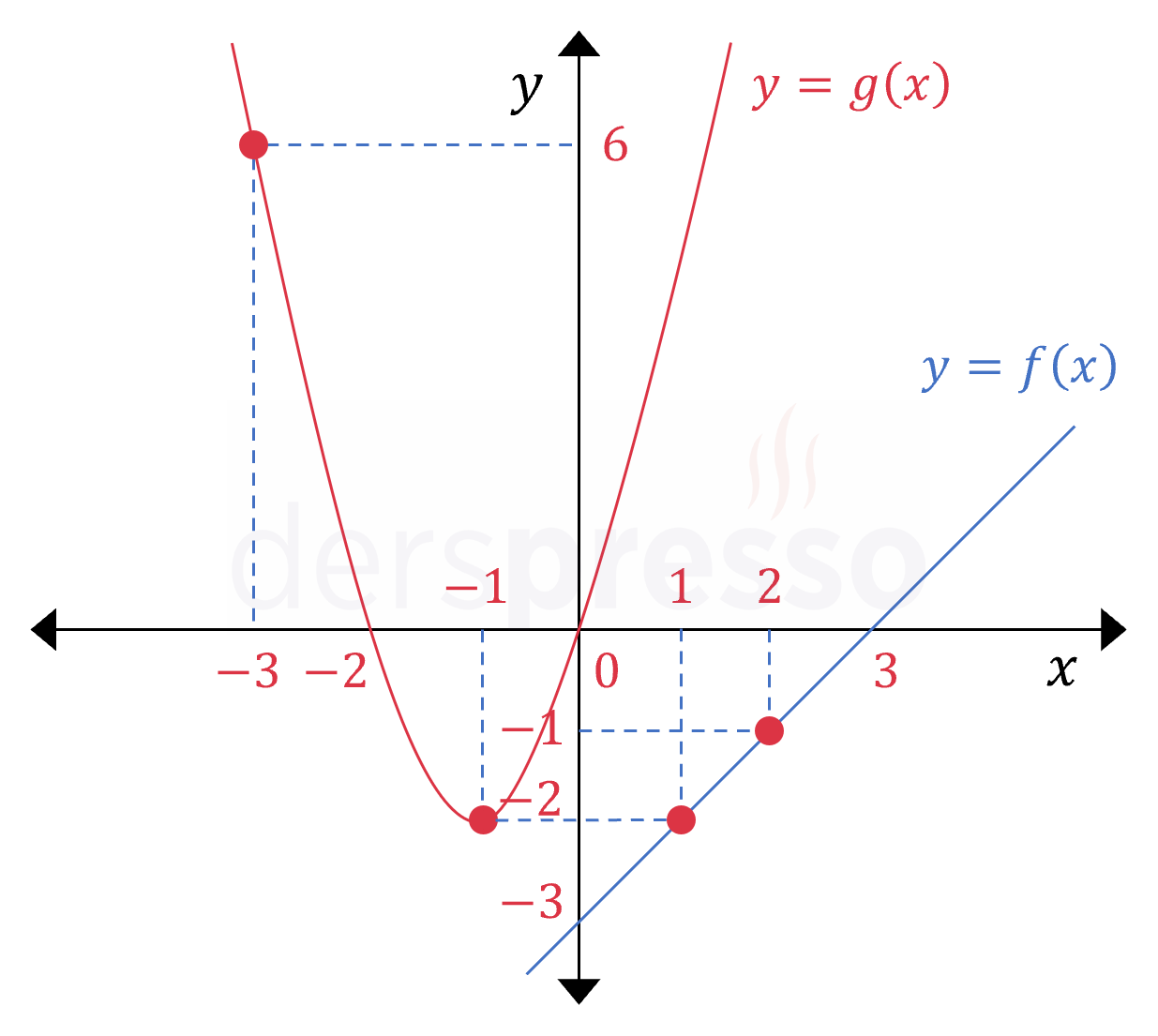
Bu iki fonksiyonun bileşkesi olan \( g \circ f \) fonksiyonunun grafiği de aşağıdaki gibidir.
\( (g \circ f)(x) = g(f(x)) \)
\( = 2x^2 - 8x + 6 \)
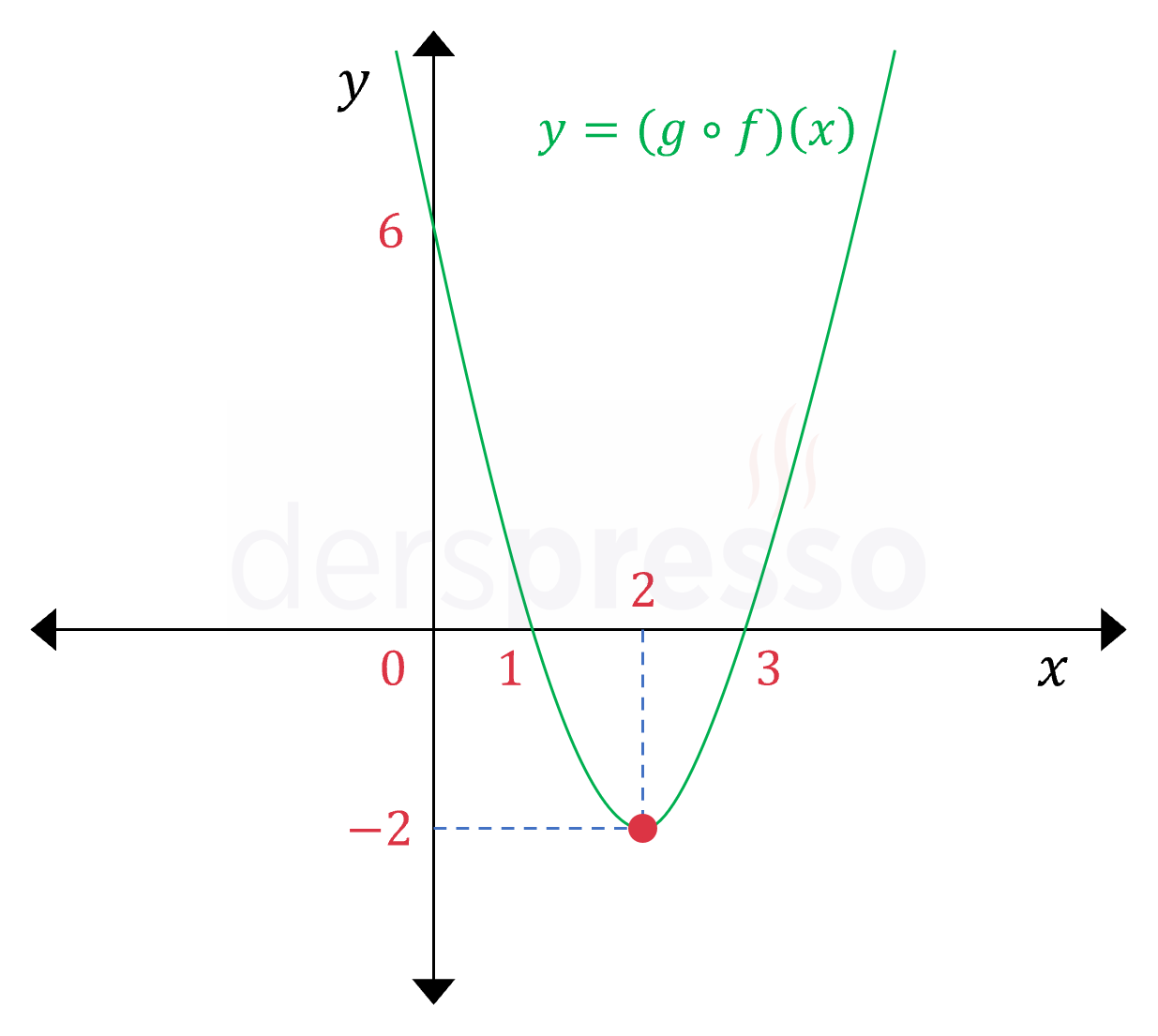
Bu grafikler üzerinde işaretli 4 nokta aşağıdaki tabloda verilmiştir. 2. ve 3. sütunlarda fonksiyonları ayrı ayrı kullanarak iki adımda elde edebildiğimiz görüntü değerlerini 4. sütunda bileşke fonksiyon grafiği ile tek adımda elde edebildiğimizi görebiliriz.
| \( x \) | \( f(x) \) | \( g(f(x)) \) | \( (g \circ f)(x) \) |
|---|---|---|---|
| \( 0 \) | \( f(0) = -3 \) | \( g(f(0)) = g(-3) = 6 \) | \( (g \circ f)(0) = 6 \) |
| \( 1 \) | \( f(1) = -2 \) | \( g(f(1)) = g(-2) = 0 \) | \( (g \circ f)(1) = 0 \) |
| \( 2 \) | \( f(2) = -1 \) | \( g(f(2)) = g(-1) = -2 \) | \( (g \circ f)(2) = -2 \) |
| \( 3 \) | \( f(3) = 0 \) | \( g(f(3)) = g(0) = 0 \) | \( (g \circ f)(3) = 0 \) |
Üç Fonksiyonun Bileşkesi
Üç fonksiyon arasında bileşke işlemi aşağıdaki şekilde tanımlanabilir.
\( (h \circ g \circ f)(x) = h(g(f(x))) \)
\( f = \{ (a, 3), (b, 1), (c, 2), (d, 4) \} \)
\( g = \{ (1, x), (2, z), (3, x), (4, w) \} \)
\( h = \{ (x, m), (y, m), (z, k), (w, n) \} \)
\( h \circ g \circ f = \{ (a, m), (b, m), (c, k), (d, n) \} \)
İki fonksiyonlu durumda olduğu gibi, bileşke fonksiyonlarda fonksiyonların yazılış sırası işlem sırasının tersidir. Dolayısıyla \( h \circ g \circ f \) şeklindeki bir bileşke fonksiyonda işlem sırası \( f \to g \to h \) şeklinde olur.
Fonksiyon - makine benzetmesini üç fonksiyonun bileşke fonksiyonuna aşağıdaki şekilde uyarlayabiliriz.
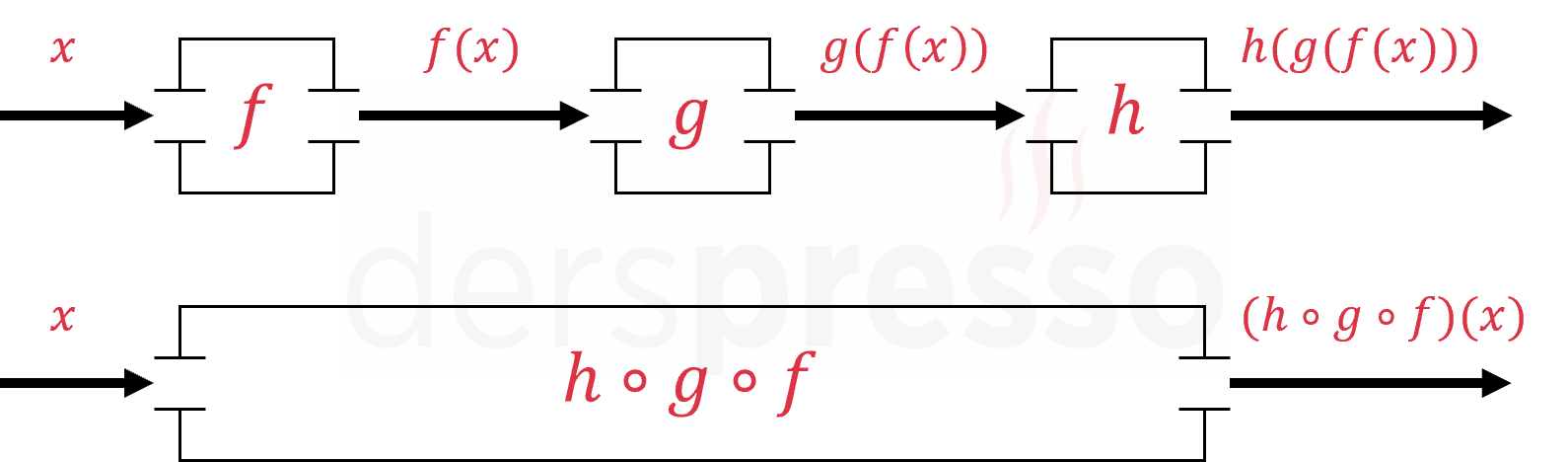
\( f(x) = x + 2 \)
\( g(x) = 3x + 1 \)
\( h(x) = x^2 - 1 \) olduğuna göre,
\( (f \circ g \circ h)(x) = 12 \) eşitliğini sağlayan \( x \) doğal sayısı kaçtır?
Çözümü Göster\( (f \circ g \circ h)(x) = f(g(h(x))) = 12 \)
Dıştan içe doğru fonksiyon değerlerini bulalım.
\( f \) fonksiyonunu 12 yapan \( x \) değerini bulalım.
\( f(x) = x + 2 = 12 \Longrightarrow x = 10 \)
Buna göre \( g(h(x)) = 10 \) olur.
\( g \) fonksiyonunu 10 yapan \( x \) değerini bulalım.
\( g(x) = 3x + 1 = 10 \Longrightarrow x = 3 \)
Buna göre \( h(x) = 3 \) olur.
\( h \) fonksiyonunu 3 yapan doğal sayı \( x \) değerini bulalım.
\( h(x) = x^2 - 1 = 3 \Longrightarrow x = \pm 2 \)
\( x \)'in bir doğal sayı olduğu belirtildiği için cevap 2 olur.
\( f(x) \) pozitif eğimli doğrusal bir fonksiyondur.
\( (f \circ f \circ f \circ f)(x) = 16x + 75 \) olduğuna göre, \( f(1) \) kaçtır?
Çözümü Göster\( f(x) \) eğimi pozitif olan doğrusal bir fonksiyon olduğuna göre \( x \)'in katsayısı pozitiftir.
\( m \gt 0 \) olmak üzere,
\( f(x) = mx + b \) diyelim.
\( (f \circ f)(x) \) bileşke fonksiyonunu bulalım.
\( (f \circ f)(x) = f(f(x)) \)
\( = m(mx + b) + b \)
\( = m^2x + mb + b \)
\( (f \circ f \circ f)(x) \) bileşke fonksiyonunu bulalım.
\( (f \circ f \circ f)(x) = (f \circ f)(f(x)) \)
\( = m^2(mx + b) + mb + b \)
\( = m^3x + m^2b + mb + b \)
\( (f \circ f \circ f \circ f)(x) \) bileşke fonksiyonunu bulalım.
\( (f \circ f \circ f \circ f)(x) = (f \circ f \circ f)(f(x)) \)
\( = m^3(mx + b) + m^2b + mb + b \)
\( = m^4x + m^3b + m^2b + mb + b \)
Bu ifade ile soruda verilen ifadeyi birbirine eşitleyelim.
\( m^4x + m^3b + m^2b + mb + b = 16x + 75 \)
Bu eşitlikte \( x \)'li terimlerin katsayıları ve sabit terimler birbirine eşittir.
\( 16 = m^4 \)
\( m = 2 \) ya da \( m = -2 \)
\( m \) pozitif olduğundan \( m = 2 \) olur.
\( m \) değerini yerine yazalım ve sabit terimlerin eşitliğinden \( b \) değerini bulalım.
\( m^3b + m^2b + mb + b = 75 \)
\( 8b + 4b + 2b + b = 75 \)
\( 15b = 75 \)
\( b = 5 \)
Buna göre \( f(x) \) fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = mx + b = 2x + 5 \)
\( f(1) = 2(1) + 5 = 7 \) bulunur.
\( f(x) = 2x^2 \)
\( g(x) = 4^x \)
olduğuna göre, \( (f \circ f \circ f \circ g \circ g)(-1) \) ifadesinin eşiti nedir?
Çözümü GösterSorudaki ifadeyi aşağıdaki şekilde yazabiliriz.
\( (f \circ f \circ f \circ g \circ g)(-1) = f(f(f(g(g(-1))))) \)
Önce \( g(-1) \) değerini bulalım.
\( g(-1) = 4^{-1} = \dfrac{1}{4} \)
\( g(g(-1)) \) değerini bulalım.
\( g(g(-1)) = 4^{\frac{1}{4}} \)
\( = 2^{\frac{1}{2}} = \sqrt{2} \)
\( f(g(g(-1))) \) değerini bulalım.
\( f(g(g(-1))) = 2(\sqrt{2})^2 = 4 \)
\( f(f(g(g(-1)))) \) değerini bulalım.
\( f(f(g(g(-1)))) = 2(4)^2 = 32 \)
\( f(f(f(g(g(-1))))) \) değerini bulalım.
\( f(f(f(g(g(-1))))) = 2(32)^2 = 2048 \) bulunur.
Parçalı Fonksiyonların Bileşkesi
\( m \) aralıktan oluşan bir parçalı fonksiyonla \( n \) aralıktan oluşan bir parçalı fonksiyonun bileşkesi \( m \cdot n \)'ye kadar aralıktan oluşabilir. Parçalı fonksiyonların bileşkesini bulurken bu aralıkların her birinin geçerli birer aralık olup olmadığı kontrol edilmelidir.
Parçalı fonksiyonun belirli bir aralığının geçerliliğini yukarıda bileşke fonksiyonların tanım kümesini bulma bölümünde kullandığımız iki koşul ile kontrol edebiliriz.
Bir örnek üzerinden parçalı fonksiyonların bileşke fonksiyonunu nasıl bulabileceğimizi gösterelim.
\( f(x) = \begin{cases} x + 4 & -3 \le x \lt -1 \\ -x + 3 & -1 \le x \le 5 \end{cases} \)
\( g(x) = \begin{cases} -2x + 1 & -2 \le x \lt 0 \\ x - 1 & 0 \le x \le 3 \end{cases} \)
\( (g \circ f)(x) \) bileşke fonksiyonunu bulalım.
\( (g \circ f)(x) = g(f(x)) \)
\( g(x) \) fonksiyon tanımında \( x \) gördüğümüz yerlere \( f(x) \) yazalım.
\( g(f(x)) = \begin{cases} -2f(x) + 1 & -2 \le f(x) \lt 0 \\ f(x) - 1 & 0 \le f(x) \le 3 \end{cases} \)
\( f(x) \) de parçalı bir fonksiyon olduğu için \( g(f(x)) \) tanımındaki her aralık birden fazla \( f(x) \) aralığına karşılık gelebilir. Bu yüzden bu iki aralığın her birini iki \( f(x) \) aralığına bölelim, her aralık için bileşke fonksiyonu bulalım ve aralığın geçerli bir tanım aralığına sahip olup olmadığını kontrol edelim.
Kontrol edeceğimiz her aralıktaki \( x \) değerleri o aralıktaki \( f \) fonksiyonunun tanım kümesinin, \( f(x) \) değerleri de o aralıktaki \( g \) fonksiyonunun tanım kümesinin elemanı olmalıdır.
| \( f(x) \) | \( g(f(x)) \) | \( x \) Tanım Aralığı | \( f(x) \) Tanım Aralığı | Kesişim Kümesi |
|---|---|---|---|---|
|
\( x + 4 \) |
\( -2f(x) + 1 \) \( = -2(x + 4) + 1 \) \( = -2x - 7 \) |
\( \textcolor{red}{-3 \le x \lt -1} \) |
\( -2 \le f(x) \lt 0 \) \( -2 \le x + 4 \lt 0 \) \( \textcolor{red}{-6 \le x \lt -4} \) |
\( \textcolor{red}{\emptyset} \) |
|
\( x + 4 \) |
\( f(x) - 1 \) \( = (x + 4) - 1 \) \( = x + 3 \) |
\( \textcolor{red}{-3 \le x \lt -1} \) |
\( 0 \le f(x) \le 3 \) \( 0 \le x + 4 \le 3 \) \( \textcolor{red}{-4 \le x \le -1} \) |
\( \textcolor{red}{-3 \le x \lt -1} \) |
|
\( -x + 3 \) |
\( -2f(x) + 1 \) \( = -2(-x + 3) + 1 \) \( = 2x - 5 \) |
\( \textcolor{red}{-1 \le x \le 5} \) |
\( -2 \le f(x) \lt 0 \) \( -2 \le -x + 3 \lt 0 \) \( \textcolor{red}{3 \lt x \le 5} \) |
\( \textcolor{red}{3 \lt x \le 5} \) |
|
\( -x + 3 \) |
\( f(x) - 1 \) \( = (-x + 3) - 1 \) \( = -x + 2 \) |
\( \textcolor{red}{-1 \le x \le 5} \) |
\( 0 \le f(x) \le 3 \) \( 0 \le -x + 3 \le 3 \) \( \textcolor{red}{0 \le x \le 3} \) |
\( \textcolor{red}{0 \le x \le 3} \) |
Buna göre kontrol ettiğimiz dört aralıktan üçü geçerli birer aralıktır. Bu üç aralıktaki tanımlardan oluşan bileşke fonksiyonu aşağıdaki gibi olur.
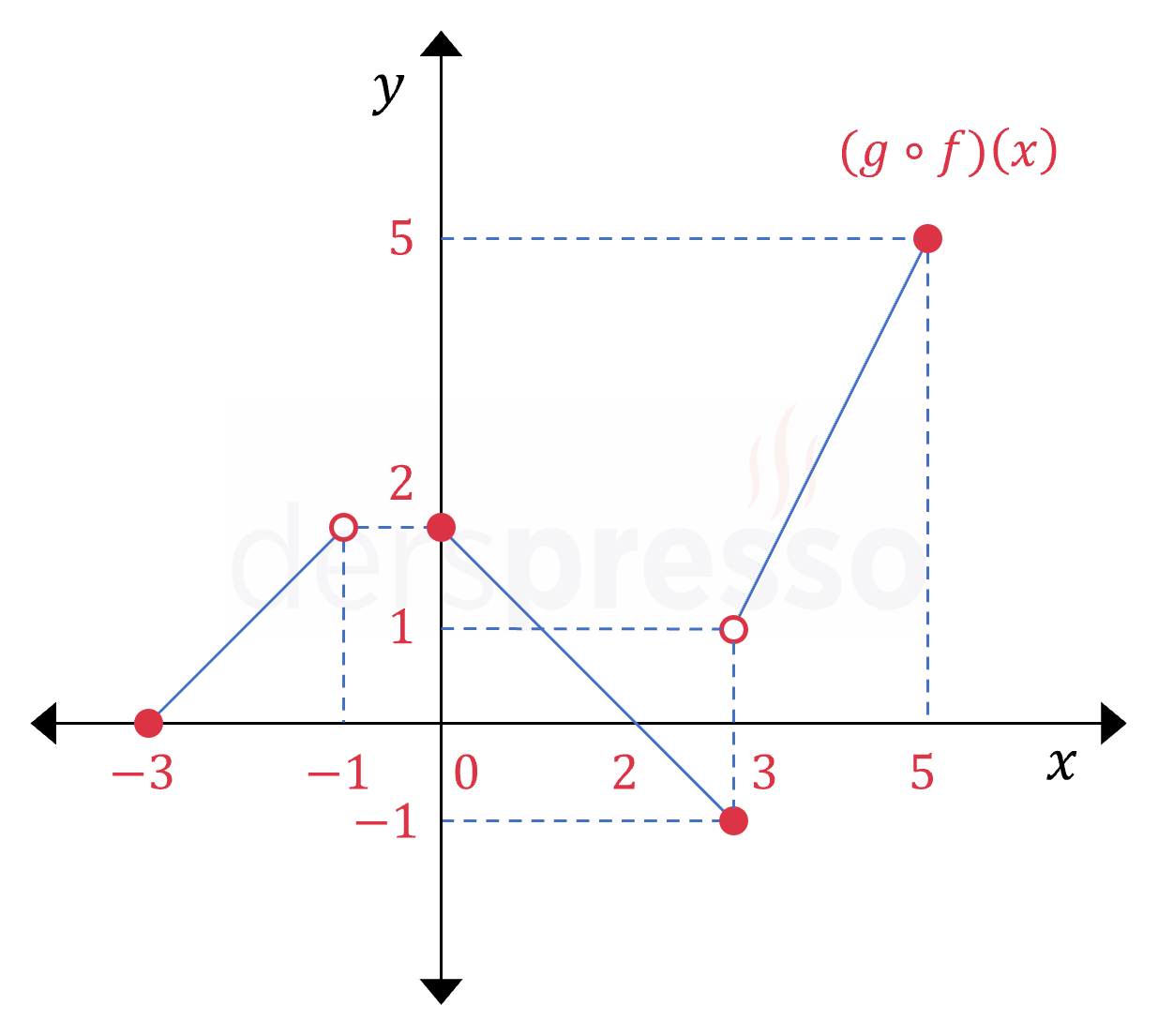
\( g(f(x)) = \begin{cases} x + 3 & -3 \le x \lt -1 \\ -x + 2 & 0 \le x \le 3 \\ 2x - 5 & 3 \lt x \le 5 \end{cases} \)
Dikkat edilirse bileşke fonksiyonun \( -1 \le x \lt 0 \) aralığında bir tanımı bulunmamaktadır.
Bulduğumuz bileşke fonksiyonun grafiği aşağıdaki gibidir.
Bileşke Fonksiyon İşlem Özellikleri
Bazı durumlarda aynı sonucu verebilse de, genel kural olarak bileşke işleminin değişme özelliği yoktur. Makine benzetmesini kullanırsak çamaşırları önce yıkayıp sonra kurutmak ile önce kurutup sonra yıkamak farklı sonuçlar verecektir.
\( g \circ f \ne f \circ g \)
\( f(x) = x^2 - 3x \)
\( g(x) = 2x + 1 \) fonksiyonları veriliyor.
\( (f \circ g)(x) \ne (g \circ f)(x) \) olduğunu gösterelim.
\( (f \circ g)(x) = f(g(x)) = f(2x + 1) \)
\( = (2x + 1)^2 - 3(2x + 1) \)
\( = 4x^2 - 2x - 2 \)
\( (g \circ f)(x) = g(f(x)) = g(x^2 - 3x) \)
\( = 2(x^2 - 3x) + 1 \)
\( = 2x^2 - 6x + 1 \)
Bulduğumuz iki bileşke fonksiyon birbirine eşit değildir.
\( (f \circ g)(x) \ne (g \circ f)(x) \)
Bileşke fonksiyon işleminin birleşme özelliği vardır. Buna göre bir bileşke işleminin yazılışında fonksiyonların sırasını değiştirmeden parantezlerin yerini değiştirerek işlemler herhangi bir sırada gerçekleştirilebilir.
\( (h \circ g) \circ f = h \circ (g \circ f) = h \circ g \circ f \)
\( f(x) = 3x + 1 \)
\( g(x) = 2\sqrt{x + 2} \)
\( h(x) = x^2 - 2 \)
\( ((f \circ g) \circ h)(x) = (f \circ (g \circ h))(x) \) olduğunu gösterelim.
İhtiyacımız olacak ikili bileşke fonksiyonları bulalım.
\( (f \circ g)(x) = f(g(x)) = f(2\sqrt{x + 2}) \)
\( = 3(2\sqrt{x + 2}) + 1 = 6\sqrt{x + 2} + 1 \)
\( (g \circ h)(x) = g(h(x)) = g(x^2 - 2) \)
\( = 2\sqrt{x^2 - 2 + 2} = 2x \)
Bu iki bileşke fonksiyonu eşitliğini göstereceğimiz ifadelerde yerlerine koyalım.
\( ((f \circ g) \circ h)(x) = (f \circ g)(h(x)) \)
\( = (f \circ g)(x^2 - 2) = 6\sqrt{x^2 - 2 + 2} + 1 \)
\( = 6x + 1 \)
\( (f \circ (g \circ h))(x) = f((g \circ h)(x)) \)
\( = f(2x) = 3(2x) + 1 \)
\( = 6x + 1 \)
Her iki durumda da \( 6x + 1 \) ifadesini elde etmiş olduk.
İSPATI GÖSTER
\( ((h \circ g) \circ f)(x) = (h \circ (g \circ f))(x) \) eşitliğini gösterelim.
\( (g \circ f)(x) = g(f(x)) \) tanımını aşağıdaki adımlarda kullanalım.
\( ((h \circ g) \circ f)(x) \) ifadesi \( h \circ g \) ve \( f \) fonksiyonları arasında bileşke işlemidir.
\( ((h \circ g) \circ f)(x) \) \( = (h \circ g)(f(x)) \)
Bu işlem \( h \) ve \( g \) fonksiyonları arasında bileşke işlemidir.
\( = h(g(f(x))) \)
\( g(f(x)) \) ifadesi \( g \) ve \( f \) fonksiyonları arasında bileşke işlemidir.
\( = h((g \circ f)(x)) \)
\( h((g \circ f)(x)) \) ifadesi \( h \) ve \( g \circ f \) fonksiyonları arasında bileşke işlemidir.
\( = (h \circ (g \circ f))(x) \)
Birleşme özelliğini makine benzetmesine uyarlarsak üç makine sıraları aynı kalmak koşuluyla herhangi bir şekilde ikili ya da üçlü birleştirilebilir.

Bileşke işleminin etkisiz elemanı \( f(x) = x \) birim fonksiyonudur ve \( I \) ile gösterilir. Yukarıda kullandığımız çamaşır/kurutma makinesi benzetmesine çamaşırlara hiçbir işlem uygulamayan ve çamaşırların girdiği şekliyle çıktığı bir makine daha eklediğimizi varsayalım (\( h(x) = I = x \)). Çamaşırları böyle bir makineye çamaşır ya da kurutma makinesinden önce ya da sonra atmamızın işlem sonucuna bir etkisi olmayacaktır.
\( f \circ I = I \circ f = f \)
\( f \circ g \circ I = f \circ I \circ g \) \( = I \circ f \circ g \) \( = f \circ g \)
İSPATI GÖSTER
\( g(x) = I = x \)
\( (g \circ f)(x) = g(f(x)) \)
\( g(x) = x \) fonksiyonunda \( x \) yerine \( f(x) \) koyarsak \( f(x) \) elde ederiz.
\( = f(x) \)
\( (f \circ g)(x) = f(g(x)) \)
\( f(x) \) fonksiyonunda \( x \) yerine \( g(x) = x \) koyarsak yine \( f(x) \) elde ederiz.
\( = f(x) \)
Her iki bileşke işleminde de sonuç olarak \( f(x) \) elde ederiz.
Bileşke Fonksiyonların Örten ve Birebir Olma Durumları
Aşağıda \( f: A \to B \) ve \( g: B \to C \) fonksiyonları ve bileşkelerinin birebir ve örten olma durumları arasındaki ilişkileri inceleyeceğiz.
\( f \) ve \( g \) fonksiyonları birebir ise \( g \circ f \) bileşke fonksiyonu da birebirdir.
Birebir fonksiyon tanımı kullanılarak bir \( f \) fonksiyonunun birebir olduğu aşağıdaki şekilde gösterilir.
- Tanım kümesinin elemanı olan herhangi iki \( x_1, x_2 \) elemanı seçilir.
- \( f(x_1) = f(x_2) \) olduğu varsayılır.
- \( x_1 = x_2 \) olduğu gösterilmeye çalışılır.
\( f: A \to B \) ve \( g: B \to C \) fonksiyonları verilmiş olsun.
\( f \) ve \( g \) fonksiyonlarının birebir olduğunu varsayalım.
\( g \circ f \) fonksiyonunun birebir olduğunu göstermeye çalışalım.
\( g \circ f \) fonksiyonunun tanım kümesinin elemanı olan herhangi iki eleman seçelim.
\( x_1, x_2 \in A \)
\( (g \circ f)(x_1) = (g \circ f)(x_2) \) olduğunu varsayalım.
Bu eşitliği aşağıdaki şekilde de ifade edebiliriz.
\( g(f(x_1)) = g(f(x_2)) \)
\( g \) fonksiyonu birebir olduğu için görüntüsü aynı olan iki elaman aynı eleman olmak zorundadır, dolayısıyla parantez içleri eşit olur.
\( f(x_1) = f(x_2) \)
Benzer şekilde \( f \) fonksiyonu da birebir olduğu için görüntüsü aynı olan iki elaman aynı eleman olmak zorundadır, dolayısıyla parantez içleri eşit olur.
\( x_1 = x_2 \)
Buna göre \( g \circ f \) fonksiyonu birebirdir.
\( f \) ve \( g \) fonksiyonları örten ise \( g \circ f \) bileşke fonksiyonu da örtendir.
\( f: A \to B \) ve \( g: B \to C \) fonksiyonları verilmiş olsun.
\( f \) ve \( g \) fonksiyonlarının örten olduğunu varsayalım.
\( g \circ f \) fonksiyonunun örten olduğunu göstermeye çalışalım.
\( g \) fonksiyonunun değer kümesinin elemanı olan herhangi bir eleman seçelim.
\( c \in C \)
\( g \) fonksiyonu örten olduğu için, görüntüsü \( c \) olan bir \( b \in B \) elemanı mutlaka vardır.
\( g(b) = c \)
\( f \) fonksiyonu örten olduğu için, görüntüsü \( b \) olan bir \( a \in A \) elemanı mutlaka vardır.
\( f(a) = b \)
Bu ikinci eşitlikteki \( b \) değerini birinci eşitlikte yerine koyalım.
\( g(f(a)) = c \)
\( (g \circ f)(a)) = c \)
Bu eşitlik, seçilecek her \( c \in C \) elemanı için \( g \circ f \) bileşke fonksiyonundaki görüntüsü \( c \) olan bir \( a \in A \) elemanının bulunduğunu gösterir.
Buna göre \( g \circ f \) fonksiyonu örtendir.
\( g \circ f \) bileşke fonksiyonu birebir ise \( f \) fonksiyonu da birebirdir.
Birebir fonksiyon tanımı kullanılarak bir \( f \) fonksiyonunun birebir olduğu aşağıdaki şekilde gösterilir.
- Tanım kümesinin elemanı olan herhangi iki \( x_1, x_2 \) elemanı seçilir.
- \( f(x_1) = f(x_2) \) olduğu varsayılır.
- \( x_1 = x_2 \) olduğu gösterilmeye çalışılır.
\( f: A \to B \) ve \( g: B \to C \) fonksiyonları verilmiş olsun.
\( g \circ f \) fonksiyonunun birebir olduğunu varsayalım.
\( f \) fonksiyonunun birebir olduğunu göstermeye çalışalım.
\( f \) fonksiyonunun tanım kümesinin elemanı olan herhangi iki eleman seçelim.
\( x_1, x_2 \in A \)
\( f(x_1) = f(x_2) \) olduğunu varsayalım.
Eşitliğin iki tarafının \( g \) fonksiyonu ile bileşkesini alalım.
\( g(f(x_1)) = g(f(x_2)) \)
Bu eşitliği aşağıdaki şekilde de ifade edebiliriz.
\( (g \circ f)(x_1) = (g \circ f)(x_2) \)
\( g \circ f \) fonksiyonu birebir olduğu için görüntüsü aynı olan iki eleman aynı eleman olmak zorundadır, dolayısıyla parantez içleri eşit olur.
\( x_1 = x_2 \)
Buna göre \( f \) fonksiyonu birebirdir.
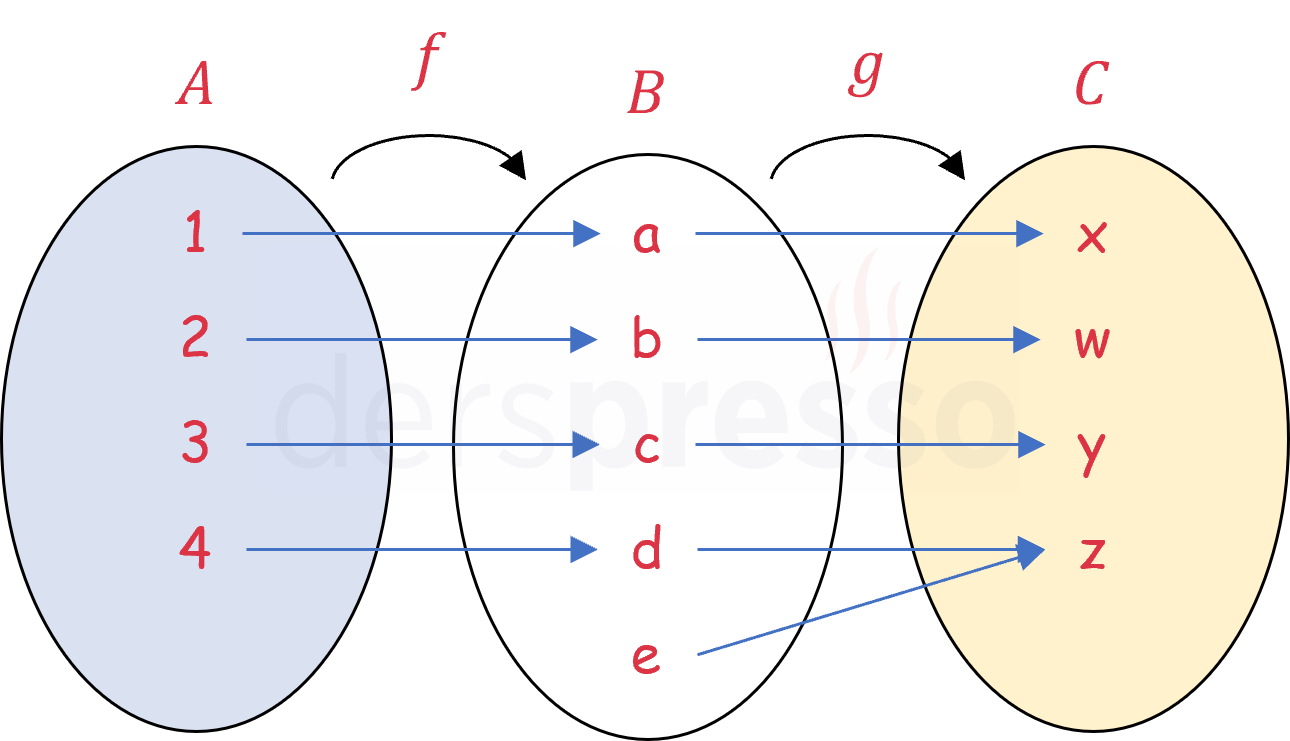
\( g \circ f \) bileşke fonksiyonu birebir ise \( g \) fonksiyonu birebir olabilir ya da olmayabilir. Aşağıda \( g \circ f \) birebir iken \( g \)'nin birebir olmadığı duruma bir örnek verilmiştir.
\( g \circ f \) bileşke fonksiyonu örten ise \( g \) fonksiyonu da örtendir.
Örten fonksiyon tanımı kullanılarak bir \( f \) fonksiyonunun örten olduğu aşağıdaki şekilde gösterilir.
- Değer kümesinin elemanı olan herhangi bir \( b \) elemanı seçilir.
- \( f(a) = b \) fonksiyon tanımı kullanılarak \( b \) değerini üreten \( a \) değeri \( b \) cinsinden yazılır.
- Birinci olarak \( a \)'nın tanım kümesinin bir elemanı olduğu gösterilir (\( a \in A \)).
- İkinci olarak \( a \)'nın \( f \) fonksiyonuna göre görüntüsünün \( b \) olduğu gösterilir (\( f(a) = b \)).
\( f: A \to B \) ve \( g: B \to C \) fonksiyonları verilmiş olsun.
\( g \circ f \) fonksiyonunun örten olduğunu varsayalım.
\( g \) fonksiyonunun örten olduğunu göstermeye çalışalım.
\( g \) fonksiyonunun değer kümesinin elemanı olan herhangi bir eleman seçelim.
\( c \in C \)
\( g \circ f \) fonksiyonu örten olduğu için, görüntüsü \( c \) olan bir \( a \in A \) elemanı mutlaka vardır.
\( (g \circ f)(a) = c \)
Bu eşitliği aşağıdaki şekilde de ifade edebiliriz.
\( g(f(a)) = c \)
Bu eşitlik, seçilecek her \( c \in C \) elemanı için \( g \) fonksiyonundaki görüntüsü \( c \) olan bir \( f(a) \in B \) elemanının bulunduğunu gösterir.
Buna göre \( g \) fonksiyonu örtendir.
\( g \circ f \) bileşke fonksiyonu örten ise \( f \) fonksiyonu örten olabilir ya da olmayabilir. Yukarıdaki şekil \( g \circ f \) örten iken \( f \) fonksiyonunun örten olmadığı duruma da bir örnektir.
\( f: \{ (1, a), (2, b), (3, c), (4, d) \} \)
\( g: \{ (a, 3), (b, 5), (c, 7), (d, 9) \} \) olduğuna göre,
\( (g \circ f)(4) + (g \circ f \circ g)(a) \) kaçtır?
Çözümü GösterSorudaki ifadeyi aşağıdaki şekilde yazabiliriz.
\( g(f(4)) + g(f(g(a))) \)
Birinci terimin sonucunu bulalım.
\( f(4) = d \)
\( g(f(4)) = g(d) = 9 \)
İkinci terimin sonucunu bulalım.
\( g(a) = 3 \)
\( f(g(a)) = f(3) = c \)
\( g(f(g(a))) = g(c) = 7 \)
İşlemin sonucunu bulalım.
\( 9 + 7 = 16 \) bulunur.
\( f(-4) = 7, \quad g(-4) = -6 \)
\( f(3) = 1, \quad g(3) = 7 \)
\( f(7) = -2, \quad g(7) = 3 \)
olduğuna göre, \( (f \circ g)(3) + (g \circ f)(-4) \) sonucu kaçtır?
Çözümü Göster\( (f \circ g)(3) + (g \circ f)(-4) = f(g(3)) + g(f(-4)) \)
\( = f(7) + g(7) \)
\( = -2 + 3 = 1 \) bulunur.
\( f(x) = 3x + 1 \) ve \( g(x) = x^2 - 3 \) olduğuna göre, \( (f \circ g)(3) \) kaçtır?
Çözümü Göster\( (f \circ g)(x) = f(g(x)) \)
\( (f \circ g)(3) = f(g(3)) \)
\( g(3) \) değerini bulalım.
\( g(3) = 3^2 - 3 = 6 \)
\( (f \circ g)(3) = f(g(3)) = f(6) \)
\( = 3 \cdot 6 + 1 = 19 \) bulunur.
\( f(x) = \dfrac{7x + 6}{4x - 3} \)
\( g(x) = 13(2x + 1) \) olduğuna göre,
\( \sqrt{g(f(f(2)))} \) ifadesinin değeri kaçtır?
Çözümü GösterÖnce \( f(2) \) değerini bulalım.
\( f(2) = \dfrac{7(2) + 6}{4(2) - 3} \)
\( = \dfrac{20}{5} = 4 \)
\( f(f(2))) \) değerini bulalım.
\( f(f(2))) = f(4) \)
\( = \dfrac{7(4) + 6}{4(4) - 3} = \dfrac{34}{13} \)
\( g(f(f(2))) \) değerini bulalım.
\( g(\dfrac{34}{13}) = 13(2(\dfrac{34}{13}) + 1) \)
\( = 68 + 13 = 81 \)
Sorudaki ifadenin değerini bulalım.
\( \sqrt{g(f(f(2)))} = \sqrt{81} = 9 \) bulunur.
\( f(x) = 4x + 5 \) ve \( (f \circ g)(2) = 17 \) olduğuna göre, \( g(2) \) kaçtır?
Çözümü Göster\( (f \circ g)(2) = f(g(2)) = 17 \)
\( f \) fonksiyonunda görüntüsü 17 olan \( x \) değerini bulalım.
\( f(x) = 4x + 5 = 17 \)
\( x = 3 \)
\( f(g(2)) = 17 = f(3) \)
\( f \) fonksiyonu doğrusal olduğu için tanım kümesindeki iki elemanın görüntüsü aynı olamaz.
Buna göre parantez içlerini eşitlersek \( g(2) = 3 \) olarak bulunur.
\( f \) bir polinom fonksiyonudur.
\( (f \circ f)(x) = 9x + 4 \) olduğuna göre,
\( f(2) \)'nin alabileceği değerler toplamı kaçtır?
Çözümü Gösterİki polinomun bileşkesinin derecesi polinomların derecelerinin çarpımına eşittir.
Buna göre sabit bir polinom fonksiyonunun kendisiyle bileşkesinin derecesi sıfır, ikinci dereceden bir polinom fonksiyonunun kendisiyle bileşkesinin derecesi 4 olur.
Verilen \( f \circ f \) fonksiyonunun derecesi 1 olduğuna göre \( f \) fonksiyonunun derecesi 1 olmalıdır.
\( f(x) = ax + b \)
\( (f \circ f)(x) = f(f(x)) = 9x + 4 \)
\( a(ax + b) + b = 9x + 4 \)
\( a^2x + ab + b = 9x + 4 \)
İki polinom birbirine eşitse aynı dereceli terimlerin katsayıları birbirine eşittir.
\( a^2 = 9 \)
\( a = 3 \) ya da \( a = -3 \)
\( ab + b = 4 \)
\( a = 3 \) için:
\( 3b + b = 4 \Longrightarrow b = 1 \)
\( a = -3 \) için:
\( -3b + b = 4 \Longrightarrow b = -2 \)
Buna göre \( (a, b) \) ikilisinin alabileceği değerler \( (3, 1) \) ve \( (-3, -2) \) olur.
Oluşan iki farklı \( f \) tanımında \( f(2) \) değerlerini bulalım.
\( f(x) = 3x + 1 \) için:
\( f(2) = 3(2) + 1 = 7 \)
\( f(x) = -3x - 2 \) için:
\( f(x) = -3(2) - 2 = -8 \)
\( f(2) \)'nin alabileceği değerler toplamı \( 7 + (-8) = -1 \) olarak bulunur.
\( f \) bir polinom fonksiyonudur.
\( (f \circ f)(x) = 9x - 8 \) olduğuna göre,
\( f \) fonksiyonunun sabit teriminin alabileceği değerler çarpımı kaçtır?
Çözümü Gösterİki polinomun bileşkesinin derecesi polinomların derecelerinin çarpımına eşittir.
Buna göre sabit bir polinom fonksiyonunun kendisiyle bileşkesinin derecesi sıfır, ikinci dereceden bir polinom fonksiyonunun kendisiyle bileşkesinin derecesi 4 olur.
Verilen \( f \circ f \) fonksiyonunun derecesi 1 olduğuna göre \( f \) fonksiyonunun derecesi 1 olmalıdır.
\( f(x) = ax + b \)
\( (f \circ f)(x) = f(f(x)) = 9x - 8 \)
\( f(ax + b) = 9x - 8 \)
\( a(ax + b) + b = 9x - 8 \)
\( a^2x + ab + b = 9x - 8 \)
İki polinom birbirine eşitse aynı dereceli terimlerin katsayıları birbirine eşittir.
\( a^2 = 9 \)
\( a = 3 \) ya da \( a = -3 \)
\( ab + b = -8 \)
\( a = 3 \) için:
\( 3b + b = -8 \)
\( b = -2 \)
\( f(x) = 3x - 2 \)
\( a = -3 \) için:
\( -3b + b = -8 \)
\( b = 4 \)
\( f(x) = -3x + 4 \)
Buna göre verilen eşitliği sağlayan iki farklı \( f \) fonksiyonu vardır.
Bu iki fonksiyonun sabit terimlerinin çarpımı \( -2 \cdot 4 = -8 \) olarak bulunur.
\( (g \circ f)(x) = 3f^2(x) - f(x) + 5 \) olduğuna göre, \( g(4) \) kaçtır?
Çözümü Göster\( (g \circ f)(x) = g(f(x)) = 3f^2(x) - f(x) + 5 \)
Bu eşitlik \( (g \circ f)(x) \) fonksiyonunu bulmak için \( g(x) \) fonksiyonunda tüm \( x \) değişkenleri yerine \( f(x) \) yazılmış fonksiyondur, dolayısıyla \( f(x) \) gördüğümüz yere \( x \) yazarak \( g(x) \) tanımını bulabiliriz.
\( g(x) = 3x^2 - x + 5 \)
\( g(4) \) değerini bulmak için \( x = 4 \) yazalım.
\( g(4) = 3(4)^2 - 4 + 5 = 49 \) bulunur.
\( f \) ve \( g \) fonksiyonları pozitif reel sayılarda tanımlıdır.
\( (f \circ g)(x) = f(x) \cdot g(x) \) ve \( f(x) = 3x - 1 \) olduğuna göre, \( g(2) \) kaçtır?
Çözümü Göster\( (f \circ g)(x) = f(x) \cdot g(x) \)
\( f(g(x)) = f(x) \cdot g(x) \)
\( f(x) \) tanımını kullanalım.
\( 3g(x) - 1 = (3x - 1)g(x) \)
\( g(2) \) değeri için \( x = 2 \) yazalım.
\( 3g(2) - 1 = (3 \cdot 2 - 1)g(2) \)
\( 3g(2) - 1 = 5g(2) \)
\( g(2) = -\dfrac{1}{2} \) bulunur.
\( f(x) = 2x - 5 \)
\( (f \circ g)(x) = 3g(x) + 2x - 2 \)
olduğuna göre, \( g(2) \) değeri kaçtır?
Çözümü Göster\( (f \circ g)(x) = f(g(x)) = 3g(x) + 2x - 2 \)
\( f \) fonksiyonunda \( x \) yerine \( g(x) \) yazalım.
\( 2g(x) - 5 = 3g(x) + 2x - 2 \)
\( g(x) = -2x - 3 \)
\( g(2) \) değerini bulmak için \( x = 2 \) yazalım.
\( g(2) = -2(2) - 3 = -7 \) bulunur.
\( (f \circ g)(x) = 5x - 6 \) ve \( f(x) = \dfrac{x + 1}{3} \) olduğuna göre, \( g(x) \) kaçtır?
Çözümü Göster\( (f \circ g)(x) = f(g(x)) = 5x - 6 \)
\( f \) fonksiyonunda \( x \) yerine \( g(x) \) yazalım.
\( \dfrac{g(x) + 1}{3} = 5x - 6 \)
\( g(x) + 1 = 15x - 18 \)
\( g(x) = 15x - 19 \) bulunur.
\( f(x) = x^3 + 6 \)
\( f(x + 4) = g(x - 2) \)
olduğuna göre, \( (f \circ g)(-7) \) kaçtır?
Çözümü Göster\( f(x) \) tanımını kullanarak \( f(x + 4) \) fonksiyonunu bulalım.
\( f(x + 4) = (x + 4)^3 + 6 = g(x - 2) \)
\( g(x) \) fonksiyonunu bulmak için \( g(x - 2) \) fonksiyonunda \( x \) yerine \( x + 2 \) yazalım.
\( g(x + 2 - 2) = (x + 2 + 4)^3 + 6 \)
\( g(x) = (x + 6)^3 + 6 \)
Sorudaki ifadenin değerini bulalım.
\( (f \circ g)(-7) = f(g(-7)) \)
\( g(-7) = (-7 + 6)^3 + 6 = 5 \)
\( (f \circ g)(-7) = f(g(-7)) = f(5) \)
\( = 5^3 + 6 = 131 \) bulunur.
\( f(x) = 2x - 1 \) ve \( g(x) = ax + b \) olarak veriliyor.
\( (f \circ g)(x) = (g \circ f)(x) \) olduğuna göre, \( g(1) \) kaçtır?
Çözümü GösterVerilen bilgileri kullanarak fonksiyonların bileşkesini alalım.
\( (f \circ g)(x) = f(g(x)) \)
\( = 2g(x) - 1 = 2(ax + b) - 1 \)
\( = 2ax + 2b - 1 \)
\( (g \circ f)(x) = g(f(x)) \)
\( = af(x) + b = a(2x - 1) + b \)
\( = 2ax - a + b \)
Soruda verilen eşitliği kullanalım.
\( 2ax + 2b - 1 = 2ax - a + b \)
\( a + b = 1 \)
\( x = 1 \) yazarak \( g(1) \) değerini bulalım.
\( g(1) = a(1) + b \)
\( = a + b = 1 \) bulunur.
\( a \in \mathbb{R}, a \ne 0 \) olmak üzere,
\( f(x) = x^2 - a \)
\( g(x) = a(x - 2) \)
\( (f \circ g)(-1) = (g \circ f)(2) \) olduğuna göre, \( a \) kaçtır?
Çözümü GösterVerilen eşitliğin sol tarafını bulalım.
\( (f \circ g)(-1) = f(g(-1)) \)
\( g(-1) = a(-1 - 2) = -3a \)
\( f(g(-1)) = f(-3a) = (-3a)^2 - a \)
\( = 9a^2 - a \)
Verilen eşitliğin sağ tarafını bulalım.
\( (g \circ f)(2) = g(f(2)) \)
\( f(2) = 2^2 - a = 4 - a \)
\( g(f(2)) = g(4 - a) = a(4 - a - 2) \)
\( = 2a - a^2 \)
İki ifadeyi birbirine eşitleyelim.
\( 9a^2 - a = 2a - a^2 \)
\( 10a^2 - 3a = 0 \)
\( a(10a - 3) = 0 \)
\( a \ne 0 \) olduğu verilmiştir.
\( a = \dfrac{3}{10} \) bulunur.
\( f(x) = x^2 + 4 \)
\( g(x) = 3x + 2 \)
\( (f \circ g)(x) = 3(g \circ f)(x) - 2 \)
eşitliğini sağlayan \( x \) değeri kaçtır?
Çözümü Göster\( (f \circ g)(x) = 3(g \circ f)(x) - 2 \)
\( f(g(x)) = 3g(f(x)) - 2 \)
\( f(3x + 2) = 3g(x^2 + 4) - 2 \)
\( (3x + 2)^2 + 4 = 3(3(x^2 + 4) + 2) - 2 \)
\( 9x^2 + 12x + 4 + 4 = 3(3x^2 + 12 + 2) - 2 \)
\( 9x^2 + 12x + 8 = 9x^2 + 40 \)
\( 12x = 32 \)
\( x = \dfrac{8}{3} \) bulunur.
\( f(x) = 2x - 2 \)
\( g(x) = 3x + 1 \) olduğuna göre,
\( (f \circ g)(a) = (\underbrace{f \circ f \circ \ldots \circ f}_\text{25 tane})(2) \) eşitliğini sağlayan \( a \) değeri nedir?
Çözümü Göster\( f(2) = 2 \cdot 2 - 2 = 2 \)
\( f(2) = 2 \) olduğu için aynı işlem 25 kez yapıldığında da sonuç 2 olur.
\( f(2) = f(f(2)) = f(f(f(2))) = \ldots = 2 \)
\( (f \circ g)(a) = f(g(a)) = 2 \)
\( f(x) \)'in değerini 2 yapan \( x \) değeri 2 olduğu için \( g(a) = 2 \) olur.
\( g(a) = 3a + 1 = 2 \)
\( a = \dfrac{1}{3} \) bulunur.
\( f(x) = 5^{x - 2} \) ve \( f(3a - 1) = f(1 - a) \) olduğuna göre \( a \) kaçtır?
Çözümü Göster\( f(3a - 1) = 5^{3a - 1 - 2} = 5^{3a - 3} \)
\( f(1 - a) = 5^{1 - a - 2} = 5^{-a - 1} \)
Bu fonksiyon değerlerini verilen eşitlikte yerine koyalım.
\( f(3a - 1) = f(1 - a) \)
\( 5^{3a - 3} = 5^{-a - 1} \)
Tabanları eşit ve -1, 0, 1'den farklı iki üslü ifadenin üsleri eşittir.
\( 3a - 3 = -a - 1 \)
\( 4a = 2 \)
\( a = \dfrac{1}{2} \) bulunur.
\( f(x) = x^2 - 10x \)
\( g(x) = e^x + 5 \) fonksiyonları veriliyor.
\( g(2x) - (f \circ g)(x) = k \)
olduğuna göre, \( k \) değeri kaçtır?
Çözümü Göster\( g(2x) \) fonksiyonunu bulalım.
\( g(2x) = e^{2x} + 5 \)
\( (f \circ g)(x) \) fonksiyonunu bulalım.
\( (f \circ g)(x) = (f(g(x)) = f(e^x + 5) \)
\( = (e^x + 5)^2 - 10(e^x + 5) \)
\( = e^{2x} + 10e^x + 25 - 10e^x - 50 \)
\( = e^{2x} - 25 \)
Bulduğumuz ifadeleri verilen eşitlikte yerine koyalım.
\( g(2x) - (f \circ g)(x) = k \)
\( (e^{2x} + 5) - (e^{2x} - 25) = k \)
\( k = 30 \) bulunur.
\( f(\dfrac{3x + 1}{2x - 3}) = \dfrac{2x - 3}{3x + 1} + 2 \) olduğuna göre, \( f(\frac{1}{14}) \) kaçtır?
Çözümü GösterParantez içindeki ifade fonksiyon tanımında çarpmaya göre ters şekilde bulunmaktadır.
\( \dfrac{3x + 1}{2x - 3} = g(x) \) diyelim.
\( f(g(x)) = \dfrac{1}{g(x)} + 2 \)
Bu eşitlik \( (f \circ g)(x) \) fonksiyonunu bulmak için \( f(x) \) fonksiyonunda tüm \( x \) değişkenleri yerine \( g(x) \) yazılmış fonksiyondur, dolayısıyla \( g(x) \) gördüğümüz yere \( x \) yazarak \( f(x) \) tanımını bulabiliriz.
\( f(x) = \dfrac{1}{x} + 2 \)
\( f(\frac{1}{14}) \) değeri için \( x = \frac{1}{14} \) yazalım.
\( f(\frac{1}{14}) = \dfrac{1}{\frac{1}{14}} + 2 \)
\( = 14 + 2 = 16 \) bulunur.
\( f(x) + f(2x + 1) = x^2 \) olduğuna göre, \( f(1) + f(15) \) kaça eşittir?
Çözümü Göster\( f(1) \) ve \( f(15) \) fonksiyonlarının bulunduğu eşitlikleri yazalım.
\( x = 1 \) verelim.
\( f(1) + f(3) = 1 \)
\( x = 7 \) verelim.
\( f(7) + f(15) = 49 \)
İki eşitliği taraf tarafa toplayalım.
\( f(1) + f(3) + f(7) + f(15) = 50 \)
\( f(3) \) ve \( f(7) \) ifadelerini eşitlikten çıkarmak için bu iki ifadenin bulunduğu bir eşitlik daha yazalım.
\( x = 3 \) verelim.
\( f(3) + f(7) = 9 \)
Toplamını bulduğumuz eşitlikten bu eşitliği çıkaralım.
\( f(1) + f(15) = 50 - 9 = 41 \) bulunur.
\( a \) ve \( b \) farklı sayılar olmak üzere,
\( f(x) = ax + b, \quad g(x) = bx + a \)
\( (f \circ g)(x) - (g \circ f)(x) = a - b \) olduğuna göre \( a + b \) kaçtır?
Çözümü Göster\( (f \circ g)(x) = a(bx + a) + b \)
\( (g \circ f)(x) = b(ax + b) + a \)
Bu değerleri verilen eşitlikte yerlerine yazalım.
\( (abx + a^2 + b) - (abx + b^2 + a) = a - b \)
\( a^2 - b^2 + 2b - 2a = 0 \)
\( (a - b)(a + b - 2) = 0 \)
\( a \) ve \( b \) farklı sayılar oldukları için \( a - b = 0 \) denklemin bir çözümü değildir.
\( a + b = 2 \) bulunur.
\( f(x + 1) = 4x - 2 \)
\( g(x + a) = 6x + 3 \)
\( (f \circ g)(3) = 54 \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( f(x) \) fonksiyonunu bulmak için \( x \) yerine \( x - 1 \) yazalım.
\( f((x - 1) + 1) = 4(x - 1) - 2 \)
\( f(x) = 4x - 6 \)
\( g(x) \) fonksiyonunu bulmak için \( x \) yerine \( x - a \) yazalım.
\( g((x - a) + a) = 6(x - a) + 3 \)
\( g(x) = 6x - 6a + 3 \)
\( f \circ g \) fonksiyonunu bulalım.
\( (f \circ g)(x) = f(g(x)) \)
\( = 4(6x - 6a + 3) - 6 \)
\( (f \circ g)(3) = 54 \)
\( 4(6 \cdot 3 - 6a + 3) - 6 = 54 \)
\( a = 1 \) bulunur.
\( \mathbb{Q} \) rasyonel sayılar kümesi olmak üzere,
\( f(x)= \begin{cases} 3x - 2 & x \in \mathbb{Q} \\ x^2 - 1 & x \notin \mathbb{Q} \end{cases} \)
Buna göre \( (f \circ f)(\frac{\sqrt{3}}{3}) \) kaçtır?
Çözümü Göster\( (f \circ f)(\frac{\sqrt{3}}{3}) = f(f(\frac{\sqrt{3}}{3})) \)
\( \frac{\sqrt{3}}{3} \) rasyonel olmadığı için parçalı fonksiyonun ikinci tanımı kullanılır.
\( f(\frac{\sqrt{3}}{3}) = (\frac{\sqrt{3}}{3})^2 - 1 \)
\( = -\dfrac{2}{3} \)
\( f(f(\frac{\sqrt{3}}{3})) = f(-\frac{2}{3}) \)
\( -\frac{2}{3} \) rasyonel olduğu için parçalı fonksiyonun ilk tanımı kullanılır.
\( f(-\frac{2}{3}) = 3(-\frac{2}{3}) - 2 \)
\( = -4 \) bulunur.
\( (f \circ g)(x) = f(x) \cdot g(x) \)
\( f(x) = 2x + 3 \)
olduğuna göre, \( g(2) \) kaçtır?
Çözümü Göster\( (f \circ g)(x) = f(x) \cdot g(x) \)
\( f(g(x)) = f(x) \cdot g(x) \)
\( 2g(x) + 3 = (2x + 3) \cdot g(x) \)
\( g(2) \) değerini bulmak için eşitlikte \( x = 2 \) yazalım.
\( 2g(2) + 3 = (2(2) + 3) \cdot g(2) \)
\( 5g(2) = 3 \)
\( g(2) = \dfrac{3}{5} \) bulunur.
\( 2f(x) - f(4 - x) = x^2 \) olduğuna göre, \( f(x) \) ifadesini bulunuz.
Çözümü GösterEşitlikte \( x \) yerine \( 4 - x \) yazalım.
\( 2f(4 - x) - f(4 - (4 - x)) = (4 - x)^2 \)
\( 2f(4 - x) - f(x) = 16 - 8x + x^2 \)
\( f(4 - x) \) ifadesini yalnız bırakalım.
\( f(4 - x) = \dfrac{f(x) + x^2 - 8x + 16}{2} \)
Bulduğumuz \( f(4 - x) \) ifadesini soruda verilen eşitlikte yerine yazalım.
\( 2f(x) - f(4 - x) = x^2 \)
\( 2f(x) - \dfrac{f(x) + x^2 - 8x + 16}{2} = x^2 \)
\( 4f(x) - f(x) - x^2 + 8x - 16 = 2x^2 \)
\( 3f(x) = 3x^2 - 8x + 16 \)
\( f(x) = x^2 - \dfrac{8x}{3} + \dfrac{16}{3} \) bulunur.
\( f(x^2 + 2x - 1) = 4x^2 + 8x + 1 \) olduğuna göre, \( f(-3) \) kaçtır?
Çözümü GösterEşitliğin iki tarafındaki ifadeleri birbirine benzetmek için eşitliğin sağ tarafını \( x^2 + 2x - 1 \) parantezine alalım.
\( f(x^2 + 2x - 1) = 4x^2 + 8x - 4 + 5 \)
\( f(x^2 + 2x - 1) = 4(x^2 + 2x - 1) + 5 \)
\( x^2 + 2x - 1 = g(x) \) diyelim.
\( f(g(x)) = 4g(x) + 5 \)
Bu eşitlik \( (f \circ g)(x) \) fonksiyonunu bulmak için \( f(x) \) fonksiyonunda tüm \( x \) değişkenleri yerine \( g(x) \) yazılmış fonksiyondur, dolayısıyla \( g(x) \) gördüğümüz yere \( x \) yazarak \( f(x) \) tanımını bulabiliriz.
\( f(x) = 4x + 5 \)
\( f(-3) \) değeri için \( x = -3 \) yazalım.
\( f(-3) = 4 \cdot (-3) + 5 = -7 \) bulunur.
\( f \) bir polinom fonksiyonudur.
\( f(x^2 + 2) = x^4 + 3x^2 + 2 \)
olduğuna göre, \( f(x^2 - 3) \) ifadesini bulunuz.
Çözümü Göster\( x^2 + 2 = u \) şeklinde değişken değiştirelim.
\( x^2 = u - 2 \)
Verilen fonksiyon ifadesinde \( x^2 = u - 2 \) yazalım.
\( f(x^2 + 2) = x^4 + 3x^2 + 2 \)
\( f(u) = (u - 2)^2 + 3(u - 2) + 2 \)
\( = u^2 - 4u + 4 + 3u - 6 + 2 \)
\( = u^2 - u \)
\( f(u) \) fonksiyonunda \( u = x^2 - 3 \) yazalım.
\( f(x^2 - 3) = (x^2 - 3)^2 - (x^2 - 3) \)
\( = x^4 - 6x^2 + 9 - x^2 + 3 \)
\( = x^4 - 7x^2 + 12 \) bulunur.
\( f(x) = \sqrt{x^2 - 9} \)
\( g(x) = \dfrac{1}{\sqrt{x}} \)
olduğuna göre, \( (f \circ g)(x) \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterBir \( x \) değerinin \( f \circ g \) bileşke fonksiyonunun tanım kümesinin elemanı olabilmesi için iki koşul sağlanmalıdır.
Koşul 1: \( x \) değeri \( g \) fonksiyonunun tanım kümesinde bulunmalıdır.
\( g \) fonksiyonu \( x \lt 0 \) olduğunda kök içi negatif olduğu için, \( x = 0 \) olduğunda payda sıfır olduğu için tanımsız olur.
Buna göre \( g \) fonksiyonunun en geniş tanım kümesi pozitif reel sayılardır.
\( x \gt 0 \)
Koşul 2: \( x \) değerinin \( g \) fonksiyonuna göre görüntüsü \( f \) fonksiyonunun tanım kümesinin elemanı olmalıdır.
\( f(x) = \sqrt{(x + 3)(x - 3)} \)
\( f \) fonksiyonu \( -3 \lt x \lt 3 \) aralığında kök içi negatif olduğu için tanımsız olur.
Buna göre \( f \) fonksiyonunun en geniş tanım kümesi bu aralık dışındaki tüm reel sayılardır.
\( x \le -3 \) ya da \( x \ge 3 \)
\( x \) değerinin \( g \) fonksiyonuna göre görüntüsü \( f \) fonksiyonunun tanım kümesinin elemanı olmalıdır.
Durum 1:
\( g(x) = \dfrac{1}{\sqrt{x}} \le -3 \)
Bir karekök ifadesi hiçbir zaman negatif olamayacağı için bu durumun reel çözümü yoktur.
\( x \in \emptyset \)
Durum 2:
\( g(x) = \dfrac{1}{\sqrt{x}} \ge 3 \)
\( 0 \lt \sqrt{x} \le \dfrac{1}{3} \)
\( 0 \lt x \le \dfrac{1}{9} \)
İki durumun birleşim kümesi ikinci koşulu sağlayan \( x \) aralığını verir.
\( 0 \lt x \le \dfrac{1}{9} \)
İki koşul için bulduğumuz aralıkların kesişim kümesi \( f \circ g \) fonksiyonunun en geniş tanım kümesini verir.
Tanım kümesi: \( x \in (0, \frac{1}{9}] \)
\( f(x) = \ln{x} \)
\( g(x) = \dfrac{2x}{x - 2} \)
olduğuna göre, \( (g \circ f)(x) \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterBir \( x \) değerinin \( g \circ f \) bileşke fonksiyonunun tanım kümesinin elemanı olabilmesi için iki koşul sağlanmalıdır.
Koşul 1: \( x \) değeri \( f \) fonksiyonunun tanım kümesinde bulunmalıdır.
\( f \) fonksiyonu \( x \le 0 \) olduğunda logaritma içi sıfır ya da negatif olduğu için tanımsız olur.
Buna göre \( f \) fonksiyonunun en geniş tanım kümesi pozitif reel sayılardır.
\( x \gt 0 \)
Koşul 2: \( x \) değerinin \( f \) fonksiyonuna göre görüntüsü \( g \) fonksiyonunun tanım kümesinin elemanı olmalıdır.
\( g \) fonksiyonu \( x = 2 \) olduğunda paydası sıfır olduğu için tanımsız olur.
Buna göre \( g \) fonksiyonunun en geniş tanım kümesi bu değer dışındaki tüm reel sayılardır.
\( x \in \mathbb{R} - \{ 2 \} \)
\( x \) değerinin \( f \) fonksiyonuna göre görüntüsü \( g \) fonksiyonunun tanım kümesinin elemanı olmalıdır.
\( f(x) = \ln{x} \ne 2 \)
\( x \ne e^2 \)
İki koşul için bulduğumuz aralıkların kesişim kümesi \( g \circ f \) fonksiyonunun en geniş tanım kümesini verir.
Tanım kümesi: \( x \in \mathbb{R^+} - \{ e^2 \} \)
\( g(x) = x + 1 \)
\( f(g(x)) = \dfrac{x^3}{3} + x^2 + x \)
olduğuna göre, \( f(x) \) fonksiyonunu bulunuz.
Çözümü Göster\( f(g(x)) = \dfrac{x^3}{3} + x^2 + x \)
\( f(x + 1) = \dfrac{x^3}{3} + x^2 + x \)
İfadeyi tek bir kesir şeklinde yazalım.
\( = \dfrac{x^3 + 3x^2 + 3x}{3} \)
İfadeye \( \frac{1}{3} \) ekleyip çıkaralım.
\( = \dfrac{x^3 + 3x^2 + 3x}{3} + \dfrac{1}{3} - \dfrac{1}{3} \)
\( = \dfrac{x^3 + 3x^2 + 3x + 1}{3} - \dfrac{1}{3} \)
\( = \dfrac{(x + 1)^3}{3} - \dfrac{1}{3} \)
\( f(x + 1) \) tanımında her \( x + 1 \) yerine \( x \) yazarak \( f(x) \) tanımını elde edebiliriz.
\( f(x + 1) = \dfrac{(x + 1)^3 - 1}{3} \)
\( f(x) = \dfrac{x^3 - 1}{3} \) bulunur.
\( f(x) = 3x + 7 \)
\( (g \circ f)(x) = 9x^2 - 27x + 88 \)
olduğuna göre, \( g(x) \) fonksiyonunu bulunuz.
Çözümü Göster\( (g \circ f)(x) = g(f(x)) \)
\( = g(3x + 7) = 9x^2 - 27x + 88 \)
\( y = 3x + 7 \) fonksiyonunun tersi \( y = \dfrac{x - 7}{3} \) fonksiyonudur.
Bu ifadeyi bileşke fonksiyonda \( x \) yerine yazalım.
\( g(3(\dfrac{x - 7}{3}) + 7) = 9(\dfrac{x - 7}{3})^2 - 27(\dfrac{x - 7}{3}) + 88 \)
\( g(x) = (x - 7)^2 - 9(x - 7) + 88 \)
\( = x^2 - 14x + 49 - 9x + 63 + 88 \)
\( = x^2 - 23x + 200 \) bulunur.
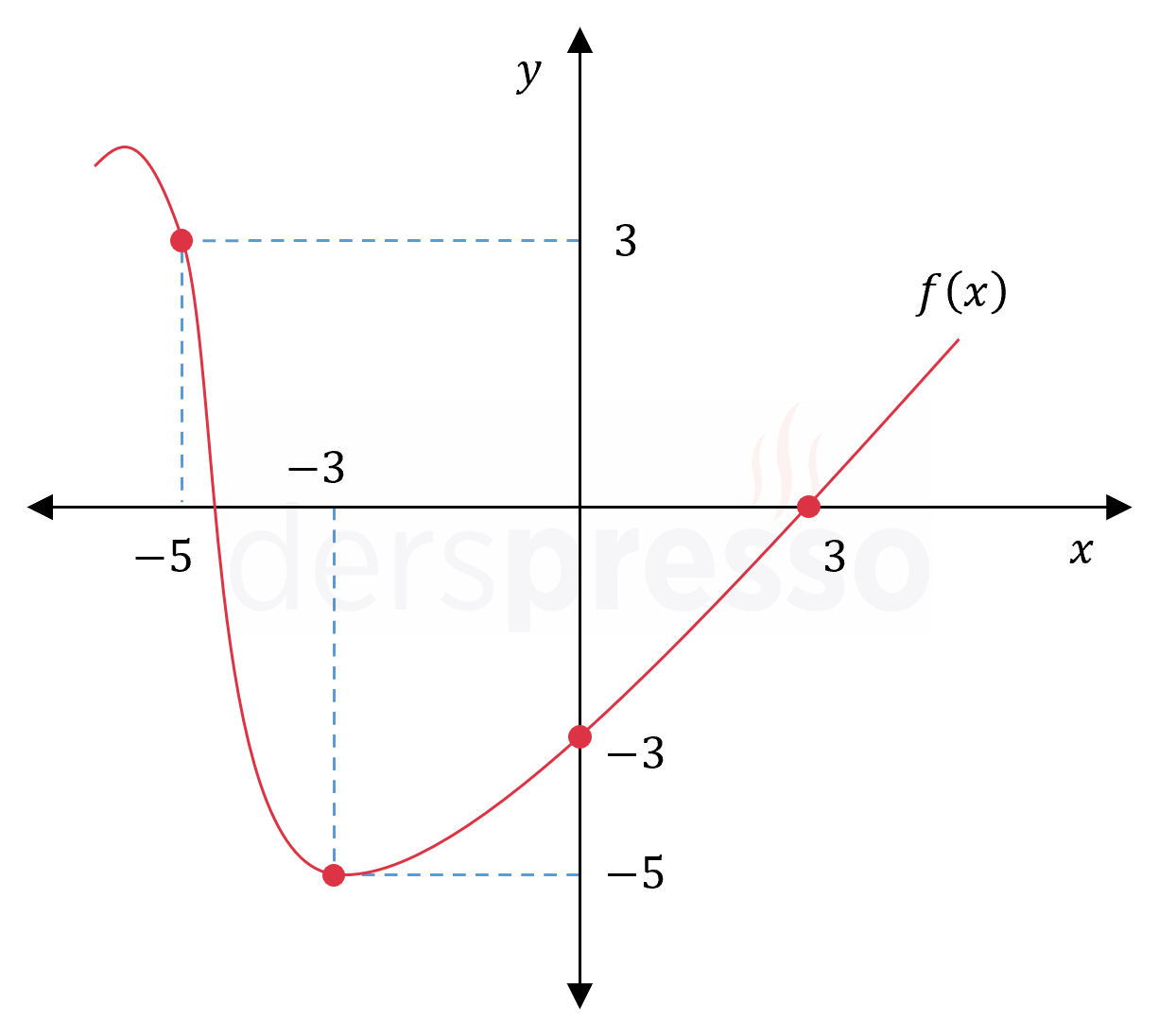
Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Buna göre, \( (\underbrace{f \circ f \circ \ldots \circ f}_\text{103 tane})(0) \) kaçtır?
Çözümü Göster\( f \) fonksiyonunun kendisiyle ilk beş bileşkesini grafiği kullanarak bulalım.
\( f(0) = -3 \)
\( f(-3) = -5 \)
\( f(-5) = 3 \)
\( f(3) = 0 \)
\( f(0) = -3 \)
Buna göre bileşke fonksiyonun değeri her dört işlemde bir kendini tekrar etmektedir.
103 sayısını 4'e böldüğümüzde kalanı bulalım.
\( 103 = 4 \cdot 25 + 3 \)
\( (\underbrace{f \circ f \circ \ldots \circ f}_\text{103 tane})(0) = (f \circ f \circ f)(0) \)
\( = 3 \) bulunur.
\( f(x) = 4x^2 + 6x + 1 \)
\( (f \circ g)(x) = 4x^4 + 16x^3 + 14x^2 - 4x - 1 \)
\( g(x) = x^2 + bx + c \)
olduğuna göre, \( b + c \) toplamı kaçtır?
Çözümü Göster\( (f \circ g)(x) = f(g(x)) \)
\( = 4(x^2 + bx + c)^2 + 6(x^2 + bx + c) + 1 \)
Üç terimli parantez karesi ifadesinin açılımını yazalım.
\( = 4(x^4 + b^2x^2 + c^2 + 2(bx^3 + cx^2 + bcx)) + 6(x^2 + bx + c) + 1 \)
\( = 4x^4 + 4b^2x^2 + 4c^2 + 8bx^3 + 8cx^2 + 8bcx + 6x^2 + 6bx + 6c + 1 \)
\( = 4x^4 + 8bx^3 + (4b^2 + 8c + 6)x^2 + (6b + 8bc)x + 4c^2 + 6c + 1 \)
Bu ifade soruda verilen \( f \circ g \) fonksiyonuna eşittir.
\( = 4x^4 + 16x^3 + 14x^2 - 4x - 1 \)
İki polinomun eşitliğinde dereceleri aynı terimlerin katsayıları birbirine eşittir.
\( 8b = 16 \Longrightarrow b = 2 \)
\( 4b^2 + 8c + 6 = 14 \)
\( 4(2)^2 + 8c + 6 = 14 \)
\( c = -1 \)
\( b + c = 2 + (-1) = 1 \) olarak bulunur.
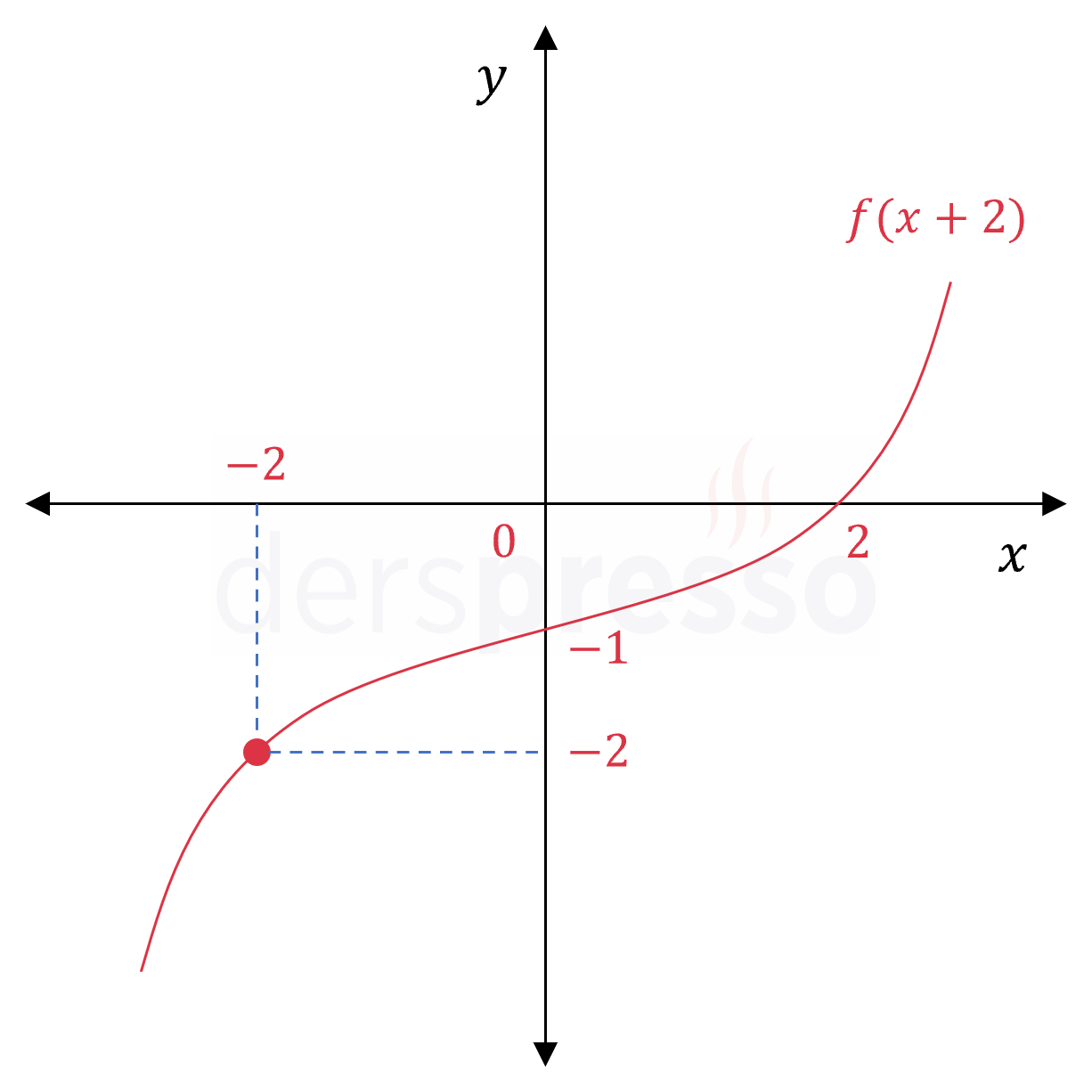
Yukarıda \( y = f(x + 2) \) fonksiyonunun grafiği verilmiştir.
Buna göre \( \dfrac{f(0) + f^{-1}(-1)}{f(2)} \) ifadesinin değeri kaçtır?
Çözümü Göster\( f(2) \) değerini bulmak için \( f(x + 2) \) grafiğinde \( x = 0 \) noktasına bakılır.
\( f(0 + 2) = f(2) = -1 \)
\( f(0) \) değerini bulmak için \( f(x + 2) \) grafiğinde \( x = -2 \) noktasına bakılır.
\( f(-2 + 2) = f(0) = -2 \)
\( f(2) = -1 \) olarak bulduğumuz için \( f^{-1}(-1) = 2 \) olur.
Bu değerleri sorudaki ifadede yerlerine koyalım.
\( \dfrac{f(0) + f^{-1}(-1)}{f(2)} = \dfrac{-2 + 2}{-1} = 0 \) bulunur.
\( f(x) = \sin{x} \)
\( g(x) = x^2 \)
Aşağıdaki her seçenekteki \( h \) fonksiyonunu elde etmek için, \( f \) ve \( g \) fonksiyonlarını kullanan bileşke fonksiyon ne olmalıdır?
(a) \( h(x) = \sin{x^2} \)
(b) \( h(x) = \sin{x^4} \)
(c) \( h(x) = \sin(\sin^2{x}) \)
(d) \( h(x) = \sin^4{x^2} \)
Çözümü Göster(a) seçeneği:
\( f \) fonksiyonunda \( x \) yerine \( g(x) = x^2 \) yazıldığında \( f(g(x)) = \sin{x^2} \) elde edilir.
\( h(x) = f(g(x)) = (f \circ g)(x) \)
(b) seçeneği:
\( g \) fonksiyonunda \( x \) yerine \( g(x) = x^2 \) yazıldığında \( g(g(x)) = x^4 \) elde edilir.
Daha sonra \( f \) fonksiyonunda \( x \) yerine \( g(g(x)) = x^4 \) yazıldığında \( f(g(g(x))) = \sin{x^4} \) elde edilir.
\( h(x) = f(g(g(x))) = (f \circ g \circ g)(x) \)
(c) seçeneği:
\( g \) fonksiyonunda \( x \) yerine \( f(x) = \sin{x} \) yazıldığında \( g(f(x)) = \sin^2{x} \) elde edilir.
Daha sonra \( f \) fonksiyonunda \( x \) yerine \( g(f(x)) = \sin^2{x} \) yazıldığında \( f(g(f(x))) = \sin(\sin^2{x}) \) elde edilir.
\( h(x) = f(g(f(x))) = (f \circ g \circ f)(x) \)
(d) seçeneği:
\( f \) fonksiyonunda \( x \) yerine \( g(x) = x^2 \) yazıldığında \( f(g(x)) = \sin{x^2} \) elde edilir.
\( g \) fonksiyonunda \( x \) yerine \( f(g(x)) = \sin{x^2} \) yazıldığında \( g(f(g(x))) = \sin^2{x^2} \) elde edilir.
\( g \) fonksiyonunda \( x \) yerine \( g(f(g(x))) = \sin^2{x^2} \) yazıldığında \( g(g(f(g(x)))) = \sin^4{x^2} \) elde edilir.
\( h(x) = g(g(f(g(x)))) = (g \circ g \circ f \circ g)(x) \)
\( A = \{1, 2, 3, 4\} \)
\( f: A \to A \) olmak üzere,
\( (f \circ f)(x) = x \) koşulunu sağlayan kaç fonksiyon yazılabilir?
Çözümü Gösterİstenen durum 3 farklı şekilde sağlanabilir.
Durum 1:
Bu durumda her eleman kendisiyle eşlenir.
\( f_1 = \{(1, 1), (2, 2), (3, 3), (4, 4)\} \)
Bu şekilde bir fonksiyon yazılabilir.
Durum 2:
Bu durumda elemanlar ikişerli şekilde birbiriyle eşlenir.
\( f_2 = \{(1, 2), (2, 1), (3, 4), (4, 3)\} \)
\( f_3 = \{(1, 3), (3, 1), (2, 3), (3, 2)\} \)
\( \vdots \)
Bu şekilde 4 eleman içinden 2 elemanın farklı seçim sayısı kadar (\( C(4, 2) = 6 \)) fonksiyon yazılabilir.
Durum 3:
Bu durumda iki eleman ikişerli şekilde birbiriyle eşlenirken diğer iki eleman kendisiyle eşlenir.
\( f_8 = \{(1, 2), (2, 1), (3, 3), (4, 4)\} \)
\( f_9 = \{(1, 3), (3, 1), (2, 2), (4, 4)\} \)
\( \vdots \)
Bu şekilde 4 eleman içinden 2 elemanın farklı seçim sayısı kadar (\( C(4, 2) = 6 \)) fonksiyon yazılabilir.
Buna göre istenen koşulu sağlayan \( 1 + 6 + 6 = 13 \) fonksiyon yazılabilir.
\( f: \mathbb{Z^+} \to \mathbb{Z^+} \) olmak üzere,
\( f \) girdi değerinin rakamları toplamını veren bir fonksiyondur.
Örnek: \( f(75) = 7 + 5 = 12 \)
\( (ab) \) iki basamaklı bir sayı olmak üzere,
\( (f \circ f)(ab) = 4 \) eşitliğini sağlayan kaç \( (ab) \) sayısı vardır?
Çözümü Göster\( (f \circ f)(ab) = f(f(ab)) \)
\( f(ab) = y \) diyelim.
\( f(y) = 4 \) sonucunu veren \( y \) sayılarını bulalım.
\( (ab) \) iki basamaklı olduğu için rakamları toplamı en az 1 (10), en çok 18 (99) olabilir.
\( 1 \le y \le 18 \)
\( f(y) = 4 \) ve \( 1 \le y \le 18 \) koşullarını sağlayan \( y \) değerlerini bulalım.
\( y \in \{4, 13\} \)
\( f(ab) = y = 4 \) koşulunu sağlayan iki basamaklı \( (ab) \) sayılarını bulalım.
\( (ab) \in \{13, 22, 31, 40\} \)
\( f(ab) = y = 13 \) koşulunu sağlayan iki basamaklı \( (ab) \) sayılarını bulalım.
\( (ab) \in \{49, 58, 67, 76, 85, 94\} \)
Bu iki durum için toplam \( 4 + 6 = 10 \) tane \( (ab) \) sayısı vardır.