Fonksiyon Olma Koşulları
Önceki bölümde verdiğimiz tanıma göre, \( A \) ve \( B \) boş kümeden farklı iki küme olmak üzere, \( A \) kümesinin her elemanını \( B \) kümesinin sadece bir elemanı ile eşleyen bağıntıya \( A \)'dan \( B \)'ye tanımlı fonksiyon denir.
Buna göre her fonksiyon bir bağıntıdır, ancak her bağıntı bir fonksiyon değildir. \( A \)'dan \( B \)'ye tanımlı bir bağıntının aynı zamanda bir fonksiyon olabilmesi için iki koşul sağlanmalıdır.
Koşul 1: \( A \) kümesinde \( B \) kümesinin bir elemanıyla eşlenmemiş açıkta eleman kalmamalıdır.
Her \( a \in A \) için,
\( (a, b) \in f \) olan en az bir \( b \in B \) elemanı vardır.
Koşul 2: \( A \) kümesinin her elemanı \( B \) kümesinde sadece bir elemanla eşlenmelidir (iyi tanımlılık).
Her \( a \in A \) ve \( b, c \in B \) için,
\( (a, b) \in f \) ve \( (a, c) \in f \) ise \( b = c \) olur.
\( A \)'dan \( B \)'ye tanımlı aşağıdaki bağıntının bir fonksiyon olup olmadığını inceleyelim.
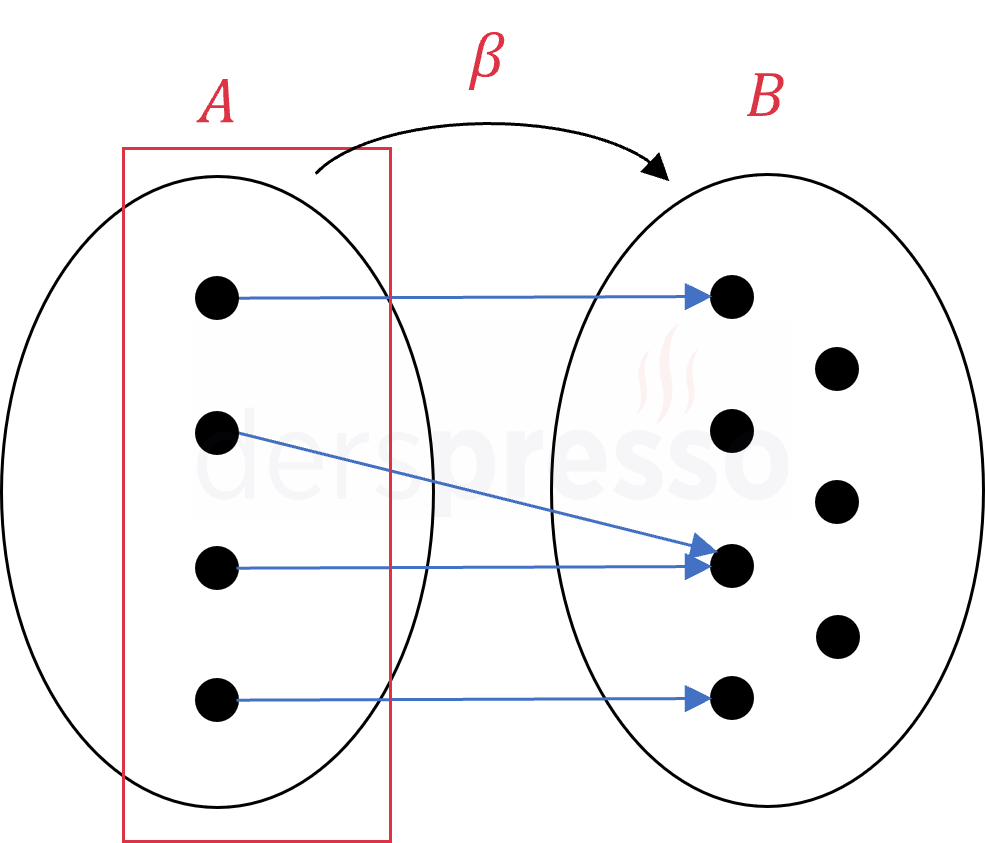
- \( A \) kümesinde \( B \) kümesinin bir elemanı ile eşlenmemiş açıkta eleman yoktur, buna göre birinci koşul sağlanmaktadır.
- \( A \) kümesinin her elemanı \( B \) kümesinde sadece bir elemanla eşlenmiştir, buna göre ikinci koşul da sağlanmaktadır.
Buna göre verilen bağıntı bir fonksiyondur.
Venn şeması gösteriminde bir bağıntının fonksiyon olup olmadığını anlamak için \( A \) kümesinin her elemanından bir ve yalnız bir ok çıktığını kontrol etmemiz yeterlidir. \( B \) kümesinde eşlemelerin nasıl gerçekleştiğinin ya da \( B \) kümesinde açıkta eleman kalıp kalmadığının bir bağıntının fonksiyon olup olmaması açısından bir önemi yoktur.
Benzer bir örneği küme liste yöntemi ile tanımlanmış bir bağıntı üzerinden de verebiliriz.
\( A = \{ a, b, c, d \} \)
\( B = \{ 1, 2, 3 \} \) olmak üzere,
\( A \)'dan \( B \)'ye tanımlı aşağıdaki bağıntıların birer fonksiyon olup olmadığını inceleyelim.
Aşağıdaki iki bağıntı \( A \) kümesinin her elemanı \( B \) kümesinin sadece bir elemanı ile eşlendiği için birer fonksiyondur.
\( \beta_1 = \{ (a, 1), (b, 2), (c, 3), (d, 3) \} \)
\( \beta_2 = \{ (a, 2), (b, 2), (c, 2), (d, 2) \} \)
Aşağıdaki bağıntı \( A \) kümesinin bir elemanı açıkta kaldığı için (birinci fonksiyon koşulu) bir fonksiyon değildir.
\( \beta_3 = \{ (a, 1), (b, 2), (c, 3) \} \)
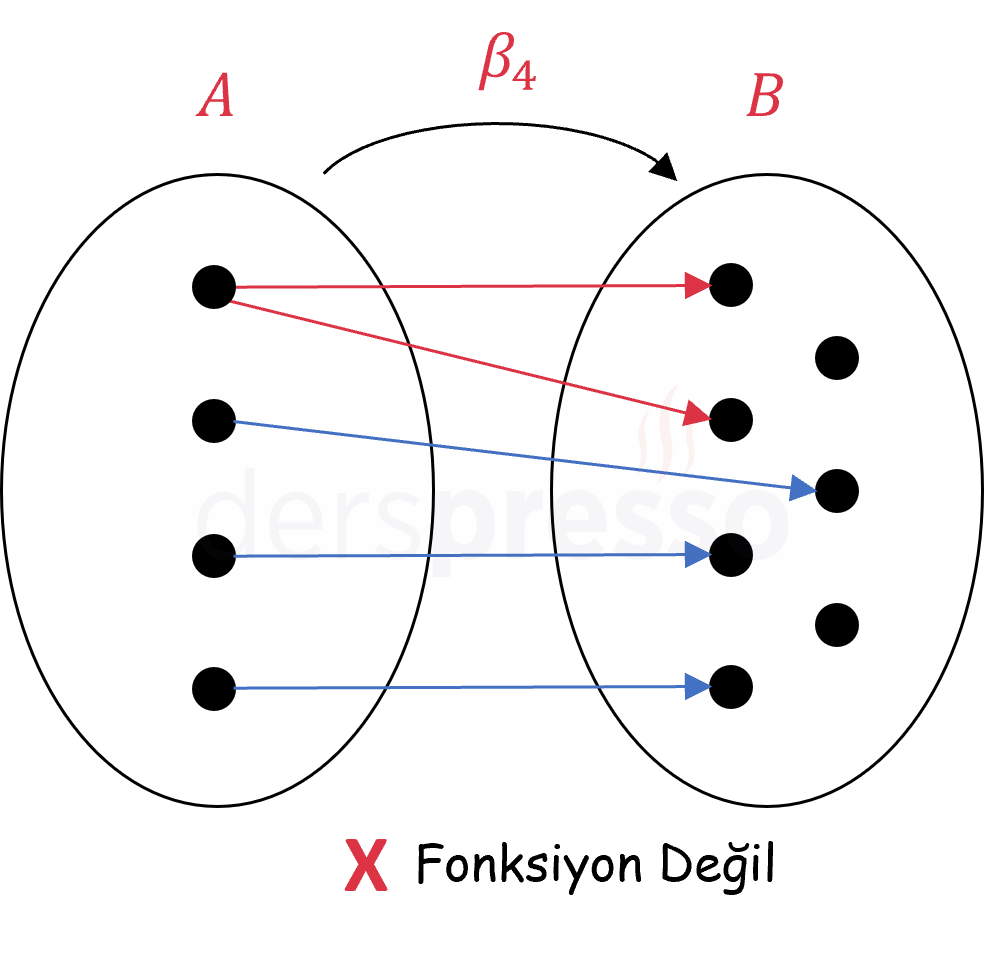
Aşağıdaki bağıntı \( A \) kümesinin bir elemanı \( B \) kümesinde iki elemanla eşlendiği için (ikinci fonksiyon koşulu) bir fonksiyon değildir.
\( \beta_4 = \{ \textcolor{red}{(a, 1)}, \textcolor{red}{(a, 2)}, (b, 3), (c, 2), (d, 1) \} \)
Küme liste yöntemi ile tanımlanmış bir bağıntının fonksiyon olup olmadığını anlamak için bağıntının tanım kümesindeki eleman sayısı kadar sıralı ikili içerdiğini ve sıralı ikililerin birinci bileşeninde tanım kümesinin her elemanının sadece bir kez yer aldığını kontrol etmemiz yeterlidir.
Bağıntı ve Fonksiyon Örnekleri
Aşağıda fonksiyon olma koşullarını sağlayan iki bağıntı verilmiştir. Bu bağıntılar \( A \) kümesinin her elemanını \( B \) kümesinin sadece bir elemanı ile eşlediği için birer fonksiyondur.
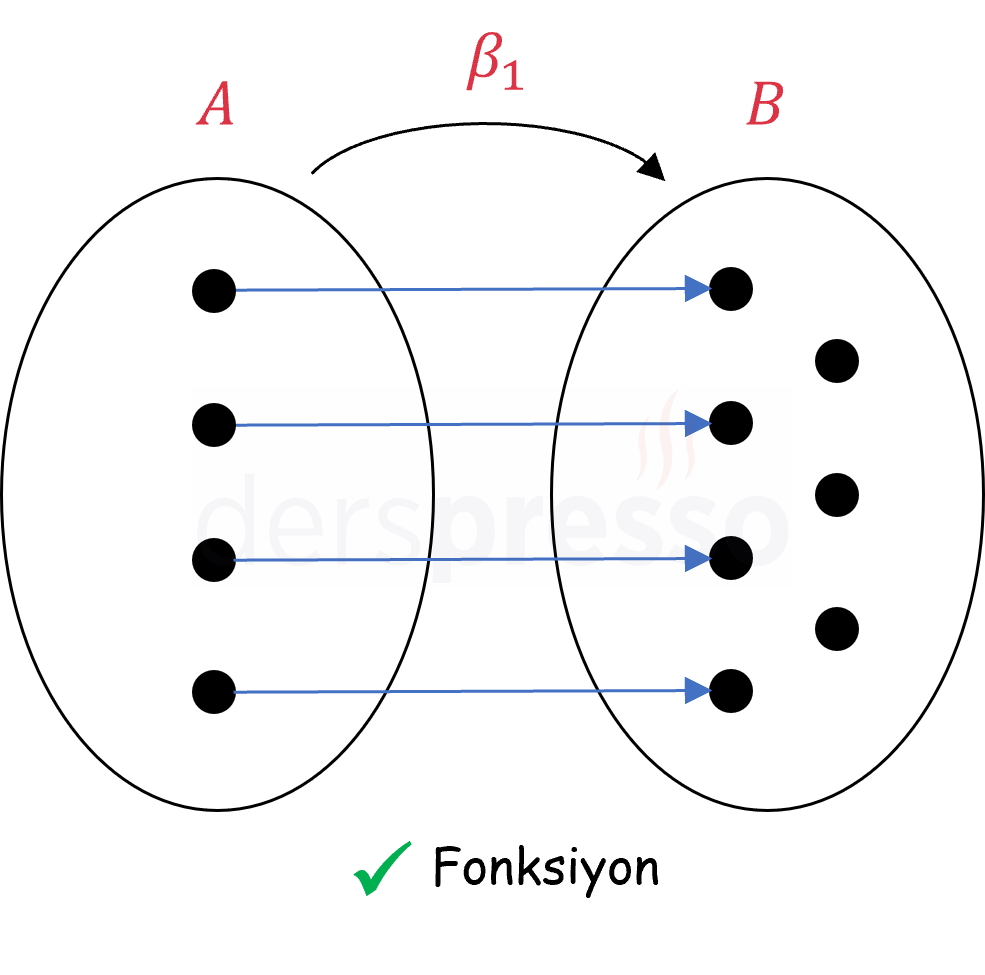
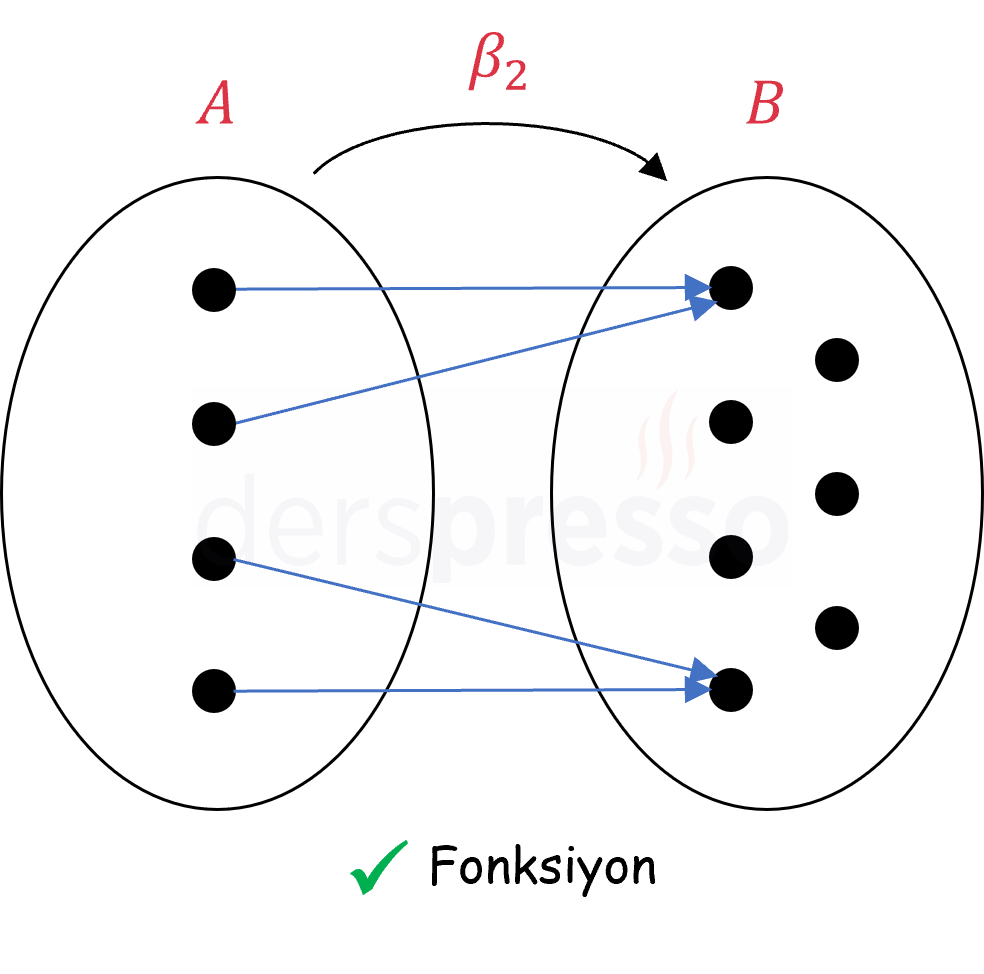
Aşağıda fonksiyon olma koşullarını sağlamayan iki bağıntı verilmiştir. Birinci bağıntı \( A \) kümesinin son elemanı açıkta kaldığı için (birinci fonksiyon koşulu), ikinci bağıntı da \( A \) kümesinin ilk elemanı \( B \) kümesinde iki elemanla eşlendiği için (ikinci fonksiyon koşulu) fonksiyon değildir.
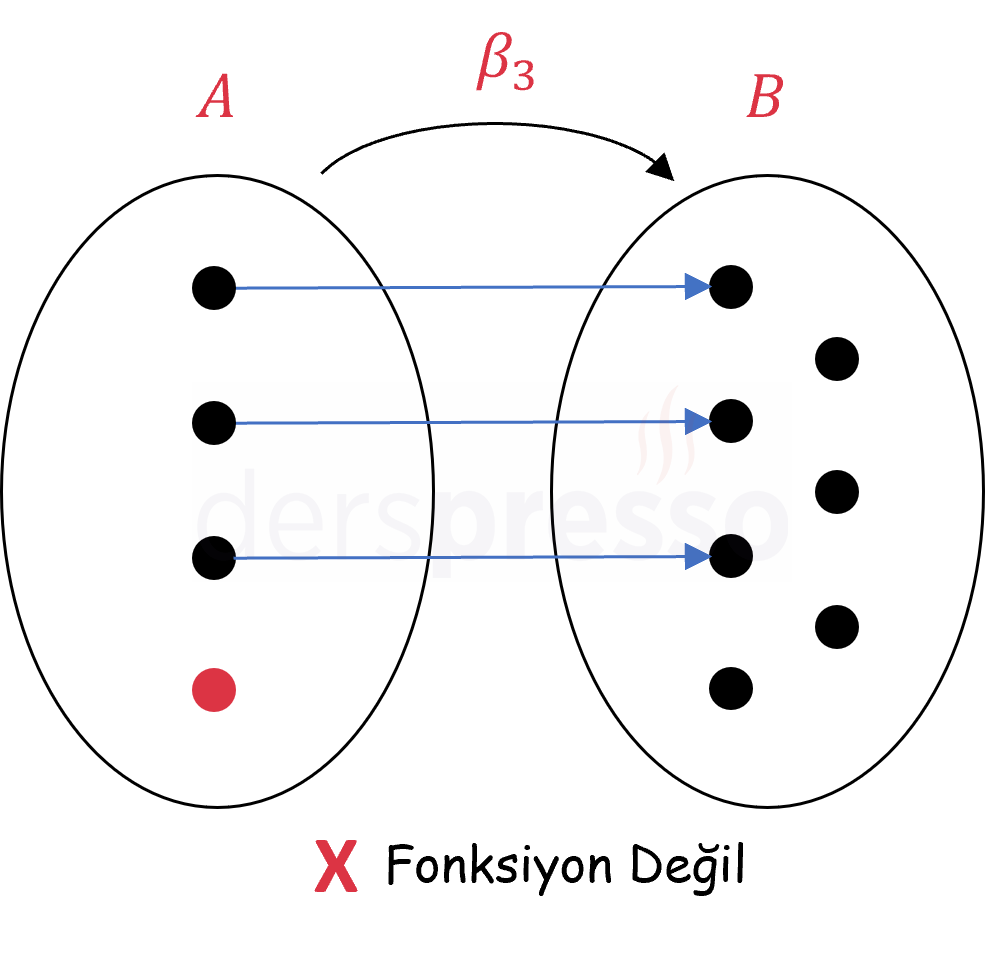
Aşağıda diğer bazı bağıntılar ve her bağıntının bir fonksiyon olup olmadığı açıklamalarıyla birlikte verilmiştir.
| Bağıntı | Fonksiyon? | Açıklama |
|---|---|---|
| Bir sınıftaki öğrenciler (\( A \)) ve doğum günleri (\( B \)) | Fonksiyon | Her öğrencinin mutlaka ve tek bir doğum günü vardır. Belirli bir günde doğmuş öğrenci olmaması ya da birden fazla öğrenci olması bağıntının fonksiyon olmasına engel değildir. |
| Reel sayılar (\( A \)) ve kareleri (\( B \)) | Fonksiyon | Her reel sayının mutlaka ve tek bir karesi vardır. Bir sayının ve ters işaretlisinin karelerinin aynı olması bağıntının fonksiyon olmasına engel değildir. |
| Bir lisede son sınıftaki öğrenciler (\( A \)) ve yerleştikleri bölümler (\( B \)) | Fonksiyon Değil | Her öğrenci tek bir bölüme yerleşebilir, ama bir bölüme yerleşmemiş öğrenciler de olabilir, dolayısıyla fonksiyon olmanın birinci koşulu sağlanmaz. \( A \) kümesi sınavda bir bölüme yerleşen öğrenciler olarak tanımlanırsa bu bağıntı bir fonksiyon olur. |
| Bir üniversitedeki öğrenciler (\( A \)) ve vatandaşı oldukları ülkeler (\( B \)) | Fonksiyon Değil | Her öğrenci mutlaka bir ülkenin vatandaşıdır, ama bazı öğrenciler birden fazla ülkenin pasaportunu taşıyor olabilir, dolayısıyla fonksiyon olmanın ikinci koşulu sağlanmaz. |
\( A = \{a, b, c\} \)
\( B = \{1, 2\} \) olmak üzere,
\( A \)'dan \( B \)'ye tanımlanabilecek tüm fonksiyonları listeleyin.
Çözümü Göster\( A \)'dan \( B \)'ye bir fonksiyon \( A \) kümesinin her elemanını \( B \) kümesinin sadece bir elemanı ile eşler.
Buna göre \( A \)'dan \( B \)'ye aşağıdaki fonksiyonlar tanımlanabilir. Dikkat edilirse tüm fonksiyonların her biri \( A \) kümesinin bir elemanına karşılık gelecek şekilde 3'er elemanı vardır.
\( f_1 = \{(a, 1), (b, 1), (c, 1)\} \)
\( f_2 = \{(a, 1), (b, 1), (c, 2)\} \)
\( f_3 = \{(a, 1), (b, 2), (c, 1)\} \)
\( f_4 = \{(a, 1), (b, 2), (c, 2)\} \)
\( f_5 = \{(a, 2), (b, 1), (c, 1)\} \)
\( f_6 = \{(a, 2), (b, 1), (c, 2)\} \)
\( f_7 = \{(a, 2), (b, 2), (c, 1)\} \)
\( f_8 = \{(a, 2), (b, 2), (c, 2)\} \)
\( A = \{ -1, 0, 1 \} \) ve \( B = \{ 2, 3 \} \) olduğuna göre aşağıdaki bağıntılardan hangileri \( A \)'dan \( B \)'ye bir fonksiyondur?
I. \( \{ (-1, 3), (0, 2), (1, 3) \} \)
II. \( \{ (-1, 2), (1, 3) \} \)
III. \( \{ (1, 2), (0, 2), (0, 3), (-1, 2) \} \)
Çözümü GösterFonksiyon olmanın koşulları, tanım kümesinde boşta eleman kalmaması ve tanım kümesindeki bir elemanın değer kümesinde sadece bir elemanla eşlenmesidir.
I. öncül bu koşulları sağladığı için fonksiyondur.
II. öncülde tanım kümesindeki \( 0 \) elemanı boşta kalmıştır, bu yüzden fonksiyon değildir.
III. öncülde tanım kümesindeki \( 0 \) elemanı hem \( 2 \) hem de \( 3 \)'le eşleştiği için fonksiyon değildir.
Buna göre sadece I. öncüldeki bağıntı bir fonksiyondur.
\( A = \{ 1, 2, 3, 4 \} \) olduğuna göre, aşağıdaki bağıntılardan hangileri \( A \) üzerinde bir fonksiyondur?
\( \beta_1 = \{ (1, 3),(3, 1),(2, 4),(4, 2) \} \)
\( \beta_2 = \{ (1, 1),(2, 3),(3, 2),(2, 4), (4, 4) \} \)
\( \beta_3 = \{ (1, 1),(2, 1),(3, 1),(4, 1) \} \)
\( \beta_4 = \{ (1, 3),(2, 4),(4, 1) \} \)
Çözümü Göster\( A \) üzerinde tanımlı bir fonksiyonun tanım ve değer kümeleri \( A \) kümesidir.
Fonksiyon olmanın koşulları, tanım kümesinde boşta eleman kalmaması ve tanım kümesindeki bir elemanın değer kümesinde sadece bir elemanla eşlenmesidir.
\( \beta_1 \) bağıntısı iki koşulu da sağladığı için fonksiyondur.
\( \beta_2 \) bağıntısı 2. koşulu sağlamadığı için fonksiyon değildir ("2" elemanı değer kümesinde iki farklı elemanla eşlenmiştir).
\( \beta_3 \) bağıntısı iki koşulu da sağladığı için fonksiyondur.
\( \beta_4 \) bağıntısı 1. koşulu sağlamadığı için fonksiyon değildir ("3" elemanının görüntüsü yoktur).
Buna göre 1. ve 3. bağıntılar birer fonksiyondur.
Aşağıdaki bağıntılardan hangileri bir fonksiyon belirtir?
I. \( \beta_1: \mathbb{R} \to \mathbb{R}, \beta_1(x) = \dfrac{x^2 + 3}{x - 4} \)
II. \( \beta_2: \mathbb{Z} \to \mathbb{N}, \beta_2(x) = 2x + 4 \)
III. \( \beta_3: \mathbb{Z} \to \mathbb{R}, \beta_3(x) = \dfrac{x^2 + 1}{x^2 - 2} \)
IV. \( \beta_4: \mathbb{R} \to \mathbb{R}, \beta_4(x) = \sqrt{x^3 - 4} \)
V. \( \beta_5: \mathbb{R} \to \mathbb{R}, \beta_5(x) = \sqrt[3]{x^3 - 5} \)
Çözümü GösterI. öncül: Tanım kümesindeki "4" değeri paydayı tanımsız yaptığı için bir görüntüsü yoktur. Bağıntı fonksiyon değildir.
II. öncül: -2'den küçük tam sayıların görüntüsü doğal sayı olmaz (\( 2(-5) + 4 = -6 \)). Bağıntı fonksiyon değildir.
III. öncül: Tanım kümesi tam sayılar kümesi olduğu için paydayı tanımsız yapan bir tam sayı değeri yoktur. Bağıntı fonksiyondur.
IV. öncül: Tanım kümesindeki bazı değerler için karekök ifadesi tanımsız olur (örneğin 0). Bağıntı fonksiyon değildir.
V. öncül: Tek dereceli köklü ifadeler tüm reel sayılarda tanımlıdır. Bağıntı fonksiyondur.
Buna göre III. ve V. öncüldeki bağıntılar birer fonksiyondur.
Aşağıdaki bağıntılardan hangileri bir fonksiyon belirtir?
I. \( \beta_1: \mathbb{R} \to \mathbb{R^+}, \beta_1 = x^4 \)
II. \( \beta_2: \mathbb{N} \to \mathbb{Z}, \beta_2 = \abs{x} \)
III. \( \beta_3: \mathbb{Z^+} \to \mathbb{Q}, \beta_3 = \sqrt{x} \)
Çözümü GösterI. öncül: Tanım kümesindeki \( x = 0 \) için \( x^4 = 0 \) değer kümesinin (pozitif reel sayılar) elemanı değildir. Bağıntı fonksiyon değildir.
II. öncül: Tüm doğal sayıların mutlak değeri tam sayılarda tanımlıdır. Bağıntı fonksiyondur.
III. öncül: Sadece tam kare olan (4, 9, 16 vb.) pozitif tam sayıların karekökü rasyoneldir, diğer pozitif tam sayıların karekökü irrasyoneldir. Bağıntı fonksiyon değildir.
Buna göre sadece II. öncüldeki bağıntı bir fonksiyondur.