Periyodik Fonksiyon
Aldığı değerler ve grafiği \( x \) ekseni boyunca düzenli aralıklarla kendini tekrarlayan fonksiyonlara periyodik fonksiyon denir.
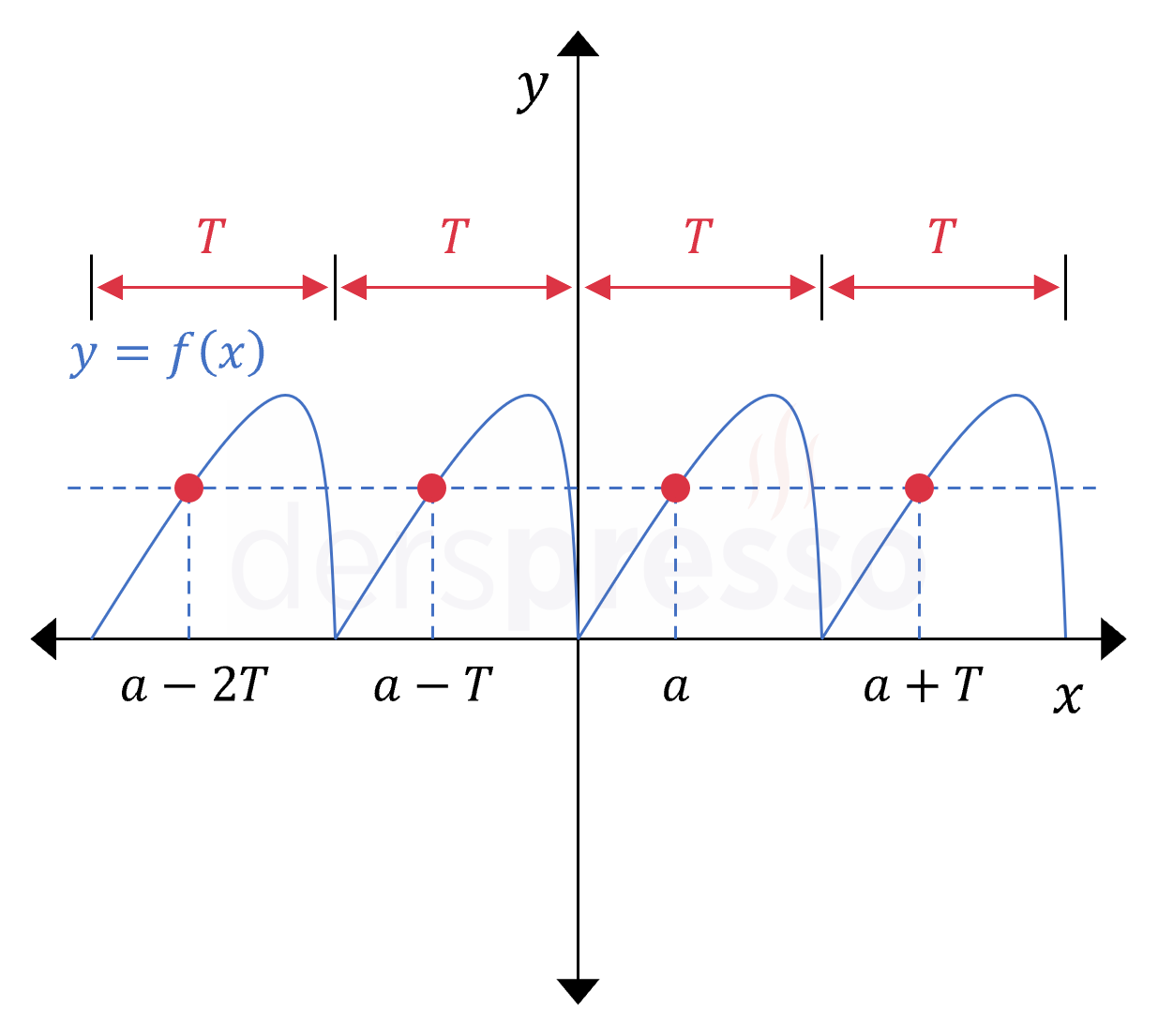
\( f: A \to B \) olmak üzere,
Her \( a \in A \) için \( f(a + T) = f(a) \) koşulunu sağlayan bir \( T \) pozitif reel sayısı varsa,
\( f \) fonksiyonu periyodik fonksiyondur ve \( T \) bu fonksiyonun bir periyodudur.
\( \ldots = f(a - 2T) = f(a - T) = f(a) \) \( = f(a + T) = \ldots \)
\( f \) periyodu 5 olan bir periyodik fonksiyon ise tanım aralığı içinde aşağıdaki eşitlikler sağlanır.
\( \ldots = f(-5) = f(0) = f(5) = f(10) = \ldots \)
\( \ldots = f(-2) = f(3) = f(8) = f(13) = \ldots \)
\( T \) bir periyodik fonksiyonun periyodu ise \( T \)'nin tam sayı katları için de aşağıdaki eşitlik sağlanır.
\( k \in \mathbb{Z} \) olmak üzere,
\( f(x + kT) = f(x) \)
Buna göre, \( T \) bir fonksiyonun periyodu ise \( T \)'nin tam sayı katları (\( 2T, 3T \) vb.) da fonksiyonun birer periyodu olur. Bu şekildeki pozitif periyot değerlerinin en küçüğüne fonksiyonun esas periyodu denir. Bir fonksiyonun periyodu dendiğinde anlamamız gereken fonksiyonun esas periyodudur.
Aşağıdaki \( f \) fonksiyonu, kendini tekrarlayan bir periyoda sahip olmadığı (her salınımda \( y \) gittikçe büyüyen değerler aldığı) için periyodik değildir. \( g \) fonksiyonu, ardışık salınımları özdeş olmasa da iki salınımda bir kendini tekrar ettiği için periyodiktir.
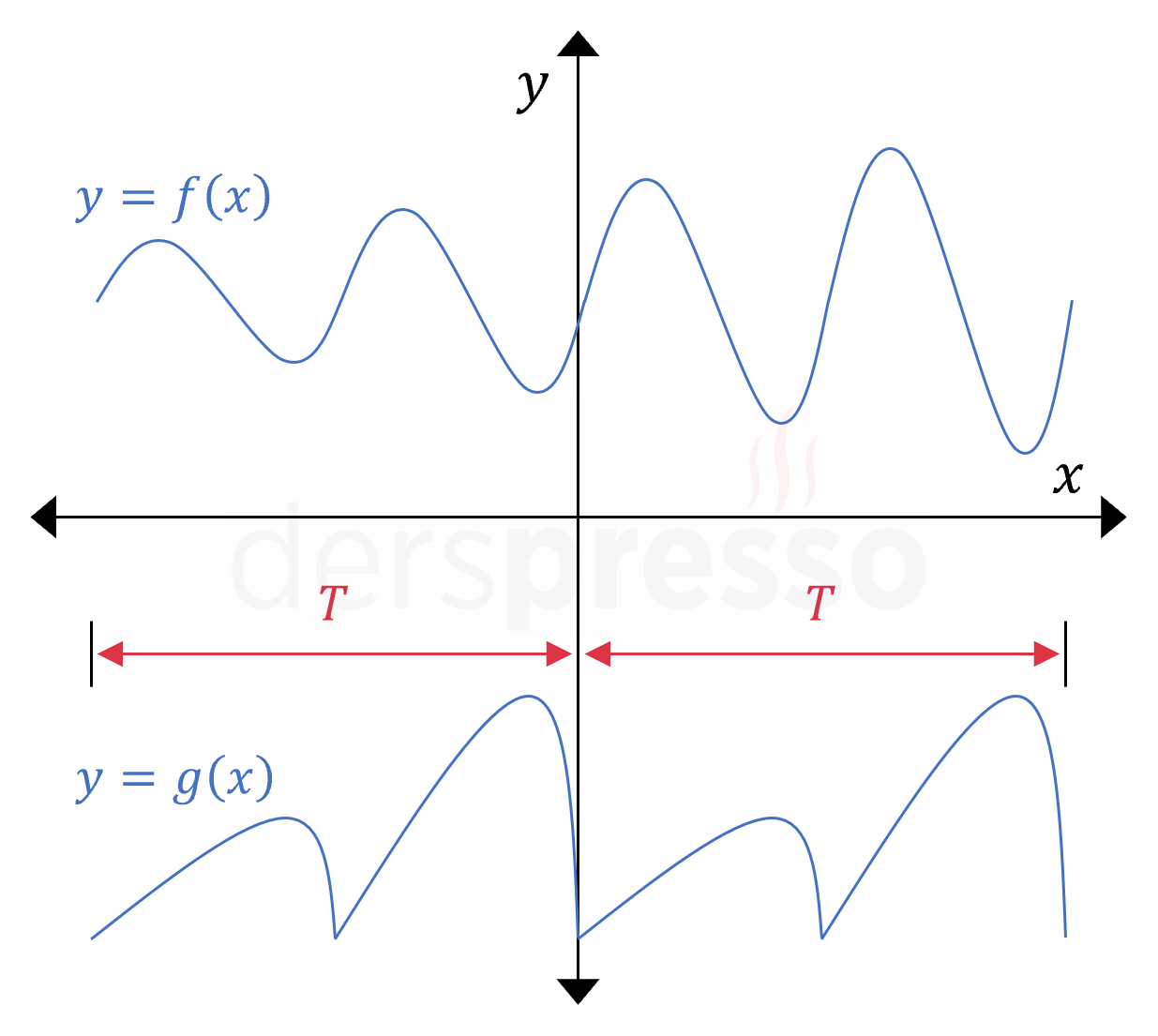
Örnek Periyodik Fonksiyonlar
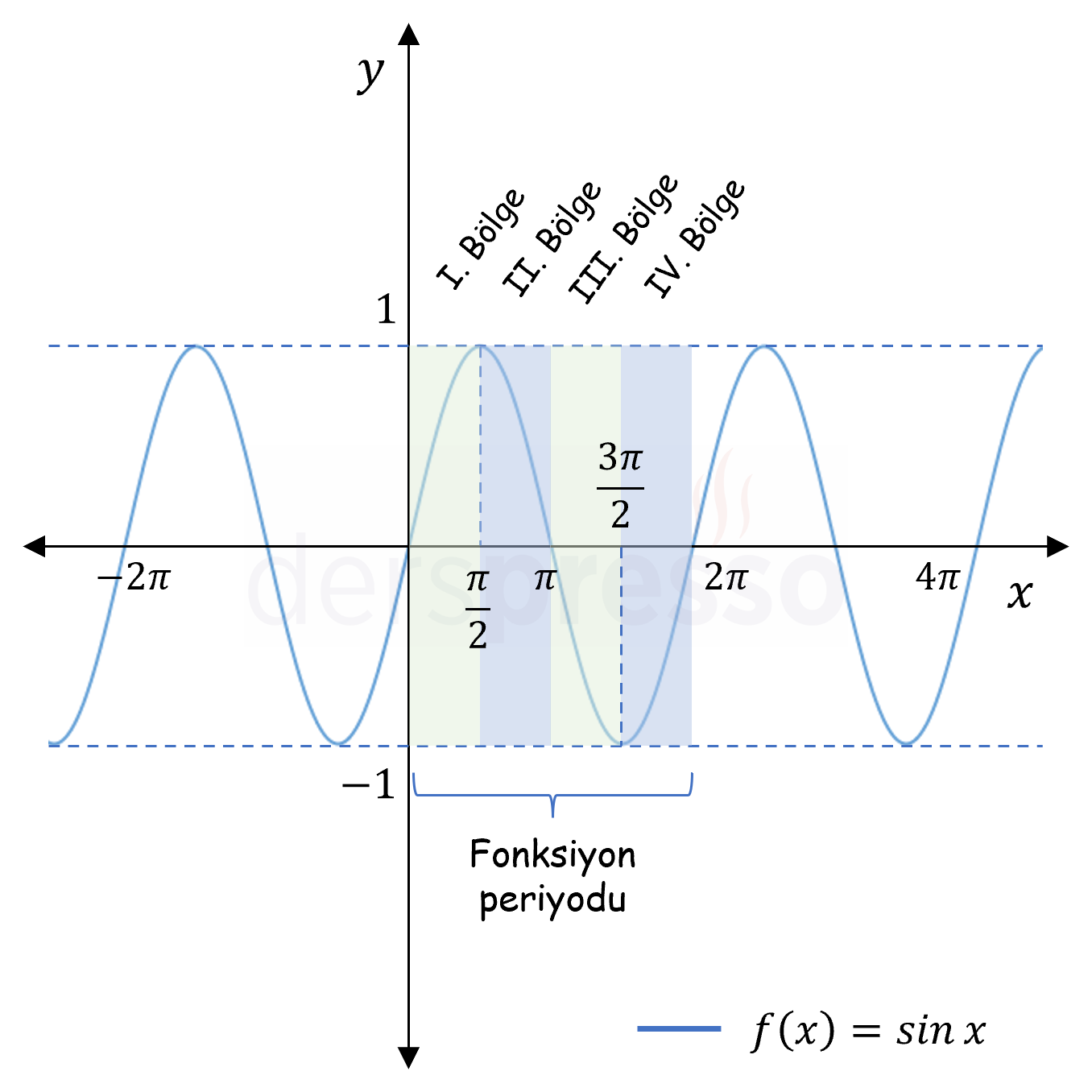
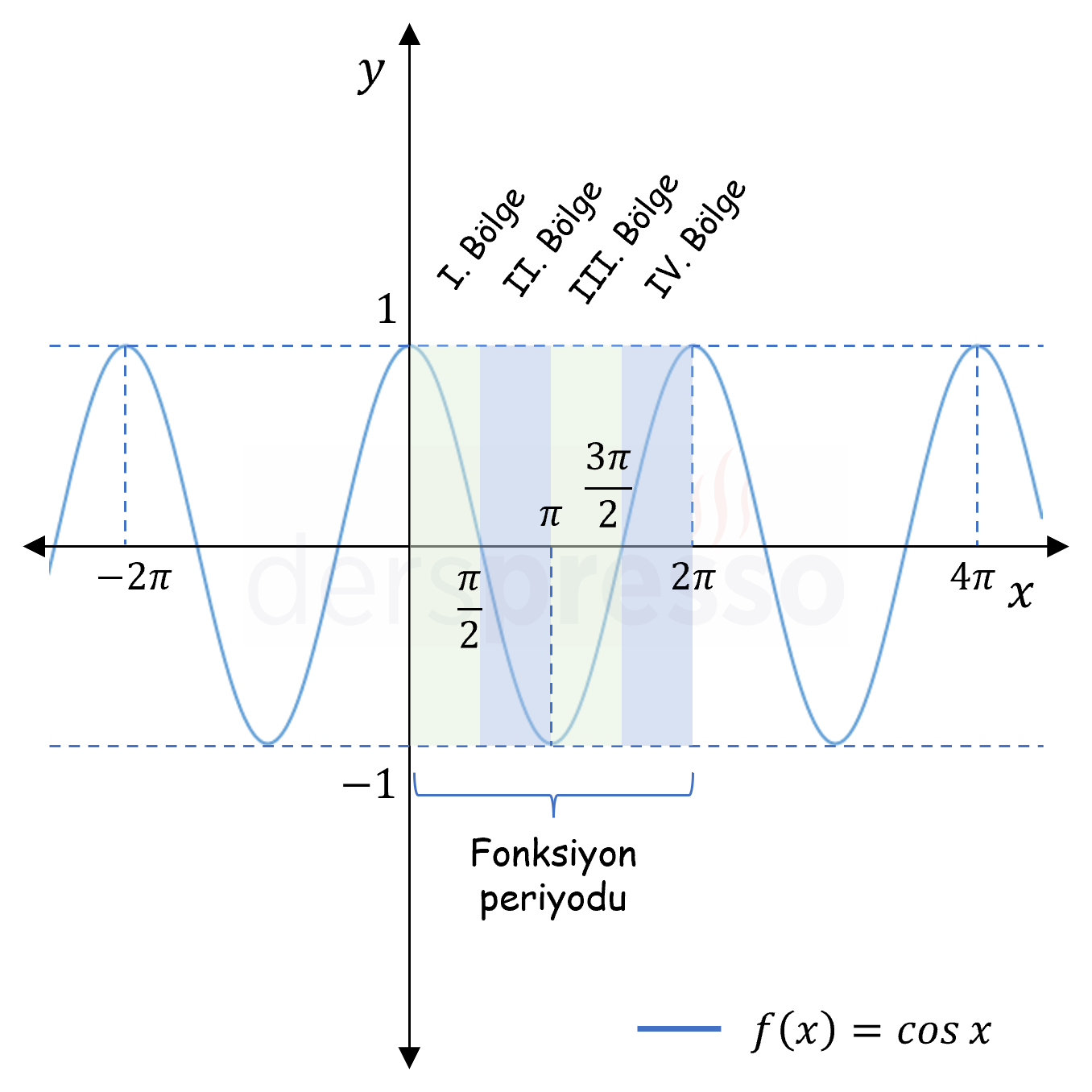
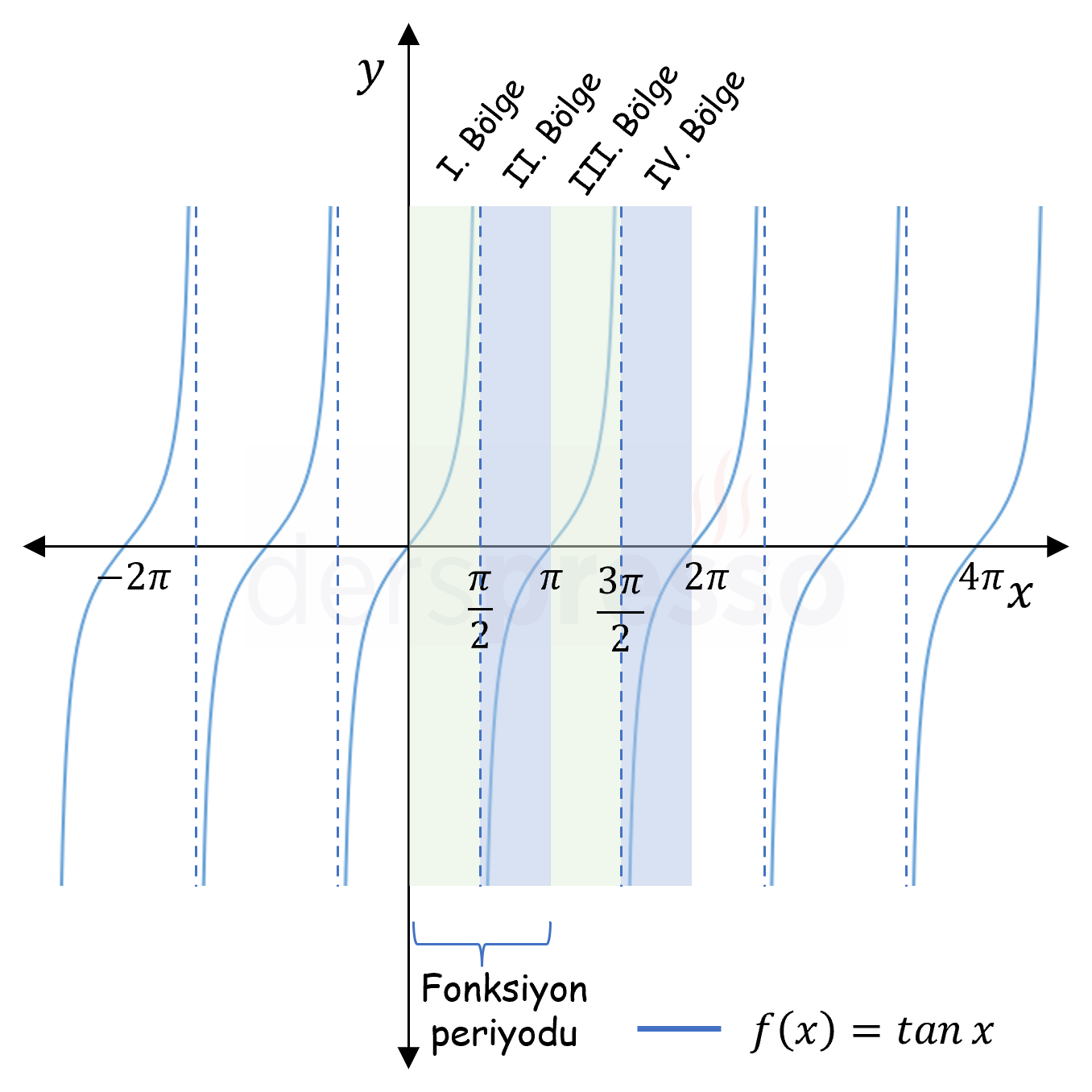
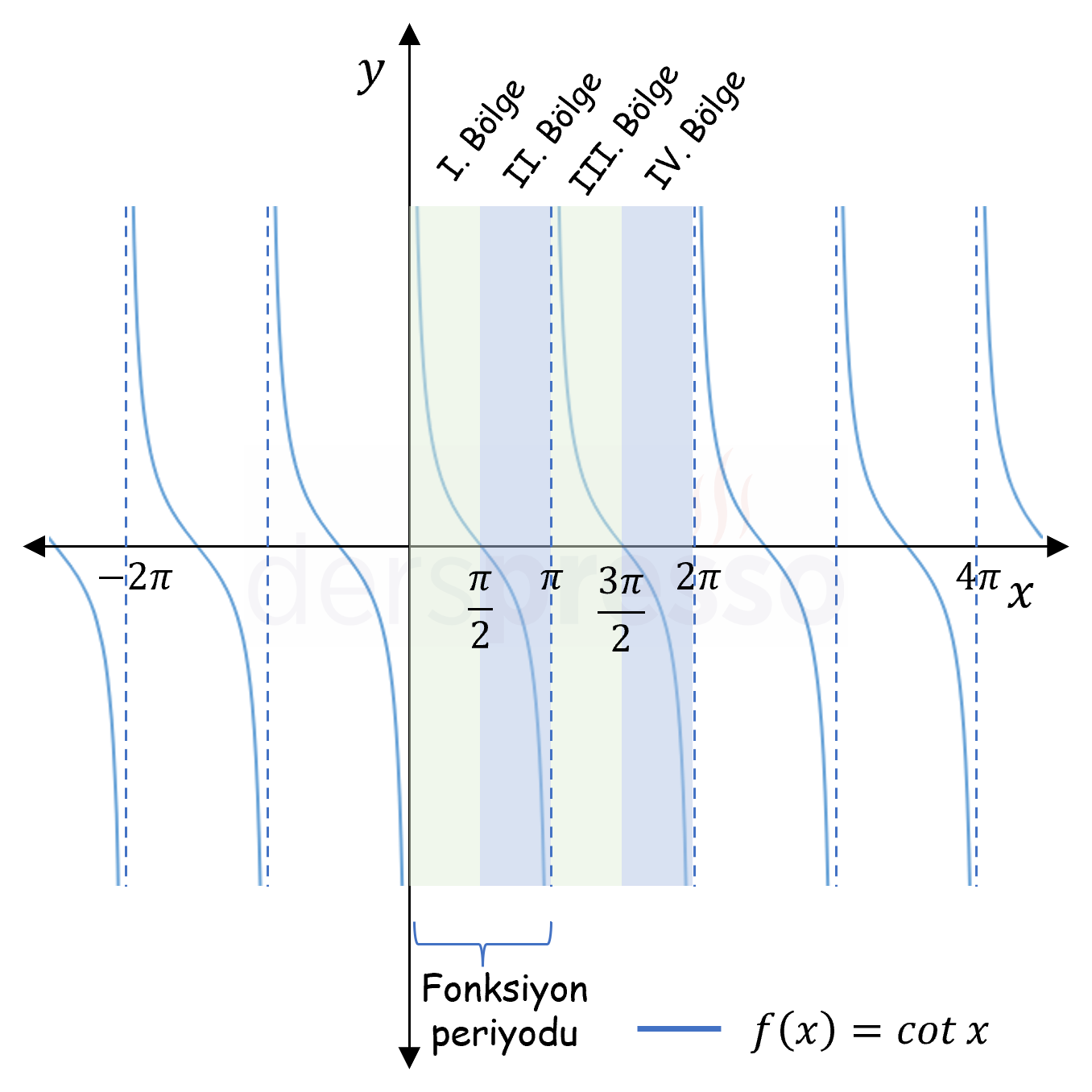
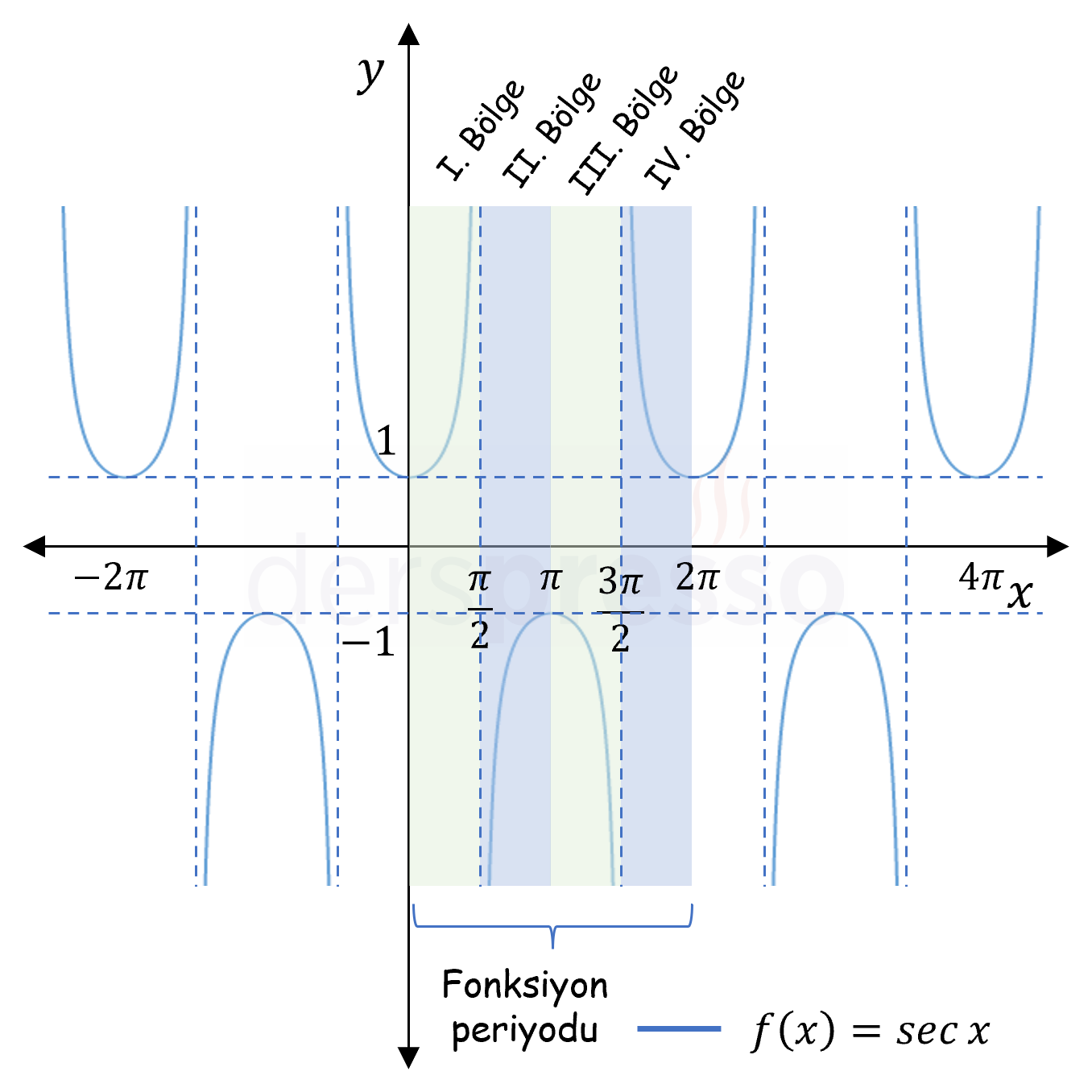
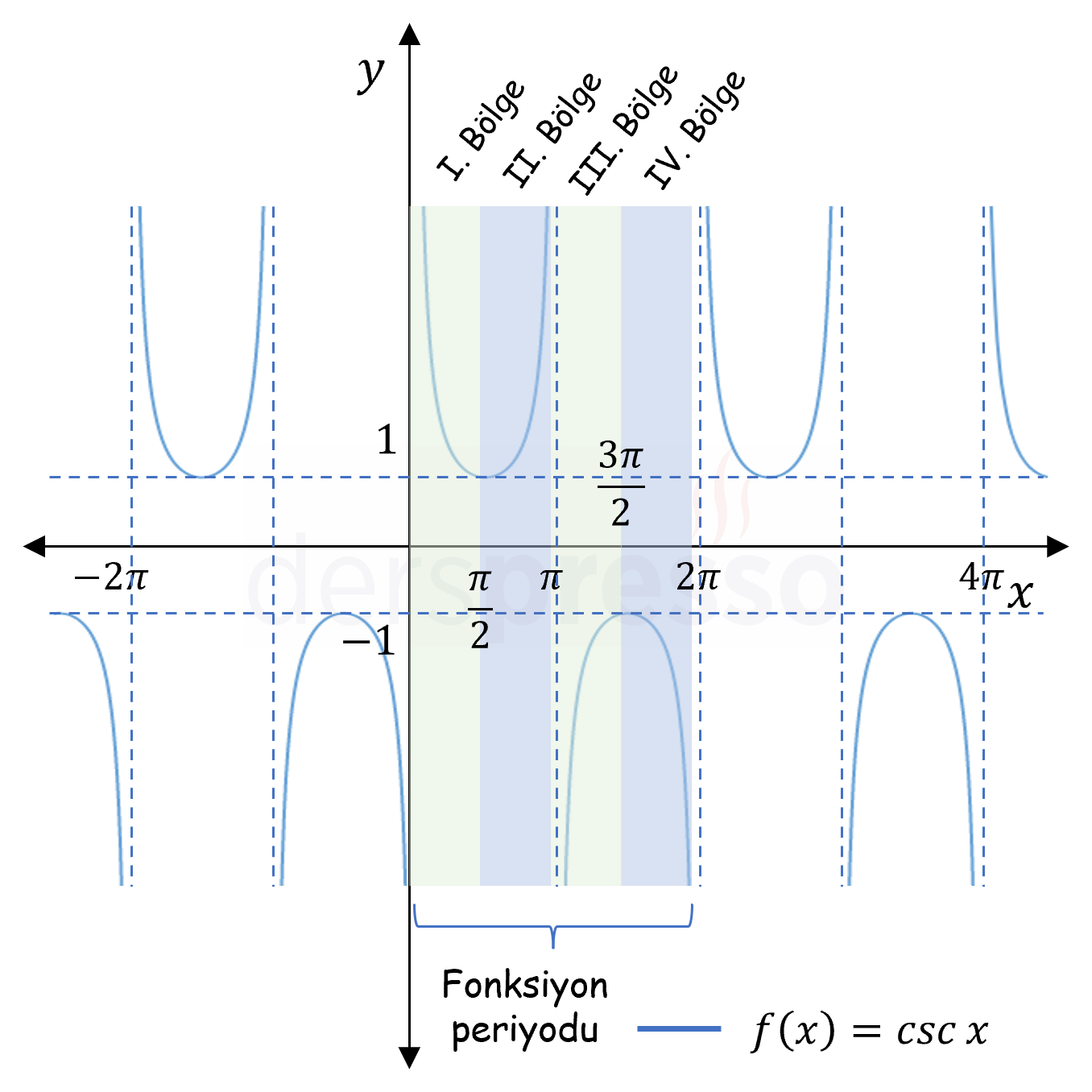
Trigonometrik fonksiyonların tümü periyodiktir. Sinüs (grafik), kosinüs (grafik), sekant (grafik) ve kosekant (grafik) fonksiyonlarının esas periyodu \( 2\pi \), tanjant (grafik) ve kotanjant (grafik) fonksiyonlarının esas periyodu \( \pi \)'dir.
\( \ldots = \sin(x - 2\pi) = \sin{x} = \sin(x + 2\pi) = \ldots \)
\( \ldots = \cos(x - 2\pi) = \cos{x} = \cos(x + 2\pi) = \ldots \)
\( \ldots = \tan(x - \pi) = \tan{x} = \tan(x + \pi) = \ldots \)
Sabit fonksiyonlar periyodik fonksiyon tanımını sağladıkları için periyodiktir, ancak her pozitif reel sayı birer periyodu olduğu için esas periyotları yoktur.
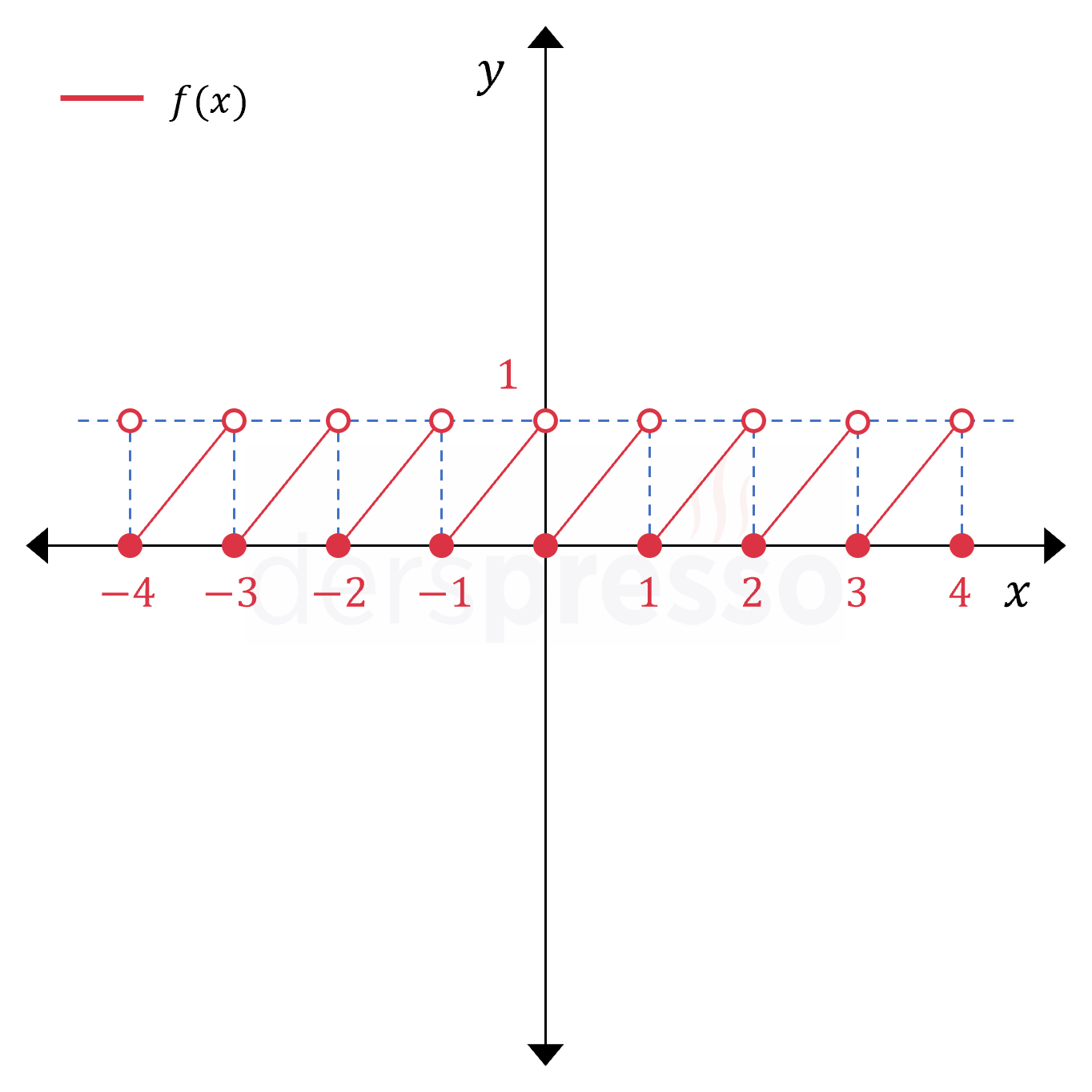
Ayrıca özel fonksiyonlar bölümünde göreceğimiz ondalık kısım fonksiyonu (grafik) da esas periyodu 1 olan bir periyodik fonksiyondur.
Periyodik Fonksiyonlarda Dönüşüm
Fonksiyon dönüşümleri konusunda detaylı göreceğimiz üzere, bir fonksiyonun tanımında belirli değişiklikler yaparak fonksiyon grafiğinde \( y \) ve \( x \) eksenleri boyunca şekil ve konum değişiklikleri yapılabilir.
\( g(x) = -a \cdot f(-b(x + c)) + k \)
Dikey dönüşümler (\( a \) ve \( k \) değerleri) fonksiyon grafiğinde \( y \) ekseni boyunca değişikliklere yol açtığı için periyodik bir fonksiyonun periyodunu değiştirmez.
Yatay öteleme dönüşümü (\( c \) değeri) fonksiyon grafiğinin şeklini değiştirmeden \( x \) ekseni boyunca konum değişikliğine yol açtığı için periyodik bir fonksiyonun periyodunu değiştirmez.
\( b \) katsayısının işaretini negatife çevirmek fonksiyon grafiğinin \( y \) eksenine göre yansımasını aldığı için periyodik bir fonksiyonun periyodunu değiştirmez.
\( b \) katsayısının mutlak değer olarak değerindeki değişiklikler ise fonksiyon grafiğinde \( x \) ekseni boyunca daralma/genişlemeye yol açar ve fonksiyonun esas periyodu bu sayı ile ters orantılı olarak değişir.
\( b \in \mathbb{R}, \quad b \ne 0 \)
\( f \) sabit olmayan periyodik bir fonksiyon olmak üzere,
\( f(x) \) fonksiyonunun esas periyodu \( T \) ise,
\( f(bx) \) fonksiyonunun esas periyodu \( \dfrac{T}{\abs{b}} \) olur.
\( f \) fonksiyonunun esas periyodu \( T \) ise, aşağıdaki fonksiyonların tümünün periyodu \( \frac{T}{2} \) olur.
\( f(\textcolor{red}{2}x + 5) - 3 \)
\( 3f(-\textcolor{red}{2}x - 4) \)
\( -2f(\textcolor{red}{2}(x + 1)) - 7 \)
Yukarıda bahsettiğimiz dönüşümler periyodik bir fonksiyon olan sinüs fonksiyonuna uygulandığında fonksiyon grafiği aşağıdaki şekillerde değişim gösterir.
İnteraktif uygulama: Sinüs Fonksiyonunda Dönüşümler
Periyodik Fonksiyonlar Arasında İşlemler
Periyodik \( f \) ve \( g \) fonksiyonlarının esas periyotları sırasıyla \( p \) ve \( q \) olsun. Bu iki fonksiyon arasındaki herhangi bir aritmetik işlem (toplama, çıkarma, çarpma, bölme) sonucunda oluşan yeni fonksiyona \( h \) diyelim.
\( p \) ve \( q \) periyotlarının en küçük ortak katı (EKOK'u) tanımlı ise \( h \) fonksiyonu da periyodik bir fonksiyondur ve periyotlarından biri \( EKOK(p, q) \) olur. \( h \) fonksiyonunun esas periyodu ise bu EKOK değeri olabilir ya da bir tam sayı katı bu EKOK değeri olan daha küçük bir değer olabilir.
\( f(x) = \sin{x}, \quad g(x) = \cos{x} \)
\( f \) ve \( g \)'nin esas periyotları \( 2\pi \)'dir.
\( h(x) = f(x) \cdot g(x) = \sin{x} \cdot \cos{x} \) \( = \frac{1}{2} \sin(2x) \) olmak üzere,
\( EKOK(2\pi, 2\pi) = 2\pi \)
\( h \) fonksiyonu da periyodiktir, ancak esas periyodu \( 2\pi \) değil, dönüşüm başlığı altında gördüğümüz üzere \( \frac{2\pi}{2} = \pi \)'dir.
\( k(x) = \dfrac{f(x)}{g(x)} = \dfrac{\sin{x}}{\cos{x}} = \tan{x} \) olmak üzere,
\( k \) fonksiyonu periyodiktir, ancak esas periyodu \( 2\pi \) değil, \( \pi \)'dir.
\( p \) ve \( q \) periyot değerlerinin EKOK'u tanımlı değilse \( h \) fonksiyonu burada detaylarına girmeyeceğimiz istisnai bazı fonksiyonlar dışında periyodik olmaz.
\( f(x) = \sin{x}, \quad g(x) = \cos(2\pi x) \)
\( f \)'nin esas periyodu \( 2\pi \), \( g \)'nin esas periyodu \( 1 \)'dir.
\( h(x) = \sin{x} + \cos(2\pi x) \)
\( EKOK(2\pi, 1) \) tanımlı değildir.
Buna göre \( h \) fonksiyonu periyodik değildir.
İki sayının EKOK'unun tanımlı olmadığı durum, sayıların birbirine oranının rasyonel sayı olmadığı durumdur. Örneğin aşağıdaki sayı ikililerinin EKOK'ları tanımlı değildir.
\( \sqrt{2} \) ve \( 1 \)
\( \sqrt{2} \) ve \( \sqrt{3} \)
\( \pi \) ve \( 1 \)
Aşağıdaki sayı ikililerinin ikisi de irrasyonel olsa da oranları rasyonel sayı olduğu için EKOK'ları tanımlıdır.
\( EKOK(\sqrt{2}, 2\sqrt{2}) = 2\sqrt{2} \)
\( EKOK(2\pi, 3\pi) = 6\pi \)
Periyodu \( T \) olan bir periyodik fonksiyonun pozitif tam sayı kuvvetleri de periyodiktir. Fonksiyonun tek sayı kuvvetlerinin periyodu yine \( T \) olurken çift sayı kuvvetlerinin periyodu fonksiyonun grafik özelliklerine göre \( T \) ya da \( \frac{T}{2} \) olabilir.
- Sinüs, kosinüs, sekant ve kosekant fonksiyonlarının periyodu \( 2\pi \)'dir. Bu fonksiyonların tek sayı kuvvetlerinin periyodu yine \( 2\pi \) iken çift sayı kuvvetlerinin periyodu \( \pi \) olur.
- Tanjant ve kotanjant fonksiyonlarının periyodu \( \pi \)'dir. Bu fonksiyonların hem tek hem çift sayı kuvvetlerinin periyodu yine \( \pi \) olur.
Reel sayılarda tanımlı ve sabit fonksiyon olmayan \( f \) fonksiyonunun periyodu 6'dır.
Buna göre \( g(x) = f(\frac{3x + 4}{2}) + 1 \) fonksiyonunun periyodu kaçtır?
Çözümü Göster\( f(x) \) fonksiyonunun esas periyodu \( T \) ise,
\( f(bx + c) + k \) fonksiyonunun esas periyodu \( \frac{T}{\abs{b}} \) olur.
\( g(x) = f(\frac{3x + 4}{2}) + 1 = f(\frac{3}{2}x + 2) + 1 \)
Buna göre \( b = \frac{3}{2} \) olur.
\( T_g = \dfrac{6}{\frac{3}{2}} = 4 \) olarak bulunur.
\( f(x) \) fonksiyonunun periyodu 5, \( g(x) \) fonksiyonunun periyodu 6'dır.
\( f(48) = 2 \) ve \( g(49) = 3 \) olduğuna göre,
\( \dfrac{f(23) + g(19)}{(f \circ g)(1)} \) ifadesinin değeri kaçtır?
Çözümü GösterPeriyodik fonksiyonlar \( x \)'in her periyot kadar artışında aynı değeri alırlar.
\( k \in \mathbb{Z} \) olmak üzere,
\( f(x) = f(x + 5k) \)
\( g(x) = g(x + 6k) \)
Sorudaki ifadelerin değerlerini bulalım.
\( f(23) = f(23 + 5 \cdot 5) = f(48) = 2 \)
\( g(19) = g(19 + 6 \cdot 5) = g(49) = 3 \)
\( (f \circ g)(1) = f(g(1)) \)
\( g(1) = g(1 + 6 \cdot 8) = g(49) = 3 \)
\( f(g(1)) = f(3) \)
\( f(3) = f(3 + 5 \cdot 9) = f(48) = 2 \)
\( f(g(1)) = f(3) = 2 \)
Bu değerleri sorudaki ifadede yerlerine koyalım.
\( \dfrac{f(23) + g(19)}{(f \circ g)(1)} = \dfrac{2 + 3}{2} \) \( = \dfrac{5}{2} \) bulunur.
Her \( x \in [-15, 15] \) için \( f(x) = \abs{3x} \)
Her \( x \in \mathbb{R} \) için \( f(x) = f(x + 30) \) olduğuna göre, \( f(257) \) kaçtır?
Çözümü GösterVerilen bilgiye göre \( f \) fonksiyonu periyodiktir ve periyodu 30'dur.
\( x = 257 \) apsis değerli noktanın periyodik fonksiyonda \( [-15, 15] \) aralığında karşılık geldiği noktayı bulalım.
\( f(227) = f(197) = \ldots = f(17) = f(-13) \)
\( f(-13) = \abs{3 \cdot (-13)} = 39 \) bulunur.
\( f(x) = 4\tan^5(2x + 1) - \sin^3(3x + 2) \) fonksiyonunun periyodu kaçtır?
Çözümü GösterTanjant fonksiyonunun ve tüm kuvvetlerinin periyodu \( \pi \)'dir. Buna göre \( \tan^5(2x + 1) \) fonksiyonunun periyodu \( \frac{\pi}{2} \) olur.
Sinüs fonksiyonunun ve tek sayı kuvvetlerinin periyodu \( 2\pi \)'dir. Buna göre \( \sin^3(3x + 2) \) fonksiyonunun periyodu \( \frac{2\pi}{3} \) olur.
İki fonksiyon arasındaki toplama/çıkarma işlemi sonucunda oluşan fonksiyonun periyodu fonksiyonların periyotlarının EKOK'una eşittir.
\( \dfrac{\pi}{2} = 90°, \quad \dfrac{2\pi}{3} = 120° \) bulunur.
\( EKOK(90°, 120°) = 360° = 2\pi \) olarak bulunur.
\( f(x) = 3 + \tan^2(8x + 5) \)
\( g(x) = 5 + \cot^4(-4x + 2) \)
\( h(x) = \sin^6(-16x + 8) \)
olduğuna göre, \( f + g + h \) fonksiyonunun periyodu kaçtır?
Çözümü GösterTanjant fonksiyonunun ve tüm kuvvetlerinin periyodu \( \pi \)'dir. Buna göre \( f \) fonksiyonunun periyodu \( \frac{\pi}{8} \) olur.
Kotanjant fonksiyonunun ve tüm kuvvetlerinin periyodu \( \pi \)'dir. Buna göre \( g \) fonksiyonunun periyodu \( \frac{\pi}{\abs{-4}} = \frac{\pi}{4} \) olur.
Sinüs fonksiyonunun periyodu \( 2\pi \), çift sayı kuvvetlerinin periyodu \( \pi \)'dir. Buna göre \( h \) fonksiyonunun periyodu \( \frac{\pi}{\abs{-16}} = \frac{\pi}{16} \) olur.
Üç fonksiyon arasındaki toplama/çıkarma işlemi sonucunda oluşan fonksiyonun periyodu fonksiyonların periyotlarının EKOK'una eşittir.
\( EKOK(\frac{\pi}{8}, \frac{\pi}{4}, \frac{\pi}{16}) = \dfrac{\pi}{4} \) olarak bulunur.
\( f \) ve \( g \) periyodik fonksiyonlardır.
\( f(4 - 3x) = g(x + 5) \)
\( f \) fonksiyonunun periyodu 6 olduğuna göre, \( g \) fonksiyonunun periyodu kaçtır?
Çözümü Göster\( f(4 - 3x) = f(-3x + 4) \)
\( f(x) \) fonksiyonun periyodu \( T \) ise \( f(bx + c) \) fonksiyonunun periyodu \( \frac{T}{\abs{b}} \) olur.
Buna göre \( f(x) \) fonksiyonun periyodu 6 ise \( f(4 - 3x) \) fonksiyonunun periyodu \( \frac{6}{\abs{-3}} = 2 \) olur.
\( f(4 - 3x) = g(x + 5) \)
\( f(4 - 3x) \) fonksiyonu \( g \) fonksiyonunun 5 birim sola ötelenmiş halidir. Yatay öteleme bir fonksiyonun periyodunu değiştirmeyeceği için \( g \) fonksiyonunun da periyodu 2 olur.
\( f(x) \) fonksiyonunun esas periyodu 5, \( g(x) \) fonksiyonunun esas periyodu 2'dir.
Buna göre \( h(x) = f(\frac{x}{3})g(x) + g(2x)f(x) \) fonksiyonunun periyodu kaçtır?
Çözümü Göster\( f(x) \) fonksiyonunun esas periyodu \( T \) ise \( f(bx) \) fonksiyonunun esas periyodu \( \frac{T}{\abs{b}} \) olur.
\( f(\frac{x}{3}) \) fonksiyonunun esas periyodunu bulalım.
\( T_1 = \dfrac{5}{\abs{\frac{1}{3}}} = 15 \)
\( g(2x) \) fonksiyonunun esas periyodunu bulalım.
\( T_2 = \dfrac{2}{\abs{2}} = 1 \)
\( f(x) \) fonksiyonunun esas periyodu 5 olarak verilmiştir.
Periyodik fonksiyonlar arası aritmetik işlemler sonucunda elde edilen fonksiyonun periyodu fonksiyonların esas periyotlarının EKOK'udur. Bulunan periyot değeri elde edilen fonksiyonun periyotlarından biri olup, esas periyodu olmayabilir.
\( h(x) \) fonksiyonunun periyodunu bulalım.
\( EKOK(15, 2, 1, 5) = 30 \) olarak bulunur.
\( k \in \mathbb{Z^+} \) olmak üzere,
\( f(x) = \cos^k(kx) \) fonksiyonunun esas periyodu \( \frac{\pi}{4} \) olduğuna göre, \( k \)'nın alabileceği değerler toplamı kaçtır?
Çözümü GösterKosinüs fonksiyonunun ve tek sayı kuvvetlerinin periyodu \( 2\pi \), çift sayı kuvvetlerinin periyodu \( \pi \)'dir.
\( k \) tek sayı ise:
\( T_f = \dfrac{2\pi}{k} = \dfrac{\pi}{4} \)
\( k = 8 \)
Bulduğumuz \( k \) değeri çift sayı olduğu için geçerli bir çözüm değildir.
\( k \) çift sayı ise:
\( T_f = \dfrac{\pi}{k} = \dfrac{\pi}{4} \)
\( k = 4 \)
Buna göre \( k \)'nın alabileceği tek değer 4 olarak bulunur.