Fonksiyonların Tanım ve Görüntü Kümesi
\( f: A \to B \) şeklindeki bir fonksiyon tanımında \( A \) tanım kümesi, \( B \) değer kümesidir. Tanım kümesi her bir elemanı değer kümesinin bir elemanı ile eşlenecek değerleri, değer kümesi de tanım kümesindeki elemanların eşlenebileceği değerleri içerir.
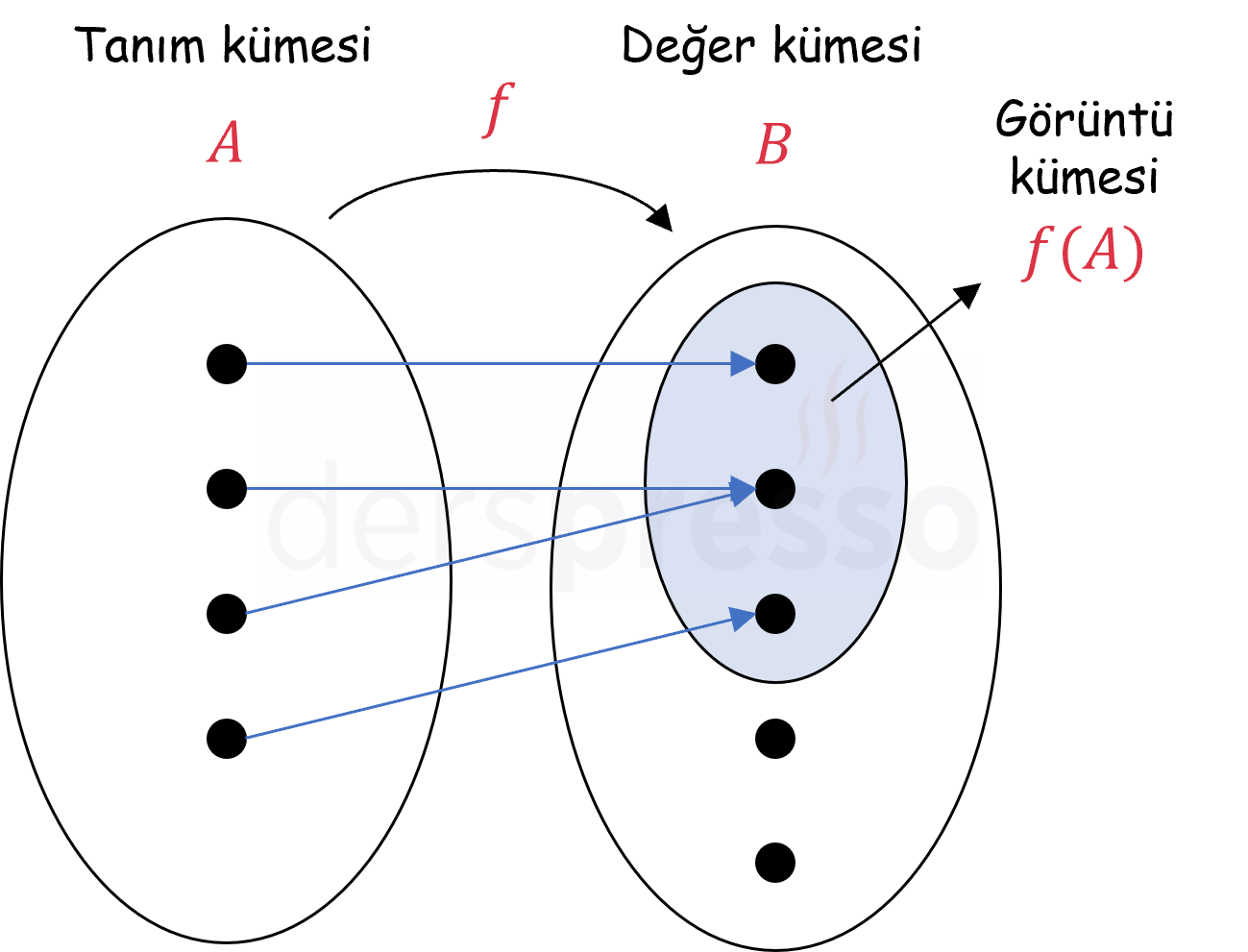
Tanım kümesindeki bir elemanın değer kümesinde eşlendiği elemana bu elemanın \( f \) fonksiyonuna göre görüntüsü denir. Fonksiyon tanımı gereği tanım kümesindeki her elemanın değer kümesinde sadece bir görüntüsü olmak zorundadır.
Tanım kümesinin tüm elemanlarının görüntülerinin oluşturduğu kümeye fonksiyonun görüntü kümesi denir ve \( f(A) \) ile gösterilir.
Tanım kümesindeki elemanların görüntüleri değer kümesindeki tüm elemanları kapsıyorsa görüntü kümesi değer kümesine eşit olur (\( f(A) = B \)), aksi takdirde (değer kümesinde açıkta elemanlar kalıyorsa) görüntü kümesi değer kümesinin bir öz alt kümesi olur (\( f(A) \subset B \)).
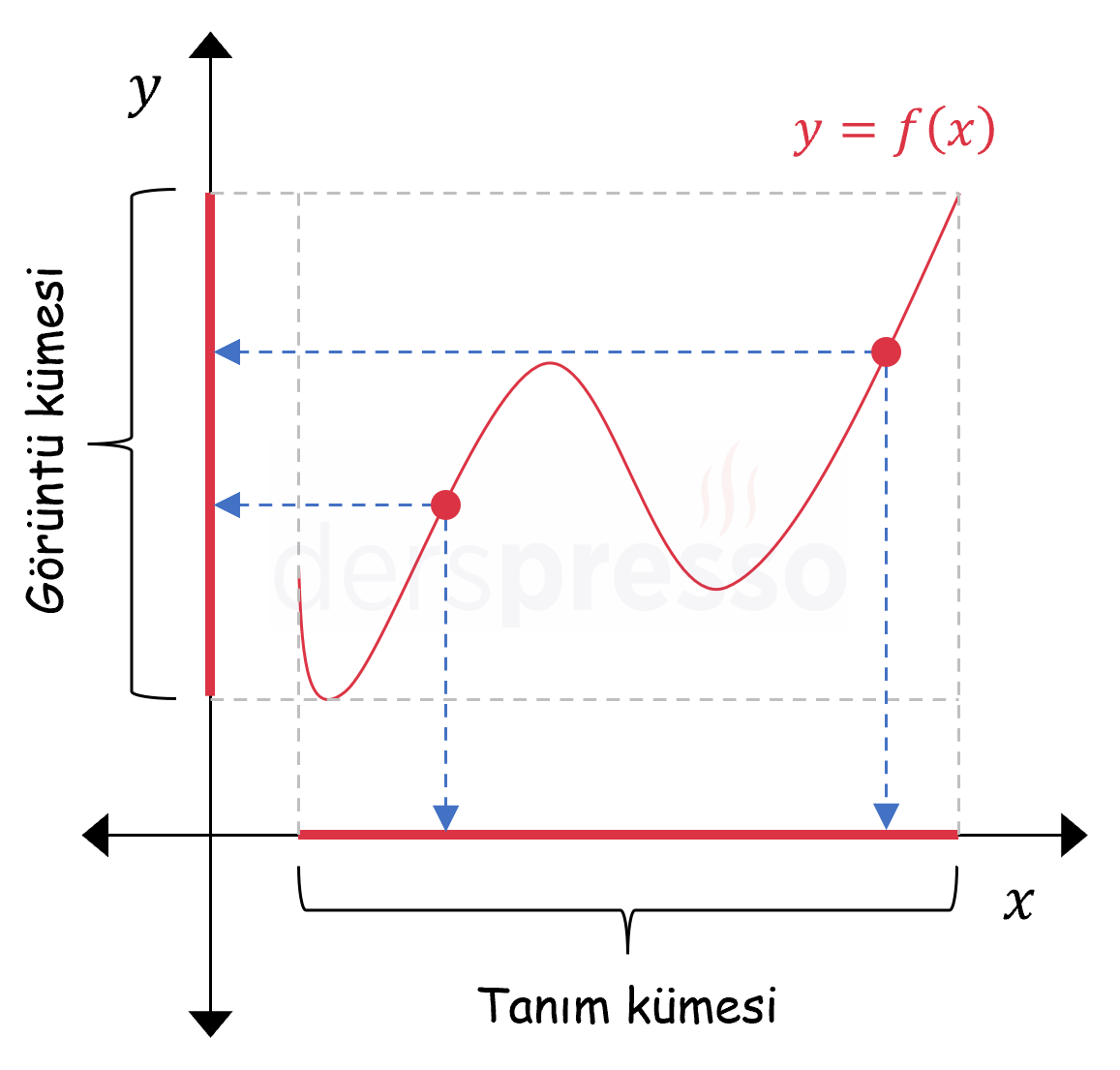
Bir fonksiyonun grafiği üzerindeki tüm noktaların \( x \) ekseni üzerindeki izdüşümleri tanım kümesini, \( y \) ekseni üzerindeki izdüşümleri de görüntü kümesini verir.
Tanım ve değer kümelerinin fonksiyon tanımında belirtilmediği durumlarda tanım kümesi fonksiyonun reel sayı sonuç verdiği en geniş aralık (örneğin polinom fonksiyonları için tüm reel sayılar, \( \sqrt{x} \) için negatif olmayan reel sayılar), değer kümesi de reel sayılar kümesi olarak kabul edilebilir.
Tanımsız Noktalar
Bir fonksiyonun tanım kümesindeki her eleman için bir değeri olması gerektiği için fonksiyonu tanımsız yapan \( x \) değerleri tanım kümesinin dışında tutulmalıdır. Bu tanımsızlık durumları aşağıdaki şekillerde olabilir.
Paydayı Sıfır Yapan Değerler
Rasyonel ifadelerde paydayı sıfır yapan \( x \) değerleri ifadeyi tanımsız yapar.
| İfade | Tanımsız Değerler |
|---|---|
| \( \dfrac{1}{x - 2} \) | Paydayı sıfır yapan \( x = 2 \) değerinde ifade tanımsız olur. |
| \( \dfrac{1}{x^2 - 5x + 6} \) | Paydayı sıfır yapan \( x \in \{ 2, 3 \} \) değerlerinde ifade tanımsız olur. |
| \( \dfrac{1}{x^2 - 4} + \dfrac{1}{x - 5} \) | Paydaları sıfır yapan \( x \in \{ -2, 2, 5 \} \) değerlerinde ifade tanımsız olur. |
| \( \dfrac{1}{\sin{x} - 1} \) | Paydayı sıfır yapan \( x \in \{\frac{\pi}{2} + 2k\pi, k \in \mathbb{Z} \} \) değerlerinde ifade tanımsız olur. |
Çift Dereceli Köklü İfadeler
Derecesi çift sayı olan köklü ifadelerin içi negatif olamayacağı için kök içini negatif yapan \( x \) değerleri ifadeyi tanımsız yapar.
| İfade | Tanımsız Değerler |
|---|---|
| \( \sqrt{x} \) | Kök içini negatif yapan \( x \lt 0 \) aralığında ifade tanımsız olur. |
| \( \sqrt{x - 2} - \sqrt[4]{6 - x} \) | Kök içini negatif yapan \( x \lt 2 \) ve \( x \gt 6 \) aralıklarında ifade tanımsız olur. |
| \( \sqrt{(x - 1)(x - 4)} \) | Kök içini negatif yapan \( 1 \lt x \lt 4 \) aralığında ifade tanımsız olur. |
Tanımsızlık İçeren Fonksiyonlar
Bir trigonometrik ya da logaritmik fonksiyonu tanımsız yapan \( x \) değerleri bu fonksiyonları içeren fonksiyonları da tanımsız yapar.
| Fonksiyon | Tanımsız Değerler |
|---|---|
| \( \tan{x} \) | Fonksiyon içini \( \{\frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) yapan \( x \) değerlerinde tanımsızdır. |
| \( \cot{x} \) | Fonksiyon içini \( \{k\pi, k \in \mathbb{Z} \} \) yapan \( x \) değerlerinde tanımsızdır. |
| \( \sec{x} \) | Fonksiyon içini \( \{\frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \) yapan \( x \) değerlerinde tanımsızdır. |
| \( \csc{x} \) | Fonksiyon içini \( \{k\pi, k \in \mathbb{Z} \} \) yapan \( x \) değerlerinde tanımsızdır. |
| \( \arcsin{x} \) | Fonksiyon içini \( [-1, 1] \) aralığı dışında bir değer yapan \( x \) değerlerinde tanımsızdır. |
| \( \arccos{x} \) | Fonksiyon içini \( [-1, 1] \) aralığı dışında bir değer yapan \( x \) değerlerinde tanımsızdır. |
| \( \arcsec{x} \) | Fonksiyon içini \( [-1, 1] \) aralığında bir değer yapan \( x \) değerlerinde tanımsızdır. |
| \( \arccsc{x} \) | Fonksiyon içini \( [-1, 1] \) aralığında bir değer yapan \( x \) değerlerinde tanımsızdır. |
| \( \log{x} \) | Logaritma içini sıfır ya da negatif yapan \( x \) değerlerinde tanımsızdır. |
| \( \ln{x} \) | Logaritma içini sıfır ya da negatif yapan \( x \) değerlerinde tanımsızdır. |
Görüntü Kümesinin Bulunması
Bir fonksiyonun grafiği verildiyse grafik üzerindeki tüm noktaların \( y \) ekseni üzerindeki izdüşümlerinin oluşturduğu küme görüntü kümesini verir.
Bir fonksiyonun grafiği verilmediyse ancak fonksiyonun grafik ve görüntü kümesi özellikleri biliniyorsa bu özellikler yardımıyla görüntü kümesi bulunabilir.
Ters fonksiyon konusunda göreceğimiz üzere, bir \( f \) fonksiyonunun görüntü kümesi ters fonksiyonu olan \( f^{-1} \) fonksiyonunun tanım kümesi ile, \( f \) fonksiyonunun tanım kümesi de \( f^{-1} \) fonksiyonunun görüntü kümesi ile aynıdır. Buna göre bir fonksiyonun ters fonksiyonunu ve ters fonksiyonunun tanım kümesini bulduğumuzda fonksiyonun görüntü kümesini de bulmuş oluruz.
\( f: [2, \infty) \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 4x + 1 \) fonksiyonunun görüntü kümesini bulalım.
Fonksiyonun ters fonksiyonu aşağıdaki gibidir.
\( f^{-1}(x) = \sqrt{x + 3} + 2 \)
Bu ters fonksiyonun tanım kümesi kök içini negatif yapan \( x \) değerleri dışında tüm reel sayılardır.
\( f^{-1} \) tanım kümesi: \( x \in [-3, \infty) \)
Buna göre \( f \) fonksiyonun görüntü kümesi de aynı aralık olur.
\( f \) görüntü kümesi: \( f(x) \in [-3, \infty) \)
\( A = \{4, 5, 7, 8\} \)
\( B = \{10, 12, 13, 15, 19, 22\} \)
\( f: A \to B \)
\( f(x) = 3x - 2 \) olduğuna göre, \( f \) fonksiyonunun görüntü kümesi nedir?
Çözümü GösterTanım kümesindeki tüm elemanların görüntüsünü bularak \( f \) fonksiyonunun görüntü kümesini bulalım.
\( f(4) = 3(4) - 2 = 10 \)
\( f(5) = 3(5) - 2 = 13 \)
\( f(7) = 3(7) - 2 = 19 \)
\( f(8) = 3(8) - 2 = 22 \)
\( f(A) = \{10, 13, 19, 22\} \) olarak bulunur.
\( f: A \to B \)
\( f(x) = \dfrac{x - 2}{2} \)
\( f(A) = \{2, 4, 6\} \) olduğuna göre, \( A \) kümesi nedir?
Çözümü Göster\( f(A) \) fonksiyonun görüntü kümesidir. Bu görüntü değerlerini veren \( x \) değerlerini bulalım.
\( \dfrac{x - 2}{2} = 2 \Longrightarrow x = 6 \)
\( \dfrac{x - 2}{2} = 4 \Longrightarrow x = 10 \)
\( \dfrac{x - 2}{2} = 6 \Longrightarrow x = 14 \)
Buna göre görüntüsü \( f(A) \) olan tanım kümesi \( A = \{ 6, 10, 14 \} \) olur.
\( f = \{ (1, 2), (2, 1), (3, 4), (4, 1) \} \)
\( f \) fonksiyonunun tanım, değer ve görüntü kümelerinden hangileri \( \{ 1, 2, 3, 4, 5 \} \) olabilir?
Çözümü GösterFonksiyonun elemanı olan ikililerdeki birinci bileşenler tanım kümesini oluşturur. Buna göre \( f \) fonksiyonunun tanım kümesi \( \{ 1, 2, 3, 4 \} \) olur.
Fonksiyonun elemanı olan ikililerdeki ikinci bileşenler görüntü kümesini oluşturur. Buna göre \( f \) fonksiyonunun görüntü kümesi \( \{ 1, 2, 4 \} \) olur.
Değer kümesi görüntü kümesini kapsayan herhangi bir küme olabilir. \( \{ 1, 2, 3, 4, 5 \} \) görüntü kümesini kapsadığı için değer kümesi olabilir.
Buna göre sadece değer kümesi \( \{ 1, 2, 3, 4, 5 \} \) olabilir.
\( f(x) = \sqrt{x^2 + 4x - 21} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterDerecesi çift sayı olan köklü ifadelerin içi negatif olamaz.
\( x^2 + 4x - 21 \ge 0 \)
\( (x + 7)(x - 3) \ge 0 \)
Bu eşitsizliğin çözüm kümesi \( (-\infty, -7] \cup [3, \infty) \) aralığıdır.
Buna göre \( f \) fonksiyonunun en geniş tanım kümesi aşağıdaki gibi bulunur.
Tanım kümesi \( = (-\infty, -7] \cup [3, \infty) \)
\( f(x) = \dfrac{3x + 1}{\abs{x + 1} - 2} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterVerilen rasyonel fonksiyon paydasını sıfır yapan değerler hariç tüm reel sayılarda tanımlıdır.
Paydayı sıfır yapan değerleri bulalım.
\( \abs{x + 1} - 2 = 0 \)
\( \abs{x + 1} = 2 \)
\( x + 1 = 2 \) veya \( x + 1 = -2 \)
\( x = 1 \) veya \( x = -3 \)
Buna göre fonksiyonun en geniş tanım kümesi aşağıdaki gibidir.
Tanım kümesi: \( \mathbb{R} - \{-3, 1\} \)
\( f(x) = \dfrac{2x + 6}{x^2 - 2x - 8} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü Göster\( f \) bir rasyonel fonksiyondur ve en geniş tanım kümesi paydayı sıfır yapan değerler hariç tüm reel sayılardır.
Paydayı sıfır yapan değerleri bulalım.
\( x^2 - 2x - 8 = 0 \)
\( (x + 2)(x - 4) = 0 \)
Buna göre fonksiyon \( x = -2 \) ve \( x = 4 \) için tanımsızdır ve en geniş tanım kümesi bu iki değer hariç tüm reel sayılardır.
Tanım kümesi \( = \mathbb{R} - \{ -2, 4 \} \)
\( f: (-2, 4] \to \mathbb{R} \)
\( f(x) = \dfrac{4x + 1}{2} \) olduğuna göre, fonksiyonun görüntü kümesindeki tam sayıların toplamı kaçtır?
Çözümü GösterFonksiyon doğrusal olduğu için tanım kümesinin sınır değerlerini fonksiyonda yerine koyarak görüntü kümesinin sınır değerlerini bulabiliriz.
\( \dfrac{4(-2) + 1}{2} = -\dfrac{7}{2} \)
\( \dfrac{4(4) + 1}{2} = \dfrac{17}{2} \)
Görüntü kümesi: \( (-\frac{7}{2}, \frac{17}{2}] \)
Fonksiyon doğrusal olduğu için bu aralıktaki her reel sayı değeri alır.
Buna göre görüntü kümesindeki tam sayılar aşağıdaki gibidir.
\( \{ -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8 \} \)
Bu sayıların toplamı \( 4 + 5 + 6 + 7 + 8 = 30 \) olur.
\( f: A \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 5 \) fonksiyonu veriliyor.
\( f(A) = \{4, 11, 20\} \) olduğuna göre, \( A \) kümesinin elemanları toplamı aşağıdakilerden hangisi olamaz?
(a) \( 0 \quad \) (b) \( 2 \quad \) (c) \( 6 \quad \) (d) \( 8 \quad \) (e) \( 10 \)
Çözümü Göster\( f \) fonksiyonuna göre görüntüsü \( f(A) \) kümesinin elemanları olabilecek değerleri bulalım.
\( x^2 - 5 = 4 \Longrightarrow x \in \{-3, 3\} \)
Hem -3 hem de 3'ün görüntüsü 4 olduğu için, tanım kümesi bu iki değerden en az birini içermelidir, ama ikisini birlikte içermek zorunda değildir.
\( x^2 - 5 = 11 \Longrightarrow x \in \{-4, 4\} \)
Hem -4 hem de 4'ün görüntüsü 11 olduğu için, tanım kümesi bu iki değerden en az birini içermelidir, ama ikisini birlikte içermek zorunda değildir.
\( x^2 - 5 = 20 \Longrightarrow x \in \{-5, 5\} \)
Hem -5 hem de 5'in görüntüsü 20 olduğu için, tanım kümesi bu iki değerden en az birini içermelidir, ama ikisini birlikte içermek zorunda değildir.
Buna göre tanım kümesi 3, 4, 5 ya da 6 elemanlı olabilir.
Seçeneklerden hangisinin tanım kümesindeki elemanların toplamı olabileceğini bulalım.
(a) \( A = \{-3, 3, -4, 4, -5, 5\} \) olduğu durumda elemanların toplamı 0 olur.
(b) \( A = \{-3, -4, 4, 5\} \) olduğu durumda elemanların toplamı 2 olur.
(c) \( A = \{-3, 4, 5\} \) olduğu durumda elemanların toplamı 6 olur.
(d) \( A = \{3, -4, 4, 5\} \) olduğu durumda elemanların toplamı 8 olur.
(e) Bu 6 değerle elemanları toplamı 10 olan bir tanım kümesi oluşturulamaz.
Doğru seçenek (e) olur.
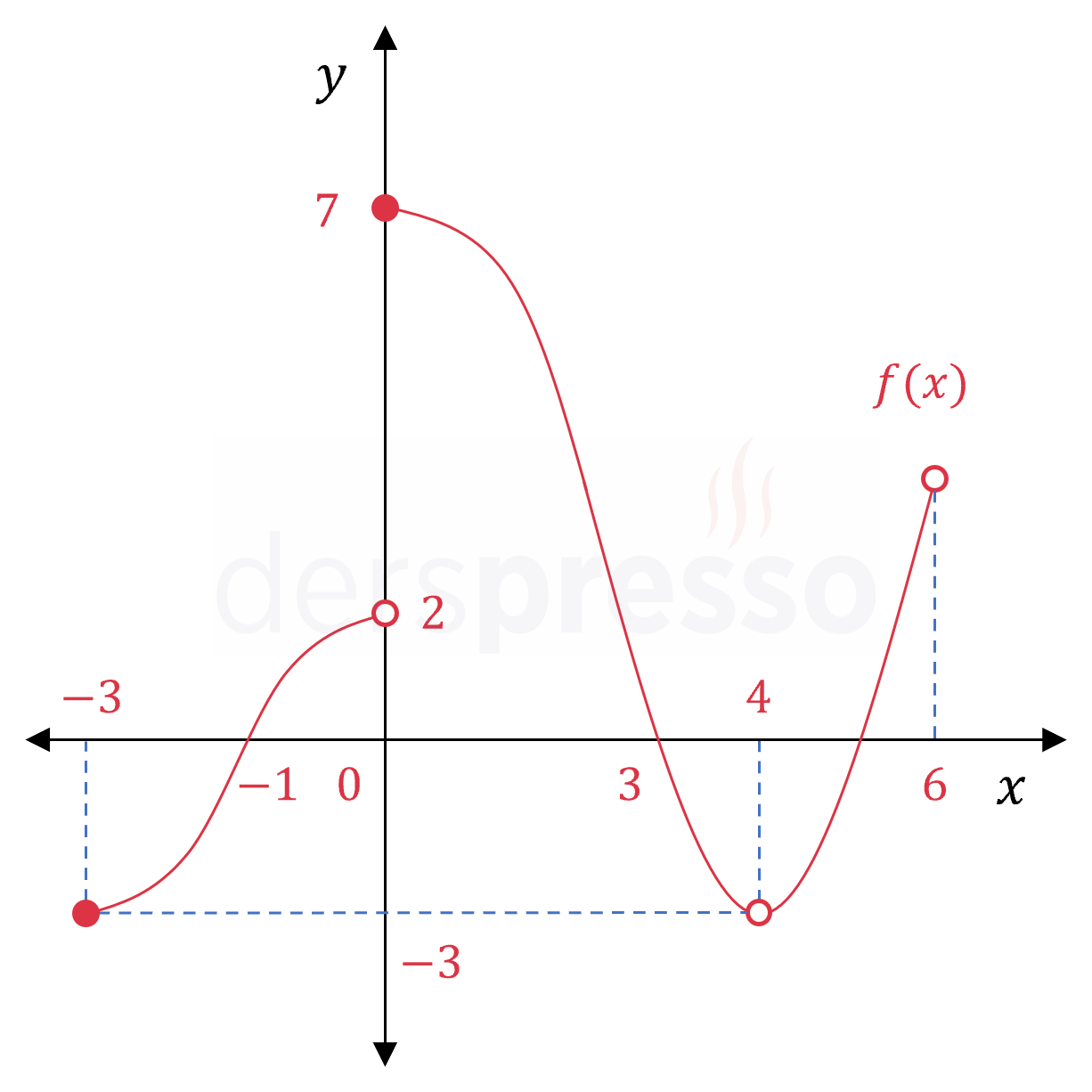
Yukarıda \( f \) fonksiyonunun grafiği verilmiştir. Buna göre aşağıdakilerden hangileri doğrudur?
I. \( f(0) = 7 \)
II. Tanım kümesi \( [-3, 6) \) aralığıdır.
III. Görüntü kümesi \( [-3, 7] \) aralığıdır.
IV. Fonksiyonun \( [-3, 6] \) aralığında tanımsız olduğu 3 nokta vardır.
V. \( f(-3) = f(4) \)
Çözümü GösterI. öncül: Fonksiyonun \( x = 0 \) noktasındaki değeri 2 değil 7'dir. Bu öncül doğrudur.
II. öncül: Fonksiyon \( x = 4 \) noktasında tanımsız olduğu için tanım kümesi \( [-3, 6) - \{4\} \) olur. Bu öncül yanlıştır.
III. öncül: Fonksiyon \( [-3, 7] \) aralığındaki tüm değerleri alır. Bu öncül doğrudur.
IV. öncül: Fonksiyonun belirtilen aralıkta tanımsız olduğu noktalar \( x = 4 \) ve \( x = 6 \)'dır. Fonksiyon \( x = 0 \) noktasında tanımlıdır ve değeri 7'dir. Bu öncül yanlıştır.
V. öncül: Fonksiyon \( x = 4 \) noktasında tanımsızdır. Bu öncül yanlıştır.
Buna göre I. ve III. öncüller doğrudur.
\( f(x) = (2x - 9)^2 + (7 - 2x)^2 \) parabolünün en küçük değeri nedir?
Çözümü GösterParantez içindeki ifadelerin açılımını yazalım.
\( f(x) = 4x^2 - 36x + 81 + 49 - 28x + 4x^2 \)
\( = 8x^2 - 64x + 130 \)
Parabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür, dolayısıyla parabol en küçük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Parabolün katsayılarını yazalım.
\( a = 8, \quad b = -64, \quad c = 130 \)
\( r = -\dfrac{b}{2a} = -\dfrac{-64}{2(8)} = 4 \)
Parabolün tepe noktasındaki değerini bulalım.
\( k = f(4) = 8(4)^2 - 64(4) + 130 \)
\( = 2 \) bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{9x + 3a}{(2a + 2)x + 2} \) olduğuna göre, \( f(a) \) kaçtır?
Çözümü GösterFonksiyonun tanım kümesi tüm reel sayılar olduğu için tanımsız olduğu bir nokta yoktur, dolayısıyla payda hiçbir \( x \) değeri için sıfır olmamalıdır.
Paydadaki \( x \)'in katsayısı sıfırdan farklı olduğunda paydayı sıfır yapan bir \( x \) değeri mutlaka olacağı için \( x \)'in katsayısı sıfır olmalıdır.
\( 2a + 2 = 0 \Longrightarrow a = -1 \)
Fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \dfrac{9x - 3}{2} \)
\( f(a) = f(-1) = \dfrac{9(-1) - 3}{2} = -6 \) bulunur.
Aşağıdaki fonksiyonlardan hangileri \( (-\infty, 0) \) aralığının tümünde reel sayı olarak tanımlıdır?
I. \( f(x) = \sqrt{-3x^3} \)
II. \( g(x) = \sqrt{-3x^2} \)
III. \( h(x) = \sqrt[3]{3x^3} \)
IV. \( k(x) = \sqrt{3x} \)
Çözümü Göster\( (-\infty, 0) \) aralığı tüm negatif reel sayılara karşılık gelir.
I. öncül:
\( x \) negatif olduğunda \( x^3 \) negatif, \( -3x^3 \) pozitif olur.
\( \sqrt{-3x^3} \) ifadesi karekök içindeki sayı pozitif olduğu için reel sayı olarak tanımlıdır.
II. öncül:
\( x \) negatif olduğunda \( x^2 \) pozitif, \( -3x^2 \) negatif olur.
\( \sqrt{-3x^3} \) ifadesi karekök içindeki sayı negatif olduğu için reel sayı olarak tanımlı değildir.
III. öncül:
\( x \) negatif olduğunda \( x^3 \) ve \( 3x^3 \) negatif olur.
Küpkök fonksiyonu kök içinin tüm reel sayı değerlerinde reel sayı olarak tanımlıdır.
IV. öncül:
\( x \) negatif olduğunda \( 3x \) negatif olur.
\( \sqrt{3x} \) ifadesi karekök içindeki sayı negatif olduğu için reel sayı olarak tanımlı değildir.
Buna göre I. ve III. öncüllerdeki fonksiyonlar \( (-\infty, 0) \) aralığının tümünde reel sayı olarak tanımlıdır.
\( f(x) = (x - 16x^{-1})^{-1} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterFonsiyonu üslerden kurtaralım.
\( f(x) = (x - \dfrac{16}{x})^{-1} \)
\( = \dfrac{1}{x - \frac{16}{x}} \)
Paydayı sıfır yapan değerler tanımsız olduğu için \( x = 0 \) değeri tanım kümesine dahil değildir.
\( = \dfrac{1}{\frac{x^2 - 16}{x}} \)
\( = \dfrac{x}{(x - 4)(x + 4)} \)
Paydayı sıfır yapan \( x = -4 \) ve \( x = 4 \) değerleri tanım kümesine dahil değildir.
\( f \) fonksiyonunun en geniş tanım kümesi bulduğumuz üç değer dışındaki tüm reel sayılardır.
Tanım kümesi: \( x \in \mathbb{R} - \{ -4, 0, 4 \} \) bulunur.
\( f(x) = \sqrt{2 - \sqrt{1 + \sqrt{x^2 - 6x + 9}}} \) fonksiyonunun en geniş tanım kümesini bulunuz.
Çözümü GösterEn dıştaki köklü ifadeden en içtekine adım adım ilerleyerek fonksiyonun tanım kümesini bulalım.
Derecesi çift sayı olan bir köklü ifadenin içi negatif olamaz.
\( 2 - \sqrt{1 + \sqrt{x^2 -6x + 9}} \ge 0 \)
\( \sqrt{1 + \sqrt{x^2 - 6x + 9}} \le 2 \)
Kök işaretinden kurtulmak için eşitsizliğin her iki tarafının karesini alalım. Ayrıca kök içi negatif olamaz.
\( 0 \le 1 + \sqrt{x^2 - 6x + 9} \le 4 \)
\( -1 \le \sqrt{x^2 - 6x + 9} \le 3 \)
Bir karekök ifadesinin sonucu negatif olamayacağı için eşitsizliğin alt sınır değerini sıfır yapalım.
\( 0 \le \sqrt{x^2 - 6x + 9} \le 3 \)
\( 0 \le \sqrt{(x - 3)^2} \le 3 \)
Kök içindeki ifade mutlak değerin tanımıdır.
\( 0 \le \abs{x - 3} \le 3 \)
\( -3 \le x - 3 \le 3 \)
\( 0 \le x \le 6 \)
Tanım kümesi: \( x \in [0, 6] \)
\( f(x) = \dfrac{\sqrt{25 - x^2}}{\sqrt{x - 4}} \)
\( g(x) = \sqrt{\dfrac{25 - x^2}{x - 4}} \)
fonksiyonlarının tanımlı olduğu \( x \) reel sayı aralıklarını bulunuz.
Çözümü GösterDerecesi çift sayı olan köklü ifadelerin içini negatif yapan ve rasyonel bir ifadenin paydasını sıfır yapan \( x \) değerleri fonksiyonu tanımsız yapar.
\( f \) fonksiyonunun tanım kümesini bulalım.
Paydaki köklü ifadenin içi negatif olamaz.
\( 25 - x^2 \ge 0 \)
\( x^2 \le 25 \)
\( -5 \le x \le 5 \)
Paydadaki köklü ifadenin içi negatif olamaz.
\( x - 4 \ge 0 \)
\( x \ge 4 \)
Paydadaki köklü ifadenin içi sıfır olamaz.
\( x \ne 4 \)
Yukarıda bulduğumuz aralıkların kesişim kümesi \( f \) fonksiyonunun tanım kümesini verir.
Tanım kümesi: \( x \in (4, 5] \)
\( g \) fonksiyonunun tanım kümesini bulalım.
Köklü ifadenin içi negatif olamaz.
\( \dfrac{25 - x^2}{x - 4} \ge 0 \)
Bu eşitsizliği çözmek için işaret tablosu yapalım.

Buna göre bu eşitsizliğin çözüm kümesi aşağıdaki aralıktır.
\( x \in (-\infty, -5] \cup (4, 5] \)
Paydadaki köklü ifadenin içi sıfır olamaz.
\( x \ne 4 \)
Bulduğumuz aralıkların kesişim kümesi \( g \) fonksiyonunun tanım kümesini verir.
Tanım kümesi: \( x \in [-\infty, 5) \cup (4, 5] \)
\( f(x) = \dfrac{x}{\sqrt{4x - 8} - 2} \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterKöklü ifadenin içi negatif olamayacağı için kök içini negatif yapan \( x \) değerleri tanım kümesinde yer alamaz.
\( 4x - 8 \ge 0 \)
\( x \ge 2 \)
İfadenin paydası sıfır olmayacağı için paydayı sıfır yapan \( x \) değerleri de tanım kümesinde yer alamaz.
\( \sqrt{4x - 8} - 2 \ne 0 \)
\( \sqrt{4x - 8} \ne 2 \)
\( 4x - 8 \ne 4 \)
\( x \ne 3 \)
Bu iki koşulu sağlayan reel sayılar fonksiyonun en geniş tanım kümesini oluşturur.
Tanım kümesi: \( [2, \infty) - \{3\} \)
\( f(x) = \dfrac{\sqrt{x - 3} + \sqrt{7 - x}}{x^2 - 9x + 20} \) fonksiyonunun en geniş tanım kümesindeki tam sayıların toplamı kaçtır?
Çözümü GösterDerecesi çift sayı olan köklü ifadelerin içi negatif olamaz.
\( x - 3 \ge 0 \Longrightarrow x \ge 3 \)
\( 7 - x \ge 0 \Longrightarrow x \le 7 \)
\( 3 \le x \le 7 \)
Rasyonel ifadelerde payda sıfır olamaz.
\( x^2 - 9x + 20 \ne 0 \)
\( (x - 4)(x - 5) \ne 0 \)
\( x \ne 4 \) ve \( x \ne 5 \)
Buna göre fonksiyonun en geniş tanım kümesindeki tam sayı değerleri \( \{ 3, 6, 7 \} \) olur.
\( 3 + 6 + 7 = 16 \) bulunur.
\( f(x) = \sqrt{6 - \sqrt{x}} \) fonksiyonunun en geniş tanım kümesinde kaç tam sayı eleman vardır?
Çözümü GösterDerecesi çift sayı olan köklü ifadelerin içi negatif olamaz.
İçteki karekök ifadesi için:
\( x \ge 0 \)
Dıştaki karekök ifadesi için:
\( 6 - \sqrt{x} \ge 0 \)
\( \sqrt{x} \le 6 \)
\( 0 \le x \le 36 \)
Bu iki aralığın kesişimini alalım.
\( 0 \le x \le 36 \)
Buna göre fonksiyonun en geniş tanım aralığında \( 36 - 0 + 1 = 37 \) tam sayı eleman vardır.
\( f(x) = \sqrt{3 - \abs{x + 1}} \) fonksiyonunun en geniş tanım kümesinde kaç tam sayı eleman vardır?
Çözümü GösterDerecesi çift sayı olan köklü ifadelerin içi negatif olamaz.
\( 3 - \abs{x + 1} \ge 0 \)
\( \abs{x + 1} \le 3 \)
\( -3 \le x + 1 \le 3 \)
\( -4 \le x \le 2 \)
Buna göre fonksiyonun en geniş tanım aralığında \( 2 - (-4) + 1 = 7 \) tam sayı eleman vardır.
\( f(x) = \dfrac{2xf(x) + 3x + 1}{3x - 2} \) olduğuna göre, \( f(x) \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü Göster\( f(x) \) ifadesini yalnız bırakalım.
\( f(x)(3x - 2) = 2xf(x) + 3x + 1 \)
\( 3xf(x) - 2f(x) = 2xf(x) + 3x + 1 \)
\( f(x)(x - 2) = 3x + 1 \)
\( f(x) = \dfrac{3x + 1}{x - 2} \)
\( f \) bir rasyonel fonksiyondur ve en geniş tanım kümesi paydayı sıfır yapan değerler hariç tüm reel sayılardır.
Buna göre fonksiyon \( x = 2 \) için tanımsızdır ve en geniş tanım kümesi bu değer hariç tüm reel sayılardır.
Tanım kümesi \( = \mathbb{R} - \{ 2 \} \)
\( f(x) = 6 - \sqrt{x - 5} \) fonksiyonunun en geniş görüntü kümesi nedir?
Çözümü GösterKarekök içindeki ifadenin alabileceği en küçük değer 0 olduğu için fonksiyonun en büyük değeri 6'dır.
Karekök içindeki ifadenin alabileceği en büyük değer pozitif sonsuz olduğu için fonksiyonun en küçük değeri negatif sonsuzdur.
Buna göre fonksiyonun en geniş görüntü kümesi aşağıdaki gibi bulunur.
Görüntü kümesi \( = (- \infty, 6] \)
\( f(x) = 3^{2 - x} + 5 \) fonksiyonunun en geniş görüntü kümesi nedir?
Çözümü GösterFonksiyonun tanımsız olduğu bir değer olmadığı için en geniş tanım kümesi tüm reel sayılardır.
\( 3^{2 - x} = (\dfrac{1}{3})^{x - 2} = 9 \cdot (\dfrac{1}{3})^x \)
\( (\frac{1}{3})^x \) ifadesi bir üstel fonksiyondur ve grafiğini düşündüğümüzde görüntü kümesi \( (0, \infty) \) aralığıdır.
Bu aralığa sabit terim olarak 5 eklediğimizde görüntü kümesi \( (5, \infty) \) olur.
\( f(x) = \sqrt{\dfrac{4^{-x} - 2}{3^x - 1 }} \) fonksiyonunun en geniş tanım kümesini bulunuz.
Çözümü GösterBu fonksiyonun tanımlı olabilmesi için kök içindeki ifade sıfıra eşit ya da sıfırdan büyük olmalıdır ve paydadaki ifade sıfırdan farklı olmalıdır.
\( \dfrac{4^{-x} - 2}{3^x - 1} \ge 0 \)
Payı sıfır yapan değeri bulalım.
\( 4^{-x} - 2 = 0 \)
\( 4^{-x} = 2 \)
\( 2^{-2x} = 2^1 \)
Üslü ifadeler arasındaki eşitlikte tabanlar birbirine eşit ve -1, 0, 1'den farklı ise üsler de eşittir.
\( -2x = 1 \)
\( x = -\dfrac{1}{2} \)
Paydayı sıfır yapan değeri bulalım.
\( 3^x - 1 = 0 \)
\( x = 0 \)
Bu değerleri kullanarak eşitsizlik için işaret tablosu yapalım.

Buna göre verilen ifade \( [-\frac{1}{2}, 0) \) aralığında tanımlıdır.
Tanım kümesi: \( x \in [-\frac{1}{2}, 0) \)
\( f(x) = 3\sqrt{4 - x^2} \) fonksiyonun reel sayılardaki en geniş tanım kümesi \( A \) ve görüntü kümesi \( B \) olduğuna göre, aşağıdaki ifadelerden hangileri doğrudur?
I. \( A = [-2, 2] \)
II. \( B = [0, 6] \)
III. \( A \cap B = [-2, 6] \)
Çözümü GösterDerecesi çift sayı olan köklü ifadelerin içi negatif olamaz.
\( 4 - x^2 \ge 0 \)
\( (2 - x)(2 + x) \ge 0 \)
\( x \in [-2, 2] \)
Buna göre fonksiyonun en geniş tanım kümesi \( A = [-2, 2] \) olur. I. öncül doğrudur.
Kök içindeki ifade negatif başkatsayılı bir paraboldür ve kolları aşağı yönlüdür. Bu parabolün alabileceği en küçük ve en büyük değerleri bulmak için tepe noktasındaki ve tanım kümesinin sınır değerlerindeki fonksiyon değerlerini bulalım.
Denklemi \( y = 4 - x^2 \) olan parabolün tepe noktasının apsis değeri \( x = -\frac{b}{2a} = -\frac{0}{-2} = 0 \) olur.
\( f(0) = 3\sqrt{4 - 0^2} = 6 \)
\( f(-2) = 3\sqrt{4 - (-2)^2} = 0 \)
\( f(2) = 3\sqrt{4 - 2^2} = 0 \)
Buna göre fonksiyonun tanım aralığında aldığı en küçük ve en büyük değerler \( 0 \) ve \( 6 \)'dır, dolayısıyla görüntü kümesi \( B = [0, 6] \) olur. II. öncül doğrudur.
Tanım ve görüntü kümelerinin kesişimi \( A \cap B = [0, 2] \) aralığıdır. III. öncül yanlıştır.
Buna göre I. ve II. öncüller doğrudur.
\( f(x) = \begin{cases} 2\sin{x} + 3 & 0 \le x \lt \pi \\ 3\cos{x} & \pi \le x \le 2\pi \end{cases} \)
şeklinde tanımlanan \( f \) fonksiyonunun görüntü kümesini bulunuz.
Çözümü GösterVerilen parçalı fonksiyonun iki aralığı için görüntü kümesini ayrı ayrı bulalım.
\( 0 \le x \lt \pi \) aralığı için:
Sinüs fonksiyonu bu aralıkta \( [0, 1] \) aralığında değer alır.
\( 0 \le \sin{x} \le 1 \)
\( 0 \le 2\sin{x} \le 2 \)
\( 3 \le 2\sin{x} + 3 \le 5 \)
\( \pi \le x \le 2\pi \) aralığı için:
Kosinüs fonksiyonu bu aralıkta \( [-1, 1] \) aralığında değer alır.
\( -1 \le \cos{x} \le 1 \)
\( -3 \le 3\cos{x} \le 3 \)
Buna göre \( f \) fonksiyonunun görüntü kümesi \( [3, 5] \cup [-3, 3] = [-3, 5] \) aralığıdır.
\( A = \{2, 3, 4, 5\} \) ve \( B = \{0, 1, 2, 3, 4\} \) olduğuna göre,
\( A \)'dan \( B \)'ye tanımlanacak bir fonksiyonun görüntü kümesi kaç farklı şekilde olabilir?
Çözümü GösterTanım kümesi 4 elemanlı olduğu için bu 4 eleman hiçbir zaman değer kümesindeki 5 elemanla eşlenemez, dolayısıyla görüntü kümesi 1, 2, 3 ya da 4 elemanlı olabilir.
5 elemanlı değer kümesinin elemanları içinden belirli sayıda eleman aşağıdaki şekillerde seçilebilir.
1 elemanlı görüntü kümeleri: \( C(5, 1) = 5 \)
2 elemanlı görüntü kümeleri: \( C(5, 2) = 10 \)
3 elemanlı görüntü kümeleri: \( C(5, 3) = 10 \)
4 elemanlı görüntü kümeleri: \( C(5, 4) = 5 \)
Buna göre görüntü kümesi \( 5 + 10 + 10 + 5 = 30 \) farklı şekilde olabilir.
\( A = \{x, y, z, t\} \)
\( B = \{1, 2, 3, 4, 5, 6, 7\} \) olmak üzere,
\( f(y) = 5 \) olacak şekilde \( A \) kümesinden \( B \) kümesine tanımlanacak \( f \) fonksiyonunun görüntü kümesi kaç farklı şekilde olabilir?
Çözümü GösterTanım kümesi 4 elemanlı olduğu için görüntü kümesi de en çok 4 elemanlı olabilir.
Durum 1: Görüntü kümesi 1 elemanlı
\( f(y) = 5 \) olarak verildiği için 1 elemanlı sadece bir görüntü kümesi olur.
Durum 2: Görüntü kümesi 2 elemanlı
"5" dışında değer kümesinin 6 elemanı içinden 1 eleman \( C(6, 1) = 6 \) farklı şekilde seçilebilir.
Durum 3: Görüntü kümesi 3 elemanlı
"5" dışında değer kümesinin 6 elemanı içinden 2 eleman \( C(6, 2) = 15 \) farklı şekilde seçilebilir.
Durum 4: Görüntü kümesi 4 elemanlı
"5" dışında değer kümesinin 6 elemanı içinden 3 eleman \( C(6, 3) = 20 \) farklı şekilde seçilebilir.
Buna göre görüntü kümesi \( 1 + 6 + 15 + 20 = 42 \) farklı şekilde olabilir.
\( f: [1, \infty) \to \mathbb{R} \) olmak üzere,
\( f(x) = (x - 3)^2 + 2 \)
fonksiyonunun grafiğini çizerek görüntü kümesini bulunuz.
Çözümü GösterParabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür.
\( f(x) = (x - r)^2 + k \) formundaki bir parabolün tepe noktası \( T(r, k) \) noktasıdır.
Buna göre verilen parabolün tepe noktası \( T(3, 2) \) olur.
\( x = 1 \) noktasındaki fonksiyon değerini bulalım.
\( f(1) = (1 - 3)^2 + 2 = 6 \)
Buna göre parabolün \( x \in [1, \infty) \) aralığındaki grafiği aşağıdaki gibidir.
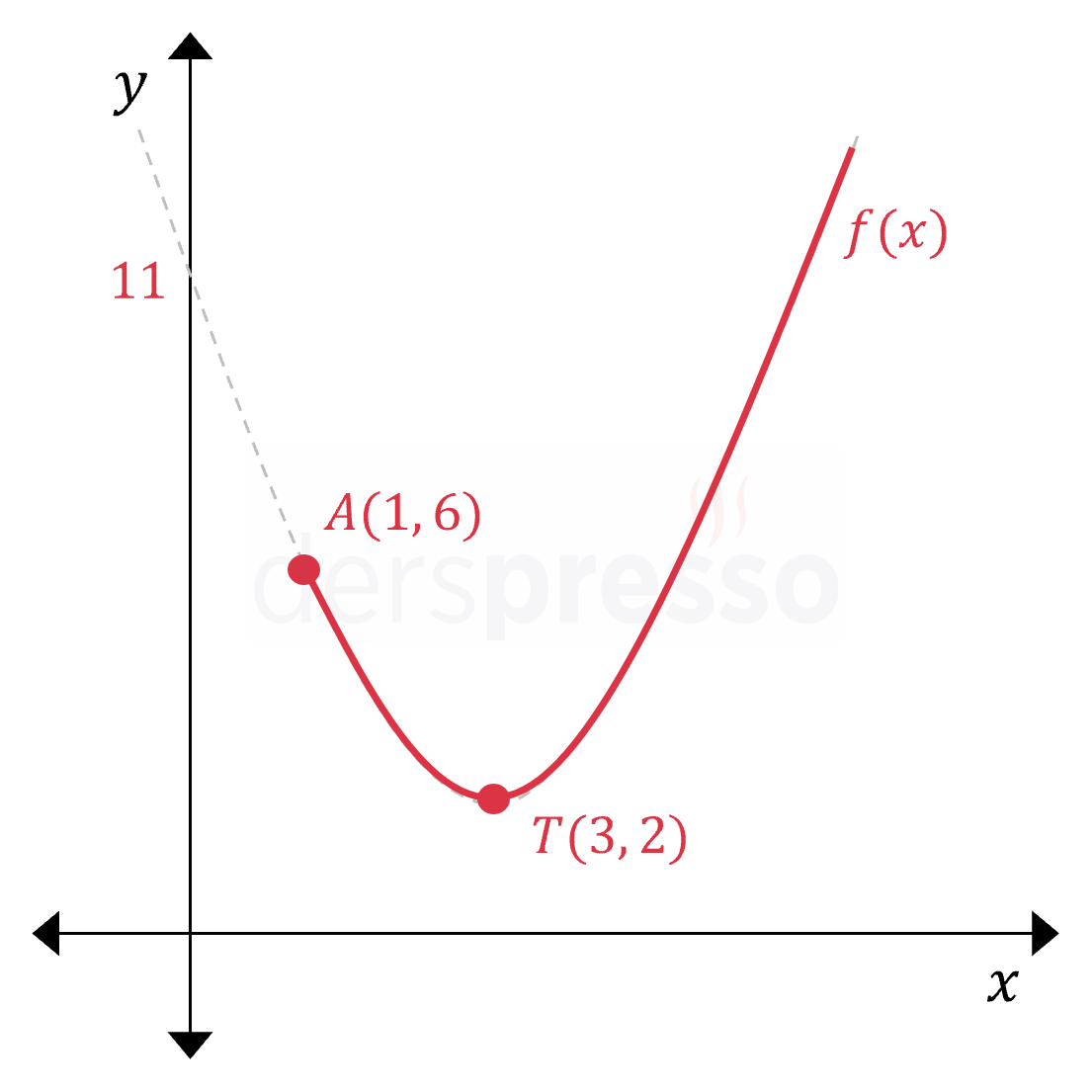
Grafikte görülebileceği üzere, parabolün en küçük değeri tepe noktasındaki \( y = 2 \) değeridir, ayrıca parabol \( x \) sonsuza giderken pozitif sonsuza gider.
Görüntü kümesi: \( f(x) \in [2, \infty) \)
\( f: [2, 8] \to \mathbb{R} \) olmak üzere,
\( f(x) = -\dfrac{1}{2}x^2 + 4x + 3 \)
fonksiyonunun grafiğini çizerek görüntü kümesini bulunuz.
Çözümü GösterParabolün başkatsayısı negatif olduğu için kolları aşağı yönlüdür.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{4}{2(-\frac{1}{2})} = 4 \)
\( k = f(4) \)
\( = -\dfrac{1}{2}(4)^2 + 4(4) + 3 = 11 \)
Buna göre verilen parabolün tepe noktası \( T(4, 11) \) olur.
Fonksiyonun tanım kümesinin uç noktalarındaki değerini bulalım.
\( f(2) = -\dfrac{1}{2}(2)^2 + 4(2) + 3 = 9 \)
\( f(8) = -\dfrac{1}{2}(8)^2 + 4(8) + 3 = 3 \)
Buna göre parabolün \( x \in [2, 8] \) aralığındaki grafiği aşağıdaki gibidir.
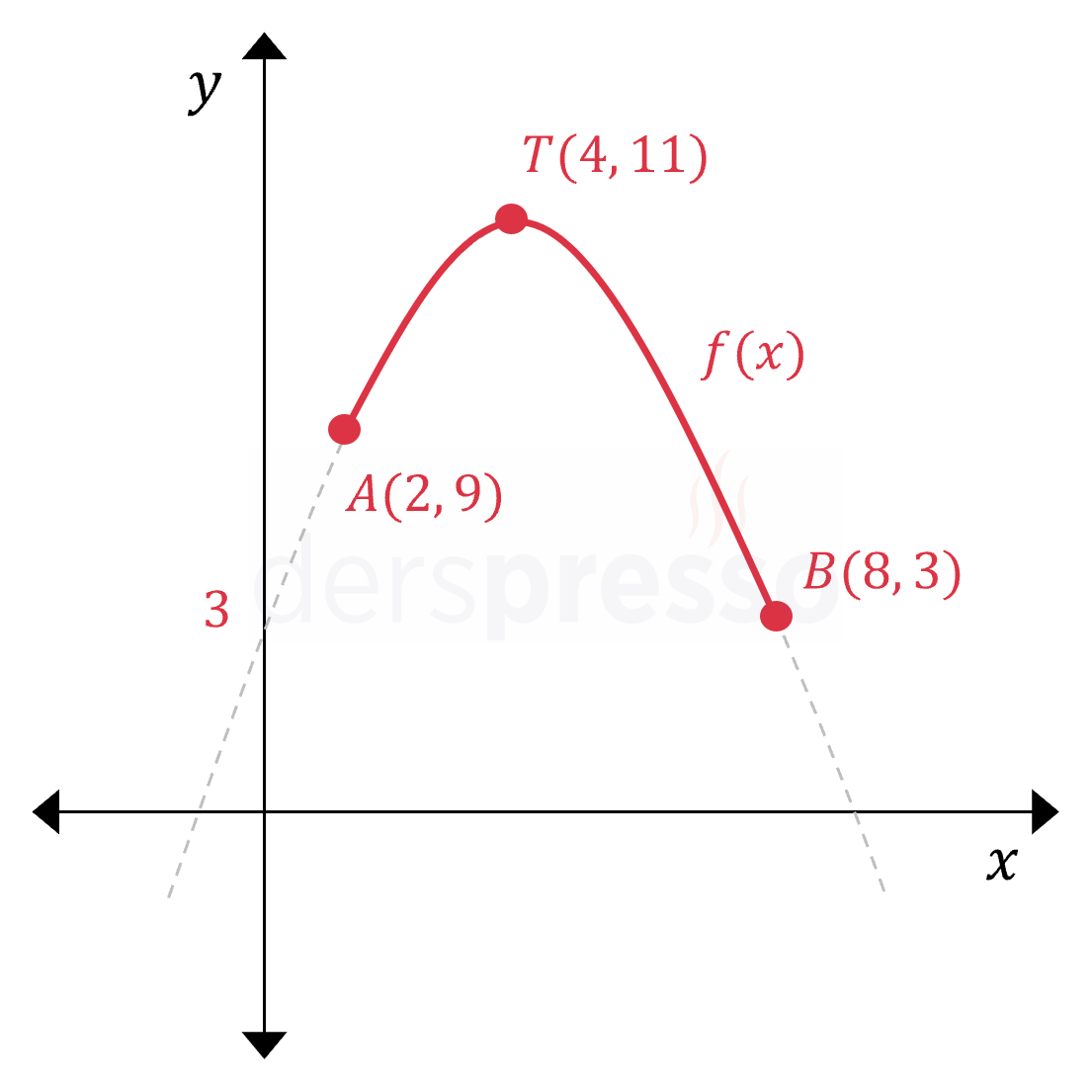
Grafikte görülebileceği üzere, parabolün en küçük değeri \( B \) noktasındaki \( y = 3 \) değeri, en büyük değeri tepe noktasındaki \( y = 11 \) değeridir.
Görüntü kümesi: \( f(x) \in [3, 11] \)

Yukarıda verilen \( f(x) \) fonksiyonunun grafiğine göre aşağıdaki ifadelerden hangileri doğrudur?
I. \( y = -f(x) \) fonksiyonunun görüntü kümesi \( [-3 , \infty) \) aralığıdır.
II. \( y = 2f(x) \) fonksiyonunun görüntü kümesi \( (-\infty, 6] \) aralığıdır.
III. \( y = f^2(x) \) fonksiyonunun görüntü kümesi \( (-\infty, 9] \) aralığıdır.
Çözümü Göster\( f(x) \) fonksiyonunun görüntü kümesi \( (- \infty, 3] \) aralığıdır.
I. öncül: \( y = -f(x) \) fonksiyonu \( f(x) \) fonksiyonunun \( x \) eksenine göre simetriğidir ve görüntü kümesi \( [-3 , \infty) \) aralığıdır. Bu öncül doğrudur.
II. öncül: \( 2f(x) \) fonksiyonunda grafik üzerindeki tüm noktalar \( x \) ekseninden iki kat uzaklaşır ve görüntü kümesi \( (-\infty, 6] \) olur. Bu öncül doğrudur.
III. öncül: \( f^2(x) \) fonksiyonunda ordinat değeri 0 ya da pozitif olan noktaların ordinat değerlerinin karesi alınır ve bu noktaların görüntü kümesi \( [0, 9] \) olur. Ordinat değeri negatif olan noktalar ise eksenin pozitif tarafına taşınır ve bu noktaların görüntü kümesi \( [0, \infty] \) olur. Sonuç olarak fonksiyonun görüntü kümesi \( [0, \infty] \) olur. Bu öncül yanlıştır.
Buna göre I. ve II öncüller doğrudur.
\( f(x) = \sqrt{x^2 - 8x + 25} \) fonksiyonunun en geniş tanım ve görüntü kümelerini bulunuz.
Çözümü GösterKök içerisindeki ifadede tam kare elde etmeye çalışalım.
\( x^2 - 8x + 25 = x^2 - 8x + 16 + 9 \)
\( = (x - 4)^2 + 9 \)
\( f(x) = \sqrt{(x - 4)^2 + 9} \)
Derecesi çift sayı olan bir köklü ifadenin içi negatif olamaz.
\( (x - 4)^2 \) ifadesi negatif olamayacağı için \( (x - 4)^2 + 9 \) ifadesi de negatif olamaz.
Dolayısıyla fonksiyon her \( x \) değeri için tanımlıdır.
Tanım kümesi: \( x \in \mathbb{R} \)
Görüntü kümesini bulmak için verilen ifadeyi inceleyelim.
\( (x - 4)^2 + 9 \) ifadesi \( x^2 \) parabolünün 4 birim sağa, 9 birim yukarı ötelenmiş halidir.
Parabolün tepe noktası \( T(4, 9) \) noktası ve başkatsayısı pozitif olduğuna göre görüntü kümesi aşağıdaki aralıkta olur.
\( 9 \le (x - 4)^2 + 9 \lt \infty \)
Eşitsizliğin taraflarının karekökünü aldığımızda \( f(x) \)'i elde ederiz.
\( 3 \le \sqrt{(x - 4)^2 + 9} \lt \infty \)
\( 3 \le f(x) \lt \infty \)
Görüntü kümesi: \( f(x) = [3, \infty) \)
\( f(x) = 3 + 2^{2x - x^2} \) fonksiyonunun en geniş görüntü kümesi nedir?
Çözümü GösterFonksiyonun tanımsız olduğu bir değer olmadığı için en geniş tanım kümesi tüm reel sayılardır.
\( 2^{2x - x^2} \) ifadesi tabanı 1'den büyük olan bir üstel fonksiyondur ve grafiğini düşündüğümüzde fonksiyon en küçük değerini üssünün en küçük değerinde, en büyük değerini üssünün en büyük değerinde alır.
\( 2x - x^2 \) ifadesi bir paraboldür ve başkatsayısı negatif olduğu için en küçük değeri \( -\infty \) olur, en büyük değerini de tepe noktasında alır.
\( T(r, k) \) parabolün tepe noktası olmak üzere,
\( a = -1, \quad b = 2, \quad c = 0 \)
\( r = -\dfrac{b}{2a} = -\dfrac{2}{-2} = 1 \)
Buna göre \( x = 1 \) noktasında \( 2x - x^2 \) parabolü, dolayısıyla \( 2^{2x - x^2} \) ifadesi ve \( f(x) \) en büyük değerini alır.
\( f(1) = 3 + 2^{2 \cdot 1 - 1^2} = 5 \)
Fonksiyonun en küçük değerini bulalım.
\( 2x - x^2 \) ifadesi negatif sonsuza giderken \( 2^{2x - x^2} \) ifadesi 0'a yaklaşır, ama 0 değerini almaz. \( f(x) \) de bu durumda sabit terim olan 3'e yaklaşır, ama 3 değerini almaz.
Buna göre fonksiyonun en geniş görüntü kümesi \( (3, 5] \) olur.
\( f(x) = 2^{2x} + 5^{2x} + 2^{-2x} + 5^{-2x} + 6 \) fonksiyonunun en geniş tanım kümesi için görüntü kümesini bulunuz.
Çözümü GösterFonksiyon sadece üstel ve sabit ifadelerden oluştuğu için terimleri tanımsız yapan bir \( x \) değeri yoktur, dolayısıyla en geniş tanım kümesi tüm reel sayılardır.
Tanım kümesi: \( x \in \mathbb{R} \)
\( 6 = 10 - 2 - 2 \) yazarak fonksiyonu düzenleyelim.
\( f(x) = 2^{2x} - 2 + 2^{-2x} + 5^{2x} - 2 + 5^{-2x} + 10 \)
\( -2 \) terimlerini düzenleyelim.
\( = (2^{2x} - 2 \cdot 2^x \cdot 2^{-x} + 2^{-2x}) + (5^{2x} - 2 \cdot 5^x \cdot 5^{-x} + 5^{-2x}) + 10 \)
Parantez içindeki ifadeler parantez karesi ifadelerinin açılımıdır.
\( = (2^x - 2^{-x})^2 + (5^x - 5^{-x})^2 + 10 \)
İlk iki terim tam kare ifadeler olduğu için negatif olamazlar, \( x = 0 \) olduğunda iki ifade de ayrı ayrı sıfıra eşit olur.
Ayrıca \( x \) pozitif sonsuza giderken iki ifade de ayrı ayrı pozitif sonsuza gider.
\( 0 \le (2^x - 2^{-x})^2 + (5^x - 5^{-x})^2 \lt \infty \)
Eşitsizliğin taraflarına 10 eklediğimizde \( f(x) \)'i elde ederiz.
\( 10 \le (2^x - 2^{-x})^2 + (5^x - 5^{-x})^2 + 10 \lt \infty \)
\( 10 \le f(x) \lt \infty \)
Görüntü kümesi: \( f(x) \in [10, \infty) \)
\( f \) fonksiyonunun tanım kümesi \( [3, 4] \), görüntü kümesi \( [-2, 1] \) aralığıdır.
\( g(x) = f^2(\sqrt{x}) + 5 \) olduğuna göre, \( g \) fonksiyonunun en geniş tanım ve görüntü kümelerini bulunuz.
Çözümü Göster\( g(x) \)'in tanımlı olabilmesi için \( f(\sqrt{x}) \) tanımlı olmalıdır.
\( f \) fonksiyonunun en geniş tanım kümesini verecek \( g(x) \) tanım kümesini bulalım.
\( f(3) = f(\sqrt{9}) \)
\( f(4) = f(\sqrt{16}) \)
Buna göre, \( g(x) \) tanım kümesi \( [9, 16] \) olmalıdır.
\( g(x) \)'in görüntü kümesi için \( f^2(\sqrt{x}) \) ifadesinin alabileceği en küçük ve en büyük değerleri bulalım.
En büyük değer için karesi en büyük değer olan \( f(\sqrt{x}) = -2 \) koyalım.
\( f^2(\sqrt{x}) + 5 = (-2)^2 + 5 = 9 \)
En küçük değer için karesi en küçük değer olan \( f(\sqrt{x}) = 0 \) koyalım.
\( f^2(\sqrt{x}) + 5 = 0^2 + 5 = 5 \)
\( g(x) \)'in görüntü kümesi \( [5, 9] \) olur.
\( g \) fonksiyonunun tanım kümesi \( [9, 16] \), görüntü kümesi \( [5, 9] \) olarak bulunur.