Birebir Fonksiyon
Bir fonksiyonun tanım kümesindeki her elemanın görüntüsü farklıysa bu fonksiyona birebir fonksiyon ya da injektif fonksiyon denir. Bir diğer ifadeyle, bir birebir fonksiyonda tanım kümesindeki birden fazla eleman değer kümesinde aynı elemanla eşlenmez.
Aşağıdaki fonksiyon tanım kümesindeki her elemanın görüntüsü farklı olduğu için birebirdir.
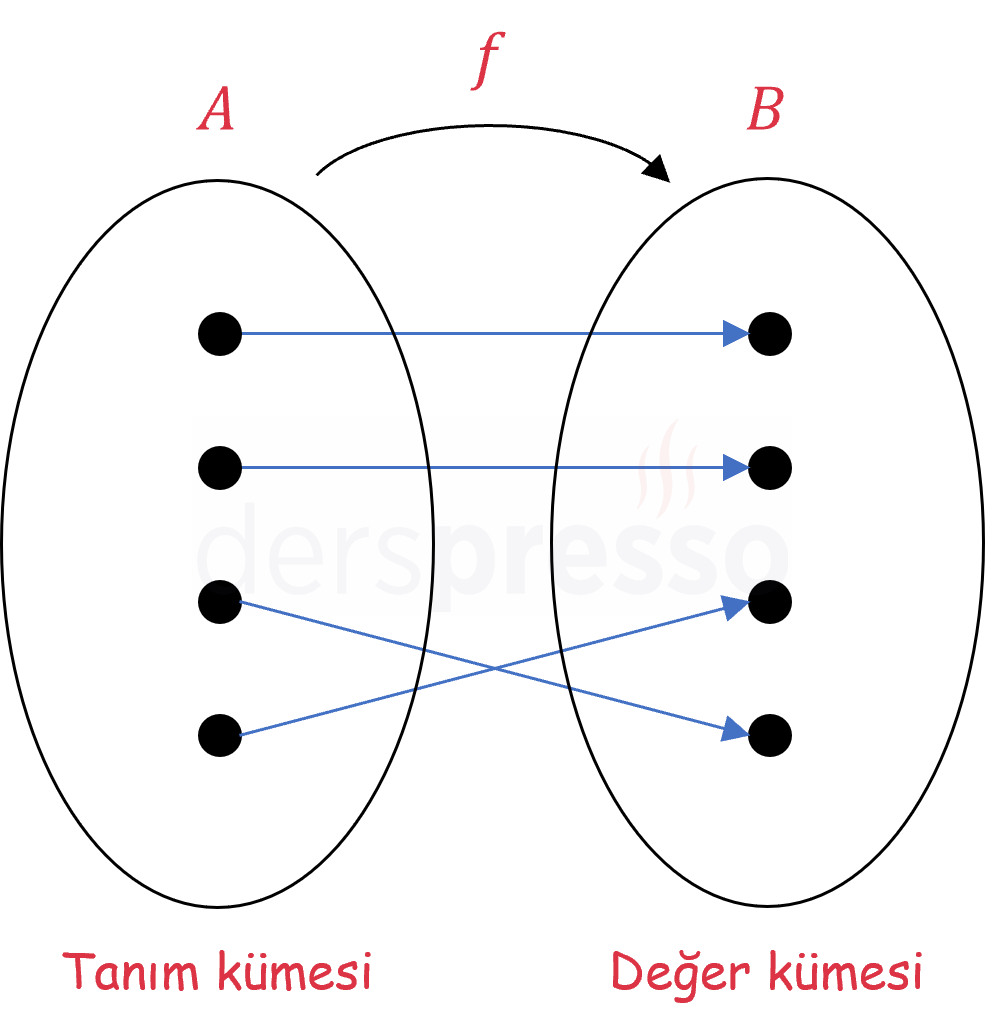
\( f: A \to B \) fonksiyonunda, her \( x_1, x_2 \in A \) için,
\( f(x_1) = f(x_2) \Longrightarrow x_1 = x_2 \)
bir diğer ifadeyle, bu önermenin karşıt tersi olan
\( x_1 \ne x_2 \Longrightarrow f(x_1) \ne f(x_2) \)
önermesi doğru ise \( f \) birebir fonksiyondur.
Karşıt ters: \( (p \Rightarrow q) \equiv (q' \Rightarrow p') \)
\( A = \{ a, b, c \} \)
\( B = \{ 1, 2, 3, 4 \} \)
\( f, g: A \to B \)
\( f \) tanım kümesindeki her elemanın görüntüsü farklı olduğu için birebirdir.
\( f = \{ (a, 3), (b, 4), (c, 1) \} \)
\( g \) tanım kümesindeki iki elemanın görüntüsü aynı olduğu için birebir değildir.
\( g = \{ (a, 3), (b, \textcolor{red}{1}), (c, \textcolor{red}{1}) \} \)
Bir fonksiyonun birebir olabilmesi için gerekli koşullardan biri, tanım kümesinin eleman sayısının değer kümesinin eleman sayısına eşit ya da ondan küçük olmasıdır. Aksi takdirde değer kümesinde tanım kümesindeki her elemanın farklı bir görüntüsü olacak kadar eleman bulunmaz.
\( f: A \to B \) fonksiyonunun birebir olabilmesi için gerekli koşul:
\( s(A) \le s(B) \)
Hem birebir hem de örten olan fonksiyonlara bijektif fonksiyon denir.
Birebir Fonksiyon Sayısı
Birebir fonksiyon sayısı aşağıdaki formülle hesaplanır.
\( f: A \to B \)
\( s(A) = n, \quad s(B) = k \) olmak üzere,
Birebir fonksiyon sayısı \( = \begin{cases} 0 & n \gt k \\ P(k, n) = \dfrac{k!}{(k - n)!} & n \le k \\ \end{cases} \)
3 elemanlı \( A \) kümesinden 5 elemanlı \( B \) kümesine tanımlanabilecek birebir fonksiyon sayısı:
Birebir fonksiyon sayısı \( = P(5, 3) = 5 \cdot 4 \cdot 3 = 60 \)
İSPATI GÖSTER
İki küme arasında yazılabilecek fonksiyon sayısını tanım kümesinin her bir elemanından değer kümesinin her bir elemanına çizilebilecek ok sayısı olarak düşünerek \( k^n \) olarak belirtmiştik.
Birebir bir fonksiyonda tanım kümesinin bir elemanı değer kümesinin bir elemanı ile eşlendikten sonra artık tanım kümesinin bir diğer elemanı aynı elemanla eşlenemeyeceği için, birebir fonksiyon sayısını permütasyon formülü ile bulabiliriz.
Buna göre tanım kümesinin 1. elemanı \( k \) elemanla, 2. elemanı \( k - 1 \) elemanla, \( n \). elemanı da \( k - n + 1 \) elemanla eşlenebilir.
Buna göre toplam farklı eşlenme sayısı aşağıdaki gibi olur.
Toplam farklı eşlenme sayısı \( = k \cdot (k - 1) \cdot \ldots \cdot (k - n + 1) = P(k, n) \)
Birebir Fonksiyonların Grafik Yorumu
Grafiği verilen bir fonksiyonun birebir olup olmadığını anlamak için görüntü kümesindeki tüm \( y \) değerleri için \( x \) eksenine paralel doğrular çizilir. Yatay doğru testi adı verilen bu yöntemde eğer doğruların hiçbiri grafiği birden fazla noktada kesmiyorsa fonksiyon birebirdir.
Bir fonksiyon belirli bir aralıkta kesin artan ya da kesin azalan ise o aralıkta birebirdir. Benzer şekilde, bir fonksiyon bir aralıkta birebir ise o aralıkta ya kesin artan ya da kesin azalandır (fonksiyon artıp azalamaz, azalıp artamaz ya da sabit kalamaz).
Aşağıda farklı fonksiyonların birebir olma durumları yatay doğru testi ile yorumlanmıştır.
| Fonksiyon | Grafik |
|---|---|
|
Sabit fonksiyon \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = c \) Yatay doğru fonksiyon grafiği ile çakışık olduğu (sonsuz noktada kestiği) için fonksiyon birebir değildir. |

|
|
Doğrusal fonksiyon \( a \ne 0 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = ax + b \) Her yatay doğru fonksiyon grafiğini sadece bir noktada keser, bu yüzden fonksiyon birebirdir. |

|
|
Mutlak değer fonksiyonu \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = \abs{x} \) Yatay doğrular fonksiyon grafiğini birden fazla noktada keser, bu yüzden fonksiyon birebir değildir. |

|
|
2. dereceden polinom fonksiyonu (parabol) \( a \ne 0 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = ax^2 + bx + c \) Yatay doğrular fonksiyon grafiğini birden fazla noktada keser, bu yüzden fonksiyon birebir değildir. Derecesi çift sayı olan tüm polinom fonksiyonları için aynı durum geçerlidir. |

|
|
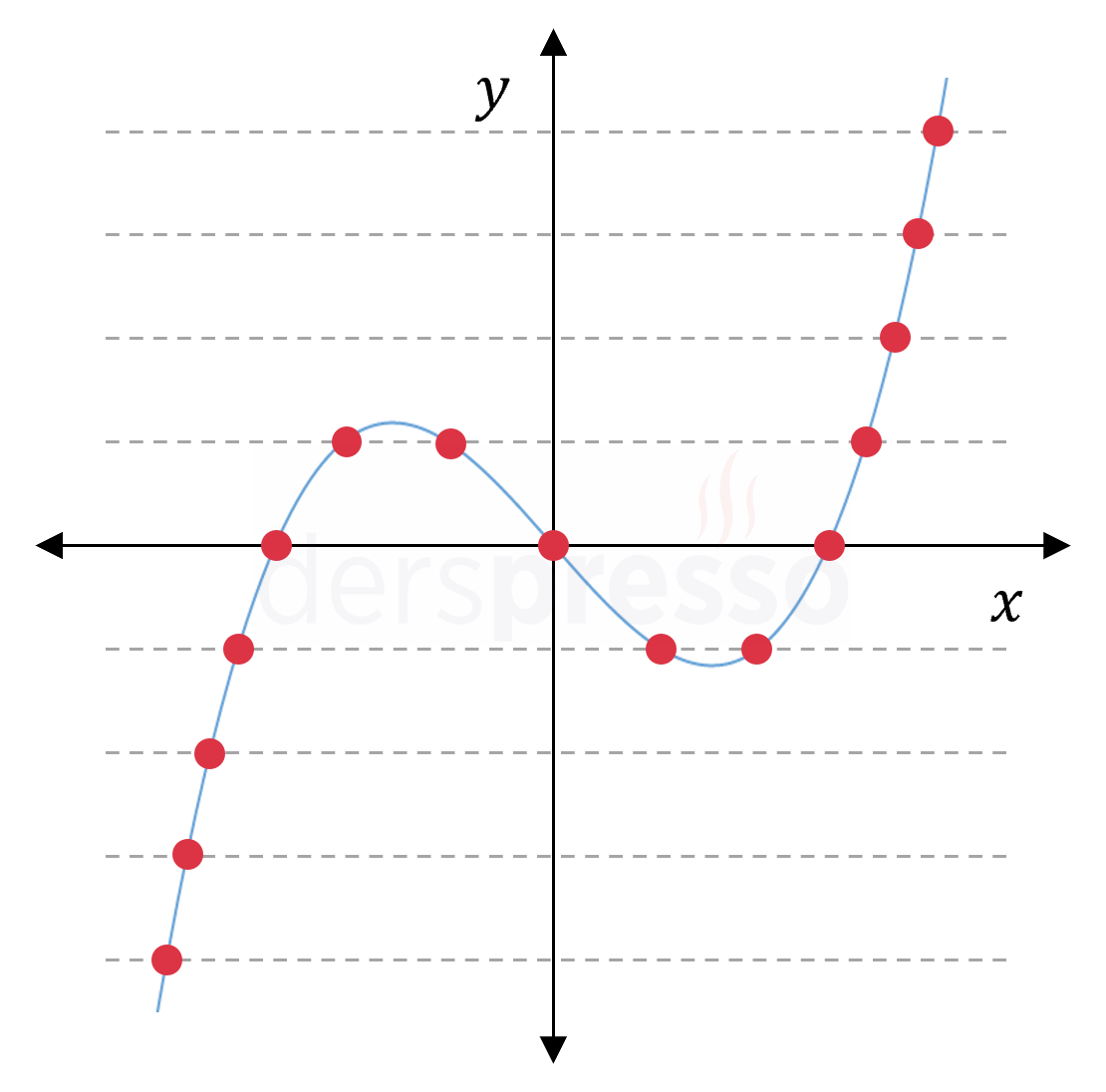
3. dereceden polinom fonksiyonu \( a \ne 0 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = ax^3 + bx^2 + cx + d \) Yandaki grafikte yatay doğrular fonksiyon grafiğini birden fazla noktada kesmektedir, bu yüzden fonksiyon birebir değildir. Ancak 3. dereceden polinom fonksiyon grafikleri kesin artan/azalan da olabilirler (örneğin \( x^3 \)), bu gibi durumlarda fonksiyonlar birebir olur. Derecesi tek sayı olan tüm polinom fonksiyonları için aynı durum geçerlidir. |
|
|
Üstel fonksiyon \( a \gt 0, a \ne 1 \) olmak üzere, \( f: \mathbb{R} \to \mathbb{R} \) \( f(x) = a^x \) Üstel fonksiyonlar taban değerine göre kesin artan ya da kesin azalan oldukları için birebirdirler. |

|
|
Logaritma fonksiyonu \( a \gt 0, a \ne 1 \) olmak üzere, \( f: \mathbb{R^+} \to \mathbb{R} \) \( f(x) = \log_a{x} \) Logaritma fonksiyonları taban değerine göre kesin artan ya da kesin azalan oldukları için birebirdirler. |

|
Yukarıda paylaştığımız birebir fonksiyon tanımı ile yatay doğru testi arasındaki paralelliğin anlaşılması önem taşımaktadır. Birebir bir fonksiyonda tanım kümesindeki iki eleman değer kümesinde aynı elemanla eşlenemezler. Yatay doğru testi de fonksiyonun değer kümesindeki elemanların (grafiğin \( y \) değerleri) tanım kümesindeki en fazla bir elemanın görüntüsü olup olmadığını test etmektedir.
Özet
Bir fonksiyonun örten, içine ya da birebir olup olmadığını anlamak için kullandığımız yatay doğru testini özetlemeye çalışalım: Bir fonksiyonun grafiğinde değer kümesindeki tüm \( y \) değerleri için \( x \) eksenine paralel doğrular çizilir. Bu doğruların aşağıdaki koşullara göre durumu fonksiyonun örten, içine ya da birebir olup olmadığını gösterir.
- Doğruların tümü grafiği en az bir noktada kesiyorsa fonksiyon örtendir.
- Doğruların bir kısmı grafiği kesiyor, bir kısmı kesmiyorsa fonksiyon içinedir.
- Doğruların hiçbiri grafiği birden fazla noktada kesmiyorsa fonksiyon birebirdir.
Bir fonksiyonun örten/içine ve birebir olma durumları aşağıdaki dört şekilde olabilir.
| Grafik | Notlar |
|---|---|
|
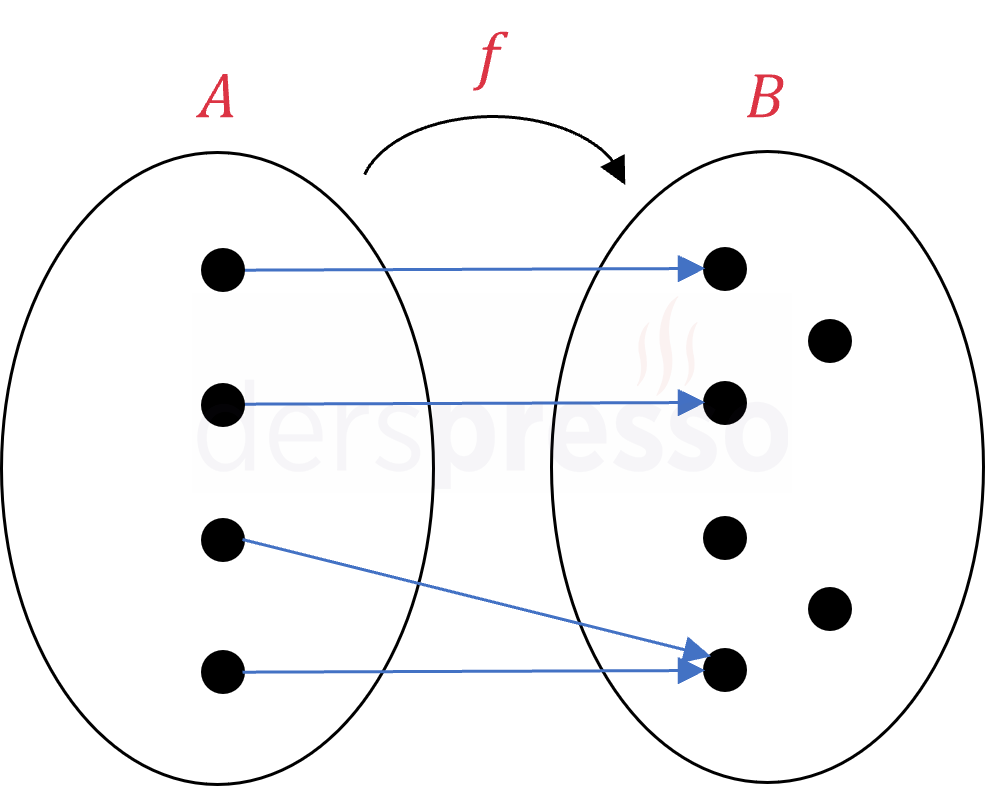
Birebir değil, içine fonksiyon Tanım kümesindeki iki eleman değer kümesinde aynı eleman ile eşlendiği için birebir değil. Değer kümesinde açıkta eleman kaldığı için içine. |

|
Birebir değil, örten fonksiyon Tanım kümesindeki iki eleman değer kümesinde aynı eleman ile eşlendiği için birebir değil. Değer kümesinde açıkta eleman kalmadığı için örten. |
|
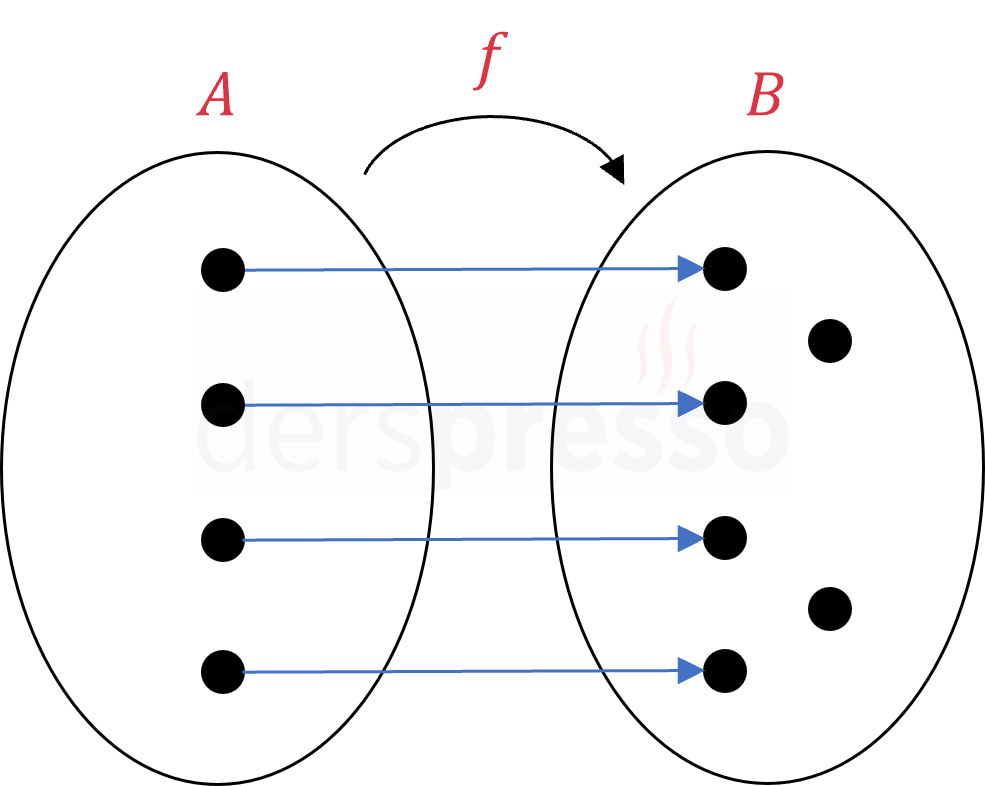
Birebir ve içine fonksiyon Tanım kümesindeki her elemanın görüntüsü farklı olduğu için birebir. Değer kümesinde açıkta eleman kaldığı için içine. |
|
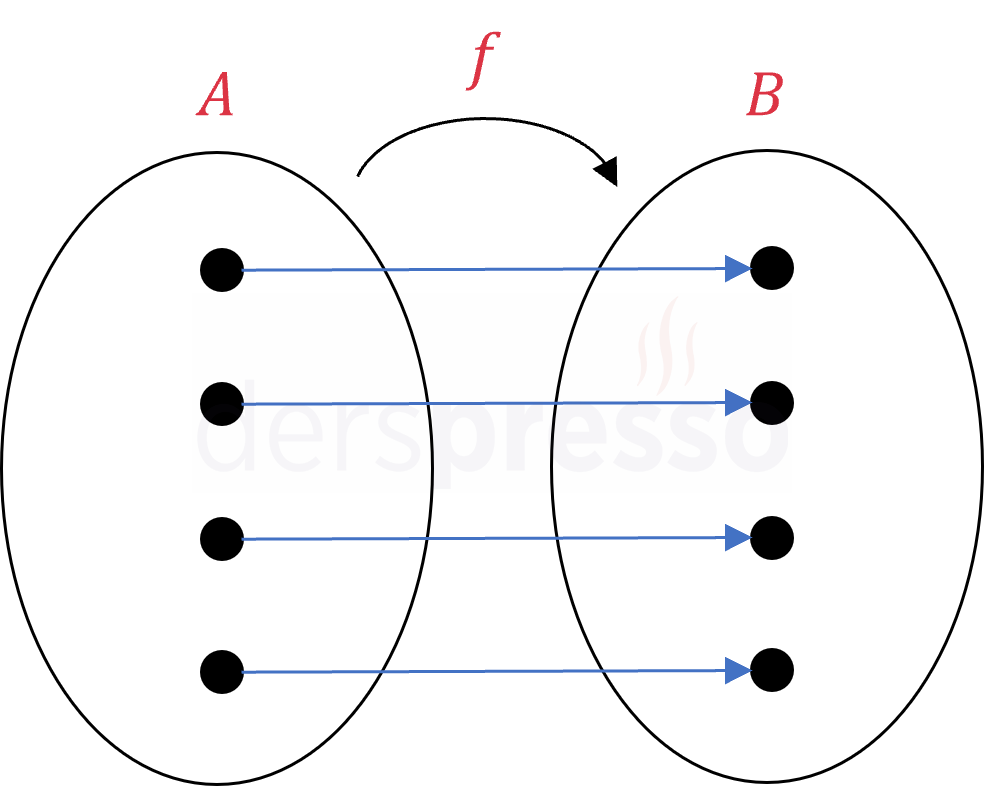
Birebir ve örten fonksiyon Tanım kümesindeki her elemanın görüntüsü farklı olduğu için birebir. Değer kümesinde açıkta eleman kalmadığı için örten. |
\( A = \{ 0, 2, 4, 6, 8, 10 \} \)
\( f: A \to A \) olmak üzere,
\( f \) fonksiyonu birebir olduğuna göre, \( f(0) + f(10) \) ifadesinin en büyük değeri kaçtır?
Çözümü Gösterİfadenin en büyük değerini elde etmek için \( f(0) \) ve \( f(10) \)'u ayrı ayrı en büyük seçmeliyiz. Fonksiyon birebir olduğu için \( f(0) \) ve \( f(10) \) için 10'u seçemeyiz, \( f(0) = 10 \) seçersek birebir özelliğini sağlamak için ikinci en büyük değer olarak \( f(10) = 8 \) seçmeliyiz.
Buna göre toplamın en büyük değeri \( f(0) + f(10) = 10 + 8 = 18 \) olur.
\( A = \{ -2, 0, 2 \} \)
\( f: A \to B \) birebir ve örten bir fonksiyondur.
\( f(2x + 4) = x + 3 \) olduğuna göre, \( B \) kümesinin elemanları toplamı kaçtır?
Çözümü GösterFonksiyonu \( f(x) \) cinsinden yazmak için \( f(2x + 4) = x + 3 \) ifadesinde \( x \) yerine \( 2x + 4 \) ifadesinin tersi olan \( \frac{x - 4}{2} \) yazalım.
\( f(2(\frac{x - 4}{2}) + 4) = \dfrac{x - 4}{2} + 3 \)
\( f(x) = \dfrac{x - 4}{2} + 3 \)
\( A \) kümesinin elemanlarının sırayla görüntülerini bulalım.
\( f(-2) = \dfrac{-2 - 4}{2} + 3 = 0 \)
\( f(0) = \dfrac{0 - 4}{2} + 3 = 1 \)
\( f(2) = \dfrac{2 - 4}{2} + 3 = 2 \)
Buna göre görüntü kümesi aşağıdaki gibi olur.
\( f(A) = \{ 0, 1, 2 \} \)
Fonksiyon örten olduğu için değer kümesi görüntü kümesine eşit olmalıdır.
\( B = f(A) = \{ 0, 1, 2 \} \)
Buna göre \( B \) kümesinin elemanları toplamı \( 0 + 1 + 2 = 3 \) olur.
\( s(A) = x^2 - 5 \) ve \( s(B) = 5x + 1 \) olmak üzere,
\( f: A \to B \) şeklinde tanımlı olan fonksiyon birebir ve örtendir.
Buna göre \( A \) kümesi kaç elemanlıdır?
Çözümü GösterBir fonksiyonun örten olabilmesi için gerekli koşullardan biri, tanım kümesinin eleman sayısının değer kümesinin eleman sayısına eşit ya da ondan büyük olmasıdır.
\( s(A) \ge s(B) \)
Bir fonksiyonun birebir olabilmesi için gerekli koşullardan biri, tanım kümesinin eleman sayısının değer kümesinin eleman sayısına eşit ya da ondan küçük olmasıdır.
\( s(A) \le s(B) \)
Buna göre bir fonksiyonun hem birebir hem örten olabilmesi için tanım kümesinin eleman sayısı değer kümesinin eleman sayısına eşit olmalıdır.
\( s(A) = s(B) \)
\( x^2 - 5 = 5x + 1 \)
\( x^2 - 5x - 6 = 0 \)
\( (x - 6)(x + 1) = 0 \)
\( x \)'in alabileceği değerler 6 ve -1'dir, ancak -1 olduğu durumda kümelerin eleman sayıları negatif olacağı için bu geçerli bir çözüm değildir.
\( x = 6 \) için \( A \) kümesinin eleman sayısını bulalım.
\( s(A) = x^2 - 5 = 6^2 - 5 = 31 \) bulunur.
\( s(A) = 3 \) ve \( s(B) = 6 \) olduğuna göre,
\( A \)'dan \( B \)'ye birebir olmayan kaç farklı fonksiyon tanımlanabilir?
Çözümü Göster\( A \) kümesinden \( B \) kümesine tanımlanabilecek birebir olmayan fonksiyon sayısı, toplam fonksiyon sayısı ile birebir fonksiyon sayısının farkına eşittir.
Birebir olmayan fonksiyon sayısı = Tüm fonksiyonların sayısı - Birebir fonksiyon sayısı
\( A \)'dan \( B \)'ye toplam fonksiyon sayısı: \( 6^3 = 216 \)
\( A \)'dan \( B \)'ye birebir fonksiyon sayısı: \( P(6, 3) = 6 \cdot 5 \cdot 4 = 120 \)
Buna göre birebir olmayan fonksiyon sayısı \( 216 - 120 = 96 \) olarak bulunur.
\( f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x^2 + 1 \)
\( g: \mathbb{Z} \to \mathbb{Z}, \quad g(x) = 7x - 3 \)
\( h: \mathbb{R^+} \to \mathbb{R}, \quad h(x) = 4x^2 + 2 \)
fonksiyonlarından hangileri birebir fonksiyondur?
Çözümü Göster\( f \) fonksiyonunda \( x^2 \) ifadesi \( x \)'in pozitif ve negatif değerleri için aynı sonucu verir, grafiği de bir parabol olduğu için çizilecek yatay doğrular grafiği iki noktada keser. Bu yüzden \( f \) fonksiyonu birebir değildir.
\( g \) fonksiyonunun grafiği eğimi pozitif olan bir doğrudur, dolayısıyla çizilecek yatay doğrular doğruyu tek bir noktada keser. Bu yüzden \( g \) fonksiyonu birebirdir.
\( h \) fonksiyonu da \( f \) fonksiyonu gibi bir paraboldür, ancak tanım kümesi pozitif reel sayılar olduğu için grafiği tepe noktasının sağındaki kısma karşılık gelir ve çizilecek yatay doğrular grafiği tek bir noktada keser. Bu yüzden \( h \) fonksiyonu birebirdir.
Buna göre \( g \) ve \( h \) fonksiyonları birebirdir.
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = ax^2 + bx + c \) fonksiyonu veriliyor.
\( f \) birebir olduğuna göre, aşağıdakilerden hangisi doğru olabilir?
(a) \( a \neq 0, b = 1, c = 1 \)
(b) \( a = 0, b = 0, c = 2 \)
(c) \( a \neq 0, b = 0, c = 2 \)
(d) \( a = 0, b \neq 0, c \neq 0 \)
(e) \( a \neq 0, b \neq 0, c \neq 0 \)
Çözümü Göster\( a \ne 0 \) olduğunda fonksiyon bir parabol olur. Paraboller tüm reel sayılarda birebir olmadıkları için \( a = 0 \) olmalıdır.
Geriye kalan \( bx + c \) ifadesi bir doğrudur. \( b = 0 \) olduğunda ifade sabit fonksiyon olur. Sabit fonksiyonlar birebir olmadıkları için \( b \ne 0 \) olmalıdır.
Buna göre seçeneklerden sadece (d) doğru olabilir.
\( f: A \to A \) fonksiyonu birebirdir.
\( A = \{ 2, 3, 4, 5, 6, 7 \} \) olduğuna göre, \( f(2) + f(3) + f(4) \) toplamının alabileceği kaç farklı değer vardır?
Çözümü Göster\( f \) fonksiyonu birebir olduğu için tanım kümesindeki her eleman değer kümesinde farklı bir elemanla eşleşmek zorundadır.
\( f(2) \), \( f(3) \) ve \( f(4) \) sırası önemsiz şekilde en küçük 2, 3 ve 4 değerlerini alabilir ve bu durumda toplamları \( 2 + 3 + 4 = 9 \) olur.
\( f(2) \), \( f(3) \) ve \( f(4) \) sırası önemsiz şekilde en büyük 5, 6 ve 7 değerlerini alabilir ve bu durumda toplamları \( 5 + 6 + 7 = 18 \) olur.
Bu toplam en küçük ve en büyük değerleri arasındaki diğer değerleri de alabilir. Buna göre verilen toplam \( 18 - 9 + 1 = 10 \) farklı değer alabilir.
\( A = \{ a, b, c \} \)
\( B = \{ 1, 2, 3, 4, 5 \} \) olmak üzere,
\( A \)'dan \( B \)'ye görüntü kümesinde 2 elemanı bulunan birebir kaç fonksiyon yazılabilir?
Çözümü GösterBu soruyu iki yöntemle çözebiliriz.
1. yöntem:
İstenen fonksiyon sayısını tüm birebir fonksiyonların sayısından görüntü kümesinde 2 bulunmayan birebir fonksiyon sayısını çıkararak bulabiliriz.
\( s(A) = 3, \quad s(B) = 5 \)
Tüm birebir fonksiyonların sayısı \( = P(5, 3) = 5 \cdot 4 \cdot 3 = 60 \)
Görüntü kümesinde 2 bulunmayan birebir fonksiyonların sayısını bulmak için değer kümesinin 2 elemanını içermediği durum için aynı formülü kullanabiliriz.
Görüntü kümesinde 2 bulunmayan birebir fonksiyonların sayısı: \( P(5 - 1, 3) = 4 \cdot 3 \cdot 2 = 24 \)
Buna göre görüntü kümesinde 2 elemanı bulunan birebir fonksiyon sayısı \( 60 - 24 = 36 \) olarak bulunur.
2. yöntem:
İlk önce tanım kümesindeki elemanlardan birini 2 elemanı ile eşleyelim. Bu eşlemeyi tanım kümesindeki her eleman için olmak üzere 3 farklı şekilde yapabiliriz.
Bu eşleme sonucunda tanım kümesinde 2, değer kümesinde 4 eleman kalır. Bu durumda yazılabilecek birebir fonksiyon sayısı: \( P(4, 2) = 4 \cdot 3 = 12 \)
Buna göre görüntü kümesinde 2 elemanı bulunan birebir fonksiyon sayısı \( 3 \cdot 12 = 36 \) olarak bulunur.
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = \begin{cases} x - 2 & x \le 1 \\ x & x \gt 1 \end{cases} \)
olduğuna göre, aşağıdaki ifadelerden hangileri doğrudur?
I. \( f \) içine fonksiyondur.
II. \( f \) birebir fonksiyondur.
III. \( f \)'in görüntü kümesi \( \mathbb{R} \)'dir.
Çözümü GösterVerilen parçalı fonksiyonun grafiği aşağıdaki gibidir.

I. öncül: Değer kümesindeki \( (-1, 1] \) aralığı görüntü kümesinde bulunmadığı için fonksiyondur içinedir. Bu öncül doğrudur.
II. öncül: Yatay doğru testi yaptığımızda doğruların hiçbiri grafiği birden fazla noktada kesmediği için fonksiyon birebirdir. Bu öncül doğrudur.
III. öncül: Görüntü kümesi \( \mathbb{R} - (-1, 1] \) olduğu için bu öncül yanlıştır.
Buna göre I. ve II. öncüller doğrudur.