Fonksiyonların Grafik Gösterimi
Bir fonksiyonun girdi ve çıktı değerleri arasındaki ilişki ve fonksiyonun davranışı hakkında en detaylı yorumları fonksiyonun grafiğini inceleyerek yapabiliriz.
Fonksiyon Grafiğini Okuma
Bir \( f \) fonksiyonunun analitik düzlemdeki grafiği ile ilgili önemli bazı noktalar şunlardır:
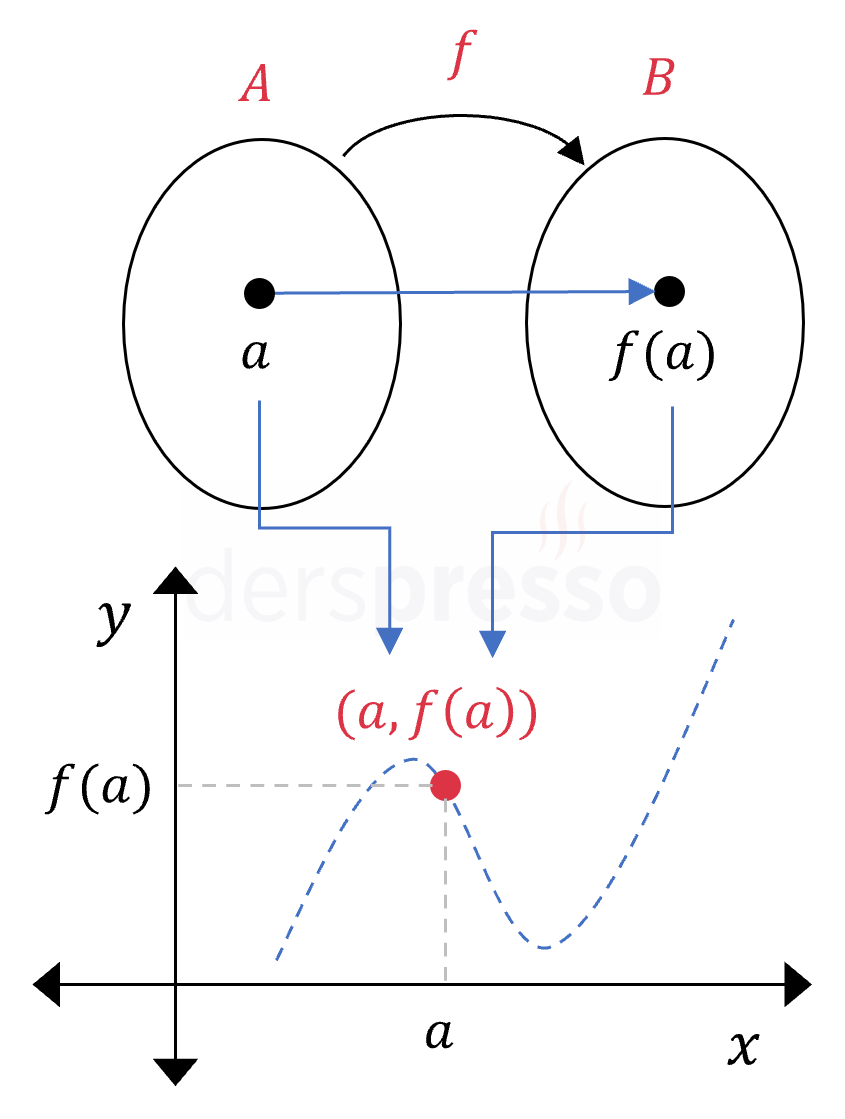
- Fonksiyonun tanım kümesi olan \( A \) kümesinin elemanları \( x \) eksenine karşılık gelir.
- Fonksiyonun değer kümesi olan \( B \) kümesinin elemanları \( y \) eksenine karşılık gelir.
- \( a \in A \) olmak üzere, bir \( a \) elemanının ve \( B \) kümesindeki görüntüsünün oluşturduğu \( (a, f(a)) \) sıralı ikilisi, analitik düzlemde apsisi \( a \) ve ordinatı \( f(a) \) olan noktaya karşılık gelir.
- \( A \) kümesinin tüm elemanları için yazılacak bu sıralı ikililerin oluşturduğu noktalar kümesi fonksiyonun grafiğini oluşturur.
Bir fonksiyonun \( a \) noktasındaki değeri, fonksiyon tanımında \( x = a \) konduğunda bulunan \( f(a) \) değeridir. Bir fonksiyonun \( x = a \) noktasındaki değerini (eşlendiği elemanı) grafik üzerinde bulmak için \( x \) ekseni üzerinde \( a \) noktasından \( x \) eksenine dik bir doğru çizilir ve doğrunun fonksiyon grafiğini kestiği noktanın ordinat değeri bulunur.
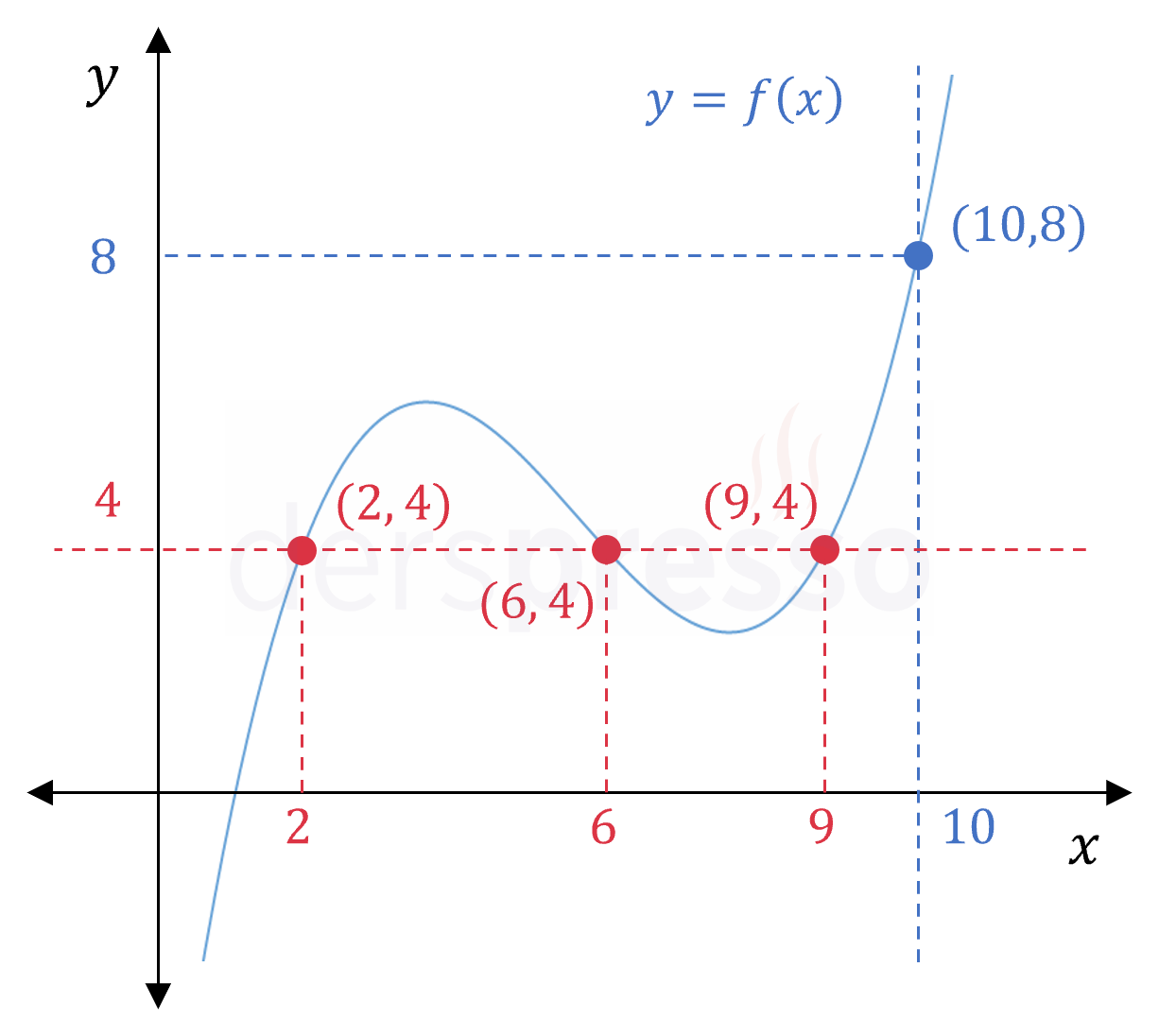
Yukarıdaki grafiğe göre, \( x = 10 \) için fonksiyonun değeri dikey kesikli mavi doğrunun grafiği kestiği noktanın ordinatı olan \( y = 8 \)'dir.
\( f(10) = 8 \)
Görüntüsü belirli bir değer olan tanım kümesi elemanlarını bulmak için, \( y \) ekseni üzerinde ordinatı bu değer olan noktadan \( y \) eksenine dik bir doğru çizilir ve doğrunun fonksiyon grafiğini kestiği noktanın/noktaların apsis değeri/değerleri bulunur.
Yukarıdaki grafiğe göre, fonksiyonun \( y = 4 \) değerini aldığı noktalar yatay kırmızı kesikli doğrunun grafiği kestiği noktaların apsis değerleri olan \( x \in \{ 2, 6, 9 \} \) değerleridir.
\( f(2) = f(6) = f(9) = 4 \)
Fonksiyon Grafiğini Yorumlama
Bir fonksiyonun grafiğini çizmek veya farklı açılardan yorumlamak oldukça kapsamlı bir bakış açısı gerektirir. Aşağıda bazı bileşenlerini listelediğimiz ve matematiğin farklı başlıkları altında incelenen bu konudaki bilgi düzeyimiz, denklemi verilen bir fonksiyonun grafiğini ve davranışını farklı açılardan yorumlamamızı kolaylaştıracaktır.
- Temel fonksiyonların grafik özellikleri (doğrusal, kuvvet, kök, mutlak değer, polinom, trigonometri, üstel, logaritma, rasyonel, parçalı vb.)
- Grafiklerin eksenleri kestikleri noktalar
- Tanımsız noktalar
- Grafiklerin dönüşümü (öteleme, daralma, genişleme)
- Simetri (tek ve çift fonksiyonlar)
- Artan, azalan ve sabit aralıklar
- Minimum ve maksimum noktaları
- Büküm noktaları
- Konveks ve konkav aralıklar
- Grafiklerin sürekliliği
- Grafiklerin \( x \) sonsuza giderkenki davranışı
- Yatay ve dikey asimptotlar
- Grafiklerin periyodu
Değer Tablosu ile Fonksiyon Grafiği Çizme
Bir fonksiyonun detaylı davranışı hakkında fikir vermese de, bir fonksiyonun grafiğini en kolay şekilde bir değer tablosu oluşturarak çizebiliriz.
Aşağıdaki fonksiyonun grafiğini bir değer tablosu yardımıyla çizelim.
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = (x - 3)^2 - 4 \)
Önce bir değer tablosu oluşturarak bazı \( x \) değerleri için fonksiyon değerlerini hesaplayalım ve fonksiyon grafiğindeki noktalara karşılık gelecek olan \( (x, f(x)) \) sıralı ikililerini bulalım.
| \( x \) | \( y = f(x) \) | Nokta \( (x, f(x)) \) |
|---|---|---|
| \( -1 \) | \( f(-1) = (-1 - 3)^2 - 4 = 12 \) | \( (-1, 12) \) |
| \( 0 \) | \( f(0) = (0 - 3)^2 - 4 = 5 \) | \( (0, 5) \) |
| \( 1 \) | \( f(1) = (1 - 3)^2 - 4 = 0 \) | \( (1, 0) \) |
| \( 2 \) | \( f(2) = (2 - 3)^2 - 4 = -3 \) | \( (2, -3) \) |
| \( 3 \) | \( f(3) = (3 - 3)^2 - 4 = -4 \) | \( (3, -4) \) |
| \( 4 \) | \( f(4) = (4 - 3)^2 - 4 = -3 \) | \( (4, -3) \) |
| \( 5 \) | \( f(5) = (5 - 3)^2 - 4 = 0 \) | \( (5, 0) \) |
| \( 6 \) | \( f(6) = (6 - 3)^2 - 4 = 5 \) | \( (6, 5) \) |
| \( 7 \) | \( f(7) = (7 - 3)^2 - 4 = 12 \) | \( (7, 12) \) |
Bulduğumuz bu noktaları analitik düzlemde işaretlediğimizde aşağıdaki kırmızı noktaları elde ederiz. Bu noktaları birleştirdiğimizde aşağıdaki parabol grafiğini elde ederiz.
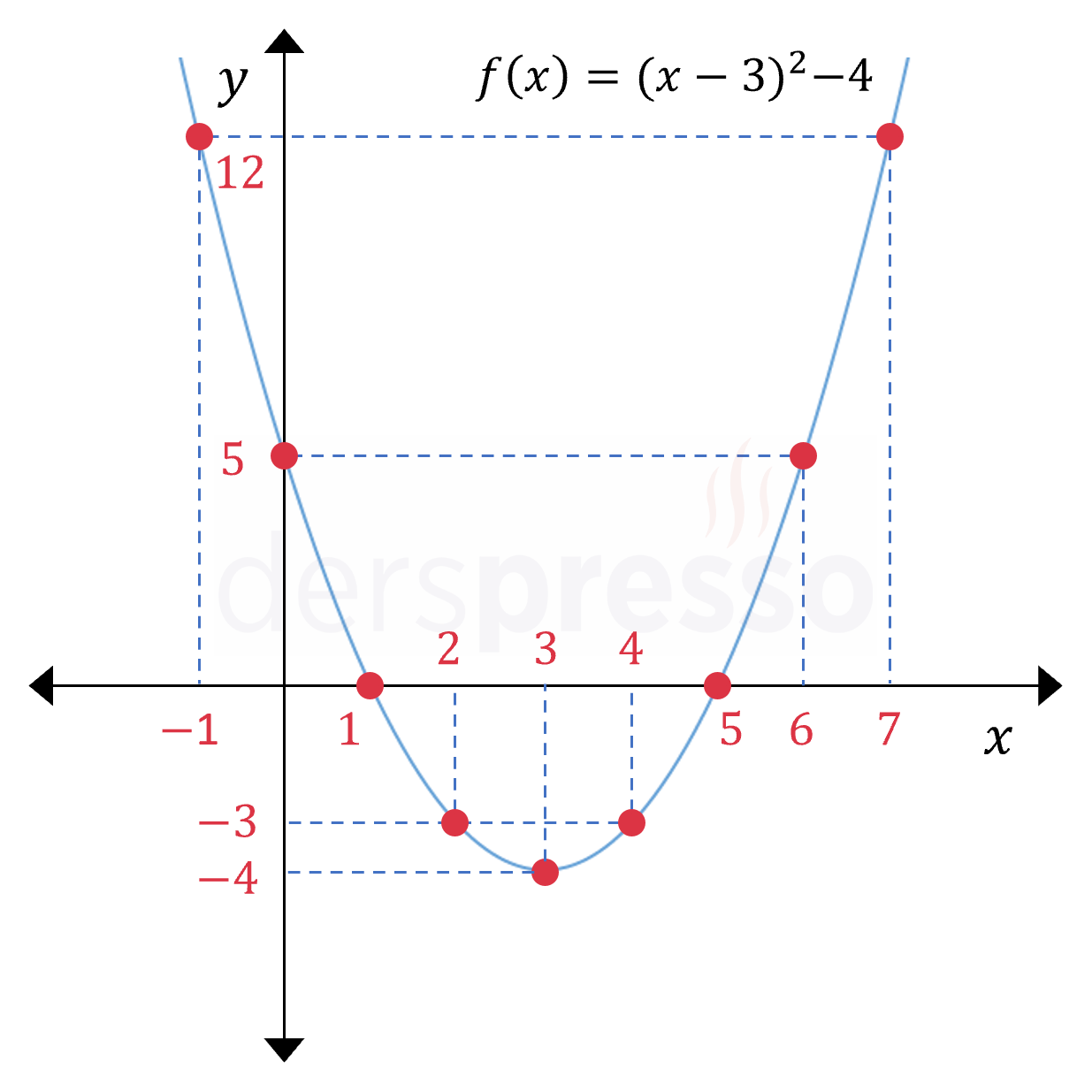
Dikey Doğru Testi
Fonksiyon tanımını yaparken bir bağıntının fonksiyon olma kuralı olarak iki koşuldan bahsetmiştik. Bir bağıntının bu koşulları sağlayıp sağlamadığını bağıntının grafiğinden de anlayabiliriz.
Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için, \( x \) ekseni üzerinde bağıntının tanımlı olduğu aralıktaki (eksen üzerinde kırmızı doğru ile gösterilen aralık) tüm noktalardan \( x \) eksenine dik doğrular çizilir. Dikey doğru testi adı verilen bu yöntemde doğruların tümü grafiği sadece bir noktada kesiyorsa bu bağıntı bir fonksiyondur.
Aşağıda fonksiyon olma koşullarını, dolayısıyla dikey doğru testini sağlayan iki bağıntının grafiği verilmiştir. Bu grafiklerde dikey doğrular grafiği sadece bir noktada kestikleri için (yani \( A \) kümesinin her elemanı \( B \) kümesinde sadece bir elemanla eşlendiği için) bu bağıntılar birer fonksiyondur.
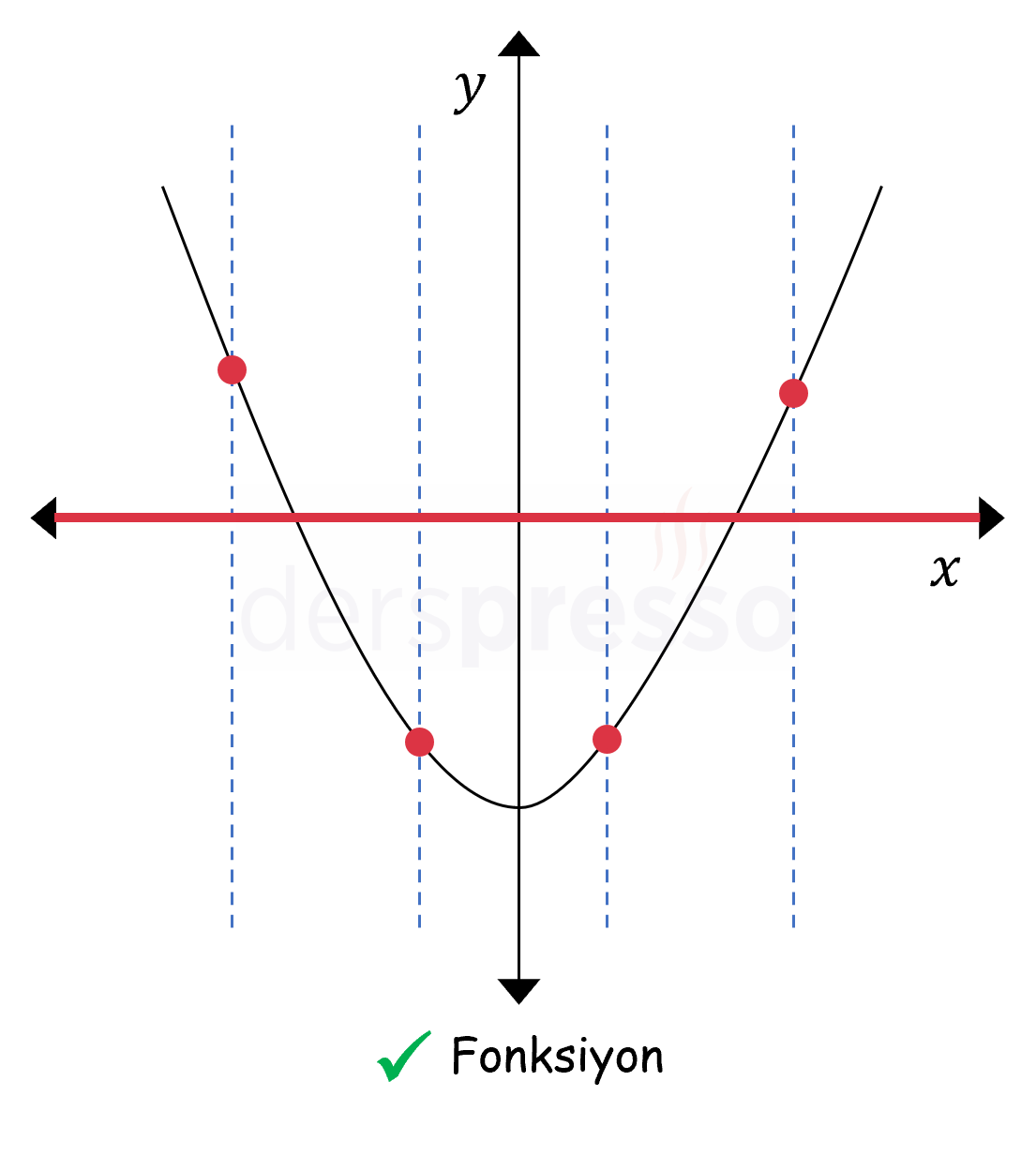
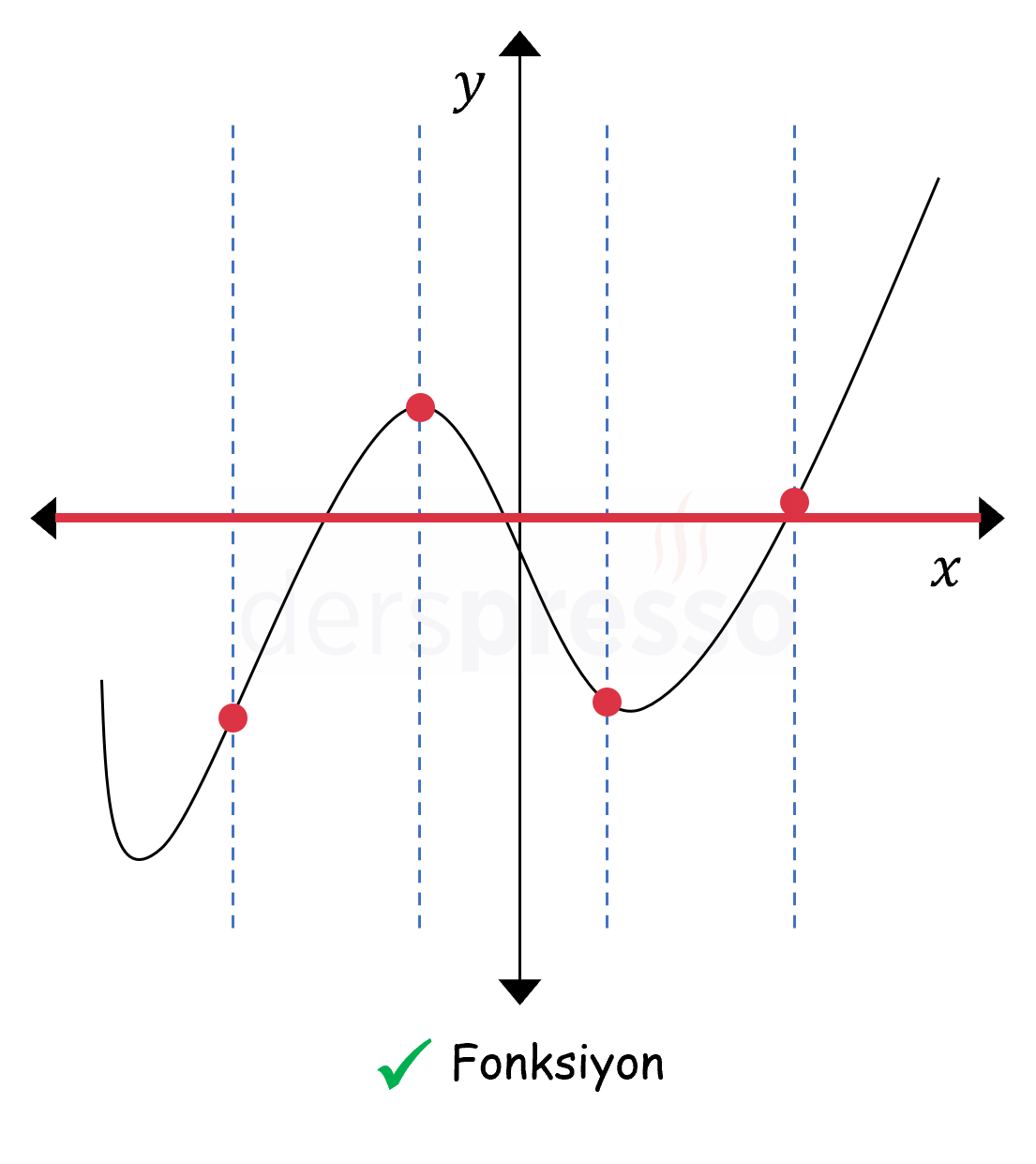
Aşağıda ikinci fonksiyon olma koşulunu, dolayısıyla dikey doğru testini sağlamayan iki bağıntının grafiği verilmiştir. Bu grafiklerde grafiği birden fazla noktada kesen dikey doğrular bulunduğu için (yani \( A \) kümesinin bazı elemanları \( B \) kümesinde birden fazla elemanla eşlendiği için) bu bağıntılar birer fonksiyon değildir.
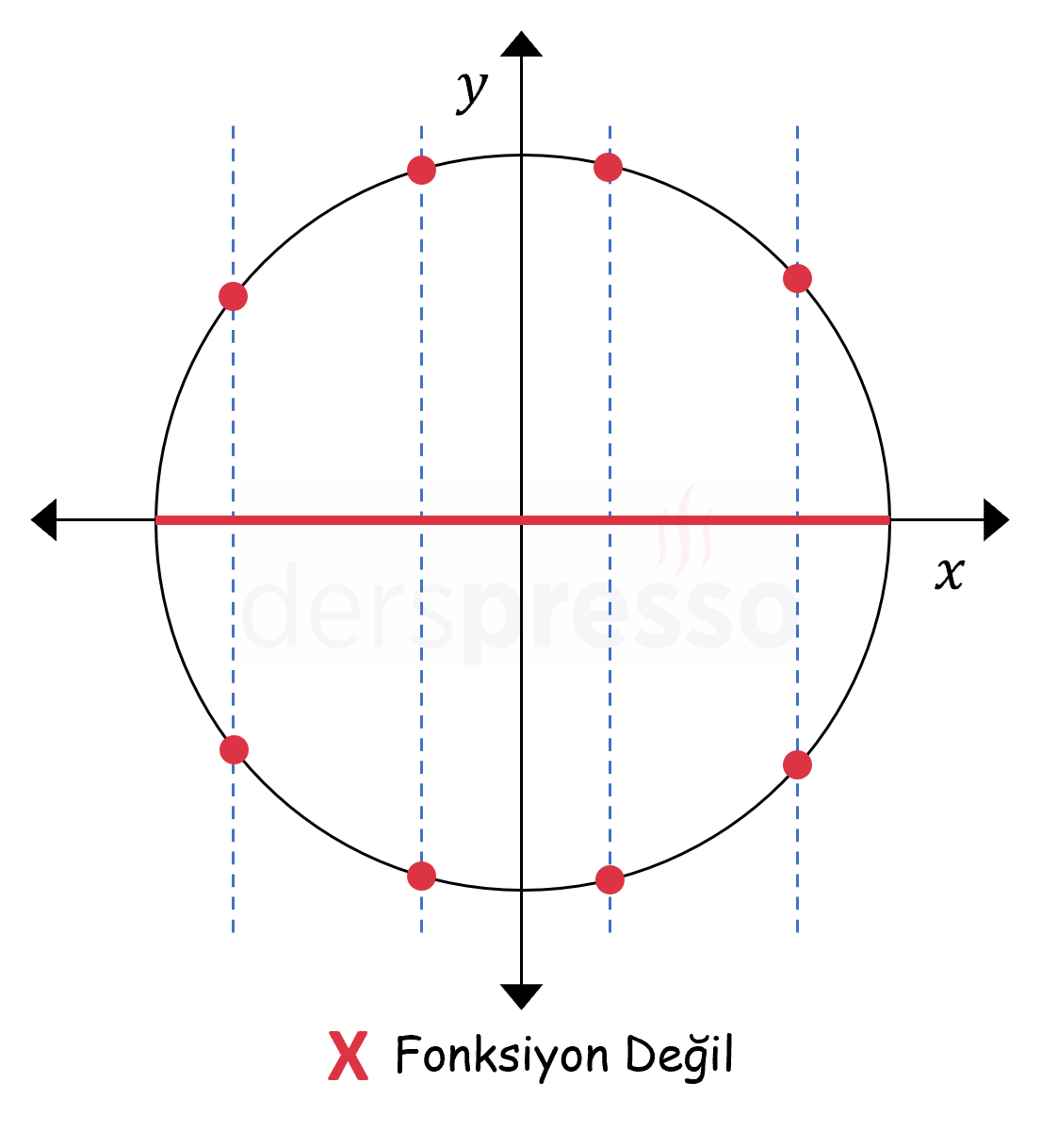
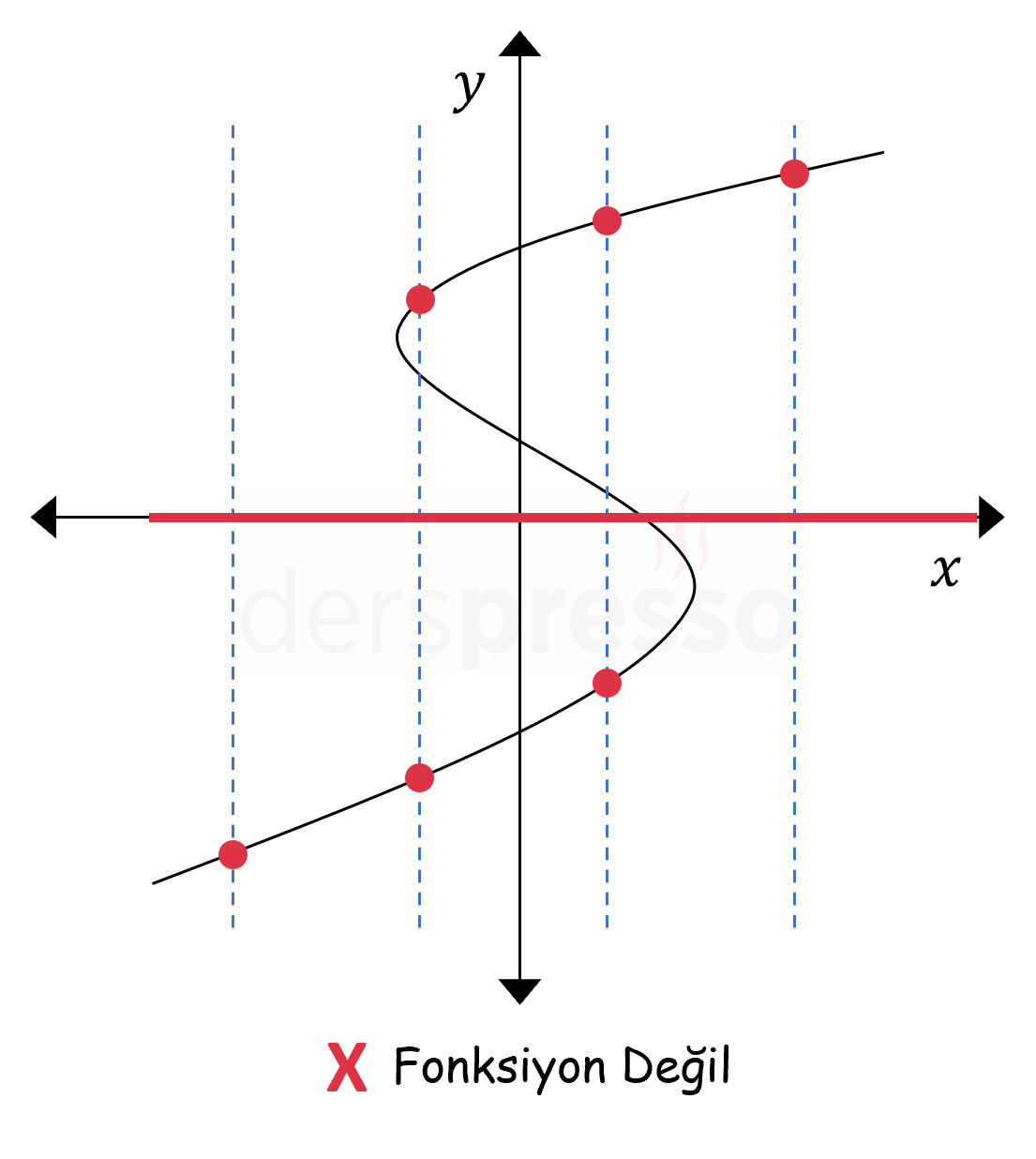
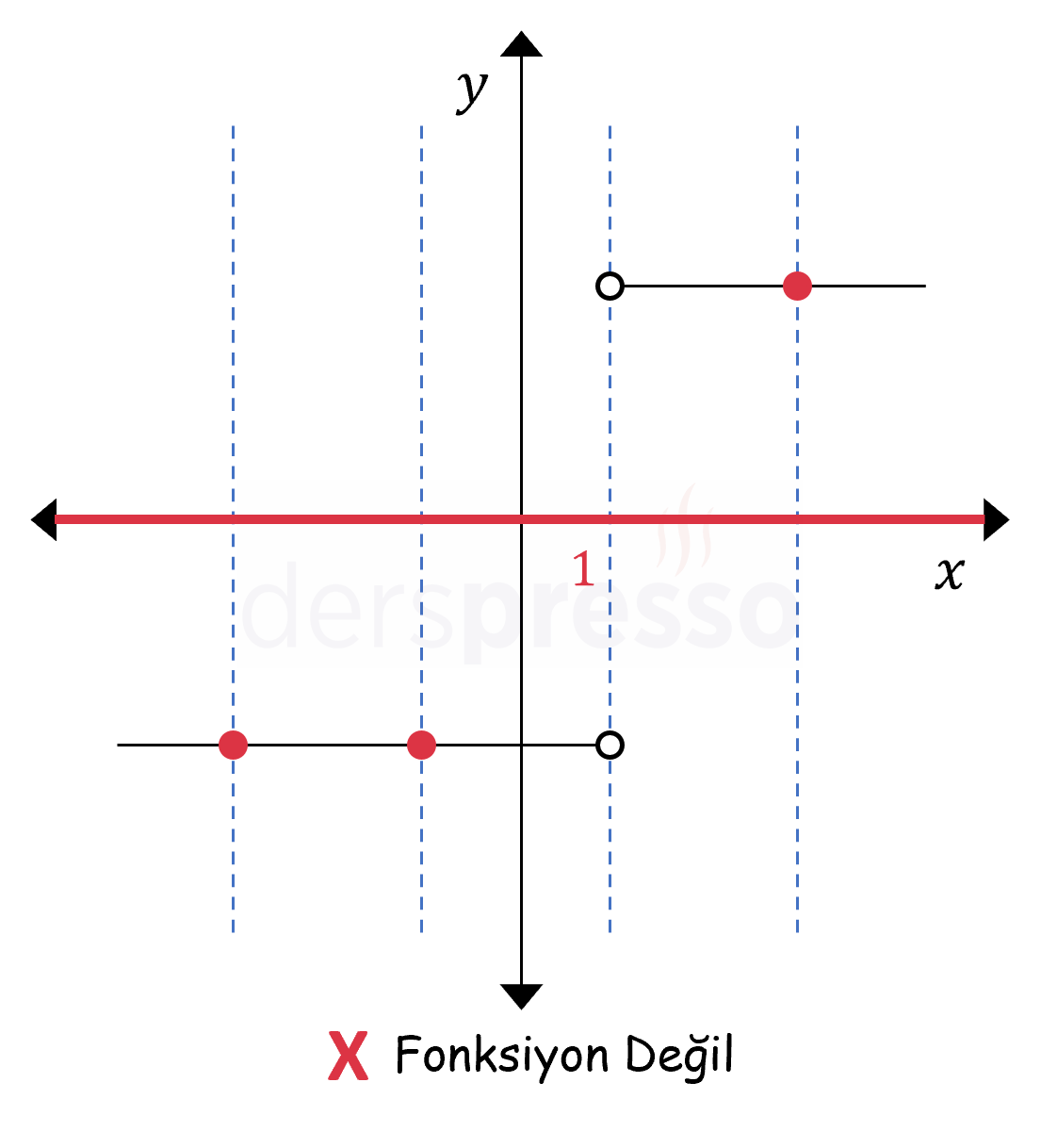
Aşağıda birinci fonksiyon olma koşulunu, dolayısıyla dikey doğru testini sağlamayan tüm reel sayılarda tanımlı bir bağıntının grafiği verilmiştir. Bu grafikte \( x = 1 \) noktasında bağıntının bir görüntüsü olmadığı için (yani nokta \( B \) kümesinde hiçbir elemanla eşlenmediği için) dikey doğru bu noktada grafiği hiçbir noktada kesmemektedir.
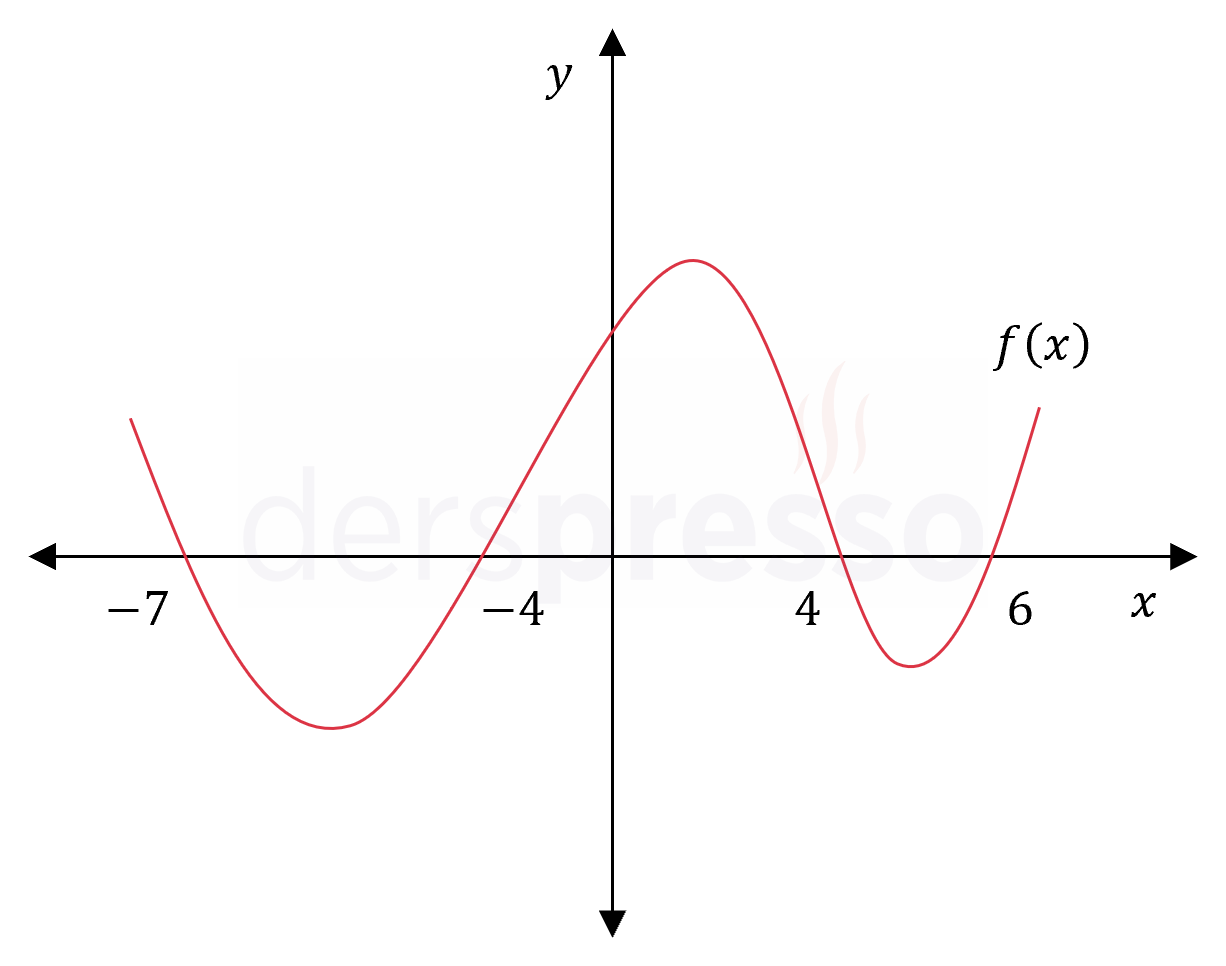
Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Verilen aralıkta fonksiyonun değerinin negatif olduğu \( x \) tam sayılarının çarpımı kaçtır?
Çözümü Göster\( f \) fonksiyonu grafiği verilen aralıkta \( x \in (-7, -4) \) ve \( x \in (4, 6) \) aralıklarında negatif değer alır.
Bu iki aralıktaki tam sayı \( x \) değerleri \( \{ -6, -5, 5 \} \) olur.
\( -6 \cdot (-5) \cdot 5 = 150 \) bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \abs{\abs{x - 3} - a} \) fonksiyonu \( x \) eksenini \( -2 \) apsis değerli noktada kestiğine göre, \( a \) kaçtır?
Çözümü GösterFonksiyon \( x \) eksenini \( -2 \) apsis değerli noktada kesiyorsa grafik \( (-2, 0) \) noktasından geçiyordur.
Bir fonksiyonun grafiği belirli bir noktadan geçiyorsa o noktanın koordinatları fonksiyon tanımını sağlar.
\( f(-2) = \abs{\abs{-2 - 3} - a} = 0 \)
\( \abs{5 - a} = 0 \)
\( a = 5 \) bulunur.
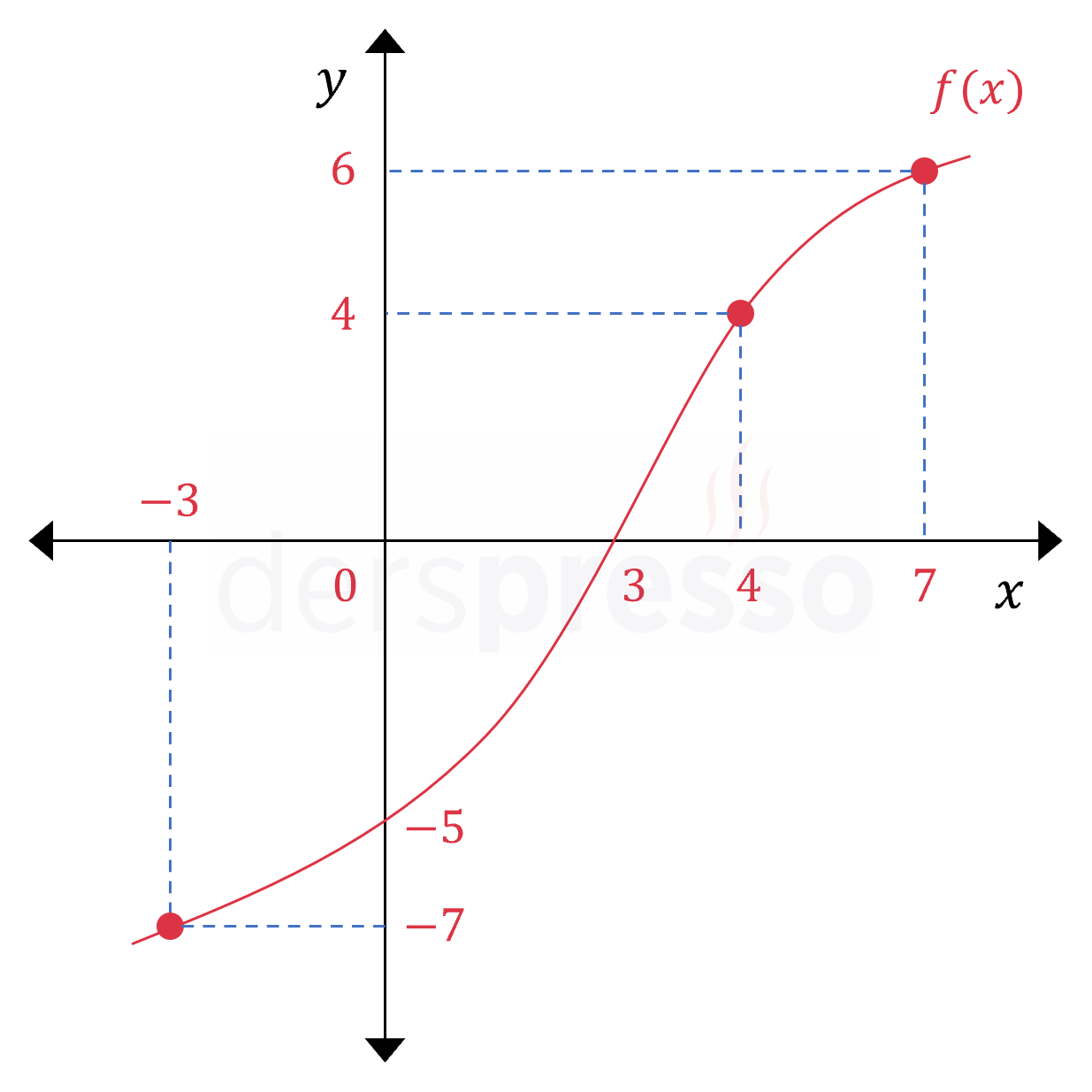
Yukarıdaki \( y = f(x) \) grafiğine göre,
\( \dfrac{f(4) + f(-3)}{f(3) + f(7) + f(0)} \) işleminin sonucu kaçtır?
Çözümü GösterSorudaki ifadedeki fonksiyon değerlerini bulalım.
\( f(4) = 4 \)
\( f(-3) = -7 \)
\( f(3) = 0 \)
\( f(7) = 6 \)
\( f(0) = -5 \)
Bu değerleri yerine koyalım.
\( \dfrac{f(4) + f(-3)}{f(3) + f(7) + f(0)} = \dfrac{4 + (-7)}{0 + 6 + (-5)} \)
\( = -3 \) bulunur.
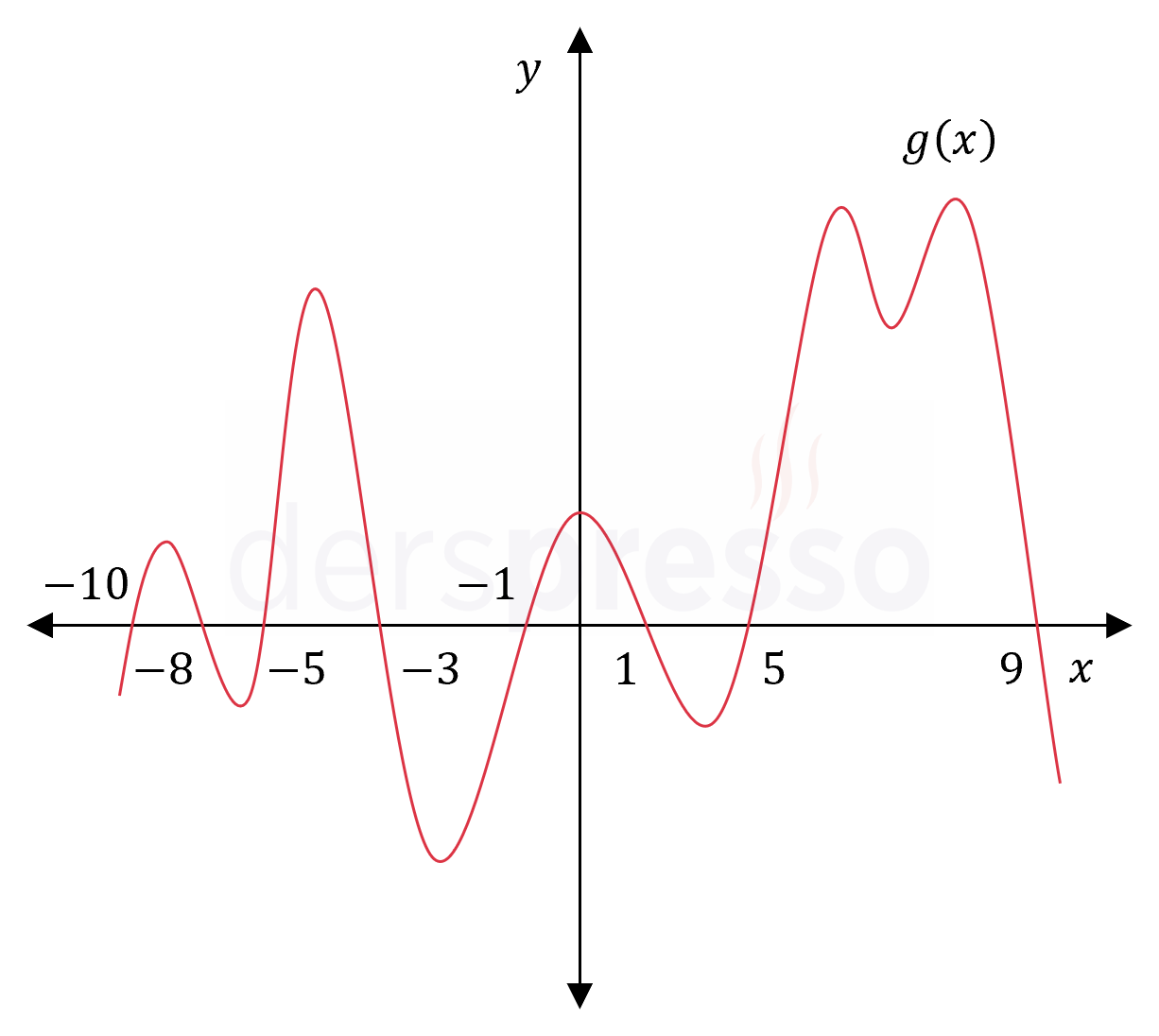
Yukarıda \( g \) fonksiyonunun grafiği verilmiştir.
Buna göre, \( -6 \lt x \le 8 \) aralığında \( g(x) \ge 0 \) koşulunu sağlayan kaç \( x \) tam sayısı vardır?
Çözümü Göster\( g \) fonksiyonunun değeri grafiği verilen aralıkta \( x \in \{ -10, -8, -5, -3, -1, 1, 5, 9 \} \) noktalarında sıfır, \( (-10, -8), (-5, -3), (-1, 1), (5, 9) \) aralıklarında pozitif, \( (-8, -5), (-3, -1), (1, 5) \) aralıklarında ise negatif değer alır.
Buna göre \( -6 \lt x \le 8 \) aralığında \( g(x) \ge 0 \) koşulunu sağlayan, yani fonksiyonun sıfır ya da pozitif olduğu \( x \) tam sayı değerleri 10 tanedir.
\( x \in \{ -5, -4, -3, -1, 0, 1, 5, 6, 7, 8 \} \)
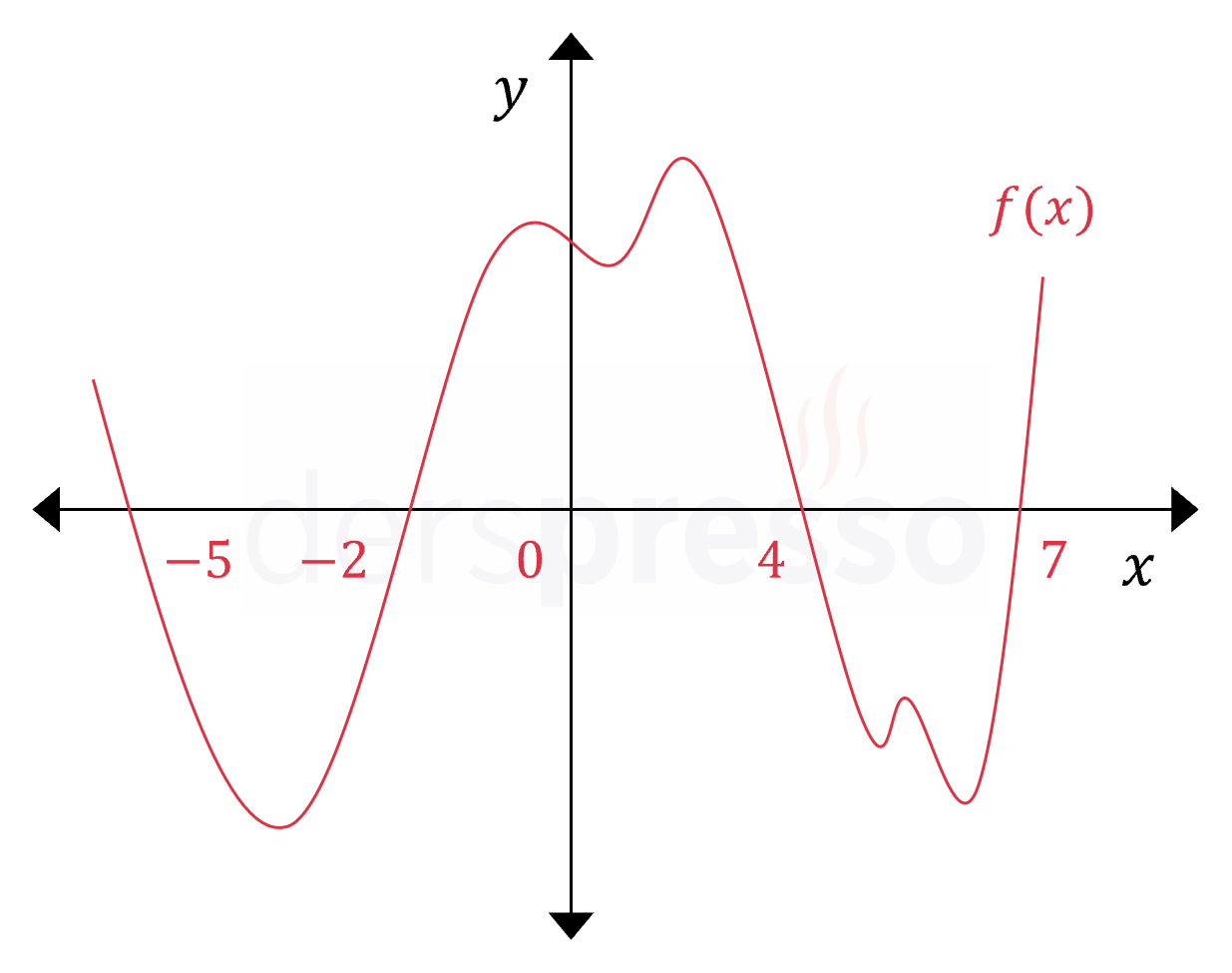
Yukarıda \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
Buna göre, grafiği verilen aralıkta \( f(x) \le 0 \) koşulunu sağlayan kaç \( x \) tam sayısı vardır?
Çözümü Göster\( f \) fonksiyonunun değeri verilen aralıkta \( x \in \{-5, -2, 4, 7\} \) noktalarında sıfır, \( (-2, 4) \) aralığında pozitif, \( (-5, -2) \) ve \( (4, 7) \) aralıklarında negatif değer alır.
Buna göre bu aralıkta \( f(x) \le 0 \) koşulunu sağlayan \( x \) tam sayı değerleri 8 tanedir.
\( x \in \{-5, -4, -3, -2, 4, 5, 6, 7\} \)
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 3ax + 5 - b \) fonksiyonunun grafiği \( (2, 3) \) ve \( (-1, -2) \) noktalarından geçtiğine göre, \( ab \) çarpımı kaçtır?
Çözümü GösterBir fonksiyonun grafiği belirli bir noktadan geçiyorsa o noktanın koordinatları fonksiyon tanımını sağlar.
\( f(2) = 2^2 - 3a(2) + 5 - b = 3 \)
\( 6a + b = 6 \)
\( f(-1) = (-1)^2 - 3a(-1) + 5 - b = -2 \)
\( 3a - b = -8 \)
İki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = -\dfrac{2}{9}, \quad b = \dfrac{22}{3} \)
\( ab = -\dfrac{2}{9} \cdot \dfrac{22}{3} = -\dfrac{44}{27} \) bulunur.
Fonksiyonlar \( ( -3, -2 ) \) noktasında kesiştiklerine göre, bu noktanın koordinatları iki denklemi de sağlar.
\( y = cx \)
\( -2 = -3c \Longrightarrow c = \dfrac{2}{3} \)
\( y = \dfrac{d}{x}\)
\( -2 = \dfrac{d}{-3} \Longrightarrow d = 6 \)
\( c \) ve \( d \) değerlerini denklemlerde yerlerine yazalım.
\( y = \dfrac{2x}{3} \)
\( y = \dfrac{6}{x} \)
İki denklemi ortak çözerek kesişim noktalarını bulalım.
\( f(x) = g(x) \)
\( \dfrac{2x}{3} = \dfrac{6}{x} \)
\( 2x^2 = 18 \)
\( x \in \{ -3, 3 \} \)
\( x = -3 \) soruda verilen kesişim noktasının apsis değeridir, buna göre ikinci kesişim noktasının apsisi \( x = 3 \) olur.
İkinci kesişim noktasının ordinatını bulmak için denklemlerden birinde \( x = 3 \) yazalım.
\( y = \dfrac{2x}{3} = \dfrac{6}{3} = 2 \)
Buna göre ikinci kesişim noktası \( (3, 2) \) noktasıdır.
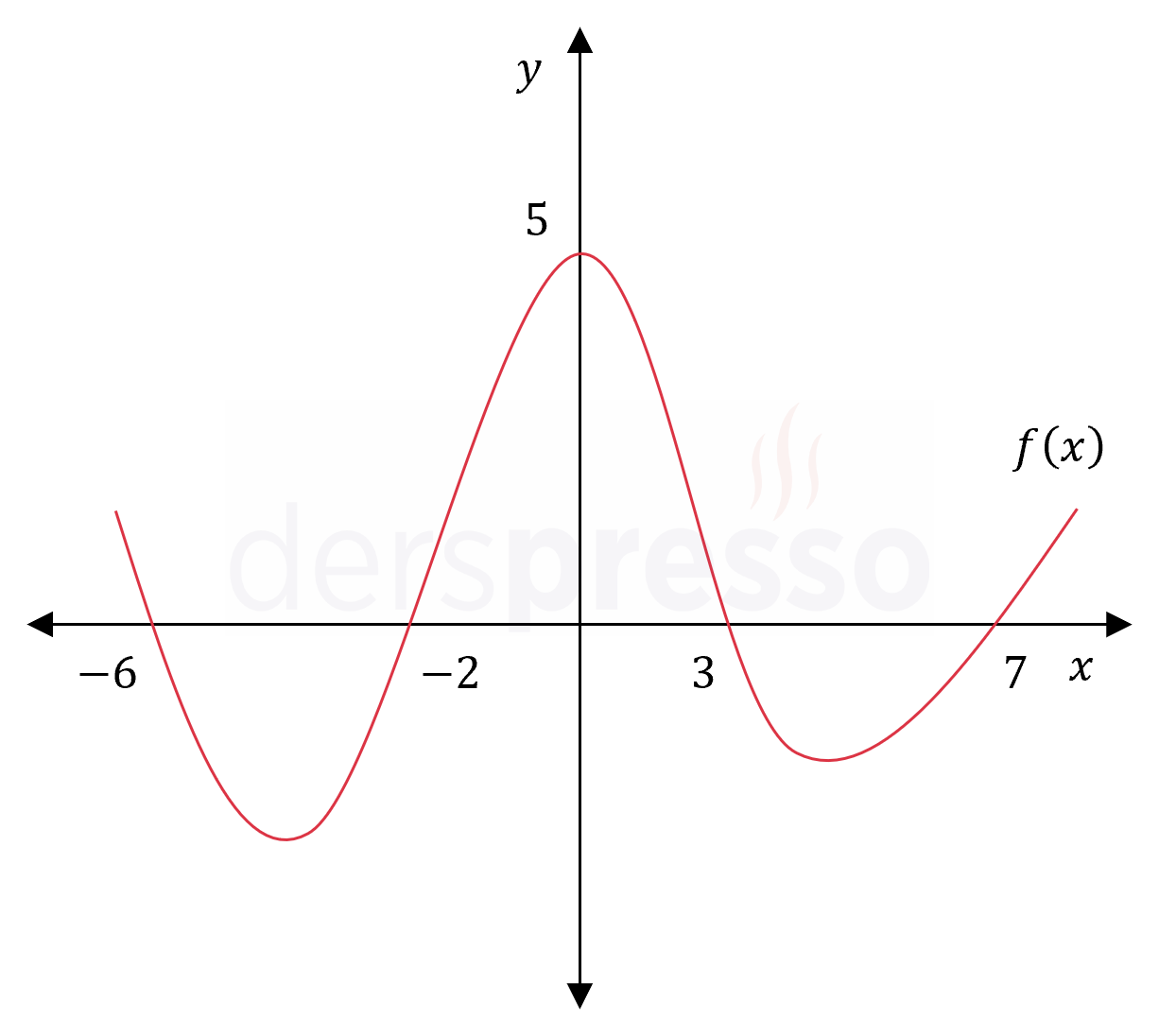
Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Verilen aralıkta \( f(m) = 0 \) ve \( f(0) = n \) eşitliğini sağlayan \( m \) ve \( n \) tam sayı değerlerinin toplamı kaçtır?
Çözümü Göster\( f(m) = 0 \) eşitliğini sağlayan \( m \) değerleri, fonksiyon grafiğinin \( x \) eksenini kestiği noktalardır.
\( m \in \{ -6, -2, 3, 7 \} \)
\( f(0) = n \) eşitliğini sağlayan \( n \) değeri, fonksiyonun \( x = 0 \) için, yani \( y \) eksenini kestiği noktadaki değeridir.
\( f(0) = n = 5 \)
Bulduğumuz \( m \) ve \( n \) tam sayı değerlerini toplayalım.
\( -6 + (-2) + 3 + 7 + 5 = 7 \) bulunur.
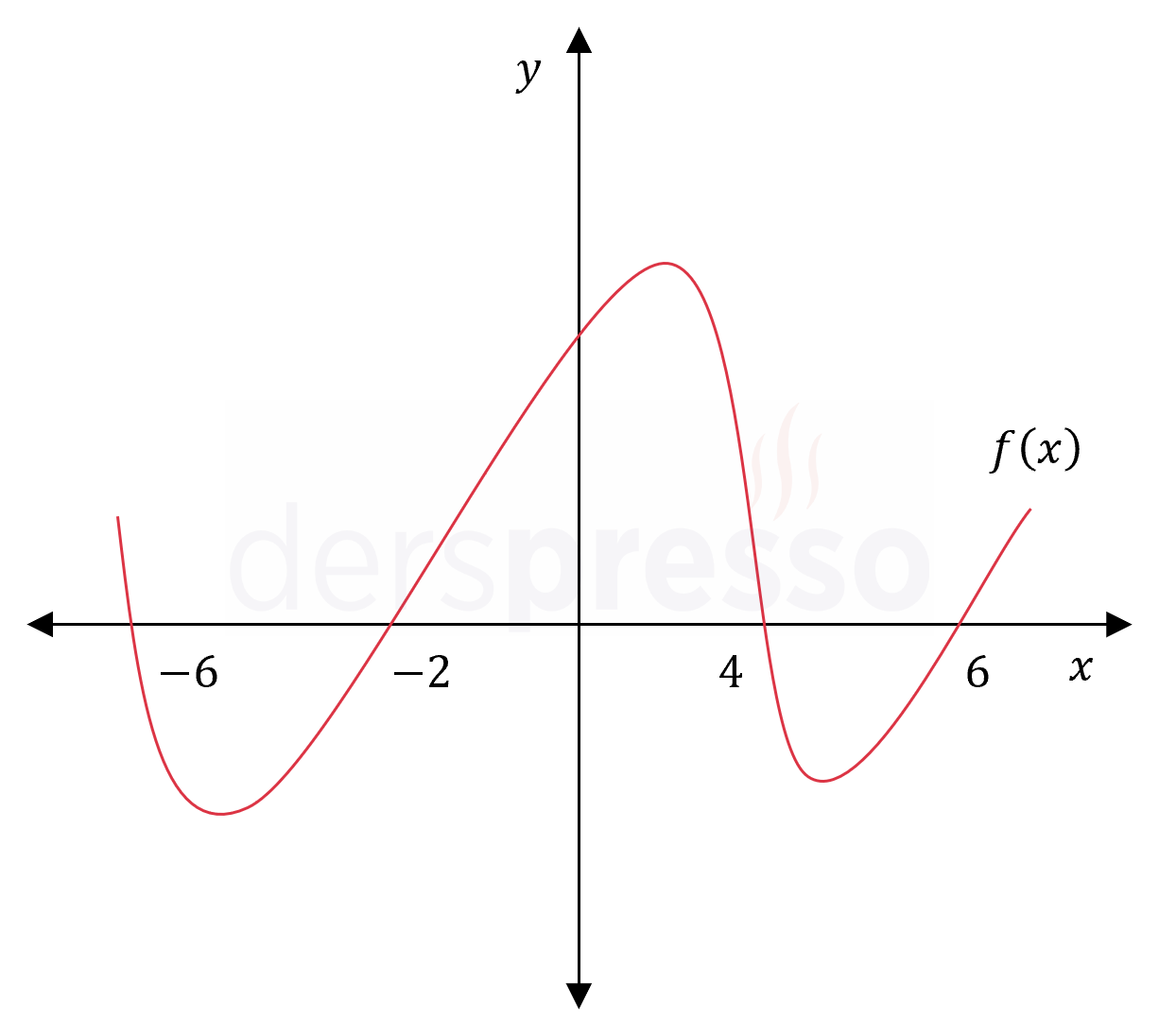
Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdaki öncüllerden hangileri doğrudur?
I. \( f(-2) \ge 0 \)
II. \( f(-4) \cdot f(2) \lt 0 \)
III. \( f(0) + f(3) \lt 0 \)
IV. \( f(-6) + f(6) \le 0 \)
Çözümü GösterVerilen öncülleri sırayla inceleyelim.
I. öncül:
\( f(-2) \ge 0 \)
Fonksiyon \( x = -2 \) noktasında \( x \) eksenini kestiği için \( f(-2) = 0 \) olur.
I. öncül doğrudur.
II. öncül:
\( f(-4) \cdot f(2) \lt 0 \)
Fonksiyon \( (-6, -2) \) aralığında negatif olduğu için \( f(-4) \lt 0 \) olur.
Fonksiyon \( (-2, 4) \) aralığında pozitif olduğu için \( f(2) \gt 0 \) olur.
\( f(-4) \cdot f(2) \lt 0 \)
II. öncül doğrudur.
III. öncül:
\( f(0) + f(3) \lt 0 \)
Fonksiyon \( y \) eksenini pozitif tarafta kestiği için \( f(0) \gt 0 \) olur.
Fonksiyon \( (-2, 4) \) aralığında pozitif olduğu için \( f(3) \gt 0 \) olur.
\( f(0) + f(3) \gt 0 \)
III. öncül yanlıştır.
IV. öncül:
\( f(-6) + f(6) \le 0 \)
Fonksiyon \( x = -6 \) ve \( x = 6 \) noktalarında \( x \) eksenini kestiği için \( f(-6) = f(6) = 0 \) olur.
\( f(-6) + f(6) = 0 \)
IV. öncül doğrudur.
Buna göre I., II. ve IV. öncüller doğrudur.
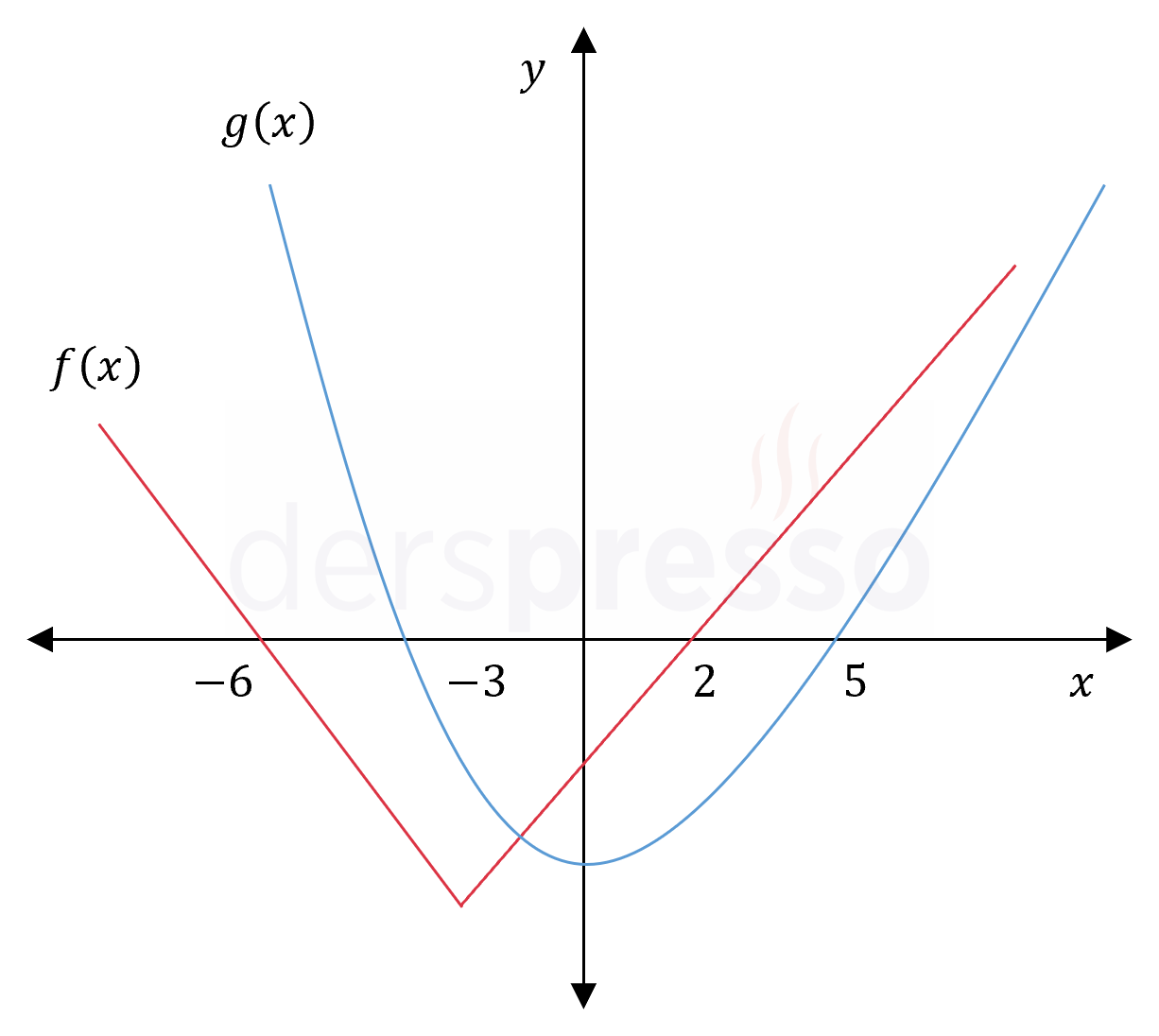
Yukarıda \( f \) ve \( g \) fonksiyonlarının grafikleri verilmiştir.
\( f(a) = g(b) = 0 \) eşitliğini sağlayan \( a \) ve \( b \) değerlerinin çarpımının en küçük değeri kaçtır?
Çözümü Göster\( f \) fonksiyonunun sıfır olduğu noktalar \( x = -6 \) ve \( x = 2 \) noktalarıdır.
\( f(-6) = f(2) = 0 \)
\( g \) fonksiyonunun sıfır olduğu noktalar \( x = -3 \) ve \( x = 5 \) noktalarıdır.
\( g(-3) = g(5) = 0 \)
\( ab \) çarpımının alabileceği farklı değerleri bulalım.
\( -6 \cdot (-3) = 18 \)
\( -6 \cdot 5 = -30 \)
\( 2 \cdot (-3) = -6 \)
\( 2 \cdot 5 = 10 \)
\( ab \) çarpımının en küçük değeri \( -30 \) olarak bulunur.
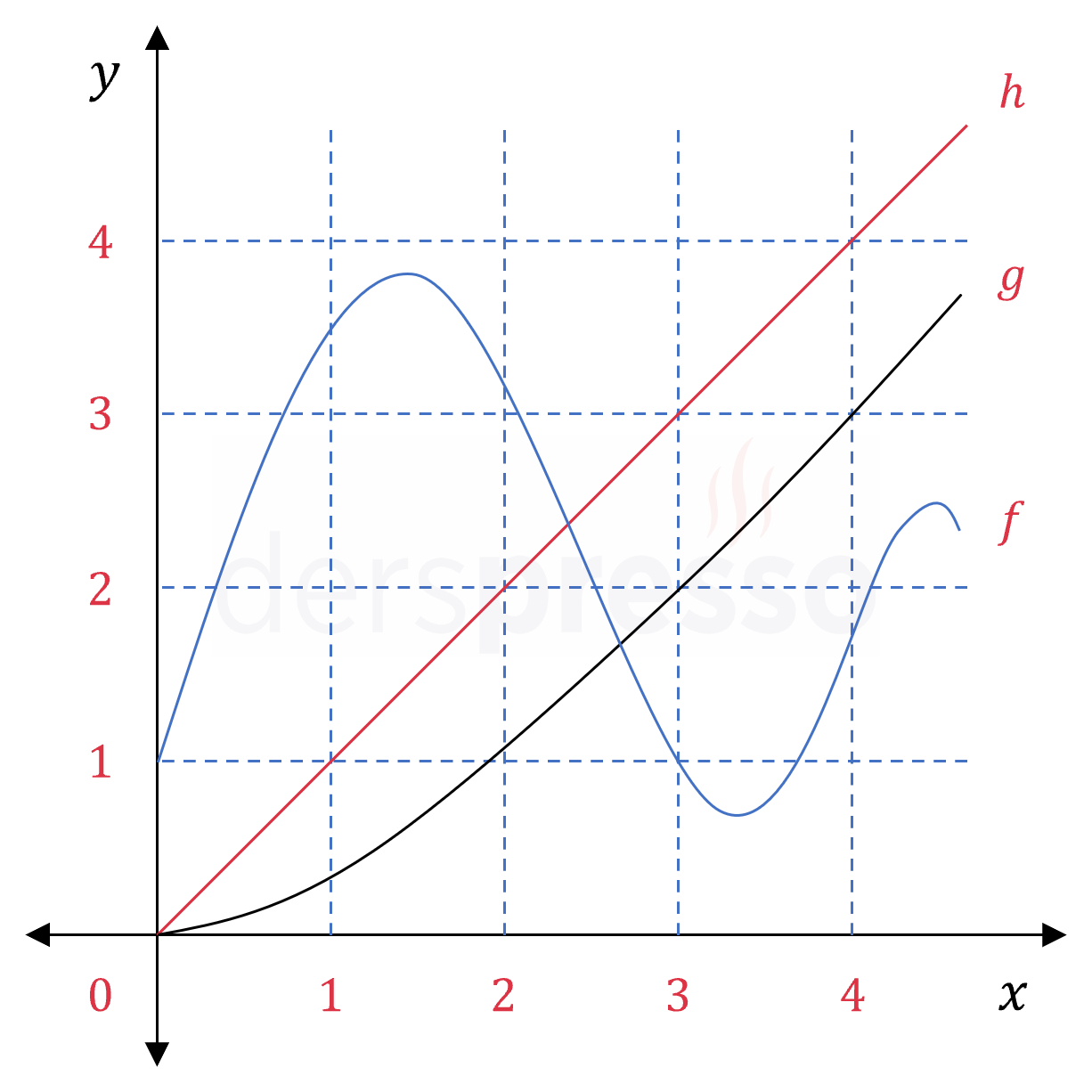
Yukarıdaki grafiğe göre, \( a \in (1, 2) \) olmak üzere,
\( f(a) = b \)
\( g(b) = c \)
\( h(c) = d \)
olduğuna göre, aşağıdakilerden hangileri doğrudur?
I. \( b \gt a \)
II. \( b \gt d \)
III. \( a \gt c \)
Çözümü Göster\( a \in (1, 2) \) olduğu biliniyor.
\( f(a) = b \) olduğuna göre \( b \in (3, 4) \) olur.
\( g(b) = c \) olduğuna göre \( c \in (2, 3) \) olur.
\( h(c) = d \) olduğuna göre \( d \in (2, 3) \) olur.
Buna göre I. ve II. öncüller doğrudur.

Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
Buna göre \( f(x - 2) = 0 \) denklemini sağlayan \( x \) reel sayılarının toplamı kaçtır?
Çözümü Göster\( f \) fonksiyonunda değeri sıfır olan \( x \) değerleri \( \{ -4, 3, 7 \} \) sayılarıdır.
\( f(x - 2) = 0 \) denklemini sağlayan \( x \) değerleri için parantez içindeki ifadeyi fonksiyonunun köklerine eşitleyelim.
\( x - 2 = -4 \Longrightarrow x = -2 \)
\( x - 2 = 3 \Longrightarrow x = 5 \)
\( x - 2 = 7 \Longrightarrow x = 9 \)
\( f(x - 2) = 0 \) eşitliğini sağlayan \( x \) değerlerinin toplamını bulalım.
\( -2 + 5 + 9 = 12 \) bulunur.
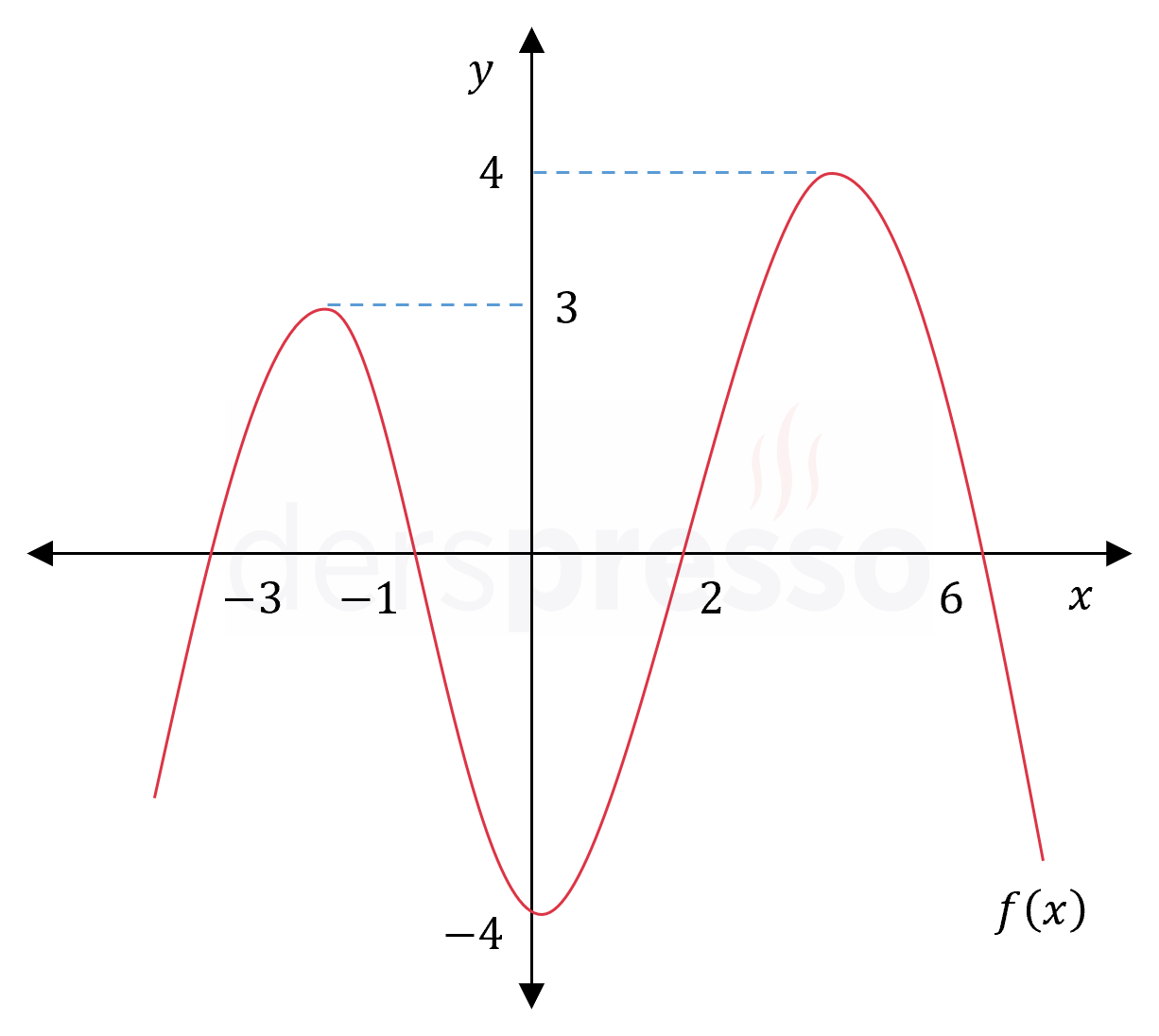
Yukarıda \( f \) fonksiyonun grafiği verilmiştir.
Buna göre verilen aralıkta aşağıdakilerden hangileri doğrudur?
I. \( f \) fonksiyonu eksenleri 4 noktada keser.
II. Fonksiyonun \( [-3, 6] \) aralığındaki en büyük değeri 6'dır.
III. \( \abs{f(x)} = 2 \) denkleminin çözüm kümesi 8 elemanlıdır.
Çözümü GösterVerilen öncülleri sırayla inceleyelim.
I. öncül:
\( f \) fonksiyonu \( x \) eksenini \( x \in \{ -3, -1, 2, 6 \} \) olmak üzere dört noktada, \( y \) eksenini \( y = -4 \) olmak üzere tek noktada keser.
I. öncül yanlıştır.
II. öncül:
Fonksiyonun en büyük değeri \( (2, 6) \) aralığında aldığı 4 değeridir.
II. öncül yanlıştır.
III. öncül:
\( \abs{f(x)} = 2 \) denkleminin çözüm kümesi, fonksiyonun \( f(x) = 2 \) ya da \( f(x) = -2 \) değerlerini aldığı \( x \) değerlerinden oluşur.
Grafik üzerinde \( y = 2 \) ve \( y = -2 \) doğrularını çizelim ve fonksiyonun bu iki doğruyu kestiği noktaları bulalım.
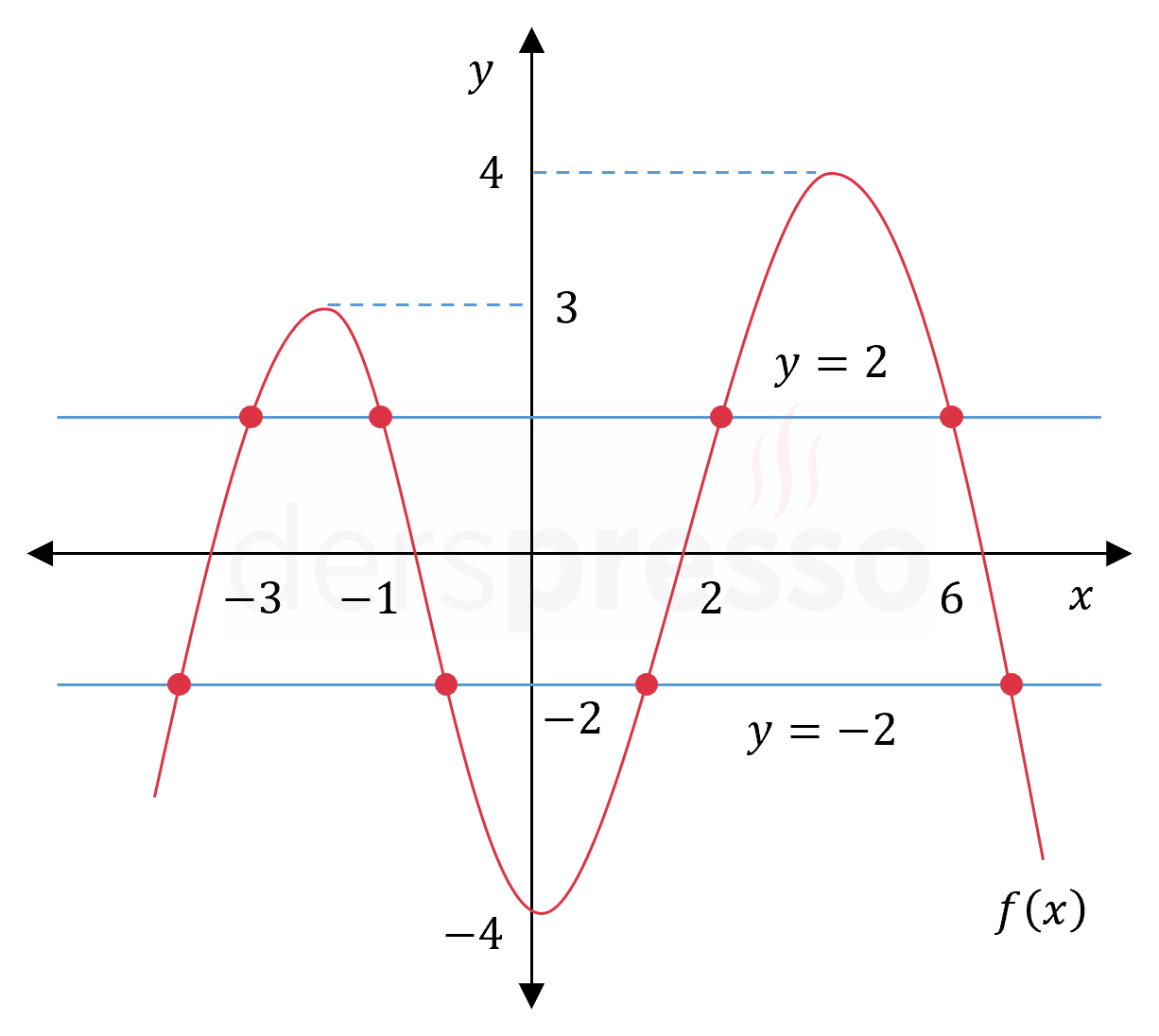
Fonksiyon doğruları işaretli 8 noktada kestiği için denklemin çözüm kümesi 8 elemanlıdır.
III. öncül doğrudur.
Buna göre sadece III. öncül doğrudur.

\( k \in (2, 3) \) olmak üzere, yukarıdaki grafikle ilgili aşağıdaki bilgiler veriliyor.
\( f(k) = l, \quad h(l) = m, \quad g(m) = n \)
Buna göre aşağıdaki ifadelerden hangileri doğrudur?
I. \( l \cdot m \cdot n \gt 0 \)
II. \( g(m) \gt h(m) \)
III. \( f(k) \lt h(l) \lt g(m) \)
Çözümü Göster\( k \in (2, 3) \) olduğu biliniyor.
\( f(k) = l \) olduğuna göre, \( l \in (-3, -2) \) olur.
\( h(l) = m \) olduğuna göre, \( m \in (-1, 0) \) olur.
\( g(m) = n \) olduğuna göre, \( n \in (2, 3) \) olur.
Bulduğumuz bu değer aralıklarını kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( l \cdot m \cdot n \gt 0 \)
\( n \) pozitif, \( l \) ve \( m \) negatif olduğundan çarpımları pozitif olur.
I. öncül doğrudur.
II. öncül:
\( g(m) \gt h(m) \)
\( m \in (-1, 0) \) aralığında \( g \) fonksiyonu \( h \) fonksiyonunun üstünde kaldığı için bu aralıkta \( g(m) \gt h(m) \) olur.
II. öncül doğrudur.
III. öncül:
\( f(k) \lt h(l) \lt g(m) \)
\( k \in (2, 3) \) aralığında \( f \) fonksiyonu \( (-3, -2) \) aralığında değer alır.
\( l \in (-3, -2) \) aralığında \( h \) fonksiyonu \( (-1, 0) \) aralığında değer alır.
\( m \in (-1, 0) \) aralığında \( g \) fonksiyonu \( (2, 3) \) aralığında değer alır.
III. öncül doğrudur.
Buna göre verilen öncüllerin tümü doğrudur.
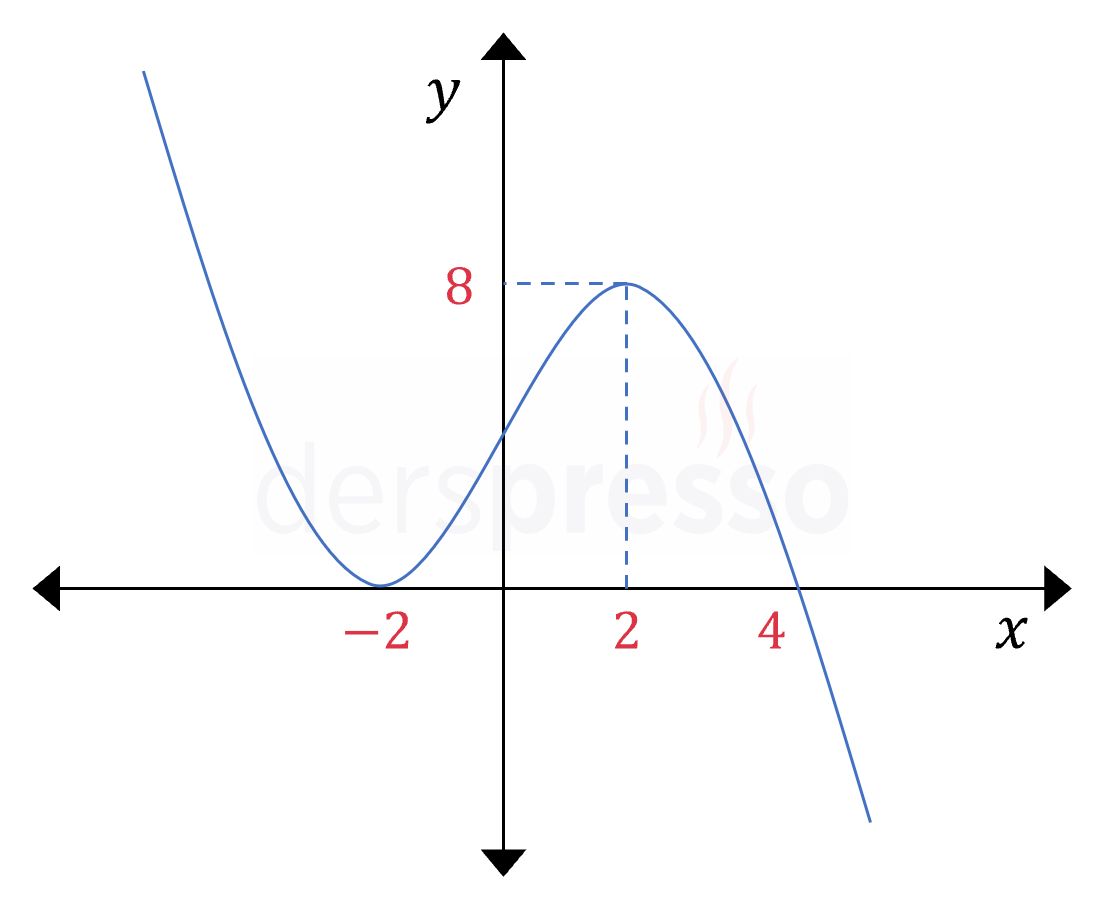
Yukarıda \( y = f(x)\) fonksiyonunun grafiği verilmiştir.
\( \abs{f(a) - 2} = 5 \) eşitliğini sağlayan kaç farklı \( a \) reel sayısı vardır?
Çözümü Göster\( \abs{f(a) - 2} = 5 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( f(a) - 2 = 5 \)
\( f(a) = 7 \)
Durum 2:
\( f(a) - 2 = -5 \)
\( f(a) = -3 \)
Bu iki eşitliği sağlayan \( a \) değerleri fonksiyon değeri 7 ya da -3 olan \( x \) değerleridir.
Fonksiyon değeri 7 olan \( x \) değerlerini bulmak için fonksiyon grafiği ile \( y = 7 \) doğrusunun kesişim noktalarını, fonksiyon değeri -3 olan \( x \) değerlerini bulmak için de fonksiyon grafiği ile \( y = -3 \) doğrusunun kesişim noktalarını bulalım.
\( f(x) \) fonksiyonu \( y = 7 \) doğrusu ile 3 noktada, \( y = -3 \) doğrusu ile 1 noktada kesişir.
Bu kesişim noktaları aşağıdaki şekilde gösterilmiştir.
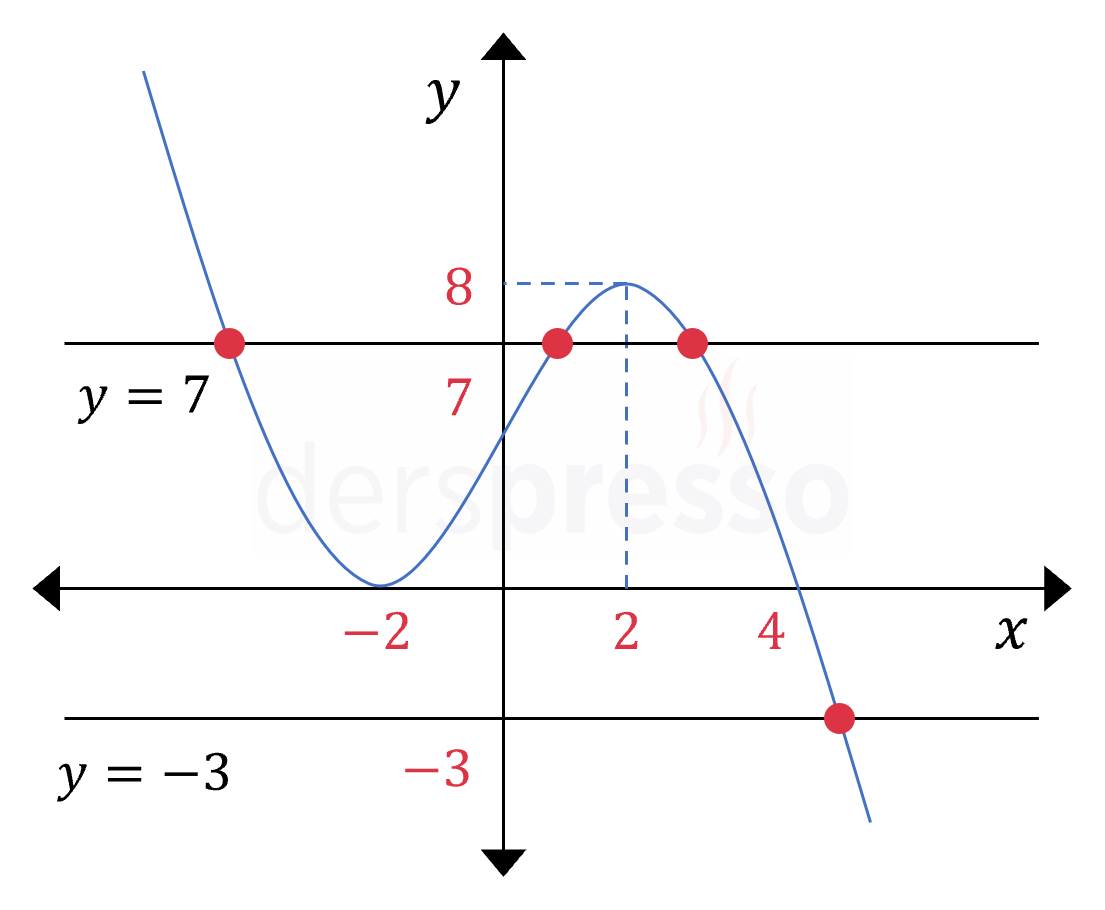
Buna göre verilen eşitliği sağlayan 4 farklı \( a \) reel sayısı vardır.
\( f \) fonksiyonu, her \( x \) değeri için \( y = x + 3 \), \( y = 4x + 6 \) ve \( y = 8 - 4x \) doğrularının en küçük değerini alacak şekilde tanımlanıyor.
Buna göre, \( f \) fonksiyonunun en büyük değeri kaçtır?
Çözümü GösterVerilen üç doğrunun grafiğini çizelim (kırmızı doğrular).

Mavi ile işaretlenmiş olan doğru parçaları, her \( x \) değeri için bu üç doğrunun aldığı değerlerin en küçüğünü, dolayısıyla \( f \) fonksiyonunu temsil etmektedir.
Bu grafiğe göre, \( f \) fonksiyonu en büyük değerini \( y = x + 3 \) ve \( y = 8 - 4x \) doğrularının kesişim noktasında alır.
\( y \) değerlerini eşitleyerek iki doğru denklemini ortak çözelim.
\( x + 3 = 8 - 4x \)
\( x = 1 \)
\( x = 1 \) için \( f \) fonksiyonunun değerini bulalım.
\( y = x + 3 = 1 + 3 = 4 \)
Buna göre \( f \) fonksiyonunun en büyük değeri 4'tür.