Harmonik Seri
Birim kesirlerin toplamından oluşan seriye harmonik seri denir.
\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{1}{n}} = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots \)
Harmonik serilerin \( n \). kısmi toplamına harmonik sayı denir ve \( H_n \) ile gösterilir.
\( H_n = \displaystyle\sum_{k = 1}^n {\dfrac{1}{k}} \)
Harmonik serilerin toplamı sonsuza gider, dolayısıyla harmonik seriler ıraksaktır.
Harmonik seriler ıraksaktır.
İSPATI GÖSTER
Harmonik serinin \( n \). kısmi toplamını yazalım.
\( H_n = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots + \dfrac{1}{n} \)
Bu toplamın her terimini analitik düzlemde genişliği 1 birim, yüksekliği terimin değerine eşit olan bir dikdörtgen olarak çizelim.
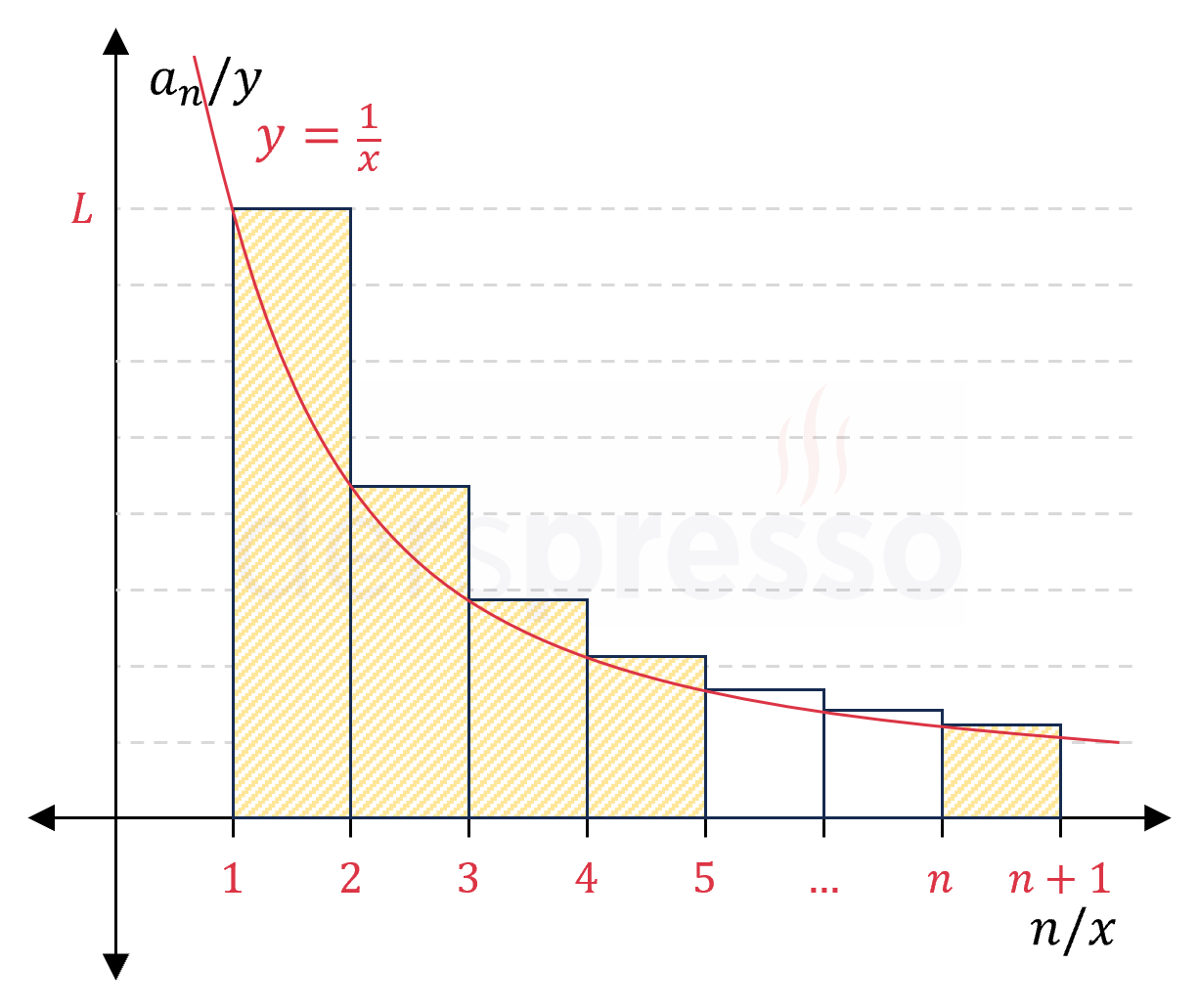
Buna göre \( H_n \) toplamı bu dikdörtgenlerin alanları toplamına eşittir.
Pozitif tam sayı değerleri için harmonik serinin terimlerinin karşılık geldiği \( f(x) = \frac{1}{x} \) fonksiyonunun aynı \( [1, n + 1] \) aralığında \( x \) ekseni ile arasında kalan alanı bulalım.
\( \displaystyle\int_1^{n+1} {\dfrac{1}{x}\ dx} = (\ln{x})|_1^{n+1} \)
\( = \ln(n + 1) - \ln{1} = \ln(n + 1) \)
Grafikte de görülebileceği gibi, harmonik serinin toplamının karşılık geldiği dikdörtgenlerin alanları toplamı fonksiyonun altında kalan alandan büyüktür.
\( H_n \gt \ln(n + 1) \)
Bu eşitsizliğin taraflarının \( n \) sonsuza giderken limitini alalım.
\( \lim\limits_{n \to \infty} {H_n} \gt \lim\limits_{n \to \infty} \ln(n + 1) \)
Eşitsizliğin sol tarafı harmonik dizinin toplamına eşittir. Eşitsizliğin sağ tarafı \( n \) sonsuza giderken sonsuza gider.
Buna göre harmonik serinin toplamı da sonsuza gider, dolayısıyla harmonik seri ıraksaktır.
Ardışık terimlerinin işaretleri birbirinden farklı olan harmonik serilere alterne harmonik seri denir.
\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{(-1)^{n-1}}{n}} = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \ldots \)
Önümüzdeki bölümlerde göstereceğimiz üzere, alterne harmonik seriler (koşullu) yakınsaktır.
\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{7}{n}} \) serisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü Göster\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{7}{n}} = 7\displaystyle\sum_{n = 1}^{\infty} {\dfrac{1}{n}} \)
\( \displaystyle\sum_{n = 1}^{\infty} {\frac{1}{n}} \) serisi bir harmonik seridir, dolayısıyla ıraksaktır.
Iraksak bir serinin sıfırdan farklı bir skaler ile çarpımı da ıraksaktır.
Buna göre, \( 7\sum {\frac{1}{n}} \) serisi de ıraksaktır.
\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{5n + 5}{n^2 + n}} \) serisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü Göster\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{5n + 5}{n^2 + n}} = \displaystyle\sum_{n = 1}^{\infty} {\dfrac{5(n + 1)}{n(n + 1)}} \)
\( = \displaystyle\sum_{n = 1}^{\infty} {\dfrac{5}{n}} \)
\( = 5\displaystyle\sum_{n = 1}^{\infty} {\dfrac{1}{n}} \)
\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{1}{n}} \) serisi bir harmonik seridir, dolayısıyla ıraksaktır.
Iraksak bir serinin sıfırdan farklı bir skaler ile çarpımı da ıraksaktır.
Buna göre, \( 5\sum {\frac{1}{n}} \) serisi de ıraksaktır.
\( \displaystyle\sum_{n = 1}^{\infty} {\dfrac{2n + 11}{n^2}} \) serisinin yakınsaklık/ıraksaklık durumunu inceleyiniz.
Çözümü Göster\( \displaystyle\sum_{n = 1}^{\infty} {a_n} = \displaystyle\sum_{n = 1}^{\infty} {\dfrac{2n + 11}{n^2}} \)
Bu seri ile aşağıdaki seri arasında direkt karşılaştırma testi uygulayalım.
\( \displaystyle\sum_{n = 1}^{\infty} {b_n} = \displaystyle\sum_{n = 1}^{\infty} {\dfrac{1}{n}} \)
İki serinin de terimleri her \( n \ge 1 \) için pozitiftir.
Paydaları eşit iki ifadeden payı büyük olan daha büyüktür (\( 2n + 11 \gt 2n \)).
\( a_n = \dfrac{2n + 11}{n^2} \gt \dfrac{2n}{n^2} \)
\( = \dfrac{2}{n} \gt \dfrac{1}{n} = b_n \)
\( \sum {b_n} \) serisi bir harmonik seridir ve ıraksaktır.
\( \sum {b_n} \) serisi ıraksak ve her \( n \ge 1 \) için \( a_n \gt b_n \) olduğu için \( \sum {a_n} \) serisi de ıraksaktır.