Bir Vektörün Bileşenleri
Önceki bölümlerde bir konum vektörünü uç noktasının koordinatları cinsinden ifade ettik ve vektörler arası işlemleri bu koordinatlar üzerinden gerçekleştirdik. Vektörleri tanımlamak ve vektörler arası işlemleri gerçekleştirmek için kullanılabilecek bir diğer yöntem vektörleri bileşenleri cinsinden yazmaktır.
Birim Vektörler
Birim vektörü büyüklüğü bir birim olan vektör olarak tanımlamıştık. Bir vektör büyüklüğüne bölündüğünde, o vektörle aynı yöndeki birim vektör elde edilir ve her vektör normu ile birim vektörünün skaler çarpımı şeklinde ifade edilebilir.
\( \hat{a} = \dfrac{\vec{a}}{\norm{\vec{a}}} \)
\( \vec{a} = \norm{\vec{a}} \hat{a} \)
Herhangi bir vektör için birim vektör tanımlanabileceği gibi, koordinat eksenleri için de birer birim vektör tanımlanabilir. \( x \) ve \( y \) eksenleri için tanımlanmış özel birim vektörler aşağıda gösterilmiştir. \( x \) ekseni için tanımlanan birim vektör \( \hat{i} \) sembolüyle, \( y \) ekseni için tanımlanan birim vektör \( \hat{j} \) sembolüyle gösterilir.

\( \hat{i} = (1, 0) \)
\( \hat{j} = (0, 1) \)
\( \norm{\vec{i}} = \norm{\vec{j}} = 1 \)
Birim Vektörlerin Nokta Çarpımı
Bir vektörün kendisiyle yaptığı açı 0° olduğu için, \( \hat{i} \) ve \( \hat{j} \) birim vektörlerinin kendileriyle nokta çarpımı 1'e eşittir.
\( \hat{i} \cdot \hat{i} = \norm{\vec{i}} \norm{\vec{i}} \cos{0°} \)
\( \hat{i} \cdot \hat{i} = 1 \cdot 1 \cdot 1 = 1 \)
\( \hat{j} \cdot \hat{j} = 1 \)
\( \hat{i} \) ve \( \hat{j} \) birim vektörleri birbirlerine dik oldukları için, nokta çarpımları 0'a eşittir.
\( \hat{i} \cdot \hat{j} = \norm{\vec{i}} \norm{\vec{j}} \cos{90°} \)
\( \hat{i} \cdot \hat{j} = 1 \cdot 1 \cdot 0 = 0 \)
Bir Vektörün Bileşenleri
Bir \( \vec{a} \) vektörünün bileşenleri, vektörün her bir eksen üzerindeki izdüşümlerinden oluşur. Aşağıda \( \vec{a} \) vektörünün \( x \) ve \( y \) eksenleri üzerindeki izdüşümü olan \( \vec{a}_x \) ve \( \vec{a}_y \) vektörleri gösterilmiştir.
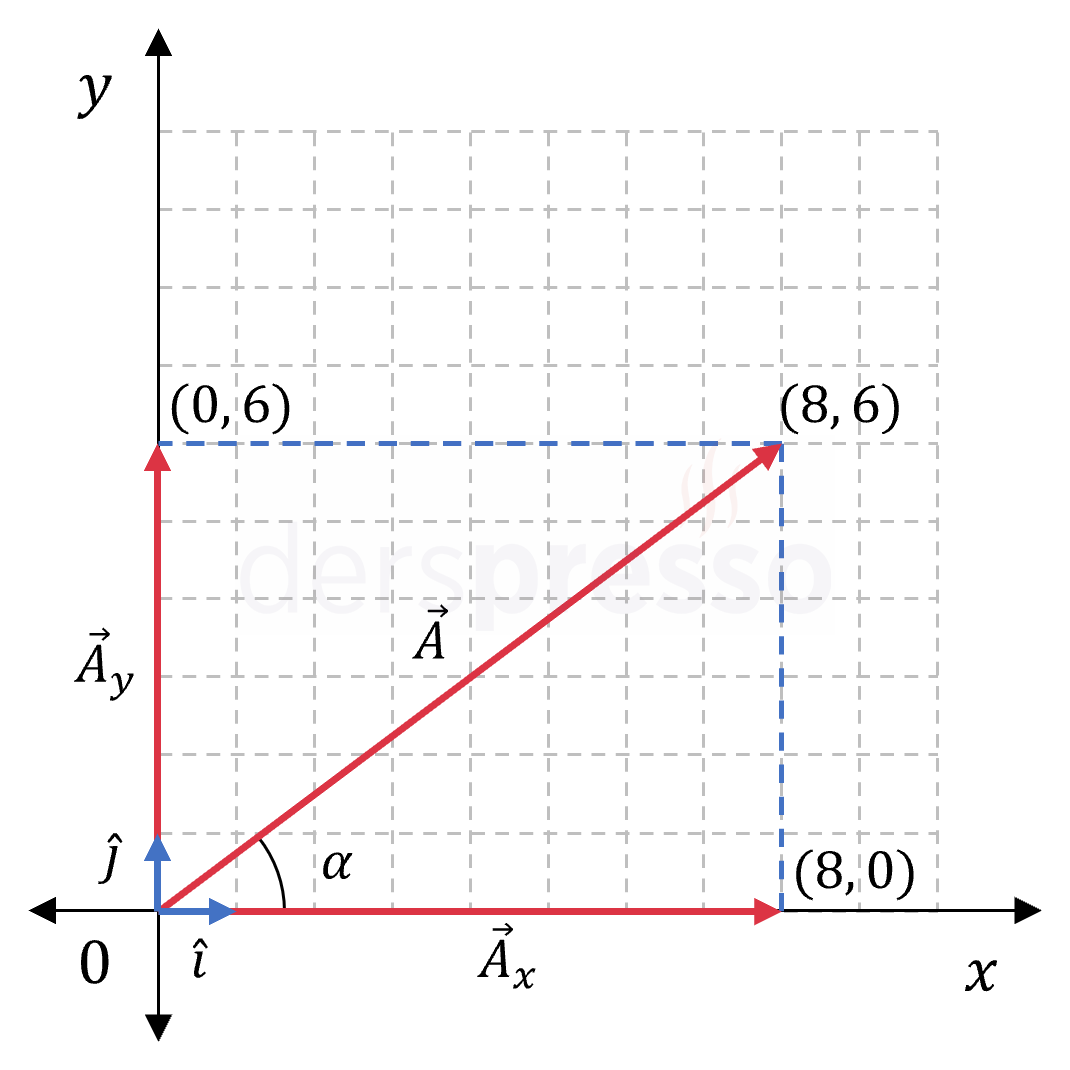
Vektörlerin toplamı konusunda iki vektörün toplamının, bu iki vektörün oluşturduğu paralelkenarın köşegeni olduğunu belirtmiştik. Yukarıdaki şekil bu açıdan incelendiğinde, \( \vec{a} \) vektörünün bileşenlerinin vektörel toplamına eşit olduğu görülebilir.
\( \vec{a} = \vec{a}_x + \vec{a}_y \)
\( (8, 6) = (8, 0) + (0, 6) \)
Bu bileşenlerin büyüklükleri trigonometrik fonksiyonlar kullanılarak aşağıdaki şekilde hesaplanabilir.
\( \norm{\vec{a_x}} = \norm{\vec{a}} \cos{\alpha} \)
\( \norm{\vec{a_y}} = \norm{\vec{a}} \sin{\alpha} \)
Her bir bileşen vektörü, vektörün büyüklüğü ile yukarıda tanımladığımız ilgili eksenin birim vektörünün çarpımı şeklinde de yazılabilir.
\( \vec{a}_x = \norm{\vec{a}_x} \hat{i} \)
\( \vec{a}_y = \norm{\vec{a}_y} \hat{j} \)
\( (8, 0) = 8(1, 0) \)
\( (0, 6) = 6(0, 1) \)
\( \norm{\vec{a}_x} \) ve \( \norm{\vec{a}_y} \) skaler büyüklükleri kısaca \( a_x \) ve \( a_y \) şeklinde ifade edilirse \( \vec{a} \) vektörü bileşenleri ve birim vektörler cinsinden aşağıdaki şekilde yazılabilir.
\( \vec{a} = a_x \hat{i} + a_y \hat{j} \)
\( (8, 6) = 8 \hat{i} + 6 \hat{j} \)
\( \hat{i} \) ve \( \hat{j} \) birim vektörleri matris şeklinde yazılarak bir vektörün ve bileşenlerinin toplamının eşitliği gösterilebilir.
\( (a_x, a_y) = a_x(1, 0) + a_y(0, 1) \)
\( = (a_x, 0) + (0, a_y) \) \( = (a_x, a_y) \)
\( (8, 6) = 8(1, 0) + 6(0, 1) \)
\( = (8, 0) + (0, 6) \)
\( = (8, 6) \)
\( \vec{a} \) vektörünün büyüklüğü Pisagor teoremi kullanılarak bileşenlerinin büyüklükleri cinsinden aşağıdaki şekilde yazılabilir.
\( \norm{\vec{a}} = \sqrt{a_x^2 + a_y^2} \)
Vektör Bileşenleriyle İşlemler
Önceki bölümlerde vektörlerle işlemleri geometrik olarak ve vektörlerin uç noktalarının koordinatları ile nasıl yapabileceğimizi görmüştük. Bu işlemler vektörlerin bileşenleri cinsinden de gerçekleştirilebilir.
Vektörlerle Toplama
İki vektörün toplamının bileşenleri, vektörlerin bileşenlerinin toplamına eşittir.
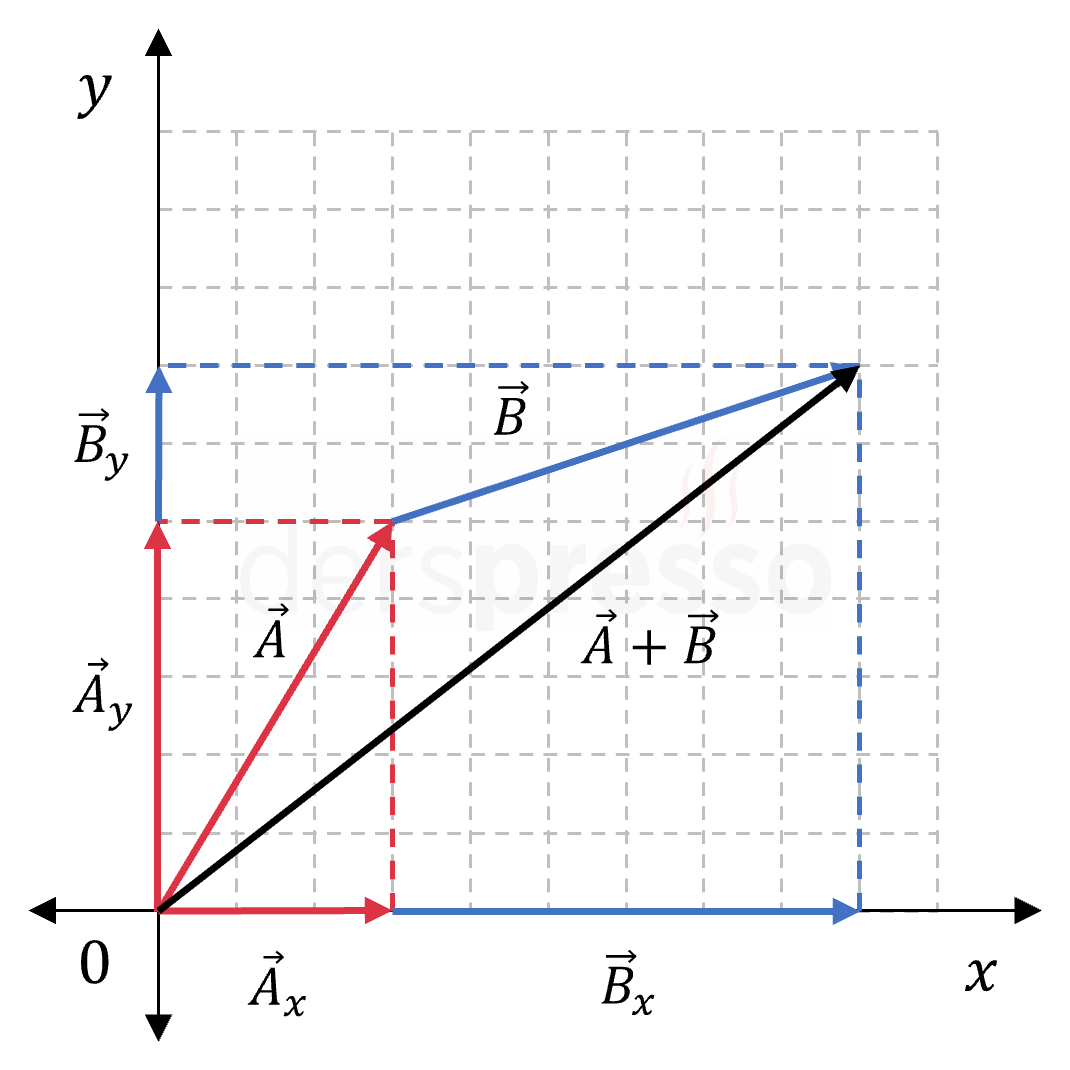
\( \vec{a} = a_x \hat{i} + a_y \hat{j} \)
\( \vec{b} = b_x \hat{i} + b_y \hat{j} \) olmak üzere,
\( \vec{a} + \vec{b} = (a_x \hat{i} + a_y \hat{j}) + (b_x \hat{i} + b_y \hat{j}) \)
\( = (a_x + b_x) \hat{i} + (a_y + b_y) \hat{j} \)
Vektörlerle Çıkarma
İki vektörün farkının bileşenleri, vektörlerin bileşenlerinin farkına eşittir.
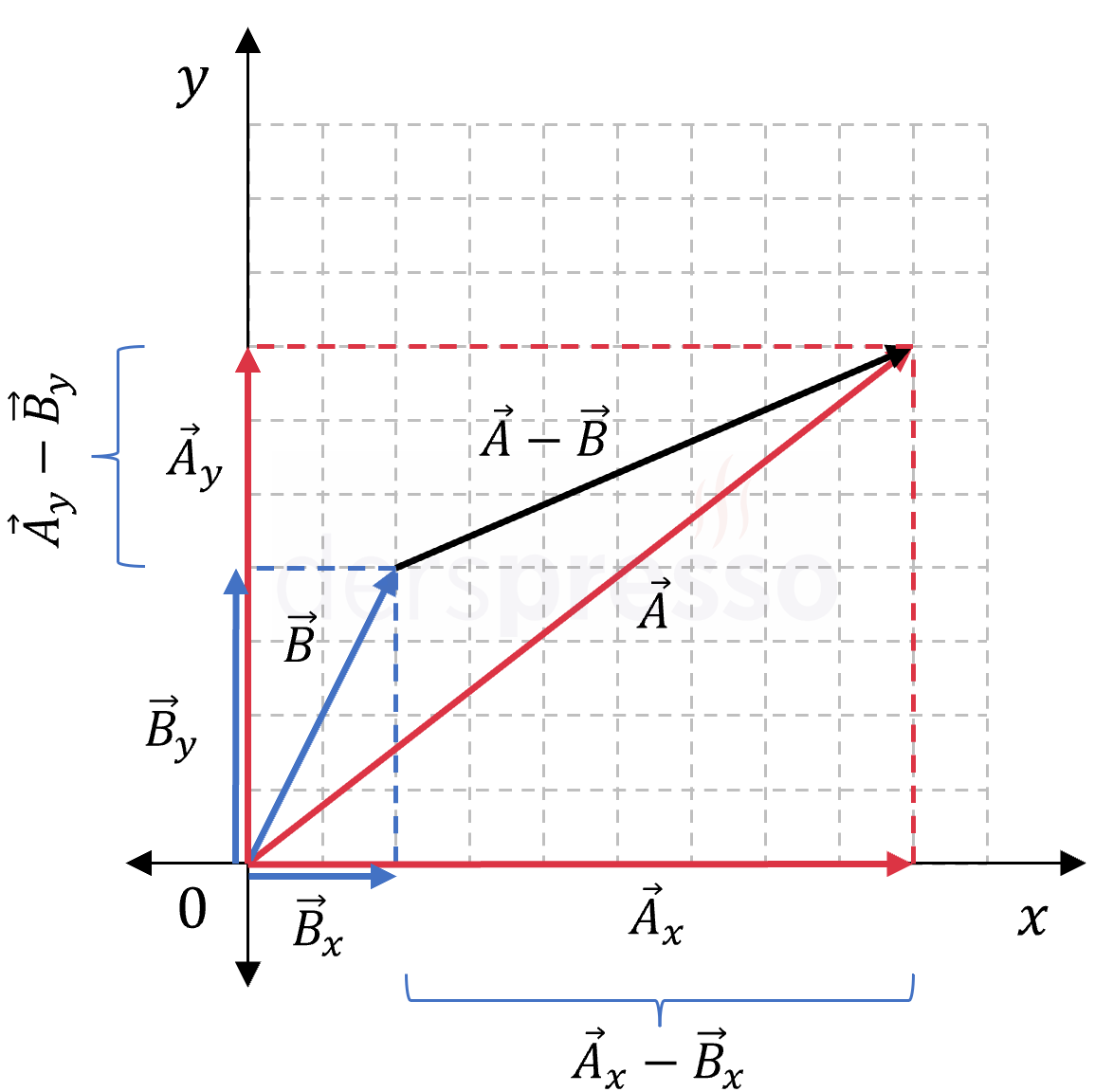
\( \vec{a} = a_x \hat{i} + a_y \hat{j} \)
\( \vec{b} = b_x \hat{i} + b_y \hat{j} \)
\( \vec{a} - \vec{b} = (a_x \hat{i} + a_y \hat{j}) - (b_x \hat{i} + b_y \hat{j}) \)
\( = (a_x - b_x) \hat{i} + (a_y - b_y) \hat{j} \)
Bir Skaler Büyüklükle Çarpma
Bir vektörün bir skaler büyüklükle çarpımının bileşenleri, vektörlerin bileşenlerinin skaler büyüklükle çarpımına eşittir.

\( k \in \mathbb{R} \)
\( \vec{a} = a_x \hat{i} + a_y \hat{j} \)
\( k \vec{a} = k(a_x \hat{i} + a_y \hat{j}) \)
\( = k a_x \hat{i} + k a_y \hat{j} \)
Nokta Çarpımı
İki vektörün nokta çarpımını bulmak için vektörlerin bileşenlerinin nokta çarpımı alınır.
\( \vec{a} = a_x \hat{i} + a_y \hat{j} \)
\( \vec{b} = b_x \hat{i} + b_y \hat{j} \) olmak üzere,
\( \vec{a} \cdot \vec{b} = (a_x \hat{i} + a_y \hat{j}) \cdot (b_x \hat{i} + b_y \hat{j}) \)
\( = a_xb_x (\hat{i} \cdot \hat{i}) \) \( + a_xby (\hat{i} \cdot \hat{j}) \) \( + a_yb_x (\hat{i} \cdot \hat{j}) \) \( + a_yb_y (\hat{j} \cdot \hat{j}) \)
Yukarıda gösterdiğimiz birim vektörler arası nokta çarpım kurallarını kullanalım.
\( = a_xb_x + a_yb_y \)
Buna göre, iki vektörün nokta çarpımı vektörlerin \( x \) ekseni bileşenlerinin büyüklüklerinin çarpımı ile \( y \) ekseni bileşenlerinin büyüklüklerinin çarpımının skaler toplamına eşittir.
Vektörel Çarpım
İki vektörün vektörel çarpımının büyüklüğünün formülünü aşağıdaki şekilde görmüştük.
\( \vec{a} = (x_1, y_1) \)
\( \vec{b} = (x_2, y_2) \) olmak üzere,
\( \norm{\vec{a} \times \vec{b}} = \abs{x_1 y_2 - x_2 y_1} \)
Bu formül vektörün bileşenlerine uyarlandığında aşağıdaki formül elde edilir.
\( \vec{a} = a_x \hat{i} + a_y \hat{j} \)
\( \vec{b} = b_x \hat{i} + b_y \hat{j} \)
\( \norm{\vec{a} \times \vec{b}} = \abs{a_x b_y - b_x a_y} \)
Vektörel çarpımın sonucunun yönü önceki bölümde gördüğümüz sağ el kuralı kullanılarak bulunabilir.
Üç Boyutlu Vektörlerin Bileşenleri
Üç boyutlu vektörleri bileşenleri cinsinden göstermek için öncelikle üçüncü bileşen için de bir birim vektör tanımlanmalıdır. Aşağıdaki şekilde, daha önce \( x \) ve \( y \) eksenleri için tanımladığımız \( \hat{i} \) ve \( \hat{j} \) birim vektörlerine ek olarak, \( z \) eksenine ait \( \hat{k} \) birim vektörü gösterilmiştir.

\( \hat{i} = (1, 0, 0) \)
\( \hat{j} = (0, 1, 0) \)
\( \hat{k} = (0, 0, 1) \)
\( \norm{\vec{i}} = \norm{\vec{j}} \) \( = \norm{\vec{k}} = 1 \)
Bir \( \vec{a} \) vektörünün bileşenlerinin koordinat sisteminde gösterimi ve bileşenleri cinsinden yazılışı aşağıda gösterilmiştir. İki boyutlu vektörlerde olduğu gibi, üç boyutlu vektörler de her bir eksen için bileşenlerinin vektörel toplamına eşittir.
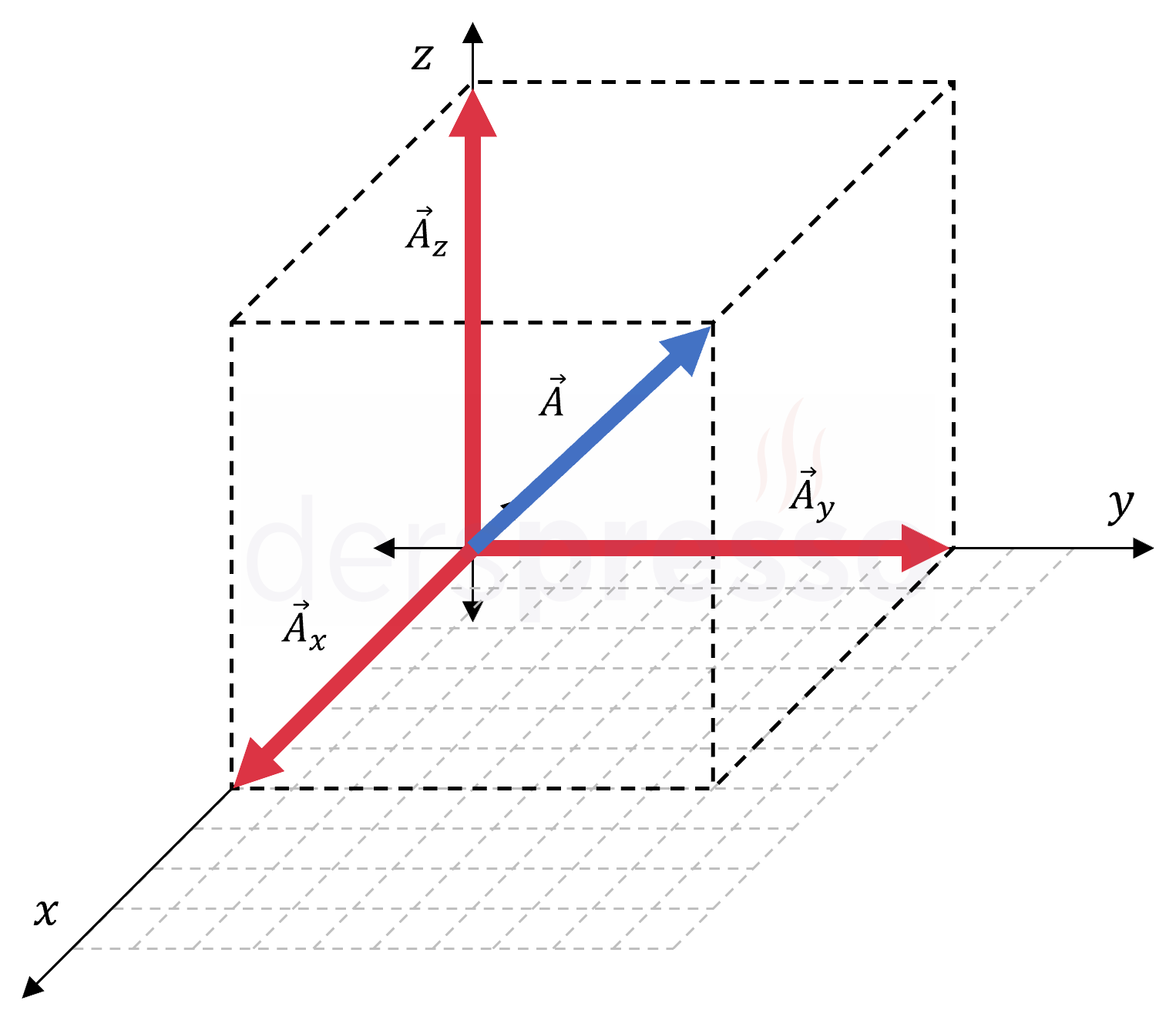
\( \vec{a} = \vec{a_x} + \vec{a_y} + \vec{a_z} \)
\( \vec{a_x} = \norm{\vec{a_x}} \hat{i} \)
\( \vec{a_y} = \norm{\vec{a_y}} \hat{j} \)
\( \vec{a_z} = \norm{\vec{a_z}} \hat{k} \)
Bileşenlerin büyüklüklerine sırasıyla \( a_x \), \( a_y \) ve \( a_z \) diyelim.
\( \vec{a} = a_x \hat{i} + a_y \hat{j} + a_z \hat{k} \)
Bileşen Gösterimi ile İşlemler
Bileşenleri cinsinden yazılmış iki vektörün toplamı olan vektör, vektörlerin \( x \), \( y \) ve \( z \) bileşenleri toplanarak bulunabilir.
\( \vec{a} = a_x \hat{i} + a_y \hat{j} + a_z \hat{k} \)
\( \vec{b} = b_x \hat{i} + b_y \hat{j} + b_z \hat{k} \)
\( \vec{a} + \vec{b} = (a_x \hat{i} + a_y \hat{j} + a_z \hat{k}) \) \( + (b_x \hat{i} + b_y \hat{j} + b_z \hat{k}) \)
\( = (a_x + b_x) \hat{i} + (a_y + b_y) \hat{j} \) \( + (a_z + b_z) \hat{k} \)
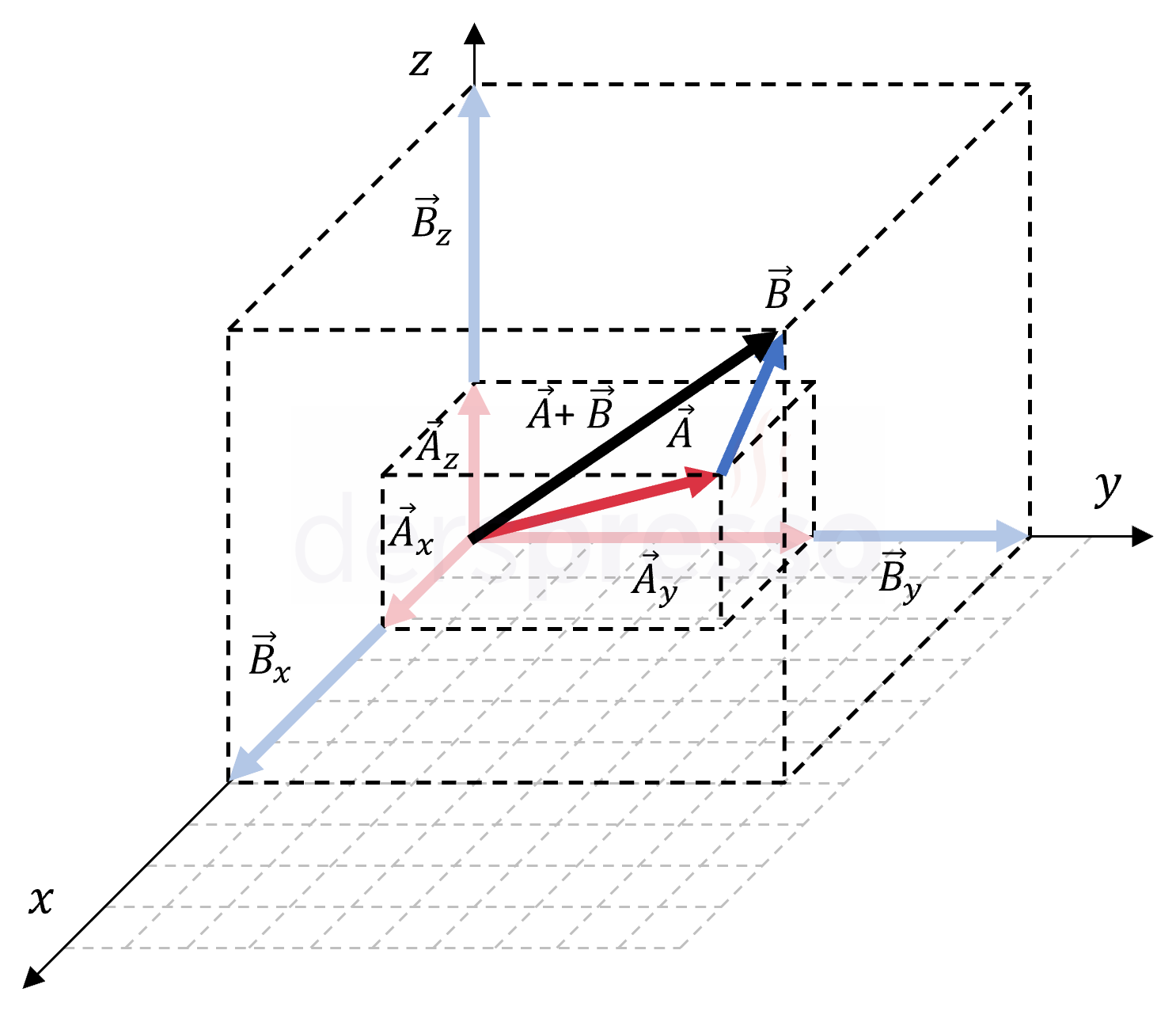
Vektörlerin bileşenleri cinsinden gösterimi kullanılarak iki vektör arasında çıkarma işlemi de benzer şekilde yapılabilir.
\( \vec{a} - \vec{b} = (a_x - b_x) \hat{i} + (a_y - b_y) \hat{j} \) \( + (a_z - b_z) \hat{k} \)
Bir vektörün skaler bir büyüklükle çarpımında, vektörün her bir bileşeni skaler büyüklükle çarpılır.
\( k \in \mathbb{R} \) olmak üzere,
\( k \vec{a} = k(a_x \hat{i} + a_y \hat{j} + a_z \hat{k}) \)
\( k \vec{a} = k a_x \hat{i} + k a_y \hat{j} + k a_z \hat{k} \)
Üç boyutlu iki vektörün nokta çarpımında, vektörlerin her bir eksen için koordinatlarının birbiriyle çarpımının toplamı alınır.
\( \vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_z \)
Önceki bölümlerde iki vektörün vektörel çarpımını alırken çarpım vektörünün büyüklüğünü ve yönünü ayrı ayrı bulmuştuk. Üç boyutlu iki vektörün bileşenleri cinsinden yazılışlarının vektörel çarpımında ise çarpım vektörünün büyüklüğü ve yönü tek bir işlemle bulabiliriz.
\( \vec{a} \times \vec{b} = (a_y b_z − a_z b_y) \hat{i} \) \( + (a_z b_x − a_x b_z) \hat{j} \) \( + (a_x b_y − a_y b_x) \hat{k} \)