Nokta (Skaler) Çarpımı
Konu tekrarı için: İzdüşüm
İki vektörün nokta çarpımı, vektörlerin birbirine karşılık gelen bileşenlerinin çarpımlarının toplamına eşittir.
\( \vec{a} = (x_1, y_1, z_1) \)
\( \vec{b} = (x_2, y_2, z_2) \) olmak üzere,
\( \vec{a} \cdot \vec{b} = (x_1, y_1, z_1) \cdot (x_2, y_2, z_2) \)
\( = x_1 x_2 + y_1 y_2 + z_1z_2 \)
\( \vec{a} = (2, 3) \)
\( \vec{b} = (-4, 5) \) olmak üzere,
\( \vec{a} \cdot \vec{b} = (2, 3) \cdot (-4, 5) \)
\( = 2 \cdot (-4) + 3 \cdot 5 = 7 \)
\( \vec{c} = (2, -3, 2) \)
\( \vec{d} = (-1, 7, 5) \) olmak üzere,
\( \vec{c} \cdot \vec{d} = (2, -3, 2) \cdot (-1, 7, 5) \)
\( = 2 \cdot (-1) + (-3) \cdot 7 + 2 \cdot 5 = -13 \)
Yukarıdaki örneklerde görülebileceği üzere, iki vektörün nokta çarpımı skaler bir büyüklüktür ve herhangi bir reel sayı değer alabilir.
Nokta çarpımında vektörler arasında nokta (\( \cdot \)) sembolü kullanılır. Sayılar arasındaki çarpma işleminde çarpanlar arasında çarpma sembolünün kullanılması zorunlu değildir (\( xy = x \cdot y \)), ancak vektörler arasındaki nokta çarpımında nokta işareti mutlaka kullanılmalıdır (\( \vec{a} \cdot \vec{b} \)).
Nokta çarpımına skaler çarpım ya da iç çarpım da denir. Nokta çarpımının bir diğer adı olan "skaler çarpım" ile önceki bölümde gördüğümüz "bir skaler ile çarpma" işlemleri karıştırılmamalıdır.
Nokta Çarpımının Geometrik Tanımı
Nokta çarpımının yukarıda yaptığımız tanıma denk olan ikinci ve geometrik tanımı aşağıdaki gibidir. Bu formüle göre; iki vektörün nokta çarpımı, vektörlerin normları ile aralarındaki açının kosinüsünün çarpımına eşittir.
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} \norm{\vec{b}} \cos{\alpha} \)
Aşağıdaki iki vektörün nokta çarpımını bulalım.
\( \vec{a} = (8, 8) \)
\( \vec{b} = (10, 0) \)
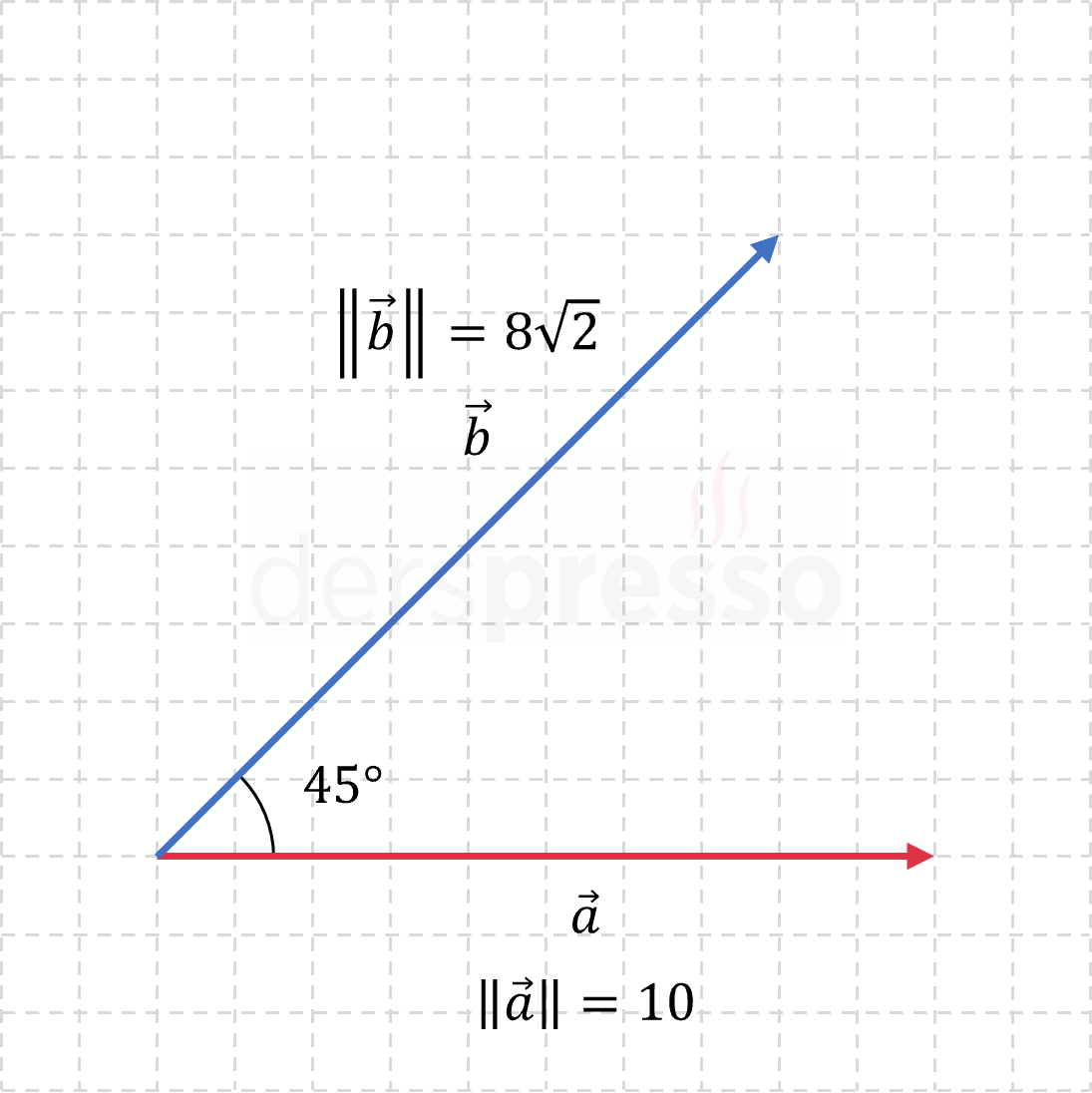
\( \norm{\vec{a}} = \sqrt{8^2 + 8^2} = 8\sqrt{2} \)
\( \norm{\vec{b}} = \sqrt{10^2 + 0^2} = 10 \)
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} \norm{\vec{b}} \cos{45°} \)
\( = 8\sqrt{2} \cdot 10 \cdot \dfrac{\sqrt{2}}{2} = 80 \)
Aynı işlemi nokta çarpımının birinci tanımını kullanarak yaptığımızda aynı sonucu elde ettiğimizi görebiliriz.
\( \vec{a} \cdot \vec{b} = (8, 8) \cdot (10, 0) \)
\( = 8 \cdot 10 + 8 \cdot 0 = 80 \)
\( \norm{\vec{a}} \) ve \( \norm{\vec{b}} \) değerleri vektörlerin normları olduğu için skaler büyüklüklerdir. İki vektör arasındaki açının kosinüs değeri de skaler bir büyüklük olduğu için, nokta çarpımının sonucunun bir vektör değil skaler olduğu bu ikinci tanımda da görülebilir.
Nokta Çarpımının Geometrik Yorumu
İki vektör arasındaki nokta çarpımı, vektörlerden birinin diğer vektör üzerindeki izdüşümünün büyüklüğü ile üzerinde izdüşüm alınan vektörün büyüklüğünün çarpımı şeklinde ifade edilebilir. Bunu iki farklı şekilde gösterelim.
Nokta çarpım işlemini önce \( \vec{b} \) vektörünün \( \vec{a} \) vektörü üzerindeki izdüşümünün büyüklüğünü bularak yapalım. Bir dik üçgendeki trigonometrik oranlar kullanılarak \( \vec{b} \) vektörünün \( \vec{a} \) vektörü üzerindeki izdüşümünün \( \norm{\vec{b}} \cos{\alpha} \) olduğu görülebilir. Bu ifade üzerinde izdüşüm alınan \( \vec{a} \) vektörünün büyüklüğü ile çarpıldığında nokta çarpım formülü elde edilir.
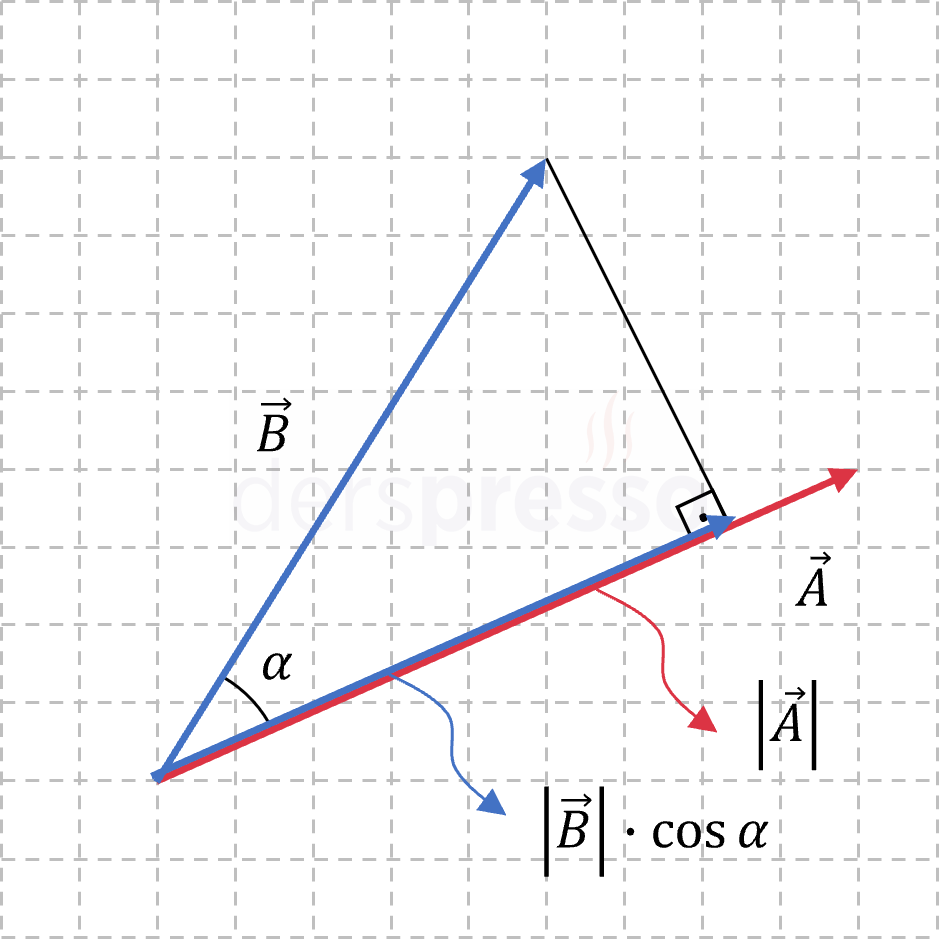
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} (\norm{\vec{b}} \cos{\alpha}) \)
\( \norm{\vec{a}} \): \( \vec{a} \) vektörünün büyüklüğü
\( \norm{\vec{b}} \cos{\alpha} \): \( \vec{b} \) vektörünün \( \vec{a} \) vektörü üzerindeki izdüşümünün büyüklüğü
Aynı işlemi şimdi de \( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki izdüşümünün büyüklüğünü bularak yapalım. Yine trigonometrik oranlar kullanılarak bu izdüşümün \( \norm{\vec{a}} \cos{\alpha} \) olduğu görülebilir. Bu ifade üzerinde izdüşüm alınan \( \vec{b} \) vektörünün büyüklüğü ile çarpıldığında aynı nokta çarpım formülü elde edilir.
\( \vec{a} \cdot \vec{b} = \norm{\vec{b}} (\norm{\vec{a}} \cos{\alpha}) \)
\( \norm{\vec{b}} \): \( \vec{b} \) vektörünün büyüklüğü
\( \norm{\vec{a}} \cos{\alpha} \): \( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki izdüşümünün büyüklüğü
Buna göre, nokta çarpımının geometrik tanımı ile ilgili aşağıdaki iki yorumu yapabiliriz.
- Nokta çarpımı birinci vektörün ikinci vektör üzerindeki izdüşümünün büyüklüğü ile ikinci vektörün büyüklüğünün çarpımına eşittir.
- Vektörlerden hangisinin birinci hangisinin ikinci vektör olarak alındığının sonuca bir etkisi yoktur.
Nokta Çarpım İşlem Özellikleri
Yukarıda geometrik olarak gösterdiğimiz üzere, nokta çarpımının değişme özelliği vardır.
\( \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \)
İSPATI GÖSTER
\( n \) boyutlu \( \vec{a} \) ve \( \vec{b} \) vektörleri tanımlayalım.
\( \vec{a} = (a_1, a_2, \ldots, a_n) \)
\( \vec{b} = (b_1, b_2, \ldots, b_n) \)
\( \vec{a} \) ve \( \vec{b} \) vektörleri arasında nokta çarpımı aşağıdaki şekilde tanımlıdır.
\( \vec{a} \cdot \vec{b} = \displaystyle\sum_{i=1}^{n} {a_ib_i} \)
Reel sayılarda çarpma işleminin değişme özelliği vardır.
\( = \displaystyle\sum_{i=1}^{n} {b_ia_i} \)
Bu toplam işlemi \( \vec{b} \cdot \vec{a} \) nokta çarpımının açılımıdır.
\( = \vec{b} \cdot \vec{a} \)
Nokta çarpımının skaler bir büyüklükle birleşme özelliği vardır.
\( (c\vec{a}) \cdot \vec{b} = c(\vec{a} \cdot \vec{b}) \)
İSPATI GÖSTER
\( n \) boyutlu \( \vec{a} \) ve \( \vec{b} \) vektörleri ve bir \( c \) reel sayısı tanımlayalım.
\( \vec{a} = (a_1, a_2, \ldots, a_n) \)
\( \vec{b} = (b_1, b_2, \ldots, b_n) \)
\( c \in \mathbb{R} \)
\( c\vec{a} \) ve \( \vec{b} \) vektörleri arasında nokta çarpımı aşağıdaki şekilde tanımlıdır.
\( (c\vec{a}) \cdot \vec{b} = \displaystyle\sum_{i=1}^{n} {(ca_i)b_i} \)
Reel sayılarda çarpma işleminin birleşme özelliği vardır.
\( = \displaystyle\sum_{i=1}^{n} {c(a_ib_i)} \)
Sabit bir sayı toplam işleminin dışına alınabilir.
\( = c\displaystyle\sum_{i=1}^{n} {a_ib_i} \)
Bu toplam işlemi \( \vec{a} \cdot \vec{b} \) nokta çarpımının açılımıdır.
\( = c(\vec{a} \cdot \vec{b}) \)
Nokta çarpımının toplama işlemi üzerinde soldan ve sağdan dağılma özelliği vardır.
\( \vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} \)
\( (\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \)
İSPATI GÖSTER
Nokta çarpımının toplama işlemi üzerinde soldan dağılma özelliğini ispatlayalım.
\( n \) boyutlu \( \vec{a} \), \( \vec{b} \) ve \( \vec{c} \) vektörleri tanımlayalım.
\( \vec{a} = (a_1, a_2, \ldots, a_n) \)
\( \vec{b} = (b_1, b_2, \ldots, b_n) \)
\( \vec{c} = (c_1, c_2, \ldots, c_n) \)
\( \vec{a} \) ve \( \vec{b} + \vec{c} \) vektörleri arasında nokta çarpımı aşağıdaki şekilde tanımlıdır.
\( \vec{a} \cdot (\vec{b} + \vec{c}) = \displaystyle\sum_{i=1}^{n} {a_i(b_i + c_i)} \)
Reel sayılarda çarpma işleminin toplama işlemi üzerinde soldan dağılma özelliği vardır.
\( = \displaystyle\sum_{i=1}^{n} (a_ib_i + a_ic_i) \)
Toplam işlemi terimlerine dağıtılabilir.
\( = \displaystyle\sum_{i=1}^{n} {a_ib_i} + \displaystyle\sum_{i=1}^{n} {a_ic_i} \)
Bu iki toplam işlemi sırasıyla \( \vec{a} \cdot \vec{b} \) ve \( \vec{a} \cdot \vec{c} \) nokta çarpımının açılımıdır.
\( = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} \)
Benzer bir ispat nokta çarpımının toplama işlemi üzerinde sağdan dağılma özelliği için de yapılabilir.
\( (\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \)
Nokta Çarpım İşlem Kuralları
Bir vektörün kendisiyle nokta çarpımı, vektörün normunun karesine eşittir.
\( \vec{a} \cdot \vec{a} = {\norm{\vec{a}}}^2 \)
İSPATI GÖSTER
\( \vec{a} \cdot \vec{a} = \norm{\vec{a}} \norm{\vec{a}} \cos{\alpha} \)
Bir vektörün kendisiyle yaptığı açı 0° olur.
\( = \norm{\vec{a}} \norm{\vec{a}} \cos{0°} \)
\( = \norm{\vec{a}} \norm{\vec{a}} \cdot 1 \)
\( = \norm{\vec{a}}^2 \)
Yönleri aynı iki vektörün nokta çarpımı, vektörlerin normlarının çarpımına eşittir.
\( \vec{a} \parallel \vec{b} \) ise,
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} \norm{\vec{b}} \)
İSPATI GÖSTER
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} \norm{\vec{b}} \cos{\alpha} \)
Yönleri aynı (paralel) iki vektörün arasındaki açı 0° olur.
\( = \norm{\vec{a}} \norm{\vec{b}} \cos{0°} \)
\( = \norm{\vec{a}} \norm{\vec{b}} \cdot 1 \)
\( = \norm{\vec{a}} \norm{\vec{b}} \)
Birbirine dik iki vektörün nokta çarpımı sıfıra eşittir. Bunu geometrik olarak açıklamak gerekirse, bir vektörün kendisine dik bir vektör üzerindeki izdüşümünün büyüklüğü sıfırdır.
\( \vec{a} \perp \vec{b} \) ise,
\( \vec{a} \cdot \vec{b} = 0 \)
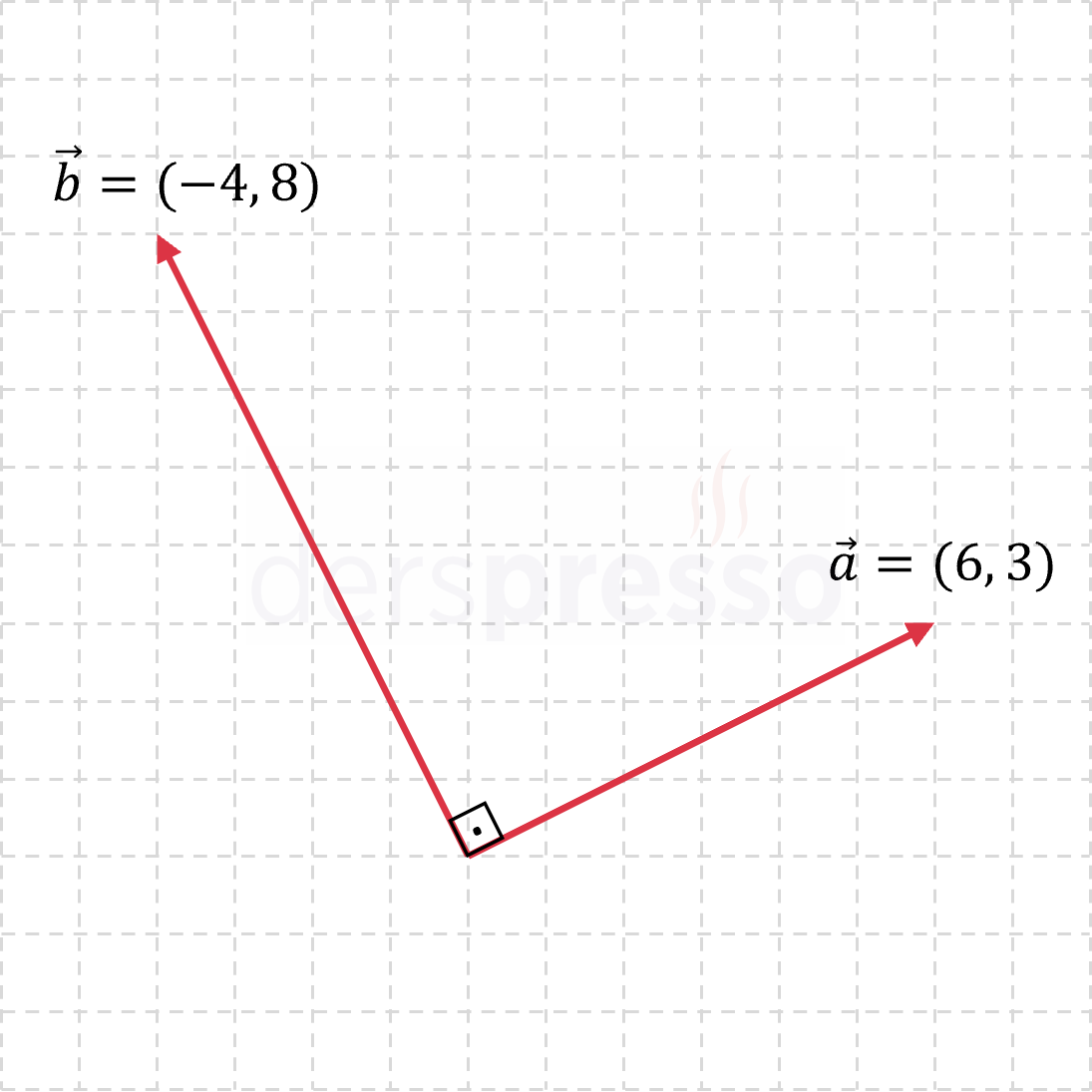
\( \vec{a} = (6, 3) \)
\( \vec{b} = (-4, 8) \)
\( \vec{a} \perp \vec{b} \)
\( \vec{a} \cdot \vec{b} = 6 \cdot (-4) + 3 \cdot 8 \)
\( = -24 + 24 = 0 \)
İSPATI GÖSTER
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} \norm{\vec{b}} \cos{\alpha} \)
Birbirine dik iki vektörün arasındaki açı 90° olur.
\( = \norm{\vec{a}} \norm{\vec{b}} \cos{90°} \)
\( = \norm{\vec{a}} \norm{\vec{b}} \cdot 0 \)
\( = 0 \)
İki vektörün nokta çarpımı sıfır ise ya vektörler birbirine diktir ya da vektörlerden biri ya da ikisi sıfır vektörüdür.
Sıfır vektörünün tüm vektörlerle nokta çarpımı sıfır olduğu için sıfır vektörü tüm vektörlere diktir.
\( \vec{a} \) herhangi bir vektör olmak üzere,
\( \vec{a} \cdot \vec{0} = 0 \)
\( \vec{a} \perp \vec{0} \)
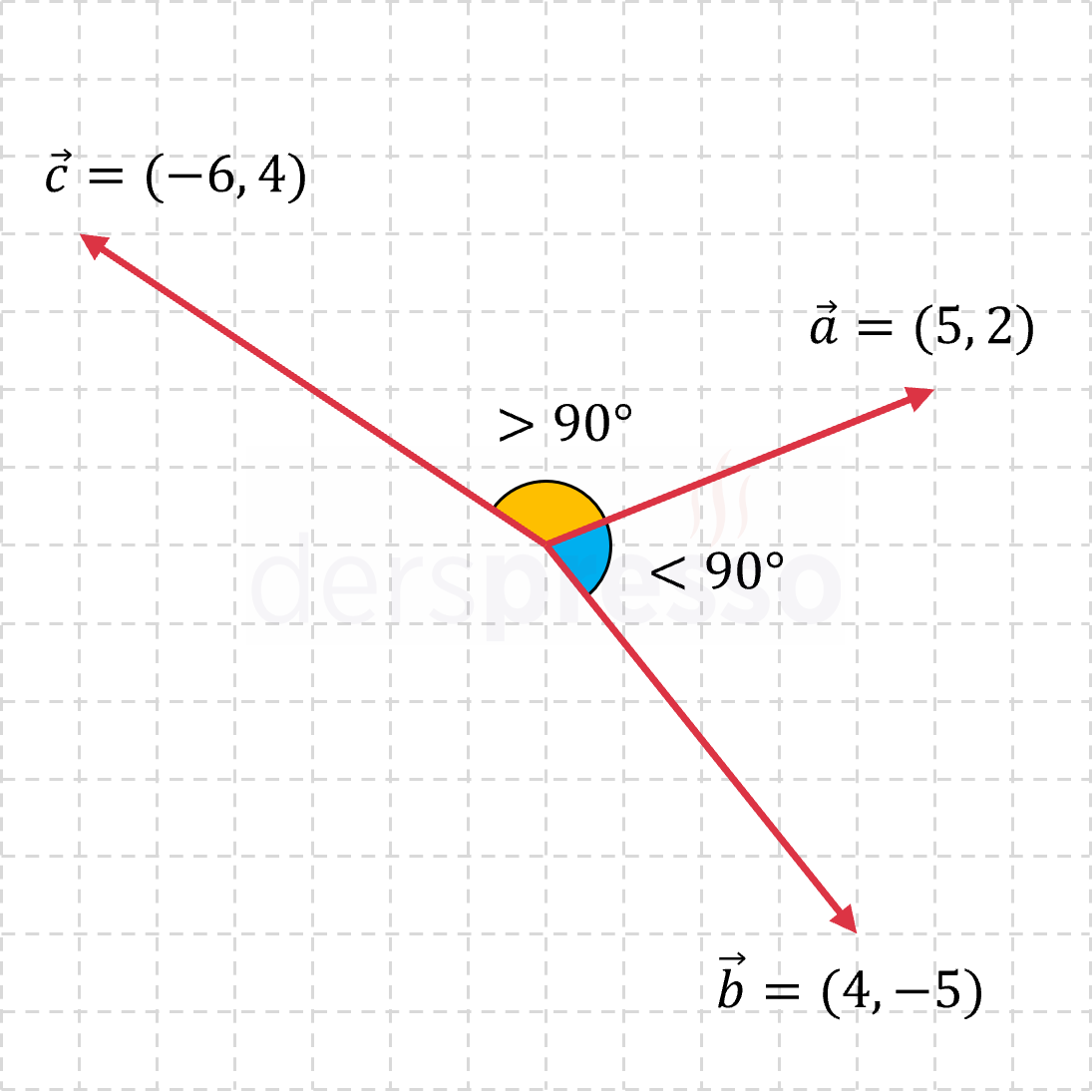
İki vektörün nokta çarpımı vektörler arasındaki açı 90°'den küçükse pozitif, 90°'den büyükse negatiftir.
\( 0 \lt \alpha \lt 90° \) ise,
\( \vec{a} \cdot \vec{b} \gt 0 \)
\( 90 \lt \alpha \lt 180° \) ise,
\( \vec{a} \cdot \vec{b} \lt 0 \)
\( \vec{a} = (5, 2) \)
\( \vec{b} = (4, -5) \)
\( \vec{c} = (-6, 4) \)
\( \vec{a} \cdot \vec{b} = 5 \cdot 4 + 2 \cdot (-5) \)
\( = 20 - 10 = 10 \gt 0 \)
\( \vec{a} \cdot \vec{c} = 5 \cdot (-6) + 2 \cdot 4 \)
\( = -30 + 8 = -22 \lt 0 \)
İSPATI GÖSTER
\( \vec{a} \ne \vec{0} \) ve \( \vec{b} \ne \vec{0} \) olmak üzere,
Sıfır vektöründen farklı bir vektörün normu pozitiftir.
\( 0 \lt \alpha \lt 90° \) ise,
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} \norm{\vec{b}} \cos{\alpha} \)
Kosinüs I. bölgede pozitiftir.
\( \vec{a} \cdot \vec{b} \gt 0 \)
\( 90 \lt \alpha \lt 180° \) ise,
\( \vec{a} \cdot \vec{b} = \norm{\vec{a}} \norm{\vec{b}} \cos{\alpha} \)
Kosinüs II. bölgede negatiftir.
\( \vec{a} \cdot \vec{b} \lt 0 \)
Üç vektörün nokta çarpımı geçerli bir işlem değildir. Bunun sebebi, iki vektörün nokta çarpımının sonucunun skaler bir büyüklük olması ve skaler ve vektörel iki büyüklük arasında nokta çarpım işlemi yapılamayacak olmasıdır.
\( \vec{a} \cdot \vec{b} = k \in \mathbb{R} \) olmak üzere,
Aşağıdaki işlem geçersiz bir işlemdir.
\( (\vec{a} \cdot \vec{b}) \cdot \vec{c} = k \cdot \vec{c} \)
Aşağıdaki işlem geçerli bir skaler ile çarpma işlemidir.
\( (\vec{a} \cdot \vec{b})\ \vec{c} = k\vec{c} \)
Nokta Çarpımı ve Kosinüs Teoremi
İki vektörün nokta çarpımı kullanılarak trigonometri konusunda gördüğümüz kosinüs teoremi formülü türetilebilir.
Aralarındaki açı \( \alpha \) olan \( \vec{a} \) ve \( \vec{b} \) vektörleri ve \( \vec{a} - \vec{b} \) farkına eşit olan bir \( \vec{c} \) vektörü tanımlayalım.
\( \vec{c} = \vec{a} - \vec{b} \)
Her iki tarafın kendisiyle nokta çarpımını alalım.
\( \vec{c} \cdot \vec{c} = (\vec{a} - \vec{b}) \cdot (\vec{a} - \vec{b}) \)
Nokta çarpımının toplama işlemi üzerinde soldan ve sağdan dağılma özelliğini kullanalım.
\( \vec{c} \cdot \vec{c} = \vec{a} \cdot \vec{a} \) \( - \vec{a} \cdot \vec{b} \) \( - \vec{b} \cdot \vec{a} \) \( + \vec{b} \cdot \vec{b} \)
Bir vektörün kendisiyle nokta çarpımı, vektörün büyüklüğünün karesine eşittir.
\( \norm{\vec{c}}^2 = \norm{\vec{a}}^2 \) \( - \vec{a} \cdot \vec{b} \) \( - \vec{b} \cdot \vec{a} \) \( + \norm{\vec{b}}^2 \)
Nokta çarpımının geometrik formülünü yazalım.
\( \norm{\vec{c}}^2 = \norm{\vec{a}}^2 \) \( - \norm{\vec{a}} \norm{\vec{b}} \cos{\alpha} \) \( - \norm{\vec{b}} \norm{\vec{a}} \cos{\alpha} \) \( + \norm{\vec{b}}^2 \)
\( \vec{a}, \vec{b}, \vec{c} \) vektörlerinin normlarına sırasıyla \( a, b, c \) diyelim.
\( c^2 = a^2 - ab\cos{\alpha} - ba\cos{\alpha} + b^2 \)
\( c^2 = a^2 + b^2 - 2ab\cos{\alpha} \)
Elde ettiğimiz bu eşitlik kosinüs teoremi formülüdür.
\( O \) noktası orijin olmak üzere, koordinat düzlemindeki \( A \) ve \( B \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(3, -2) \)
\( \vec{BA} = (-2, -2) \)
Buna göre;
(a) \( \norm{\vec{OB}} \) uzunluğu nedir?
(b) \( \widehat{AOB} \) açısının ölçüsü nedir?
Çözümü Göster(a) seçeneği:
\( \vec{OA} \) konum vektörünü tanımlayalım.
\( \vec{OA} = (3, -2) \)
\( \vec{BA} \) vektörü başlangıç noktası \( B \) ve bitiş noktası \( A \) olan vektörü temsil eder.
\( \vec{BA} \) vektörü \( \vec{OA} \) konum vektöründen \( \vec{OB} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{BA} = \vec{OA} - \vec{OB} \)
\( \vec{OB} = \vec{OA} - \vec{BA} \)
İki vektör arasındaki çıkarma işleminde, vektörlerin birbirine karşılık gelen bileşenlerinin ayrı ayrı farkı alınır.
\( = (3, -2) - (-2, -2) \)
\( = (3 - (-2), -2 - (-2)) \)
\( = (5, 0) \)
\( \vec{OB} \) vektörünün normunu bulalım.
\( \norm{\vec{OB}} = \sqrt{5^2 + 0^2} = 5 \)
(b) seçeneği:
\( \widehat{AOB} \) açısı, \( \vec{OA} \) ve \( \vec{OB} \) vektörleri arasında kalan açıdır. Bu açıya \( \alpha \) diyelim.
İki vektör arasındaki açıyı bulmak için nokta çarpımı formülünü kullanalım.
\( \vec{OA} \cdot \vec{OB} = \norm{\vec{OA}} \norm{\vec{OB}} \cos{\alpha} \)
\( \cos{\alpha} = \dfrac{\vec{OA} \cdot \vec{OB}}{\norm{\vec{OA}} \norm{\vec{OB}}} \)
İki vektörün nokta çarpımı, vektörlerin birbirine karşılık gelen bileşenlerinin çarpımlarının toplamına eşittir.
\( \vec{OA} \cdot \vec{OB} = (3, -2) \cdot (5, 0) \)
\( = 3 \cdot 5 + (-2) \cdot 0 \)
\( = 15 \)
\( \vec{OA} \) vektörünün normunu bulalım.
\( \norm{\vec{OA}} = \sqrt{3^2 + (-2)^2} \)
\( = \sqrt{13} \)
Bulduğumuz değerleri nokta çarpımı formülünde yerine koyalım.
\( \cos{\alpha} = \dfrac{15}{\sqrt{13} \cdot 5} \)
\( = \dfrac{3}{\sqrt{13}} = \dfrac{3\sqrt{13}}{13} \)
\( \alpha = \arccos{\dfrac{3\sqrt{13}}{13}} \)
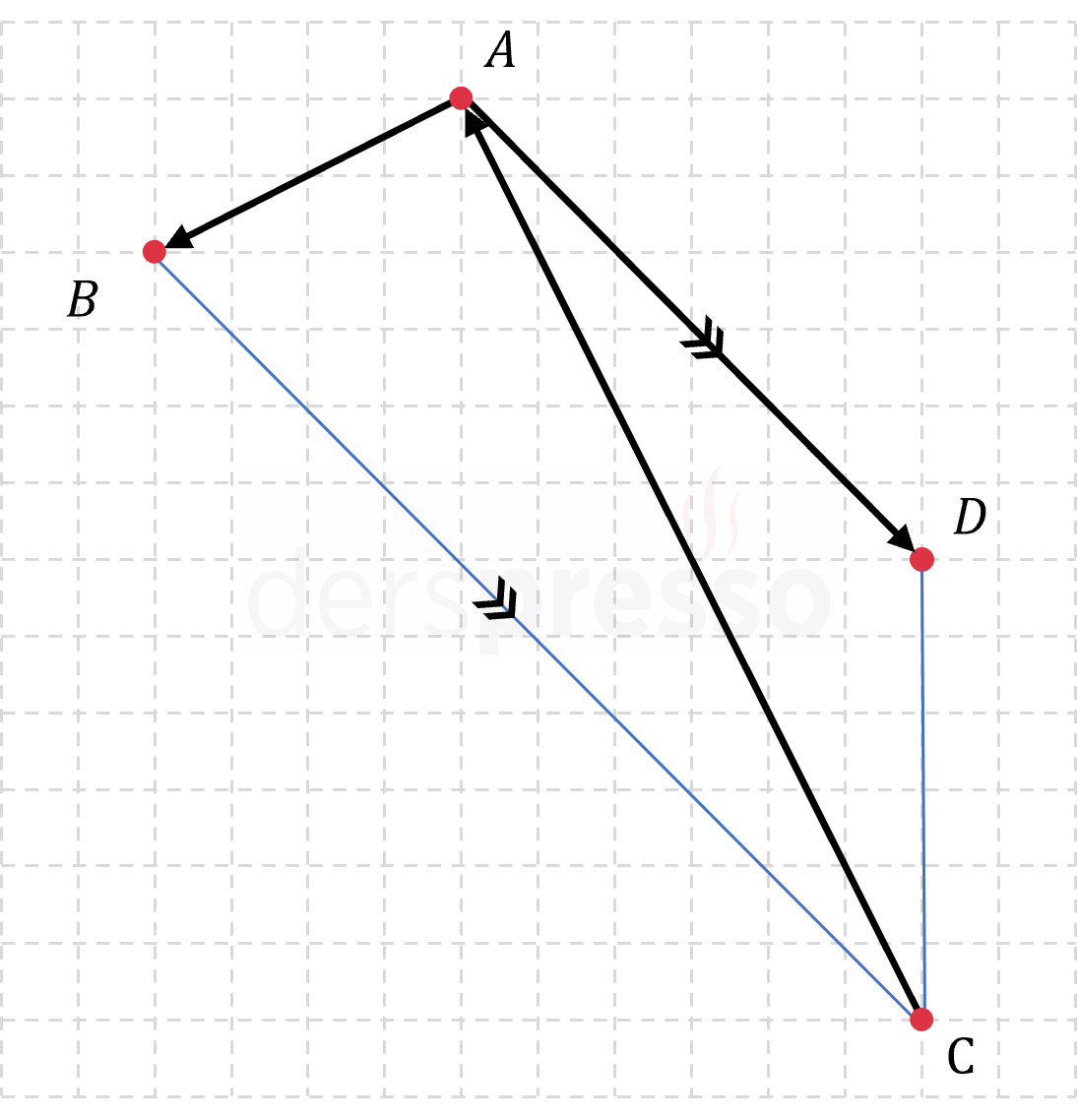
Şekildeki \( ABCD \) yamuğu ile ilgili aşağıdaki bilgiler veriliyor.
\( \vec{AD} \parallel \vec{BC} \)
\( \vec{AB} = (-2, -1) \)
\( \vec{AD} = (3, k) \)
\( \vec{CA} = (-3, 6) \)
Buna göre;
(a) \( \vec{BC} \) vektörünü bulunuz.
(b) \( \vec{AD} \) vektörünü bulunuz.
(c) \( \norm{\vec{DC}} \) uzunluğu nedir?
(d) \( \widehat{ACD} \) açısının ölçüsü nedir?
Çözümü Göster(a) seçeneği:
\( \vec{BC} \) vektörünü uç uca ekleme yöntemini kullanarak bulalım.
\( \vec{BC} = \vec{BA} + \vec{AC} \)
\( = -\vec{AB} + (-\vec{CA}) \)
İki vektör arasındaki toplama işleminde, vektörlerin birbirine karşılık gelen bileşenlerinin ayrı ayrı toplamı alınır.
\( = -(-2, -1) + [-(-3, 6)] \)
\( = (2, 1) + (3, -6) \)
\( = (2 + 3, 1 + (-6)) \)
\( = (5, -5) \)
(b) seçeneği:
\( \vec{AD} = (3, k) \)
\( \vec{AD} \parallel \vec{BC} \)
Paralel iki vektörün bileşenleri orantılıdır.
\( \dfrac{3}{5} = \dfrac{k}{-5} \)
\( k = -3 \)
\( \vec{AD} = (3, -3) \)
(c) seçeneği:
\( \vec{DC} \) vektörünü uç uca ekleme yöntemini kullanarak bulalım.
\( \vec{DC} = \vec{DA} + \vec{AC} \)
\( = -\vec{AD} + (-\vec{CA}) \)
\( = -(3, -3) + [-(-3, 6)] \)
\( = (-3, 3) + (3, -6) \)
\( = (-3 + 3, 3 + (-6)) \)
\( = (0, -3) \)
\( \vec{DC} \) vektörünün normunu bulalım.
\( \norm{\vec{DC}} = \sqrt{0^2 + (-3)^2} \)
\( = 3 \)
(d) seçeneği:
\( \widehat{ACD} \) açısı, \( \vec{CA} \) ve \( \vec{CD} \) vektörleri arasında kalan açıdır. Bu açıya \( \alpha \) diyelim.
İki vektör arasındaki açıyı bulmak için nokta çarpımı formülünü kullanalım.
\( \vec{CA} \cdot \vec{CD} = \norm{\vec{CA}} \norm{\vec{CD}} \cos{\alpha} \)
\( \cos{\alpha} = \dfrac{\vec{CA} \cdot \vec{CD}}{\norm{\vec{CA}} \norm{\vec{CD}}} \)
İki vektörün nokta çarpımı, vektörlerin birbirine karşılık gelen bileşenlerinin çarpımlarının toplamına eşittir.
\( \vec{CA} \cdot \vec{CD} = \vec{CA} \cdot (-\vec{DC}) \)
\( = (-3, 6) \cdot [-(0, -3)] \)
\( = (-3, 6) \cdot (0, 3) \)
\( = (-3) \cdot 0 + 6 \cdot 3 = 18 \)
\( \vec{CA} \) vektörünün normunu bulalım.
\( \norm{\vec{CA}} = \sqrt{(-3)^2 + 6^2} \)
\( = 3\sqrt{5} \)
\( \norm{\vec{CD}} = \norm{\vec{DC}} = 3 \)
Bulduğumuz değerleri nokta çarpımı formülünde yerine koyalım.
\( \cos{\alpha} = \dfrac{18}{3\sqrt{5} \cdot 3} \)
\( = \dfrac{2\sqrt{5}}{5} \)
\( \alpha = \arccos{\dfrac{2\sqrt{5}}{5}} \)
\( O \) noktası orijin olmak üzere, koordinat düzlemindeki \( A, B, C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( \vec{OA} = (1, -1, 1) \)
\( \vec{OB} = (2, 1, 2) \)
\( \vec{OC} = (3, -1, 1) \)
Buna göre \( ABC \) üçgeninin alanı nedir?
Çözümü Göster\( \vec{AB} \) vektörünü bulalım.
\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
İki vektör arasındaki çıkarma işleminde, vektörlerin birbirine karşılık gelen bileşenlerinin ayrı ayrı farkı alınır.
\( = (2, 1, 2) - (1, -1, 1) \)
\( = (2 - 1, 1 - (-1), 2 - 1) \)
\( = (1, 2, 1) \)
\( \vec{BC} \) vektörünü bulalım.
\( \vec{BC} = \vec{OC} - \vec{OB} \)
\( = (3, -1, 1) - (2, 1, 2) \)
\( = (3 - 2, -1 - 1, 1 - 2) \)
\( = (1, -2, -1) \)
\( \vec{BA} \) ve \( \vec{BC} \) vektörleri arasındaki açıyı bulmak için nokta çarpımı formülünü kullanalım.
İki vektör arasındaki açıya \( \alpha \) diyelim.
\( \vec{BA} \cdot \vec{BC} = \norm{\vec{BA}} \norm{\vec{BC}} \cos{\alpha} \)
\( (-\vec{AB}) \cdot \vec{BC} = \norm{\vec{AB}} \norm{\vec{BC}} \cos{\alpha} \)
\( \cos{\alpha} = \dfrac{(-\vec{AB}) \cdot \vec{BC}}{\norm{\vec{AB}} \norm{\vec{BC}}} \)
İki vektörün nokta çarpımı, vektörlerin birbirine karşılık gelen bileşenlerinin çarpımlarının toplamına eşittir.
\( (-\vec{AB}) \cdot \vec{BC} = [-(1, 2, 1)] \cdot (1, -2, -1) \)
\( = (-1, -2, -1) \cdot (1, -2, -1) \)
\( = (-1) \cdot 1 + (-2) \cdot (-2) + (-1) \cdot (-1) \)
\( = -1 + 4 + 1 = 4 \)
\( \vec{AB} \) vektörünün normunu bulalım.
\( \norm{\vec{AB}} = \sqrt{1^2 + 2^2 + 1^2 } \)
\( = \sqrt{6} \)
\( \vec{BC} \) vektörünün normunu bulalım.
\( \norm{\vec{BC}} = \sqrt{1^2 + (-2)^2 + (-1)^2 } \)
\( = \sqrt{6} \)
Bulduğumuz değerleri nokta çarpımı formülünde yerine koyalım.
\( \cos{\alpha} = \dfrac{4}{\sqrt{6} \cdot \sqrt{6}} \)
\( = \dfrac{2}{3} \)
Pisagor özdeşliğini kullanalım.
\( \sin^2{\alpha} + \cos^2{\alpha} = 1 \)
\( \sin^2{\alpha} + (\dfrac{2}{3})^2 = 1 \)
\( \sin{\alpha} = \pm \dfrac{\sqrt{5}}{3} \)
\( \alpha \) açısı \( ABC \) üçgeninin bir iç açısıdır.
\( 0 \lt \alpha \lt 180 \)
Sinüs I. ve II. bölgelerde pozitiftir.
\( \sin{\alpha} = \dfrac{\sqrt{5}}{3} \)
Sinüs alan formülünü kullanalım.
\( A(ABC) = \dfrac{1}{2}\norm{\vec{BA}}\norm{\vec{BC}}\sin{\alpha} \)
\( = \dfrac{1}{2} \cdot \sqrt{6} \cdot \sqrt{6} \cdot \dfrac{\sqrt{5}}{3} \)
\( = \sqrt{5} \) bulunur.
Koordinat uzayındaki \( A, B, C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( k \in \mathbb{R} \) olmak üzere,
\( \vec{AB} = (4, 1, 1) \)
\( \vec{BC} = (k, -2k, 8) \)
\( \vec{AB} \perp \vec{BC} \)
Buna göre;
(a) \( k \) kaçtır?
(b) \( ABC \) üçgeninin alanı nedir?
Çözümü Göster(a) seçeneği:
Aralarındaki açı 90° (birbirine dik) olan iki vektörün nokta çarpımı sıfıra eşittir.
\( \vec{AB} \cdot \vec{BC} = 0 \)
İki vektörün nokta çarpımı, vektörlerin birbirine karşılık gelen bileşenlerinin çarpımlarının toplamına eşittir.
\( (4, 1, 1) \cdot (k, -2k, 8) = 0 \)
\( 4 \cdot k + 1 \cdot (-2k) + 1 \cdot 8 = 0 \)
\( 4k - 2k + 8 = 0 \)
\( k = -4 \) bulunur.
(b) seçeneği:
\( \vec{AB} \) vektörünün normunu bulalım.
\( \norm{\vec{AB}} = \sqrt{4^2 + 1^2 + 1^2} \)
\( = \sqrt{18} = 3\sqrt{2} \)
Bulduğumuz \( k \) değerini \( \vec{BC} \) vektöründe yerine yazalım.
\( \vec{BC} = (k, -2k, 8) \)
\( = (-4, -2(-4), 8) \)
\( = (-4, 8, 8) \)
\( \vec{BC} \) vektörünün normunu bulalım.
\( \norm{\vec{BC}} = \sqrt{(-4)^2 + 8^2 + 8^2} \)
\( = \sqrt{144} = 12 \)
\( \vec{AB} \perp \vec{BC} \) soruda verilmiştir.
Dik üçgen alan formülünü kullanalım.
\( A(ABC) = \dfrac{\norm{\vec{AB}} \cdot \norm{\vec{BC}}}{2} \)
\( = \dfrac{3\sqrt{2} \cdot 12}{2} \)
\( = 18\sqrt{2} \) bulunur.