Vektörel Çarpım
Vektörel çarpım işleminin gösterimi aşağıdaki gibidir. Vektörel çarpım işleminde vektörler arasında çarpı (\( \times \)) sembolü kullanılır. Vektörel çarpım işleminin sonucu yine bir vektördür.
\( \vec{c} = \vec{a} \times \vec{b} \)
Vektörel çarpım işleminde sonucun büyüklüğü ve yönü ayrı ayrı bulunur.
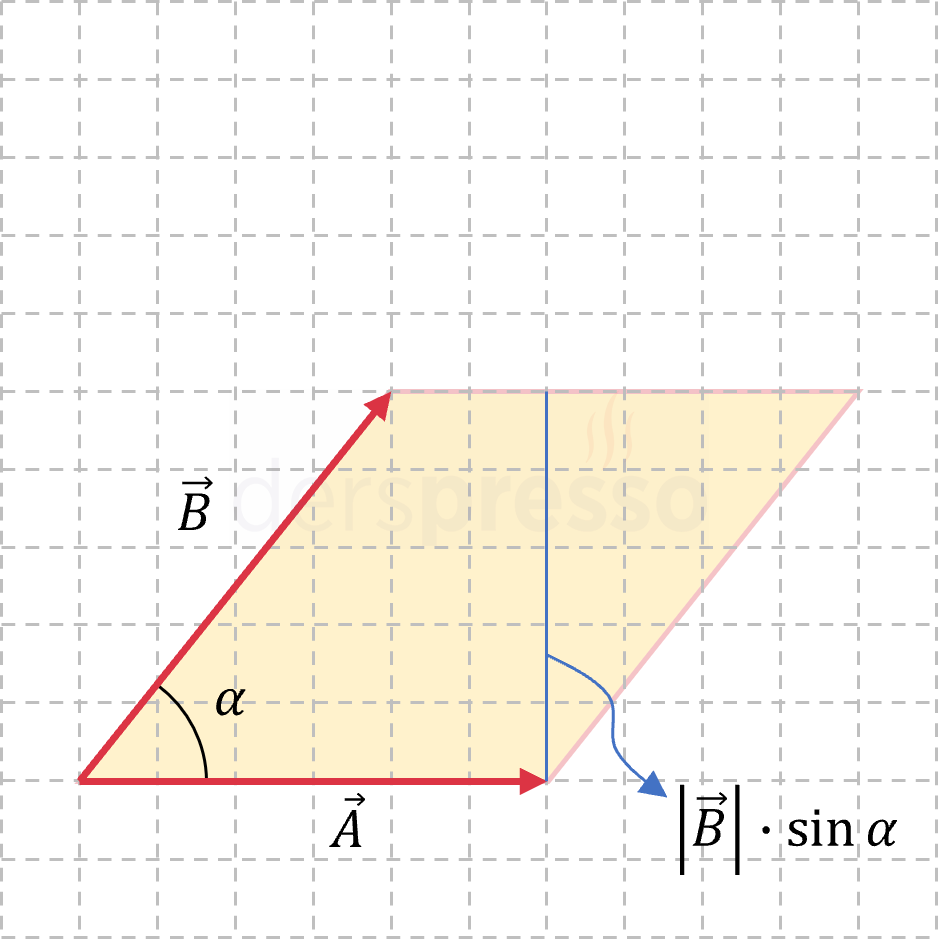
Vektörel çarpım işleminin sonucunun büyüklüğü, bu iki vektör aşağıdaki şekildeki gibi bir paralelkenara tamamlandığında oluşan paralelkenarın alanına eşittir. Aralarındaki açı \( \alpha \) olan iki vektörün oluşturduğu paralelkenarın alanı aşağıdaki formülle hesaplanabilir. Bu formülde \( \norm{\vec{a}} \) paralelkenarın taban uzunluğunu, \( \norm{\vec{b}}\sin{\alpha} \) da yüksekliğini vermektedir.
\( \norm{\vec{c}} = \norm{\vec{a} \times \vec{b}} = \norm{\vec{a}} \norm{\vec{b}} \sin{\alpha} \)
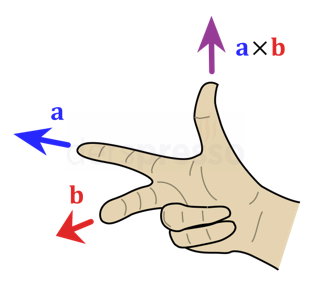
İki vektörün çarpım vektörü, bu iki vektörün bulunduğu düzleme dik bir yöndedir. Bu vektörün düzleme hangi yönde dik olduğu sağ el kuralı olarak bilinen yöntemle bulunabilir. Aşağıdaki şekilde gösterildiği gibi, sağ elimizi işaret parmağı birinci vektörü, orta parmak ikinci vektörü gösterecek şekilde tuttuğumuzda baş parmağımızın gösterdiği yön çarpım vektörünün yönüdür.
Bu kuralı yukarıdaki örneğe uyguladığımızda, vektörel çarpım vektörünün \( \vec{a} \) ve \( \vec{b} \) vektörlerine yukarı yönde dik olduğunu buluruz. Buna göre bu iki vektörün vektörel çarpımının sonucu olan \( \vec{c} \) vektörü, \( \vec{a} \) ve \( \vec{b} \) vektörlerinin bulunduğu \( xy \) düzlemine dik ve üçüncü bir \( z \) ekseni boyunca olmaktadır.
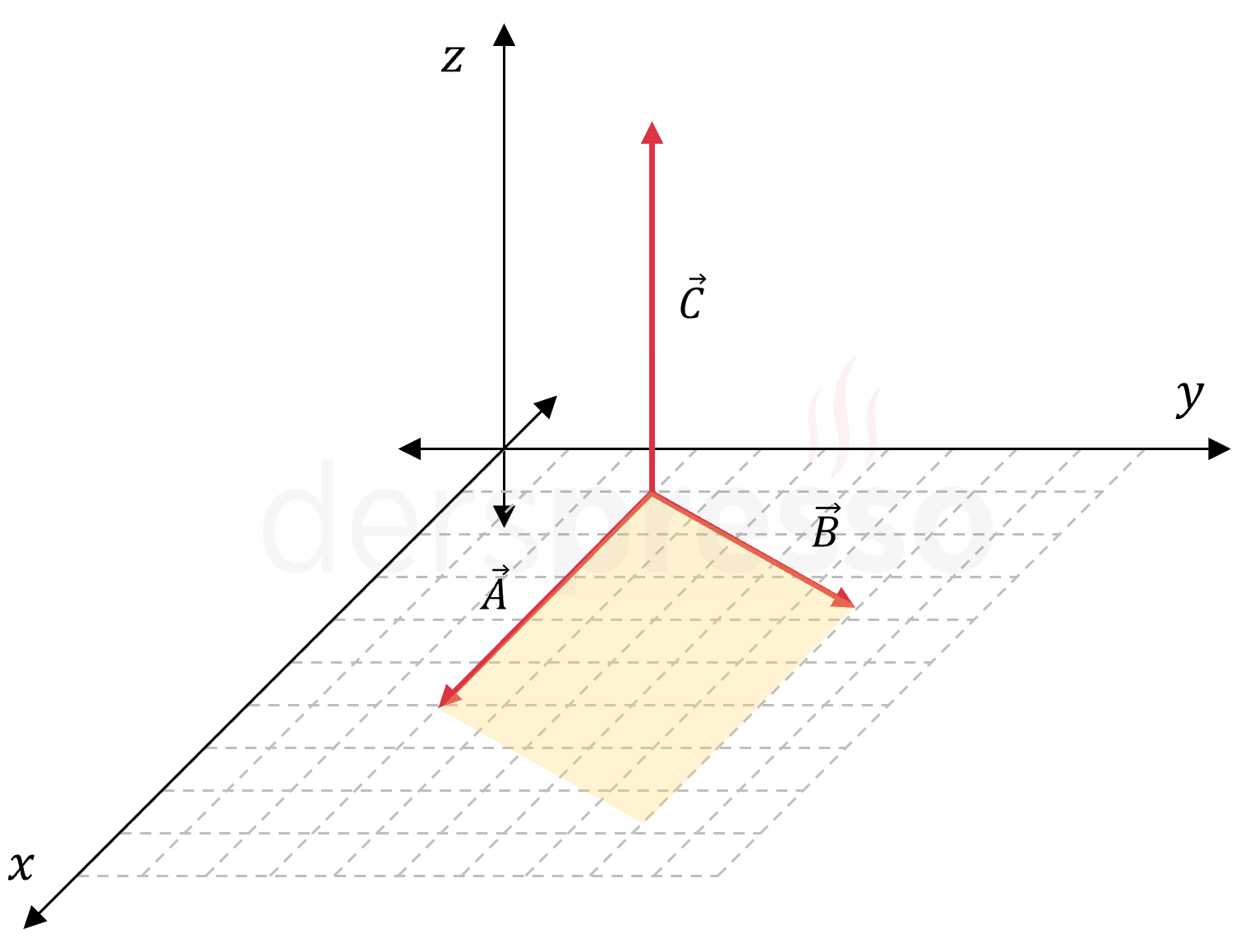
Vektörel çarpım işleminde koordinat sisteminin sağ el kuralı ile tutarlı bir şekilde tanımlanması gerekmektedir. Örneğin \( x \) ve \( y \) eksenlerinin aralarında yer değiştirdiği bir koordinat sistemi kullanılırsa sağ el kuralı ile bulunan çarpım vektörü ters ve yanlış yönlü olacaktır. Yukarıdaki üç boyutlu koordinat sistemi sağ el kuralı ile uyumlu olacak şekilde tanımlanmıştır.
Vektörel Çarpmanın İşlem Özellikleri
Vektörel çarpım işleminde vektörlerin sırası değiştirildiğinde, büyüklüğü aynı, yönü zıt yönde bir vektör elde edilir. Vektörlerin sırası değiştirildiğinde büyüklüğü temsil eden paralelkenarın alanı değişmemekte, ama sağ el kuralı gereği baş parmağımızın gösterdiği yön ters yönde olmaktadır.
\( \vec{a} \times \vec{b} = -\vec{b} \times \vec{a} \)
Vektörel çarpım işleminin toplama işlemi üzerine soldan dağılma özelliği vardır.
\( \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c} \)
Vektörel Çarpmanın İşlem Kuralları
Bir vektörün sıfır vektörü ile vektörel çarpımının sonucu sıfır vektörüdür (bir vektör ile sıfır vektörü arasında bir paralelkenar oluşmaz).
\( \vec{a} \cdot \vec{0} = \vec{0} \cdot \vec{a} = \vec{0} \)
Bir vektörün kendisiyle yaptığı açı 0° olduğu için, bir vektörün kendisiyle vektörel çarpımının sonucu sıfır vektörüdür (bir vektör ile kendisi arasında bir paralelkenar oluşmaz).
\( \vec{a} \cdot \vec{a} = \vec{0} \)
Skaler ve Vektörel Çarpım Karşılaştırması
İki vektörün nokta ve vektörel çarpımları aşağıdaki şekilde karşılaştırılabilir.
| Skaler Çarpım | Vektörel Çarpım |
|---|---|
| Çarpım sonucu bir skalerdir (sayıdır). | Çarpım sonucu bir vektördür. |
| Sonucun büyüklüğü vektörler arasındaki açının kosinüs değerine göre değişir. | Sonuç vektörünün büyüklüğü vektörler arasındaki açının sinüs değerine göre değişir. |
| Vektörlerin arasındaki açı 0° olduğunda sonuç maksimum değerini alır, 90° olduğunda sıfır olur. | Vektörlerin arasındaki açı 0° olduğunda sonuç sıfır vektörü olur, 90° olduğunda vektörün büyüklüğü maksimum değerini alır. |
| Vektörlerin arasındaki açı 0-90° aralığında arttıkça sonuç pozitif değer olarak küçülür. | Vektörlerin arasındaki açı 0-90° aralığında arttıkça sonuç vektörünün büyüklüğü artar. |
| Vektörlerin arasındaki açı 90-180° aralığında arttıkça sonuç negatif değer olarak küçülür. | Vektörlerin arasındaki açı 90-180° aralığında arttıkça sonuç vektörünün büyüklüğü azalır. |