Bir Vektörün İzdüşümü
\( \vec{a} \) vektörünün sıfır vektöründen farklı bir \( \vec{b} \) vektörü üzerindeki vektör izdüşümü, \( \vec{a} \) vektörünün başlangıç ve bitiş noktalarının \( \vec{b} \) vektörü üzerindeki dik izdüşümlerinin oluşturduğu vektördür.
\( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki vektörel izdüşümü \( \text{Proj}_{\vec{b}}(\vec{a}) \) şeklinde gösterilir ve bir vektörel büyüklüktür.

\( \vec{b} \ne \vec{0} \) olmak üzere,
\( \text{Proj}_{\vec{b}}(\vec{a}) = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}^2}\vec{b} \)
\( \vec{a} = (5, 2, -3) \) vektörünün \( \vec{b} = (-1, 2, -2) \) vektörü üzerindeki vektörel izdüşümünü bulalım.
\( \vec{a} \cdot \vec{b} = 5(-1) + 2(2) + (-3)(-2) = 5 \)
\( \norm{\vec{b}} = \sqrt{(-1)^2 + 2^2 + (-2)^2} = 3 \)
\( \text{Proj}_{\vec{b}}(\vec{a}) = \dfrac{5}{9}(-1, 2, -2) \)
\( = (-\dfrac{5}{9}, \dfrac{10}{9}, -\dfrac{10}{9}) \)
İSPATI GÖSTER
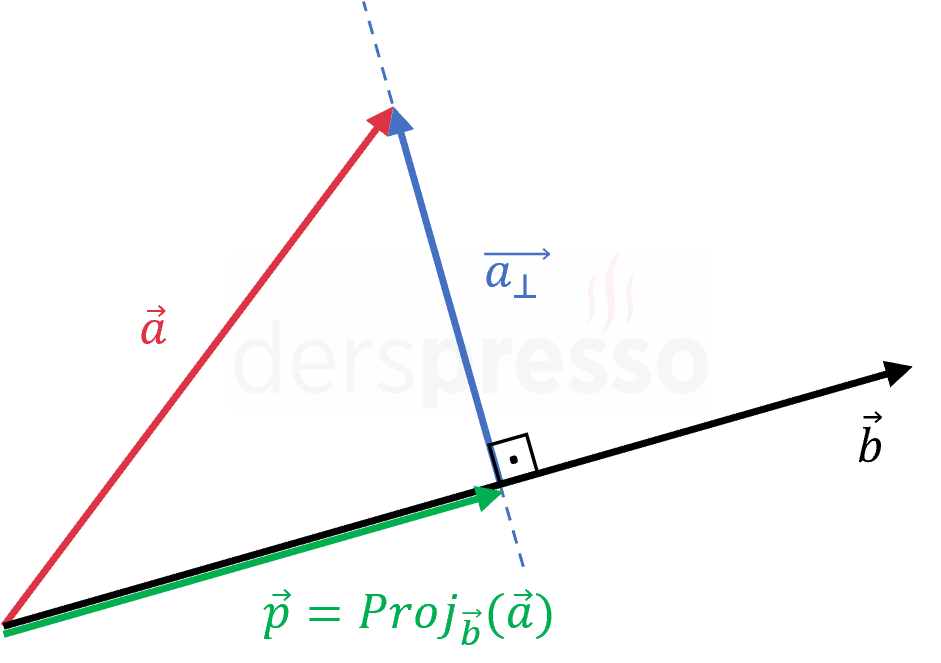
\( \vec{a} \) vektörünü, \( \vec{b} \) vektörü üzerindeki izdüşümü olan \( \vec{p} \) vektörü ile \( \vec{b} \) vektörüne dik bir doğru üzerindeki izdüşümü olan \( \vec{a_{\perp}} \) vektörünün toplamı şeklinde yazabiliriz.
\( \vec{a} = \vec{p} + \vec{a_{\perp}} \)
\( \vec{p} \) ve \( \vec{b} \) vektörlerinin yönleri aynı olduğu (iki vektör paralel oldukları) için, \( \vec{p} \) vektörünü \( \vec{b} \) vektörünün bir skaler ile çarpımı şeklinde ifade edebiliriz.
\( \vec{p} \parallel \vec{b} \)
\( c \in \mathbb{R} \) olmak üzere,
\( \vec{p} = c\vec{b} \)
\( \vec{a_{\perp}} \) vektörü \( \vec{b} \) vektörüne dik olduğu için iki vektörün nokta çarpımı sıfır olur.
\( \vec{a_{\perp}} \cdot \vec{b} = 0 \)
\( (\vec{a} - \vec{p}) \cdot \vec{b} = 0 \)
Nokta çarpımının dağılma özelliğini kullanalım.
\( \vec{a} \cdot \vec{b} - \vec{p} \cdot \vec{b} = 0 \)
\( \vec{a} \cdot \vec{b} = \vec{p} \cdot \vec{b} \)
\( \vec{p} \) vektörü yerine yukarıda bulduğumuz \( \vec{b} \) cinsinden karşılığını yazalım.
\( \vec{a} \cdot \vec{b} = c\vec{b} \cdot \vec{b} \)
Bir vektörün kendisiyle nokta çarpımı, vektörün normunun karesine eşittir.
\( \vec{a} \cdot \vec{b} = c\norm{\vec{b}}^2 \)
\( c \) sayısını yalnız bırakalım.
\( c = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}^2} \)
Bu \( c \) değerini yukarıdaki formülde yerine koyduğumuzda vektörel izdüşüm formülünü elde ederiz.
\( \vec{p} = c\vec{b} \)
\( \vec{p} = \text{Proj}_{\vec{b}}(\vec{a}) = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}^2}\vec{b} \)
Bu formüldeki vektörel ve skaler çarpanlar arasındaki ayrıma dikkat edilmelidir.
\( \text{Proj}_{\vec{b}}(\vec{a}) = \underbrace{\dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}^2}}_{\text{skaler}}\underbrace{\vec{b}}_{\text{vektör}} \)
Vektörel izdüşümün büyüklüğü skaler izdüşüm olarak adlandırılır ve vektörel izdüşümün normuna eşittir.

\( \norm{\text{Proj}_{\vec{b}}(\vec{a})} = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}} \)
\( \vec{a} = (0, -5, 4) \) vektörünün \( \vec{b} = (2, 3, -6) \) vektörü üzerindeki skaler izdüşümünü bulalım.
\( \vec{a} \cdot \vec{b} = 0(2) + (-5)(3) + 4(-6) = -39 \)
\( \norm{\vec{b}} = \sqrt{2^2 + 3^2 + (-6)^2} = 7 \)
\( \norm{\text{Proj}_{\vec{b}}(\vec{a})} = \dfrac{-39}{7} \)
İSPATI GÖSTER
\( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki vektörel izdüşümünün formülünü aşağıdaki şekilde bulmuştuk.
\( \text{Proj}_{\vec{b}}(\vec{a}) = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}^2}\vec{b} \)
Bu ifadeyi düzenleyelim.
\( = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}}\dfrac{\vec{b}}{\norm{\vec{b}}} \)
\( \frac{\vec{b}}{\norm{\vec{b}}} \) ifadesi \( \vec{b} \) vektörü ile aynı yöndeki \( \hat{b} \) birim vektörüne eşittir.
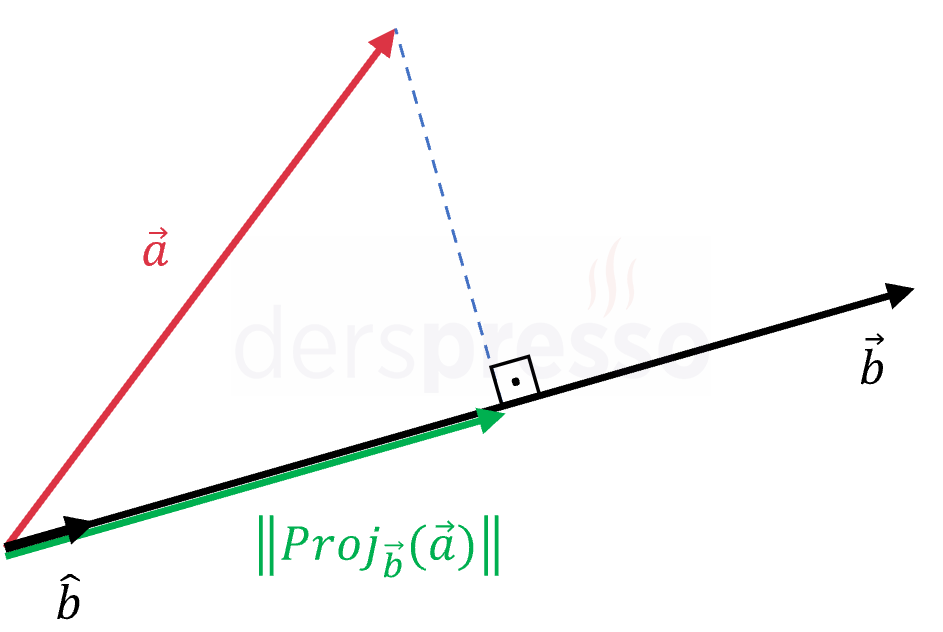
\( = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}}\hat{b} \)
Bu vektörel izdüşümün normunu bulalım.
\( \norm{\text{Proj}_{\vec{b}}(\vec{a})} = \norm{\dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}}\hat{b}} \)
\( \norm{\vec{b}} \) ifadesi pozitif bir skaler büyüklük olduğu için norm ifadesinin dışına olduğu gibi çıkar.
\( = \dfrac{1}{\norm{\vec{b}}}\norm{(\vec{a} \cdot \vec{b})\hat{b}} \)
\( \vec{a} \cdot \vec{b} \) nokta çarpımının sonucu skaler bir büyüklük olduğu için (pozitif, negatif ya da sıfır) norm dışına mutlak değer içinde çıkar.
\( = \dfrac{\abs{\vec{a} \cdot \vec{b}}}{\norm{\vec{b}}}\norm{\hat{b}} \)
Birim vektörün normu 1'e eşittir.
\( \norm{\text{Proj}_{\vec{b}}(\vec{a})} = \dfrac{\abs{\vec{a} \cdot \vec{b}}}{\norm{\vec{b}}} \)
Vektörel izdüşüm, büyüklüğü skaler izdüşüme eşit olan ve yönü \( \hat{b} \) birim vektörü ile aynı olan bir vektör olduğu için, bu ikisinin skaler çarpımı şeklinde de ifade edilebilir.

\( \text{Proj}_{\vec{b}}(\vec{a}) = \norm{\text{Proj}_{\vec{b}}(\vec{a})}\hat{b} \)
\( \text{Proj}_{\vec{b}}(\vec{a}) = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}}\hat{b} \)
\( \vec{a} = (2, -1, 8) \) vektörünün \( \vec{b} = (-12, 4, 3) \) vektörü üzerindeki vektörel izdüşümünü bulalım.
\( \vec{a} \cdot \vec{b} = 2(-12) + (-1)(4) + 8(3) = -4 \)
\( \norm{\vec{b}} = \sqrt{(-12)^2 + 4^2 + 3^2} = 13 \)
\( \hat{b} = \dfrac{(-12, 4, 3)}{13} = (\dfrac{-12}{13}, \dfrac{4}{13}, \dfrac{3}{13}) \)
\( \text{Proj}_{\vec{b}}(\vec{a}) = \dfrac{-4}{13}(\dfrac{-12}{13}, \dfrac{4}{13}, \dfrac{3}{13}) \)
\( = (\dfrac{48}{169}, -\dfrac{16}{169}, -\dfrac{12}{169}) \)
Bir Vektörün Paralel ve Dik Bileşenleri
Bir vektör diğer bir vektör üzerindeki paralel ve dik bileşenlerine ayrılabilir.
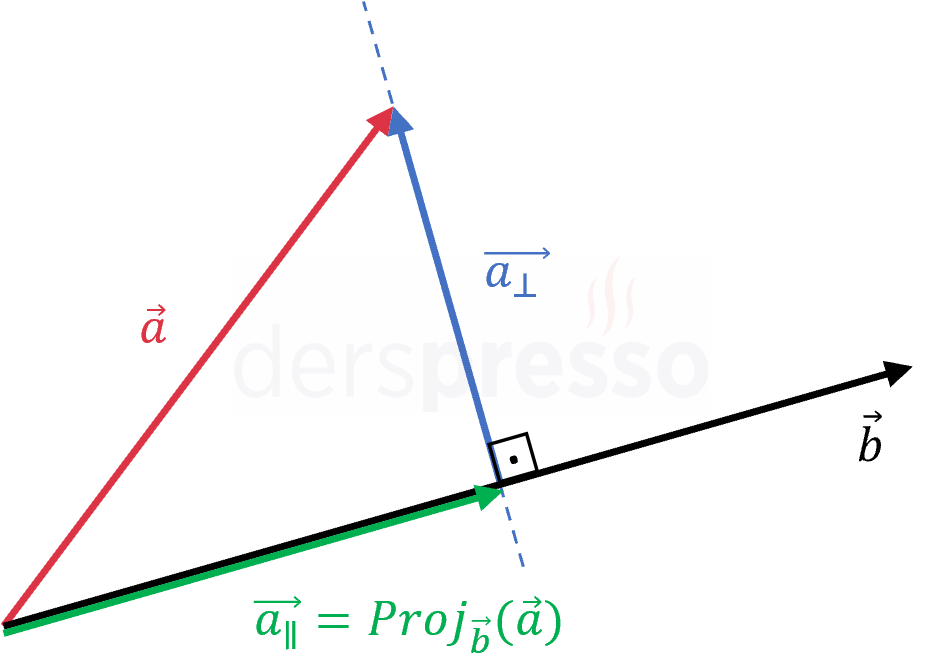
Bir \( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki paralel ve dik bileşenlerinin toplamı \( \vec{a} \) vektörüne eşittir.
\( \vec{a_{\parallel}} \): \( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki paralel bileşeni
\( \vec{a_{\perp}} \): \( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki dik bileşeni
\( \vec{a} = \vec{a_{\parallel}} + \vec{a_{\perp}} \)
\( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki paralel bileşeni \( \vec{b} \) vektörü üzerindeki izdüşümüdür.
\( \vec{a_{\parallel}} = \text{Proj}_{\vec{b}}(\vec{a}) \)
\( = \dfrac{\vec{a} \cdot \vec{b}}{\norm{\vec{b}}^2}\vec{b} \)
\( \vec{a} \) vektörünün \( \vec{b} \) vektörü üzerindeki dik bileşeni bu izdüşüm vektörüne dik olan vektördür.
\( \vec{a_{\perp}} = \vec{a} - \vec{a_{\parallel}} \)
\( = \vec{a} - \text{Proj}_{\vec{b}}(\vec{a}) \)
İzdüşüm ile Uzaklık
Skaler izdüşüm formülünün bir uygulaması olarak, bir \( B \) noktasının bir doğruya (ya da vektöre/düzleme) olan en yakın uzaklığı, bu doğru (vektör/düzlem) üzerindeki herhangi bir \( A \) noktasından \( B \) noktasına çizilen vektörün bu doğruya (vektöre/düzleme) dik bir vektör üzerindeki izdüşümünün normuna eşittir.

\( d = \abs{BC} = \norm{\text{Proj}_{\vec{n}}(\vec{AB})} \)
\( = \dfrac{\abs{\vec{AB} \cdot \vec{n}}}{\norm{\vec{n}}} \)
Bu formülü ileriki bölümlerde bir noktanın üç boyutlu uzayda bir doğruya ya da düzleme olan uzaklığını bulmak için sıklıkla kullanıyor olacağız.