Vektör Tipleri
Birim Vektör
Uzunluğu (normu) bir birim olan vektörlere birim vektör denir. Bir \( \vec{a} \) vektörü ile aynı yöndeki birim vektör \( \hat{a} \) şeklinde gösterilir.
\( \norm{\hat{a}} = 1 \)
\( \vec{a} = (\cos{30°}, \sin{30°}) \)
\( \norm{\vec{a}} = \sqrt{\cos^2{30°} + \sin^2{30°}} = 1 \)
Buna göre \( \vec{a} \) bir birim vektördür.
Birim vektörler herhangi bir yönde olabilir. Aşağıda üç farklı vektör ile aynı yöndeki birim vektörler gösterilmiştir.
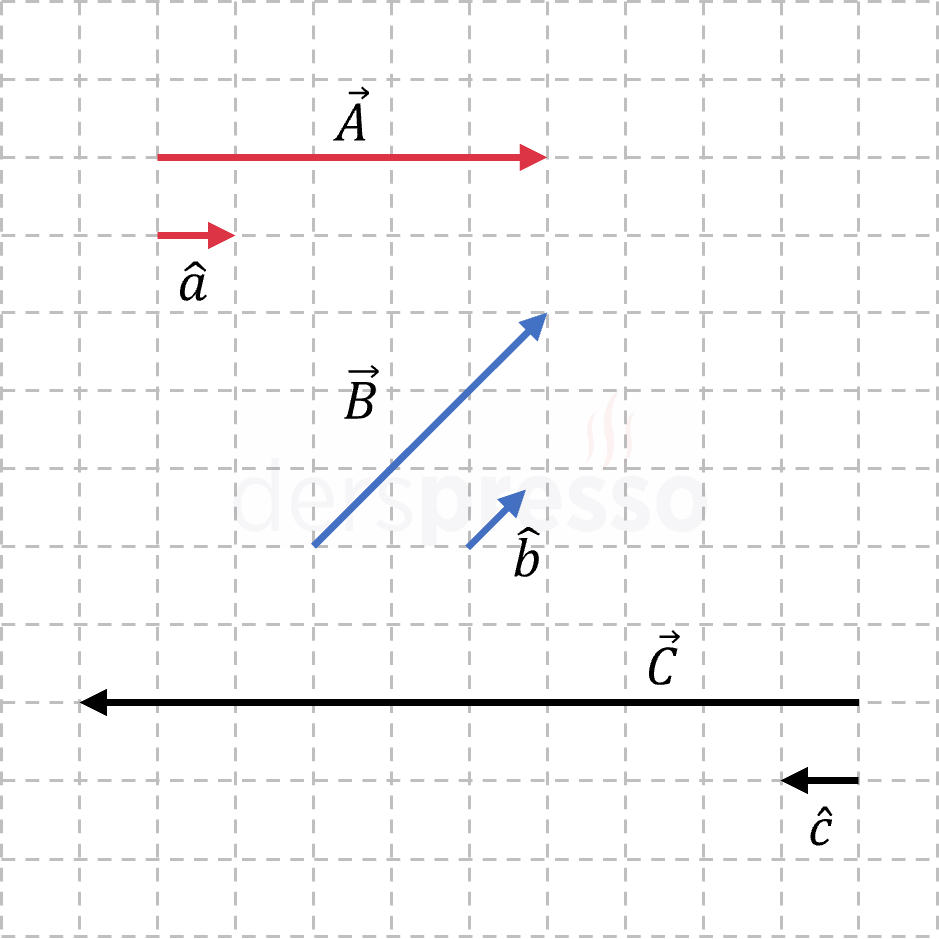
Bir vektörün normuna oranı, o vektör ile aynı yöndeki birim vektörü verir.
\( \hat{a} = \dfrac{\vec{a}}{\norm{\vec{a}}} \)
\( \norm{\hat{a}} = 1 \)
\( \vec{a} = (-3, 4) \)
\( \norm{\vec{a}} = \sqrt{(-3)^2 + 4^2} = 5 \)
\( \hat{a} = \dfrac{1}{5}(-3, 4) \)
\( = (-\dfrac{3}{5}, \dfrac{4}{5}) \)
\( \norm{\hat{a}} = \sqrt{(-\frac{3}{5})^2 + (\frac{4}{5})^2} = 1 \)
İSPATI GÖSTER
\( \vec{a} \) vektörü ile aynı yöndeki birim vektöre \( \hat{a} \) diyelim.
\( \hat{a} = \dfrac{\vec{a}}{\norm{\vec{a}}} \)
\( \hat{a} \) vektörünün normunu bulalım.
\( \norm{\hat{a}} = \norm{\dfrac{\vec{a}}{\norm{\vec{a}}}} \)
\( = \dfrac{\norm{\vec{a}}}{\norm{\norm{\vec{a}}}} \)
Norm skaler ve negatif olmayan bir büyüklük olduğu için normun tekrar normunun alınması sonucu değiştirmez.
\( = \dfrac{\norm{\vec{a}}}{\norm{\vec{a}}} = 1 \)
Buna göre her vektör, normu ve kendisiyle aynı yöndeki birim vektörün skaler çarpımı şeklinde ifade edilebilir.
\( \vec{a} = \norm{\vec{a}} \hat{a} \)
\( \vec{a} = (4, 3) \)
\( \norm{\vec{a}} = \sqrt{4^2 + 3^2} = 5 \)
\( \hat{a} = \dfrac{1}{5}(4, 3) = (\dfrac{4}{5}, \dfrac{3}{5}) \)
\( \vec{a} = 5\hat{a} \)

Sıfır Vektörü
Tüm bileşenleri sıfır olan, bir diğer ifadeyle uzunluğu sıfır olan vektörlere sıfır vektörü denir ve \( \vec{0} \) şeklinde gösterilir.
Sıfır vektörünün büyüklüğü sıfırdır, ayrıca başlangıç ve bitiş noktaları aynıdır ve bir yönü yoktur.
\( \norm{\vec{0}} = 0 \)
\( \vec{0} = (0, 0) \)
\( \vec{0} = (0, 0, 0) \)
Zıt Vektörler
Büyüklükleri aynı, yönleri zıt yönlü olan vektörlere zıt vektör denir. Zıt vektörler vektörel olarak birbirlerinin negatifine eşittir.
\( \vec{a} = -\vec{b} \)
\( \norm{\vec{a}} = \norm{\vec{b}} \)
Aşağıdaki vektör ikilileri zıt vektörlerdir.
\( (3, -5) \) ve \( (-3, 5) \)
\( (0, 4) \) ve \( (0, -4) \)
Aşağıdaki iki vektör zıt vektörlerdir.

Eşit Vektörler
Yönleri ve büyüklükleri aynı olan vektörlere eşit vektörler denir. Vektörlerin eşitliği "=" sembolüyle gösterilir.
\( \vec{a} = \vec{b} = \vec{c} \)
\( \norm{\vec{a}} = \norm{\vec{b}} = \norm{\vec{c}} \)
Büyüklükleri ve yönleri aynı olan aşağıdaki üç vektör eşittir.
\( \vec{a} = \vec{b} = \vec{c} \)

Aşağıdaki vektörler eşit değildir.
\( (3, 5) \ne (5, 3) \)
\( (2, 2, 2) \ne (2, 2) \)
Eşit vektörlerin bileşen sayıları ve birbirine karşılık gelen bileşenleri eşittir. Benzer şekilde, birbirine karşılık gelen bileşenleri eşit olan vektörler eşit vektörlerdir.
\( \vec{a} = (m, -2, k) \)
\( \vec{b} = (3, n, m + n) \)
\( \vec{a} = \vec{b} \) ise,
\( m = 3 \)
\( n = -2 \)
\( k = m + n = 1 \)
\( \vec{a} = \vec{b} = (3, -2, 1) \)