Genelleştirilmiş İntegral
Şu ana kadar gördüğümüz integral ifadeleri aşağıdaki iki koşulu sağlıyordu.
- İntegral aralığı sonlu ve kapalı bir \( [a, b] \) aralığı idi.
- İntegrali alınan fonksiyon bu aralıkta alttan ve üstten sınırlı idi.
Genelleştirilmiş integral ya da diğer adıyla has olmayan integral, bu iki koşuldan en az birinin sağlanmadığı durumlarda kullanılan bir yöntemdir. Genelleştirilmiş integral, her biri yukarıdaki iki koşuldan birinin sağlanmadığı duruma karşılık gelecek şekilde iki tipte olabilir.
- Tip I - Sınırsız integral aralığı: Bu durumda integral aralığının sınır değerlerinden en az biri sonsuzdur. Bir diğer ifadeyle integral yatay yönde sınırsızdır.
- Tip II - Sınırsız fonksiyon değeri: Bu durumda fonksiyon değeri integral aralığında bir noktada sonsuza gider ve bu noktada bir dikey asimptot oluşur. Bir diğer ifadeyle integral dikey yönde sınırsızdır.
Genelleştirilmiş integralde amaç, yukarıdaki iki durumda da ifadeyi belirli integral koşullarını sağlayan bir forma getirmek ve integral sonucu bir reel sayı olarak tanımlı ise bu değeri bulmaktır. Aşağıda göreceğimiz üzere, genelleştirilmiş integrali belirli integrale dönüştürmek için limit işlemi kullanılır.
Tip I: Sınırsız İntegral Aralığı
Bu tipteki integralde integral aralığının sınır değerlerinden en az biri sonsuzdur. Bu şekildeki bir genelleştirilmiş integral, limit işlemi yardımıyla belirli integrale dönüştürülür.
Aralık Üstten Sınırsız
İntegral aralığı \( [a, \infty) \) şeklinde ise ve fonksiyon diğer tüm integrallenebilirlik koşullarını sağlıyorsa genelleştirilmiş integral aşağıdaki şekilde tanımlanır.
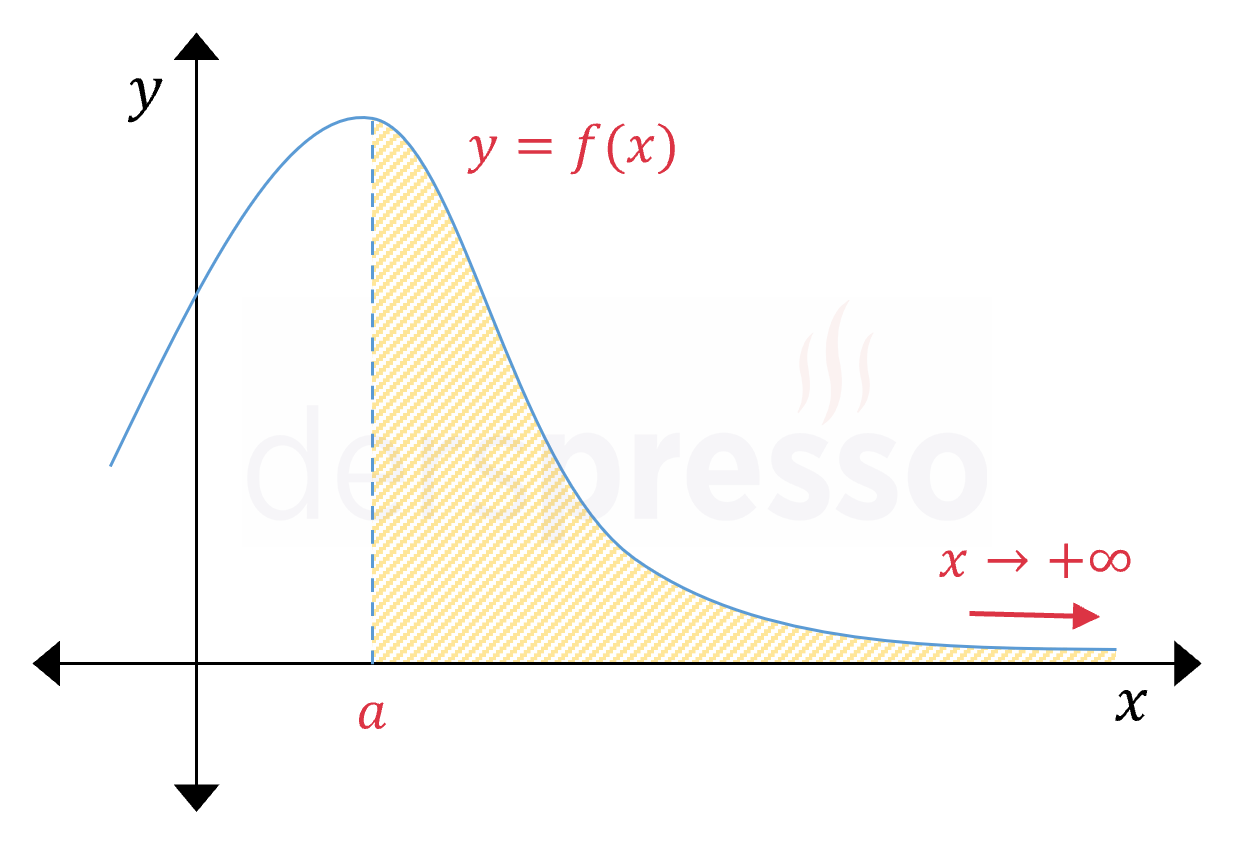
\( \displaystyle\int_a^{\infty} {f(x)\ dx} = \lim\limits_{t \to \infty} \displaystyle\int_a^t {f(x)\ dx} \)
Bu eşitlikte (ve aşağıda paylaşacağımız diğer benzer eşitliklerde) sol taraftaki integral bir genelleştirilmiş integral, limit içindeki integral ise belirli integraldir. Burada kullanılan yöntem; integralin üst sınır değerini reel sayı bir değişken olarak tanımlayarak belirli integrali hesaplamak, daha sonra belirli integral sonucunun bu değişken pozitif sonsuza giderkenki limitini almaktır.
Fonksiyonun bu aralıktaki genelleştirilmiş integrali yukarıdaki limit ifadesi bir reel sayı olarak tanımlı ise tanımlıdır. Limit ifadesi tanımsız ya da sonsuz ise bu aralıkta genelleştirilmiş integral de tanımsızdır.
Bir fonksiyonun bir aralıktaki genelleştirilmiş integrali bir reel sayı olarak tanımlı ise bu integral yakınsaktır, aksi takdirde ıraksaktır. Benzer şekilde, bir genelleştirilmiş integralin yakınsak olması integralin bir reel sayı olarak tanımlı olduğunu, ıraksak olması ise tanımsız ya da sonsuz olduğunu gösterir.
\( \displaystyle\int_0^{\infty} {e^{-x}\ dx} \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulalım.
İntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_0^{\infty} {e^{-x}\ dx} = \lim\limits_{t \to \infty} \displaystyle\int_0^t {e^{-x}\ dx} \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to \infty} (-e^{-x})|_0^t \)
\( = \lim\limits_{t \to \infty} (-e^{-t} + e^0) \)
\( t \to \infty \) iken \( e^{-t} = \frac{1}{e^t} \) ifadesi sıfıra yaklaşır.
\( = 0 + 1 = 1 \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri 1'dir.
Aralık Alttan Sınırsız
İntegral aralığı \( (-\infty, b] \) şeklinde ise ve fonksiyon diğer tüm integrallenebilirlik koşullarını sağlıyorsa genelleştirilmiş integral aşağıdaki şekilde tanımlanır.
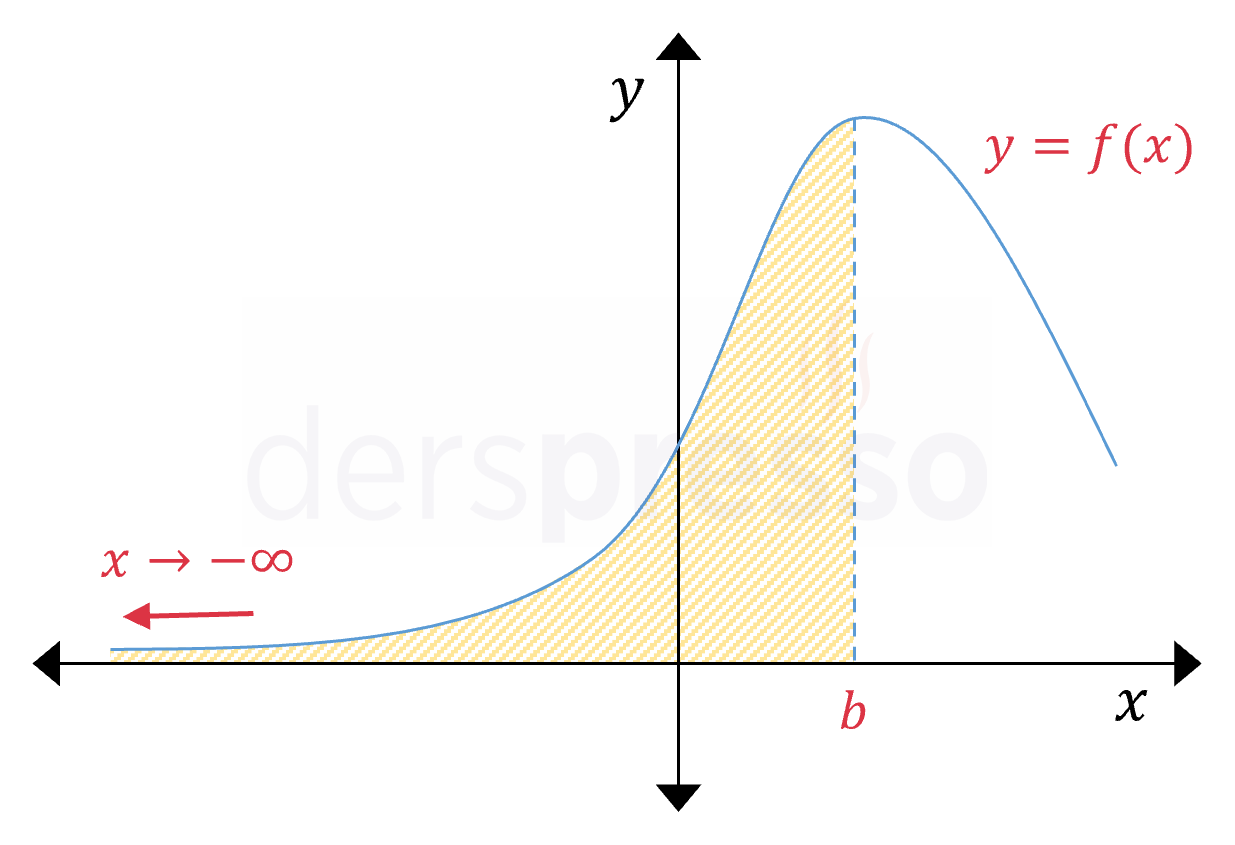
\( \displaystyle\int_{-\infty}^b {f(x)\ dx} = \lim\limits_{t \to -\infty} \displaystyle\int_t^b {f(x)\ dx} \)
Fonksiyonun bu aralıktaki genelleştirilmiş integrali yukarıdaki limit ifadesi bir reel sayı olarak tanımlı ise tanımlıdır. Limit ifadesi tanımsız ya da sonsuz ise bu aralıkta genelleştirilmiş integral de tanımsızdır.
\( \displaystyle\int_{-\infty}^0 {\dfrac{x}{\sqrt{x^2 + 1}}\ dx} \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulalım.
İntegral aralığının alt sınırı negatif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_{-\infty}^0 {\dfrac{x}{\sqrt{x^2 + 1}}\ dx} = \lim\limits_{t \to -\infty} \displaystyle\int_t^0 {\dfrac{x}{\sqrt{x^2 + 1}}\ dx} \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to -\infty} (\sqrt{x^2 + 1})|_t^0 \)
\( = \lim\limits_{t \to -\infty} (\sqrt{0^2 + 1} - \sqrt{t^2 + 1}) \)
\( t \to -\infty \) iken \( \sqrt{t^2 + 1} \) ifadesi pozitif sonsuza gider.
\( = 1 - \infty = -\infty \)
Buna göre verilen integral ifadesi ıraksaktır.
Aralık Alttan ve Üstten Sınırsız
İntegral aralığı \( (-\infty, \infty) \) şeklinde ise ve fonksiyon diğer tüm integrallenebilirlik koşullarını sağlıyorsa genelleştirilmiş integral aşağıdaki şekilde tanımlanır.
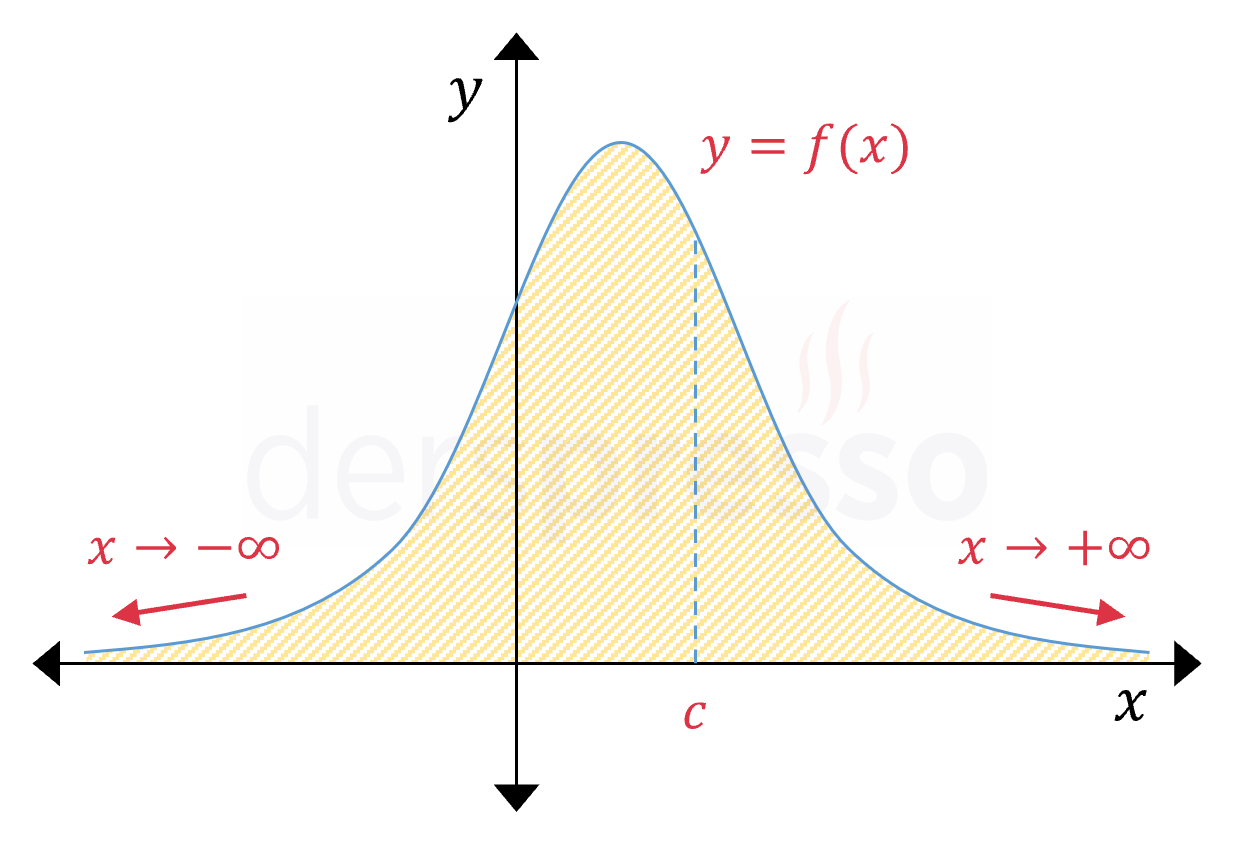
\( \displaystyle\int_{-\infty}^{\infty} {f(x)\ dx} = \displaystyle\int_{-\infty}^c {f(x)\ dx} + \displaystyle\int_c^{\infty} {f(x)\ dx} \)
Bu tanımda toplamı alınan iki integral, yukarıda tanımladığımız integral aralığının alt ya da üst sınır değerleri sonsuz olan I. tipte genelleştirilmiş integrallerdir.
Formüldeki \( x = c \) noktası \( (a, b) \) aralığında herhangi bir nokta olarak seçilebilir.
\( (-\infty, \infty) \) aralığındaki genelleştirilmiş integralin yakınsak olması için hem \( \int_{-\infty}^c {f(x)\ dx} \) hem de \( \int_c^{\infty} {f(x)\ dx} \) genelleştirilmiş integrali yakınsak olmalıdır. Bu integrallerden en az birinin ıraksak olması durumunda \( \int_{-\infty}^{\infty} {f(x)\ dx} \) genelleştirilmiş integrali de ıraksak olur.
\( \displaystyle\int_{-\infty}^{\infty} {\dfrac{1}{1 + x^2}\ dx} \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulalım.
İntegral aralığının hem alt hem de üst sınırı sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_{-\infty}^{\infty} {\dfrac{1}{1 + x^2}\ dx} = \displaystyle\int_{-\infty}^c {\dfrac{1}{1 + x^2}\ dx} + \displaystyle\int_c^{\infty} {\dfrac{1}{1 + x^2}\ dx} \)
\( c \) değeri olarak \( c = 0 \) seçelim ve \( (-\infty, 0] \) aralığı için (birinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_{-\infty}^0 {\dfrac{1}{1 + x^2}\ dx} = \lim\limits_{t \to -\infty} \displaystyle\int_t^0 {\dfrac{1}{1 + x^2}\ dx} \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to -\infty} (\arctan{x})|_t^0 \)
\( = \lim\limits_{t \to -\infty} (\arctan{0} - \arctan{t}) \)
\( t \to -\infty \) iken arc tanjant fonksiyonu \( -\frac{\pi}{2} \) değerine yaklaşır.
\( = 0 - (-\frac{\pi}{2}) = \frac{\pi}{2} \)
\( [0, \infty) \) aralığı için (ikinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_0^{\infty} {\dfrac{1}{1 + x^2}\ dx} = \lim\limits_{t \to \infty} \displaystyle\int_0^t {\dfrac{1}{1 + x^2}\ dx} \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to \infty} (\arctan{x})|_0^t \)
\( = \lim\limits_{t \to \infty} (\arctan{t} - \arctan{0}) \)
\( t \to \infty \) iken arc tanjant fonksiyonu \( \frac{\pi}{2} \) değerine yaklaşır.
\( = \frac{\pi}{2} - 0 = \frac{\pi}{2} \)
\( (-\infty, \infty) \) aralığı için genelleştirilmiş integrali bulmak için \( (-\infty, 0] \) ve \( [0, \infty) \) aralıkları için bulduğumuz değerlerin toplamını alalım.
\( \displaystyle\int_{-\infty}^{\infty} {\dfrac{1}{1 + x^2}\ dx} = \frac{\pi}{2} + \frac{\pi}{2} = \pi \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( \pi \)'dir.
Tip II: Sınırsız Fonksiyon Değeri
Bu tipteki integralde fonksiyon integral aralığındaki bir \( x = c \) noktasında sonsuza gider ve bu noktada bir dikey asimptot oluşur. Bu şekildeki bir genelleştirilmiş integral, yine limit işlemi yardımıyla belirli integrale dönüştürülür.
Fonksiyon Üst Sınır Noktasında Sonsuz
Fonksiyon değeri integral aralığının üst sınırında sonsuza gidiyorsa ve fonksiyon diğer tüm integrallenebilirlik koşullarını sağlıyorsa genelleştirilmiş integral aşağıdaki şekilde tanımlanır.

\( f \) fonksiyonu \( x = b \) noktasında sonsuza gidiyorsa,
\( \displaystyle\int_a^b {f(x)\ dx} = \lim\limits_{t \to b^-} \displaystyle\int_a^t {f(x)\ dx} \)
Bu eşitlikte (ve aşağıda paylaşacağımız diğer benzer eşitliklerde) sol taraftaki integral bir genelleştirilmiş integral, limit içindeki integral ise belirli integraldir. Burada kullanılan yöntem; fonksiyonun sonsuza gittiği (dikey asimptotun oluştuğu) noktanın apsis değerini bir değişken olarak tanımlayarak belirli integrali hesaplamak, daha sonra belirli integral sonucunun değişken bu noktaya soldan yaklaşırkenki limitini almaktır.
Fonksiyonun bu aralıktaki genelleştirilmiş integrali yukarıdaki limit ifadesi bir reel sayı olarak tanımlı ise tanımlıdır. Limit ifadesi tanımsız ya da sonsuz ise bu aralıkta genelleştirilmiş integral de tanımsızdır.
\( \displaystyle\int_0^3 {\dfrac{1}{\sqrt{6 - 2x}}\ dx} \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulalım.
İntegral aralığının üst sınırı olan \( x = 3 \) değeri paydayı sıfır yaptığı için bu noktada bir dikey asimptot oluşur, bu yüzden üst sınır noktasında sonsuza giden II. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_0^3 {\dfrac{1}{\sqrt{6 - 2x}}\ dx} = \lim\limits_{t \to 3^-} \displaystyle\int_0^t {\dfrac{1}{\sqrt{6 - 2x}}\ dx} \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to 3^-} (-\sqrt{6 - 2x})|_0^t \)
\( = \lim\limits_{t \to 3^-} (-\sqrt{6 - 2t} + \sqrt{6 - 2(0)}) \)
\( t \to 3^- \) iken \( \sqrt{6 - 2t} \) ifadesi 0'a yaklaşır.
\( = 0 + \sqrt{6} = \sqrt{6} \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( \sqrt{6} \) dır.
Fonksiyon Alt Sınır Noktasında Sonsuz
Fonksiyon değeri integral aralığının alt sınırında sonsuza gidiyorsa ve fonksiyon diğer tüm integrallenebilirlik koşullarını sağlıyorsa genelleştirilmiş integral aşağıdaki şekilde tanımlanır.
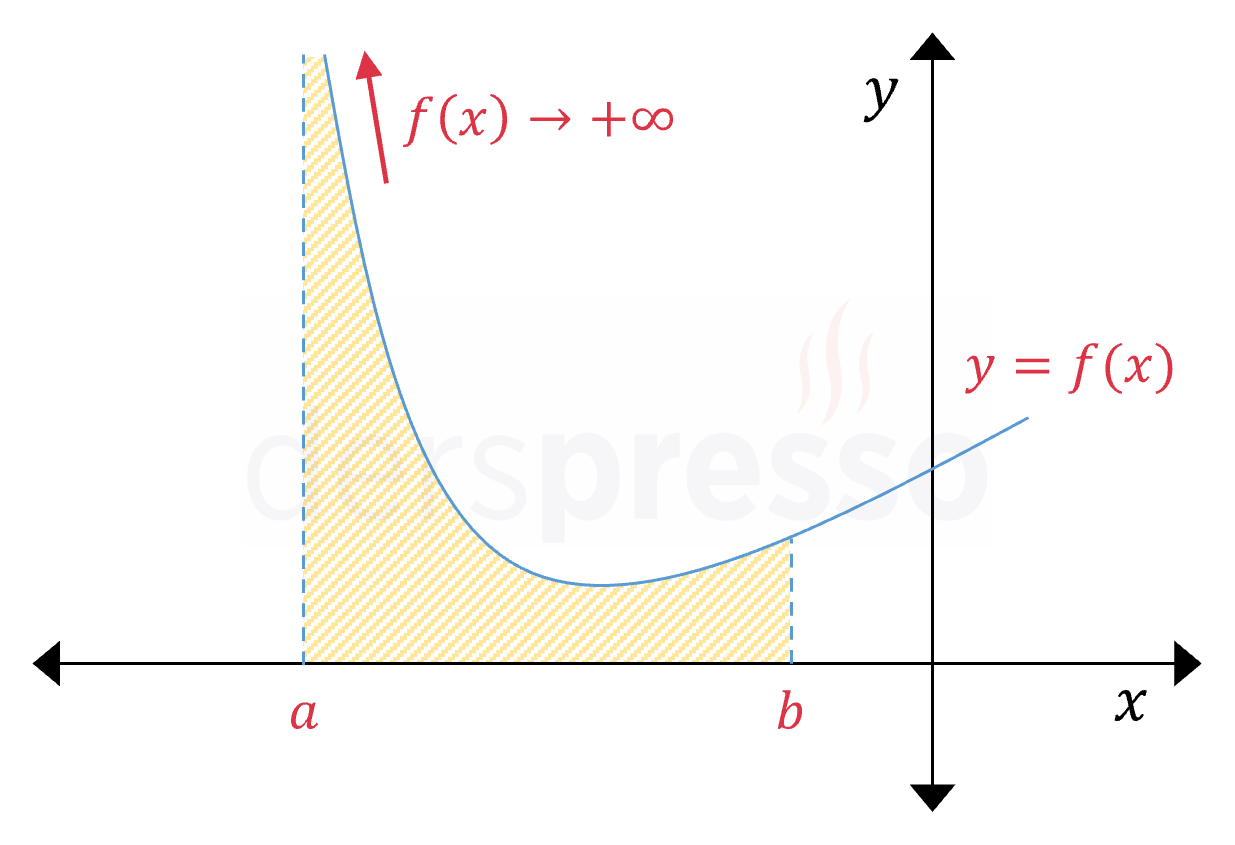
\( f \) fonksiyonu \( x = a \) noktasında sonsuza gidiyorsa,
\( \displaystyle\int_a^b {f(x)\ dx} = \lim\limits_{t \to a^+} \displaystyle\int_t^b {f(x)\ dx} \)
Fonksiyonun bu aralıktaki genelleştirilmiş integrali yukarıdaki limit ifadesi bir reel sayı olarak tanımlı ise tanımlıdır. Limit ifadesi tanımsız ya da sonsuz ise bu aralıkta genelleştirilmiş integral de tanımsızdır.
\( \displaystyle\int_1^e {\dfrac{1}{x(\ln{x})^2}\ dx} \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulalım.
İntegral aralığının alt sınırı olan \( x = 1 \) değeri \( \ln{x} \) ifadesini ve paydayı sıfır yaptığı için bu noktada bir dikey asimptot oluşur, bu yüzden alt sınır noktasında sonsuza giden II. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_1^e {\dfrac{1}{x(\ln{x})^2}\ dx} = \lim\limits_{t \to 1^+} \displaystyle\int_t^e {\dfrac{1}{x(\ln{x})^2}\ dx} \)
\( u = \ln{x} \) ve \( du = \frac{1}{x}\ dx \) değişken değiştirmesi ile ifadenin integralini alalım.
\( = \lim\limits_{t \to 1^+} (-\dfrac{1}{\ln{x}})|_t^e \)
\( = \lim\limits_{t \to 1^+} (-\dfrac{1}{\ln{e}} + \dfrac{1}{\ln{t}}) \)
\( t \to 1^+ \) iken \( \ln{t} \) ifadesi 0'a pozitif taraftan yaklaşır, dolayısıyla \( \frac{1}{\ln{t}} \) ifadesi pozitif sonsuza gider.
\( = -1 + \infty = +\infty \)
Buna göre verilen integral ifadesi ıraksaktır.
Fonksiyon Bir Ara Noktada Sonsuz
Fonksiyonun sonsuza gittiği nokta \( (a, b) \) açık aralığında bir \( x = c \) noktası ise genelleştirilmiş integral aşağıdaki şekilde tanımlanır.

\( f \) fonksiyonu \( (a, b) \) açık aralığında bir \( x = c \) noktasında sonsuza gidiyorsa,
\( \displaystyle\int_a^b {f(x)\ dx} = \displaystyle\int_a^c {f(x)\ dx} + \displaystyle\int_c^b {f(x)\ dx} \)
Bu tanımda toplamı alınan iki integral, yukarıda tanımladığımız II. tipteki genelleştirilmiş integrallerdir.
Tanımdaki \( x = c \) noktası; I. tipte olduğu gibi \( (a, b) \) aralığında seçilen herhangi bir nokta değil, fonksiyon değerinin sonsuza gittiği noktadır.
İntegral aralığındaki ara bir noktada sonsuza giden bir genelleştirilmiş integralin yakınsak olması için hem \( \int_a^c {f(x)\ dx} \) hem de \( \int_c^b {f(x)\ dx} \) genelleştirilmiş integrali yakınsak olmalıdır. Bu integrallerden en az birinin ıraksak olması durumunda \( \int_a^b {f(x)\ dx} \) integrali de ıraksak olur.
\( \displaystyle\int_0^9 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulalım.
İntegral aralığının ara bir noktası olan \( x = 1 \) değeri paydayı sıfır yaptığı için bu noktada bir dikey asimptot oluşur, bu yüzden ara bir noktasında sonsuza giden II. tipte genelleştirilmiş integral formülünü kullanalım.
Formüldeki \( c \) değeri dikey asimptotun oluştuğu \( x = 1 \) değeri olur.
\( \displaystyle\int_0^9 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} = \displaystyle\int_0^1 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} + \displaystyle\int_1^9 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} \)
\( [0, 1) \) aralığı için (birinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_0^1 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} = \lim\limits_{t \to 1^-} \displaystyle\int_0^t {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to 1^-} (3\sqrt[3]{x - 1})|_0^t \)
\( = \lim\limits_{t \to 1^-} (3\sqrt[3]{t - 1} - 3\sqrt[3]{0 - 1}) \)
\( t \to 1^- \) iken \( \sqrt[3]{t - 1} \) ifadesi 0'a yaklaşır.
\( = 0 - (-3) = 3 \)
\( (1, 9] \) aralığı için (ikinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_1^9 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} = \lim\limits_{t \to 1^+} \displaystyle\int_t^9 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to 1^+} (3\sqrt[3]{x - 1})|_t^9 \)
\( = \lim\limits_{t \to 1^+} (3\sqrt[3]{9 - 1} - 3\sqrt[3]{t - 1}) \)
\( t \to 1^+ \) iken \( \sqrt[3]{t - 1} \) ifadesi 0'a yaklaşır.
\( = 6 - 0 = 6 \)
\( [0, 9] \) aralığı için genelleştirilmiş integrali bulmak için \( [0, 1) \) ve \( (1, 9] \) aralıkları için bulduğumuz değerlerin toplamını alalım.
\( \displaystyle\int_0^9 {\dfrac{1}{\sqrt[3]{(x - 1)^2}}\ dx} = 3 + 6 = 9 \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri 9'dur.
Her ne kadar kullanılan integral sembolleri aynı olsa da, genelleştirilmiş integral belirli integralden farklı bir işlemdir. I. tipte genelleştirilmiş integralde sınır değerlerinden en az biri sonsuz olduğu için bu integralin belirli integralden ayırt edilmesi kolaydır, ancak II. tipte böyle bir ayrım söz konusu olmadığı için dikkatli olunmalı ve sonsuzluk içeren bir aralıkta genelleştirilmiş integral yerine belirli integral kullanılmamalıdır.
Bu durumun gözden kaçırılması durumunda nasıl yanlış sonuç elde edilebileceğini bir örnekle gösterelim.
\( \displaystyle\int_0^{\pi} \tan{x}\ dx \) integralinin sonucunu bulalım.
Tanjant fonksiyonu verilen aralıkta sonsuza gittiği gerçeğini gözden kaçırdığımızı varsayarak ifadenin integralini önce (hatalı bir şekilde) normal belirli integral yöntemi ile alalım.
\( \displaystyle\int_0^{\pi} \tan{x}\ dx = (\ln{\abs{\sec{x}}})|_0^\pi \)
\( = \ln{\abs{\sec{\pi}}} - \ln{\abs{\sec{0}}} \)
\( = \ln{\abs{-1}} - \ln{\abs{1}} \)
\( = \ln{1} - \ln{1} \)
\( = 0 - 0 = 0 \)
Her ne kadar reel sayı bir sonuç elde etmiş olsak da, tanjant fonksiyonu bu aralıktaki \( x = \frac{\pi}{2} \) noktasında sonsuza gider, dolayısıyla integrali belirli integral yerine genelleştirilmiş integral yöntemi ile almamız gerekir.
Ara bir noktasında sonsuza giden II. tipte genelleştirilmiş integral formülünü kullanalım.
Formüldeki \( c \) değeri fonksiyonda dikey asimptotun oluştuğu \( x = \frac{\pi}{2} \) değeri olur.
\( \displaystyle\int_0^{\pi} \tan{x}\ dx = \displaystyle\int_0^{\frac{\pi}{2}} \tan{x}\ dx + \displaystyle\int_{\frac{\pi}{2}}^{\pi} \tan{x}\ dx \)
\( [0, \frac{\pi}{2}) \) aralığı için (birinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_0^{\frac{\pi}{2}} \tan{x}\ dx = \lim\limits_{t \to \frac{\pi}{2}^-} \displaystyle\int_0^t \tan{x}\ dx \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to \frac{\pi}{2}^-} (\ln{\abs{\sec{x}}})|_0^t \)
\( = \lim\limits_{t \to \frac{\pi}{2}^-} (\ln{\abs{\sec{t}}} - \ln{\abs{\sec{0}}}) \)
\( = \lim\limits_{t \to \frac{\pi}{2}^-} (\ln{\abs{\sec{t}}} - \ln{\abs{1}}) \)
\( = \lim\limits_{t \to \frac{\pi}{2}^-} \ln{\abs{\sec{t}}} \)
Aşağıdaki sekant grafiğinde görebileceğimiz üzere, \( t \to \frac{\pi}{2}^- \) iken \( \sec{t} \) ifadesi pozitif sonsuza gider, dolayısıyla doğal logaritma ifadesi de pozitif sonsuza gider.
\( = +\infty \)
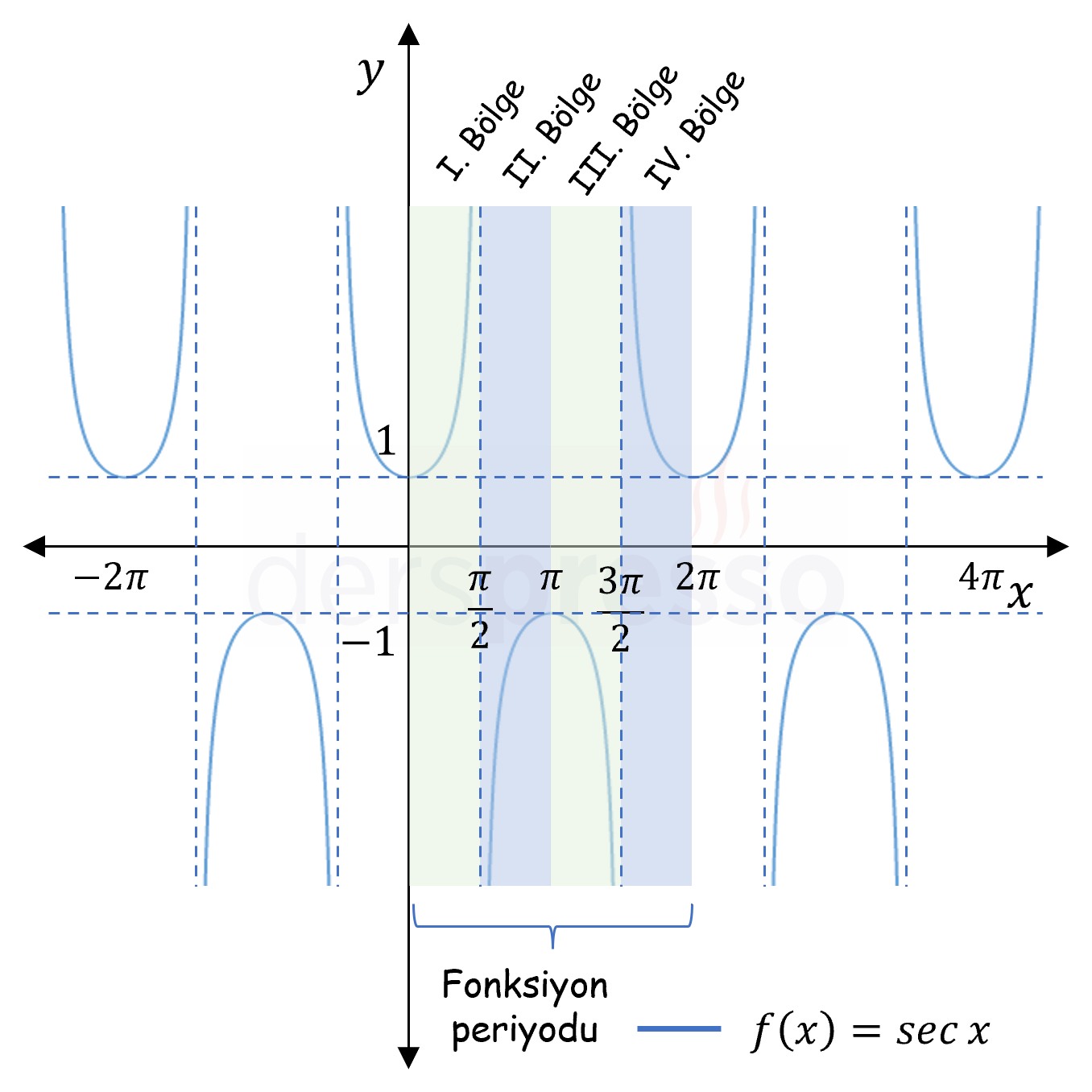
\( [0, \frac{\pi}{2}) \) aralığında pozitif sonsuz sonucu elde ettiğimiz için \( (\frac{\pi}{2}, \pi] \) aralığı için benzer bir hesaplama yapmamıza gerek yoktur.
Verilen integral ifadesi ıraksaktır.
\( \displaystyle\int_0^{\infty} \cos{x}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_0^{\infty} \cos{x}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_0^t \cos{x}\ dx \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to \infty} (\sin{x})|_0^t \)
\( = \lim\limits_{t \to \infty} (\sin{t} - \sin{0}) \)
\( = \lim\limits_{t \to \infty} \sin{t} \)
Sinüs fonksiyonu periyodik bir fonksiyon olduğu için \( t \to \infty \) iken belirli bir değere yaklaşmaz, dolayısıyla limiti tanımsızdır.
Buna göre verilen integral ifadesi ıraksaktır.
Verilen ifadeyi belirli integralin alan anlamı açısından düşündüğümüzde, periyodik bir fonksiyonun \( x \) ekseni ile arasında kalan alanın \( x \) sonsuza giderken kesin bir değeri olamayacağını görebiliriz.
\( \displaystyle\int_{e}^{\infty} \dfrac{6}{x\ln^4{x}}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_{e}^{\infty} \dfrac{6}{x\ln^4{x}}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_{e}^{t} \dfrac{6}{x\ln^4{x}}\ dx \)
İfadenin integralini alalım.
\( u = \ln{x} \) ve \( du = \dfrac{1}{x}\ dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to \infty} (-\dfrac{2}{\ln^3{x}})|_{e}^{t} \)
\( = \lim\limits_{t \to \infty} (-\dfrac{2}{\ln^3{t}} - (-\dfrac{2}{\ln^3{e}})) \)
\( t \to \infty\) iken \( -\dfrac{2}{\ln^3{t}} \) ifadesi sıfıra yaklaşır.
\( = \lim\limits_{t \to \infty} (-0 - (-\dfrac{2}{1^3})) \)
\( = 2 \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( 2 \) olarak bulunur.
\( \displaystyle\int_{-\infty}^{0} \dfrac{4e^x}{e^{2x} + 1}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının alt sınırı negatif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_{-\infty}^0 \dfrac{4e^x}{e^{2x} + 1}\ dx = \lim\limits_{t \to -\infty} \displaystyle\int_t^0 \dfrac{4e^x}{e^{2x} + 1}\ dx \)
İfadenin integralini alalım.
\( u = e^x \) ve \( du = e^x\ dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to -\infty} (4\arctan{e^x})|_t^0 \)
\( = \lim\limits_{t \to -\infty} (4\arctan{e^0} - 4\arctan{e^t}) \)
\( \arctan{e^0} = \arctan{1} = \dfrac{\pi}{4} \)
\( t \to -\infty \) iken \( e^t \) ifadesi sıfıra pozitif taraftan yaklaşır.
\( e^t \to 0^+ \) iken \( \arctan{e^t} \) ifadesi sıfıra yaklaşır.
Buna göre yukarıdaki limit ifadesinin sonucu aşağıdaki gibi olur.
\( = 4 \cdot \dfrac{\pi}{4} - 4 \cdot 0 \)
\( = \pi \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( \pi \) olarak bulunur.
\( \displaystyle\int_3^{\infty} \dfrac{4}{x^2 - 4}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_3^{\infty} \dfrac{4}{x^2 - 4}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_{3}^{t} \dfrac{4}{x^2 - 4}\ dx \)
\( = \lim\limits_{t \to \infty} \displaystyle\int_3^t \dfrac{4}{(x - 2)(x + 2)}\ dx \)
İfadeyi basit kesirlerin toplamı şeklinde yazalım.
\( = \lim\limits_{t \to \infty} \displaystyle\int_3^t (\dfrac{1}{x - 2} - \dfrac{1}{x + 2})\ dx \)
Kesirlerin ayrı ayrı integrallerini alalım.
\( = \lim\limits_{t \to \infty} (\ln{\abs{x - 2}} - \ln{\abs{x + 2}})|_3^t \)
\( = \lim\limits_{t \to \infty} (\ln{\abs{\dfrac{x - 2}{x + 2}}})|_3^t \)
\( t \to \infty \) iken pay ve payda pozitif olacağı için mutlak değeri kaldırabiliriz.
\( = \lim\limits_{t \to \infty} (\ln{\dfrac{x - 2}{x + 2}})|_3^t \)
\( = \lim\limits_{t \to \infty} (\ln{\dfrac{t - 2}{t + 2}} - \ln{\dfrac{3 - 2}{3 + 2}}) \)
İfadeyi düzenleyelim.
\( = \lim\limits_{t \to \infty} (\ln{\dfrac{t(1 - \frac{2}{t})}{t(1 + \frac{2}{t})}} - \ln{\dfrac{1}{5}}) \)
\( = \lim\limits_{t \to \infty} (\ln{\dfrac{1 - \frac{2}{t}}{1 + \frac{2}{t}}} + \ln{5}) \)
\( t \to \infty \) iken \( \dfrac{2}{t} \) ifadesi sıfıra yaklaşır.
\( = \ln{1} + \ln{5} \)
\( = \ln{5} \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( \ln{5} \) olarak bulunur.
\( \displaystyle\int_2^{\infty} -\dfrac{7}{(2x + 3)(3x + 1)}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_2^{\infty} -\dfrac{7}{(2x + 3)(3x + 1)}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_2^t -\dfrac{7}{(2x + 3)(3x + 1)}\ dx \)
İfadeyi basit kesirlerin toplamı şeklinde yazalım.
\( = \lim\limits_{t \to \infty} \displaystyle\int_2^t (\dfrac{2}{2x + 3} - \dfrac{3}{3x + 1})\ dx \)
Kesirlerin ayrı ayrı integrallerini alalım.
\( = \lim\limits_{t \to \infty} (\ln{\abs{2x + 3}} - \ln{\abs{3x + 1}})|_2^t \)
\( = \lim\limits_{t \to \infty} (\ln{\abs{\dfrac{2x + 3}{3x + 1}}})|_2^t \)
\( t \to \infty \) iken pay ve payda pozitif olacağı için mutlak değeri kaldırabiliriz.
\( = \lim\limits_{t \to \infty} (\ln{\dfrac{2x + 3}{3x + 1}})|_2^t \)
\( = \lim\limits_{t \to \infty} (\ln{\dfrac{2t + 3}{3t + 1}}- \ln{\dfrac{4 + 3}{6 + 1}}) \)
İlk terimin limitini bulmak için ifadeyi düzenleyelim.
\( = \lim\limits_{t \to \infty} \ln{\dfrac{2t + 3}{3t + 1}} = \lim\limits_{t \to \infty} \ln{\dfrac{t(2 + \frac{3}{t})}{t(3 + \frac{1}{t})}} \)
\( = \lim\limits_{t \to \infty} \ln{\dfrac{2 + \frac{3}{t}}{3 + \frac{1}{t}}} \)
\( t \to \infty \) iken \( \dfrac{3}{t} \) ve \( \dfrac{1}{t} \) ifadeleri sıfıra yaklaşır.
\( = \lim\limits_{t \to \infty} \ln{\dfrac{2 + 0}{3 + 0}} = \ln{\dfrac{2}{3}} \)
Buna göre yukarıdaki limit ifadesinin sonucu aşağıdaki gibi olur.
\( = \ln{\dfrac{2}{3}} - \ln{1} \)
\( = \ln{\dfrac{2}{3}} \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( \ln{\dfrac{2}{3}} \) olarak bulunur.
\( \displaystyle\int_0^{\infty} (\dfrac{4}{1 + x} - \dfrac{8x}{1 + 2x^2})\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_0^{\infty} (\dfrac{4}{1 + x} - \dfrac{8x}{1 + 2x^2})\ dx = \lim\limits_{t \to \infty} \displaystyle\int_0^t (\dfrac{4}{1 + x} - \dfrac{8x}{1 + 2x^2})\ dx \)
Kesirlerin ayrı ayrı integrallerini alalım.
İkinci terimin integralini alınırken \( u = 1 + 2x^2 \) ve \( du = 4x\ dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to \infty} (4\ln{\abs{1 + x}} - 2\ln{\abs{1 + 2x^2}})|_0^t \)
\( t \to \infty \) iken pay ve payda pozitif olacağı için mutlak değeri kaldırabiliriz.
\( = 2\lim\limits_{t \to \infty} (\ln{\dfrac{(1 + x)^2}{1 + 2x^2}})|_0^t \)
\( = 2\lim\limits_{t \to \infty} (\ln{\dfrac{(1 + t)^2}{1 + 2t^2}} - \ln{\dfrac{(1 + 0)^2}{1 + 2(0)^2}}) \)
\( = 2\lim\limits_{t \to \infty} (\ln{\dfrac{1 + 2t + t^2}{1 + 2t^2}} - \ln{1}) \)
\( = 2\lim\limits_{t \to \infty} \ln{\dfrac{t^2 + 2t + 1}{2t^2 + 1}} \)
İfadeyi düzenleyelim.
\( = 2\lim\limits_{t \to \infty} \ln{\dfrac{t^2(1 + \frac{2}{t} + \frac{1}{t^2})}{t^2(2 + \frac{1}{t^2})}} \)
\( = 2\lim\limits_{t \to \infty} \ln{\dfrac{1 + \frac{2}{t} + \frac{1}{t^2}}{2 + \frac{1}{t^2}}} \)
\( t \to \infty \) iken \( \dfrac{2}{t} \) ve \( \dfrac{1}{t^2} \) ifadeleri sıfıra yaklaşır.
\( = 2\lim\limits_{t \to \infty} \ln{\dfrac{1}{2}} \)
\( = -2\ln{2} \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( -2\ln{2} \) olarak bulunur.
\( \displaystyle\int_0^1 \dfrac{1}{5x^{0,99}}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının alt sınırı olan \( x = 0 \) değeri paydayı sıfır yaptığı için bu noktada bir dikey asimptot oluşur, bu yüzden alt sınır noktasında sonsuza giden II. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_0^1 \dfrac{1}{5x^{0,99}}\ dx = \lim\limits_{t \to 0^+} \displaystyle\int_t^1 \dfrac{1}{5x^{0,99}}\ dx \)
İfadeyi düzenleyelim.
\( = \lim\limits_{t \to 0^+} \displaystyle\int_t^1 \dfrac{1}{5x^{\frac{99}{100}}}\ dx \)
\( = \lim\limits_{t \to 0^+} \displaystyle\int_t^1 \dfrac{1}{5\sqrt[100]{x^{99}}}\ dx \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to 0^+} (\dfrac{100\sqrt[100]{x}}{5})|_t^1 \)
\( = \lim\limits_{t \to 0^+} (20\sqrt[100]{1} - 20\sqrt[100]{t}) \)
\( t \to 0^+ \) iken \( \sqrt[100]{t} \) ifadesi sıfıra yaklaşır.
\( = 20 - 0 = 20 \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( 20 \) olarak bulunur.
\( \displaystyle\int_{-\infty}^{\infty} \dfrac{12x^3}{(x^4 + 4)^2}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının hem alt hem de üst sınırı sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_{-\infty}^{\infty} \dfrac{12x^3}{(x^4 + 4)^2}\ dx = \displaystyle\int_{-\infty}^c \dfrac{12x^3}{(x^4 + 4)^2}\ dx + \displaystyle\int_c^{\infty} \dfrac{12x^3}{(x^4 + 4)^2}\ dx \)
\( c \) değeri olarak \( c = 0 \) seçelim ve \( (-\infty, 0] \) aralığı için (birinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_{-\infty}^0 \dfrac{12x^3}{(x^4 + 4)^2}\ dx = \lim\limits_{t \to -\infty} \displaystyle\int_t^0 \dfrac{12x^3}{(x^4 + 4)^2}\ dx \)
İfadenin integralini alalım.
\( u = x^4 + 4 \) ve \( du = 4x^3\ dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to -\infty} (-\dfrac{3}{x^4 + 4})|_t^0 \)
\( = \lim\limits_{t \to -\infty} (-\dfrac{3}{0^4 + 4} - (-\dfrac{3}{t^4 + 4})) \)
\( t \to -\infty \) iken \( \dfrac{3}{t^4 + 4} \) ifadesi sıfıra yaklaşır.
\( = -\dfrac{3}{4} + 0 = -\dfrac{3}{4} \)
\( [0, \infty) \) aralığı için (ikinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_0^{\infty} \dfrac{12x^3}{(x^4 + 4)^2}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_0^t \dfrac{12x^3}{(x^4 + 4)^2}\ dx \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to \infty} (-\dfrac{3}{x^4 + 4})|_0^t \)
\( = \lim\limits_{t \to \infty} (-\dfrac{3}{t^4 + 4} - (-\dfrac{3}{0^4 + 4})) \)
\( t \to \infty \) iken \( \dfrac{3}{t^4 + 4} \) ifadesi sıfıra yaklaşır.
\( = 0 + \dfrac{3}{4} = \dfrac{3}{4}\)
\( (-\infty, \infty) \) aralığı için genelleştirilmiş integrali bulmak için \( (-\infty, 0] \) ve \( [0, \infty) \) aralıkları için bulduğumuz değerlerin toplamını alalım.
\( \displaystyle\int_{-\infty}^{\infty} \dfrac{12x^3}{(x^4 + 4)^2}\ dx = -\dfrac{3}{4} + \dfrac{3}{4} = 0 \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( 0 \) olarak bulunur.
\( \displaystyle\int_5^{\infty} 4xe^{-2x}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_5^{\infty} 4xe^{-2x}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_5^{t} 4xe^{-2x}\ dx \)
İfadenin integralini alalım.
\( u = x \) ve \( dv = e^{-x}\ dx \) olmak üzere kısmi integral yöntemini kullanalım.
\( = \lim\limits_{t \to \infty} (-2xe^{-2x} - e^{-2x})|_5^t \)
\( = \lim\limits_{t \to \infty} [(-2te^{-2t} - e^{-2t}) - (-10e^{-10} - e^{-10})] \)
\( = \lim\limits_{t \to \infty} (-e^{-2t}(2t + 1) + 11e^{-10}) \)
\( \lim\limits_{t \to 0^+} -e^{-2t}(2t + 1) \) limitini bulmak için önce ifadeyi \( \frac{\infty}{\infty} \) belirsizliği içerecek şekilde düzenleyelim.
\( \lim\limits_{t \to \infty} -e^{-2t}(2t + 1) = \lim\limits_{t \to \infty} - \dfrac{2t + 1}{e^{2t}} = \dfrac{\infty}{\infty} \)
Belirsizliği gidermek için L'Hospital kuralını kullanalım ve payın/paydanın türevini alalım.
\( = \lim\limits_{t \to \infty} -e^{-2t} \)
\( t \to \infty \) iken \( e^{-2t} = \dfrac{1}{e^{2t}} \) ifadesi sıfıra yaklaşır.
Buna göre yukarıdaki limit ifadesinin sonucu aşağıdaki gibi olur.
\( = 0 + 11e^{-10} \)
\( = 11e^{-10} \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( 11e^{-10} \) olarak bulunur.
\( \displaystyle\int_{-\infty}^{\infty} 3x^5e^{-x^6}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının hem alt hem de üst sınırı sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_{-\infty}^{\infty} 3x^5e^{-x^6}\ dx = \displaystyle\int_{-\infty}^c 3x^5e^{-x^6}\ dx + \displaystyle\int_c^{\infty} 3x^5e^{-x^6}\ dx \)
\( c \) değeri olarak \( c = 0 \) seçelim ve \( (-\infty, 0] \) aralığı için (birinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_{-\infty}^0 3x^5e^{-x^6}\ dx = \lim\limits_{t \to -\infty} \displaystyle\int_t^0 3x^5e^{-x^6}\ dx \)
İfadenin integralini alalım.
\( u = -x^6 \) ve \( du = -6x^5\ dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to -\infty} (-\dfrac{e^{-x^6}}{2})|_t^0 \)
\( = \lim\limits_{t \to -\infty} (-\dfrac{e^{-0^6}}{2} - (-\dfrac{e^{-t^6}}{2})) \)
\( t \to -\infty \) iken \( \dfrac{e^{-t^6}}{2} = \dfrac{1}{2e^{t^6}} \) ifadesi sıfıra yaklaşır.
\( = -\dfrac{1}{2} + 0 = -\dfrac{1}{2} \)
\( [0, \infty) \) aralığı için (ikinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_0^{\infty} 3x^5e^{-x^6}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_0^t 3x^5e^{-x^6}\ dx \)
İfadenin integralini alalım.
\( = \lim\limits_{t \to \infty} (-\dfrac{e^{-x^6}}{2})|_0^t \)
\( = \lim\limits_{t \to \infty} (-\dfrac{e^{-t^6}}{2} - (-\dfrac{e^{-0^6}}{2})) \)
\( t \to \infty \) iken \( \dfrac{e^{-t^6}}{2} = \dfrac{1}{2e^{t^6}} \) ifadesi sıfıra yaklaşır.
\( = 0 + \dfrac{1}{2} = \dfrac{1}{2}\)
\( (-\infty, \infty) \) aralığı için genelleştirilmiş integrali bulmak için \( (-\infty, 0] \) ve \( [0, \infty) \) aralıkları için bulduğumuz değerlerin toplamını alalım.
\( \displaystyle\int_{-\infty}^{\infty} 3x^5e^{-x^6}\ dx = -\dfrac{1}{2} + \dfrac{1}{2} = 0 \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( 0 \)'dır.
\( \displaystyle\int_0^{2e} 2x^3\ln(2x)\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının alt sınırı olan \( x = 0 \) değeri \( \ln(2x) \) ifadesini tanımsız yaptığı için bu noktada bir dikey asimptot oluşur, bu yüzden alt sınır noktasında sonsuza giden II. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_0^{2e} 2x^3\ln(2x)\ dx = \lim\limits_{t \to 0^+} \displaystyle\int_t^{2e} 2x^3\ln(2x)\ dx \)
İfadenin integralini alalım.
\( u = \ln(2x) \) ve \( dv = 2x^3\ dx \) olmak üzere kısmi integral yöntemini kullanalım.
\( = \lim\limits_{t \to 0^+} (\dfrac{x^4\ln(2x)}{2} - \dfrac{x^4}{8})|_t^{2e} \)
\( = \lim\limits_{t \to 0^+} [(\dfrac{(2e)^4\ln(4e)}{2} - \dfrac{(2e)^4}{8}) - (\dfrac{t^4\ln(2t)}{2} - \dfrac{t^4}{8})] \)
\( = \lim\limits_{t \to 0^+} (8e^4(\ln{4} + 1) - 2e^4 - \dfrac{t^4\ln(2t)}{2} + \dfrac{t^4}{8}) \)
\( = \lim\limits_{t \to 0^+} (8e^4\ln{4} + 6e^4 - \dfrac{t^4\ln(2t)}{2} + \dfrac{t^4}{8}) \)
\( t \to 0^+ \) iken \( \dfrac{t^4}{8} \) ifadesi sıfıra yaklaşır.
\( \lim\limits_{t \to 0^+} \dfrac{t^4\ln(2t)}{2} \) limitini bulmak için önce ifadeyi \( \frac{\infty}{\infty} \) belirsizliği içerecek şekilde düzenleyelim.
\( \lim\limits_{t \to 0^+} \dfrac{t^4\ln(2t)}{2} = \lim\limits_{t \to 0^+} \dfrac{\ln(2t)}{2 \cdot \frac{1}{t^4}} = \dfrac{\infty}{\infty} \)
Belirsizliği gidermek için L'Hospital kuralını kullanalım ve payın/paydanın türevini alalım.
\( = \lim\limits_{t \to 0^+} \dfrac{(\ln(2t))'}{(2 \cdot \frac{1}{t^4})'} \)
\( = \lim\limits_{t \to 0^+} (-\dfrac{t^4}{8}) \)
\( t \to +0 \) iken \( -\dfrac{t^4}{8} \) ifadesi sıfıra yaklaşır.
Buna göre yukarıdaki limit ifadesinin sonucu aşağıdaki gibi olur.
\( = 8e^4\ln{4} + 6e^4 - 0 + 0 \)
\( = 2e^4(4\ln{4} + 3) \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( 2e^4(4\ln{4} + 3) \) olarak bulunur.
\( \displaystyle\int_0^{\infty} \dfrac{1}{(x^2 + 1)(\arccot(x) + 1)}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegral aralığının üst sınırı pozitif sonsuz olduğu için I. tipte genelleştirilmiş integral formülünü kullanalım.
\( \displaystyle\int_0^{\infty} \dfrac{1}{(x^2 + 1)(\arccot(x) + 1)}\ dx = \lim\limits_{t \to \infty} \displaystyle\int_0^t \dfrac{1}{(x^2 + 1)(\arccot(x) + 1)}\ dx \)
İfadenin integralini alalım.
\( u = \arccot(x) + 1 \) ve \( du = -\dfrac{1}{x^2 + 1}\ dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to \infty} (-\ln{\abs{\arccot{x} + 1}})|_0^t \)
\( = \lim\limits_{t \to \infty} (-\ln{\abs{\arccot{t} + 1}} - (-\ln{\abs{\arccot{0} + 1}})) \)
\( t \to \infty \) iken \( \arccot{t} \) ifadesi \( 0 \) değerine yaklaşır.
\( \arccot{0} = \dfrac{\pi}{2} \)
\( = -\ln{1} + \ln(\dfrac{\pi}{2} + 1) \)
\( = -0 + \ln{(\frac{\pi}{2} + 1)} \)
\( = \ln(\dfrac{\pi}{2} + 1) \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( \ln(\dfrac{\pi}{2} + 1) \) olarak bulunur.
\( \displaystyle\int_{-10}^{15} \dfrac{1}{\sqrt[4]{(x + 1)^2}}\ dx \) integralinin yakınsak mı ıraksak mı olduğunu, yakınsak ise integral değerini bulunuz.
Çözümü Gösterİntegrali düzenleyelim.
\( \displaystyle\int_{-10}^{15} \dfrac{1}{\sqrt[4]{(x + 1)^2}}\ dx = \displaystyle\int_{-10}^{15} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx \)
İntegral aralığında ara bir nokta olan \( x = -1 \) değeri paydayı sıfır yaptığı için bu noktada bir dikey asimptot oluşur, bu yüzden ara bir noktasında sonsuza giden II. tipte genelleştirilmiş integral formülünü kullanalım.
Formüldeki \( c \) değeri sonsuz süreksizliğin oluştuğu \( x = -1 \) değeri olur.
\( \displaystyle\int_{-10}^{15} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx = \displaystyle\int_{-10}^{-1} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx + \displaystyle\int_{-1}^{15} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx \)
\( [-10, -1) \) aralığı için (birinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_{-10}^{-1} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx = \lim\limits_{t \to -1^-} \displaystyle\int_{-10}^t \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx \)
İfadeyi düzenleyelim.
\( [-10, -1) \) aralığı için:
\( \lim\limits_{t \to -1^-} \displaystyle\int_{-10}^t \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx = \lim\limits_{t \to -1^-} \displaystyle\int_{-10}^t \dfrac{1}{\sqrt{-x - 1}}\ dx \)
İfadenin integralini alalım.
\( u = -x - 1 \) ve \( du = -dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to -1^-} (-2\sqrt{-x - 1})|_{-10}^t \)
\( = \lim\limits_{t \to -1^-} (-2\sqrt{-t - 1} - (-2\sqrt{-(-10) - 1})) \)
\( t \to -1^- \) iken \( 2\sqrt{-t - 1} \) ifadesi sıfıra yaklaşır.
\( = 0 + 2\sqrt{9} = 6 \)
\( [-1, 15) \) aralığı için (ikinci terim) genelleştirilmiş integral formülünü yazalım.
\( \displaystyle\int_{-1}^{15} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx = \lim\limits_{t \to -1^+} \displaystyle\int_t^{15} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx \)
İfadeyi düzenleyelim.
\( (-1, 15] \) aralığı için:
\( \lim\limits_{t \to -1^+} \displaystyle\int_{-1}^{15} \dfrac{1}{\sqrt{\abs{x + 1}}}\ dx = \lim\limits_{t \to -1^+} \displaystyle\int_{-1}^{15} \dfrac{1}{\sqrt{x + 1}}\ dx \)
İfadenin integralini alalım.
\( u = x + 1 \) ve \( du = dx \) şeklinde değişken değiştirme uygulayalım.
\( = \lim\limits_{t \to -1^+} (2\sqrt{x + 1})|_t^{15} \)
\( = \lim\limits_{t \to -1^+} (2\sqrt{15 + 1} - 2\sqrt{t + 1}) \)
\( t \to -1^+ \) iken \( 2\sqrt{t + 1} \) ifadesi sıfıra yaklaşır.
\( = 2\sqrt{16} - 0 = 8 \)
\( [-10, 15] \) aralığı için genelleştirilmiş integrali bulmak için \( [-10, -1) \) ve \( (-1, 15] \) aralıkları için bulduğumuz değerlerin toplamını alalım.
\( \displaystyle\int_{-10}^{15} \dfrac{1}{\sqrt[4]{(x + 1)^2}}\ dx = 6 + 8 = 14 \)
Buna göre verilen integral ifadesi yakınsaktır ve değeri \( 14 \) olarak bulunur.