Yay Uzunluğu Bulma
Bir eğri üzerindeki iki nokta arasında eğri boyunca olan mesafeye yay uzunluğu denir. Yay uzunluğunu eğri üzerinde yürüyen bir karıncanın bu aralıkta katedeceği toplam mesafe olarak düşünebiliriz. Belirli integralin uygulamalarından biri de denklemi verilen bir eğrinin bir aralıktaki yay uzunluğunun bulunmasıdır.
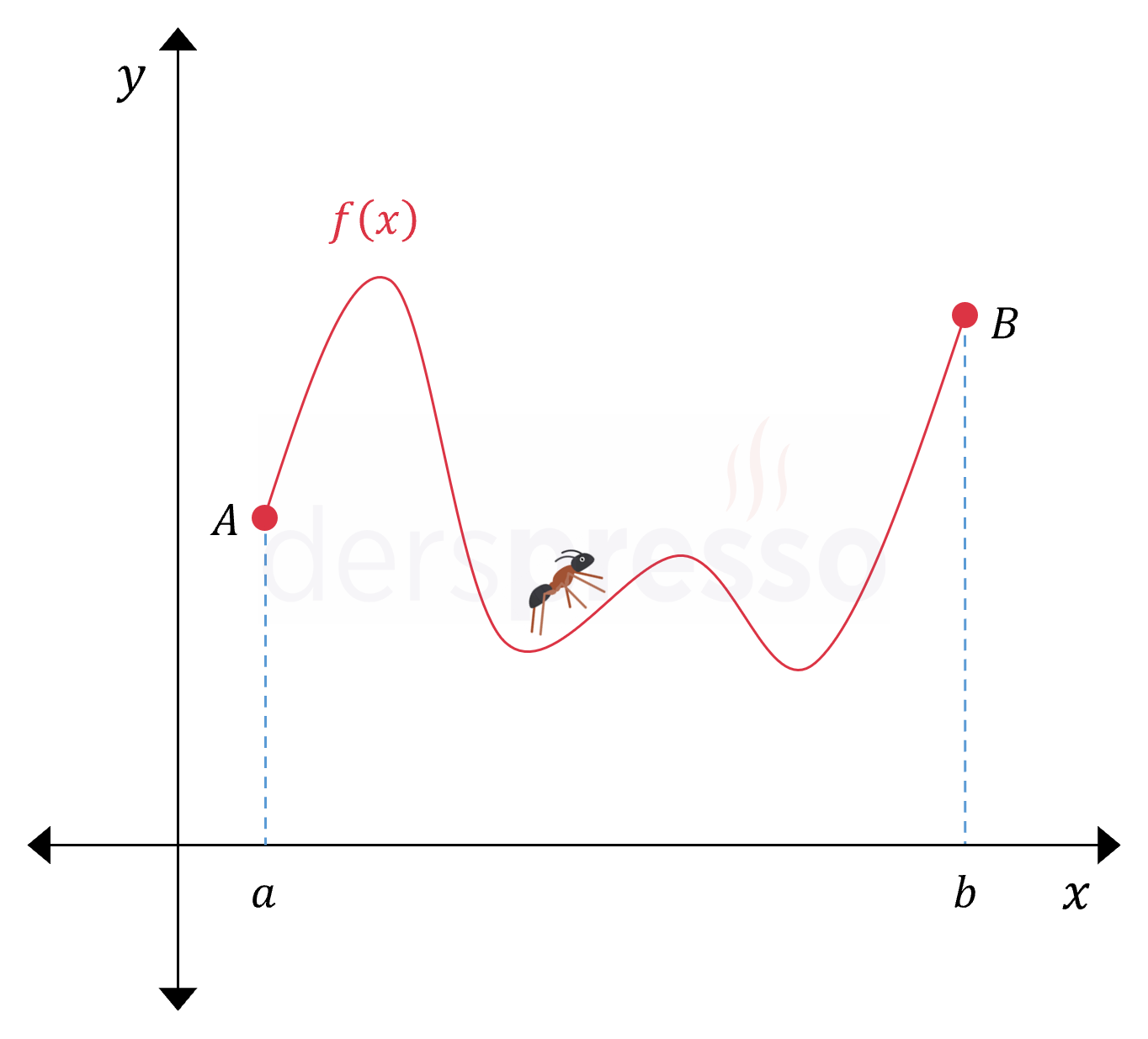
Yukarıdaki gibi bir eğrinin \( [a, b] \) aralığındaki yay uzunluğunun gerçek değerini bulmak için elimizde geometrik bir yöntem olmasa da, yaklaşık değerini bulmak için alan hesaplamasında kullandığımıza benzer bir yöntem kullanabiliriz.
- Aralık \( n \) alt aralığa bölünür ve her aralıktaki yaklaşık yay uzunluğunu bulmak için bir formül geliştirilir.
- Bu uzunlukların toplamından oluşan ve tüm \( [a, b] \) aralığı için yaklaşık yay uzunluğunu verecek olan Riemann toplam formülü yazılır.
- \( n \) sonsuza giderken, yani aralık genişlikleri sıfıra yaklaşırken bu Riemann toplamının limiti yay uzunluğunun gerçek değerini verir.
Bu yöntemi yay uzunluğu hesaplama problemine uygulayalım ve önce \( [a, b] \) aralığını aşağıdaki koşul sağlanacak şekilde eşit ya da farklı genişliklerde \( n \) alt aralığa bölelim.
\( a = x_0 \lt x_1 \lt x_2 \lt \ldots \lt b = x_n \)
Her bir aralıktaki yay uzunluğunun yaklaşık değerini bulmak için aralıkların uç noktalarını birleştiren doğru parçaları çizelim. Aşağıda \( n = 6 \) için bu aralıklar ve doğru parçaları verilmiştir.

\( i \). aralıktaki doğru parçasının uzunluğuna \( L_i \) dersek, bu uzunluğu iki nokta arasındaki uzaklık formülü ile aşağıdaki şekilde hesaplayabiliriz.
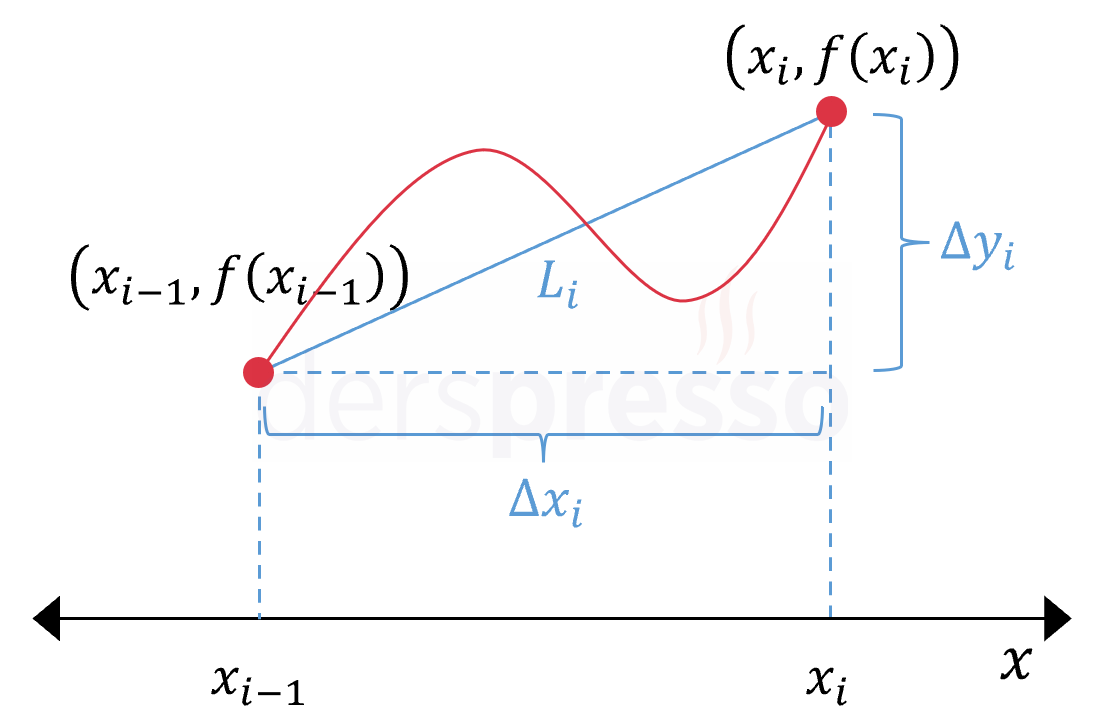
\( i \). aralığın genişliği ve yüksekliği sırasıyla \( \Delta x_i \) ve \( \Delta y_i \) olmak üzere,
\( \Delta x_i = x_i - x_{i-1} \)
\( \Delta y_i = f(x_i) - f(x_{i-1}) \)
\( L_i = \sqrt{(\Delta x_i)^2 + (\Delta y_i)^2} \)
Yaklaşık yay uzunluğunu verecek genel formülü bulmak için bu formülü düzenleyelim.
Kök içindeki ifadeyi \( (\Delta x_i)^2 \) parantezine alalım ve \( \Delta x_i \) ifadesini kökün dışına çıkaralım.
\( L_i = \sqrt{(1 + \frac{(\Delta y_i)^2}{(\Delta x_i)^2}) \cdot (\Delta x)^2} \)
\( = \sqrt{(1 + (\frac{\Delta y_i}{\Delta x_i})^2} \cdot \Delta x_i \)
\( \frac{\Delta y_i}{\Delta x_i} \) değeri \( [x_{i-1}, x_i] \) aralığındaki ortalama değişim oranıdır. Ortalama değer teoremine göre, bu aralıkta türev değeri bu ortalama değişim oranına eşit olan en az bir \( x_i^* \in [x_{i-1}, x_i] \) noktası vardır. Dolayısıyla \( i \). aralıktaki doğru parçasının uzunluğunu aşağıdaki şekilde yazabiliriz.
\( L_i = \sqrt{(1 + [f'(x_i^*)]^2} \cdot \Delta x_i \)
Tüm aralıklar için bu uzunlukların toplamını aldığımızda \( [a, b] \) aralığındaki yay uzunluğu için Riemann toplamını (\( S_n \)) buluruz. Gerçek yay uzunluğuna \( L \) dersek bu Riemann toplamı aynı zamanda \( L \) için bulduğumuz yaklaşık değer olur.
\( S_n \approx L \) olmak üzere,
\( S_n = \displaystyle\sum_{i = 1}^{n}{L_i} \)
\( = \displaystyle\sum_{i = 1}^{n}{\sqrt{(1 + [f'(x_i^*)]^2} \cdot \Delta x_i} \)
Riemann toplamının alan uygulamasından bildiğimiz üzere, \( n \) değeri büyüdükçe bulduğumuz yaklaşık değerler gerçek yay uzunluğuna yaklaşır. Riemann toplamının \( n \) sonsuza giderkenki limiti ise gerçek yay uzunluğunu verir.
\( L = \lim\limits_{n \to \infty} S_n \)
\( L = \lim\limits_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{\sqrt{(1 + [f'(x_i^*)]^2} \cdot \Delta x_i} \)
Belirli integralin limit tanımına göre, bu limit ifadesi \( \sqrt{(1 + [f'(x)]^2} \) fonksiyonunun bu aralıktaki belirli integraline eşittir.
\( f \) fonksiyonu türevlenebilir ve \( f' \) fonksiyonu sürekli olmak üzere,
\( L = \displaystyle\int_a^b {\sqrt{1 + [f'(x)]^2}\ dx} \)
Fonksiyonun \( y \) değişkeni cinsinden ifade edildiği durumlarda formül aşağıdaki şekilde olur.
\( x = f(y) \) olmak üzere,
\( L = \displaystyle\int_a^b {\sqrt{1 + [f'(y)]^2}\ dy} \)
Yay uzunluğu hesaplaması için sade gözüken bir formül elde etmiş olsak da, çoğu temel fonksiyon için bu formülün integrali zor ifadeler üreteceği akılda tutulmalıdır.
Bu formülün bir örnek üzerinde uygulamasını gösterelim.
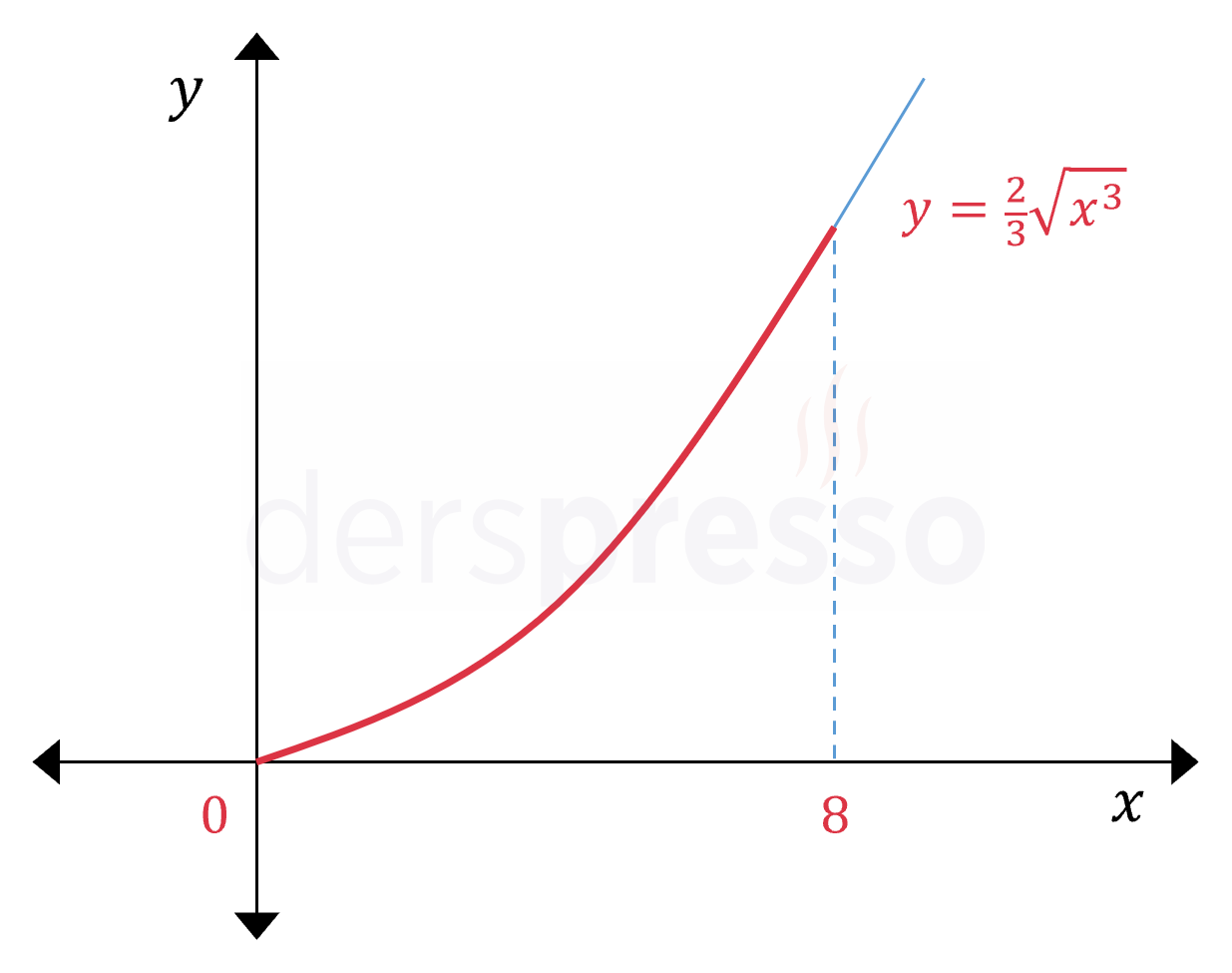
\( f(x) = \dfrac{2}{3}\sqrt{x^3} \)
Yukarıda denklemi verilen fonksiyonun \( [0, 8] \) aralığındaki yay uzunluğunu bulalım.
Fonksiyonun türevini alalım.
\( f'(x) = \sqrt{x} \)
\( [0, 8] \) aralığı için yay uzunluk formülünü yazalım.
\( \displaystyle\int_0^8 {\sqrt{1 + [f'(x)]^2}\ dx} \)
\( = \displaystyle\int_0^8 {\sqrt{1 + (\sqrt{x})^2}\ dx} \)
\( = \displaystyle\int_0^8 {\sqrt{1 + x}\ dx} \)
\( = \left[\dfrac{2}{3}\sqrt{(1 + x)^3}\right]_0^8 \)
\( = \dfrac{2}{3}\sqrt{(1 + 8)^3} - \dfrac{2}{3}\sqrt{(1 + 0)^3} \)
\( = 18 - \dfrac{2}{3} = \dfrac{52}{3} \) bulunur.
\( f(x) = \dfrac{x^2}{8} − \ln{x} \)
Yukarıda denklemi verilen fonksiyonun \( [1, e] \) aralığındaki yay uzunluğu nedir?
Çözümü GösterFonksiyonun türevini alalım.
\( f'(x) = \dfrac{x}{4} − \dfrac{1}{x} \)
\( [1, e] \) aralığı için yay uzunluk formülünü yazalım.
\( \displaystyle\int_1^e {\sqrt{1 + [f'(x)]^2}\ dx} \)
\( = \displaystyle\int_1^e {\sqrt{1 + \left(\dfrac{x}{4} − \dfrac{1}{x}\right)^2}\ dx} \)
\( = \displaystyle\int_1^e {\sqrt{1 + \dfrac{x^2}{16} − \dfrac{1}{2} + \dfrac{1}{x^2}}\ dx} \)
\( = \displaystyle\int_1^e {\sqrt{\dfrac{x^2}{16} + \dfrac{1}{2} + \dfrac{1}{x^2}}\ dx} \)
\( = \displaystyle\int_1^e {\sqrt{\left(\dfrac{x}{4} + \dfrac{1}{x}\right)^2}\ dx} \)
\( = \displaystyle\int_1^e {\abs{\dfrac{x}{4} + \dfrac{1}{x}}\ dx} \)
Mutlak değer içindeki ifade verilen aralıkta pozitiftir.
\( = \displaystyle\int_1^e {(\dfrac{x}{4} + \dfrac{1}{x})\ dx} \)
\( = \left[\dfrac{x^2}{8} + \ln{x}\right]_1^e \)
\( = \left(\dfrac{e^2}{8} + \ln{e}\right) - \left(\dfrac{1^2}{8} + \ln{1}\right) \)
\( = \dfrac{e^2}{8} + 1 - \dfrac{1}{8} - 0 \)
\( = \dfrac{e^2 + 7}{8} \) bulunur.