Yüzey Alanı Bulma
Bir eğrinin belirli bir aralıktaki bölümünü \( x \) ekseni etrafında 360° döndürdüğümüzü varsayalım. Belirli integralin uygulamalarından biri de bu şekilde oluşan 3 boyutlu şeklin yanal yüzey alanının bulunmasıdır.
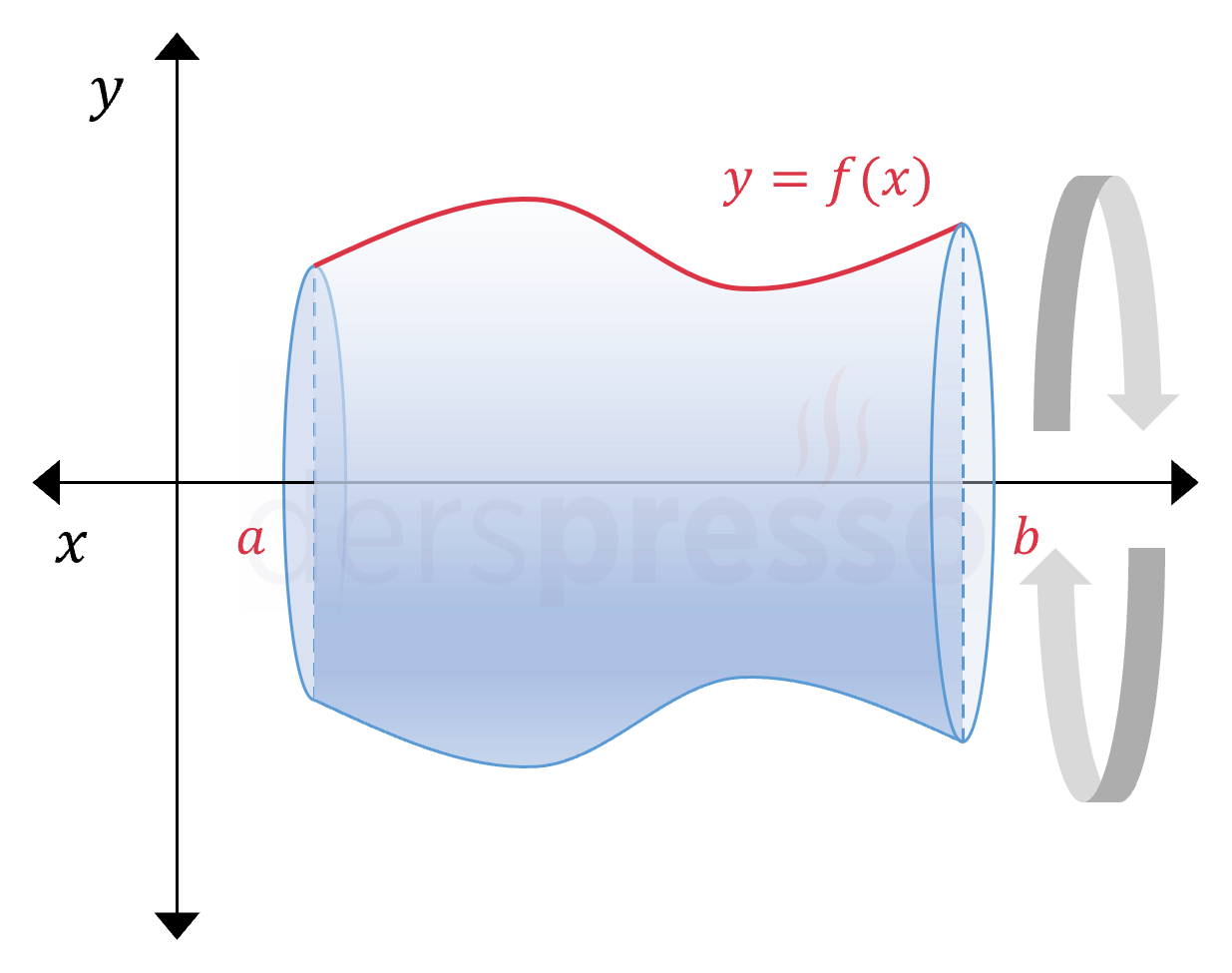
Yukarıdaki gibi bir eğrinin \( [a, b] \) aralığındaki bölümü için oluşan bu cismin yanal yüzey alanının gerçek değerini bulmak için elimizde geometrik bir yöntem olmasa da, yaklaşık değerini bulmak için alan hesaplamasında kullandığımıza benzer bir yöntem kullanabiliriz.
- Aralık \( n \) alt aralığa bölünür ve her aralıktaki yüzey alanını bulmak için bir formül geliştirilir.
- Bu alanların toplamından oluşan ve tüm \( [a, b] \) aralığı için yaklaşık yüzey alanını verecek olan Riemann toplam formülü yazılır.
- \( n \) sonsuza giderken, yani aralık genişlikleri sıfıra yaklaşırken bu Riemann toplamının limiti yüzey alanının gerçek değerini verir.
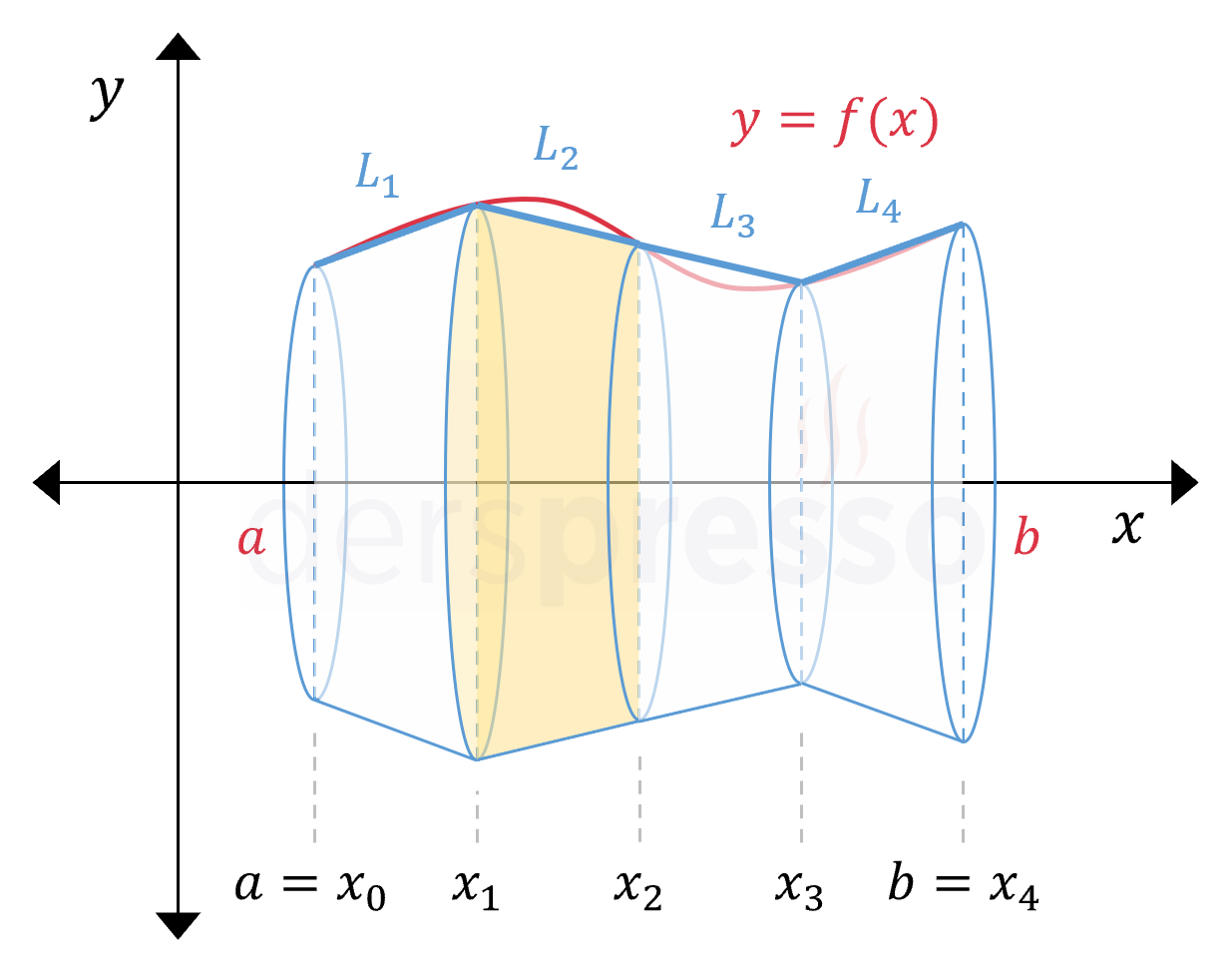
Bu yöntemi yüzey alanı hesaplama problemine uygulayalım ve önce \( [a, b] \) aralığını aşağıdaki koşul sağlanacak şekilde eşit ya da farklı genişliklerde \( n \) alt aralığa bölelim.
\( a = x_0 \lt x_1 \lt x_2 \lt \ldots \lt b = x_n \)
Her bir aralıktaki yüzey alanının yaklaşık değerini bulmak için aralıkların uç noktalarını birleştiren doğru parçaları çizelim. Aşağıda \( n = 4 \) için bu aralıklar ve doğru parçaları verilmiştir.
Her bir aralıkta oluşan üç boyutlu cisimler birer kesik konidir. Kesik koninin yanal alan formülü aşağıdaki gibidir.
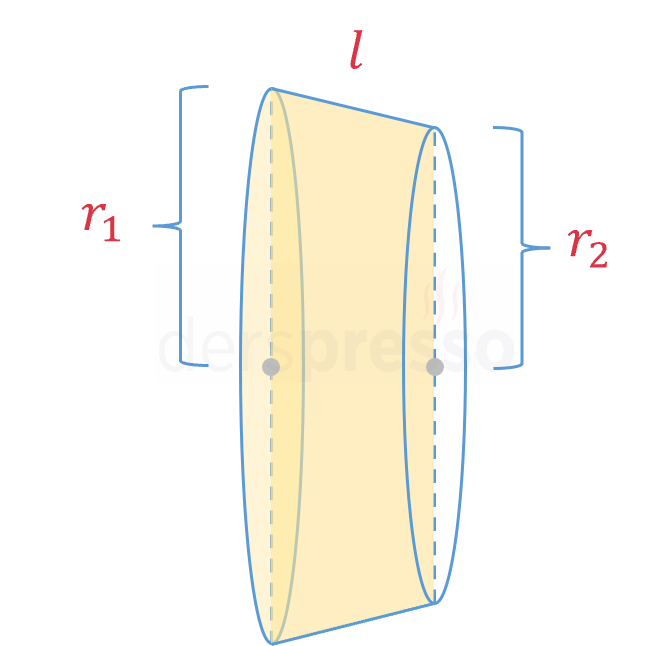
Kesik koninin yanal yüzey alan formülü:
\( A = \pi (r_1 + r_2)l \)
\( r_1, r_2 \): Alt ve üst tabanların yarıçapları
\( l \): Yan kenar uzunluğu
\( i \). aralıkta oluşan cismin yanal yüzey alanına \( A_i \) dersek, kesik koni yanal alan formülünü bu alana aşağıdaki şekilde uyarlayabiliriz.
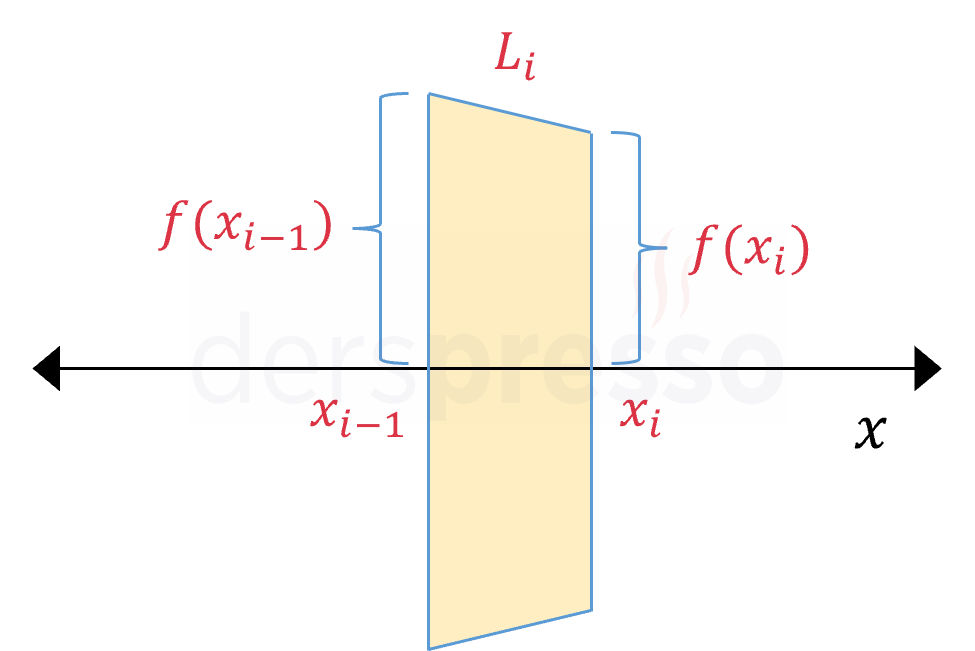
\( i \). aralıktaki yüzey alanı formülü:
\( A_i = \pi (f(x_{i-1}) + f(x_i))L_i \)
\( f(x_{i-1}), f(x_i) \): Alt ve üst tabanların yarıçapları
\( L_i \): Yay uzunluğu bölümünde hesapladığımız yay uzunluğu
\( L_i = \sqrt{1 + [f'(x_i^*)]^2} \cdot \Delta x_i \)
Tüm aralıklar için bu alanların toplamını aldığımızda \( [a, b] \) aralığındaki toplam yüzey alanı için Riemann toplamını (\( S_n \)) buluruz. Gerçek yüzey alanına \( A \) dersek bu Riemann toplamı aynı zamanda \( A \) için bulduğumuz yaklaşık değer olur.
\( S_n \approx A \) olmak üzere,
\( S_n = \displaystyle\sum_{i = 1}^{n}{A_i} \)
\( = \displaystyle\sum_{i = 1}^{n}{\pi (f(x_{i-1}) + f(x_i))\sqrt{1 + [f'(x_i^*)]^2} \cdot \Delta x_i} \)
Riemann toplamının alan uygulamasından bildiğimiz üzere, \( n \) değeri büyüdükçe bulduğumuz yaklaşık değerler gerçek yüzey alanına yaklaşır. Riemann toplamının \( n \) sonsuza giderkenki limiti ise gerçek yüzey alanını verir.
\( A = \lim\limits_{n \to \infty} S_n \)
\( A = \lim\limits_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{\pi (f(x_{i-1}) + f(x_i))\sqrt{1 + [f'(x_i^*)]^2} \cdot \Delta x_i} \)
\( n \) sonsuza giderken \( f(x_{i-1}) \) ve \( f(x_i) \) değerleri bu aralıktaki \( f(x_i^*) \) değerine yaklaşır.
\( = \lim\limits_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{2\pi f(x_i^*)\sqrt{1 + [f'(x_i^*)]^2} \cdot \Delta x_i} \)
Belirli integralin limit tanımına göre, bu limit ifadesi toplamı alınan ifadenin bu aralıktaki belirli integraline eşittir.
\( f' \) fonksiyonu sürekli olmak üzere,
\( A = 2\pi \displaystyle\int_a^b {f(x)\sqrt{1 + [f'(x)]^2}\ dx} \)
Bu formülün bir örnek üzerinde uygulamasını gösterelim.

\( f(x) = \sqrt{16 - x^2} \)
Yukarıda denklemi ve grafiği verilen fonksiyonun \( [-4, 4] \) aralığındaki kısmının \( x \) ekseni etrafında döndürülmesi ile oluşan şeklin yüzey alanını bulalım.
Grafiği belirtilen aralıkta \( x \) ekseni etrafında döndürdüğümüzde aşağıdaki küreyi elde ederiz.

Fonksiyonun türevini alalım.
\( f'(x) = \dfrac{-x}{\sqrt{16 - x^2}} \)
\( [-4, 4] \) aralığı için yüzey alanı formülünü yazalım.
\( = 2\pi \displaystyle\int_{-4}^4 {\sqrt{16 - x^2}\sqrt{1 + [\frac{-x}{\sqrt{16 - x^2}}]^2}\ dx} \)
\( = 2\pi \displaystyle\int_{-4}^4 {\sqrt{16 - x^2}\sqrt{1 + \frac{x^2}{16 - x^2}}\ dx} \)
\( = 2\pi \displaystyle\int_{-4}^4 {\sqrt{16 - x^2}\sqrt{\frac{16}{16 - x^2}}\ dx} \)
\( = 2\pi \displaystyle\int_{-4}^4 {\sqrt{16 - x^2}\frac{\sqrt{16}}{\sqrt{16 - x^2}}\ dx} \)
\( = 2\pi \displaystyle\int_{-4}^4 {4 \ dx} \)
\( = 2\pi (4x)|_{-4}^4 \)
\( = 2\pi (4 \cdot 4 - 4 \cdot (-4)) = 64\pi \) bulunur.
\( f(x) = x^3 \)
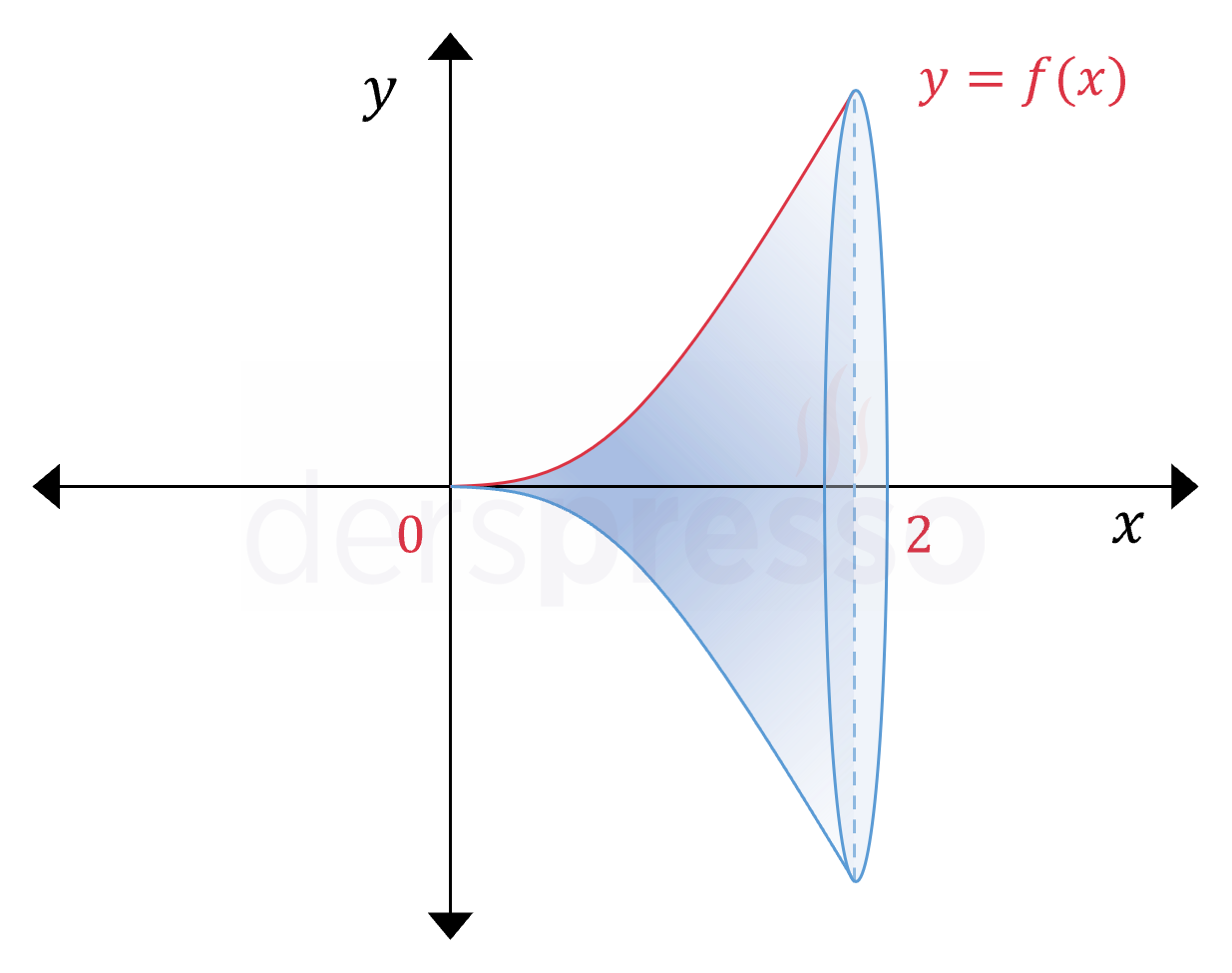
Yukarıda denklemi ve grafiği verilen fonksiyonun \( [0, 2] \) aralığındaki kısmının \( x \) ekseni etrafında döndürülmesi ile oluşan şeklin yüzey alanını bulunuz.
Çözümü GösterGrafiği belirtilen aralıkta \( x \) ekseni etrafında döndürdüğümüzde aşağıdaki şekli elde ederiz.
Fonksiyonun türevini alalım.
\( f'(x) = 3x^2 \)
\( [0, 2] \) aralığı için yüzey alanı formülünü yazalım.
\( = \displaystyle\int_0^2 {2\pi x^3\sqrt{1 + [3x^2]^2}\ dx} \)
\( = \displaystyle\int_0^2 {2\pi x^3\sqrt{1 + 9x^4}\ dx} \)
\( = (\dfrac{2\pi \cdot 2}{3 \cdot 9 \cdot 4}\sqrt{(1 + 9x^4)^3})|_0^2 \)
\( = (\dfrac{\pi}{27}\sqrt{(1 + 9x^4)^3})|_0^2 \)
\( = \dfrac{\pi}{27}\sqrt{(1 + 9(2)^4)^3} - \dfrac{\pi}{27}\sqrt{(1 + 9(0)^4)^3} \)
\( = \dfrac{\pi}{27}\sqrt{145^3} - \dfrac{\pi}{27}\sqrt{1^3} \)
\( = \dfrac{\pi}{27}(145\sqrt{145} - 1) \) bulunur.