Eğri ile y-Ekseni Arasında Kalan Alan
\( x = f(y) \) şeklinde \( x \) değişkeninin \( y \) cinsinden yazıldığı bir fonksiyonun \( y \) değişkeninin bir aralığında ve \( y \) değişkenine göre belirli integrali, fonksiyon grafiğinin \( y \) ekseni ile arasında kalan net alanı verir.

Bir fonksiyonun değerinin pozitif olduğu (\( f(y) \gt 0 \)), yani grafiğinin \( y \) ekseninin sağında kaldığı bir aralıktaki belirli integrali pozitif işaretlidir. Bu aralıkta fonksiyon grafiği ile \( y \) ekseni arasında kalan alan da bu pozitif integral değerine eşittir.
\( A_1 = \displaystyle\int_a^b {f(y)\ dy} \)
\( (+) = (+) \)

Bir fonksiyonun değerinin negatif olduğu (\( f(y) \lt 0 \)), yani grafiğinin \( y \) ekseninin solunda kaldığı bir aralıktaki belirli integrali negatif işaretlidir. Alan pozitif bir büyüklük olduğu için, bu aralıkta fonksiyon grafiği ile \( y \) ekseni arasında kalan alan bu negatif integral değerinin ters işaretlisine eşittir.
\( A_2 = -\displaystyle\int_a^b {f(y)\ dy} \)
\( (+) = -(-) \)
Buna göre, bir fonksiyonun aşağıdaki gibi hem pozitif hem negatif değerler aldığı bir aralıkta grafiğinin \( y \) ekseni ile arasında kalan toplam alanı, fonksiyonun \( y \) ekseninin sağında kaldığı aralıklardaki belirli integralinden solunda kaldığı aralıklardaki belirli integralini çıkararak bulabiliriz.
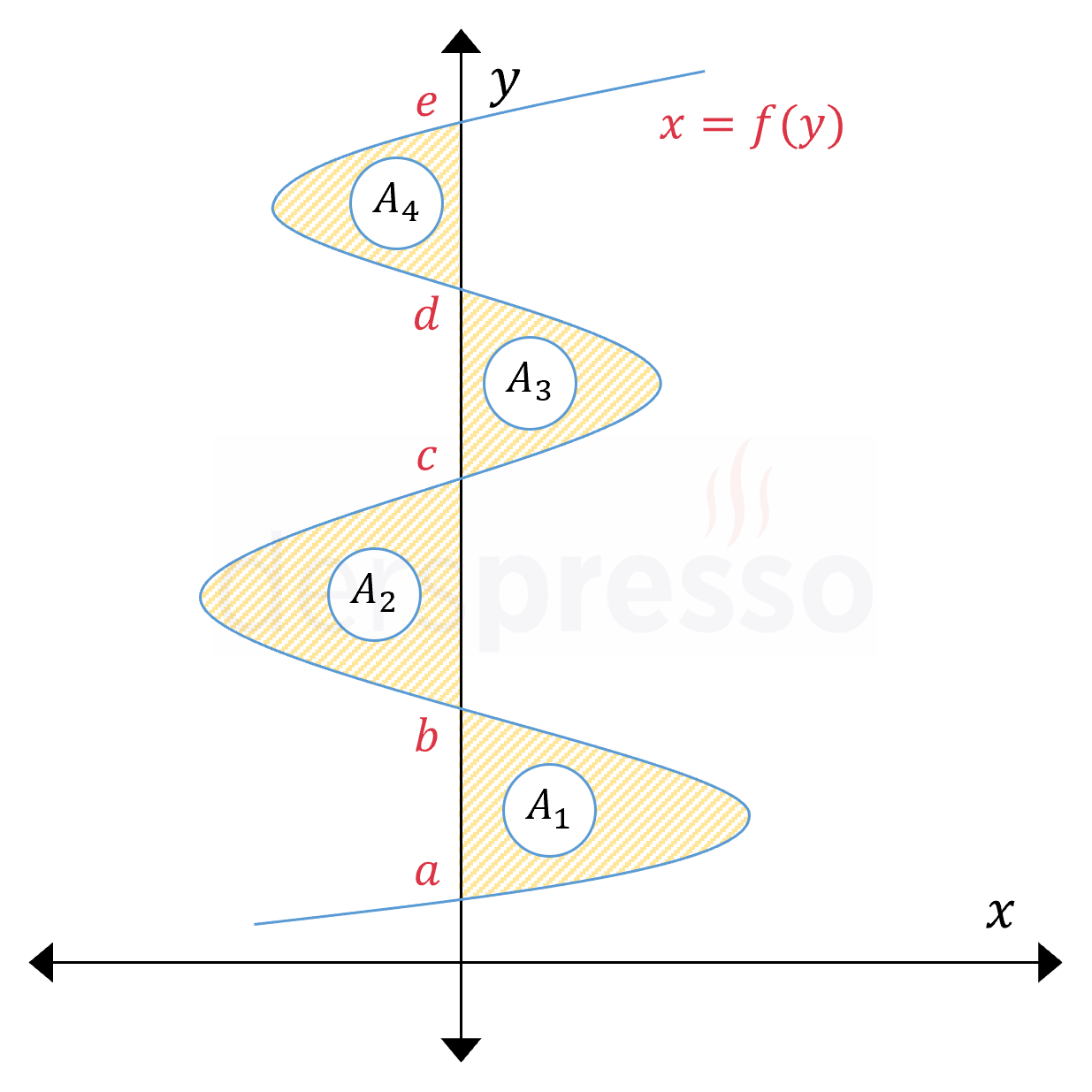
\( A = A_1 + A_2 + A_3 + A_4 \) olmak üzere,
\( A = \displaystyle\int_a^b {f(y)\ dy} \textcolor{red}{- \displaystyle\int_b^c {f(y)\ dy}} + \displaystyle\int_c^d {f(y)\ dy} \textcolor{red}{- \displaystyle\int_d^e {f(y)\ dy}} \)
Benzer şekilde, bir fonksiyonun bir aralıktaki belirli integrali, bu aralıkta \( y \) ekseninin sağında kalan alanlarla solunda kalan alanların farkına eşittir.
\( \displaystyle\int_a^e {f(y)\ dy} = (A_1 + A_3) - (A_2 + A_4) \)
Bir fonksiyonun belirli integrali ile \( y \) ekseni ile arasında kalan alan ilişkisini birkaç örnek üzerinden inceleyelim.
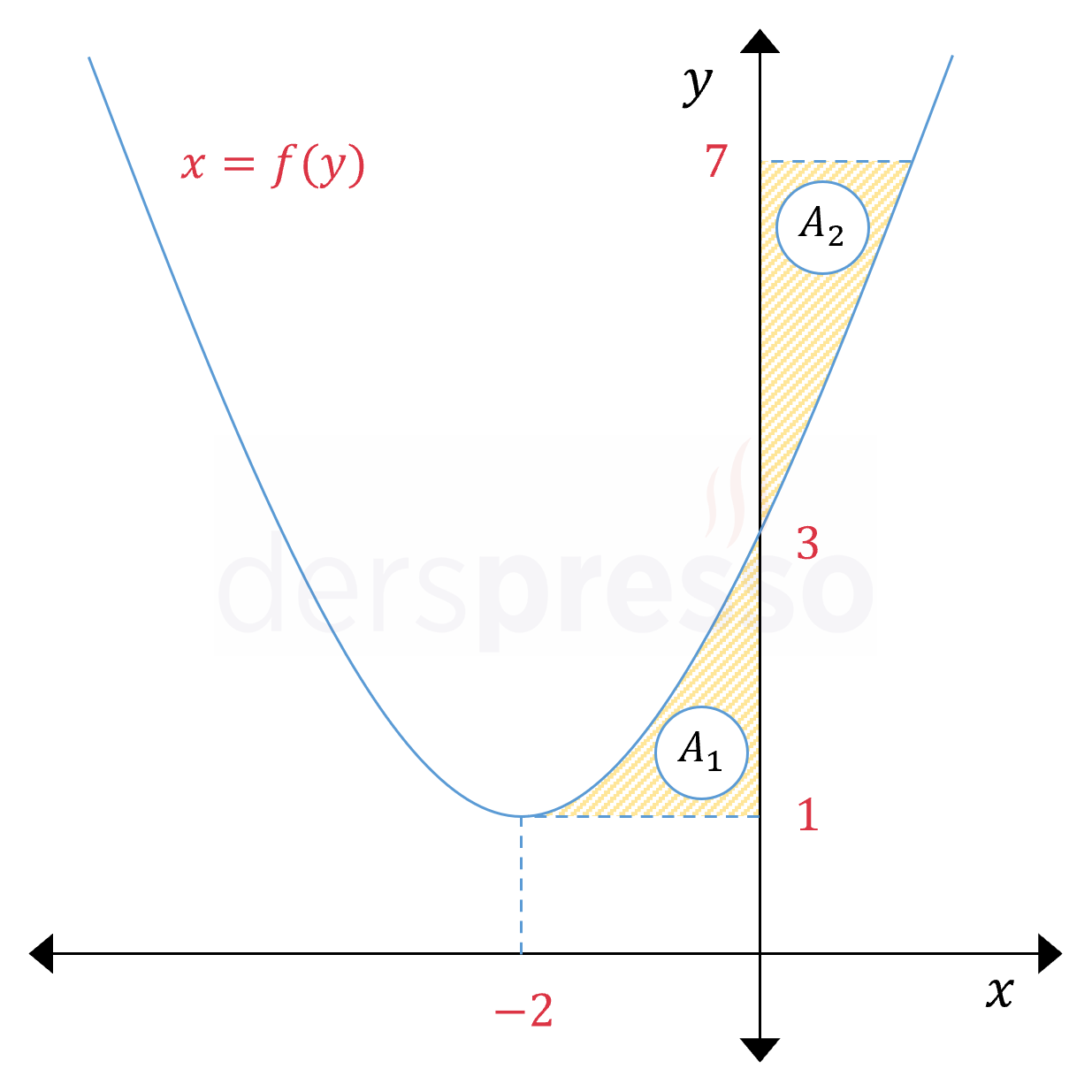
\( f(x) = \frac{1}{2}(x + 2)^2 + 1 \)
Yukarıda denklemi ve grafiği verilen fonksiyonun grafiğindeki taralı bölgenin alanını bulalım.
Taralı alan \( [1, 7] \) aralığında fonksiyon grafiği ile \( y \) ekseni arasında kalan alana karşılık gelmektedir.
Grafiğin \( y \) ekseni ile arasında kalan alanı bulmak için fonksiyonu \( y \) cinsinden yazalım.
\( y = \frac{1}{2}(x + 2)^2 + 1 \)
\( 2y - 2 = (x + 2)^2 \)
\( x = \pm\sqrt{2y - 2} - 2 \)
Bu denklemin \( x = +\sqrt{2y - 2} - 2 \) hali parabolün tepe noktasının sağında kalan kısmı, \( x = -\sqrt{2y - 2} - 2 \) hali solunda kalan kısmı temsil etmektedir.
Parabolün tepe noktasının sağında kalan kısımla ilgilendiğimiz için birinci denklemi baz alabiliriz.
\( x = \sqrt{2y - 2} - 2 \)
Taralı alan fonksiyonun \( y \) ekseninin sağında ve solunda kaldığı bölgelerden oluştuğu için aralığı fonksiyonun \( y \) eksenini kestiği noktalara göre alt aralıklara bölmemiz ve her aralık için ayrı integral hesaplamamız gerekir.
Fonksiyon \( [1, 3] \) aralığında \( y \) ekseninin solunda kaldığı için bu aralıktaki integral değeri negatiftir ve \( A_1 \) bu integral değerinin ters işaretlisine eşittir.
\( A_1 = -\displaystyle\int_1^3 {(\sqrt{2y - 2} - 2)\ dy} \)
\( = -(\dfrac{\sqrt{(2y - 2)^3}}{3} - 2y)|_1^3 \)
\( = -[(\dfrac{\sqrt{(2(3) - 2)^3}}{3} - 2(3)) - (\dfrac{\sqrt{(2(1) - 2)^3}}{3} - 2(1))] \)
\( = -[-\dfrac{10}{3} - (-2)] = \dfrac{4}{3} \)
Fonksiyon \( [3, 7] \) aralığında \( y \) ekseninin sağında kaldığı için bu aralıktaki integral değeri pozitiftir ve \( A_2 \) bu integral değerine eşittir.
\( A_2 = \displaystyle\int_3^7 {(\sqrt{2y - 2} - 2)\ dy} \)
\( = (\dfrac{\sqrt{(2y - 2)^3}}{3} - 2y)|_3^7 \)
\( = (\dfrac{\sqrt{(2(7) - 2)^3}}{3} - 2(7)) - (\dfrac{\sqrt{(2(3) - 2)^3}}{3} - 2(3)) \)
\( = (8\sqrt{3} - 14) - (-\dfrac{10}{3}) \)
\( = \dfrac{24\sqrt{3} - 32}{3} \)
Taralı bölgenin alanı bu iki bölgenin alanları toplamına eşittir.
\( A = A_1 + A_2 \)
\( = \dfrac{4}{3} + (8\sqrt{3} - \dfrac{32}{3}) \)
\( = \dfrac{24\sqrt{3} - 28}{3} \)
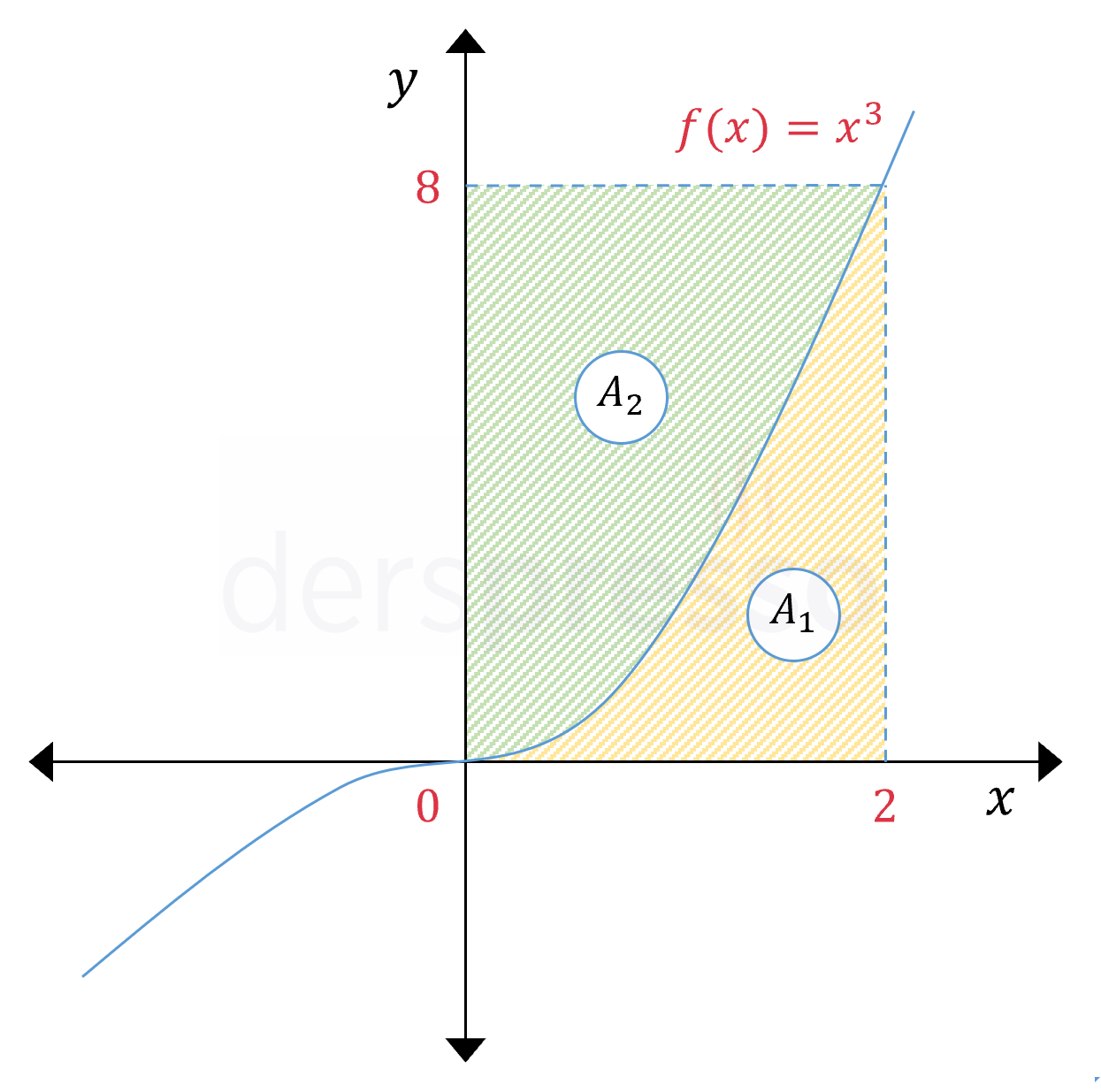
\( f(x) = x^3 \) fonksiyonunun grafiğinin \( x \) ve \( y \) eksenleri ile arasında kalan bölgelerin alanları toplamının bu iki bölgenin oluşturduğu dikdörtgenin alanına eşit olduğunu gösterelim.
Fonksiyon \( x \in [0, 2] \) aralığında \( x \) ekseninin üstünde kaldığı için, \( A_1 \) fonksiyonun bu aralıktaki integral değerine eşittir.
\( A_1 = \displaystyle\int_0^2 {x^3\ dx} \)
\( = (\dfrac{1}{4}x^4)|_0^2 \)
\( = \dfrac{1}{4}2^4 - \dfrac{1}{4}0^4 \)
\( = 4 - 0 = 4 \)
Grafiğin \( y \) ekseni ile arasında kalan alanı bulmak için fonksiyonu \( y \) cinsinden yazalım.
\( x = \sqrt[3]{y} \)
Fonksiyon \( y \in [0, 8] \) aralığında \( y \) ekseninin sağ tarafında kaldığı için, \( A_2 \) fonksiyonun bu aralıktaki integral değerine eşittir.
\( A_2 = \displaystyle\int_0^8 {\sqrt[3]{y}\ dy} \)
\( = (\dfrac{3}{4}\sqrt[3]{y^4})|_0^8 \)
\( = (\dfrac{3}{4}\sqrt[3]{8^4}) - (\dfrac{3}{4}\sqrt[3]{0^4}) \)
\( = 12 - 0 = 12 \)
Buna göre taralı iki alanın toplamı \( 4 + 12 = 16 \) olarak bulunur, bu da kenar uzunlukları 2 ve 8 birim olan dikdörtgenin alanına eşittir.
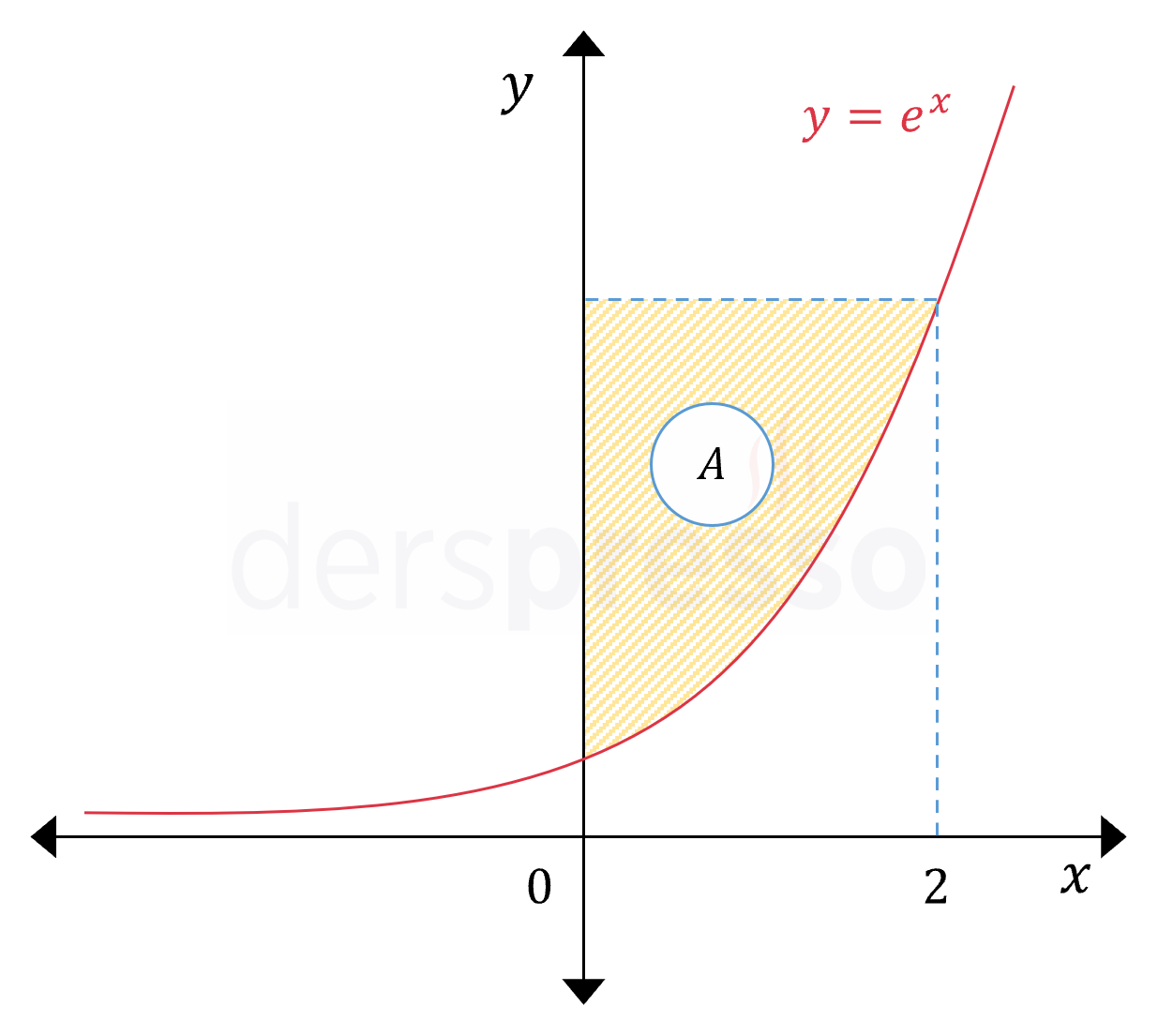
Yukarıdaki şekildeki taralı bölgenin alanı nedir?
Çözümü GösterFonksiyonun apsis değerleri verilen iki noktasının ordinat değerlerini bulalım.
\( f(0) = e^0 = 1 \)
\( f(2) = e^2 = e^2 \)
Buna göre taralı alan \( [1, e^2] \) aralığında fonksiyon grafiği ile \( y \) ekseni arasında kalan alana karşılık gelmektedir.
Grafiğin \( y \) ekseni ile arasında kalan alanı bulmak için fonksiyonu \( y \) cinsinden yazalım.
\( y = e^x \)
\( x = \ln{y} \)
\( f \) fonksiyonu bu aralıkta \( y \) ekseninin sağında kaldığı için belirli integrali pozitif işaretlidir. Bu aralıkta fonksiyon grafiği ile \( y \) ekseni arasında kalan alan da bu pozitif integral değerine eşittir.
\( A = \displaystyle\int_1^{e^2} \ln{y}\ dy \)
Bu ifadenin integralini kısmi integral yöntemi sayfasında aşağıdaki şekilde bulmuştuk.
\( = (y\ln{y} - y)|_1^{e^2} \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = (e^2\ln{e^2} - e^2) - (1\ln{1} - 1) \)
\( = e^2 + 1 \) bulunur.
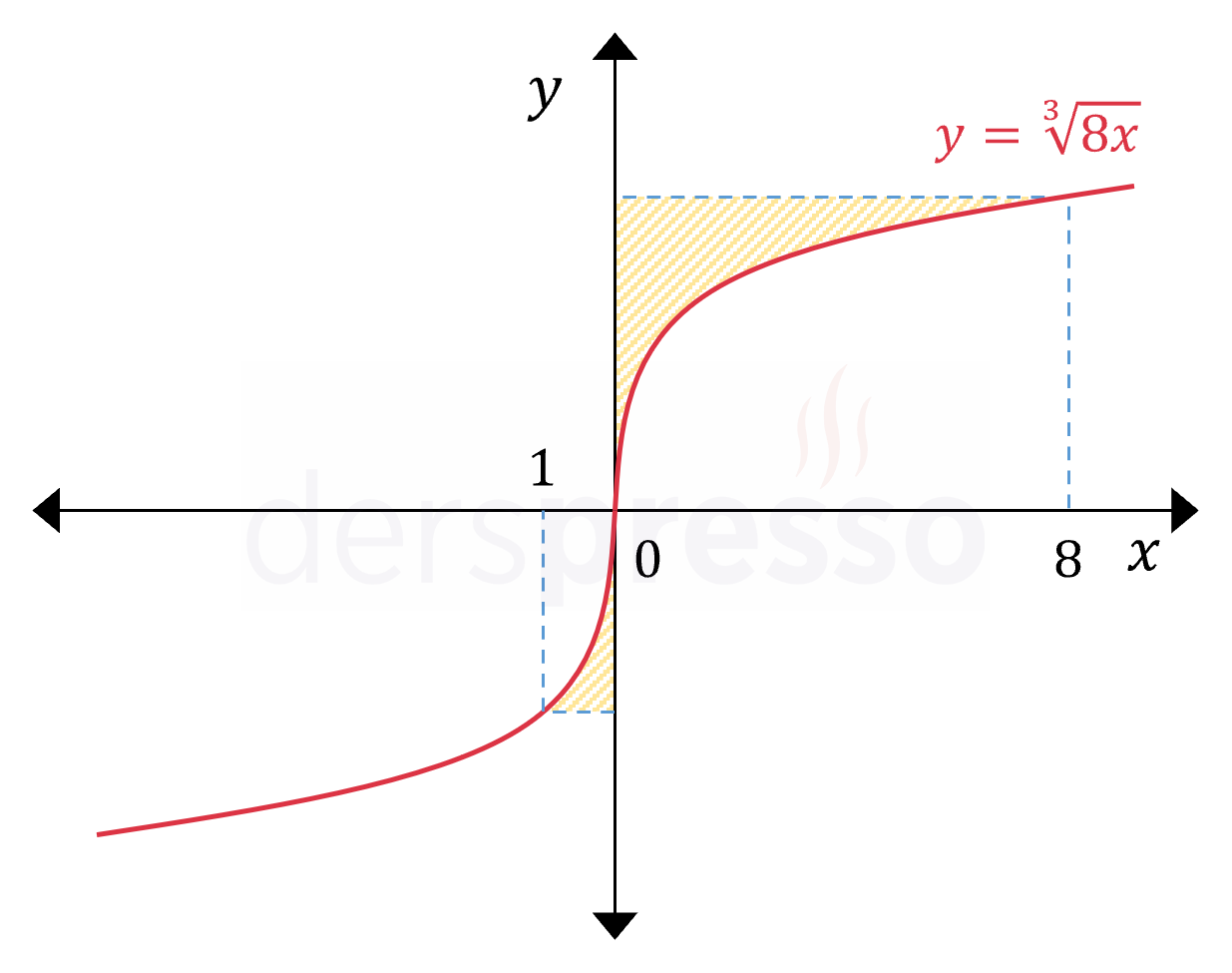
Yukarıdaki şekildeki taralı bölgenin alanı nedir?
Çözümü GösterFonksiyonun apsis değerleri verilen üç noktasının ordinat değerlerini bulalım.
\( f(-1) = \sqrt[3]{8(-1)} = -2 \)
\( f(0) = \sqrt[3]{8(0)} = 0 \)
\( f(8) = \sqrt[3]{8(8)} = 4 \)
Buna göre taralı alan \( [-2, 4] \) aralığında fonksiyon grafiği ile \( y \) ekseni arasında kalan alana karşılık gelmektedir.
Grafiğin \( y \) ekseni ile arasında kalan alanı bulmak için fonksiyonu \( y \) cinsinden yazalım.
\( y = \sqrt[3]{8x} \)
\( x = \dfrac{y^3}{8} \)
Taralı alan fonksiyonun \( y \) ekseninin sağında ve solunda kaldığı bölgelerden oluştuğu için, bu alanı fonksiyonun \( y \) ekseninin sağında kaldığı aralıklardaki belirli integralinden solunda kaldığı aralıklardaki belirli integralini çıkarak bulabiliriz.
\( A = \displaystyle\int_0^4 \dfrac{y^3}{8}\ dy - \displaystyle\int_{-2}^0 \dfrac{y^3}{8}\ dy \)
İfadenin integralini alalım.
\( = (\dfrac{y^4}{32})|_0^4 - (\dfrac{y^4}{32})|_{-2}^0 \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = (\dfrac{4^4}{32} - \dfrac{0^4}{32}) - (\dfrac{0^4}{32} - \dfrac{(-2)^4}{32}) \)
\( = (8 - 0) - (0 - \dfrac{1}{2}) \)
\( = 8\dfrac{1}{2} \) bulunur.
\( f \) sürekli bir fonksiyon olup \( [0, 5] \) aralığında kesin artandır.
\( f(0) = 0, \quad f(5) = 7 \)
\( g \) fonksiyonu \( f \) fonksiyonunun tersi olduğuna göre,
\( \displaystyle\int_0^5 f(x)\ dx + \displaystyle\int_0^7 g(y)\ dy \) ifadesi kaça eşittir?
Çözümü Göster\( f \) fonksiyonunun tahmini grafiğini çizelim.

\( f \) fonksiyonu \( [0, 5] \) aralığında \( x \) ekseninin üzerinde kaldığı için \( x \) ekseni ile arasında kalan alan fonksiyonun bu aralıktaki belirli integraline eşittir.
\( A_1 = \displaystyle\int_0^5 f(x)\ dx \)
\( g \) fonksiyonu \( f \) fonksiyonunun tersi olduğu için, \( [f(0) = 0, f(5) = 7] \) aralığında \( y \) ekseni ile arasında kalan alan \( g(y) = f^{-1}(x) \) fonksiyonunun bu aralıktaki belirli integraline eşittir.
\( A_2 = \displaystyle\int_0^7 g(y)\ dy \)
Bu iki alanın toplamı \( 5 \cdot 7 = 35 \) birimkarelik dikdörtgenin alanına karşılık gelir.
\( A_1 + A_2 = 35 \) olarak bulunur.
\( f \) birebir ve örten bir fonksiyondur.
\( f(3) = 6, \quad f(8) = 2 \)
\( \displaystyle\int_3^8 f(x)\ dx = 15 \) olduğuna göre, \( \displaystyle\int_2^6 f^{-1}(x)\ dx \) kaça eşittir?
Çözümü Göster\( f \) fonksiyonunun tahmini grafiğini çizelim.
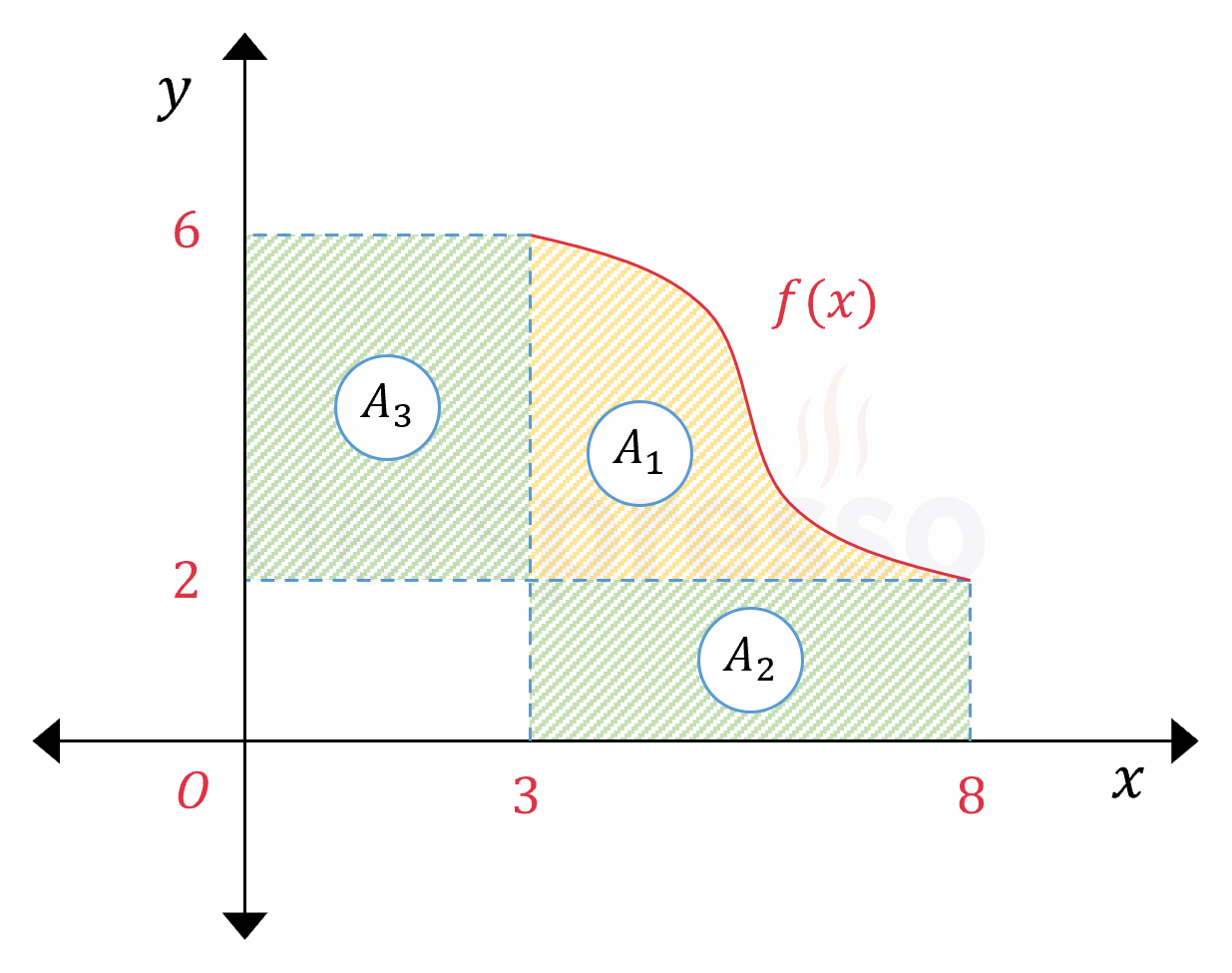
\( \displaystyle\int_3^8 f(x)\ dx \) integrali \( f \) fonksiyonunun \( [3, 8] \) aralığında \( x \) ekseni ile arasında kalan alanı ifade eder.
\( \displaystyle\int_3^8 f(x)\ dx = A_1 + A_2 \)
\( A_2 \) değerini dikdörtgen alan formülü ile bulabiliriz.
\( A_2 = (8 - 3) \cdot 2 = 10 \)
\( A_1 \) değerini bulalım.
\( \displaystyle\int_3^8 f(x)\ dx = A_1 + A_2 \)
\( 15 = A_1 + 10 \)
\( A_1 = 5 \)
\( f \) fonksiyonunun ters fonksiyonu için \( \displaystyle\int_2^6 f^{-1}(x)\ dx \) integrali \( f \) fonksiyonunun \( [f(8) = 2, f(3) = 6] \) aralığında \( y \) ekseni ile arasında kalan alanı ifade eder.
\( \displaystyle\int_2^6 f^{-1}(x)\ dx = A_1 + A_3 \)
\( A_3 \) değerini dikdörtgen alan formülü ile bulabiliriz.
\( A_3 = (6 - 2) \cdot 3 = 12 \)
Soruda istenen integral değerini bulalım.
\( \displaystyle\int_2^6 f^{-1}(x)\ dx = A_1 + A_3 \)
\( = 5 + 12 = 17 \) bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(0) = 0, \quad f(7) = 5 \)
\( f'(x) \gt 0, \quad f''(x) \lt 0 \) veriliyor.
Buna göre \( \displaystyle\int_0^7 f(x)\ dx \) ve \( \displaystyle\int_0^5 f^{-1}(y)\ dy \) integralleri arasındaki ilişkiyi bulunuz.
Çözümü GösterVerilen iki integral ifadesinden birincisi \( f(x) \) fonksiyonunun \( x \in [0, 7] \) aralığında \( x \) ekseni ile arasında kalan alana, ikincisi de \( y \in [0, 5] \) aralığında \( y \) ekseni ile arasında kalan alana karşılık gelir.
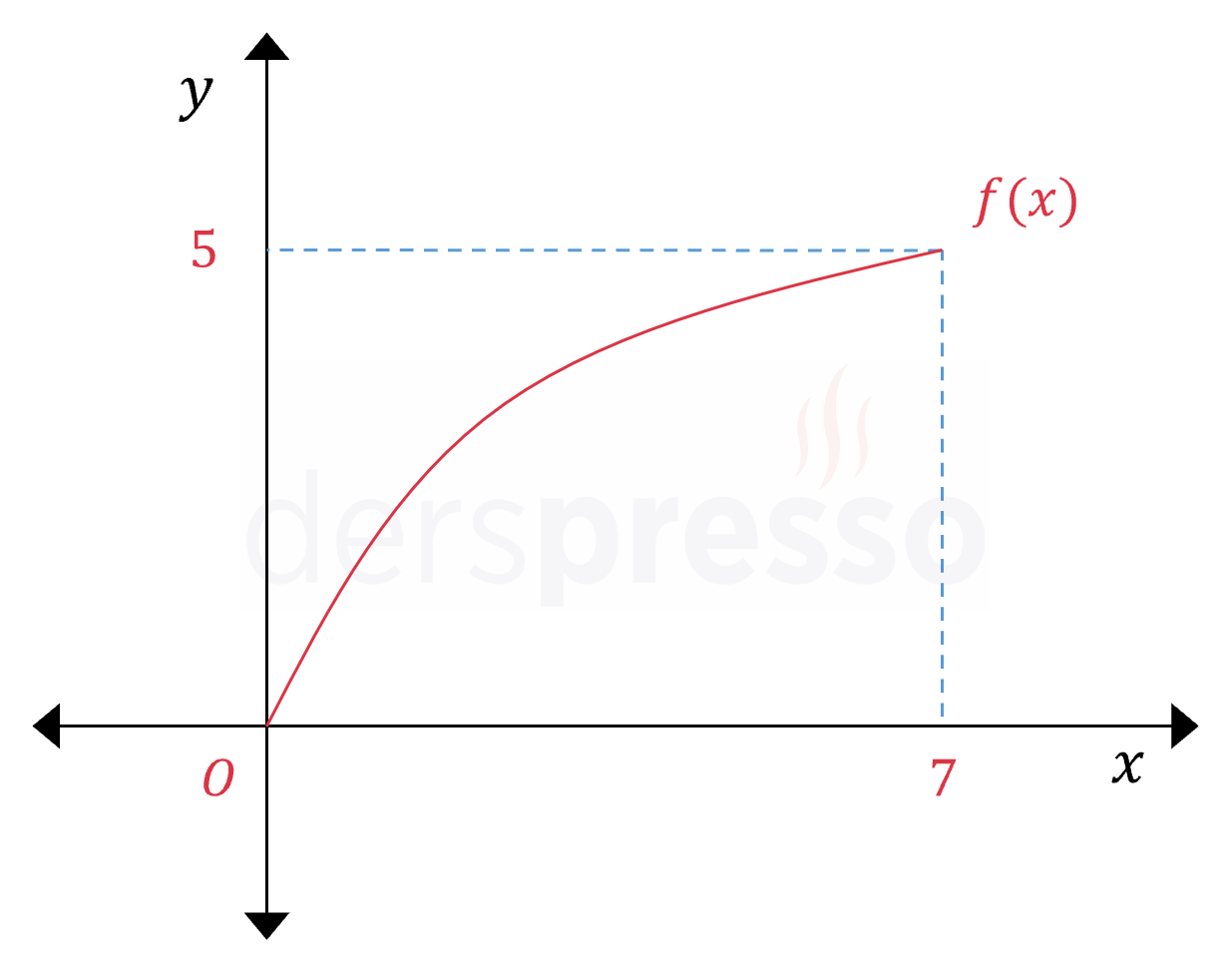
Fonksiyonun birinci türevi pozitif olduğu için grafiği şekildeki gibi sürekli artandır.
Fonksiyonun ikinci türevi negatif olduğu için eğimi sürekli azalandır, dolayısıyla grafiği şekildeki gibi konkavdır.
Bu yüzden eğri ile \( x \) ekseni arasında kalan bölge, \( y \) ekseni ile arasında kalan bölgeden daha büyük olur.
\( \displaystyle\int_0^7 f(x)\ dx \gt \displaystyle\int_0^5 f^{-1}(y)\ dy \)
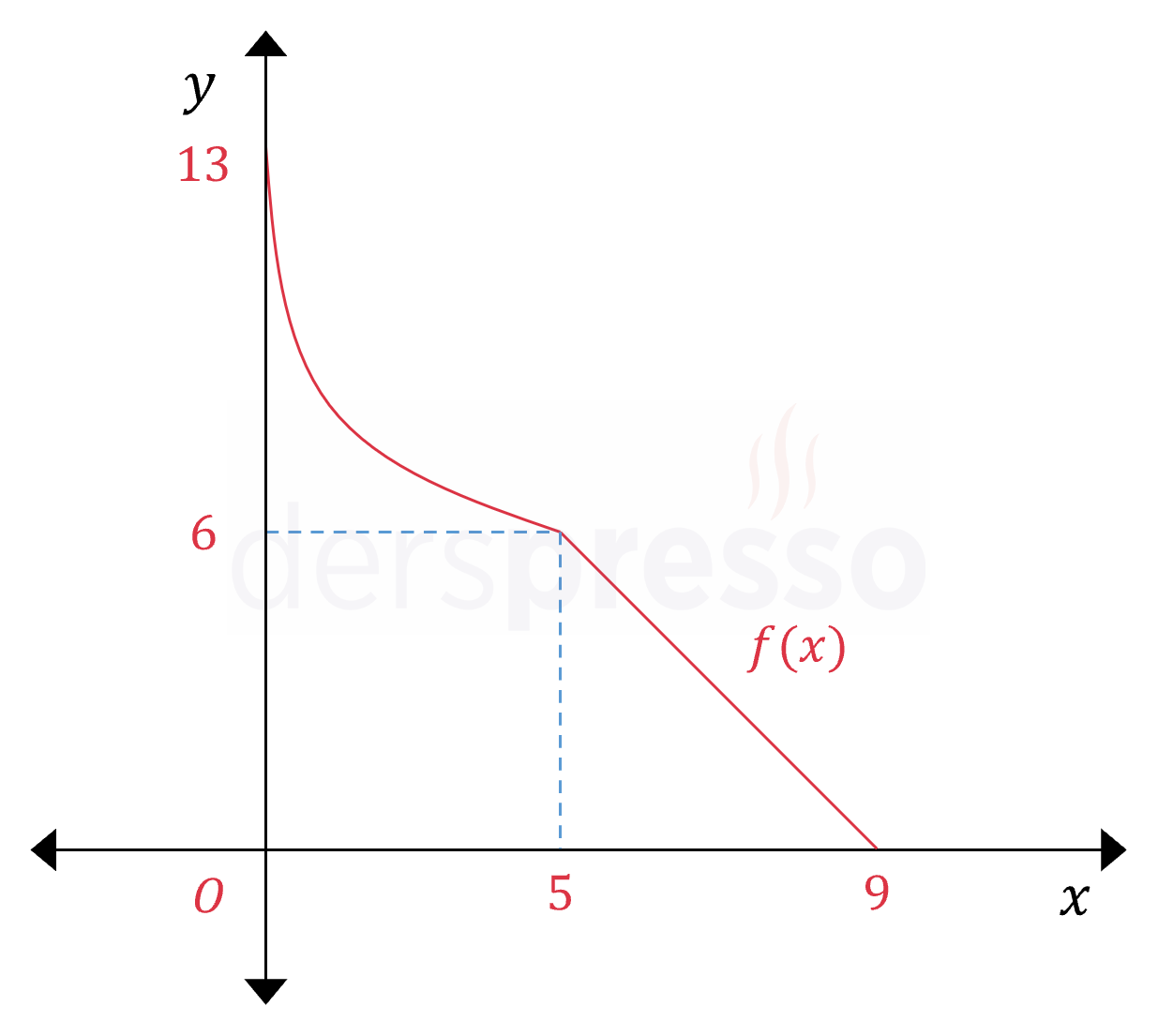
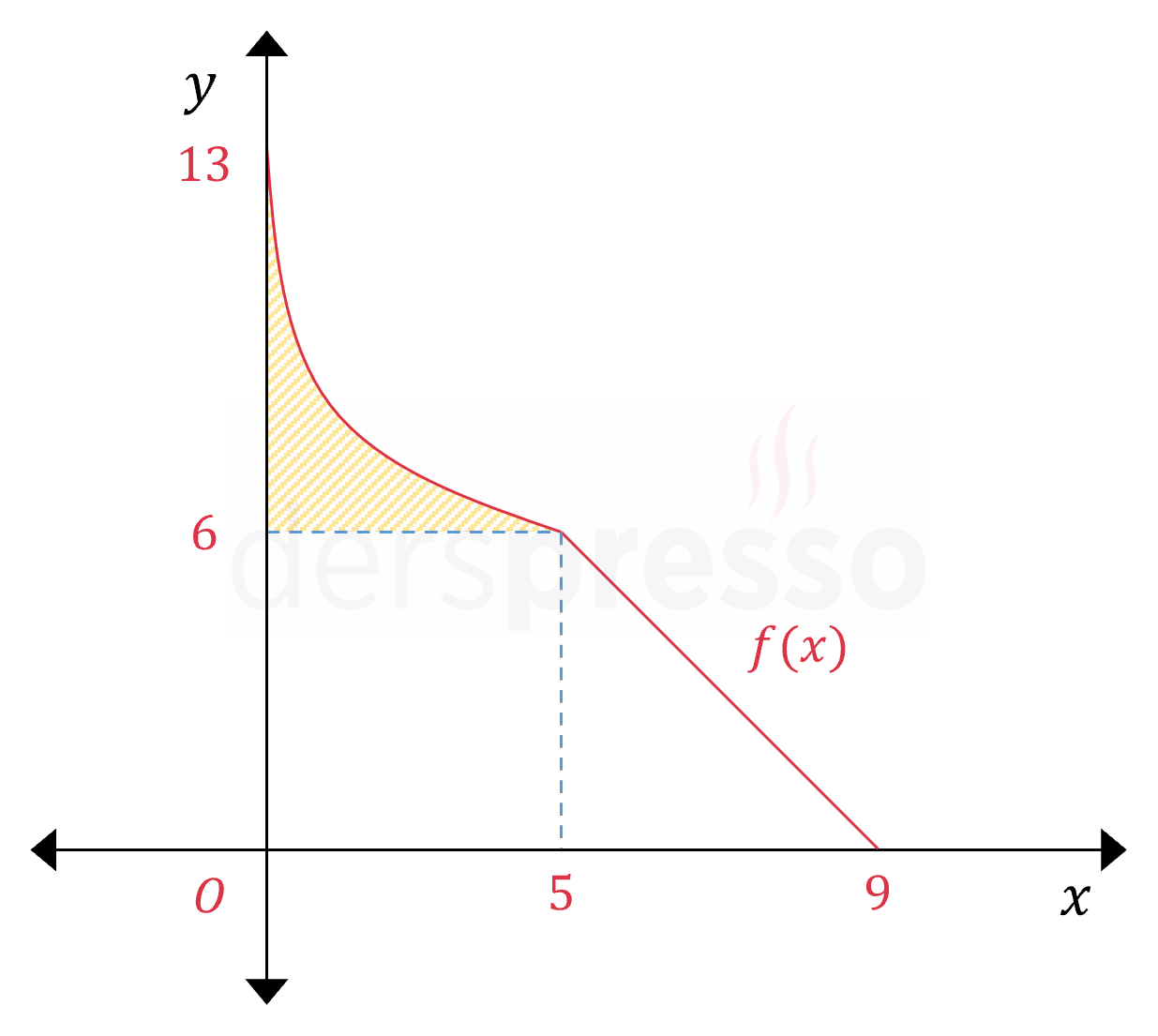
Şekildeki birebir ve örten \( f(x) \) fonksiyonu \( [5, 9] \) aralığında doğrusaldır.
\( \displaystyle\int_6^{13}{f^{-1}(x)}\ dx = 11 \) olduğuna göre,
\( \displaystyle\int_{-4}^5{2xf(x^2 - 16)}\ dx \) integralinin sonucu kaçtır?
Çözümü Göster\( f^{-1} \) fonksiyonunun \( [6, 13] \) aralığındaki belirli integrali fonksiyonun bu aralıkta \( y \) ekseni ile arasında kalan taralı alanı verir.
Değeri sorulan ifadenin integralini almak için değişken değiştirme yöntemini kullanalım.
\( x^2 - 16 = u \)
\( \Longrightarrow 2x\ dx = du \)
\( u \) değişkeni için sınır değerlerini bulalım.
\( u(-4) = (-4)^2 - 16 = 0 \)
\( u(5) = 5^2 - 16 = 9 \)
\( x \) değişkenlerinin \( u \) karşılıklarını yazalım.
\( \displaystyle\int_{-4}^5{2xf(x^2 - 16)}\ dx = \displaystyle\int_0^9{f(u)}\ du \)
Buna göre değeri istenen ifade \( [0, 9] \) aralığında \( f(x) \) fonksiyonunun \( x \) ekseni ile arasında kalan alana eşittir.
Bu alanı bulmak için köşeleri orijin, \( (9, 0) \), \( (5, 6) \) ve \( (0, 6) \) noktaları olan yamuğun alanı ile taralı alana karşılık gelen \( f^{-1} \) fonksiyonunun \( [6, 13] \) aralığındaki belirli integralini toplayalım.
Yamuğun alanını bulalım.
\( \dfrac{9 + 5}{2} \cdot 6 = 42 \)
Fonksiyonun \( [0, 9] \) aralığında \( x \) ekseni ile arasında kalan alanı bulalım.
\( \displaystyle\int_0^9{f(u)}\ du = 42 + 11 \)
\( = 53 \) olarak bulunur.
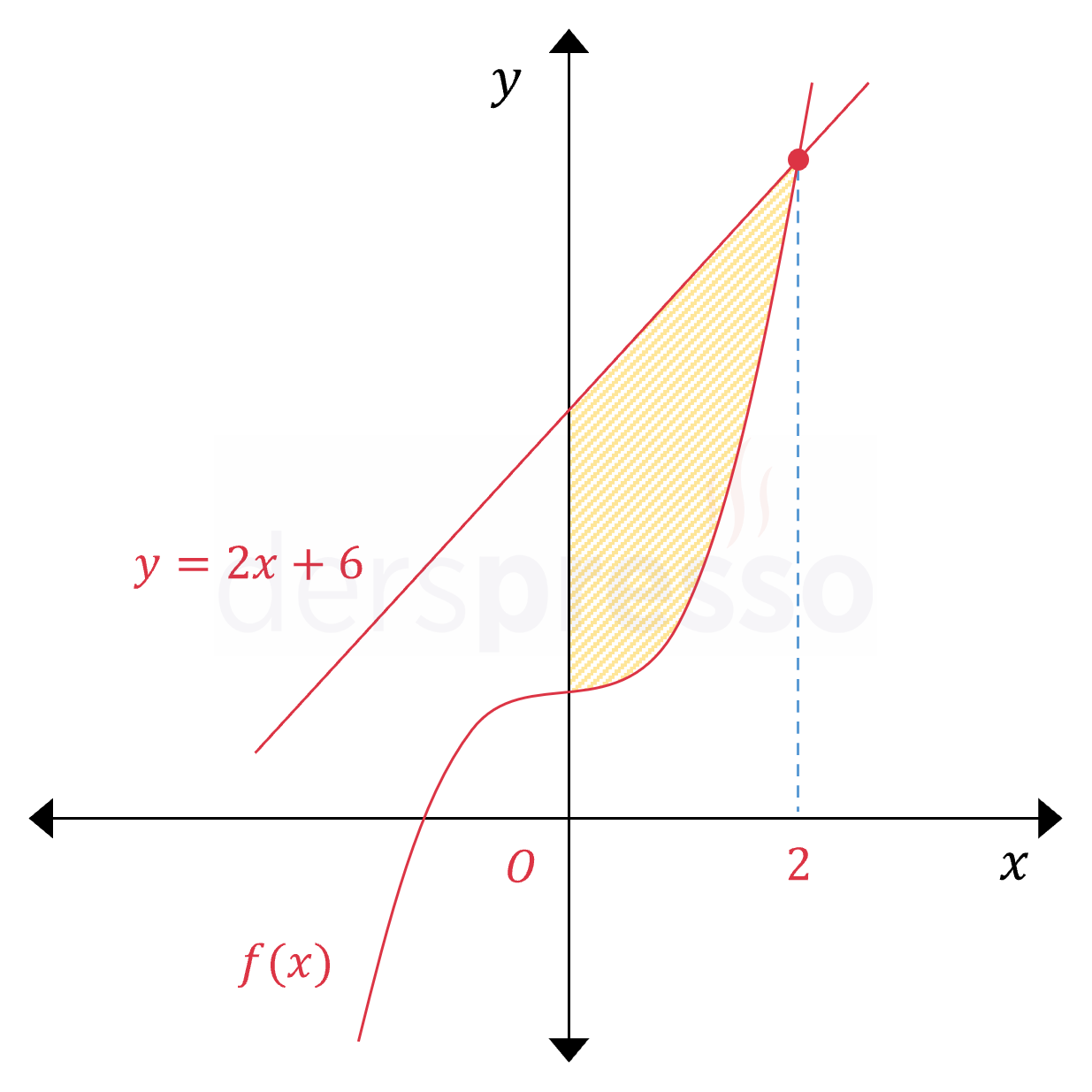
Yukarıda \( f(x) = x^3 + 2 \) eğrisi ile \( y = 2x + 6 \) doğrusunun grafiği verilmiştir.
Eğri ile doğru \( x = 2 \) apsisli noktada kesiştiğine göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü GösterDoğru ile eğrinin kesişim noktasının koordinatlarını bulmak için doğru ya da eğrinin denkleminde \( x = 2 \) yazalım.
\( y = 2(2) + 6 = 10 \)
Kesişim noktası: \( (2, 10) \)
Doğrunun \( y \) eksenini kestiği noktayı bulalım.
\( y = 2(0) + 6 = 6 \)
Doğru \( y \) eksenini \( (0, 6) \) noktasında keser.
Eğrinin \( y \) eksenini kestiği noktayı bulalım.
\( f(0) = 0^3 + 2 = 2 \)
Eğri \( y \) eksenini \( (0, 2) \) noktasında keser.
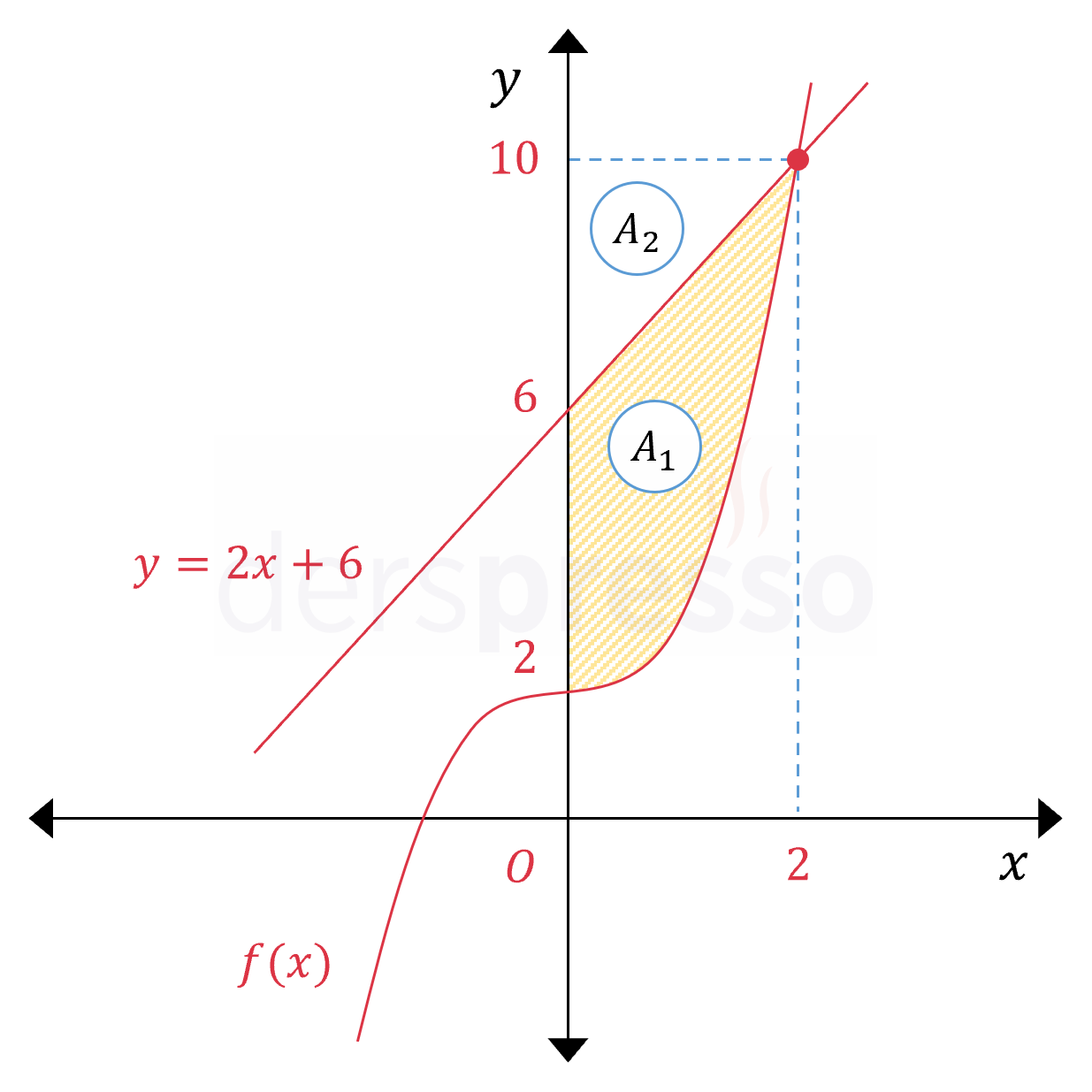
Taralı bölgenin alanını bulmak için \( f(x) \) fonksiyonunun \( [2, 10] \) aralığında \( y \) ekseni ile arasında kalan alandan köşeleri \( (0, 6) \), \( (0, 10) \) ve \( (2, 10) \) olan üçgenin alanını çıkaralım.
Üçgenin alanını bulalım.
\( A_2 = \dfrac{(10 - 6) \cdot 2}{2} = 4 \)
\( f(x) \) fonksiyonunun \( [2, 10] \) aralığında \( y \) ekseni ile arasında kalan alanı bulmak için fonksiyonu \( y \) cinsinden yazalım.
\( x^3 + 2 = y \)
\( x^3 = y - 2 \)
\( x = f(y) = \sqrt[3]{y - 2} \)
Fonksiyon bu aralıkta \( y \) ekseninin sağ tarafında kaldığı için, alan fonksiyonun bu aralıktaki belirli integraline eşittir.
\( \displaystyle\int_2^{10}{\sqrt[3]{y - 2}}\ dy \)
İfadenin integralini alalım.
\( = (\dfrac{3(y - 2)^{\frac{4}{3}}}{4})|_2^{10} \)
\( = \dfrac{3(10 - 2)^{\frac{4}{3}}}{4} - \dfrac{3(2 - 2)^{\frac{4}{3}}}{4} \)
\( = \dfrac{3(16)}{4} - \dfrac{3(0)}{4} \)
\( = 12 \)
Taralı bölgenin alanını bulalım.
\( A_1 = 12 - A_2 = 8 \) olarak bulunur.