Bir Fonksiyonun Ortalama Değeri
Belirli integralin bir diğer uygulaması bir fonksiyonun belirli bir aralıktaki ortalama değerinin bulunmasıdır. Örneğin hız fonksiyonu verilen bir aracın bir zaman aralığındaki ortalama hızını bu yöntemle hesaplayabiliriz.
Sonlu sayıda sayının ortalamasını bulmak için sayıların toplamını sayı adedine böleriz. Örneğin 5 öğrencinin bir sınavdan aldıkları notların ortalamasını aşağıdaki şekilde bulabiliriz.
\( \dfrac{71 + 52 + 93 + 86 + 68}{5} = 74 \)
Ancak bu yöntemi aşağıdaki gibi sürekli ve tanım kümesinde sonsuz sayıda eleman bulunan bir fonksiyonun bir aralıktaki ortalama değerini (\( f_{ort} \)) bulmak için kullanamayız.
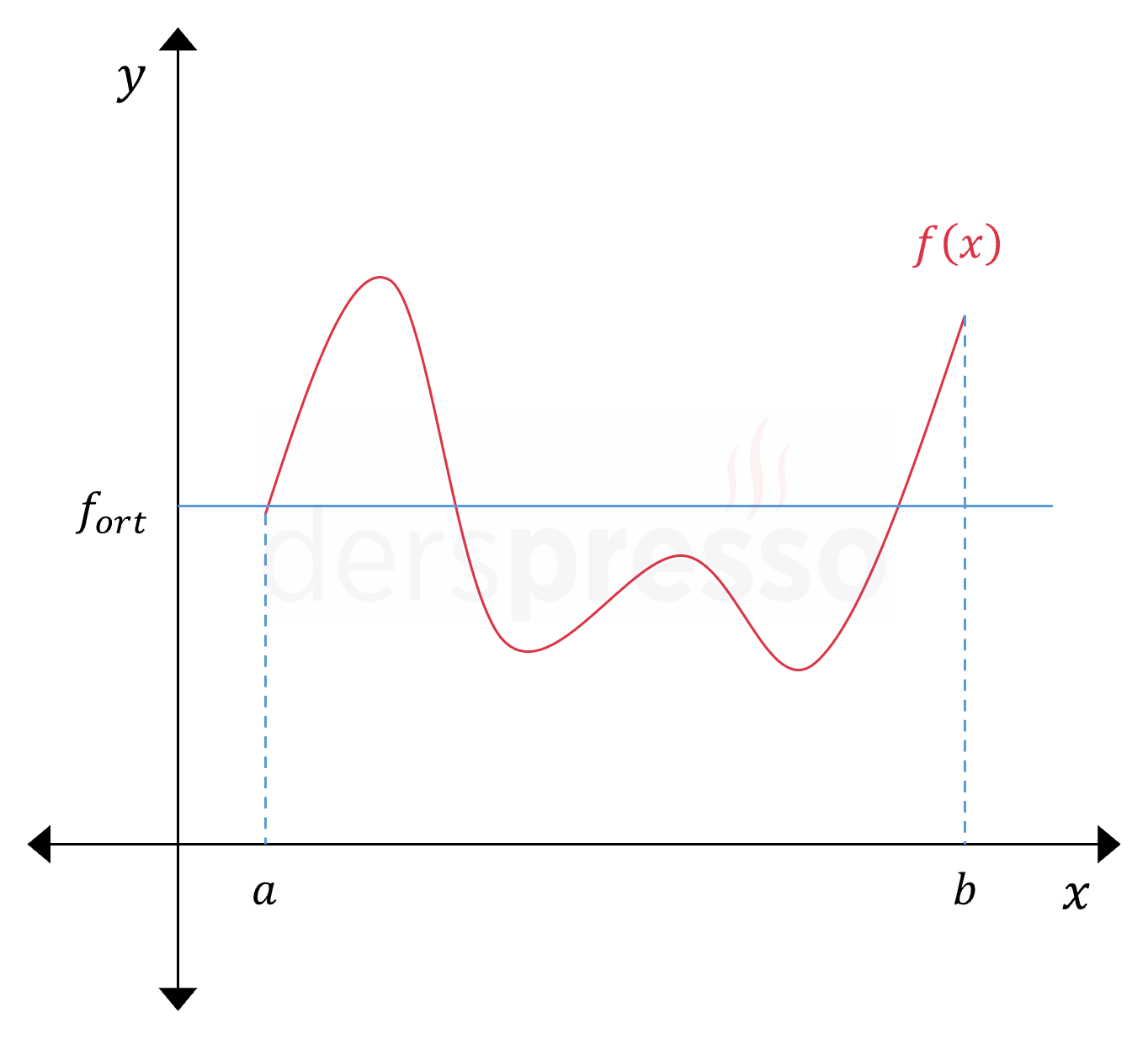
Gerçek ortalama değerini vermeyecek olsa da, bu durumda yaklaşık ortalama değeri bulmak için alan hesaplamasında kullandığımız Riemann toplamı yöntemini kullanabiliriz. Buna göre, bu aralığı belirli sayıda alt aralığa bölmeyi ve her aralıkta seçeceğimiz \( x \) değerleri için hesaplayacağımız fonksiyon değerlerinin ortalamasını almayı deneyebiliriz.
Bunun için önce \( [a, b] \) aralığını genişlikleri eşit 8 alt aralığa bölelim ve her aralıkta seçeceğimiz bir \( x_i^* \) noktası için \( f(x_i^*) \) fonksiyon değerini bulalım. Bu 8 fonksiyon değerinin ortalaması bize fonksiyonun bu aralıktaki yaklaşık ortalama değerini verecektir. Alan problemi bölümünde gördüğümüz üzere, \( x_i^* \) noktasını farklı kurallara göre seçebilecek olsak da, bu seçim belirli integral işlemi sonucunda bulacağımız gerçek ortalama değerini etkilememektedir.
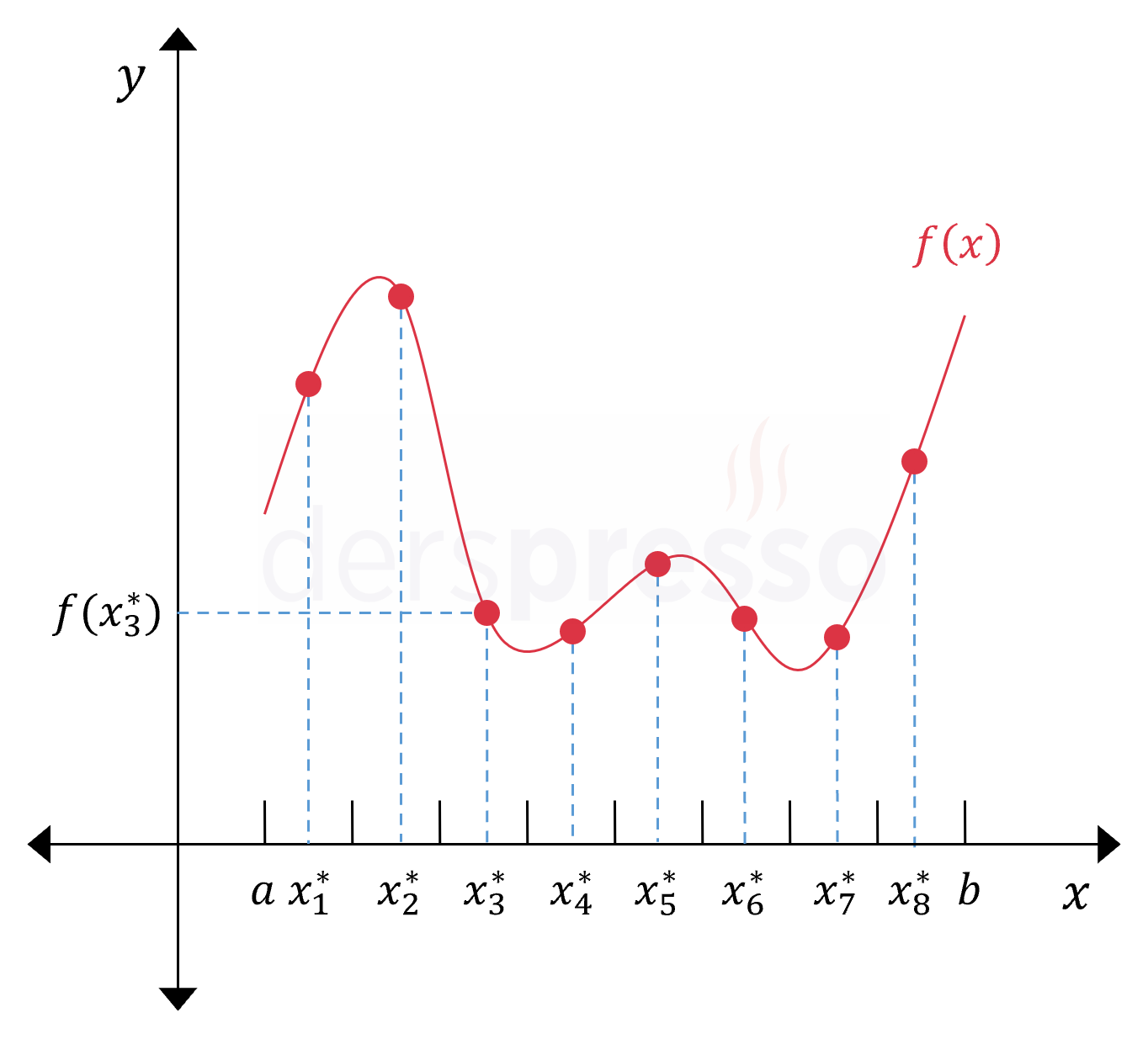
\( [a, b] \) aralığı için gerçek ortalama değerine \( f_{ort} \), Riemann toplamı yöntemi ile hesaplayacağımız yaklaşık ortalama değerine \( \overline{f_{ort}} \) dersek yaklaşık değeri aşağıdaki formülle bulabiliriz.
\( \overline{f_{ort}} = \dfrac{f(x_1^*) + f(x_2^*) + \ldots + f(x_8^*)}{8} \)
\( [a, b] \) aralığını \( n \) eşit alt aralığa böldüğümüz durumda ise genel ortalama değer formülünü aşağıdaki şekilde yazabiliriz.
\( \Delta x = \dfrac{b - a}{n} \) olmak üzere,
\( \overline{f_{ort}} = \dfrac{f(x_1^*) + f(x_2^*) + \ldots + f(x_n^*)}{n} \)
Fonksiyon değerlerinin toplamını toplam sembolü şeklinde yazalım.
\( = \dfrac{1}{n}\displaystyle\sum_{i = 1}^{n}{f(x_i^*)} \)
\( \Delta x \) formülünden \( n \) değerini yerine koyalım.
\( = \dfrac{\Delta x}{b - a}\displaystyle\sum_{i = 1}^{n}{f(x_i^*)} \)
\( \Delta x \) sabit olduğu için toplam sembolü içine alabiliriz.
\( = \dfrac{1}{b - a}\displaystyle\sum_{i = 1}^{n}{f(x_i^*)\Delta x} \)
Buna göre farklı \( n \) değerleri için hesaplayacağımız yaklaşık ortalama değeri yukarıdaki formülle bulabiliriz. Riemann toplamının farklı uygulamalarında gördüğümüz gibi, \( n \) sayısı büyüdükçe, yani \( \Delta x \) aralıkları daraldıkça bulduğumuz yaklaşık değer gerçek değere gitgide yaklaşır. Bu yaklaşık değerin \( n \) sonsuza giderkenki limiti ise bize fonksiyonun bu aralıktaki gerçek ortalama değerini verir.
\( f_{ort} = \lim_{n \to \infty} \overline{f_{ort}} \)
\( = \lim_{n \to \infty} \dfrac{1}{b - a}\displaystyle\sum_{i = 1}^{n}{f(x_i^*)\Delta x} \)
\( = \dfrac{1}{b - a}\lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*)\Delta x} \)
\( n \) sonsuza giderkenki bu limit ifadesi aynı zamanda belirli integralin tanımıdır.
\( f \), \( [a, b] \) aralığında sürekli bir fonksiyon olmak üzere,
\( f_{ort} = \dfrac{1}{b - a}\displaystyle\int_a^b {f(x)\ dx} \)
değeri \( f \) fonksiyonunun \( [a, b] \) aralığındaki ortalama değerini verir.
Bu formüle göre, bir fonksiyonun bir aralıktaki ortalama değeri fonksiyonun bu aralıkta \( x \) ekseni ile arasında kalan alanın aralığın genişliğine oranına eşittir.
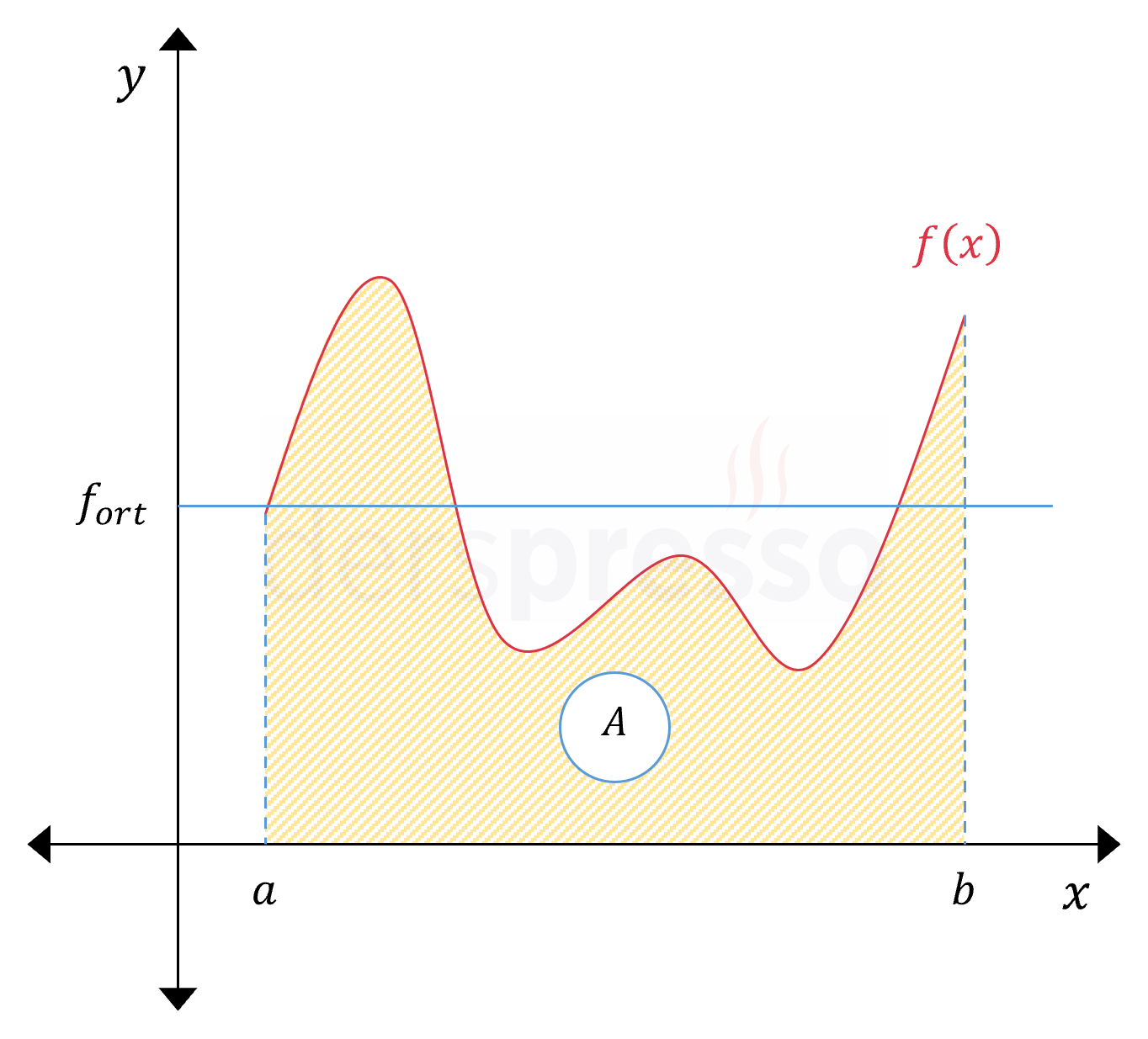
\( f_{ort} = \dfrac{A}{b - a} \)
Elde ettiğimiz bu formüle integral için ortalama değer teoremi de denir. Türev konusunda gördüğümüz ortalama değer teoremi bir fonksiyonun belirli bir aralıkta, türevi bu aralıktaki ortalama değişim oranına eşit en az bir noktası olduğunu söyler. İntegral için ortalama değer teoremi ise bu aralıktaki ortalama fonksiyon değerini bulur.
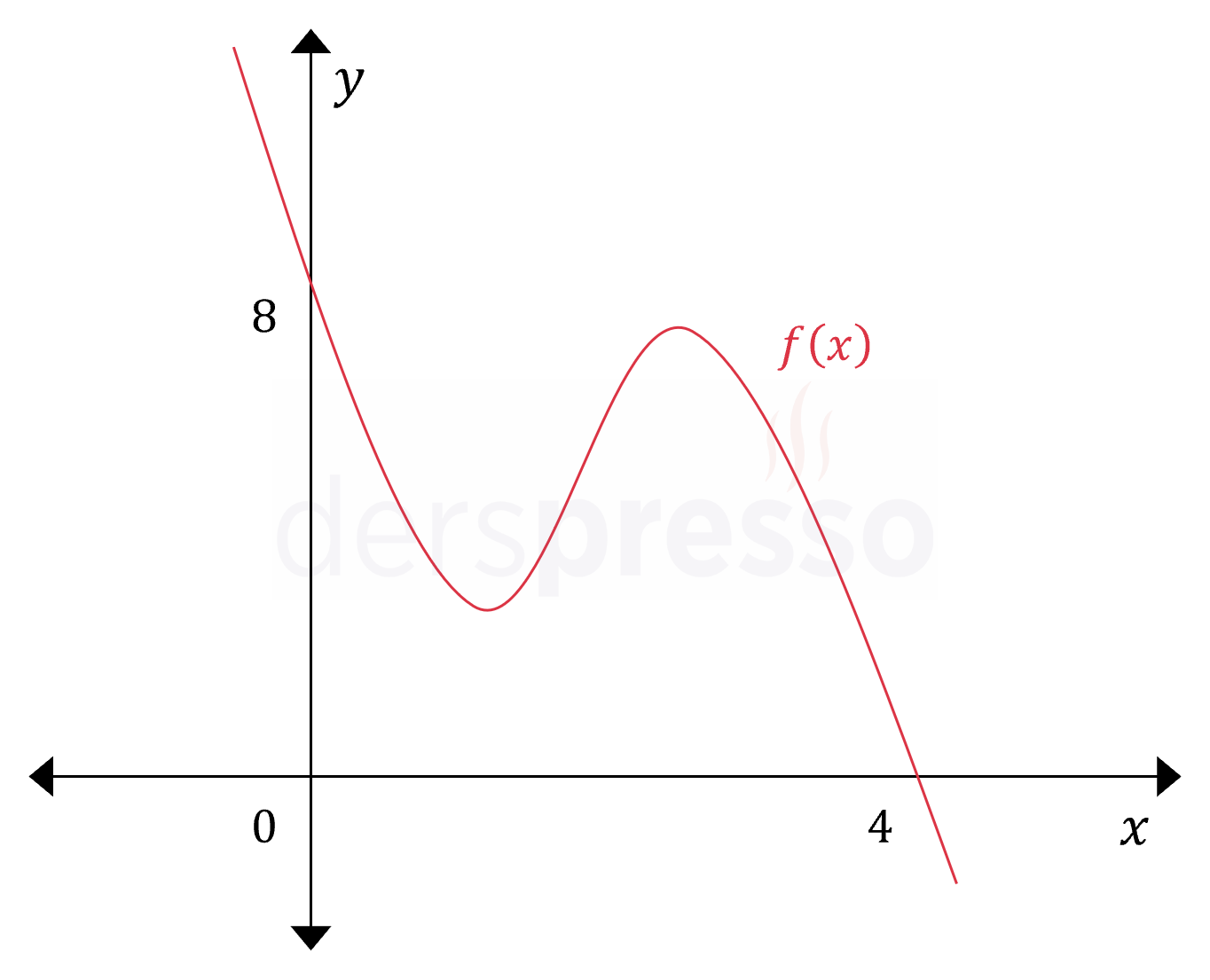
\( f(x) = -x^3 + 6x^2 - 10x + 8 \)
Yukarıda denklemi ve grafiği verilen fonksiyonun \( [0, 4] \) aralığındaki ortalama değerini bulalım.
Ortalama değer formülünü yazalım.
\( f_{ort} = \dfrac{1}{4 - 0}\displaystyle\int_0^4 {(-x^3 + 6x^2 - 10x + 8)\ dx} \)
İfadenin integralini alalım.
\( = \dfrac{1}{4}[-\dfrac{x^4}{4} + 2x^3 - 5x^2 + 8x]_0^4 \)
\( = \dfrac{1}{4}[(-\dfrac{4^4}{4} + 2(4)^3 \) \( - 5(4)^2 + 8(4)) \) \( - (-\dfrac{0^4}{4} + 2(0)^3 \) \( - 5(0)^2 + 8(0))] \)
\( = \dfrac{1}{4}[(-64 + 128 - 80 + 32) \) \( - (-0 + 0 - 0 + 0)] \)
\( = 4 \)
Bulduğumuz ortalama değeri fonksiyon grafiği üzerinde işaretleyelim.
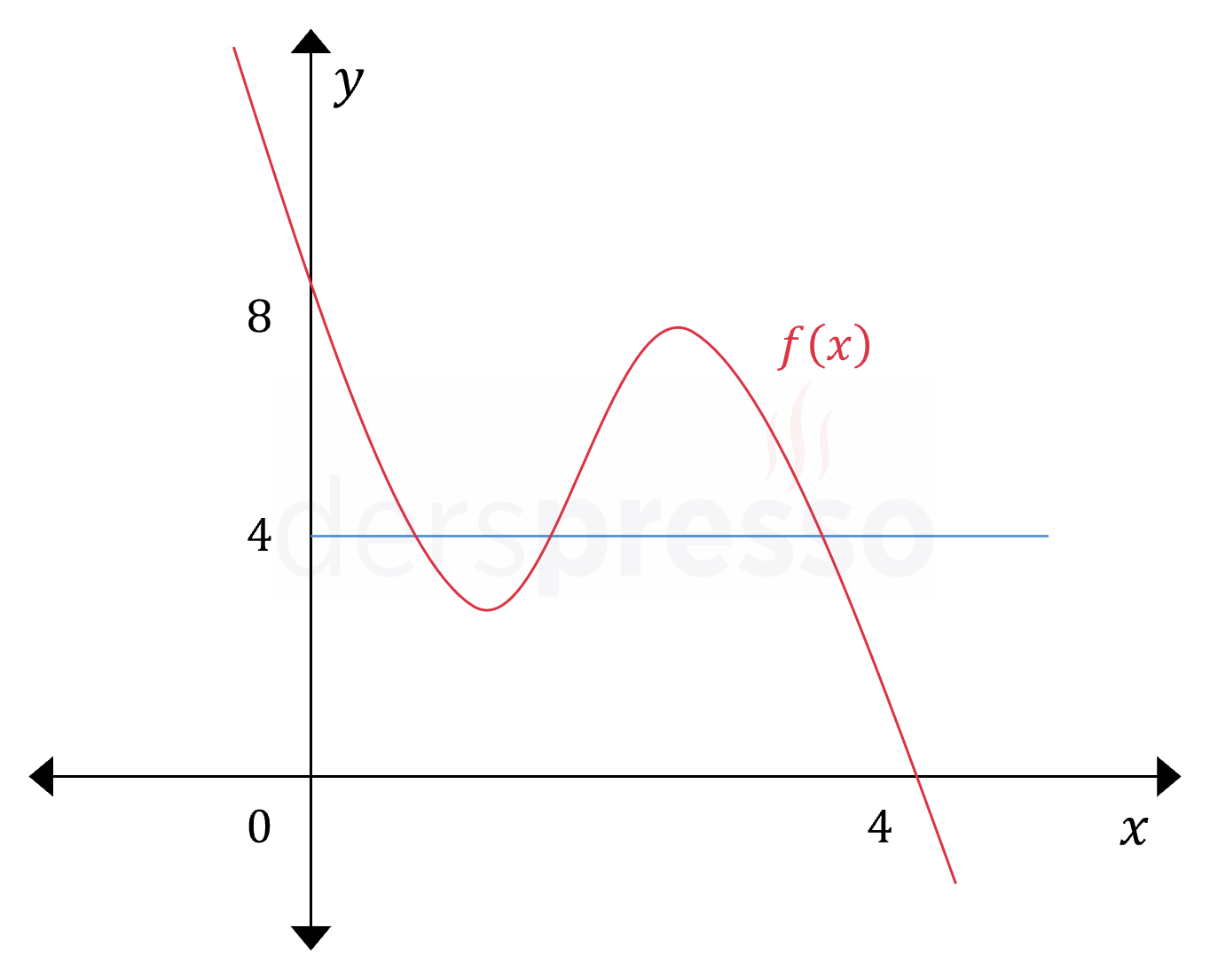
Tek fonksiyonların \( [-a, a] \) gibi \( y \) eksenine göre simetrik iki nokta arasında belirli integral değerleri sıfır olduğu için bu aralıkta ortalama değerleri de sıfırdır.
\( f(x) = \sin{x} \) fonksiyonunun \( [0, \pi] \) aralığındaki ortalama değerini bulunuz.
Çözümü GösterOrtalama değer formülünü yazalım.
\( f_{ort} = \dfrac{1}{b - a}\displaystyle\int_a^b {f(x)\ dx} \)
\( = \dfrac{1}{\pi - 0}\displaystyle\int_0^{\pi} \sin{x}\ dx \)
\( = \dfrac{1}{\pi}(-\cos{x})_0^{\pi} \)
\( = \dfrac{1}{\pi}(-\cos{\pi} + \cos{0}) \)
\( = \dfrac{1}{\pi}(1 + 1) \)
\( = \dfrac{2}{\pi} \) bulunur.
Kenar uzunlukları 2 m ile 5 m arasında olan tüm karelerin ortalama alanı nedir?
Çözümü GösterVerilen aralıkta sonsuz sayıda kare olduğu için bu karelerin alanlarını toplayıp toplam kare sayısına bölerek ortalama alanı hesaplayamayız.
Karenin alanını bir fonksiyon olarak yazarsak ortalama değer teoremi ile verilen aralıkta fonksiyonun belirli integralini aralığın genişliğine bölerek ortalama alanı hesaplayabiliriz.
Bir fonksiyonun belirli bir aralıktaki ortalama değeri aşağıdaki formülle bulunur.
\( f \), \( [a, b] \) aralığında sürekli bir fonksiyon olmak üzere,
\( f_{ort} = \dfrac{1}{b - a}\displaystyle\int_a^b {f(x)\ dx} \)
değeri \( f \) fonksiyonunun \( [a, b] \) aralığındaki ortalama değerini verir.
Bir kenarı \( x \) birim olan karenin alanını \( f(x) = x^2 \) fonksiyonu ile ifade edebiliriz.
\( f_{ort} = \dfrac{1}{5 - 2}\displaystyle\int_2^5 {x^2\ dx} \)
İfadenin integralini alalım.
\( = \dfrac{1}{3}(\dfrac{x^3}{3})|_2^5 \)
\( = \dfrac{1}{3}(\dfrac{125}{3} - \dfrac{8}{3}) \)
\( = \dfrac{117}{9} = 13 \) bulunur.