İntegral Teoremleri

Önceki bölümlerde geometrik alan formüllerini kullanarak ve Riemann toplamlarının limitini alarak integral hesaplaması yapabileceğimizi gördük, ancak bu yöntemler basit fonksiyonlar için bile uzun işlemler gerektirebildiği için pratik yöntemler olduklarını söyleyemeyiz. Kalkülüsün birinci teoremi, integral işlemi ile kalkülüsün bir diğer önemli başlığı olan türev arasında tam da bu noktada ihtiyaç duyduğumuz ilişkiyi kurmaktadır.

Alan Fonksiyonu

Aşağıdaki gibi bir \( f(t) \) fonksiyonu tanımlayalım. Bu fonksiyonun bağlı olduğu değişken olarak \( t \)'yi seçmiş olsak da \( x \) dışında herhangi bir değişken seçilebilir.

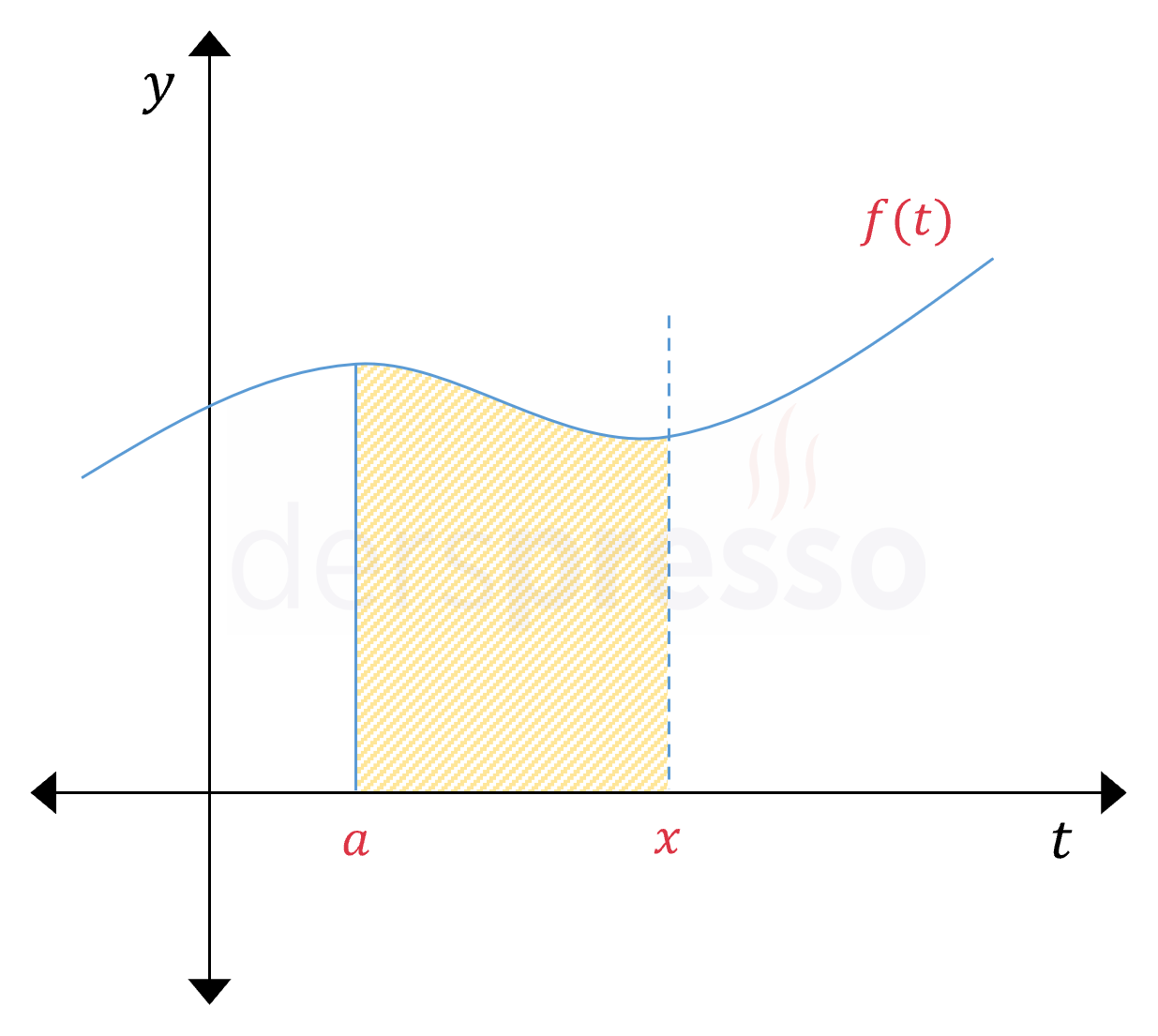
Daha sonra \( t = x \) noktasından bir dikey çizgi çizelim ve aşağıdaki gibi bir \( A(x) \) fonksiyonu tanımlayalım.

\( A(x) = \displaystyle\int_a^x {f(t)\ dt} \)

İntegralin alan anlamını düşündüğümüzde bu fonksiyonun \( [a, x] \) aralığında \( f(t) \) fonksiyonunun altında kalan alanı veren ve \( x \) değişkenine bağlı bir fonksiyon olduğunu görebiliriz. Buna göre \( x \) değişkeni farklı değerler aldıkça ve \( t = x \) doğrusu \( t \) ekseni boyunca hareket ettikçe \( A(x) \) fonksiyonu \( [a, x] \) aralığında \( f(t) \) eğrisinin altında kalan alanı verecektir.

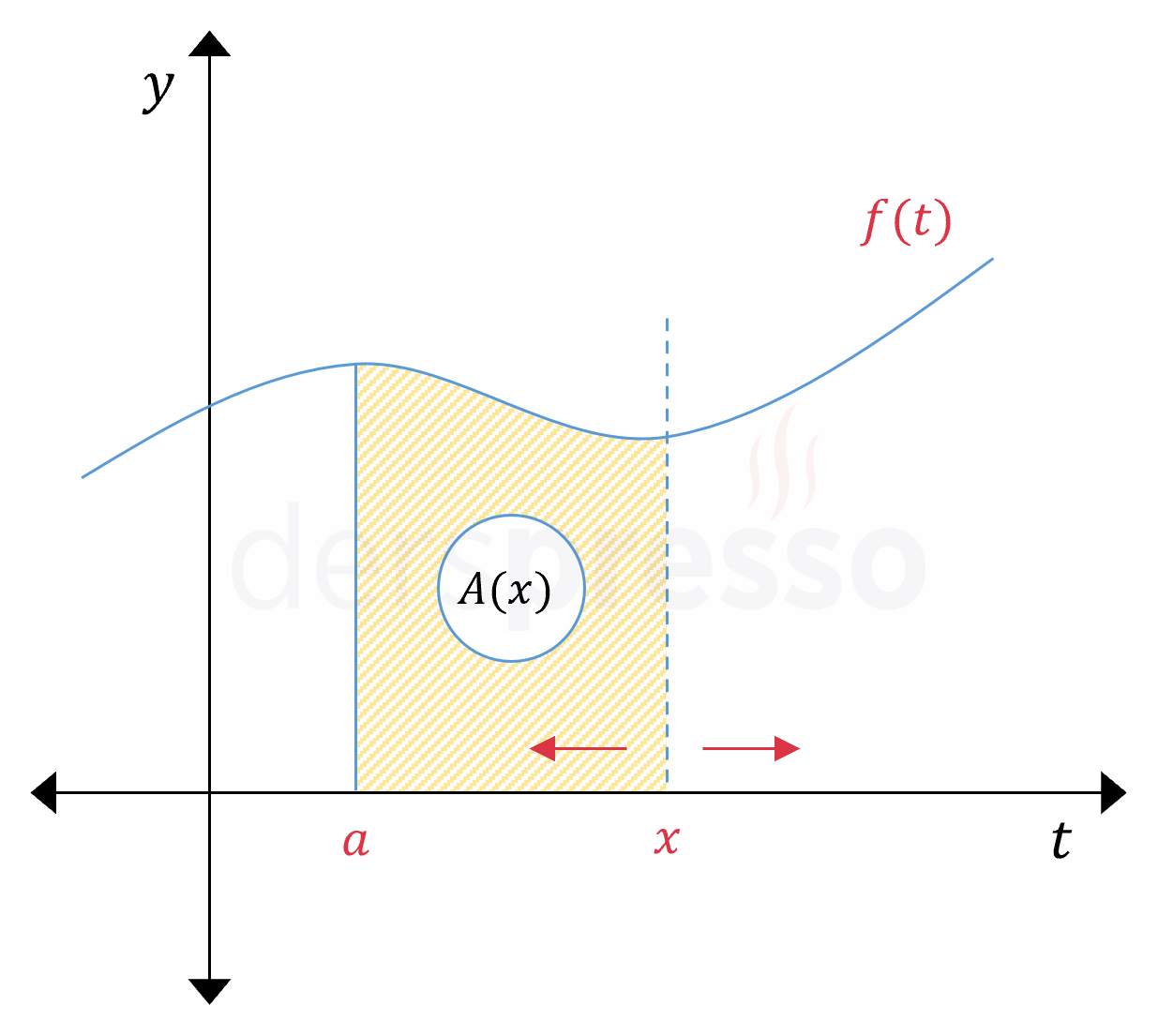
Bu şekilde diğer bir \( f(t) \) fonksiyonuna ve \( x \) değişkenine bağlı olarak tanımladığımız \( A(x) \) fonksiyonuna alan fonksiyonu denir. Alan fonksiyonu ile ilgili önemli birkaç nokta aşağıdaki gibidir.

Alan fonksiyonunun bağlı olduğu değişken integrali alınan fonksiyonun \( t \) değişkeni değil, integralin alt ya da üst sınırındaki \( x \) değişkenidir.
İntegralin alt ve üst sınırı sabit birer sayı olursa integral sonucu da sabit bir değer olacağı için bu bir alan fonksiyonu değil sabit fonksiyon olur.
\( f(t) \) fonksiyonu \( [a, x] \) aralığında negatif değer almıyorsa (\( f(t) \ge 0 \)) alan fonksiyonu \( f(t) \) fonksiyon grafiğinin altında kalan toplam alanı verir.
\( f(t) \) fonksiyonu \( [a, x] \) aralığında negatif değer de alabiliyorsa alan fonksiyonu \( f(t) \) fonksiyon grafiğinin altında kalan net alanı verir (\( x \) ekseninin üstünde kalan eksi altında kalan alan).

Kalkülüsün Birinci Temel Teoremi

Kalkülüsün birinci temel teoremi türev ve integral arasındaki ilişkiyi kurar.

\( f \) fonksiyonu \( [a, b] \) aralığında sürekli bir fonksiyon olmak üzere, \( f \) fonksiyon grafiğinin altındaki alanı hesaplayan bir \( F \) alan fonksiyonu tanımlayalım.

\( a \le x \le b \) olmak üzere,

\( F(x) = \displaystyle\int_a^x {f(t)\ dt} \)

Kalkülüsün birinci temel teoremine göre, bu \( F \) fonksiyonu da aynı \( [a, b] \) aralığında süreklidir, türevlenebilirdir ve türevi \( f(x) \) fonksiyonudur.

\( F'(x) = \dfrac{d}{dx} \displaystyle\int_a^x {f(t)\ dt} = f(x) \)

İSPATI GÖSTER

\( F \) fonksiyonunun tanımını yazalım.

\( F(x) = \displaystyle\int_a^x {f(t)\ dt} \)

\( F \) fonksiyonunun türevinin limit tanımını yazalım.

\( F'(x) = \lim_{h \to 0} \dfrac{F(x + h) - F(x)}{h} \)

\( = \lim_{h \to 0} \dfrac{1}{h}[F(x + h) - F(x)] \)

\( F \) fonksiyonu yerine yukarıdaki integral tanımını yazalım.

\( = \lim_{h \to 0} \dfrac{1}{h}[\displaystyle\int_a^{x+h} {f(t)\ dt} - \displaystyle\int_a^x {f(t)\ dt}] \)

Bu ifadedeki birinci integral aşağıdaki grafikte \( [a, x + h] \) aralığındaki taralı alana, ikinci integral de \( [a, x] \) aralığındaki taralı alana karşılık gelir.

Kalkülüsün birinci temel teoremi (ispat)

Belirli integral aralıkların birleşimi özelliğine göre, \( f(t) \) fonksiyonunun \( [a, x + h] \) aralığındaki integral değerinden \( [a, x] \) aralığındaki integral değerini çıkarırsak \( [x, x + h] \) aralığındaki integral değerini elde ederiz.

\( = \lim_{h \to 0} \dfrac{1}{h}\displaystyle\int_x^{x+h} {f(t)\ dt} \)

Bu ifadedeki integral yukarıdaki grafikte \( [x, x + h] \) aralığındaki mavi alana karşılık gelir.

Yine bu ifadedeki \( \frac{1}{h}\displaystyle\int_x^{x+h} {f(t)\ dt} \) ifadesi ise \( f \) fonksiyonunun \( [x, x + h] \) aralığında aldığı ortalama değere eşittir.

Ortalama değer teoremine göre, \( [x, x + h] \) aralığında sürekli olan \( f \) fonksiyonunun bu aralıktaki ortalama değerini aldığı en az bir \( c \in [x, x + h] \) noktası vardır.

Fonksiyonun bu aralıkta ortalama değerini aldığı \( c \) noktasındaki değeri de \( f(c) \) olur.

\( \dfrac{1}{h}\displaystyle\int_x^{x+h} {f(t)\ dt} = f(c) \)

Bu durumda yukarıdaki eşitliği aşağıdaki şekilde ifade edebiliriz.

\( F'(x) = \lim_{h \to 0} f(c) \)

Eşitliğin sağ tarafındaki limit değerini bulmak için limit konusunda gördüğümüz sıkıştırma teoremini kullanalım.

\( c \in [x, x + h] \) olduğunu biliyoruz.

\( x \le c \le x + h \)

Eşitsizliğin üç tarafının limitini alalım.

\( \lim_{h \to 0} x \le \lim_{h \to 0} c \le \lim_{h \to 0} (x + h) \)

\( x \le \lim_{h \to 0} c \le x \)

Buna göre \( h \) sıfıra giderken \( c \) de \( x \) değerine yaklaşır.

\( \lim_{h \to 0} c = x \)

\( h \) sıfıra giderken \( c \) değeri \( x \) değerine yaklaşıyorsa \( f(c) \) değeri de \( f(x) \) değerine yaklaşır.

\( \lim_{h \to 0} f(c) = f(x) \)

Bu durumda aşağıdaki eşitliği elde ederiz.

\( F'(x) = f(x) \)

İspatta hata bildirin

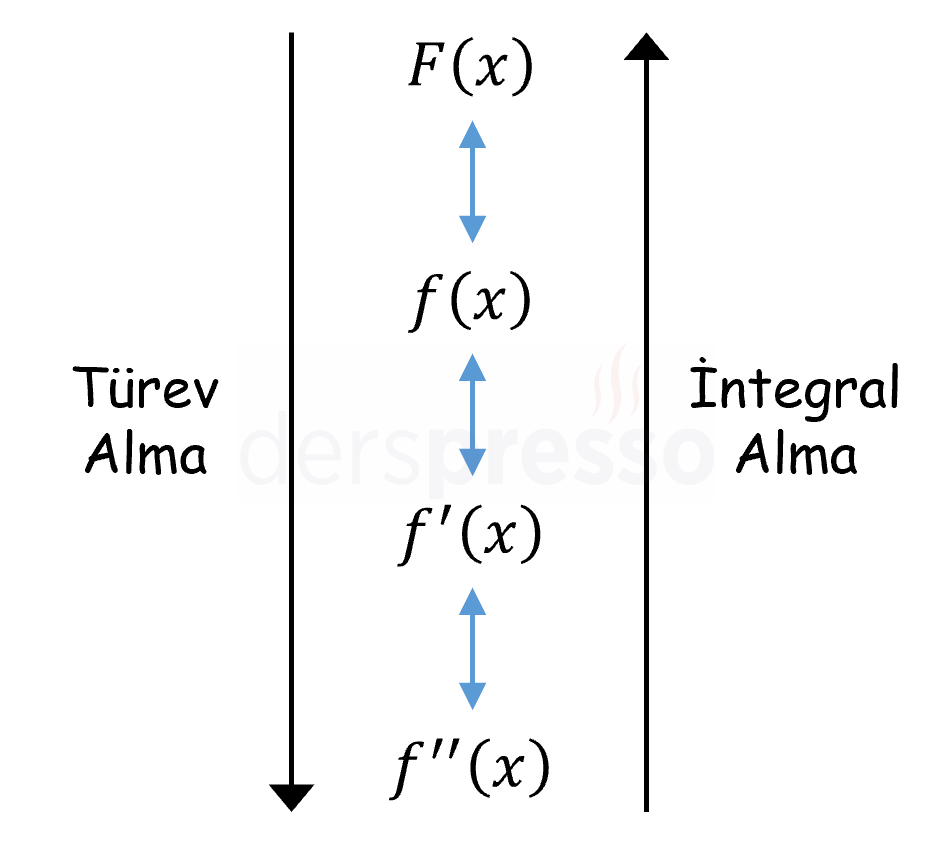
Bu teoreme göre, bir \( f \) fonksiyonunun altında kalan alanı veren alan fonksiyonunun türevi \( f \) fonksiyonunun kendisine eşittir. Buradan çıkarabileceğimiz en önemli sonuç, integral ve türev işlemlerinin birbirinin ters işlemleri olduğudur.

Bu teoremden çıkarabileceğimiz diğer bazı sonuçlar aşağıdaki gibidir.

Bir fonksiyonun integralini almak için türevi o fonksiyon olan fonksiyonu bulmamız yeterlidir.
Bir \( f \) fonksiyonunun integralinin türevi yine \( f \) fonksiyonunu verir.
Benzer şekilde, bir \( F \) fonksiyonunun türevinin integrali, önümüzdeki bölümde bahsedeceğimiz üzere sabit terim dışında orijinal fonksiyonu verir.

Yine bu teoreme göre her sürekli fonksiyonun integrali vardır.

Kalkülüsün İkinci Temel Teoremi

Bu teoreme göre, bir \( f \) fonksiyonun integrali olan fonksiyonu biliyorsak \( f \) fonksiyonunun \( [a, b] \) aralığındaki belirli integrali integral fonksiyonunun bu aralığın uç noktalarındaki fonksiyon değerlerinin farkına eşittir.

\( f \) fonksiyonu \( [a, b] \) aralığında sürekli bir fonksiyon ve \( F'(x) = f(x) \) ise,

\( \displaystyle\int_a^b {f(x)\ dx} = F(x)|_a^b = F(b) - F(a) \)

ÖRNEK:

\( \displaystyle\int_1^3 {x^3\ dx} = \dfrac{x^4}{4}|_1^3 \) \( = \dfrac{3^4}{4} - \dfrac{1^4}{4} = 20 \)

İSPATI GÖSTER

Bu iki teorem alt sınırın sabit bir sayı, üst sınırın \( x \) olduğu duruma aşağıdaki şekilde uygulanabilir. Alt sınırın integral değeri sabit bir sayı olacağı için, türevi sıfır olacaktır.

\( F(x) = \displaystyle\int_a^x {f(t)\ dt} \)

\( F'(x) = \dfrac{d}{dx} \displaystyle\int_a^x {f(t)\ dt} \) \( = \dfrac{d}{dx} (F(x) - F(a)) \) \( = f(x) - 0 = f(x) \)

Alt sınırın da \( x \) cinsinden bir fonksiyon olması durumunda teorem aşağıdaki şekilde uygulanabilir.

\( F(x) = \displaystyle\int_{g(x)}^{h(x)} {f(t)\ dt} \)

\( F'(x) = \dfrac{d}{dx} \displaystyle\int_{g(x)}^{h(x)} {f(t)\ dt} \) \( = \dfrac{d}{dx} (F(h(x)) - F(g(x))) \) \( = f(h(x)) \cdot h'(x) - f(g(x)) \cdot g'(x) \)

Net Değişim Teoremi

Net değişim teoremine göre, bir fonksiyonun değerinde belirli bir aralıktaki değişim, o fonksiyonun türevinin (anlık değişim hızının) o aralıktaki belirli integraline eşittir.

\( \displaystyle\int_a^b {F'(x)\ dx} = F(b) - F(a) \)

Bir diğer ifadeyle, fonksiyonun bir aralığın sonundaki değeri, aralığın başındaki değeri ile fonksiyonun türevinin bu aralıktaki belirli integral değerinin toplamına eşittir.

\( F(b) = F(a) + \displaystyle\int_a^b {F'(x)\ dx} \)