Rolle ve Ortalama Değer Teoremleri
Rolle ve ortalama değer teoremleri analizin önemli teoremlerindendir ve ileriki konularda karşılaşacağımız diğer bazı teoremlerin ispatında kullanılırlar.
Rolle Teoremi
Rolle teoremine göre, iki farklı noktada aynı değere sahip türevlenebilir bir fonksiyonda bu iki nokta arasında türevi sıfır olan en az bir nokta bulunur.
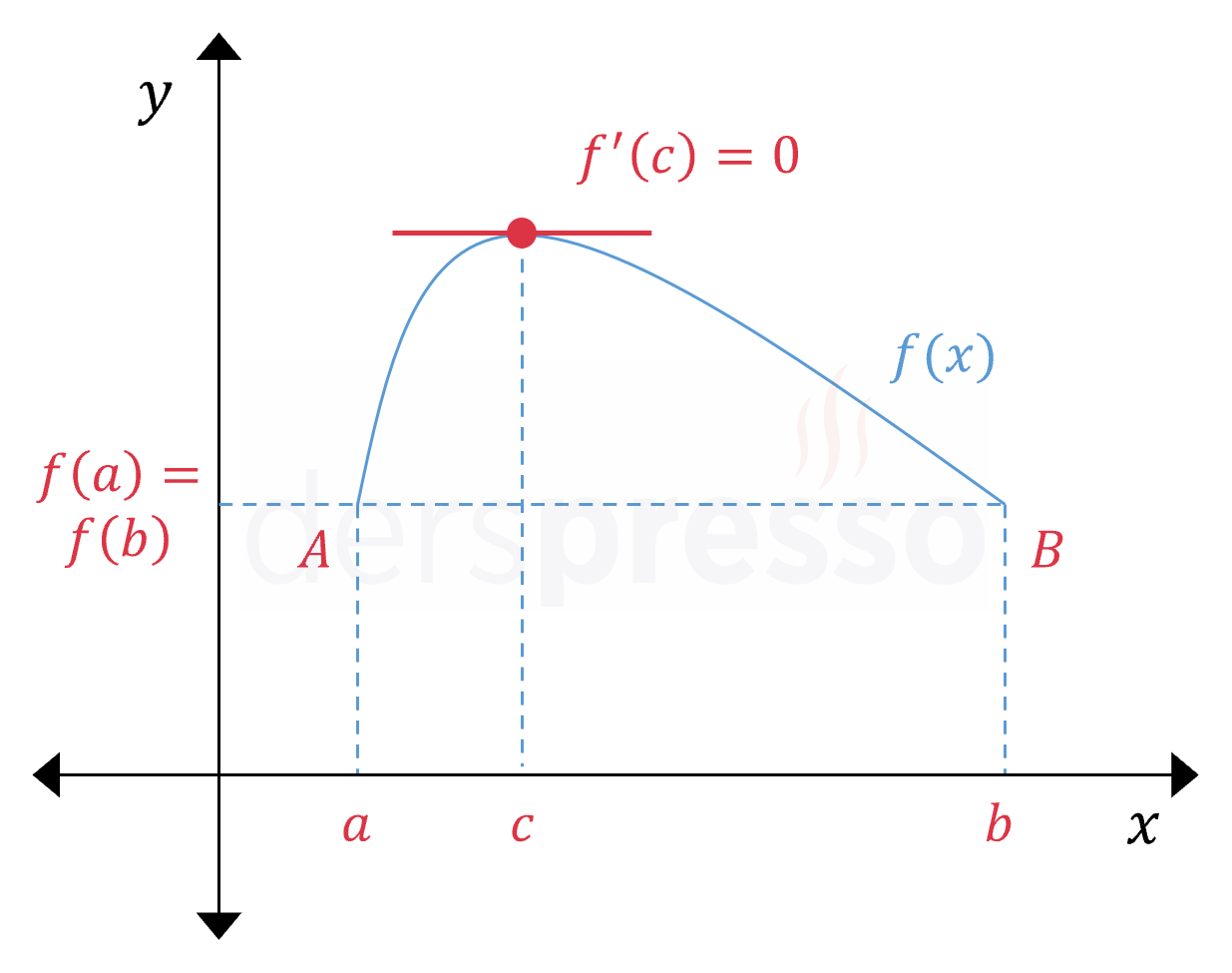
Rolle teoreminin tanımı aşağıdaki gibidir.
\( f \) fonksiyonu \( [a, b] \) aralığında sürekli, \( (a, b) \) aralığında türevlenebilir olmak üzere,
\( f(a) = f(b) \) ise,
\( (a, b) \) aralığında türevi sıfır olan en az bir \( x = c \) noktası vardır.
\( f'(c) = 0 \)
İSPATI GÖSTER
Rolle teoreminin ispatını fonksiyonun \( (a, b) \) aralığında sahip olabileceği üç farklı davranış için ayrı ayrı yapalım.
\( f(a) = f(b) = k \) olmak üzere,
Durum 1: Tüm \( x \in (a, b) \) noktaları için \( f(x) = k \)
Bu durumda fonksiyon \( (a, b) \) aralığında sabit fonksiyondur.

Fonksiyon \( (a, b) \) aralığında sabit olduğu için bu aralıktaki her nokta için \( f'(x) = 0 \) olur, dolayısıyla Rolle teoremi sağlanır.
Durum 2: Bazı \( x \in (a, b) \) noktaları için \( f(x) \gt k \)
Bu durumda fonksiyon \( (a, b) \) aralığında bazı noktalarda \( k \) değerinden büyük değerler alır.
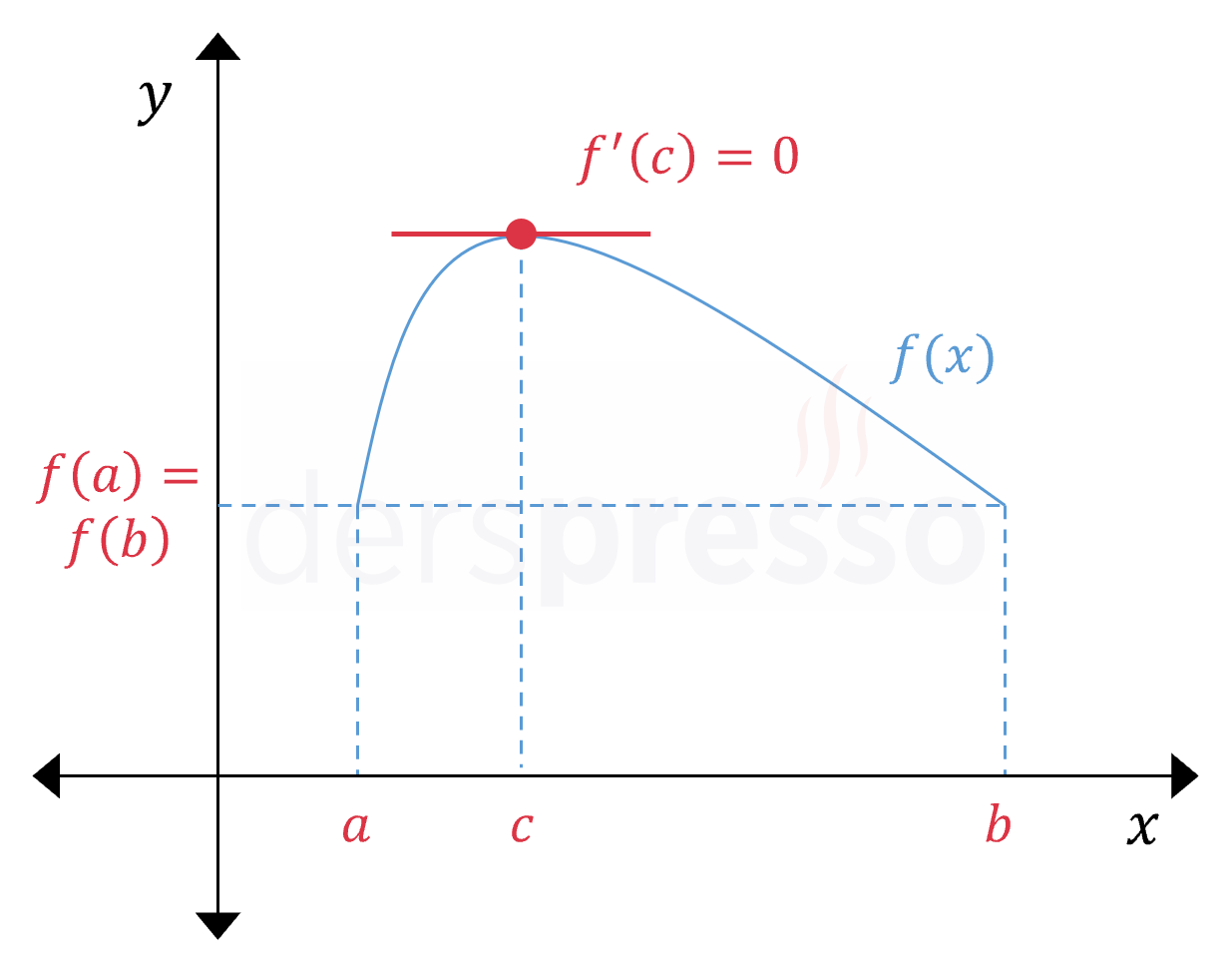
\( f \) fonksiyonu \( [a, b] \) aralığında sürekli olduğu için, uç değer teoremine göre bu aralıkta bir mutlak minimum ve maksimum noktasına sahiptir.
Bu aralıkta \( f(x) \gt k \) olan bir nokta bulunduğu için fonksiyonun mutlak maksimum noktasındaki değeri \( k \) değerinden büyük olmalıdır, dolayısıyla mutlak maksimum noktası \( [a, b] \) kapalı aralığının uç noktalarında olamaz.
Bunun bir sonucu olarak mutlak maksimum noktası \( (a, b) \) açık aralığında bir nokta olmalıdır.
\( f \) fonksiyonu \( (a, b) \) açık aralığında türevlenebilir olduğu için, bu aralıkta bulunan mutlak maksimum noktasında türevi sıfır olur, dolayısıyla Rolle teoremi sağlanır.
Durum 3: Bazı \( x \in (a, b) \) noktaları için \( f(x) \lt k \)
Bu durumda fonksiyon \( (a, b) \) aralığında bazı noktalarda \( k \) değerinden küçük değerler alır.
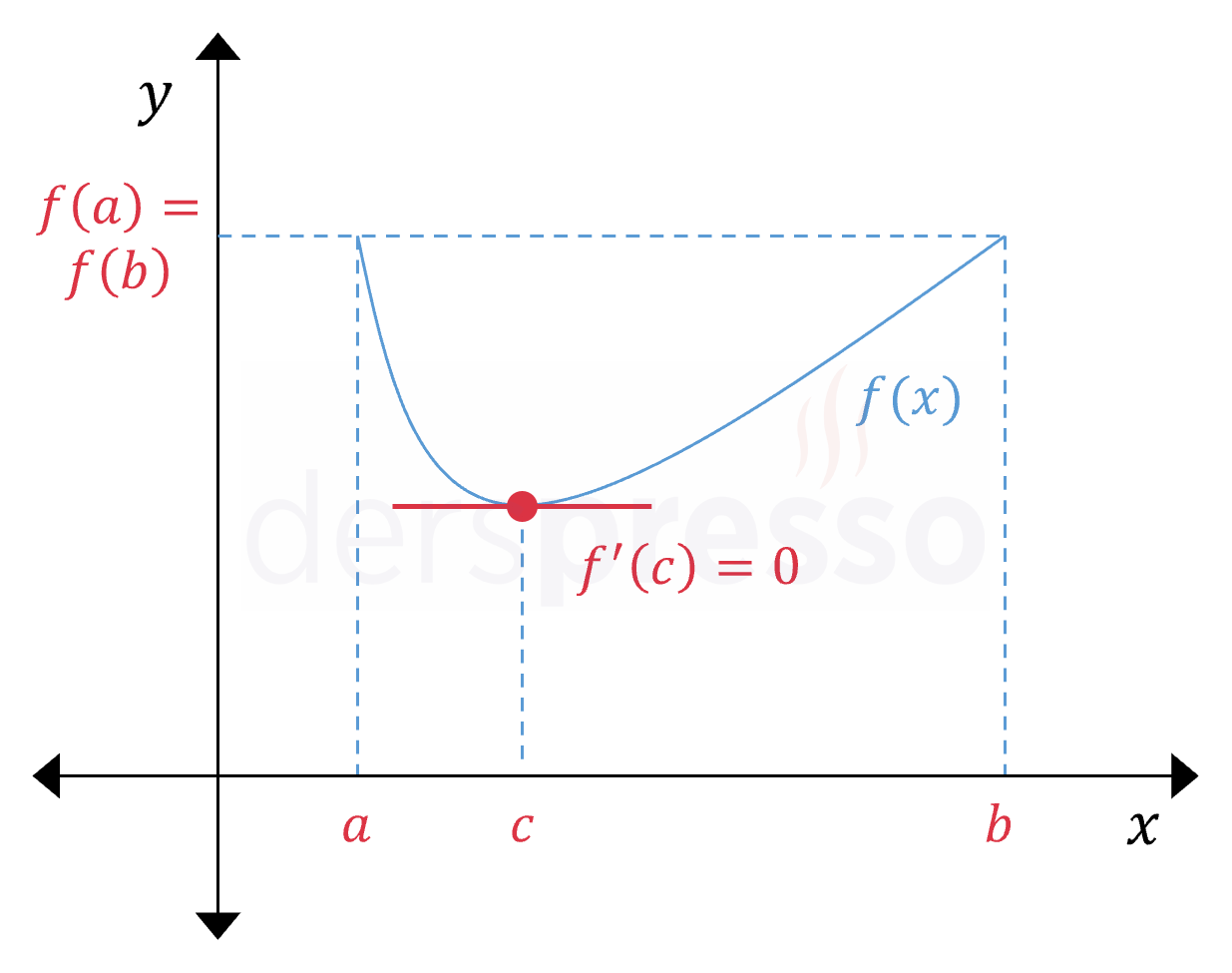
Durum 2'deki ispatın bir benzeri bu durum için de yapılabilir.
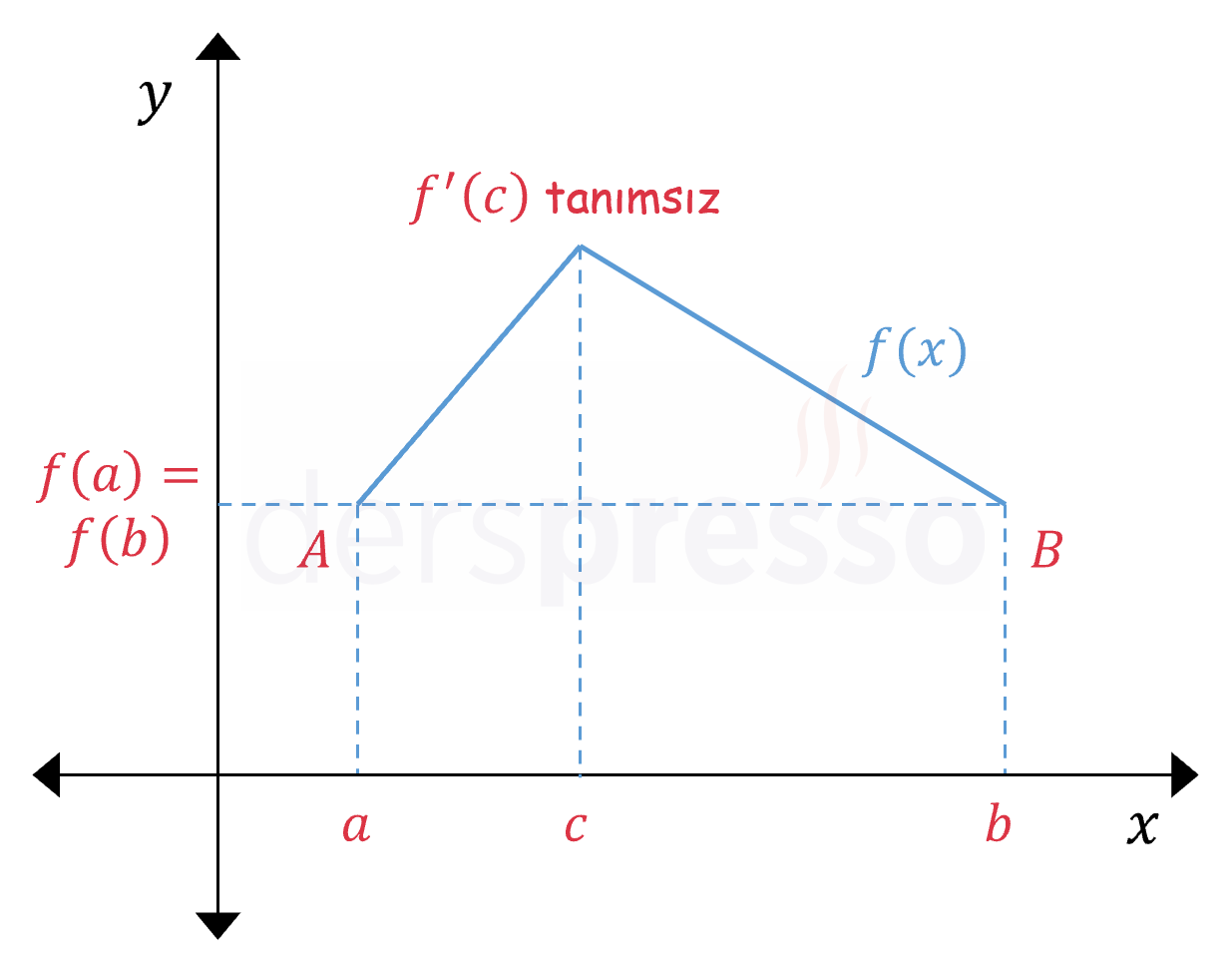
Aşağıdaki şekildeki fonksiyon \( x = c \) noktasında türevlenebilir olmadığı için Rolle teoremi koşulunu sağlamaz, dolayısıyla bu aralıkta türevi sıfır olan bir nokta bulunmaması teoreme aykırı bir durum oluşturmaz.
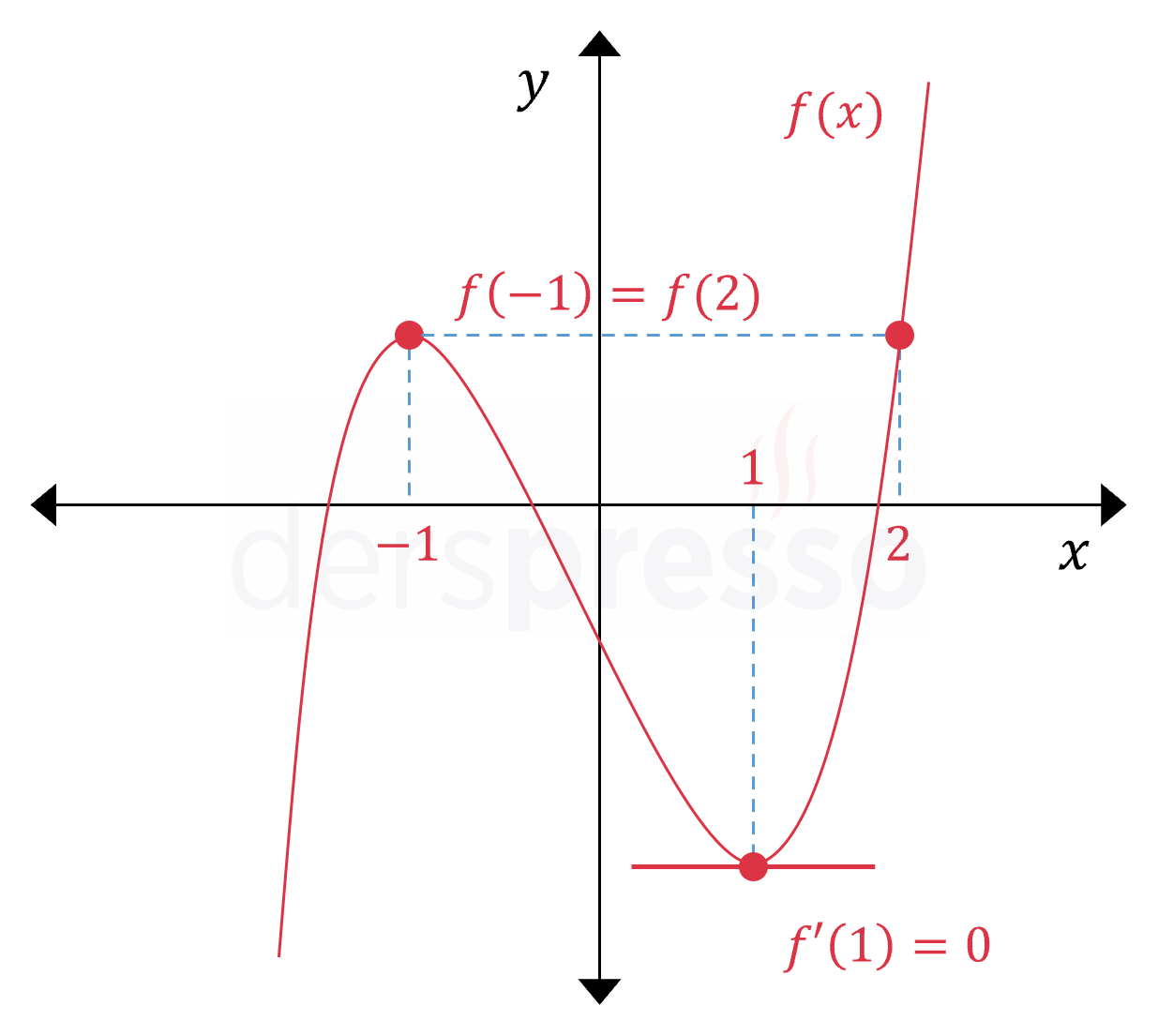
\( f(x) = x^3 - 3x - 1 \) fonksiyonu için \( (-1, 2) \) aralığında Rolle teoremini sağlayan en az bir nokta bulunduğunu gösterelim.
\( f \) bir polinom fonksiyonu olduğu için tüm reel sayılarda sürekli ve türevlenebilirdir, dolayısıyla verilen aralıkta Rolle teoremi koşullarını sağlar.
Fonksiyonun verilen aralığın uç noktalarındaki değerini bulalım.
\( f(-1) = (-1)^3 - 3(-1) - 1 = 1 \)
\( f(2) = 2^3 - 3(2) - 1 = 1 \)
Fonksiyonun bu iki noktadaki değeri birbirine eşittir.
\( f(-1) = f(2) = 1 \)
Fonksiyonun türevini alalım.
\( f'(x) = 3x^2 - 3 \)
Verilen aralıkta türevi sıfıra eşit olan \( x \) değer ya da değerlerini bulalım.
\( f'(c) = 3c^2 - 3 = 0 \)
\( c = \pm 1 \)
Bu iki değerden \( c = 1 \) verilen \( (-1, 2) \) aralığındadır.
Buna göre \( (-1, 2) \) aralığında türevi sıfır olan en az bir nokta bulunduğunu göstermiş olduk.
\( f'(1) = 0 \)
Bu sonucu grafiksel olarak aşağıdaki şekilde görebiliriz.
\( g(x) = \dfrac{1}{(x + 2)(x - 3)} \) fonksiyonu için \( (-4, 5) \) aralığında Rolle teoremini sağlayan bir \( x = c \) değeri bulunup bulunmadığını inceleyelim.
Fonksiyonun verilen aralığın uç noktalarındaki değerini bulalım.
\( g(-4) = g(5) = \dfrac{1}{14} \)
Fonksiyonun verilen aralığın uç noktalarındaki değeri birbirine eşittir, ancak Rolle teoremini kullanabilmemiz için fonksiyon verilen aralıkta sürekli ve türevlenebilir olmalıdır.
\( g \) fonksiyonu verilen aralıktaki \( x = -2 \) ve \( x = 3 \) noktalarında tanımsızdır, dolayısıyla bu noktalarda sürekli ve türevlenebilir değildir.
Bu durumda Rolle teoremini verilen fonksiyon ve aralıkta kullanamayız.
Ortalama Değer Teoremi
Ortalama değer teoremine göre, bir \( (a, b) \) aralığında türevi \( (a, f(a)) \) ve \( (b, f(b)) \) noktalarını birleştiren doğrunun eğimine eşit olan en az bir nokta bulunur. Bu iki noktayı birleştiren doğrunun eğimi aynı zamanda fonksiyonun bu aralıktaki ortalama değişim oranına eşittir.
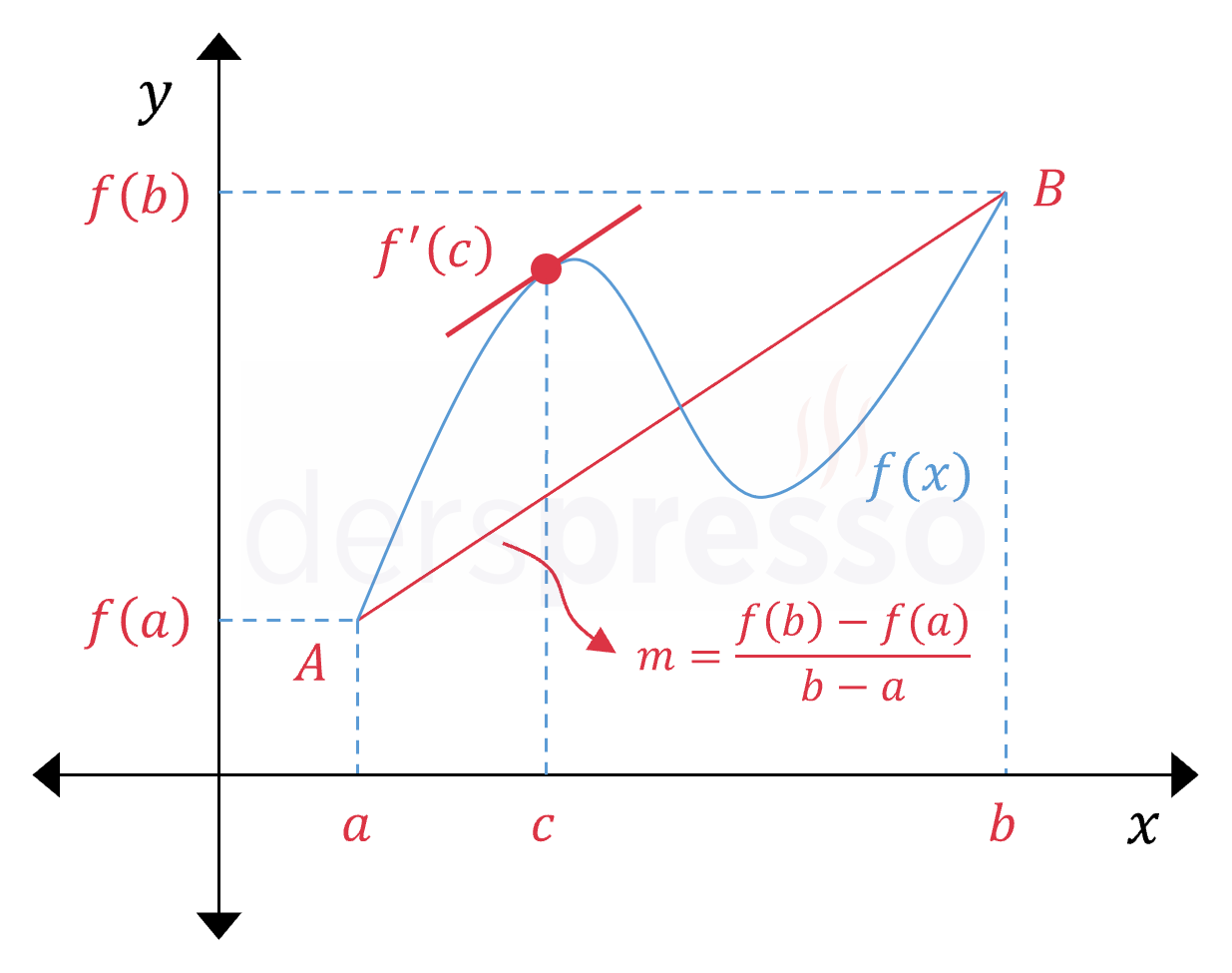
Ortalama değer teoreminin tanımı aşağıdaki gibidir.
\( f \) fonksiyonu \( [a, b] \) aralığında sürekli, \( (a, b) \) aralığında türevlenebilir olmak üzere,
\( (a, b) \) aralığında türevi bu aralıktaki ortalama değişim oranına eşit olan en az bir \( x = c \) noktası vardır.
\( f'(c) = \dfrac{f(b) - f(a)}{b - a} \)
İSPATI GÖSTER
\( A(a, f(a)) \) ve \( B(b, f(b)) \) noktalarını bir doğru ile birleştirelim.
Bu doğrunun eğimini aşağıdaki şekilde yazabiliriz.
\( m = \dfrac{f(b) - f(a)}{b - a} \)
\( A(a, f(a)) \) noktasından geçen ve eğimi bu değer olan doğrunun denklemi aşağıdaki gibidir.
\( \dfrac{y - f(a)}{x - a} = \dfrac{f(b) - f(a)}{b - a} \)
\( y = \dfrac{f(b) - f(a)}{b - a}(x - a) + f(a) \)
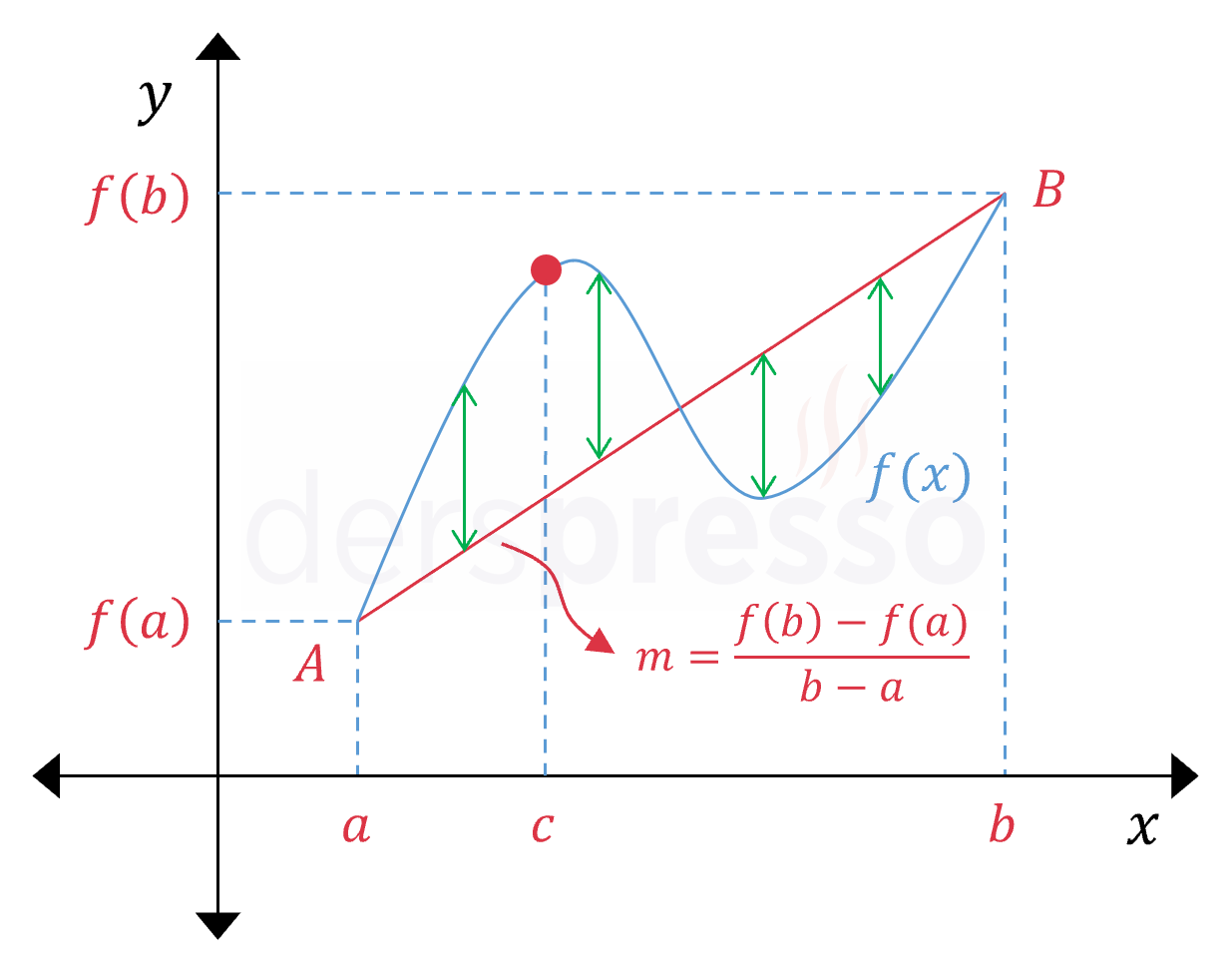
\( f(x) \) fonksiyonu ve \( [AB] \) doğrusunun denklemlerinin farkını veren bir \( g(x) \) fonksiyonu tanımlayalım.
Bu fonksiyon her \( x \) değeri için iki grafik arasındaki dikey mesafeyi verir. Bu dikey mesafeler yukarıdaki grafikte yeşil oklarla belirtilmiştir.
\( g(x) = f(x) - [\dfrac{f(b) - f(a)}{b - a}(x - a) + f(a)] \)
\( f(x) \) fonksiyonu ve \( [AB] \) doğrusu \( a \) ve \( b \) noktalarında kesiştikleri için bu iki noktada bu dikey mesafeler sıfır olur.
\( g(a) = g(b) = 0 \)
\( f \) fonksiyonu ve \( [AB] \) doğrusu \( [a, b] \) aralığında sürekli oldukları için \( g \) fonksiyonu da bu aralıkta süreklidir.
\( f \) fonksiyonu ve \( [AB] \) doğrusu \( (a, b) \) aralığında türevlenebilir oldukları için \( g \) fonksiyonu da bu aralıkta türevlenebilirdir.
Buna göre \( g \) fonksiyonu Rolle teoreminin süreklilik ve türevlenebilirlik koşullarını sağlar ve ayrıca aralığın uç noktalarındaki fonksiyon değerleri birbirine eşittir.
Buna göre Rolle teoremine göre \( g \) fonksiyonu için \( (a, b) \) aralığında aşağıdaki koşulu sağlayan en az bir \( c \in (a, b) \) noktası vardır.
\( g'(c) = 0 \)
Yukarıdaki \( g \) fonksiyon tanımını kullanarak türevini alalım.
\( g(x) = f(x) - [\dfrac{f(b) - f(a)}{b - a}(x - a) + f(a)] \)
\( g'(x) = f'(x) - \dfrac{f(b) - f(a)}{b - a} \)
\( c \) noktası için fonksiyonu sıfıra eşitleyelim
\( g'(c) = f'(c) - \dfrac{f(b) - f(a)}{b - a} = 0 \)
\( f'(c) = \dfrac{f(b) - f(a)}{b - a} \)
Buna göre \( (a, b) \) aralığında en az bir noktanın türevi bu aralıktaki ortalama değişim oranına eşittir.
Bu teoreme Lagrange'ın ortalama değer teoremi de denir. Teoremin adındaki "ortalama" ifadesi fonksiyonun verilen aralıktaki "ortalama" değişim oranına işaret etmektedir.
Ortalama değer teoremi şu şekilde de ifade edilebilir: \( (a, b) \) aralığında anlık değişim oranı bu aralıktaki ortalama değişim oranına eşit olan en az bir nokta vardır. Örneğin, iki şehir arasında ortalama 90 km/saat hızla seyahat eden bir aracın anlık hızı yolculuk sırasında en az bir kez 90 km/saat olmak zorundadır.
İki teoremi karşılaştırdığımızda Rolle teoreminin ortalama değer teoreminin \( f(a) = f(b) \) koşulunu içeren özel bir durumu olduğunu ve ortalama değer teoreminin Rolle teoremini de kapsadığını söyleyebiliriz.
Her iki teorem de \( (a, b) \) aralığında verilen koşulları sağlayan en az bir \( x = c \) noktasının var olduğunu söyler, ancak bu noktanın konumunu vermez.
\( f(x) = x^3 - 6x + 4 \) fonksiyonu için \( (-3, 3) \) aralığında ortalama değer teoremini sağlayan en az bir nokta bulunduğunu gösterelim.
\( f \) bir polinom fonksiyonu olduğu için tüm reel sayılarda sürekli ve türevlenebilirdir, dolayısıyla verilen aralıkta ortalama değer teoremi koşullarını sağlar.
Fonksiyonun \( [-3, 3] \) aralığındaki ortalama değişim oranını bulalım.
\( \dfrac{\Delta y}{\Delta x} = \dfrac{f(3) - f(-3)}{3 - (-3)} \)
Fonksiyonun verilen aralığın uç noktalarındaki değerini bulalım.
\( f(3) = 3^3 - 6(3) + 4 = 13 \)
\( f(-3) = (-3)^3 - 6(-3) + 4 = -5 \)
Bu değerleri ortalama değişim oranı formülünde yerine koyalım.
\( \dfrac{\Delta y}{\Delta x} = \dfrac{13 - (-5)}{3 - (-3)} = 3 \)
Buna göre fonksiyonun \( [-3, 3] \) aralığındaki ortalama değişim oranı 3'tür.
Fonksiyonun türevini alalım.
\( f'(x) = 3x^2 - 6 \)
Verilen aralıkta türev değeri 3'e eşit olan \( x \) değer ya da değerlerini bulalım.
\( f'(c) = 3c^2 - 6 = 3 \)
\( c = \pm \sqrt{3} \)
Her iki değer de \( (-3, 3) \) aralığındadır.
Buna göre \( (-3, 3) \) aralığında türevi bu aralıktaki ortalama değişim oranına eşit olan en az bir nokta bulunduğunu göstermiş olduk.
\( x \in \{-\sqrt{3}, \sqrt{3}\} \)
Bu iki nokta aşağıdaki şekilde fonksiyonun grafiği üzerinde gösterilmiştir.
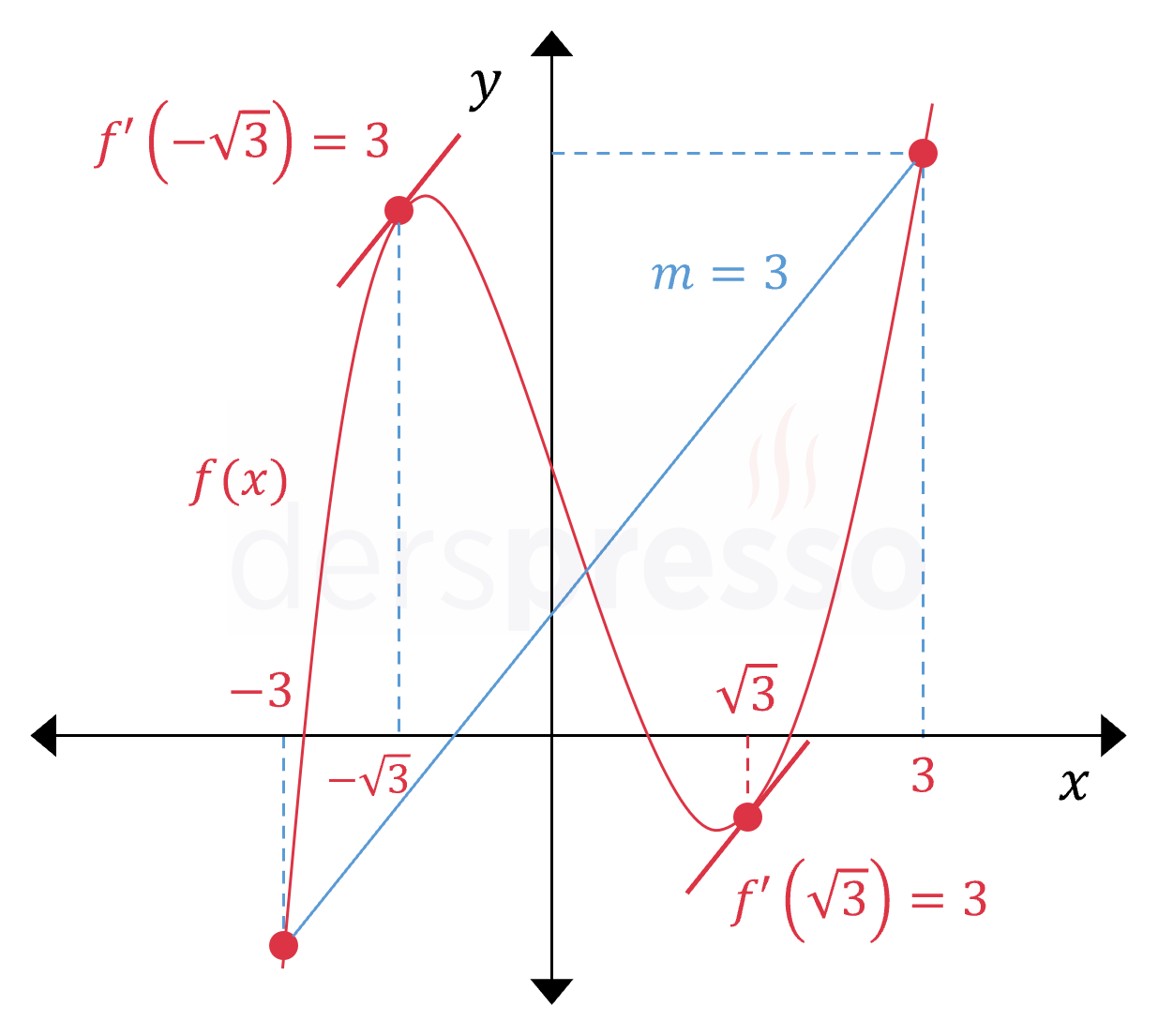
\( g(x) = \dfrac{3}{x - 3} \) fonksiyonu için \( (2, 4) \) aralığında ortalama değer teoremini sağlayan bir \( x = c \) değeri bulunup bulunmadığını inceleyelim.
Ortalama değer teoremini kullanabilmemiz için fonksiyon verilen aralıkta sürekli ve türevlenebilir olmalıdır.
\( g \) fonksiyonu verilen aralıktaki \( x = 3 \) noktasında tanımsızdır, dolayısıyla bu noktada sürekli ve türevlenebilir değildir.
Bu durumda ortalama değer teoremini verilen fonksiyon ve aralıkta kullanamayız.
Ortalama değer teoreminden çıkarılabilecek üç sonuç aşağıdaki gibidir.
Sonuç 1: Sabit Fonksiyon
Bir sabit fonksiyonun türevinin sıfır olduğunu biliyoruz. Ortalama değer teoremine göre bunun karşıtı da doğrudur, yani belirli bir aralıkta türevi sıfır olan bir fonksiyon bu aralıkta sabit fonksiyondur.
Her \( x \in (a, b) \) için \( f'(x) = 0 \) ise,
\( f(x) \) fonksiyonu \( (a, b) \) aralığında sabit fonksiyondur.
İSPATI GÖSTER
\( (a, b) \) aralığında birbirinden farklı \( x_1 \) ve \( x_2 \) noktaları seçelim.
\( x_1, x_2 \in (a, b), \quad x_1 \ne x_2 \)
Ortalama değer teoremine göre, \( (x_1, x_2) \) aralığında türevi bu aralıktaki ortalama değişim oranına eşit olan en az bir \( x = c \) noktası vardır.
\( f'(c) = \dfrac{f(x_2) - f(x_1)}{x_2 - x_1} \)
\( x_1 \) ve \( x_2 \) noktalarını içine alan aralıkta fonksiyonun türevi sıfır olduğu için \( x = c \) noktasındaki türev değeri de sıfırdır.
\( \dfrac{f(x_2) - f(x_1)}{x_2 - x_1} = 0 \)
\( x_1 \ne x_2 \) olduğuna göre,
\( f(x_2) - f(x_1) = 0 \)
\( f(x_2) = f(x_1) \)
\( (a, b) \) aralığında seçilecek her \( (x_1, x_2) \) ikilisi için aynı durum geçerli olacağı için \( f \) fonksiyonu \( (a, b) \) aralığında sabit fonksiyondur.
Sonuç 2: Türevleri Eşit Fonksiyonlar
İki fonksiyonun belirli bir aralıkta türevleri birbirine eşitse bu iki fonksiyonun birbirinden farkı bir sabit sayıdır.
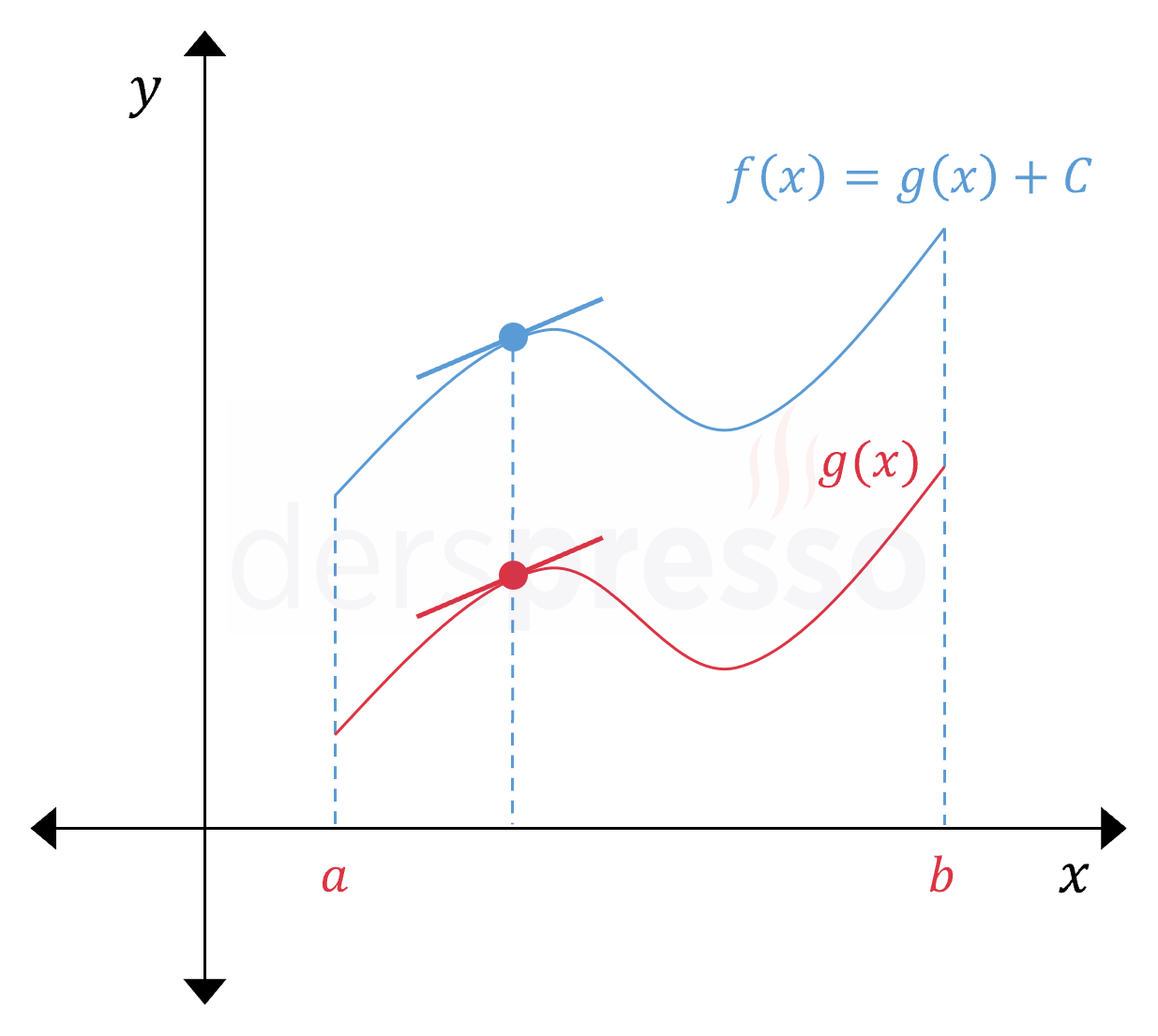
\( C \in \mathbb{R} \) olmak üzere,
Her \( x \in (a, b) \) için \( f'(x) = g'(x) \) ise,
\( (a, b) \) aralığında \( f(x) = g(x) + C \) olur.
İSPATI GÖSTER
\( (a, b) \) aralığında \( f \) ve \( g \) fonksiyonlarının farkını temsil eden \( h \) fonksiyonu tanımlayalım.
\( h(x) = f(x) - g(x) \)
Eşitliğin iki tarafının türevini alalım.
\( h'(x) = (f(x) - g(x))' \)
\( h'(x) = f'(x) - g'(x) \)
\( (a, b) \) aralığında \( f \) ve \( g \) fonksiyonlarının türevleri birbirine eşittir.
\( h'(x) = 0 \)
Yukarıda ispatıyla birlikte verdiğimiz sonuç 1'e göre, bir aralıkta türevi sıfır olan bir fonksiyon bu aralıkta sabit fonksiyondur.
\( h(x) = C \)
Buna göre \( f \) ve \( g \) fonksiyonlarının farkı da sabit fonksiyondur.
\( f(x) - g(x) = C \)
\( f(x) = g(x) + C \)
Sonuç 3: Artan/Azalan Fonksiyon
Türevi belirli bir aralıkta pozitif olan fonksiyonlar bu aralıkta kesin artan, negatif olan fonksiyonlar da kesin azalandır.
Her \( x \in (a, b) \) için,
\( f'(x) \gt 0 \) ise \( f \) fonksiyonu \( [a, b] \) aralığında kesin artandır.
\( f'(x) \lt 0 \) ise \( f \) fonksiyonu \( [a, b] \) aralığında kesin azalandır.
İSPATI GÖSTER
\( (a, b) \) aralığındaki her \( x \) için \( f'(x) \gt 0 \) olduğunu kabul edelim.
Bu aralıkta \( x_1 \lt x_2 \) olmak üzere iki nokta seçelim.
\( x_1, x_2 \in (a, b), \quad x_1 \lt x_2 \)
Ortalama değer teoremine göre, \( (x_1, x_2) \) aralığında türevi bu aralıktaki ortalama değişim oranına eşit olan en az bir \( x = c \) noktası vardır.
\( f'(c) = \dfrac{f(x_2) - f(x_1)}{x_2 - x_1} \)
\( f'(c)(x_2 - x_1) = f(x_2) - f(x_1) \)
\( x_1 \lt x_2 \) olduğu için \( x_2 - x_1 \) ifadesi pozitiftir.
\( (a, b) \) aralığında \( f'(x) \gt 0 \) olarak kabul ettiğimiz için bu aralıktaki \( x = c \) noktası için de \( f'(c) \gt 0 \) olur.
Buna göre \( f(x_2) - f(x_1) \) ifadesi de pozitif olur.
\( f(x_2) - f(x_1) \gt 0 \Longrightarrow f(x_2) \gt f(x_1) \)
\( (a, b) \) aralığında seçilecek her \( (x_1, x_2) \) ikilisi için aynı durum geçerli olacağı için \( f \) fonksiyonu \( (a, b) \) aralığında kesin artandır.
\( (a, b) \) aralığındaki her \( x \) için \( f'(x) \lt 0 \) olduğunu kabul ederek \( f \) fonksiyonunun bu aralıkta kesin azalan olduğunu benzer şekilde gösterebiliriz.
\( h(x) = 2\abs{x - 4} \) fonksiyonu için \( (1, 5) \) aralığında ortalama değer teoremini sağlayan bir \( x = c \) noktası bulunup bulunmadığını inceleyin.
Çözümü GösterOrtalama değer teoremini kullanabilmemiz için fonksiyon verilen aralıkta sürekli ve türevlenebilir olmalıdır.
\( h \) fonksiyonunu verilen aralıkta tanımsız yapan bir değer yoktur. Ayrıca mutlak değer fonksiyonu tüm reel sayılarda süreklidir.
Mutlak değer içini sıfır yapan \( x = 4 \) noktasında fonksiyonun soldan ve sağdan türevleri tanımlı olsa da bu iki türev değeri birbirinden farklıdır.
\( f'(4^-) = -2 \)
\( f'(4^+) = 2 \)
Bu sebeple fonksiyon bu noktada türevlenebilir değildir ve ortalama değer teoremini bu aralıkta kullanamayız.
\( f(x) = \sqrt{x - 6} \) fonksiyonu için \( (10, 15) \) aralığında ortalama değer teoremini sağlayan \( x = c \) noktalarını bulunuz.
Çözümü GösterSoruda verilen fonksiyon bir karekök fonksiyonudur ve \( (6, \infty) \) aralığında sürekli ve türevlenebilirdir.
Bu durumda ortalama değer teoremini verilen aralıkta kullanabiliriz.
Ortalama değer teoremine göre, bir \( (a, b) \) aralığında türevi \( (a, f(a)) \) ve \( (b, f(b)) \) noktalarını birleştiren doğrunun eğimine eşit olan en az bir nokta bulunur.
Fonksiyonun \( [10, 15] \) aralığındaki ortalama değişim oranını bulalım.
\( \dfrac{\Delta y}{\Delta x} = \dfrac{f(15) - f(10)}{15 - 10} \)
Fonksiyonun verilen aralığın uç noktalarındaki değerini bulalım.
\( f(15) = \sqrt{15 - 6} = 3 \)
\( f(10) = \sqrt{10 - 6} = 2 \)
Bulduğumuz değerleri formülde yerine koyalım.
\( \dfrac{\Delta y}{\Delta x} = \dfrac{3 - 2}{15 - 10} = \dfrac{1}{5} \)
Fonksiyonun türevini alalım.
\( f'(x) = (\sqrt{x - 6})' = \dfrac{1}{2\sqrt{x - 6}} \)
Verilen aralıkta türev değeri \( \frac{1}{5} \)'e eşit olan \( x \) değerlerini bulalım.
\( f'(c) = \dfrac{1}{2\sqrt{c - 6}} = \dfrac{1}{5} \)
\( 2\sqrt{c - 6} = 5 \)
\( c = \dfrac{49}{4} \)
Bulduğumuz değer \( (10, 15) \) aralığındadır.
Buna göre fonksiyonun \( x = \frac{49}{4} \) noktasındaki türevi, \( (10, 15) \) aralığındaki ortalama değişim oranına eşittir.
\( f: (-\frac{\pi}{2}, \frac{\pi}{2}) \to \mathbb{R} \) olmak üzere,
\( f(x) = \sec^2(x) - \tan^2(x) \)
Ortalama değer teoremi kullanılarak \( f \) fonksiyonunun tipi hakkında ne söylenebilir?
Çözümü GösterSekant ve tanjant fonksiyonları verilen aralıkta sürekli ve türevlenebilirdir.
Sekant ve tanjant fonksiyonlarının türevleri aşağıdaki gibidir.
\( \sec'(x) = \tan(x)\sec(x) \)
\( \tan'(x) = \sec^2(x) \)
\( f \) fonksiyonunun türevini alalım.
\( f'(x) = (\sec^2(x))' - (\tan^2(x))' \)
\( = 2\sec(x)\sec'(x) - 2\tan(x)\tan'(x) \)
\( = 2\sec(x)\tan(x)\sec(x) - 2\tan(x)\sec^2(x) \)
\( = 2\tan(x)\sec^2(x) - 2\tan(x)\sec^2(x) \)
\( = 0 \)
Ortalama değer teoremine göre, verilen aralıkta \( f'(x) = 0 \) olduğuna göre \( f \) fonksiyonu bu aralıkta bir sabit fonksiyondur.
320 metre yükseklikten serbest bırakılan bir elma serbest düşüş yapıyor. Elmanın \( t \) saniye sonraki yüksekliğini veren fonksiyon aşağıdaki gibidir.
\( x(t) = 320 - 5t^2 \)
Buna göre aşağıdaki soruları cevaplayın.
(a) Elma kaç saniye sonra yere düşer?
(b) Yere düşene kadar geçen sürede elmanın ortalama hızı kaçtır?
(c) Elmanın yere düşerken anlık hızının ortalama hızına eşit olduğu anda elmanın yerden yüksekliği nedir?
Çözümü Göster(a) seçeneği:
Elma yere düştüğü anda yüksekliği (\( x \) değeri) 0 metredir. Elmanın yere düştüğü ana \( a \) saniye diyelim.
\( x(a) = 320 - 5a^2 = 0 \)
\( 5a^2 = 320 \)
\( a^2 = 64 \)
\( a = 8 \)
Elma 8 saniye sonra yere düşer.
(b) seçeneği:
Elmanın ortalama hızını son konumu ile ilk konumunun farkını toplam süreye bölerek bulabiliriz.
Elmanın 8 saniyede düştüğünü biliyoruz.
\( v_{ort} = \dfrac{x(8) - x(0)}{8 - 0} \)
\( x(8) = 320 - 5(8)^2 = 0 \)
\( x(0) = 320 - 5(0)^2 = 320 \)
\( v_{ort} = \dfrac{0 - 320}{8} = -40 \)
Elmanın düştüğü süredeki ortalama hızı -40 m/s'dir. Elma aşağı yönlü (\( y \) değeri azalacak şekilde) hareket ettiği için hız negatif değer almaktadır.
(c) seçeneği:
Konum fonksiyonunun türevi anlık hızı verir.
\( x'(t) = (320 - 5t^2)' = -10t \)
Anlık hızın ortalama hıza eşit olduğu \( t \) değerini bulalım.
\( -10t = -40 \)
\( t = 4 \)
Buna göre elmanın 4. saniyedeki anlık hızı tüm düşüş boyuncaki ortalama hızına eşit olmaktadır.
\( t = 4 \) anında elmanın yerden yüksekliğini bulalım.
\( x(4) = 320 - 5(4)^2 \)
\( = 240 \) metre bulunur.