Büküm Noktaları
Fonksiyon grafiklerine giriş bölümünde konkavlik kavramından bahsetmiştik. Özetle, bir fonksiyon ikinci türevinin pozitif olduğu bir aralıkta yukarı konkavdır ve grafiği \( x \) artarken sola doğru kıvrılır, ikinci türevinin negatif olduğu bir aralıkta ise aşağı konkavdır ve grafiği \( x \) artarken sağa doğru kıvrılır.
Bir fonksiyonun grafiğinin konkavlık durumunun değiştiği, yani yukarı konkav iken aşağı konkav olduğu ya da aşağı konkav iken yukarı konkav olduğu noktalara büküm noktası ya da dönüm noktası denir.

Büküm noktaları, bir fonksiyonun grafiğinde eğimin (yani birinci türevin) artarken azalmaya ya da azalırken artmaya başladığı noktalardır.
Bir noktanın büküm noktası olabilmesi için aşağıdaki iki koşul sağlanmalıdır.
Aşağıdaki iki koşulu sağlayan noktalar bir fonksiyonun büküm noktalarıdır.
(1) Fonksiyon bu noktada süreklidir.
(2) İkinci türev bu noktada işaret değiştirir.
Bir noktanın büküm noktası olabilmesi için yeterli olmasa da gerekli bir koşul, fonksiyonun ikinci türevinin bu noktada sıfır ya da tanımsız olmadıdır.
Fonksiyonun birinci ve ikinci türevlerinin bir büküm noktasında tanımlı olma zorunluluğu yoktur, önemli olan ikinci türevin büküm noktasında işaret değiştirmesidir. Aşağıda birinci ve/veya ikinci türevin tanımlı olduğu ve olmadığı büküm noktalarına farklı örnekler vereceğiz.
Büküm Noktası Tipleri
Büküm noktaları aşağıdaki dört tip altında incelenebilir. Yukarıda yaptığımız tanıma göre, bu noktaların ortak özelliği (1) fonksiyonun bu noktalarda sürekli olması ve (2) fonksiyonun ikinci türevinin işaret değiştirmesidir.
| Grafik | Açıklama |
|---|---|

|
Yatay (durağan) büküm noktası: Bu büküm noktalarında teğet doğrusu vardır ve eğimi sıfırdır, dolayısıyla birinci türev de tanımlıdır ve sıfırdır. \( f'(a) \) tanımlı ve \( f'(a) = 0 \) |

|
Durağan olmayan büküm noktası: Bu büküm noktalarında teğet doğrusu vardır ve eğimi sıfırdan farklıdır, dolayısıyla birinci türev de tanımlıdır ve sıfırdan farklıdır. \( f'(a) \) tanımlı ve \( f'(a) \ne 0 \) |

|
Dikey büküm noktası: Bu büküm noktalarında teğet doğrusu vardır ve eğimi sonsuzdur, dolayısıyla birinci türev soldan ve sağdan pozitif ya da negatif sonsuza yaklaşır. \( f'(a) \) tanımsız ve \( f'(a) = \pm \infty \) |

|
Sivri büküm noktası: Bu büküm noktalarında teğet doğrusu yoktur, dolayısıyla birinci türev tanımsızdır (soldan ve sağdan farklı değerlere yaklaşır). \( f'(a) \) tanımsız ve \( f'(a) \ne \pm \infty \) |
Teğet doğrusunun tanımlı olduğu ilk üç tipteki büküm noktalarının ortak bir özelliği olarak, fonksiyonun grafiği teğet doğrusunu keserek doğrunun diğer tarafına geçer.
Büküm Noktalarının Bulunması
Bir fonksiyonun büküm noktaları aşağıdaki yöntemle bulunabilir.
Adım 1: Aday noktaları belirleme
Fonksiyonun birinci ve ikinci türevleri bulunur.
Bir fonksiyonun büküm noktalarında ikinci türevi sıfır ya da tanımsızdır, dolayısıyla büküm noktası olmaya aday noktaları bulmak için önce bu koşulları sağlayan noktalar bulunur.
\( f''(x) = 0 \) ya da \( f''(x) \) tanımsız
Adım 2: Süreklilik kontrolü
Fonksiyonun aday noktalardaki sürekliliği kontrol edilir.
Adım 3: İkinci türevin işaret değişimi
İkinci türev fonksiyonu için bir işaret tablosu oluşturulur ve aday noktalardan hangilerinde ikinci türevin işaret değiştirdiği bulunur.
Sürekli olan ve ikinci türevi işaret değiştiren aday noktalar birer büküm noktasıdır.
İşaret tablosu hazırlamaya alternatif bir yöntem olarak, fonksiyonun ikinci türevinin sıfır olduğu bir noktada üçüncü türevi tanımlı ve sıfırdan farklı ise bu nokta bir büküm noktasıdır. Bu alternatif yöntemin üçüncü ve dördüncü tipteki büküm noktaları için kullanılamayacağı akılda tutulmalıdır.
Adım 4: Büküm noktasının tipini belirleme
Opsiyonel olarak, büküm noktası olduğu bulunan noktaların birinci türevi kontrol edilerek her birinin tipi belirlenir.
Bir fonksiyonun büküm noktalarını bulmayı bir örnek üzerinde gösterelim.
\( f(x) = \dfrac{1}{2}x^4 - 3x^2+ 4x + 2 \) fonksiyonunun büküm noktalarını ve tiplerini bulalım.
\( f \) bir polinom fonksiyonu olduğu için kendisi ve türevleri tüm reel sayılarda süreklidir.
Büküm noktası olmaya aday noktaları bulmak için ikinci türevin sıfır ya da tanımsız olduğu noktaları bulalım.
\( f'(x) = 2x^3 - 6x + 4 \)
\( f''(x) = 6x^2 - 6 \)
\( = 6(x + 1)(x - 1) \)
İkinci türevin sıfır olduğu noktaları bulalım.
\( 6(x + 1)(x - 1) = 0 \)
\( x \in \{ -1, 1 \} \)
İkinci türevin tanımsız olduğu nokta yoktur.
Aday noktalar: \( x \in \{ -1, 1 \} \)
Büküm noktaları ikinci türevin işaret değiştirdiği noktalarda oluşur.
İkinci türevin aday noktalarda işaret değiştirip değiştirmediğini bulmak için bir işaret tablosu hazırlayalım.
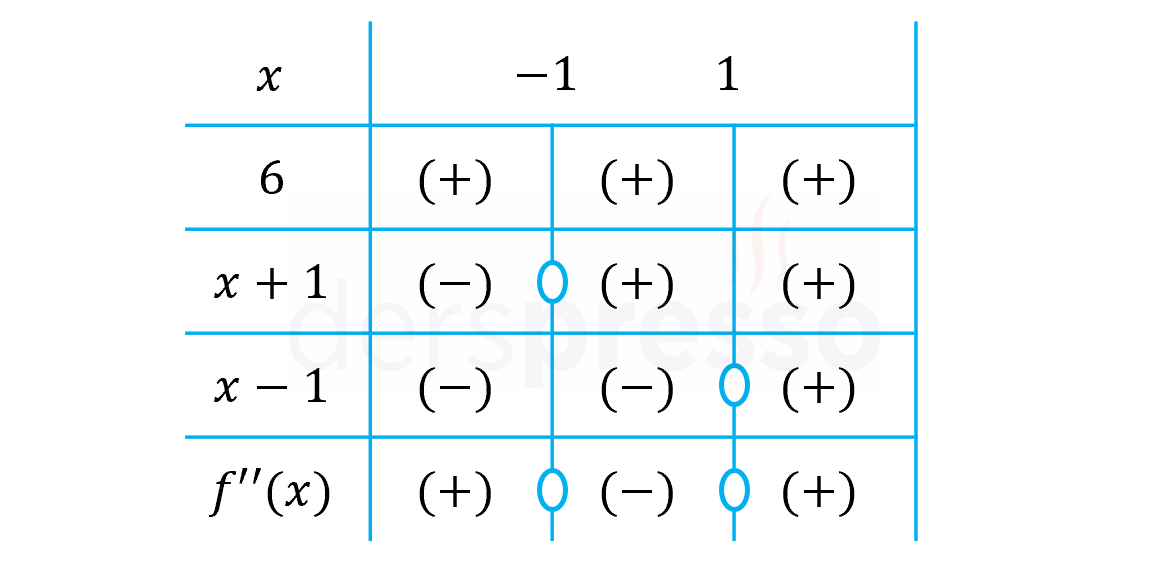
Tabloya göre fonksiyon \( (-\infty, -1) \) ve \( (1, \infty) \) aralıklarında yukarı konkav, \( (-1, 1) \) aralığında aşağı konkavdır.
İkinci türev \( x = -1 \) ve \( x = 1 \) noktalarında işaret değiştirdiği için (ve bu noktalarda konkavlığı değiştiği için) bu iki nokta birer büküm noktasıdır.
Bu büküm noktalarının tipini bulmak için apsis değerlerini birinci türevde yerine koyalım.
\( f'(-1) = 2(-1)^3 - 6(-1) + 4 = 8 \)
\( f'(-1) \) tanımlı ve \( f'(-1) \ne 0 \) olduğu için \( x = -1 \) noktası durağan olmayan bir büküm noktasıdır.
\( f'(1) = 2(1)^3 - 6(1) + 4 = 0 \)
\( f'(1) \) tanımlı ve \( f'(1) = 0 \) olduğu için \( x = 1 \) noktası yatay (durağan) bir büküm noktasıdır.
Fonksiyonun grafiği ve büküm noktaları aşağıdaki şekilde gösterilmiştir.
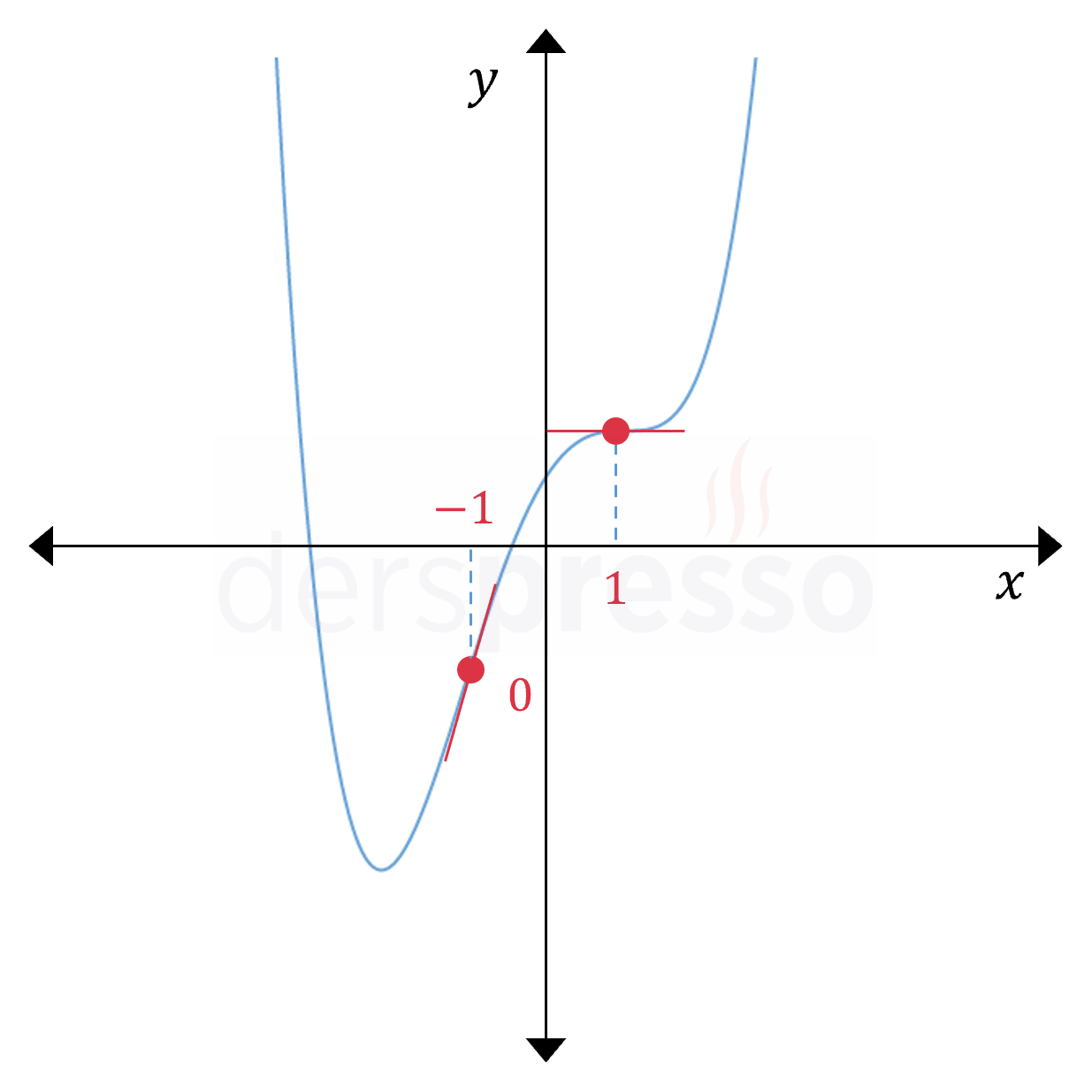
Bir fonksiyonun büküm noktalarını bulmayı ikinci bir örnek üzerinde gösterelim.
\( f: (-2\pi, 2\pi) \to \mathbb{R} \) olmak üzere,
\( f(x) = \abs{x} + \sin{x} \) fonksiyonunun büküm noktalarını ve tiplerini bulalım.
\( f \) iki sürekli fonksiyonun toplamından oluştuğu için tüm reel sayılarda süreklidir.
Büküm noktası olmaya aday noktaları bulmak için ikinci türevin sıfır ya da tanımsız olduğu noktaları bulalım.
\( \abs{x} \) fonksiyonu sıfır ve pozitif reel sayılarda \( y = x \), negatif reel sayılarda \( y = -x \) doğrusuna karşılık geldiği için türevini \( \frac{\abs{x}}{x} \) şeklinde ifade edebiliriz.
\( f'(x) = \dfrac{\abs{x}}{x} + \cos{x} \)
Birinci türev \( x = 0 \) noktasında tanımsızdır.
\( f': (-2\pi, 2\pi) - \{0\} \to \mathbb{R} \)
\( \frac{\abs{x}}{x} \) ifadesi sadece \( -1 \) ve \( 1 \) sabit değerlerini aldığı için türevi sıfırdır.
\( f''(x) = -\sin{x} \)
Birinci türev \( x = 0 \) noktasında tanımsız olduğu için ikinci türev de bu noktada tanımsızdır.
\( f'': (-2\pi, 2\pi) - \{0\} \to \mathbb{R} \)
İkinci türevin \( (-2\pi, 2\pi) \) aralığında sıfır olduğu iki nokta vardır.
\( x \in \{ -\pi, \pi \} \)
İkinci türevin \( (-2\pi, 2\pi) \) aralığında tanımsız olduğu tek nokta vardır.
\( x = 0 \)
Aday noktalar: \( x \in \{ -\pi, 0, \pi \} \)
Büküm noktaları ikinci türevin işaret değiştirdiği noktalarda oluşur.
İkinci türevin aday noktalarda işaret değiştirip değiştirmediğini bulmak için bir işaret tablosu hazırlayalım.

Tabloya göre fonksiyon \( (-\pi, 0) \) ve \( (\pi, 2\pi) \) aralıklarında yukarı konkav, \( (-2\pi, -\pi) \) ve \( (0, \pi) \) aralıklarında aşağı konkavdır.
İkinci türev \( x = -\pi \), \( x = 0 \) ve \( x = \pi \) noktalarında işaret değiştirdiği için (ve bu noktalarda konkavlığı değiştiği için) bu üç nokta birer büküm noktasıdır.
Bu büküm noktalarının tipini bulmak için apsis değerlerini birinci türevde yerine koyalım.
\( f'(-\pi) = \dfrac{\abs{-\pi}}{-\pi} + \cos(-\pi) = -1 + (-1) = -2 \)
\( f'(-\pi) \) tanımlı ve \( f'(-\pi) \ne 0 \) olduğu için \( x = -\pi \) noktası durağan olmayan bir büküm noktasıdır.
\( f'(0) = \dfrac{\abs{0}}{0} + \cos{0} = \) Tanımsız
\( f'(0) \) tanımsız ve \( f'(0) \ne \infty \) olduğu için \( x = 0 \) noktası sivri tipte bir büküm noktasıdır.
\( f'(\pi) = \dfrac{\abs{\pi}}{\pi} + \cos{\pi} = 1 + (-1) = 0 \)
\( f'(\pi) \) tanımlı ve \( f'(\pi) = 0 \) olduğu için \( x = \pi \) noktası yatay (durağan) bir büküm noktasıdır.
Fonksiyonun grafiği ve büküm noktaları aşağıdaki şekilde gösterilmiştir.

\( f(x) = 2x^3 + ax^2 - bx + 4 \)
fonksiyonunun \( x = 1 \) noktasında yerel maksimum noktası ve \( x = -2 \) noktasında büküm noktası olduğuna göre, \( f(-1) \) kaçtır?
Çözümü Göster\( f \) bir polinom fonksiyonu olduğu için tüm reel sayılarda türevlenebilirdir.
Fonksiyonun türevlenebilir olduğu \( x = 1 \) noktasında yerel maksimum noktası olduğuna göre, bu noktada birinci türevi sıfır olmalıdır.
\( f'(x) = 6x^2 + 2ax - b \)
\( f'(1) = 0 \)
\( 6(1)^2 + 2a(1) - b = 0 \)
\( 2a - b = -6 \)
Fonksiyonun \( x = -2 \) noktasında büküm noktası olduğuna göre, bu noktada ikinci türevi sıfır olmalıdır.
\( f''(x) = 12x + 2a \)
\( f''(-2) = 0 \)
\( 12(-2) + 2a = 0 \)
\( a = 12 \)
\( 2a - b = -6 \Longrightarrow b = 30 \)
Buna göre \( f \) fonksiyonunun tanımı aşağıdaki gibidir.
\( f(x) = 2x^3 + 12x^2 - 30x + 4 \)
\( f(-1) = 2(-1)^3 + 12(-1)^2 - 30(-1) + 4 \)
\( = -2 + 12 + 30 + 4 = 44 \) bulunur.